过剩载流子的产生及其影响

1 . Lecture #6 OUTLINE – Generation and recombination – Excess carrier concentrations – Minority carrier lifetime Reading: Chapter 3.3 Spring 2003 EE130 Lecture 6, Slide 1 Clarification: Quasi-Neutrality • If the dopant concentration profile varies gradually with position, then the majority-carrier concentration distribution does not differ much from the dopant concentration distribution. N D ( x ) + p ( x ) = N A ( x ) + n( x ) – n-type material: n( x) ≅ N D ( x) − N A ( x) – p-type material: p ( x) ≅ N A ( x) − N D ( x) kT  1  dn kT  1  dN D → =   =   in n-type material q  n  dx q  N D  dx Spring 2003 EE130 Lecture 6, Slide 2 1 

2 .Carrier Drift (Band Diagram Visualization) Ec Ev Spring 2003 EE130 Lecture 6, Slide 3 Generation and Recombination • Generation: • Recombination: • Recombination and Generation processes act to change the carrier concentrations, and thereby indirectly affect current flow Spring 2003 EE130 Lecture 6, Slide 4 2 

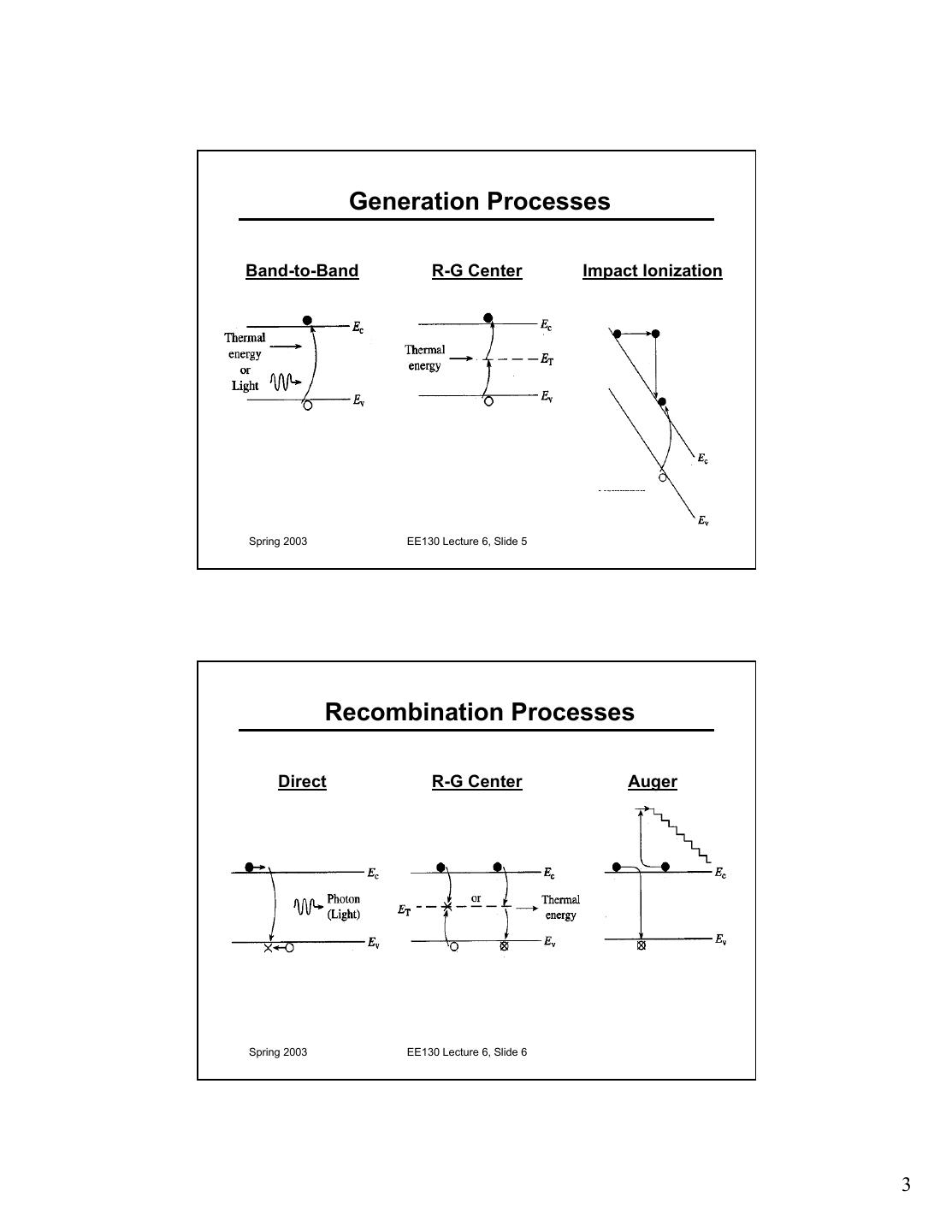
3 . Generation Processes Band-to-Band R-G Center Impact Ionization Spring 2003 EE130 Lecture 6, Slide 5 Recombination Processes Direct R-G Center Auger Spring 2003 EE130 Lecture 6, Slide 6 3 

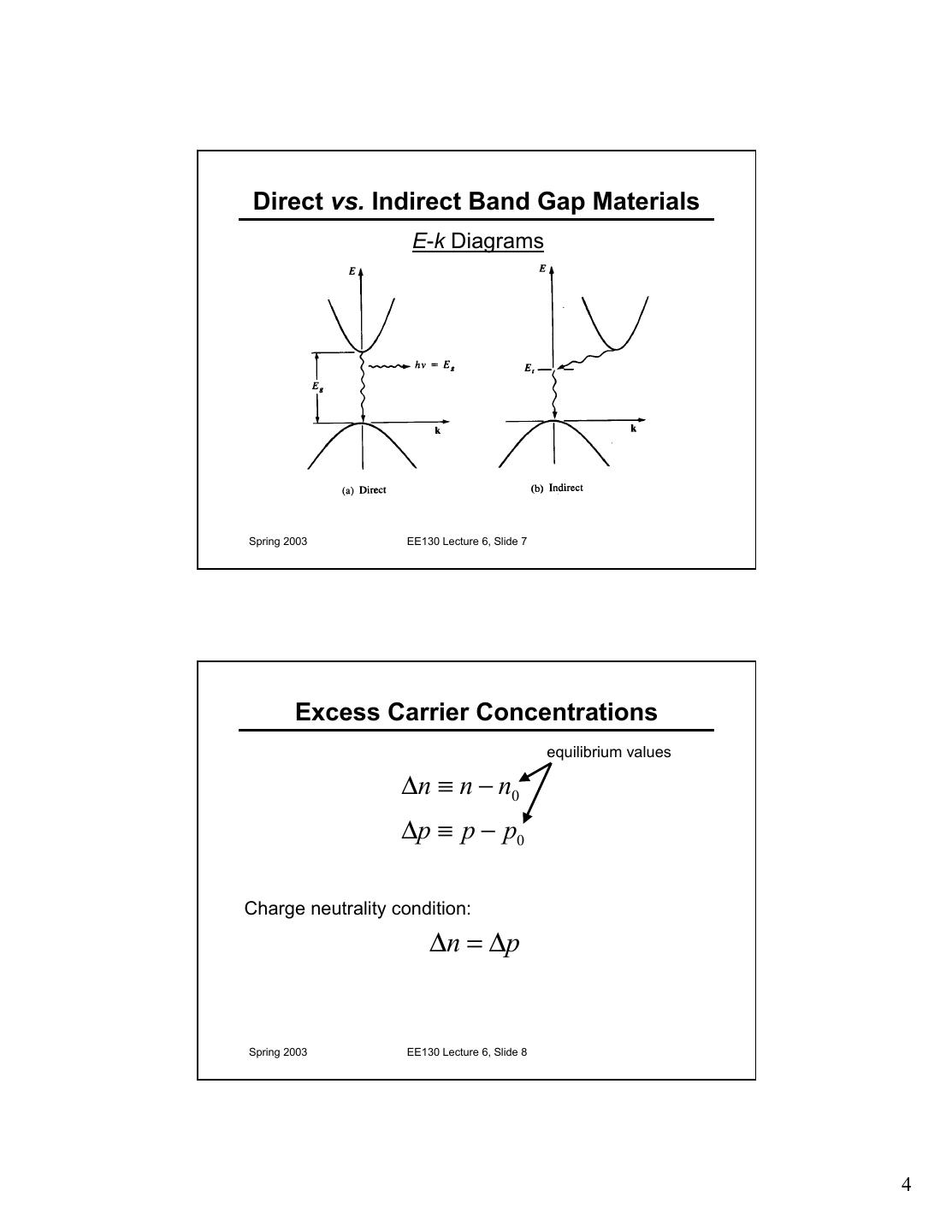
4 . Direct vs. Indirect Band Gap Materials E-k Diagrams Spring 2003 EE130 Lecture 6, Slide 7 Excess Carrier Concentrations equilibrium values ∆n ≡ n − n0 ∆p ≡ p − p0 Charge neutrality condition: ∆n = ∆p Spring 2003 EE130 Lecture 6, Slide 8 4 

5 . “Low-Level Injection” • Often the disturbance from equilibrium is small, such that the majority-carrier concentration is not affected significantly: – For an n-type material: | ∆n |=| ∆p |<< n0 so n ≅ n0 – For a p-type material: | ∆n |=| ∆p |<< p0 so p ≅ p0 • However, the minority carrier concentration can be significantly affected Spring 2003 EE130 Lecture 6, Slide 9 Indirect Recombination Rate • Consider hole recombination in n-Si through a number of traps, NT: ∂p ∂t R = −c p N T p • Since total generation = recombination at equilibrium: ∂p ∂t G = − ∂∂pt = c p N T p0 R • If we introduce excess carriers (e.g. using light) and watch the decay in ∆p: ∂p ∂t R −G = −c p N T ( p − p0 ) ≡ − τ∆pp τ p = c 1N p T Spring 2003 EE130 Lecture 6, Slide 10 5 

6 . Recombination Lifetime The minority carrier lifetime τ is the average time an excess minority carrier “survives” in a sea of majority carriers τ ranges from 1 ns to 1 ms in Si and depends on the density of metallic impurities (contaminants) such as Au and Pt, and the density of crystalline defects. These deep traps capture electrons or holes to facilitate recombination and are called recombination-generation centers. Spring 2003 EE130 Lecture 6, Slide 11 Example: Photoconductor Consider a sample of Si doped with 1015 cm-3 boron, with recombination lifetime 10 µs. It is exposed to light such that electron-hole pairs are generated throughout the sample at the rate of 1020/s·cm3. Find: (a) n0 and p0 (b) ∆n and ∆p (c) p, n, and the np product Spring 2003 EE130 Lecture 6, Slide 12 6 

7 . Solution: (a) What is p0? p0 = Na = 1015 cm-3 (b) What is n0 ? n0 = ni2/p0 = 105 cm-3 (c) What is ∆p? In steady-state, the rate of generation is equal to the rate of recombination. 1020/s-cm3 = ∆p/τ ∴ ∆p = 1020/s-cm3 · 10-5s = 1015 cm-3 Spring 2003 EE130 Lecture 6, Slide 13 (d) What is ∆n? ∆n = ∆p= 1015 cm-3 (e) What is p? p = p0 + ∆p = 1015cm-3 + 1015cm-3 = 2×1015cm-3 (f) What is n? n = n0 + ∆n = 105cm-3 + 1015cm-3 ~ 1015cm-3 since n0 << ∆n (g) What is np? np ~ 2×1015cm-3 · 1015cm-3 = 2×1030cm-6 >> ni2 = 1020cm-6. Note: The np product can be very different from ni2. Spring 2003 EE130 Lecture 6, Slide 14 7