- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
静电学
展开查看详情
1 . Lecture #10 ANNOUNCEMENT – Quiz #2 next Thursday (2/27) covering • carrier action (drift, diffusion, R-G) • continuity & minority-carrier diffusion equations • metal-semiconductor contacts OUTLINE • pn junction electrostatics Reading: Chapter 5 Spring 2003 EE130 Lecture 10, Slide 1 pn Junctions Donor s N- type P- type I – V + I N P V Reverse bias Forward bias diode symbol Spring 2003 EE130 Lecture 10, Slide 2 1
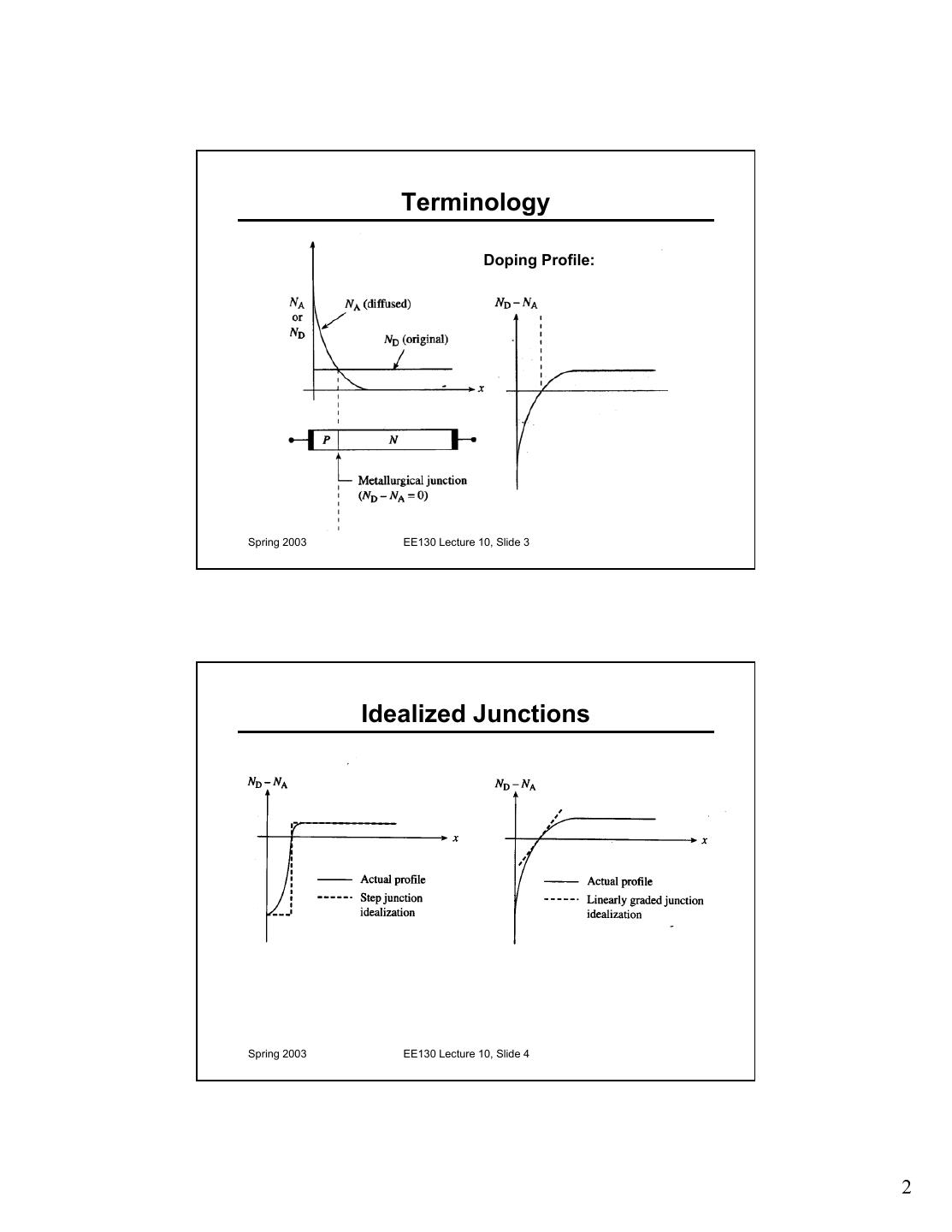
2 . Terminology Doping Profile: Spring 2003 EE130 Lecture 10, Slide 3 Idealized Junctions Spring 2003 EE130 Lecture 10, Slide 4 2
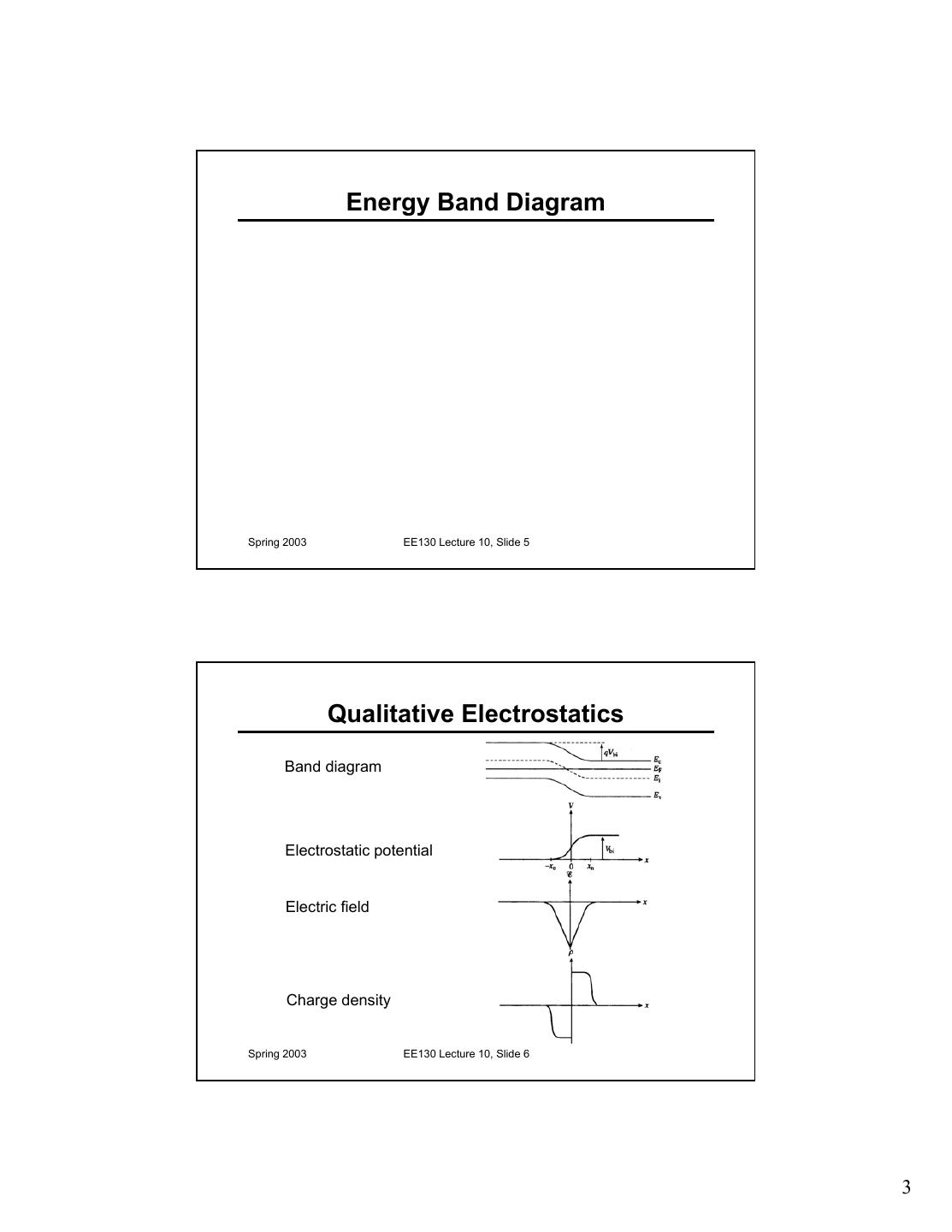
3 . Energy Band Diagram Spring 2003 EE130 Lecture 10, Slide 5 Qualitative Electrostatics Band diagram Electrostatic potential Electric field Charge density Spring 2003 EE130 Lecture 10, Slide 6 3
4 .“Game Plan” for Obtaining ρ(x), (x), V(x) • Find the built-in potential Vbi • Use the depletion approximation → ρ (x) (depletion-layer widths xp, xn unknown) • Integrate ρ (x) to find (x) – boundary conditions (-xp)=0, (xn)=0 • Integrate (x) to obtain V(x) – boundary conditions V(-xp)=0, V(xn)=Vbi • For (x) to be continuous at x=0, NAxp = NDxn → solve for xp, xn Spring 2003 EE130 Lecture 10, Slide 7 Built-In Potential Vbi qVbi = Φ S p −side − Φ S n −side = ( Ei − EF ) p −side + ( EF − Ei ) n −side For non-degenerately doped material: p n ( Ei − E F ) p − side = kT ln ( E F − Ei ) n − side = kT ln ni ni N N = kT ln A = kT ln D ni ni Spring 2003 EE130 Lecture 10, Slide 8 4
5 . Vbi for “One-Sided” pn Junctions qVbi = ( Ei − E F ) p − side + ( E F − Ei ) n − side p+n junction n+p junction Spring 2003 EE130 Lecture 10, Slide 9 The Depletion Approximation On the p-side, ρ = –qNA d qN =− A dx εs qN A -qNA ( x) = − x + C1 = (x + x p ) εs εs On the n-side, ρ = qND -qN D ( x) = ( xn − x ) εs Spring 2003 EE130 Lecture 10, Slide 10 5
6 . Electric Field in the Depletion Layer The electric field is continuous at x = 0 ⇒ NAxp = NDxn Spring 2003 EE130 Lecture 10, Slide 11 Electrostatic Potential in the Depletion Layer On the p-side: qN A V ( x) = ( x + x p ) 2 + D1 2ε s (arbitrarily choose the voltage at x = xp to be 0) On the n-side: qN D qN D V ( x) = − ( xn − x ) 2 + D2 = Vbi − ( xn − x ) 2 2ε s 2ε s Spring 2003 EE130 Lecture 10, Slide 12 6
7 .• At x = 0, expressions for p-side and n-side must be equal: • We also know that NAxp = NDxn Spring 2003 EE130 Lecture 10, Slide 13 Depletion Layer Width • Eliminating xp, we have: 2ε sVbi NA xn = q ND (N A + ND ) • Eliminating xn, we have: 2ε sVbi ND xp = q N A(N A + ND ) • Summing, we have: 2ε sVbi 1 1 xn + x p = W = + q N A ND Spring 2003 EE130 Lecture 10, Slide 14 7
8 . One-Sided Junctions If NA >> ND as in a p+n junction: 2ε sVbi W= ≈ xn qN D x p = xn N D N A ≅ 0 What about a n+p junction? 1 1 1 1 W = 2ε s Vbi qN where = + ≈ N N D N A lighter dopant density Spring 2003 EE130 Lecture 10, Slide 15 Peak Electric Field ∫ ε dx = 2 ε (0) W = Vbi − VA 1 2ε s • For a one-sided junction, W ≅ (Vbi − VA ) qN so ε (0) = 2(V W− V ) ≅ bi A 2qN (Vbi − VA ) εs Spring 2003 EE130 Lecture 10, Slide 16 8
9 . Example A p+n junction has NA=1020 cm-3 and ND =1017cm-3. What is a) its built in potential, b)W , c)xn , and d) xp ? Solution: a) EG kT N D Vbi = + ln ≈1V 2q q ni 1/ 2 b) W ≈ 2ε sVbi = 2 × 12 × 8.85 × 10 × 1 −14 1.6 × 10−19 × 1017 = 0.12 µm qN D c) xn ≈ W = 0.12 µm d) x p = xn N D N A = 1.2 × 10−4 µm = 1.2 Å ≈ 0 Spring 2003 EE130 Lecture 10, Slide 17 Linearly Graded Junction Spring 2003 EE130 Lecture 10, Slide 18 9
10 . Biased PN Junctions REQUIREMENT: VA < Vbi, otherwise, we cannot assume low-level injection Spring 2003 EE130 Lecture 10, Slide 19 Current Flow - Qualitative Spring 2003 EE130 Lecture 10, Slide 20 10
11 . Effect of Bias on Electrostatics Spring 2003 EE130 Lecture 10, Slide 21 11