- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
半导体载流子迁移率,电阻率的计算
展开查看详情
1 . Lecture #4 ANNOUNCEMENTS • Prof. King will not hold office hours this week, but will hold an extra office hour next Mo (2/3) from 11AM-12:30PM • Quiz #1 will be given at the beginning of class on Th 2/6 – covers material in Chapters 1 & 2 (HW#1 & HW#2) – closed book; one page of notes allowed OUTLINE – Drift (Chapter 3.1) » carrier motion » mobility » resistivity Spring 2003 EE130 Lecture 4, Slide 1 Nondegenerately Doped Semiconductor • Recall that the expressions for n and p were derived using the Boltzmann approximation, i.e. we assumed Ev + 3kT ≤ EF ≤ Ec − 3kT The semiconductor is said to be nondegenerately doped in this case. Spring 2003 EE130 Lecture 4, Slide 2 1
2 . Degenerately Doped Semiconductor • If a semiconductor is very heavily doped, the Boltzmann approximation is not valid. In Si at T=300K: Ec-EF < 3kT if ND > 1.6x1018 cm-3 EF-Ev < 3kT if NA > 9.1x1017 cm-3 The semiconductor is said to be degenerately doped in this case. Ev + 3kT ≤ EF ≤ Ec − 3kT Spring 2003 EE130 Lecture 4, Slide 3 Band Gap Narrowing • If the dopant concentration is a significant fraction of the silicon atomic density, the energy-band structure is perturbed Æ the band gap is reduced by ∆EG N = 1018 cm-3: N = 1019 cm-3: Spring 2003 EE130 Lecture 4, Slide 4 2
3 . Free Carriers in Semiconductors • Three primary types of carrier action occur inside a semiconductor: – drift – diffusion – recombination-generation Spring 2003 EE130 Lecture 4, Slide 5 Electrons as Moving Particles F = (-q) = moa F = (-q) = mn*a where mn* is the electron effective mass Spring 2003 EE130 Lecture 4, Slide 6 3
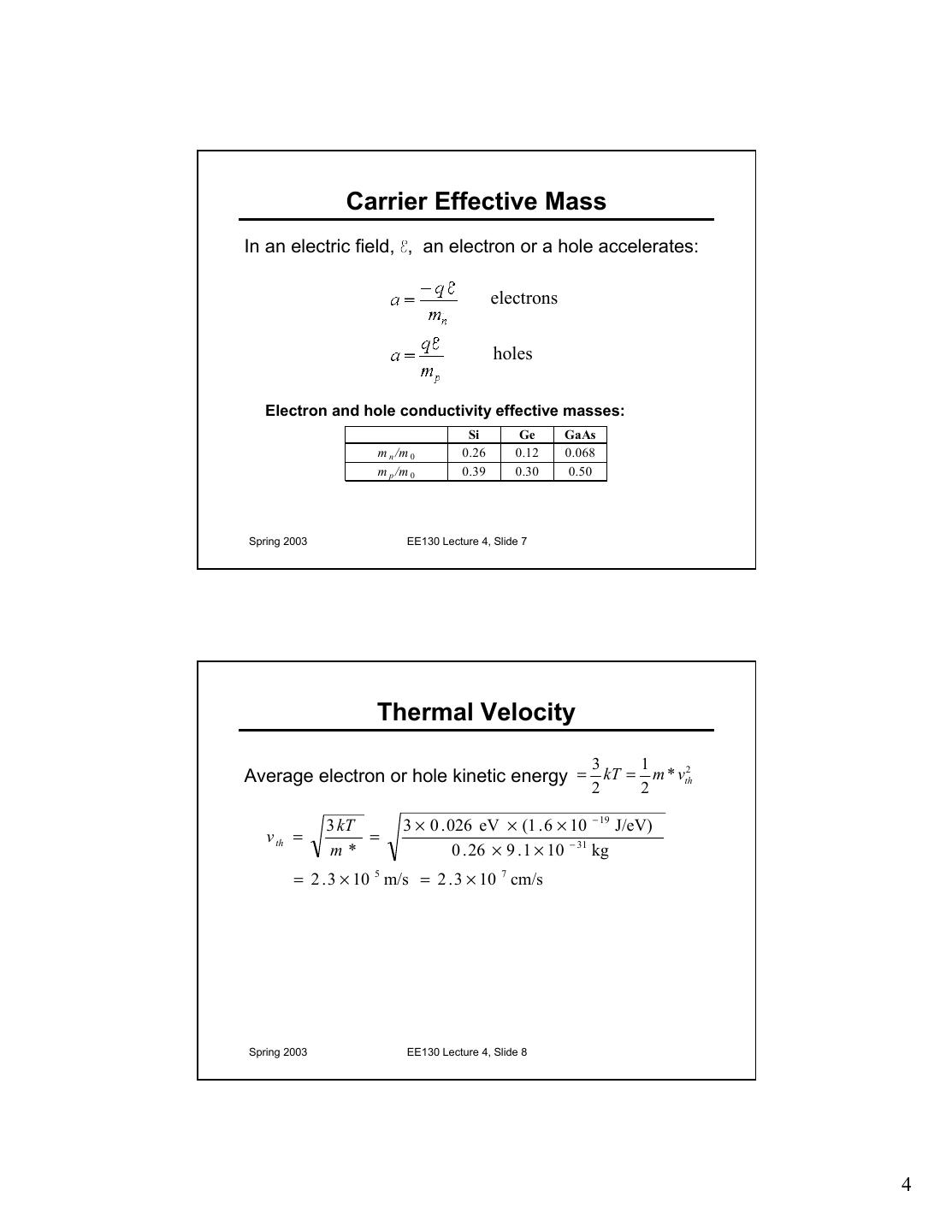
4 . Carrier Effective Mass In an electric field, , an electron or a hole accelerates: electrons holes Electron and hole conductivity effective masses: Si Ge GaAs m n /m 0 0.26 0.12 0.068 m p /m 0 0.39 0.30 0.50 Spring 2003 EE130 Lecture 4, Slide 7 Thermal Velocity 3 1 Average electron or hole kinetic energy = kT = m * vth 2 2 2 3 kT 3 × 0 . 026 eV × (1 . 6 × 10 − 19 J/eV) v th = = m* 0 . 26 × 9 . 1 × 10 − 31 kg = 2 . 3 × 10 5 m/s = 2 . 3 × 10 7 cm/s Spring 2003 EE130 Lecture 4, Slide 8 4
5 . Carrier Scattering • Mobile electrons and atoms in the Si lattice are always in random thermal motion. – Electrons make frequent collisions with the vibrating atoms • “lattice scattering” or “phonon scattering” – increases with increasing temperature – Average velocity of thermal motion for electrons: ~107 cm/s @ 300K • Other scattering mechanisms: – deflection by ionized impurity atoms – deflection due to Coulombic force between carriers • “carrier-carrier scattering” • only significant at high carrier concentrations • The net current in any direction is zero, if no electric field is applied. 2 3 1 4 electron Spring 2003 EE130 Lecture 4, Slide 9 5 Carrier Drift • When an electric field (e.g. due to an externally applied voltage) is applied to a semiconductor, mobile charge- carriers will be accelerated by the electrostatic force. This force superimposes on the random motion of electrons: 2 3 1 4 electron 5 • Electrons drift in the direction opposite to the electric field Æ current flows Because of scattering, electrons in a semiconductor do not achieve constant acceleration. However, they can be viewed as quasi-classical particles moving at a constant average drift velocity vd Spring 2003 EE130 Lecture 4, Slide 10 5
6 . Electron Momentum • With every collision, the electron loses momentum mn*vd • Between collisions, the electron gains momentum (-q) τmn where τmn = average time between scattering events Spring 2003 EE130 Lecture 4, Slide 11 Carrier Mobility mn*vd = (-q) τmn |vd| = q τmn / mn* = µn • µn ≡ [qτmn / mn*] is the electron mobility Similarly, for holes: |vd| = q τmp / mp* ≡ µp • µp ≡ [qτmp / mp*] is the hole mobility Spring 2003 EE130 Lecture 4, Slide 12 6
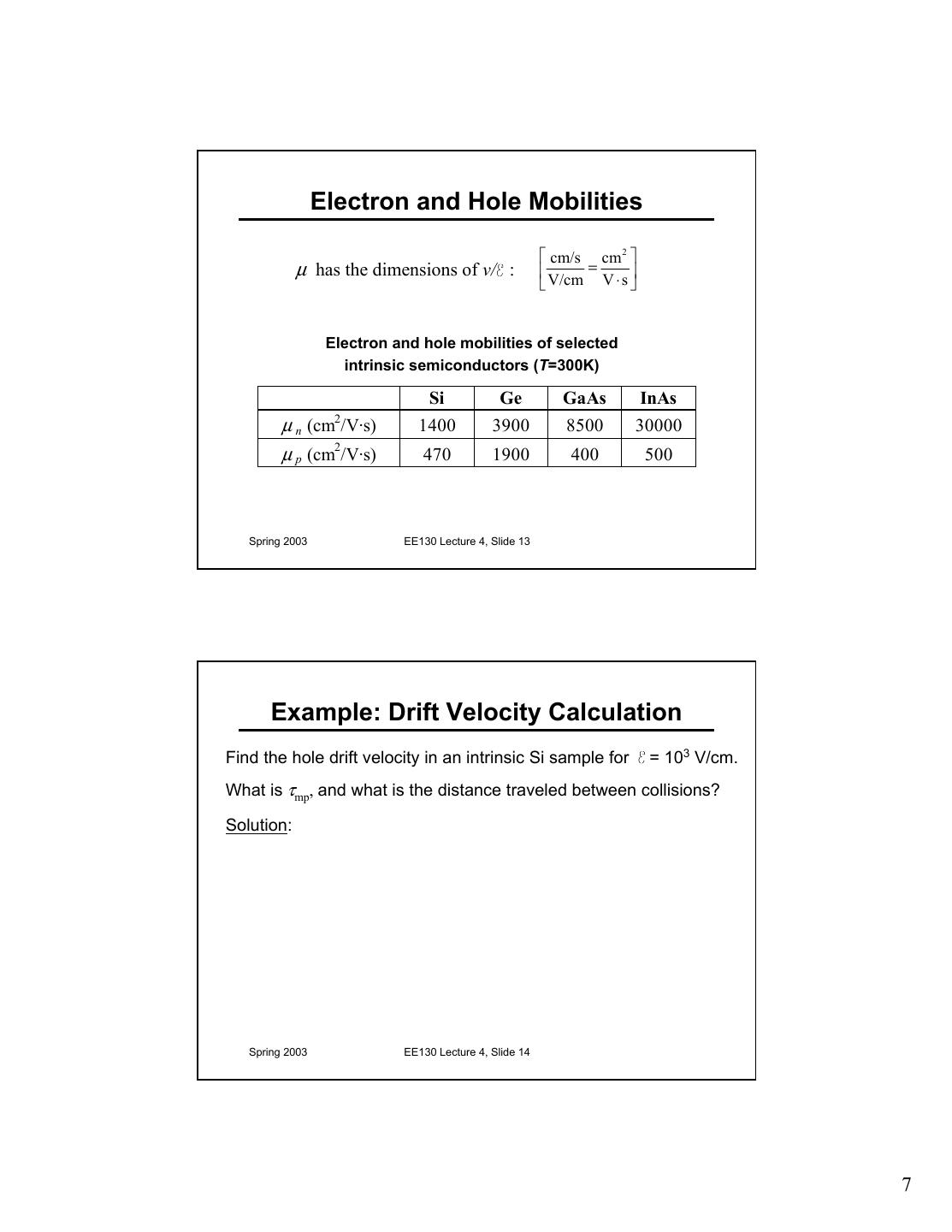
7 . Electron and Hole Mobilities cm/s cm 2 µ has the dimensions of v/ : = V/cm V ⋅ s Electron and hole mobilities of selected intrinsic semiconductors (T=300K) Si Ge GaAs InAs 2 µ n (cm /V·s) 1400 3900 8500 30000 µ p (cm2/V·s) 470 1900 400 500 Spring 2003 EE130 Lecture 4, Slide 13 Example: Drift Velocity Calculation Find the hole drift velocity in an intrinsic Si sample for = 103 V/cm. What is τmp, and what is the distance traveled between collisions? Solution: Spring 2003 EE130 Lecture 4, Slide 14 7
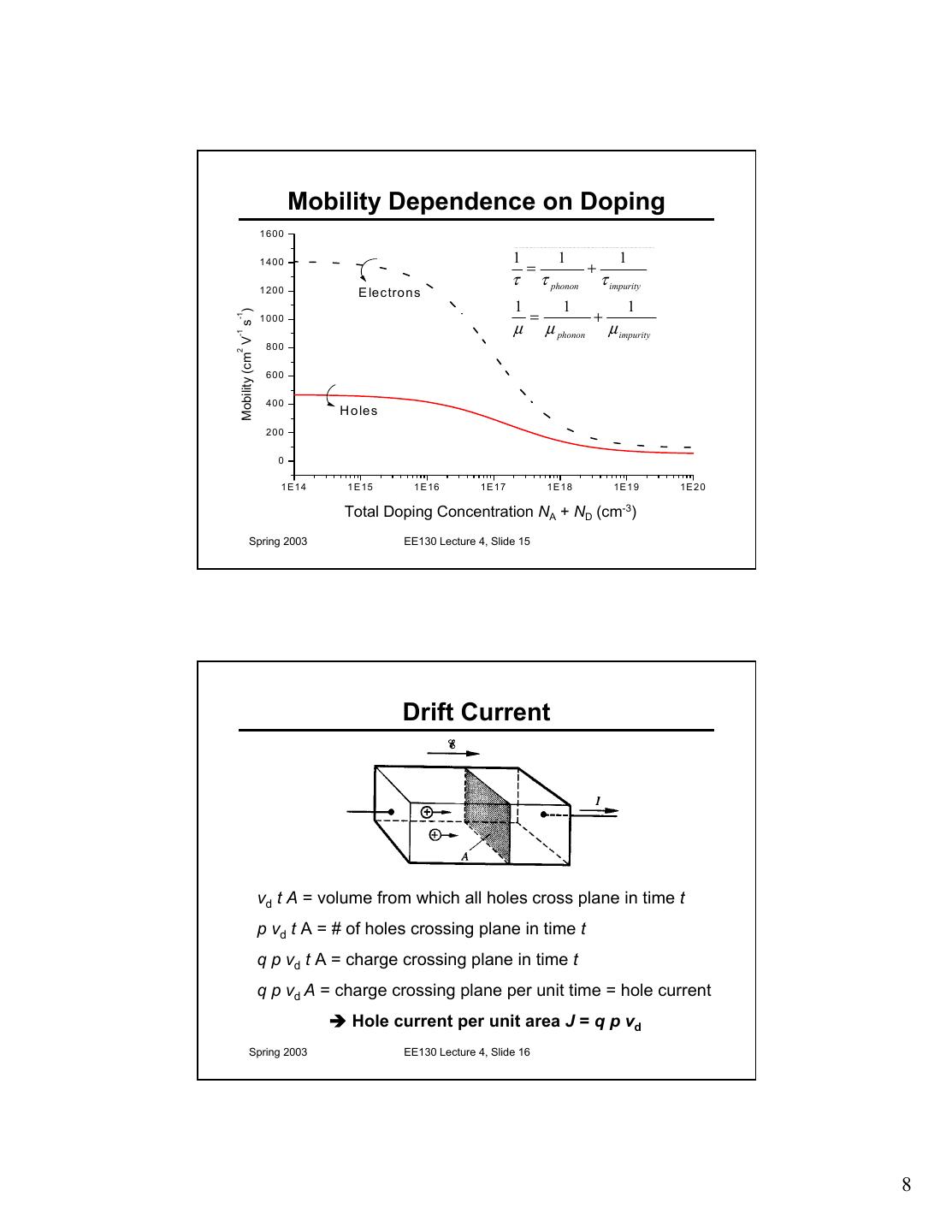
8 . Mobility Dependence on Doping 1600 1400 1 1 1 = + 1200 τ τ phonon τ impurity E lectrons 1 1 1 = + Mobility (cm V s ) -1 1000 µ µ phonon µ impurity -1 800 2 600 400 H o les 200 0 1E 14 1E 15 1E 16 1E 17 1E 18 1E 19 1E 20 -3 Total Doping T otal Concentration Im p urity C on ce nra tio nN(a A + ND (cm ) to m s cm -3) Spring 2003 EE130 Lecture 4, Slide 15 Drift Current vd t A = volume from which all holes cross plane in time t p vd t A = # of holes crossing plane in time t q p vd t A = charge crossing plane in time t q p vd A = charge crossing plane per unit time = hole current Î Hole current per unit area J = q p vd Spring 2003 EE130 Lecture 4, Slide 16 8
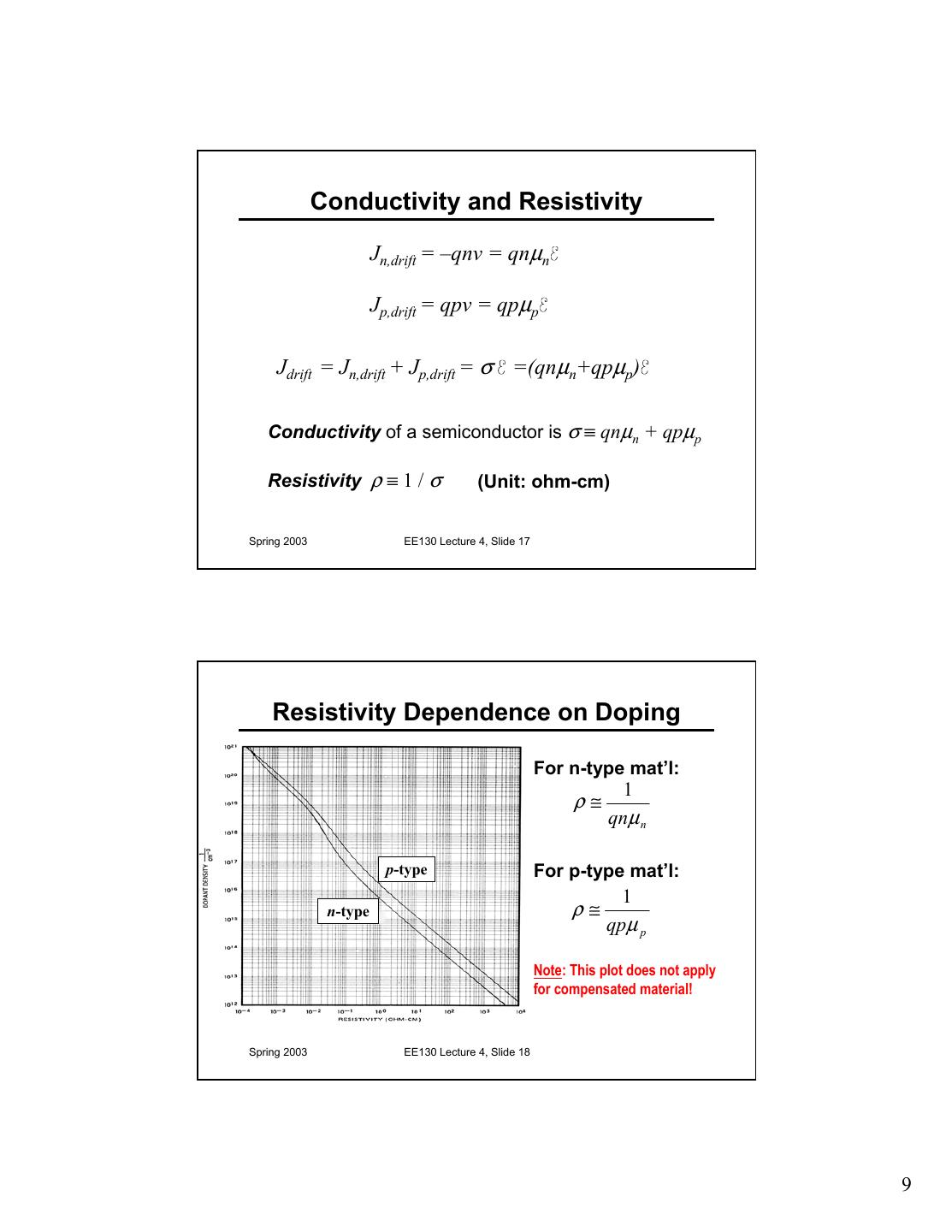
9 . Conductivity and Resistivity Jn,drift = –qnv = qnµn Jp,drift = qpv = qpµp Jdrift = Jn,drift + Jp,drift = σ =(qnµn+qpµp) Conductivity of a semiconductor is σ ≡ qnµn + qpµp Resistivity ρ ≡ 1 / σ (Unit: ohm-cm) Spring 2003 EE130 Lecture 4, Slide 17 Resistivity Dependence on Doping For n-type mat’l: 1 ρ≅ qnµ n p-type For p-type mat’l: 1 n-type ρ≅ qpµ p Note: This plot does not apply for compensated material! Spring 2003 EE130 Lecture 4, Slide 18 9
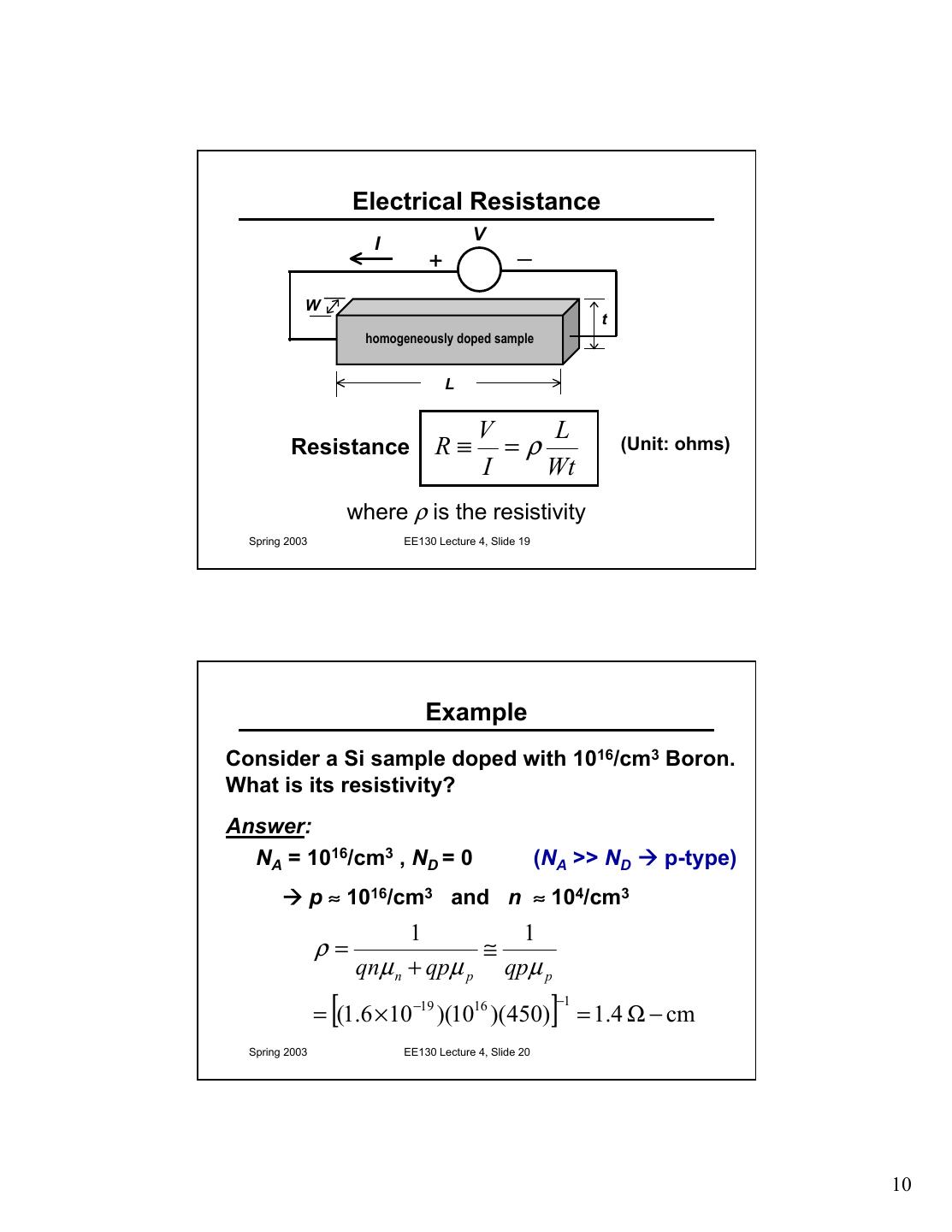
10 . Electrical Resistance V I _ + W t homogeneously doped sample L V L Resistance R≡ =ρ (Unit: ohms) I Wt where ρ is the resistivity Spring 2003 EE130 Lecture 4, Slide 19 Example Consider a Si sample doped with 1016/cm3 Boron. What is its resistivity? Answer: NA = 1016/cm3 , ND = 0 (NA >> ND Æ p-type) Æ p ≈ 1016/cm3 and n ≈ 104/cm3 1 1 ρ= ≅ qnµ n + qpµ p qpµ p [ = (1.6 × 10 −19 )(1016 )(450) ]−1 = 1.4 Ω − cm Spring 2003 EE130 Lecture 4, Slide 20 10
11 . Example: Dopant Compensation Consider the same Si sample, doped additionally with 1017/cm3 Arsenic. What is its resistivity? Answer: NA = 1016/cm3, ND = 1017/cm3 (ND>>NA Æ n-type) Æ n ≈ 9x1016/cm3 and p ≈ 1.1x103/cm3 1 1 ρ= ≅ qnµ n + qpµ p qnµ n [ = (1.6 ×10 −19 )(9 × 1016 )(600) ] −1 = 0.12 Ω − cm Spring 2003 EE130 Lecture 4, Slide 21 Summary • Electrons and holes moving under the influence of an electric field can be modelled as quasi-classical particles with average drift velocity |vd| = µ • The conductivity of a semiconductor is dependent on the carrier concentrations and mobilities σ = qnµn + qpµp 1 1 • Resistivity ρ= = σ qnµ n + qpµ p Spring 2003 EE130 Lecture 4, Slide 22 11