04 编译器原理与技术---语法制导的翻译

1 .第 4 章 语法 制导的翻译 编译原理与技术

2 .介绍 语义描述的一种形式方法：语法制导的翻译，它包括两种具体形式 语法 制导的定义 翻译 方案 介绍 语法制导翻译的实现方法 4 语法制导的翻译 内容提要

3 .4.1 语法制导的定义 第 4 章 语法 制导的翻译

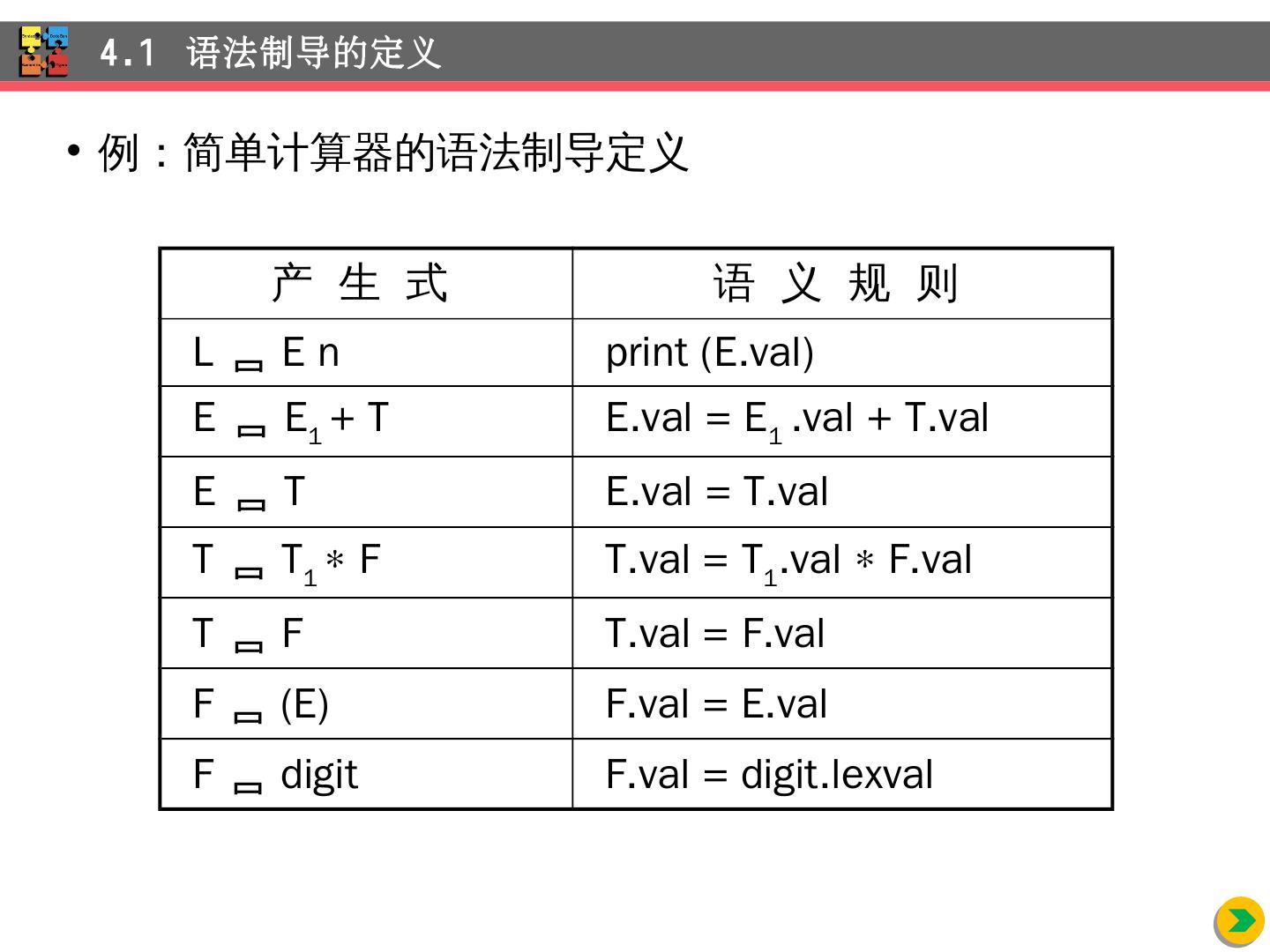
4 .例：简单 计算器的语法制导定义 4.1 语法制导的定义 产 生 式 语 义 规 则 L  E n print (E.val) E  E 1 + T E.val = E 1 .val + T.val E  T E.val = T.val T  T 1  F T.val = T 1 .val  F.val T  F T.val = F.val F  (E) F.val = E.val F  digit F.val = digit.lexval

5 .4.1.1 语法制导定义的形式 基础 文法 每个文法符号有一组属性 每个文法产生 式 A  α 有 一组形式 为 b=f(c 1 , c 2 , …, c k ) 的语义规则，其中 b 和 c 1 , c 2 , …, c k 是该产生式文法符号的属性， f 是函数 综合属性 ：如果 b 是 A 的属性， c 1 , c 2 , …, c k 是产生式右部文法符号的属性或 A 的其它属性 继承属性 ：如果 b 是右部某文法符号 X 的属性 4.1 语法制导的定义

6 .4.1.2 综合属性 S 属性定义 ：仅使用综合属性的语法制导定义 4.1 语法制导的定义 产 生 式 语 义 规 则 L  E n print (E.val) E  E 1 + T E.val = E 1 .val + T.val E  T E.val = T.val T  T 1  F T.val = T 1 .val  F.val T  F T.val = F.val F  (E) F.val = E.val F  digit F.val = digit.lexval

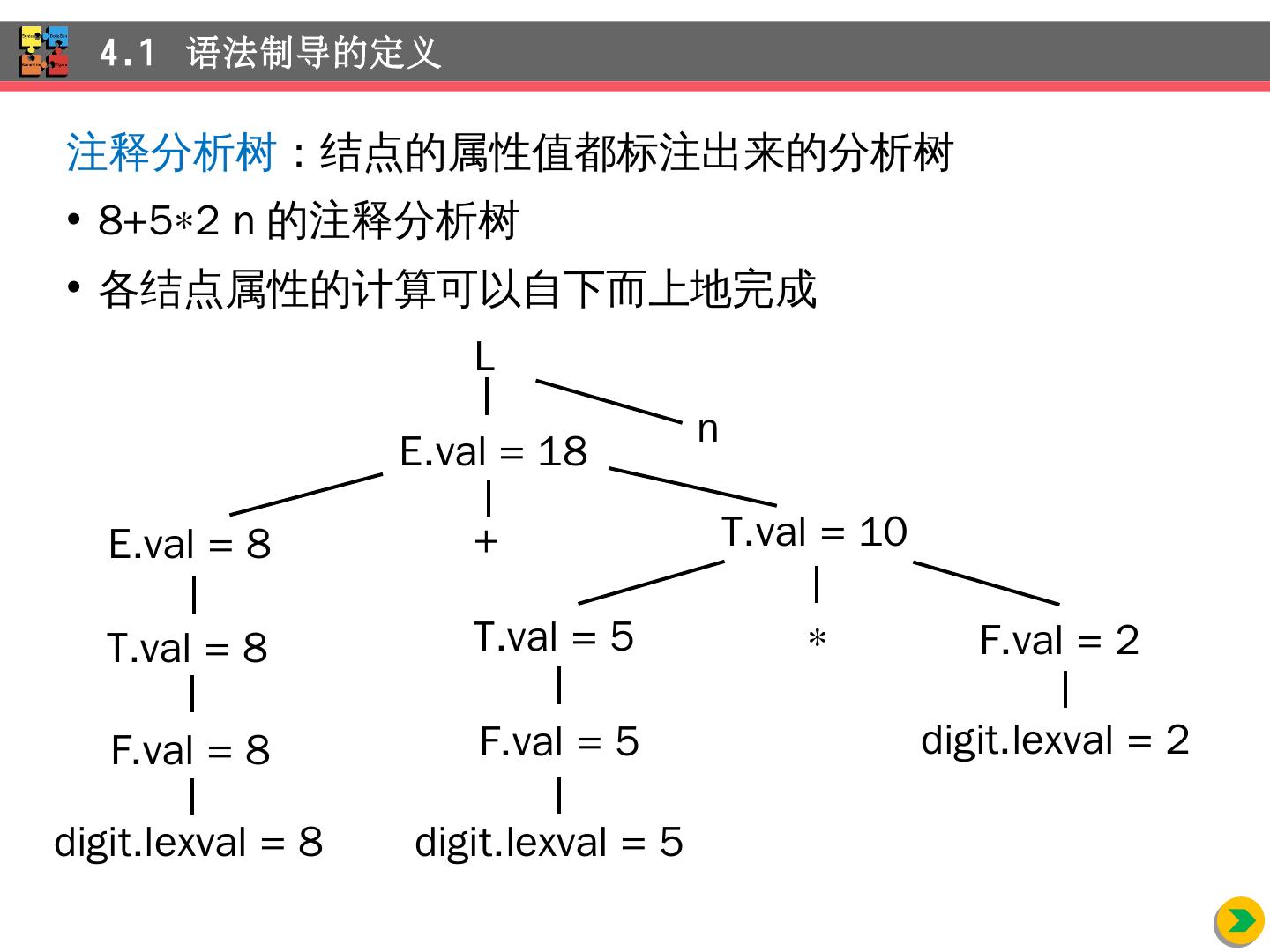
7 .注释 分析树 ： 结点 的属性值都标注出来的分析树 8+5  2 n 的注释分析树 各 结点属性的计算可以自下而上地 完成 4.1 语法制导的定义 digit.lexval = 2 E.val = 18 T.val = 10 E.val = 8 T.val = 8 F.val = 8 digit.lexval = 8 T.val = 5 F.val = 5 F.val = 2 digit.lexval = 5 L n + 

8 .4.1.3 继承属性 例： int id 1 , id 2 , id 3 4.1 语法制导的定义 产 生 式 语 义 规 则 D  TL L.in = T.type T  int T. type = integer T  real T. type = real L  L 1 , id L 1 .in = L.in; addType(id.entry, L.in) L  id addType ( id.entry , L.in)

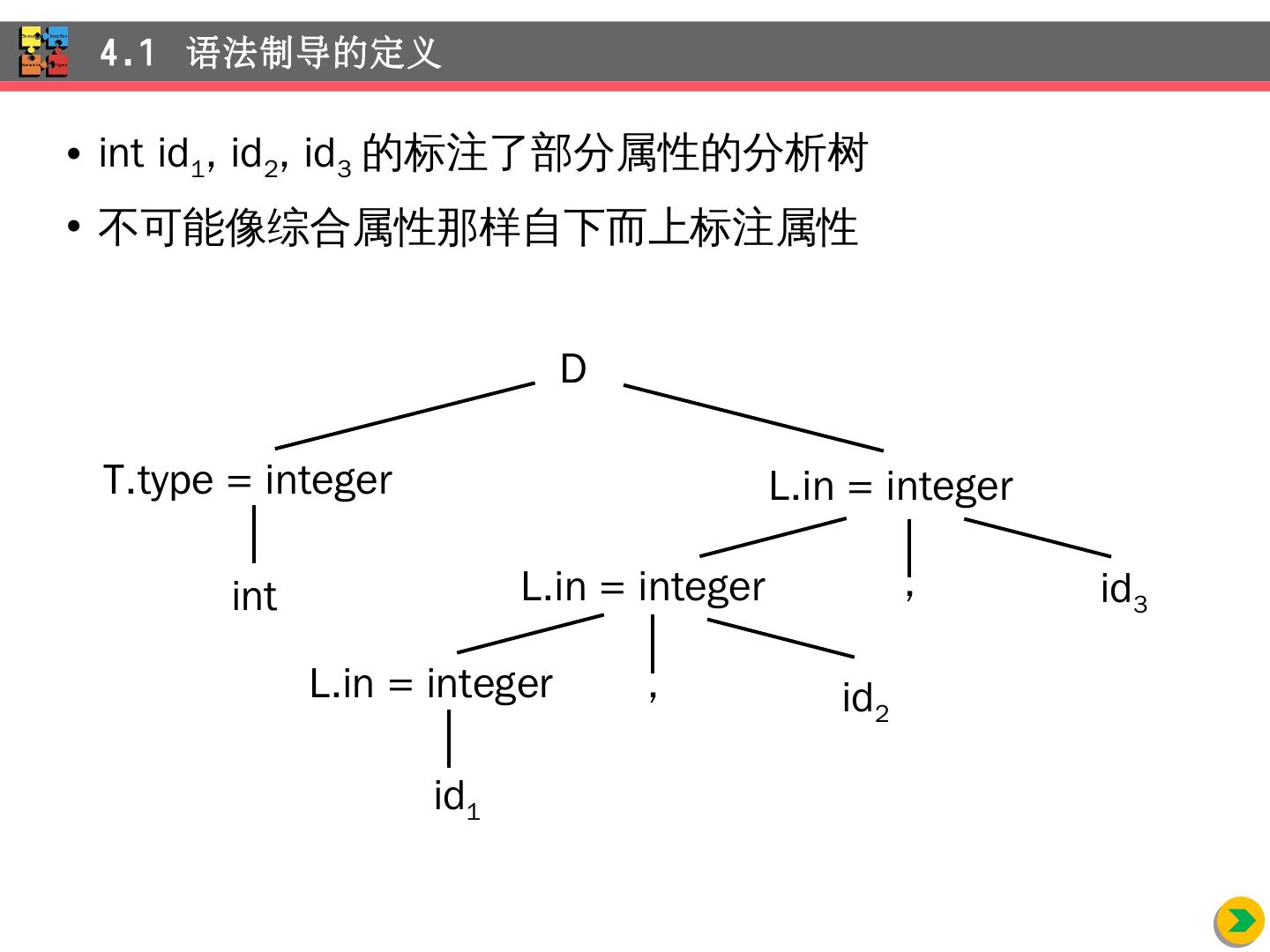
9 .int id 1 , id 2 , id 3 的标注了部分属性的分析树 不可能像 综合属性那样自下而上标注属性 4.1 语法制导的定义 D int T.type = integer , id 3 L.in = integer L.in = integer L.in = integer id 2 id 1 ,

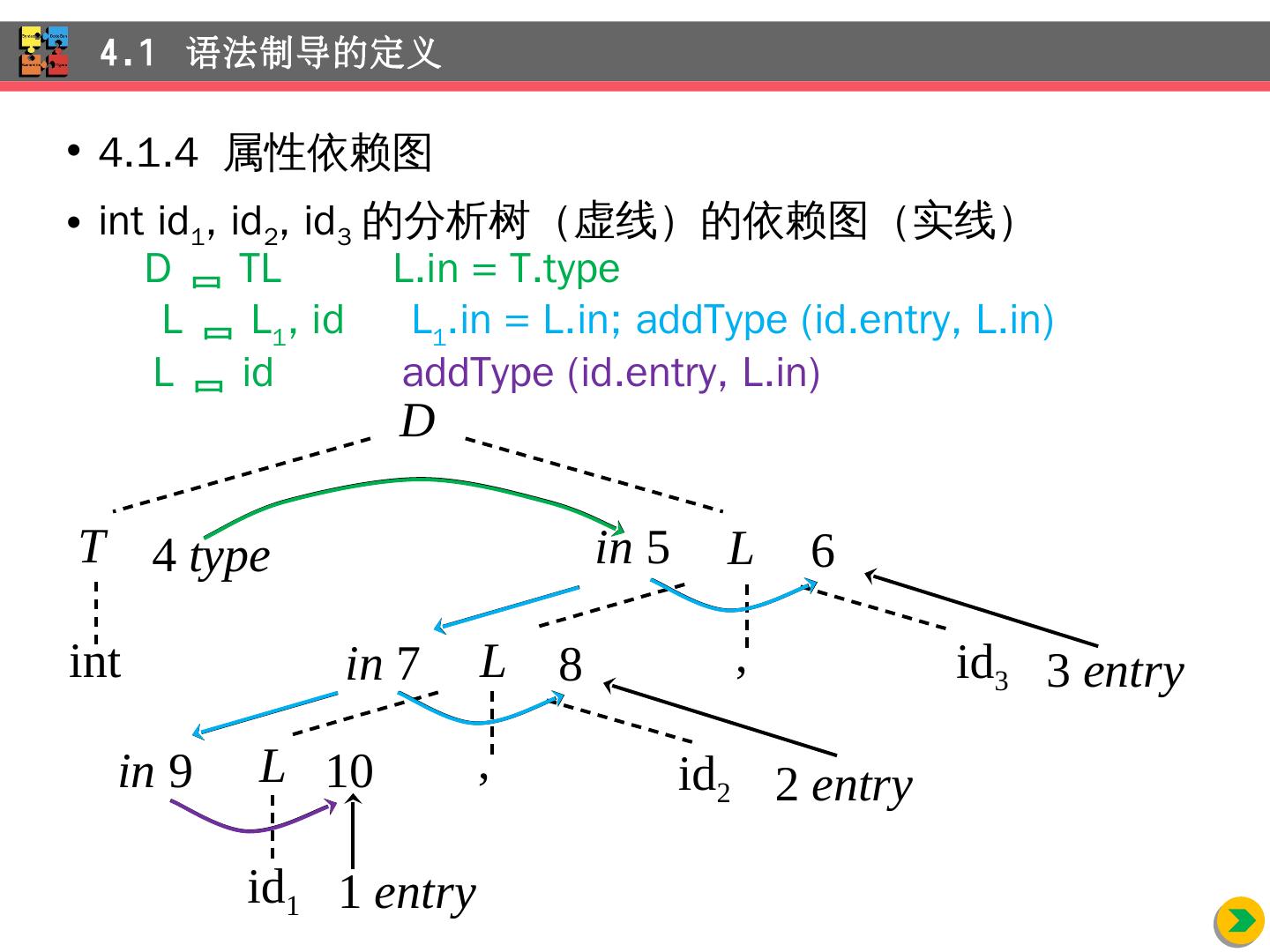
10 .4.1.4 属性依赖图 int id 1 , id 2 , id 3 的分析树（虚线）的依赖图（实线） 4.1 语法制导的定义 D int T , id 3 L L L id 2 id 1 , 1 entry 10 2 entry 3 entry in 9 8 in 7 6 in 5 4 type D  TL L.in = T.type L  L 1 , id L 1 .in = L.in ; addType ( id.entry , L.in) L  id addType ( id.entry , L.in)

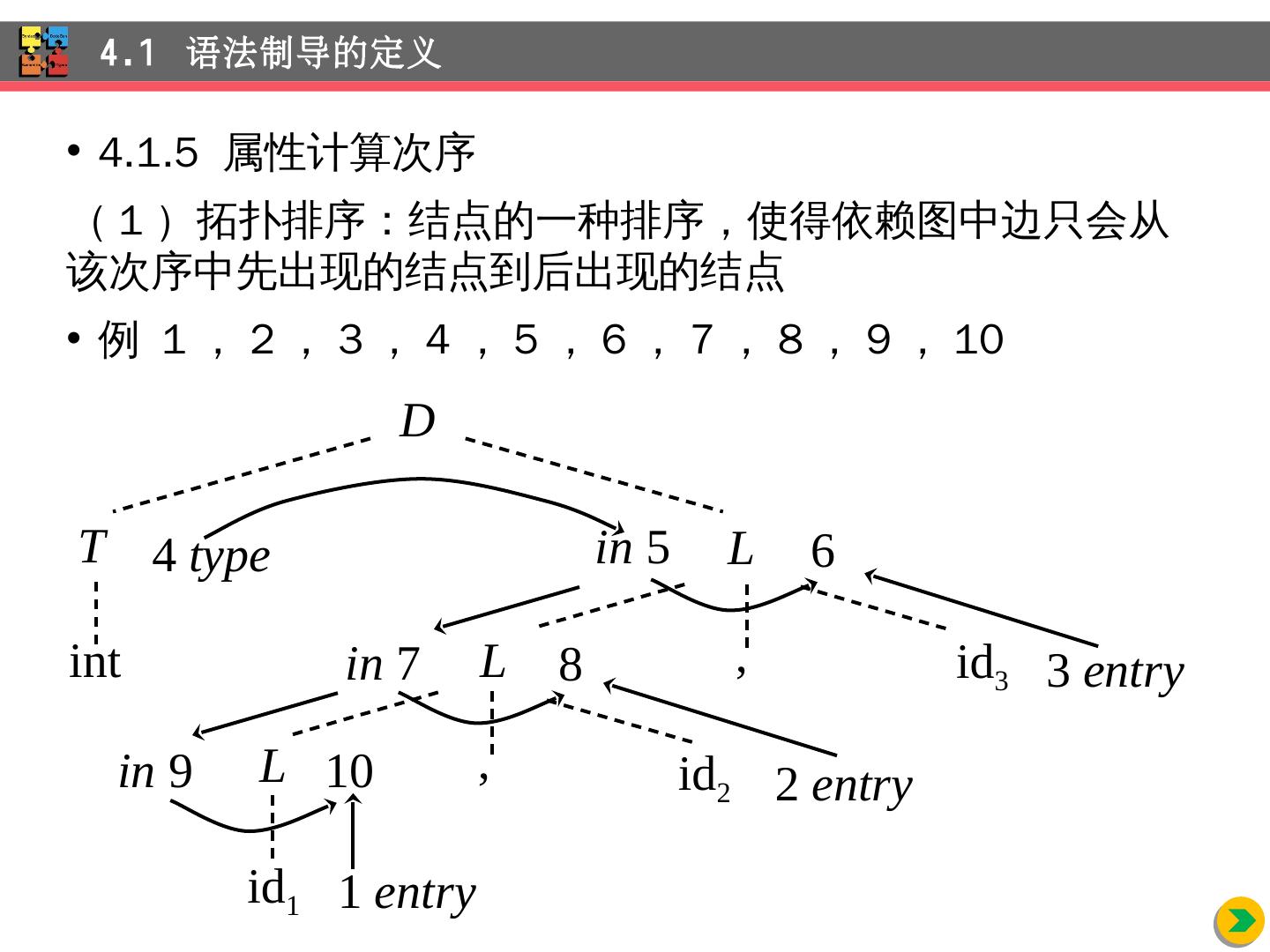
11 .4.1.5 属性计算次序 （ 1 ）拓扑 排序：结点的一种排序， 使得依赖图中边 只会从该次序中先出现的结点到后出现的结点 例 1 ， 2 ， 3 ， 4 ， 5 ， 6 ， 7 ， 8 ， 9 ， 10 4.1 语法制导的定义 D int T , id 3 L L L id 2 id 1 , 1 entry 10 2 entry 3 entry in 9 8 in 7 6 in 5 4 type

12 .（ 2 ）属性 计算次序 ： 1 ）构造 输入的 分析树 2 ）构造 属性 依赖图 3 ）对 结点进行拓扑 排序 4 ）按 拓扑排序的次序计算属性 4.1 语法制导的定义 D int T , id 3 L L L id 2 id 1 , 1 entry 10 2 entry 3 entry in 9 8 in 7 6 in 5 4 type

13 .语义规则的计算方法 分析树方法：刚才介绍的方法，动态确定计算次序，效率 低。　 概念 上的一般方法 基于 规则的方法：（ 编译器实现者 ）静态确定（ 编译器设计者提供的 ）语义规则的计算 次序。　 适用于 手工构造的方法 忽略 规则的方法：（ 编译器实现者 ）事先确定属性的计算策略（如边分析边计算） , （ 编译器设计者提供的 ）语义规则必须符合所选分析方法的 限制。 　 适用于 自动生成的方法 4.1 语法制导的定义

14 .4.2 S 属性定义的自下而上计算 第 4 章 语法 制导的翻译

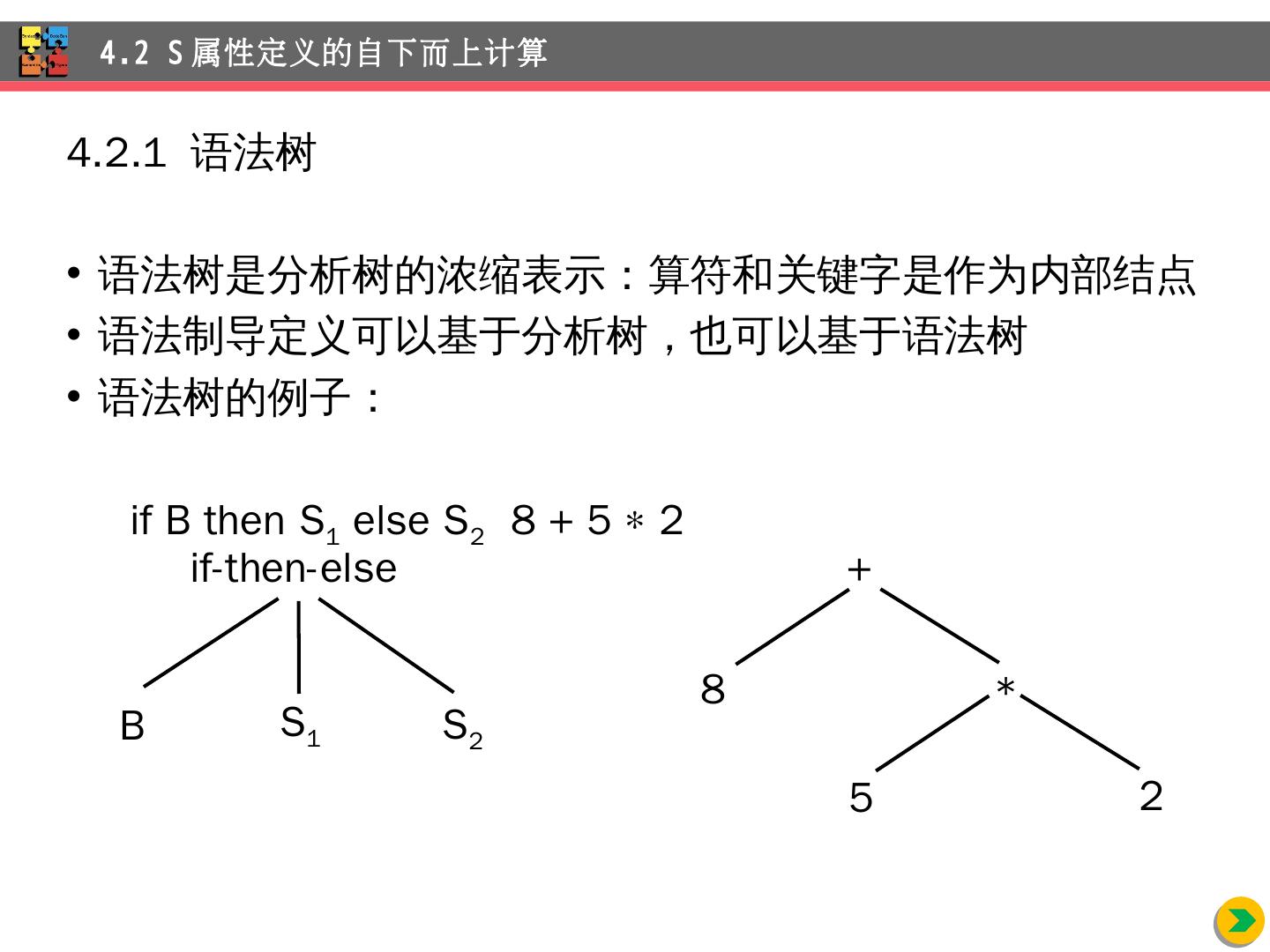
15 .4.2.1 语法树 语法 树是分析树的浓缩表示：算符和关键字是作为内部结点 语法制导定义可以基于分析树，也可以基于语法树 语法树的例子： if B then S 1 else S 2 8 + 5  2 4.2 S 属性定义的自下而上计算 if-then-else B S 1 S 2 + * 2 5 8

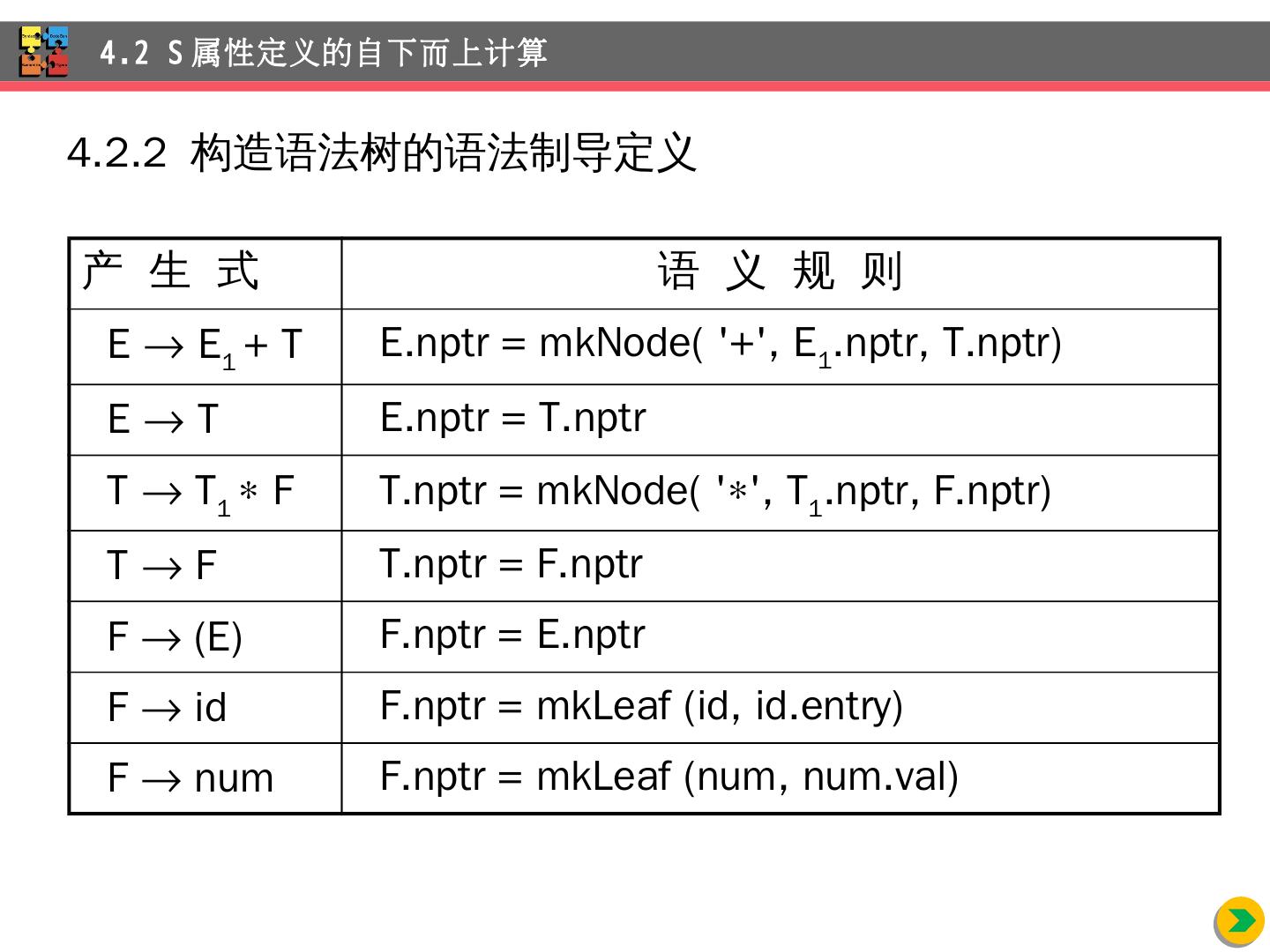
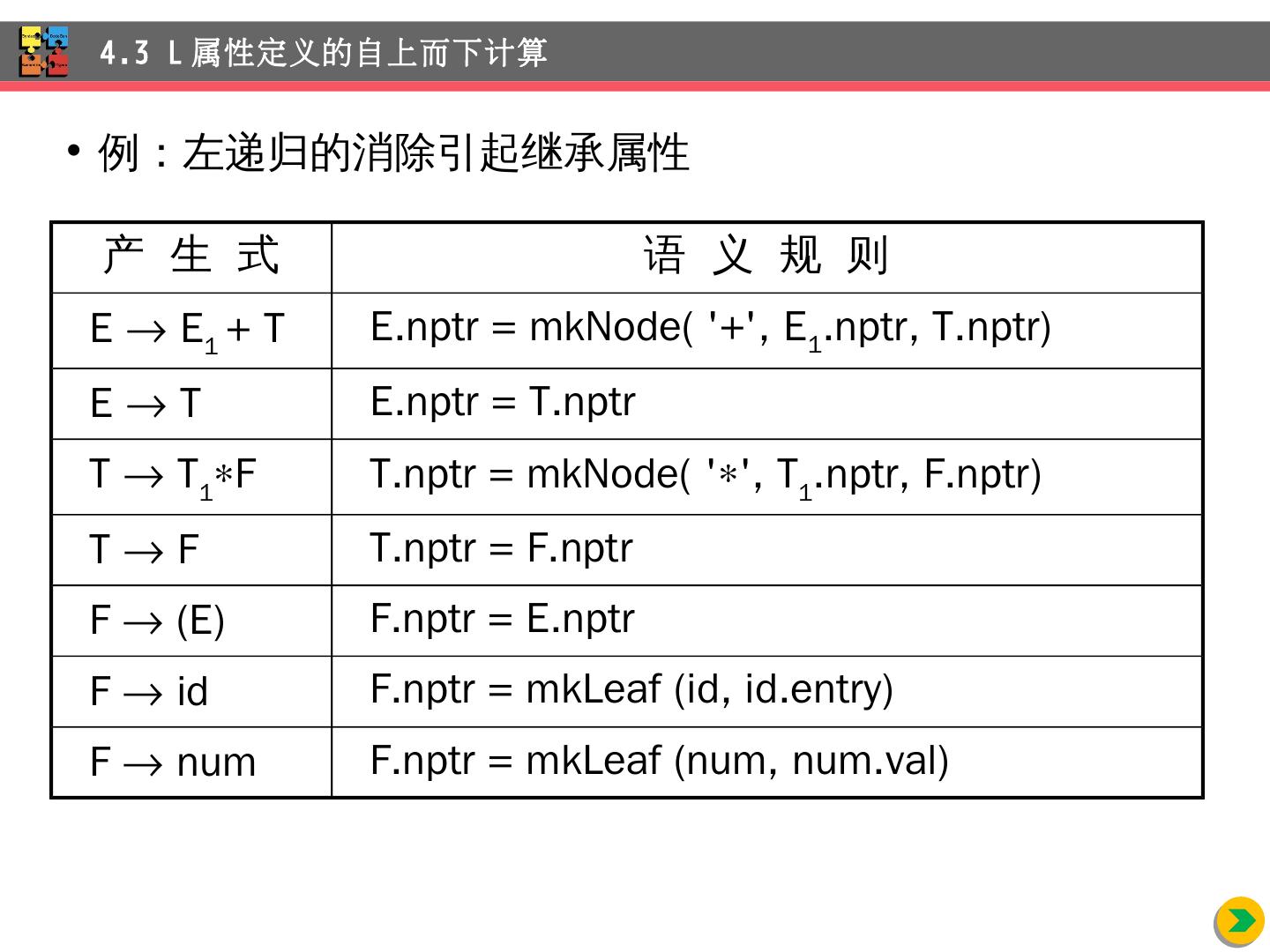
16 .4.2.2 构造语法树的语法制导定义 4.2 S 属性定义的自下而上计算 产 生 式 语 义 规 则 E  E 1 + T E.nptr = mkNode ( +, E 1 .nptr, T.nptr ) E  T E.nptr = T.nptr T  T 1  F T.nptr = mkNode (  , T 1 .nptr, F.nptr ) T  F T.nptr = F.nptr F  (E) F.nptr = E.nptr F  id F.nptr = mkLeaf (id, id.entry) F  num F.nptr = mkLeaf ( num , num.val )

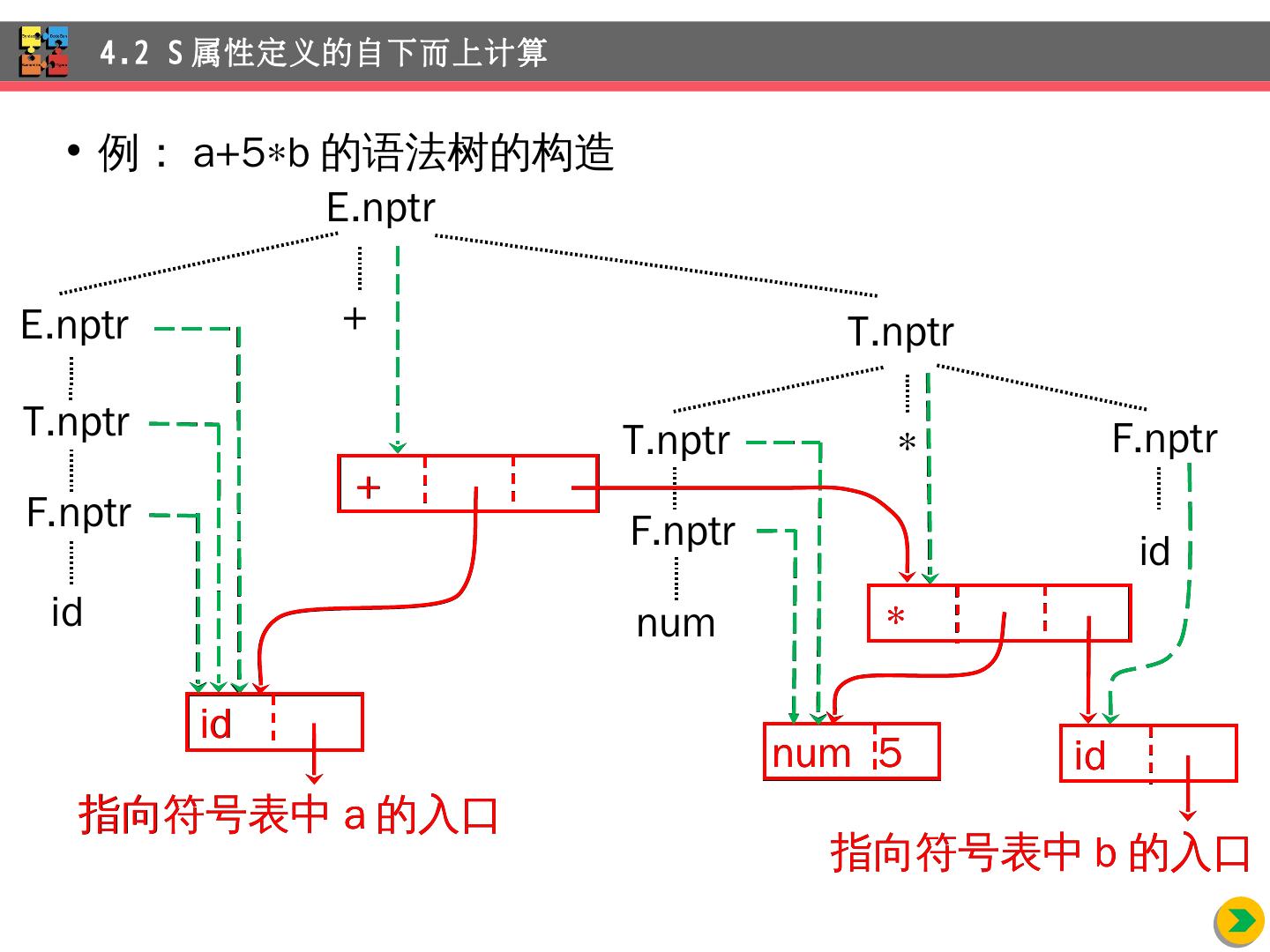
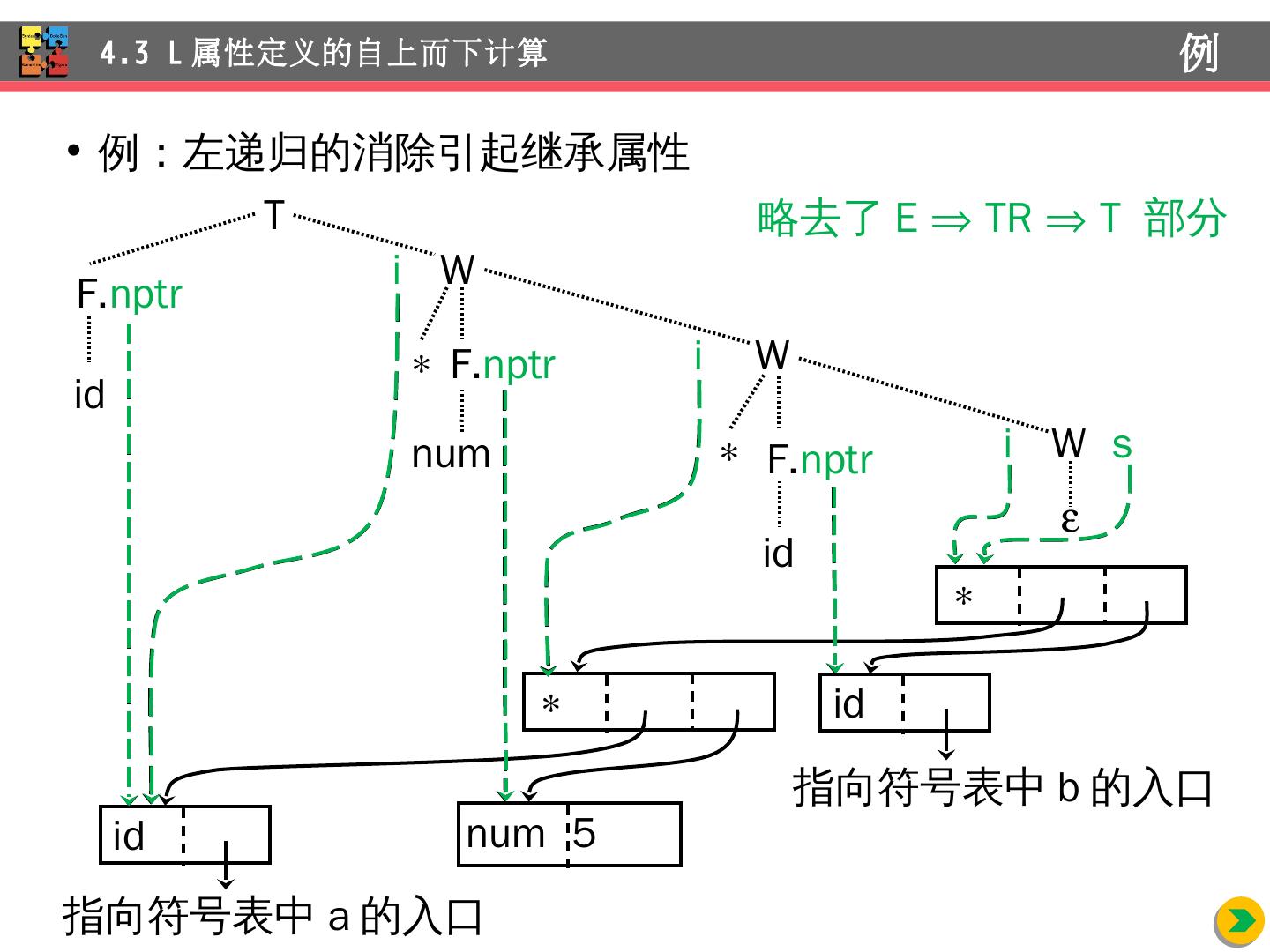
17 .例： a+5  b 的语法树的构造 4.2 S 属性定义的自下而上计算 E.nptr T.nptr E.nptr T.nptr F.nptr id T.nptr +  F.nptr F.nptr id num id id num 5  + 指向符号表中 a 的入口 指向符号表中 b 的入口 id 指向符号表中 a 的入口 num 5 id 指向符号表中 b 的入口  +

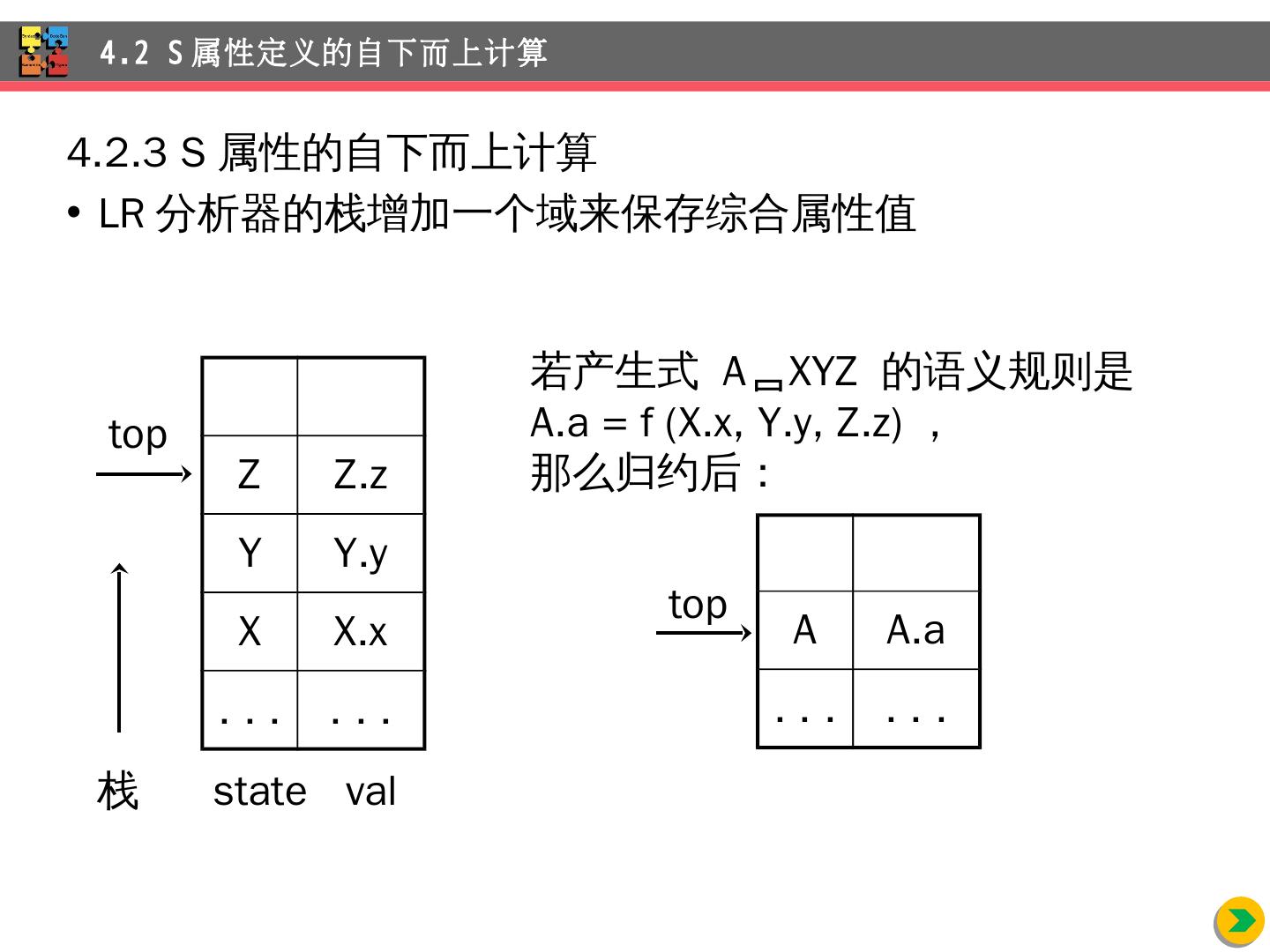
18 .4.2.3 S 属性的自下而上计算 LR 分析器的栈增加一个域来保存综合属性值 4.2 S 属性定义的自下而上计算 A A.a . . . . . . 若产生 式 A  XYZ 的 语义规则是 A.a = f ( X.x , Y.y , Z.z )， 那么归约后： top Z Z.z Y Y.y X X.x . . . . . . 栈 state val top

19 .例：简单 计算器的语法制导定义改成栈操作代码 4.2 S 属性定义的自下而上计算 产 生 式 语 义 规 则 代 码 段 L  E n print (E.val) E  E 1 + T E.val =E 1 .val +T.val E  T E.val = T.val T  T 1  F T.val = T 1 .val  F.val T  F T.val = F.val F  (E) F.val = E.val F  digit F.val = digit.lexval print ( val [ top  1] ) val [top  2 ] = val [top  2]+ val [top] val [top  2 ] = val [top  2 ]  val [top] val [top  2 ] = val [top  1] —— ——

20 .例：简单 计算器的语法制导定义改成栈操作代码 4.2 S 属性定义的自下而上计算 产 生 式 语 义 规 则 代 码 段 L  E n print (E.val) E  E 1 + T E.val =E 1 .val +T.val E  T E.val = T.val T  T 1  F T.val = T 1 .val  F.val T  F T.val = F.val F  (E) F.val = E.val F  digit F.val = digit.lexval print ( val [ top  1] ) val [top  2 ] = val [top  2]+ val [top] val [top  2 ] = val [top  2 ]  val [top] val [top  2 ] = val [top  1] —— ——

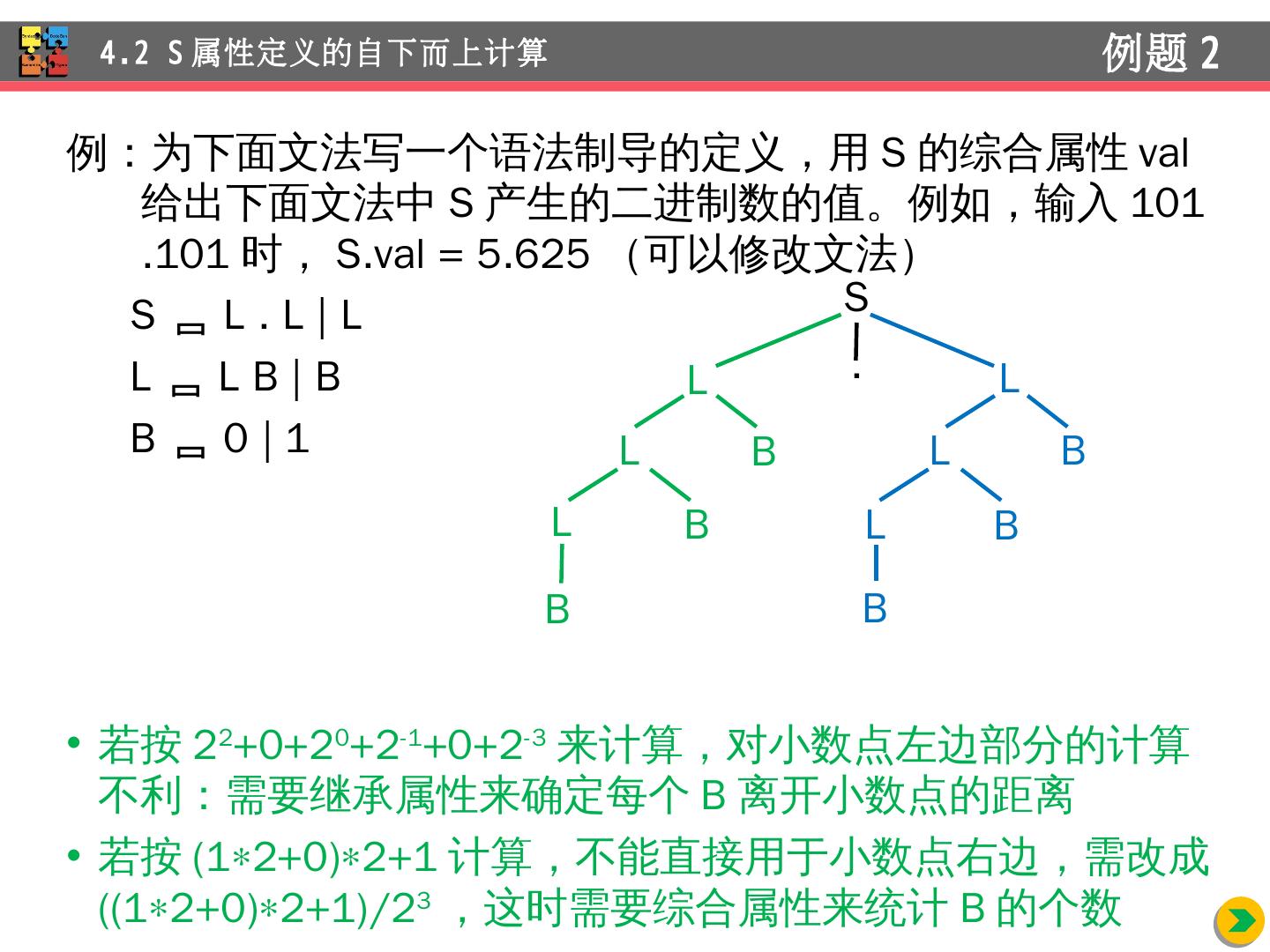
21 .例：为 下面文法写一个语法制导的定义，用 S 的综合属性 val 给 出下面文法中 S 产生的二进制数的值。例如， 输入 101.101 时， S.val = 5.625 （可以修改文法 ） S  L . L | L L  L B | B B  0 | 1 若 按 2 2 +0+2 0 +2 -1 +0+2 -3 来计算 ，对小数点左边 部分的计算 不利：需要 继承属性来确定每个 B 离开 小数点的距离 若按 ( 1  2+0)  2+1 计算，不能直接 用于小数点右边，需改成 (( 1  2+0)  2+1 )/2 3 ，这时 需要综合属性来统计 B 的 个数 4.2 S 属性定义的自下而上计算 例题 2 S . L L B L B B L L B L B B

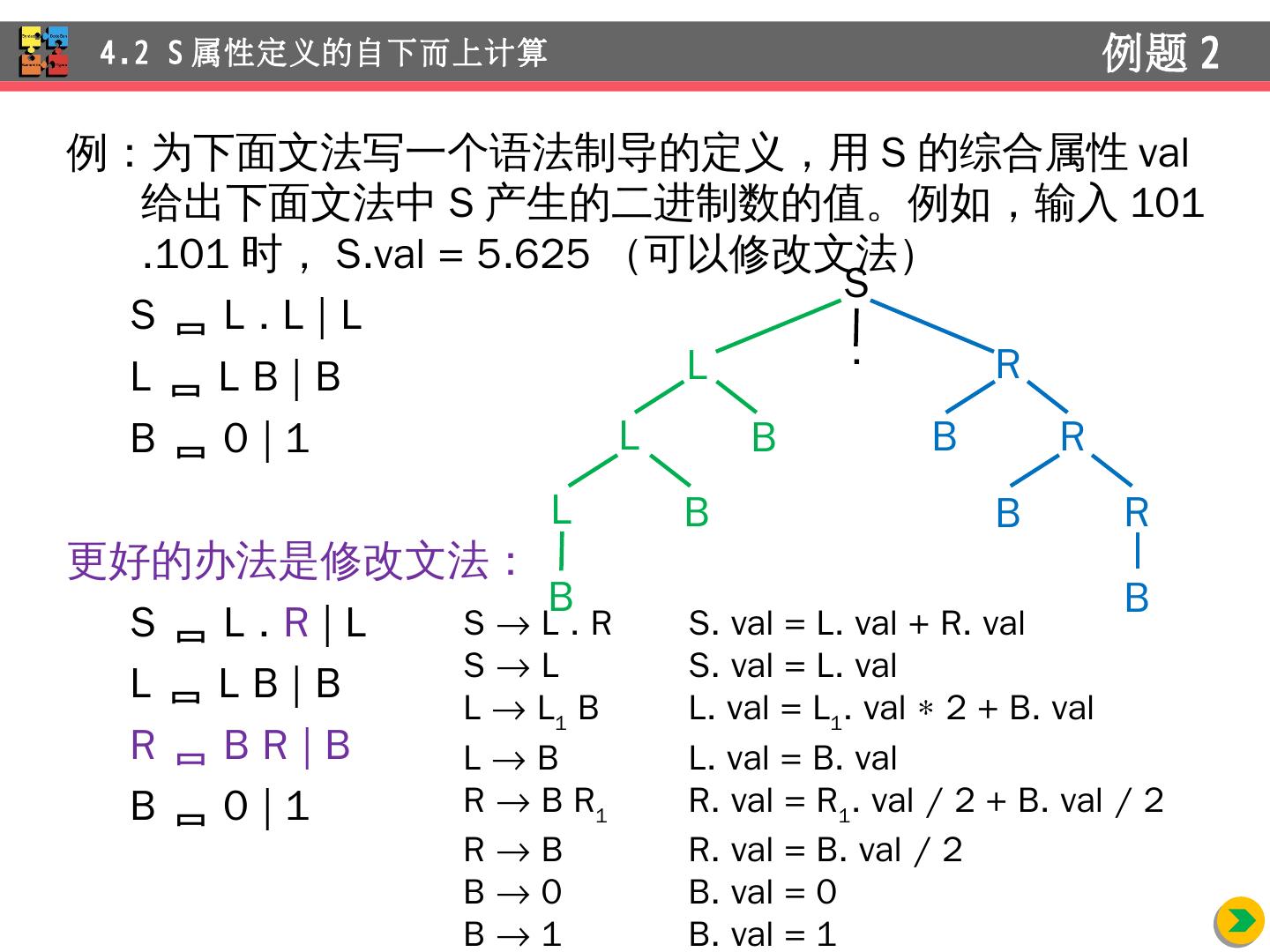
22 .例：为 下面文法写一个语法制导的定义，用 S 的综合属性 val 给 出下面文法中 S 产生的二进制数的值。例如， 输入 101.101 时， S.val = 5.625 （可以修改文法 ） S  L . L | L L  L B | B B  0 | 1 更好的 办法 是修改文法： S  L . R | L L  L B | B R  B R | B B  0 | 1 4.2 S 属性定义的自下而上计算 例题 2 S . L L B L B B R R B R B B S  L . R S . val = L. val + R. val S  L S . val = L. val L  L 1 B L . val = L 1 . val  2 + B. val L  B L . val = B. val R  B R 1 R . val = R 1 . val / 2 + B. val / 2 R  B R . val = B. val / 2 B  0 B . val = 0 B  1 B . val = 1

23 .4.3 L 属性 定义的 自上而 下 计算 第 4 章 语法 制导的翻译

24 .边分析边翻译的方式能否用于继承属性？ 属性的计算次序一定受分析方法所限定的分析树结点建立次序的限制 分析树的结点是自左向右生成 如果属性信息是自左向右流动，那么就有可能在分析的同时完成属性计算 4.3 L 属性 定义的 自上而下计算

25 .4.3.1 L 属性定义 如果每个产生 式 A  X 1 …X j-1 X j … X n 的 每条语义规则计算的属性是 A 的综合属性；或者 是 X j 的继承属性，但它仅依赖： 该产生式中 X j 左边符号 X 1 , X 2 , …, X j-1 的属性； A 的继承属性 S 属性定义属于 L 属性定义 4.3 L 属性 定义的自上而下计算

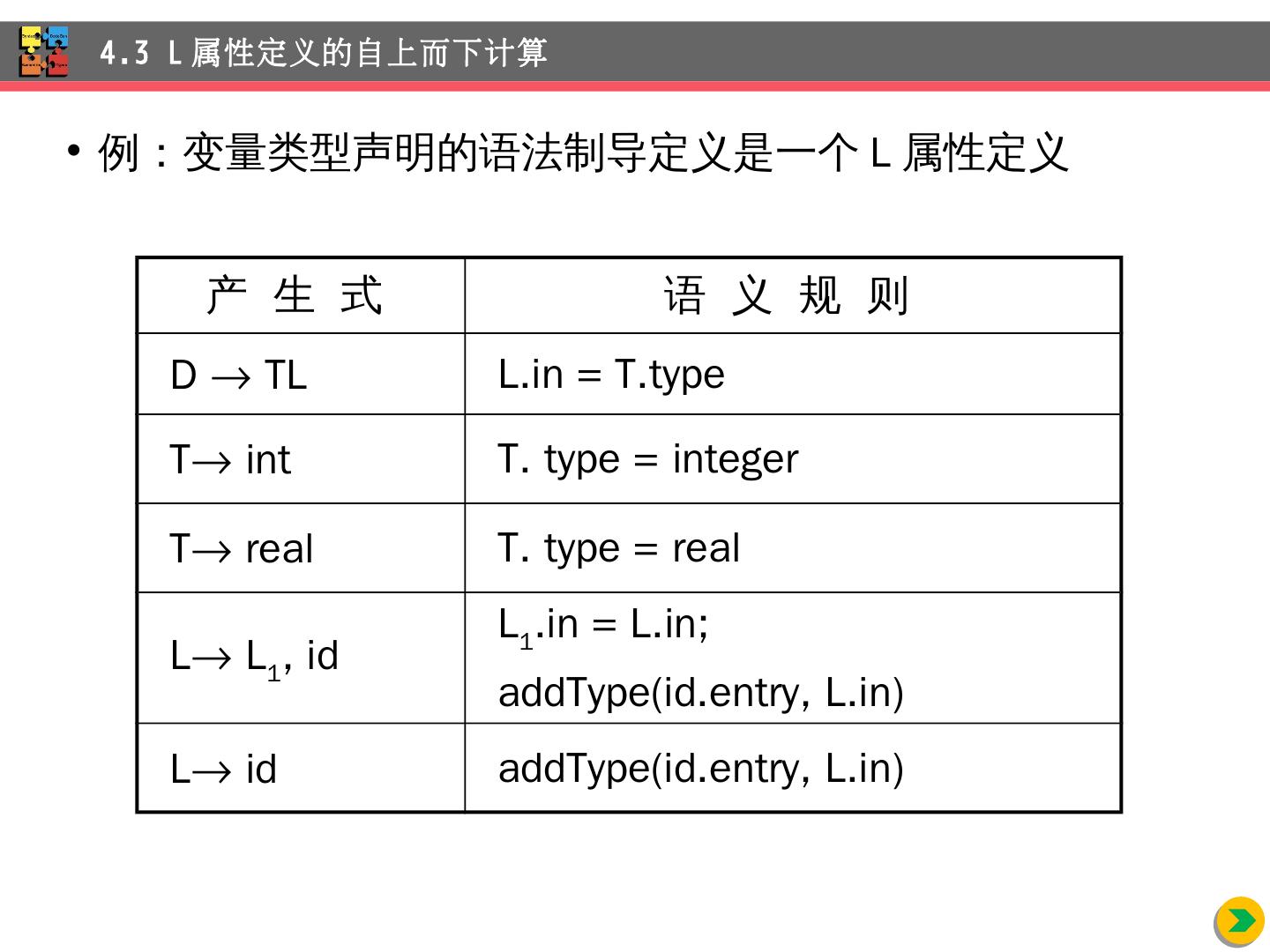
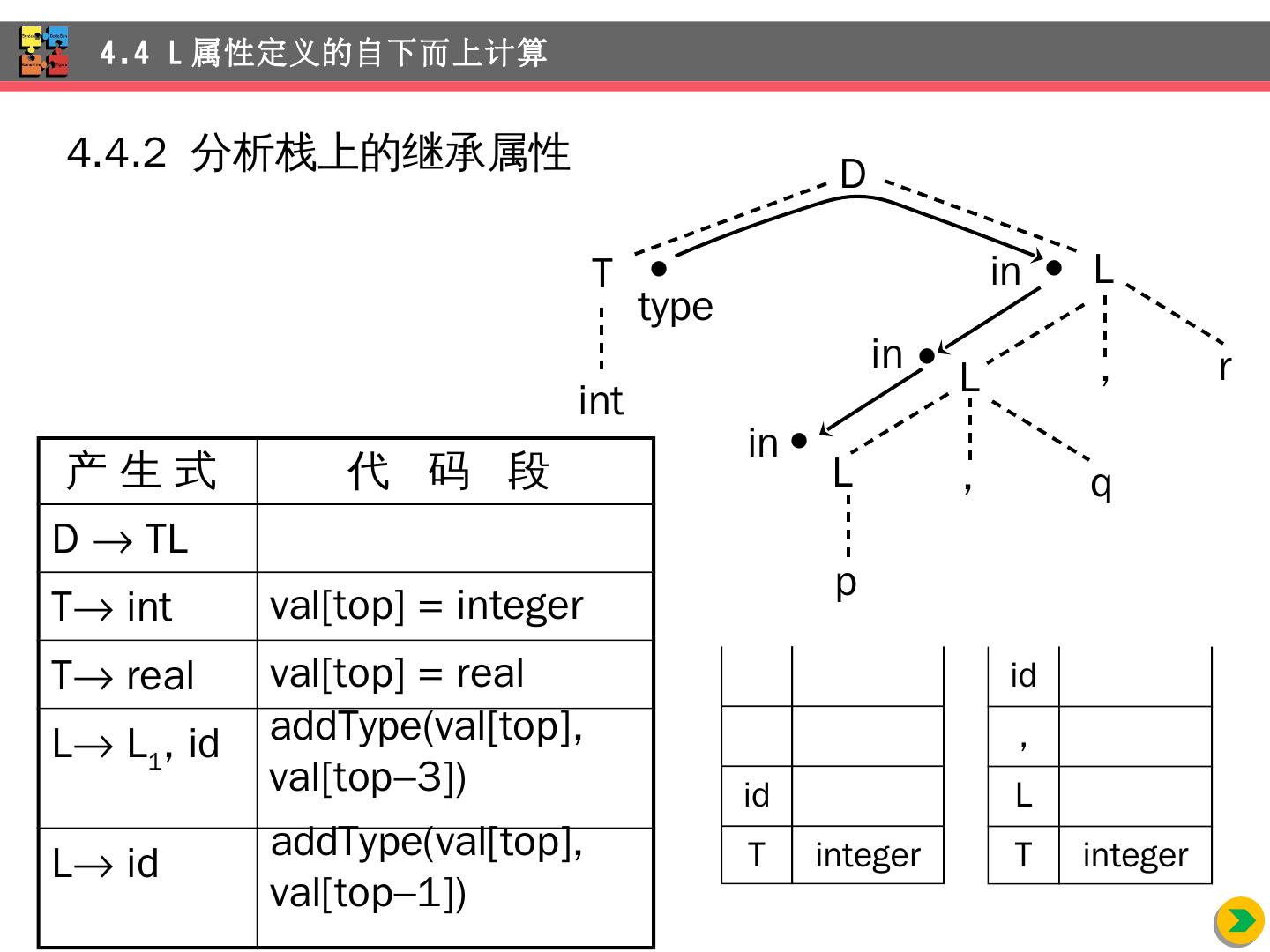
26 .例：变量 类型声明的语法制导定义是一个 L 属性定义 4.3 L 属性 定义的自上而下计算 产 生 式 语 义 规 则 D  TL L.in = T.type T  int T. type = integer T  real T. type = real L  L 1 , id L 1 .in = L.in; addType ( id.entry , L.in) L  id addType ( id.entry , L.in)

27 .4.3.2 翻译 方案 例：把 有加和减的中缀表达式翻译成后缀表达式 如果 输入是 8+5-2 ，则输出是 8 5 + 2 - E  T R R  addop T {print ( addop.lexeme )} R1 | ε T  num {print ( num.val )} E  T R  num {print (8)} R  num {print (8)} addop T {print (+)} R  num {print(8)} addop num {print(5)}{print (+)} R … {print(8)}{print(5)}{print(+)} addop T {print (-)} R … {print(8)}{print(5)}{print(+)}{print(2)}{print (-)} 4.3 L 属性 定义的自上而下计算

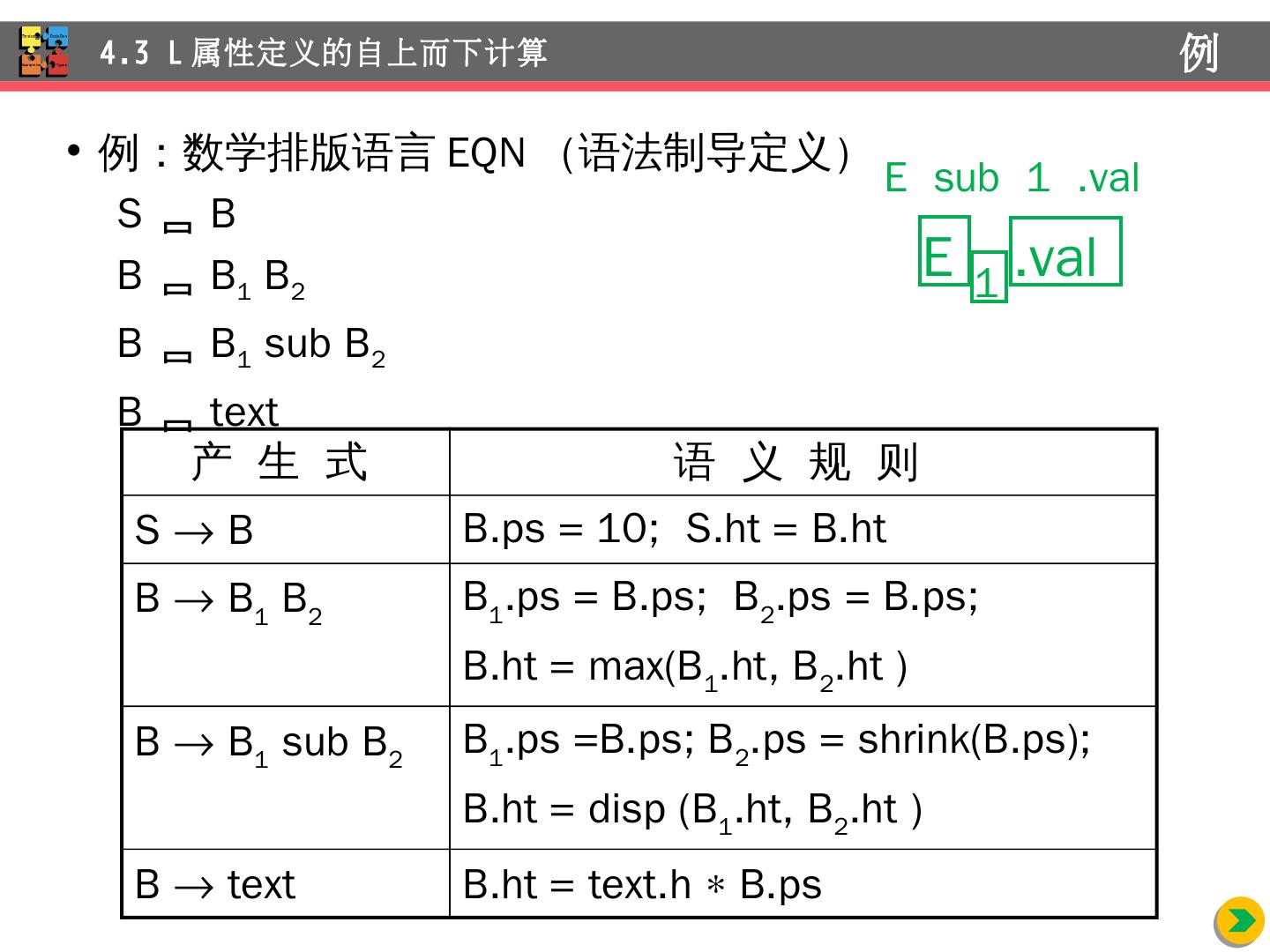
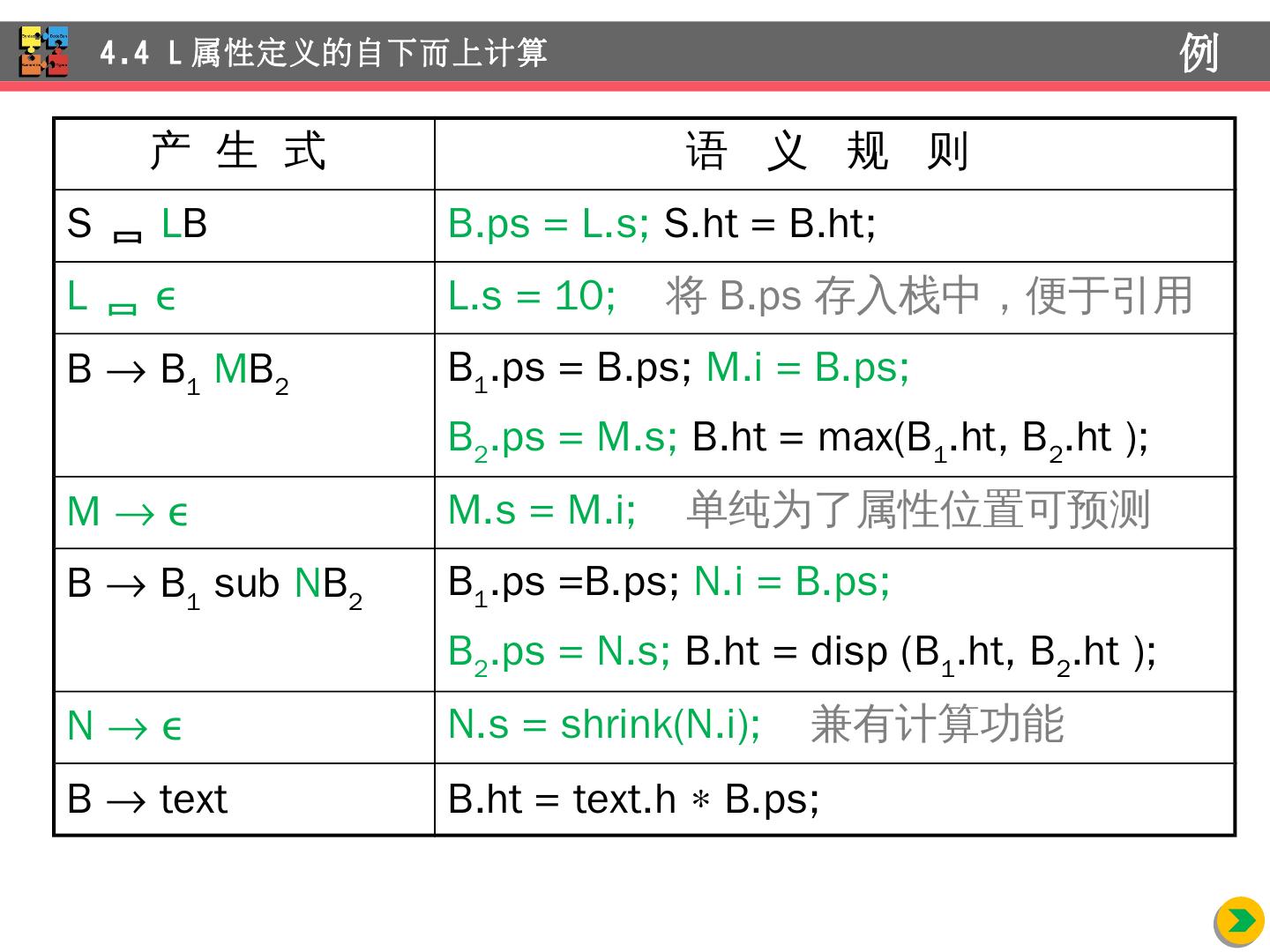
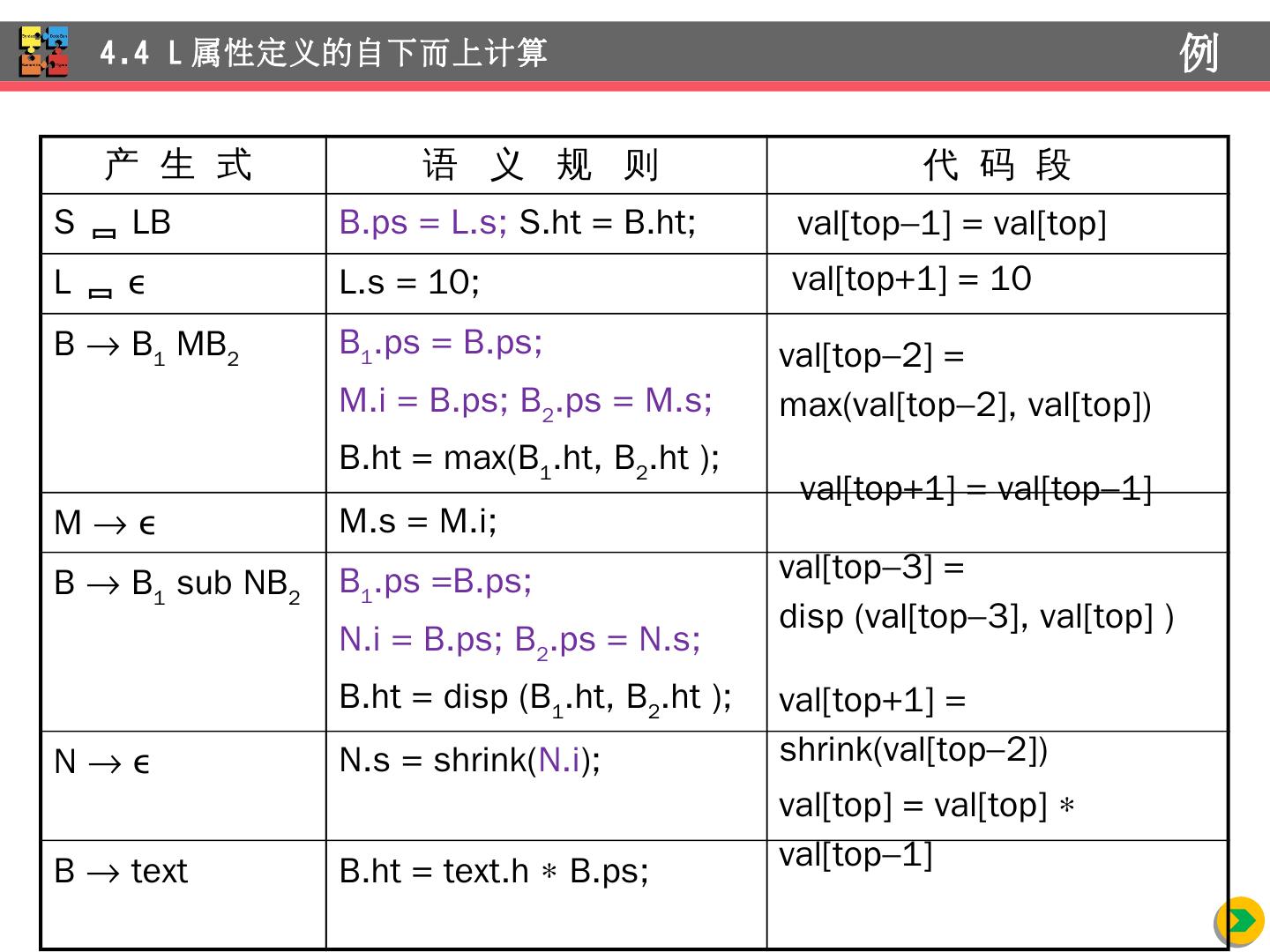
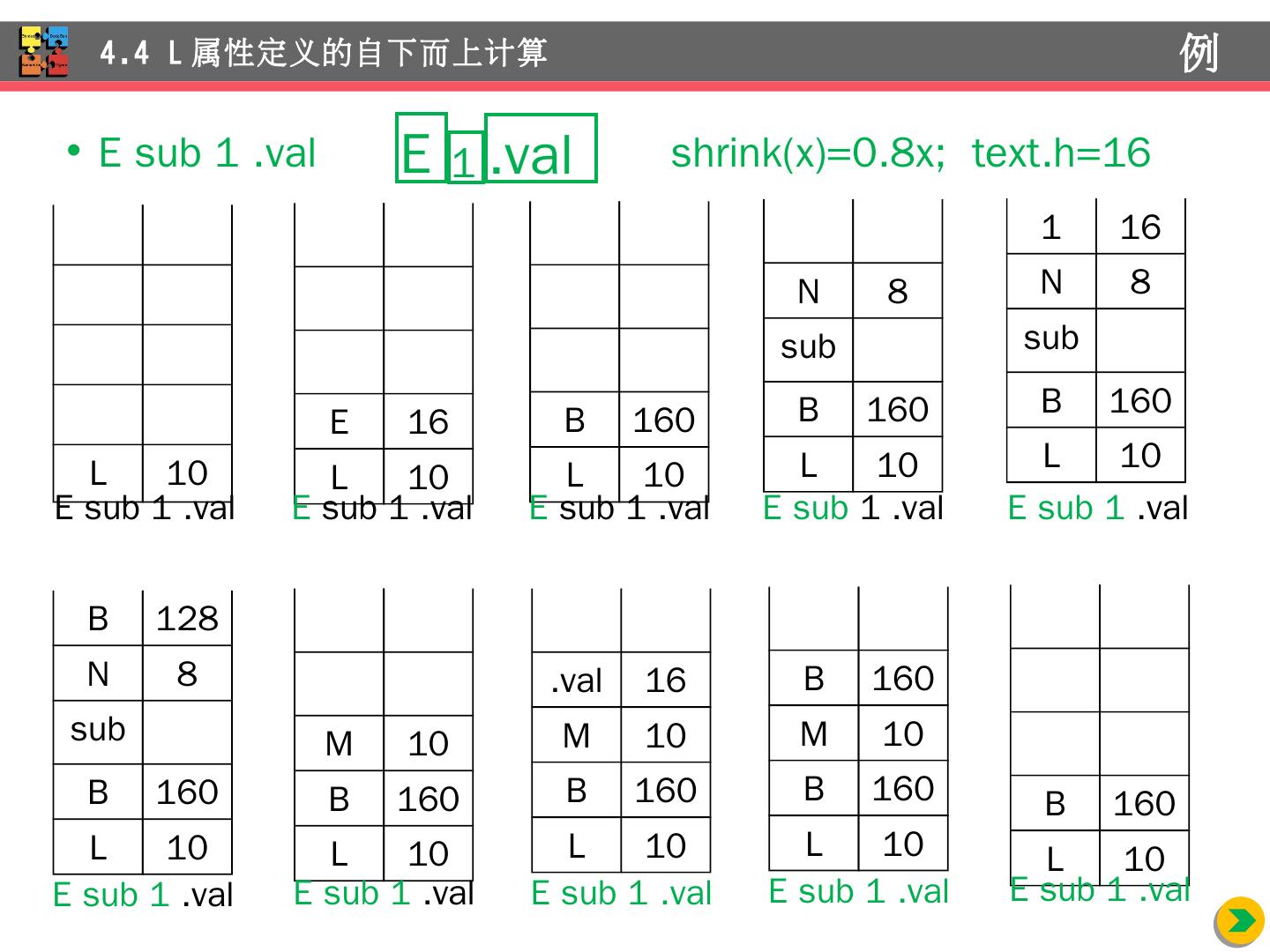
28 .例：数学 排版语言 EQN （语法 制导 定义） S  B B  B 1 B 2 B  B 1 sub B 2 B  text 4.3 L 属性 定义的自上而下计算 例 产 生 式 语 义 规 则 S  B B.ps = 10; S.ht = B.ht B  B 1 B 2 B 1 .ps = B.ps; B 2 .ps = B.ps; B.ht = max(B 1 .ht, B 2 .ht ) B  B 1 sub B 2 B 1 .ps =B.ps; B 2 .ps = shrink(B.ps); B.ht = disp (B 1 .ht, B 2 .ht ) B  text B.ht = text.h  B.ps E 1 . val E sub 1 . val

29 .例：数学 排版语言 EQN （翻译方案） S  {B.ps = 10 } //B 继承属性的计算位于 B 的左边 B {S.ht = B.ht } //S 综合 属性的计算放在右部末端 B  {B 1 .ps = B.ps } B 1 {B 2 .ps = B.ps } B 2 {B.ht = max(B 1 .ht, B 2 .ht ) } B  { B 1 .ps =B.ps } B 1 sub { B 2 .ps = shrink(B.ps) } B 2 {B.ht = disp (B 1 .ht, B 2 .ht ) } B  text {B.ht = text.h  B.ps } 4.3 L 属性 定义的自上而下计算 例