02 编译器原理与技术---词法分析

1 .第 2 章 词法分析 编译原理与技术

2 .词法分析器：把构成源程序的字符流翻译成记号流，还完成和用户接口的一些任务 围绕 词法分析器的自动生成展开 介绍正规式、状态转换图和有限自动机 概念 2 词法分析 内容提要     词法分析器 语法分析器 符号表 记号 (token) 取下一个记号 源程序

3 .2.1 词法记号及属性 第 2 章 词法分析

4 .2.1.1 词法记号、模式、词法单元 记号 名 词法单元例举 模式的非形式描述 if if 字符 i , f for for 字符 f, o, r relation < , <= , = , … < 或 <= 或 = 或 … id sum, count, D5 由 字母开头的字母数字串 number 3.1 , 10, 2.8E12 任何 数值常数 literal " seg . error" 引号 " 和 " 之间 任意不含 　 引号 本身的字符串 2.1 词法 记号及属性

5 .历史上词法定义中的一些问题 忽略空格带来的困难 DO 8 I = 3. 75 等同于 DO8I=3 . 75 DO 8 I = 3, 75 关键字 不保留 IF THEN THEN THEN=ELSE ； ELSE … 关键字 、保留字和标准标识符的区别 保留字是语言预先确定了含义的词法单元 标准标识符也是预先确定了含义的标识符，但程序可以重新声明它的 含义 2.1 词法 记号及属性

6 .2.1.2 词法记号的属性 position = initial + rate  60 的记号和属性值： < id ，指向符号表中 position 条目的 指针 > < assign_op > < id ，指向符号表中 initial 条目的 指针 > < add_op > < id ，指向符号表中 rate 条目的 指针 > < mul _ op > < number ，整数值 60> 2.1 词法 记号及属性

7 .2.1.3 词法 错误 词法分析器对源程序采取非常局部的观点 例：难以发现下面的错误 fi (a == f (x) ) … 在实数是“数字串 . 数字串”格式下，可以发现下面的错误 123.x 紧急方式的错误恢复 删 掉当前若干个字符，直至能读出正确的记号 错误修补 进行 增、删、替换和交换字符的尝试 2.1 词法 记号及属性

8 .下面 C 语言编译器编译下面的函数时，报告 parse error before else long gcd ( p,q ) long p,q ; { if ( p%q == 0) /  then part  / return q 此处遗漏分号 else /  else part  / return gcd (q, p%q ); } 2.1 词法 记号及属性 例题

9 .现在少了第一个注释的结束符号后，反而 不报 错 了 long gcd ( p,q ) long p,q ; { if ( p%q == 0) /  then part return q else /  else part  / return gcd (q, p%q ); } 2.1 词法 记号及属性 例题

10 .2.2 词法 记号的描述与识别 第 2 章 词法分析

11 .2.2.1 串和 语言 字母表 ： 符号 的有限集合， 例 ： Σ = { 0, 1} 串 ： 符号 的有穷序列，例： 0110, ε 语言 ： 字母表 上的一个串集 { ε , 0, 00, 000, …}, { ε }, Ø 句子 ： 属于语言的串 串 的运算 连接（积） xy ， s ε = ε s = s 幂 s 0 为 ε ， s i 为 s i-1 s （ i > 0 ） 2.2 词法 记号的描述与识别

12 .语言的运算 并： L ∪ M = {s | s ∈ L 或 s ∈ M } 连接： LM = { st | s ∈ L 且 t ∈ M} 幂： L 0 是 { ε } ， L i 是 L i-1 L 闭包： L  = L 0 ∪ L 1 ∪ L 2 ∪ … 正闭包 ： L + = L 1 ∪ L 2 ∪ … 例 L: { A, B, …, Z, a, b, …, z }, D: { 0, 1, …, 9 } L ∪ D, LD, L 6 , L  , L(L ∪ D )  , D + 2.2 词法 记号的描述与识别

13 .2.2.2 正规式 正规式用来表示简单的语言， 叫做 正规语言 或 正规 集 正规 式 定义的 语言 备注 ε { ε } a { a} a ∈ Σ (r) | (s) L(r )∪L(s) r 和 s 是正规式 (r)(s) L(r)L(s ) r 和 s 是正规式 (r )  ( L(r ))  r 是正规式 (r) L(r ) r 是正规式 ((a) (b )  )| (c) 可以写成 ab  | c 2.2 词法 记号的描述与识别

14 .正规式 的例子 Σ = {a, b} a | b { a, b} (a | b) (a | b ) { aa, ab, ba , bb} aa | ab | ba | bb {aa, ab, ba , bb} a  由 字母 a 构成的所有串集 (a | b )  由 a 和 b 构成的所有串集 复杂 的例子 ( 00 | 11 | ( (01 | 10) (00 | 11)  (01 | 10) ) )  句子： 01001101 00 00 10000010 11 1001 描述： 0 和 1 的个数都是偶数的 01 串 2.2 词法 记号的描述与识别 例题

15 .2.2.3 正规 定义 对 正规式命名，使表示简洁 d 1  r 1 d 2  r 2 . . . d n  r n 　各个 d i 的 名字都不同 　每个 r i 都是 Σ ∪ { d 1 , d 2 , …, d i-1 } 上的正规式 2.2 词法 记号的描述与识别

16 .正规定义的例子 C 语言的标识符是字母、数字和下划线组成的串 letter_  A | B | … | Z | a | b | … | z | _ digit  0 | 1 | … | 9 id  letter_(letter_ |digit )  2.2 词法 记号的描述与识别

17 .正规定义的例子 无 符号数集合，例 1946,11.28,63E8,1.99E-6 digit  0 | 1 | … | 9 digits  digit digit  optional_fraction  . digits| ε optional_exponent  ( E ( + | - | ε ) digits ) | ε number  digits optional_fraction optional_exponent 简化 表示 number  digit + (.digit + )? (E (+|-)? digit + )? 2.2 词法 记号的描述与识别

18 .正规定义的例子（进行下一步讨论的例子） while  while do  do relop  < | < = | = | < > | > | > = letter  A | B | … | Z | a | b | … | z id  letter (letter | digit )  number  digit + (.digit + )? (E (+|-)? digit + )? delim  blank | tab | newline ws  delim + 2.2 词法 记号的描述与识别

19 .写出语言“所有相邻数字都不相同的非空数字串”的正规定义 123 0 313571 0 6798 0 3579 0 123 answer  (0 | no_0 0 ) (no_0 0 )  (no_0 | ε ) | no_0 answer  (0 | ε ) (no_0 0 )  (no_0 | ε ) | no_0 上式包含空串，不符合定义 no_0  (1 | no_0-1 1 ) (no_0-1 1 )  (no_0-1 | ε ) | no_0-1 . . . no_0-8  9 将这些正规定义逆序排列就是答案 2.2 词法 记号的描述与识别 例题

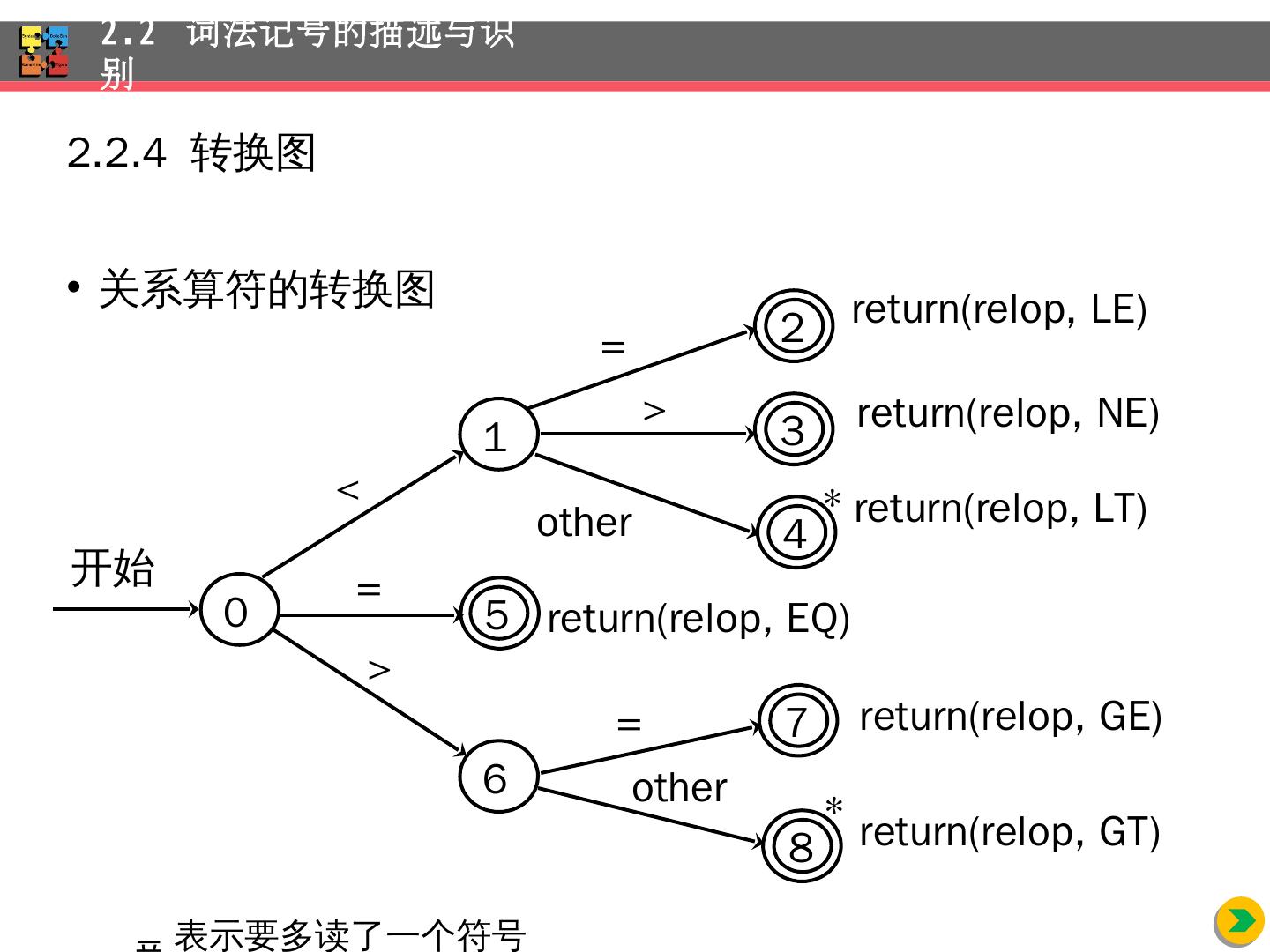
20 .2.2.4 转换图 关系 算符的转换图  表示要多读了一个符号 2.2 词法 记号的描述与识别   0 5 1 6 2 4 8 3 7 return(relop, LE) return( relop , NE) return(relop, LT) return(relop, GE) return(relop, GT) return(relop, EQ) 开始 < = > = > =   other other

21 .标识符 和关键字的转换图 id  letter (letter | digit )  2.2 词法 记号的描述与识别 9 10 11 开始 letter other  letter 或 digit return( installId ( ))

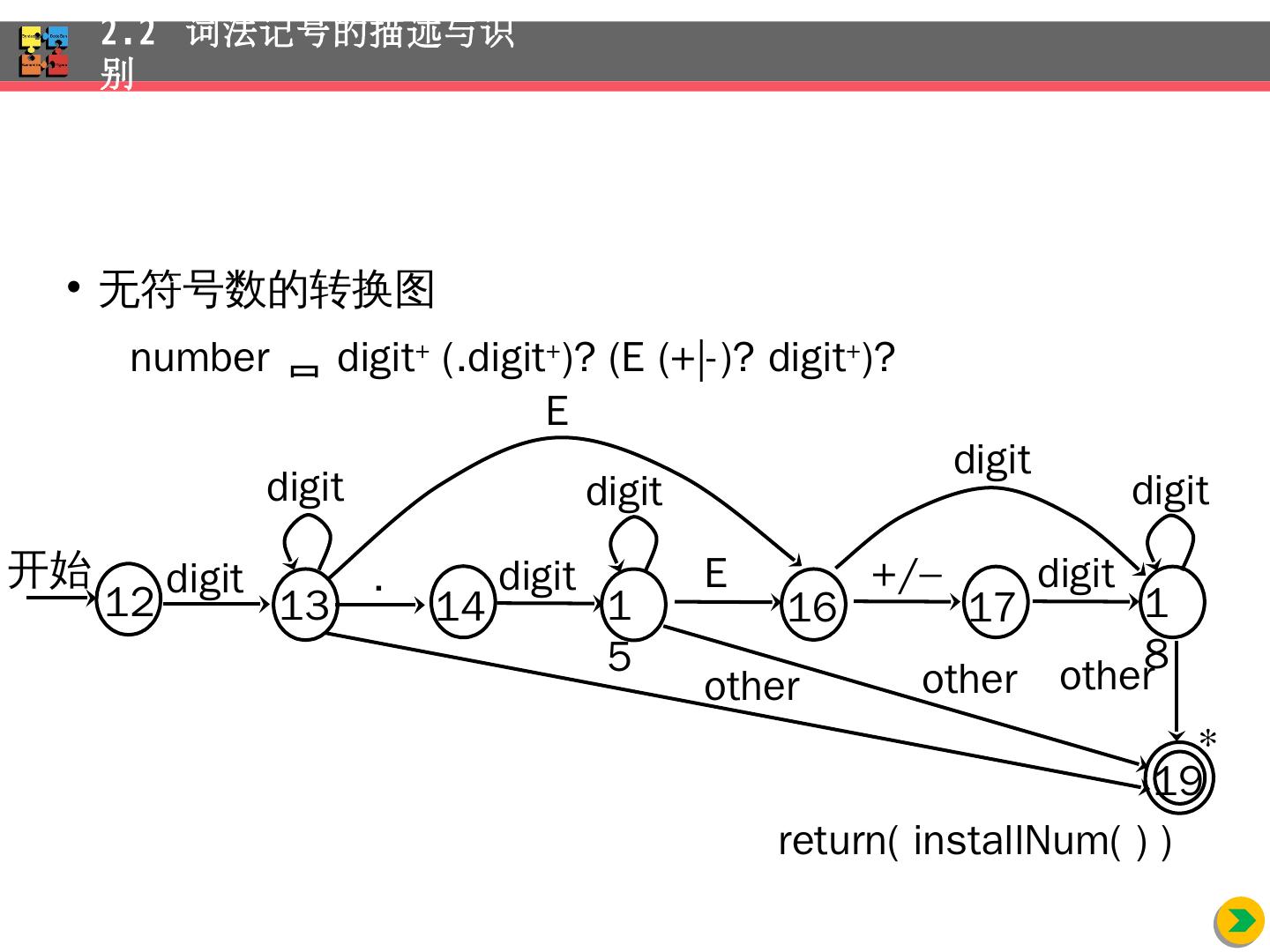
22 .无 符号数的转换图 number  digit + (.digit + )? (E (+|-)? digit + )? 2.2 词法记号的描述与识别 开始 19 digit digit digit digit digit digit other . E +/  E digit other other return( installNum ( ) )  12 13 14 15 16 17 18

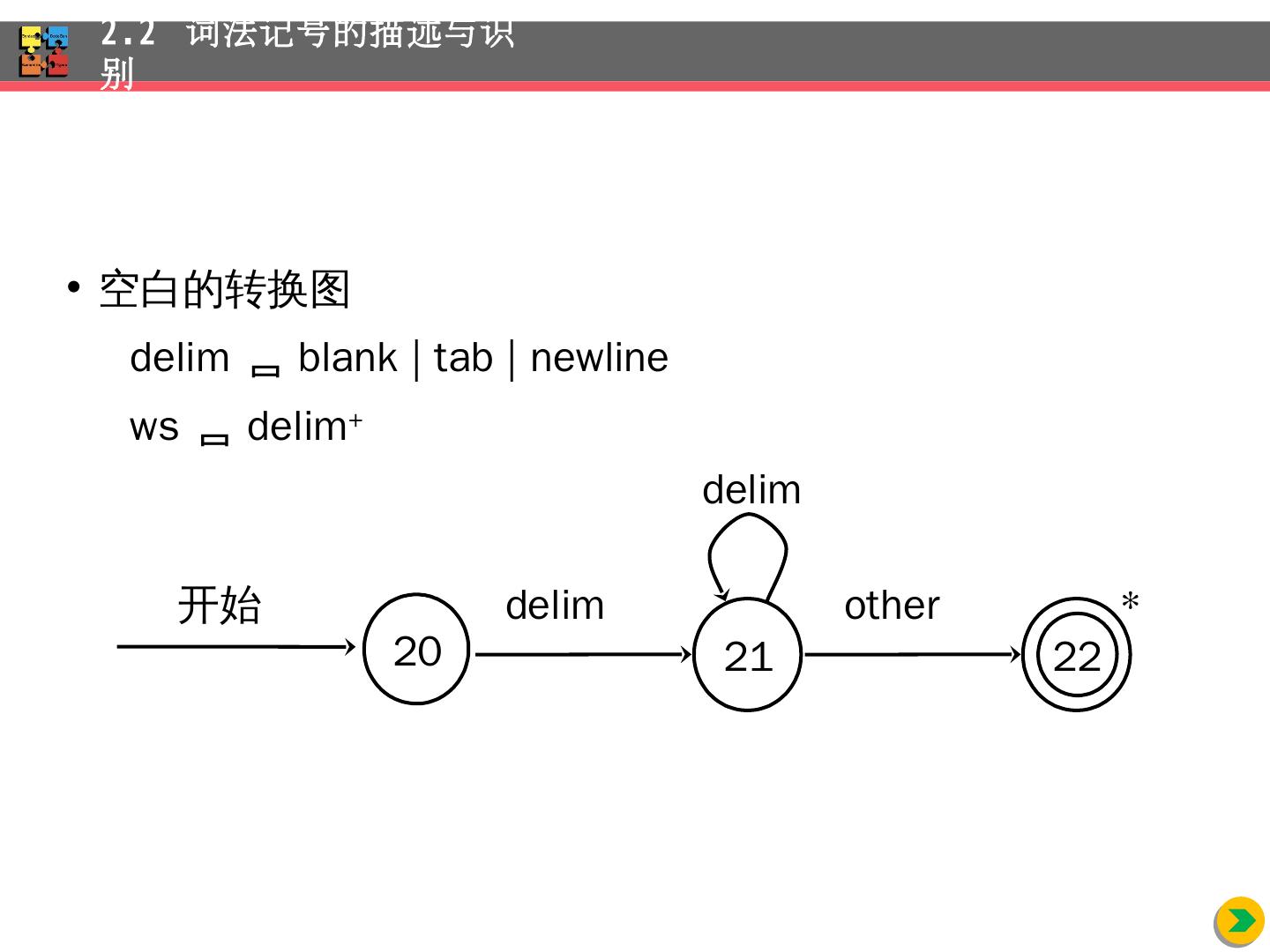
23 .空白的转换图 delim  blank | tab | newline ws  delim + 2.2 词法记号的描述与识别 21 22 开始 delim other  delim 20

24 .2.3 有限自动机 第 2 章 词法分析

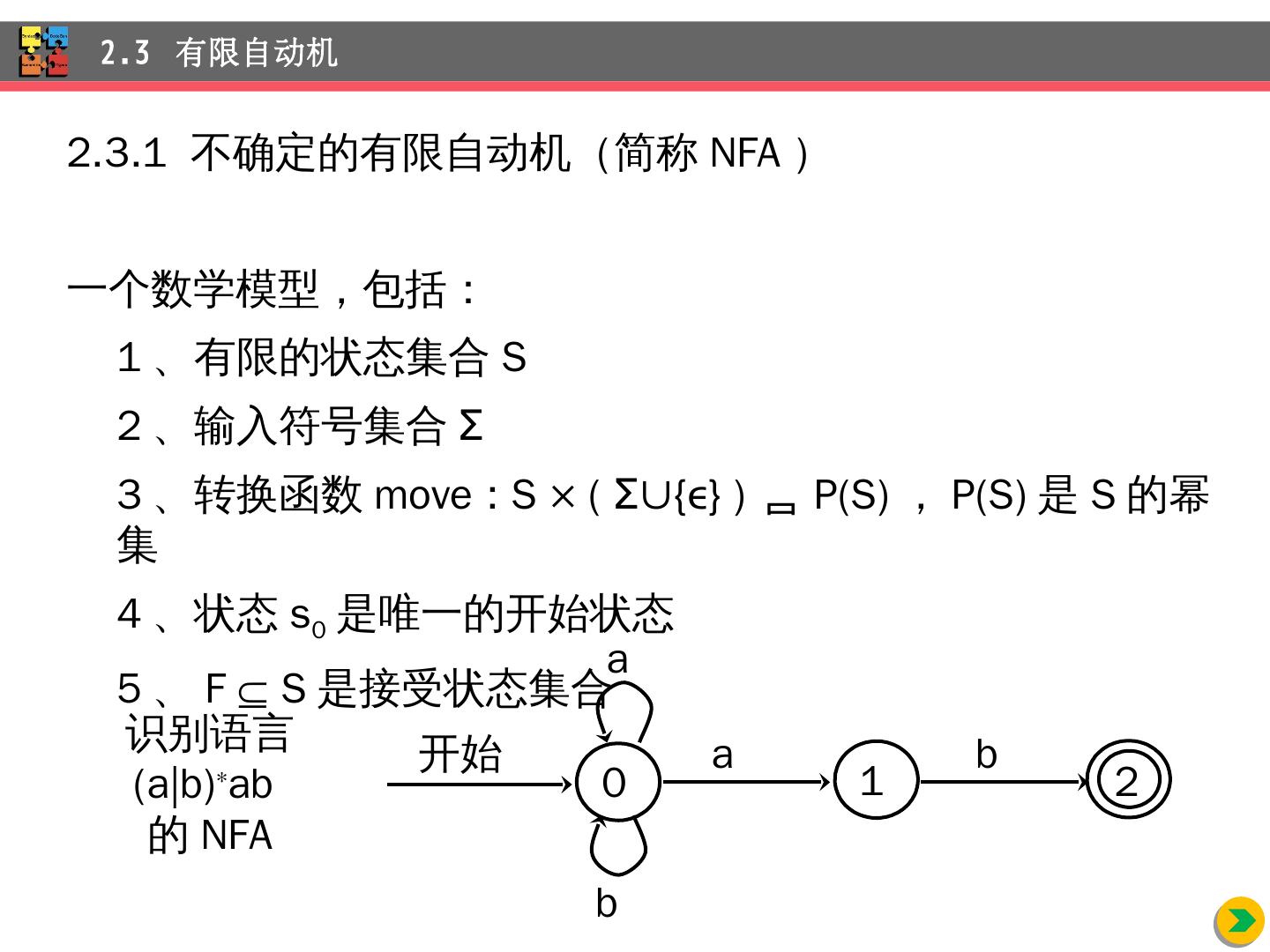
25 .2.3.1 不确定的有限自动机（简称 NFA ） 一 个数学模型 ，包括 ： 1 、有限的状态集合 S 2 、输入符号 集合 Σ 3 、转换函数 move : S × ( Σ ∪{ ε } )  P(S ) ， P(S) 是 S 的幂集 4 、状态 s 0 是唯一的开始状态 5 、 F  S 是接受状态集合 2.3 有限自动机 识别语言 ( a|b )  ab 的 NFA 1 2 开始 a 0 a b b

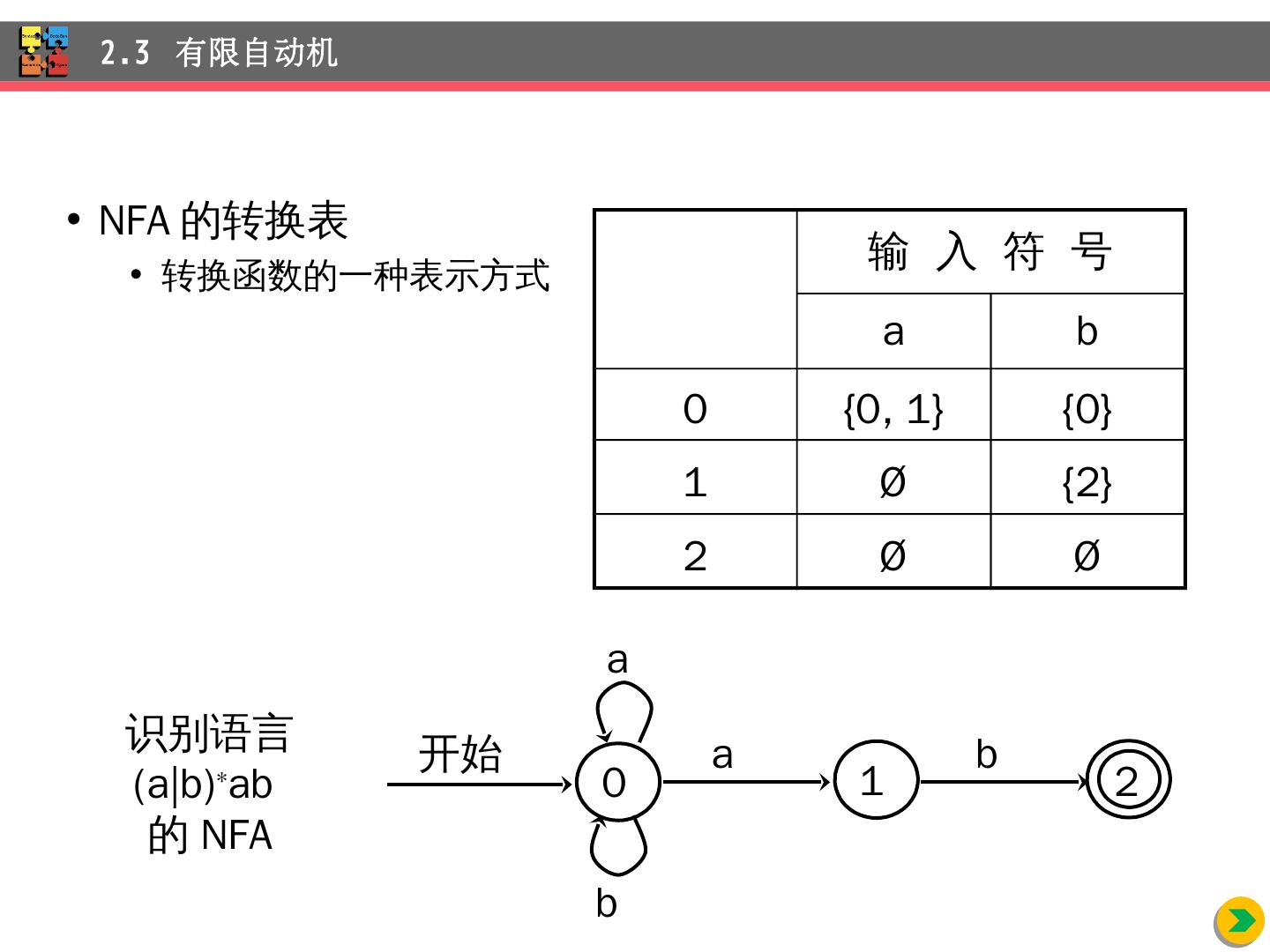
26 .NFA 的转换 表 转换 函数的一种表示方式 2.3 有限自动机 识别语言 ( a|b )  ab 的 NFA 1 2 开始 a 0 a b b 输 入 符 号 a b 0 {0, 1} {0} 1 Ø {2} 2 Ø Ø

27 .识别 aa  |bb  的 NFA 2.3 有限自动机 例题 1 2 开始 a 0 a b b 3 4  

28 .2.3.2 确定的有限自动机（简称 DFA ) 一 个 数学模型， 包括 ： 1 、有限的状态集合 S 2 、输入字母 集合 Σ 3 、转换函数 move : S × Σ  S ，且 可以是部分函数 4 、状态 s 0 是唯一的开始状态 5 、 F  S 是接受状态集合 2.3 有限自动机 识别语言 ( a|b )  ab 的 DFA 1 2 开始 a 0 a b b a b

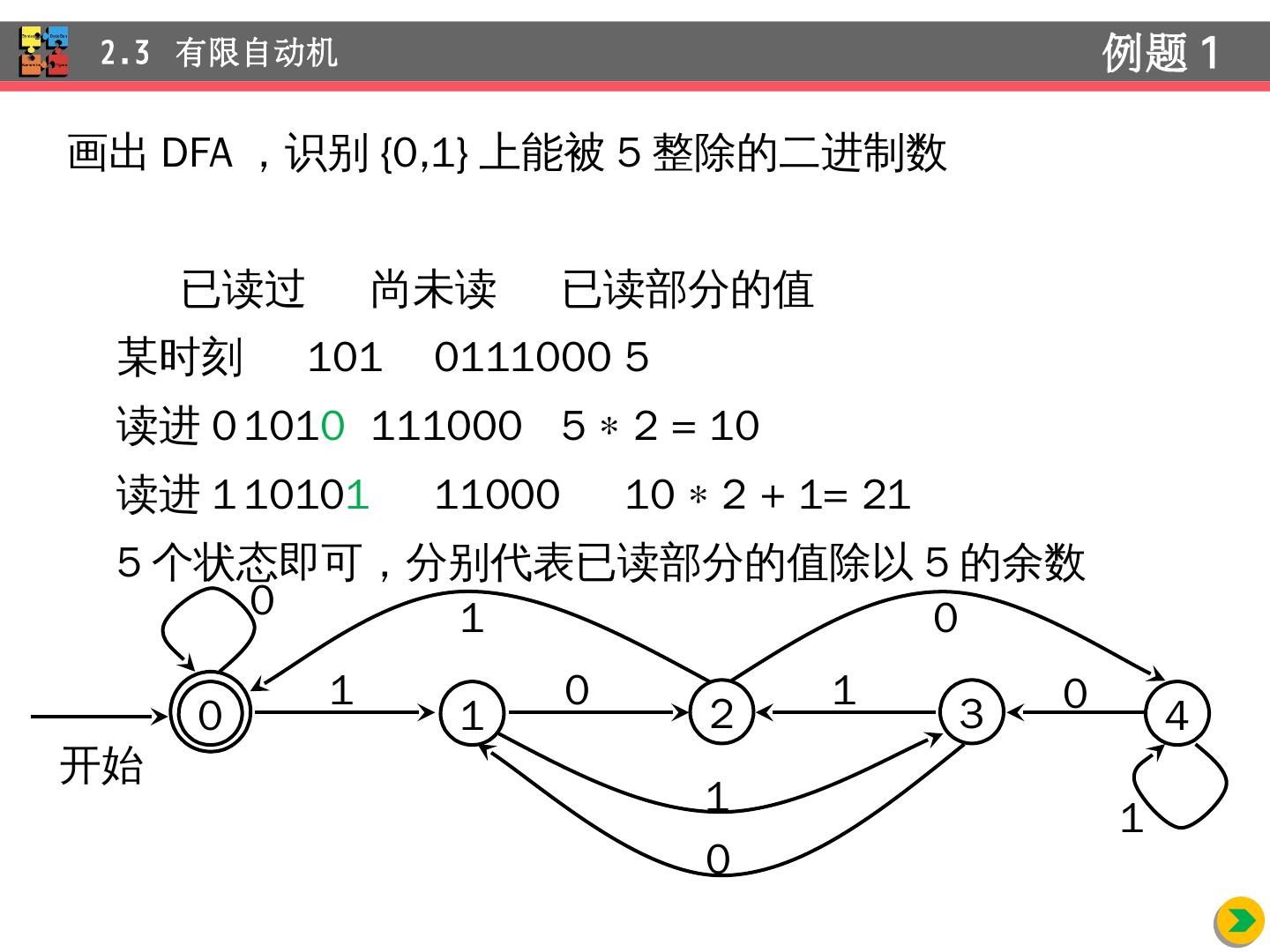
29 .画出 DFA ，识别 {0,1} 上能被 5 整除的二进制数 已读过 尚未读 已读部分的值 某 时刻 101 0111000 5 读 进 0 101 0 111000 5  2 = 10 读 进 1 1010 1 11000 10  2 + 1= 21 5 个状态即可，分别代表已读部分的值除以 5 的余数 2.3 有限自动机 例题 1 0 1 2 3 开始 4 1 0 0 1 0 1 0 1 0 1