09 编译原理---机器无关的优化

1 .第九章 机器无关的优化 许畅 南京大学计算机系 2018年春季 

2 .主要内容  引言  优化的来源  数据流分析  部分冗余消除  循环的识别、分析和优化 2 

3 .引言  代码优化或者代码改进  在目标代码中消除不必要的指令  把一个指令序列替换为一个完成相同功能的更快的指 令序列  全局优化  具体的优化实现基于数据流分析技术  用以收集程序相关信息的算法 3 

4 .优化的主要来源  编译器只能通过一些相对低层的语义等价转换来 优化代码  冗余运算的原因  源程序中的冗余  高级程序设计语言编程的副产品，比如"A[i][j].f = 0; A[i][j].k = 1;"中的冗余运算  语义不变的优化  公共子表达式消除  复制传播  死代码消除  常量折叠 4 

5 .优化的例子 (1)  快速排序算法 5 

6 .优化的例子 (2)  三地址代码 6 

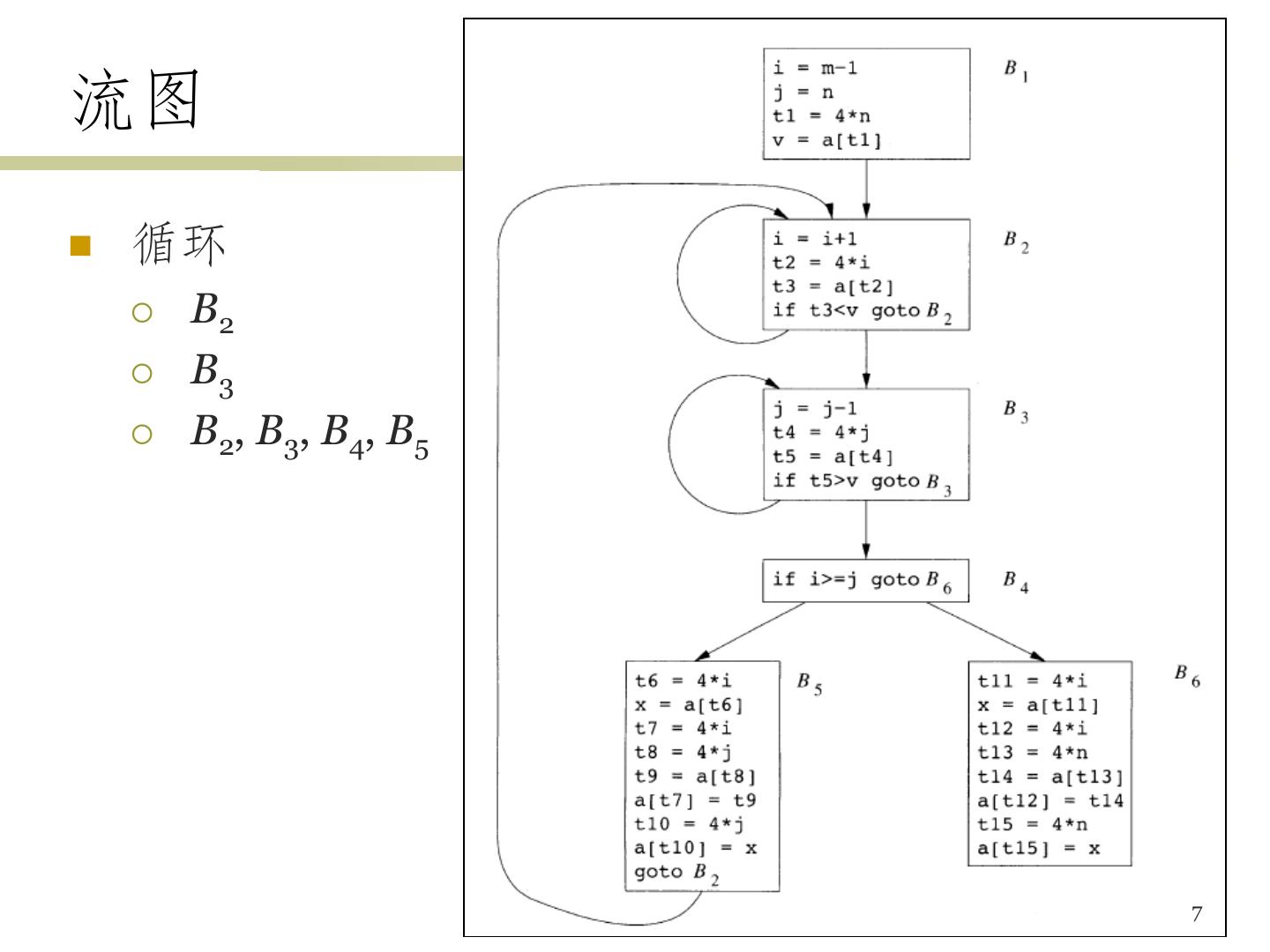
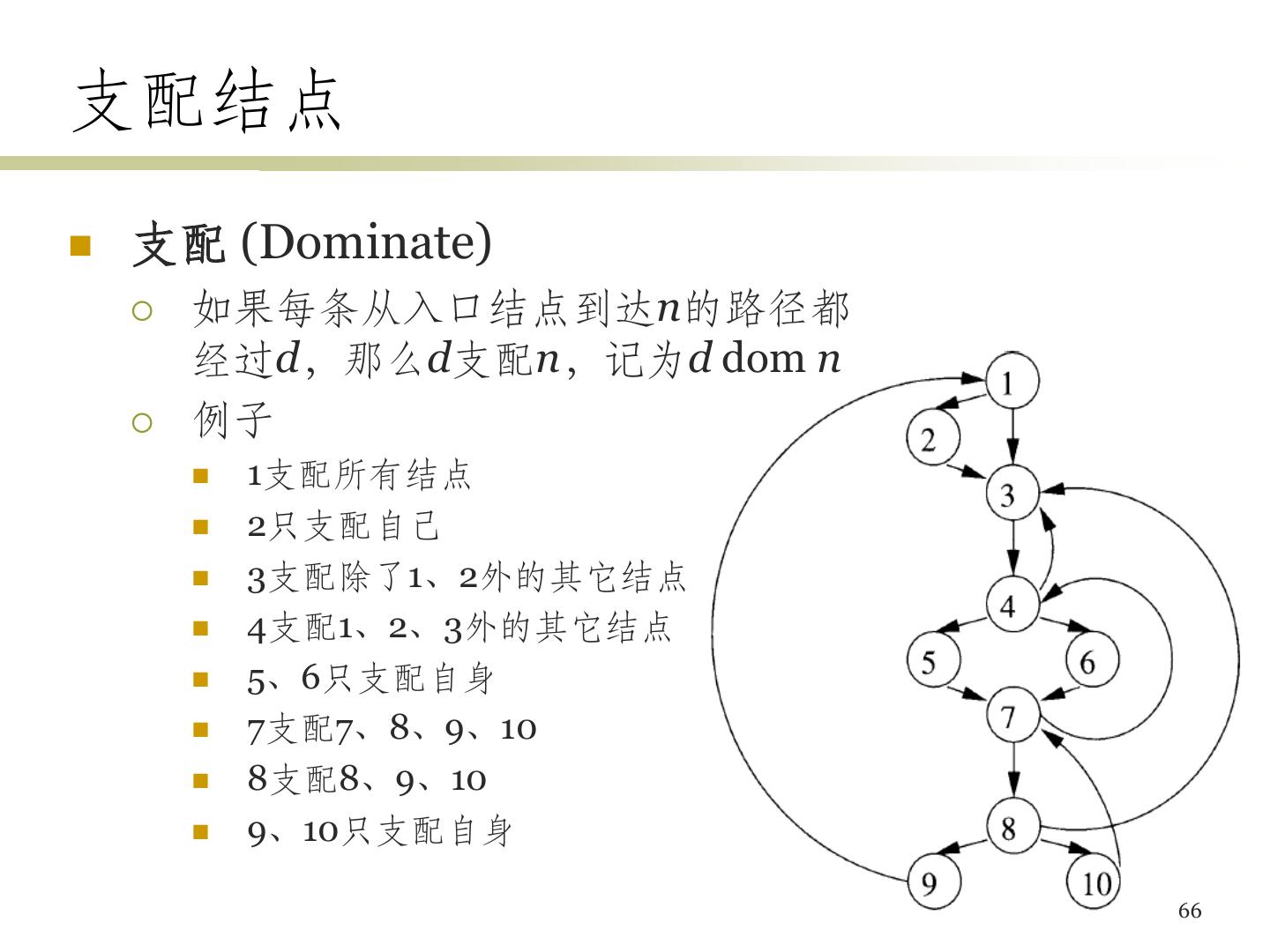
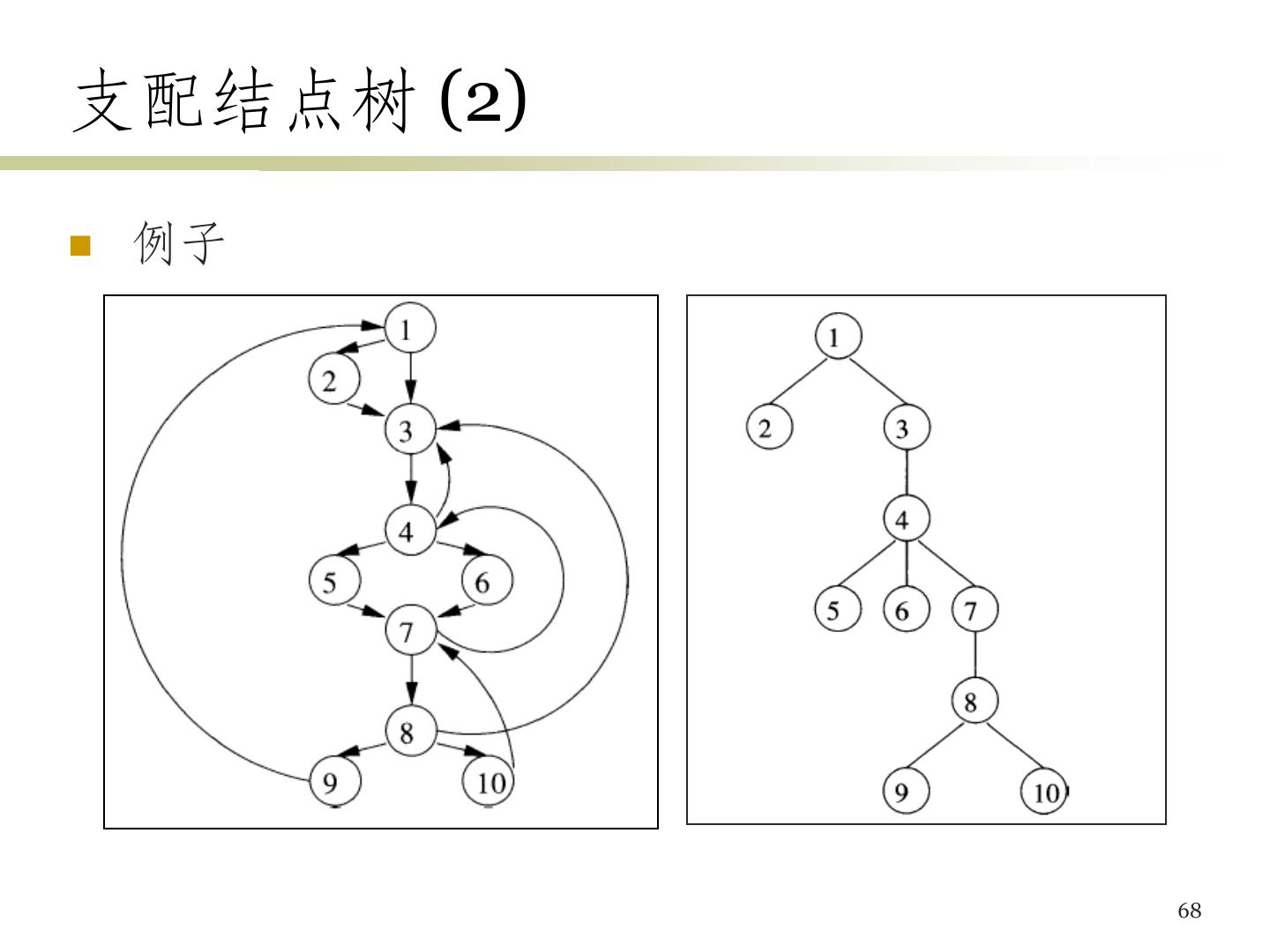
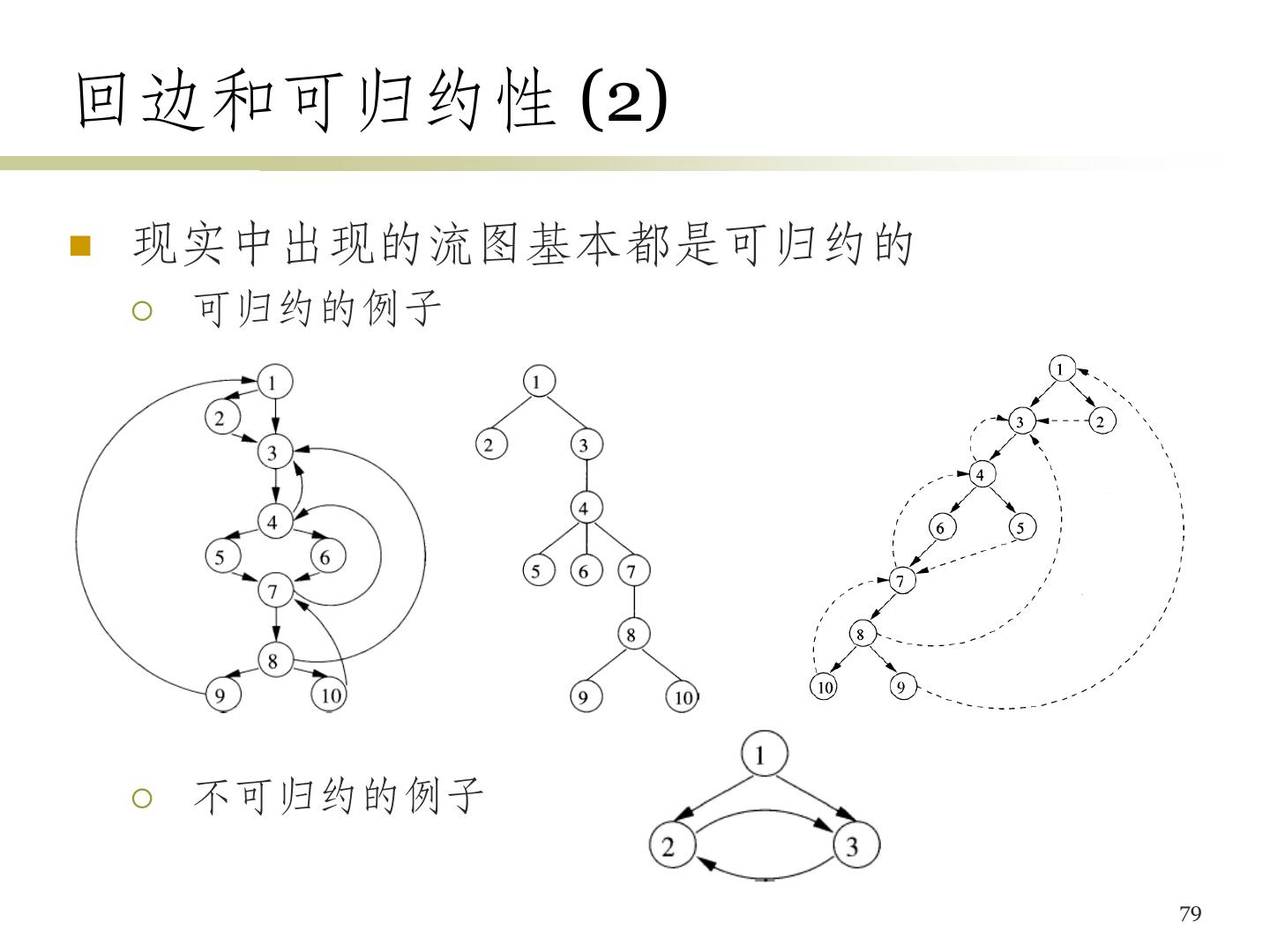
7 .流图  循环  B2  B3  B2, B3, B4, B5 7 

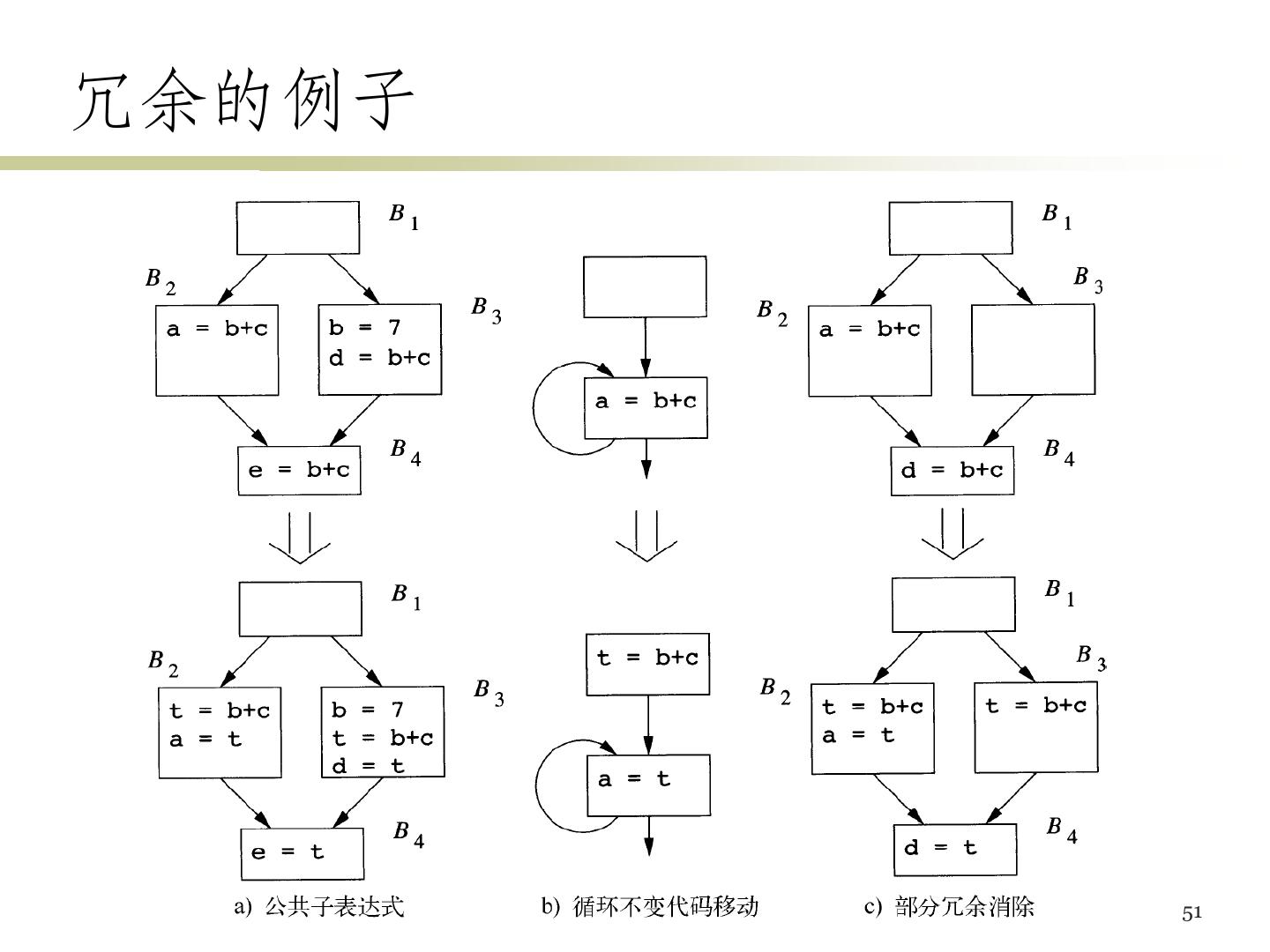
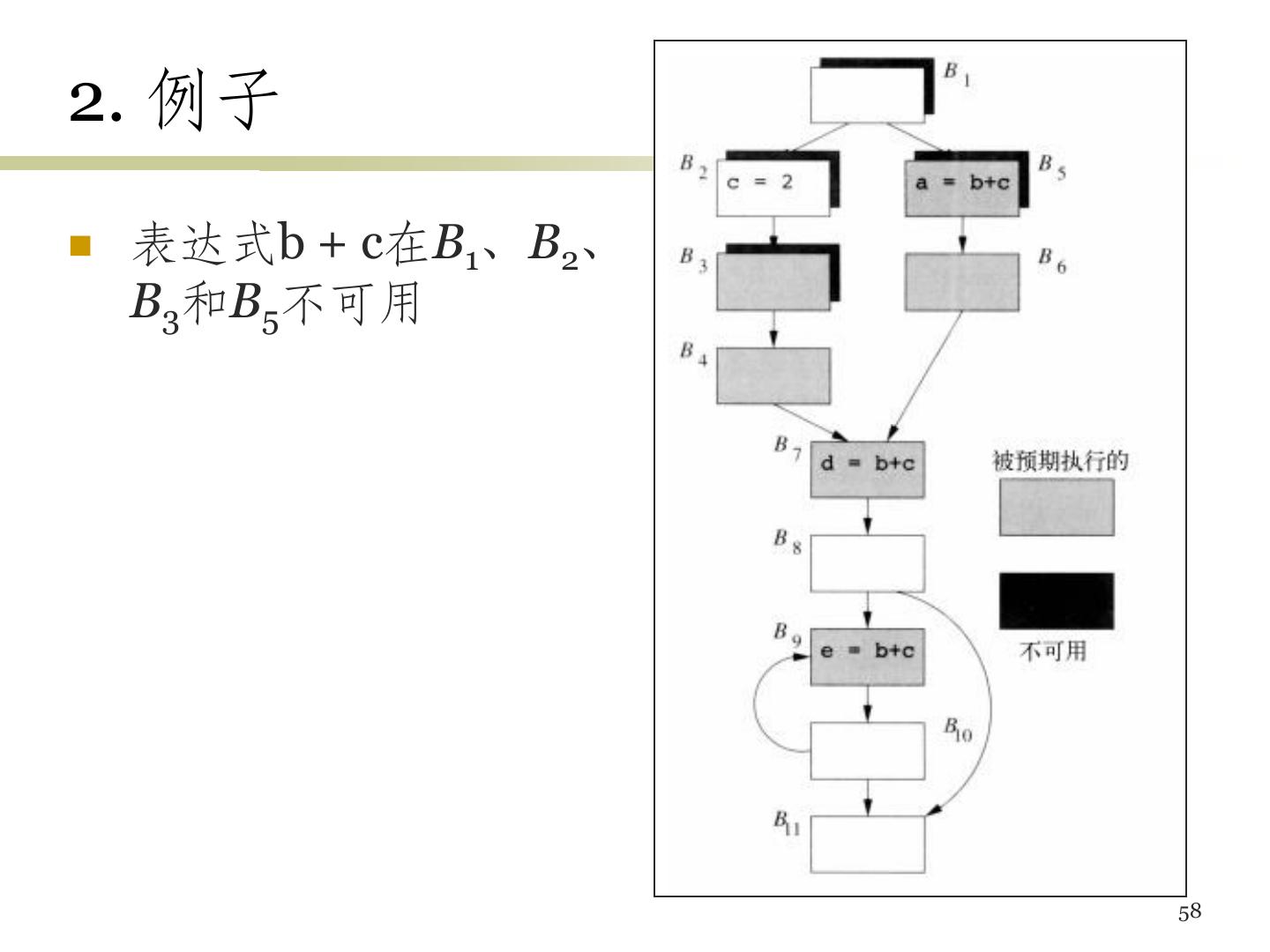
8 .全局公共子表达式  如果E  在某次出现之前必然已被计 算过，且  E的运算分量在该次计算之 后没有被改变  那么，E的本次出现就是一 个公共子表达式 t7 => t6 t10 => t8  如果上一次E的值赋给了x， 且x的值没有被修改过，那 例子： 么我们可以使用x，而不需 t7 = 4 * i 要计算E t10 = 4 * j 不需要重新计算 8 

9 .例子 • B2、B3中计算了4 * i和 4 * j，且到达B5之前必 然经过B2、B3 • t2、t4在赋值后没有被 改变过，因此B5中可直 接使用它们 • B5中赋给x的值 (a[t6]) 和B2中赋给t3的值 (a[t2]) 相同 • t4替换t8后，B5中a[t8] 和B3中a[t4]又相同 t6, t7 => t2 • B6中的a[t13]和B1中的 a[t1]不同，因为B5可能 t8, t10 改变a的值 => t4 9 

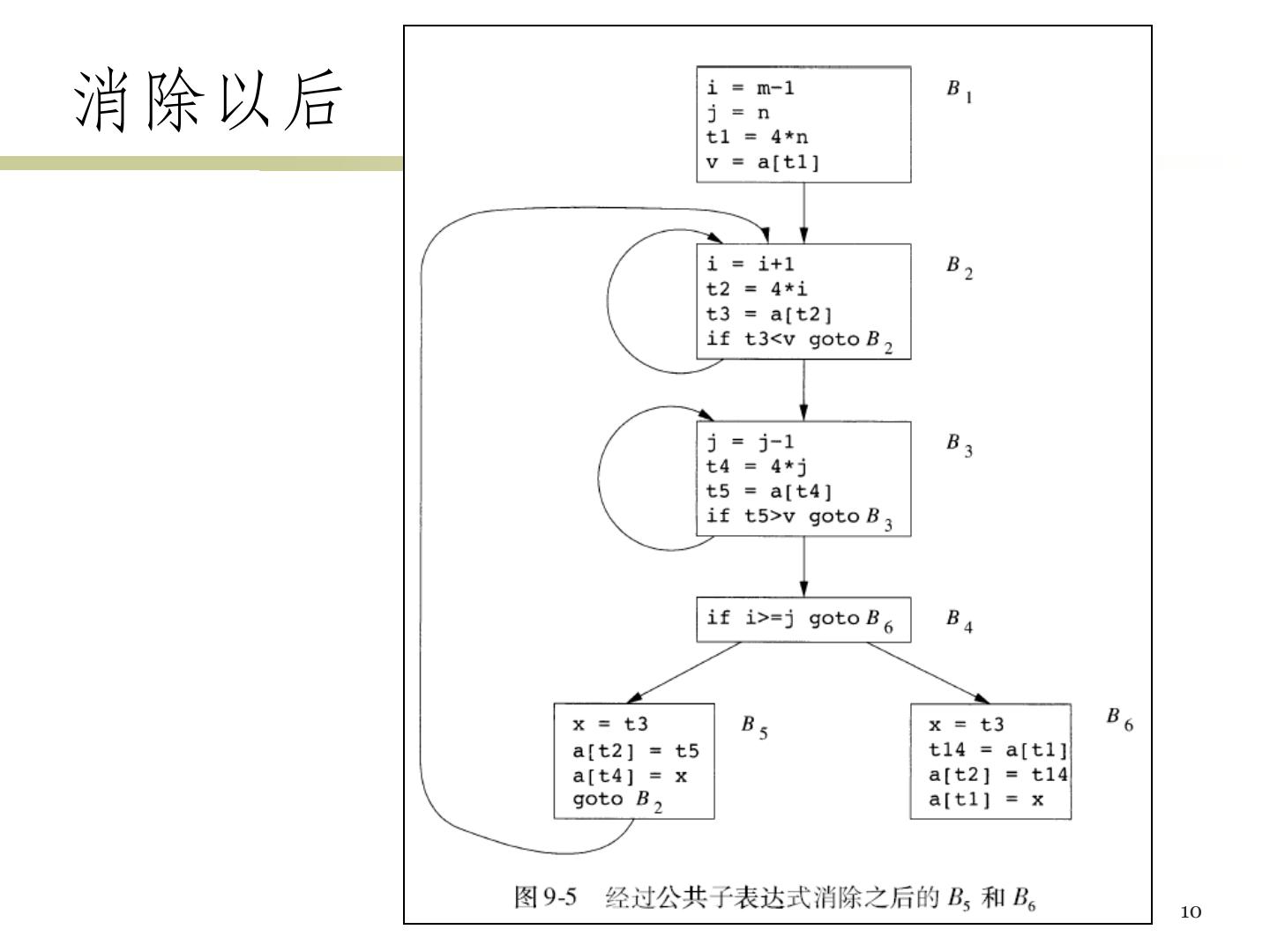
10 .消除以后 10 

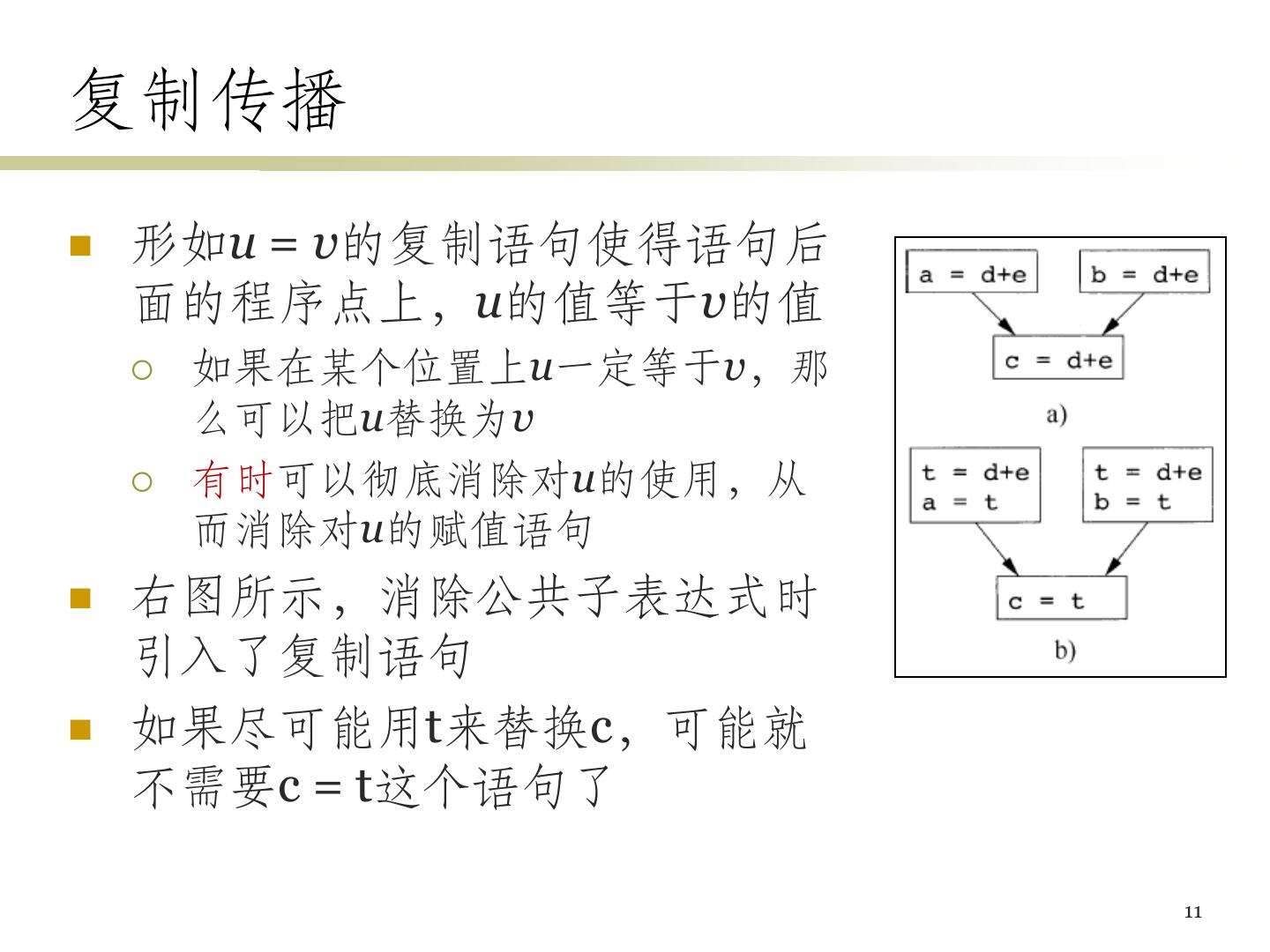
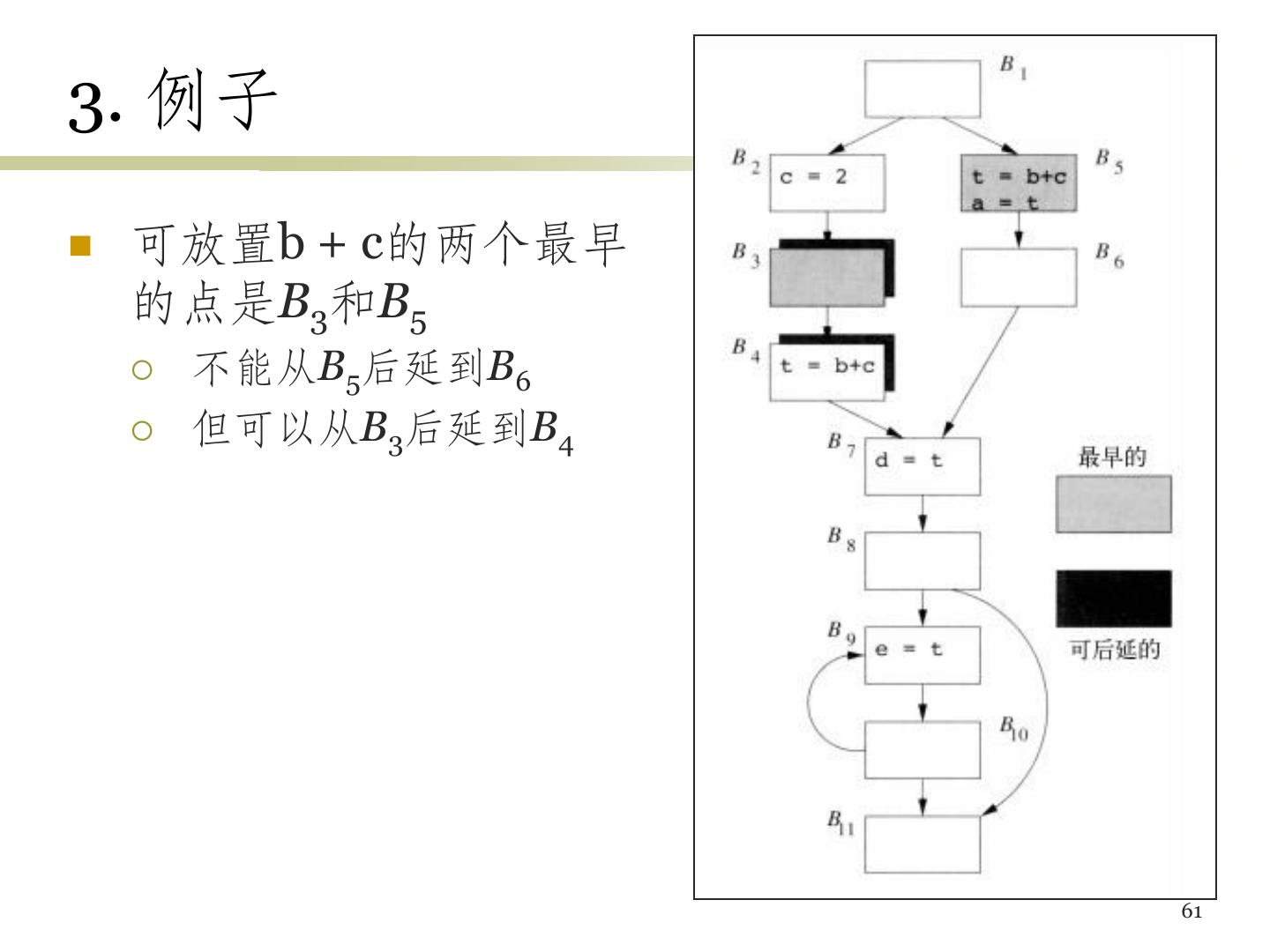
11 .复制传播  形如u = v的复制语句使得语句后 面的程序点上，u的值等于v的值  如果在某个位置上u一定等于v，那 么可以把u替换为v  有时可以彻底消除对u的使用，从 而消除对u的赋值语句  右图所示，消除公共子表达式时 引入了复制语句  如果尽可能用t来替换c，可能就 不需要c = t这个语句了 11 

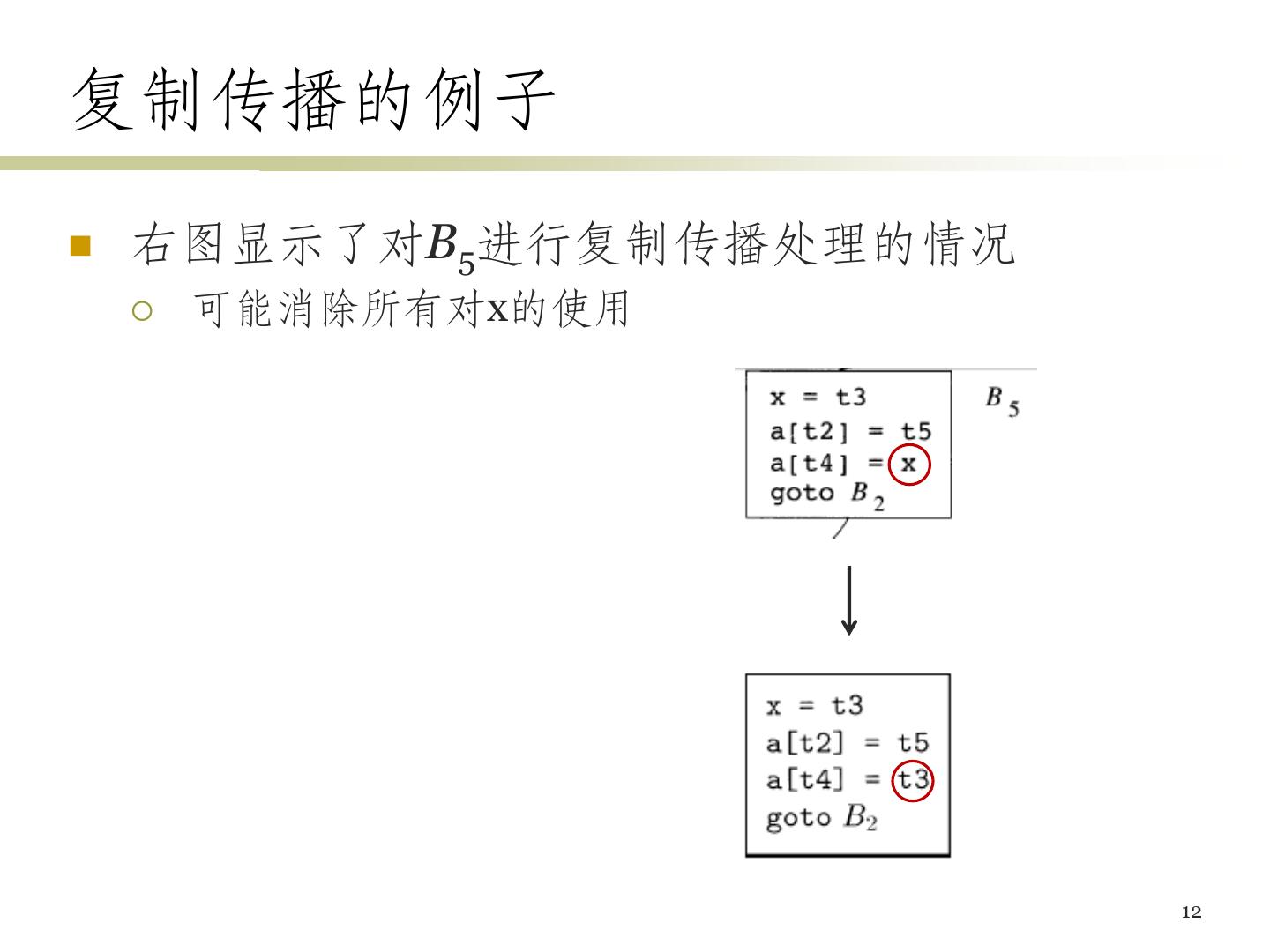
12 .复制传播的例子  右图显示了对B5进行复制传播处理的情况  可能消除所有对x的使用 12 

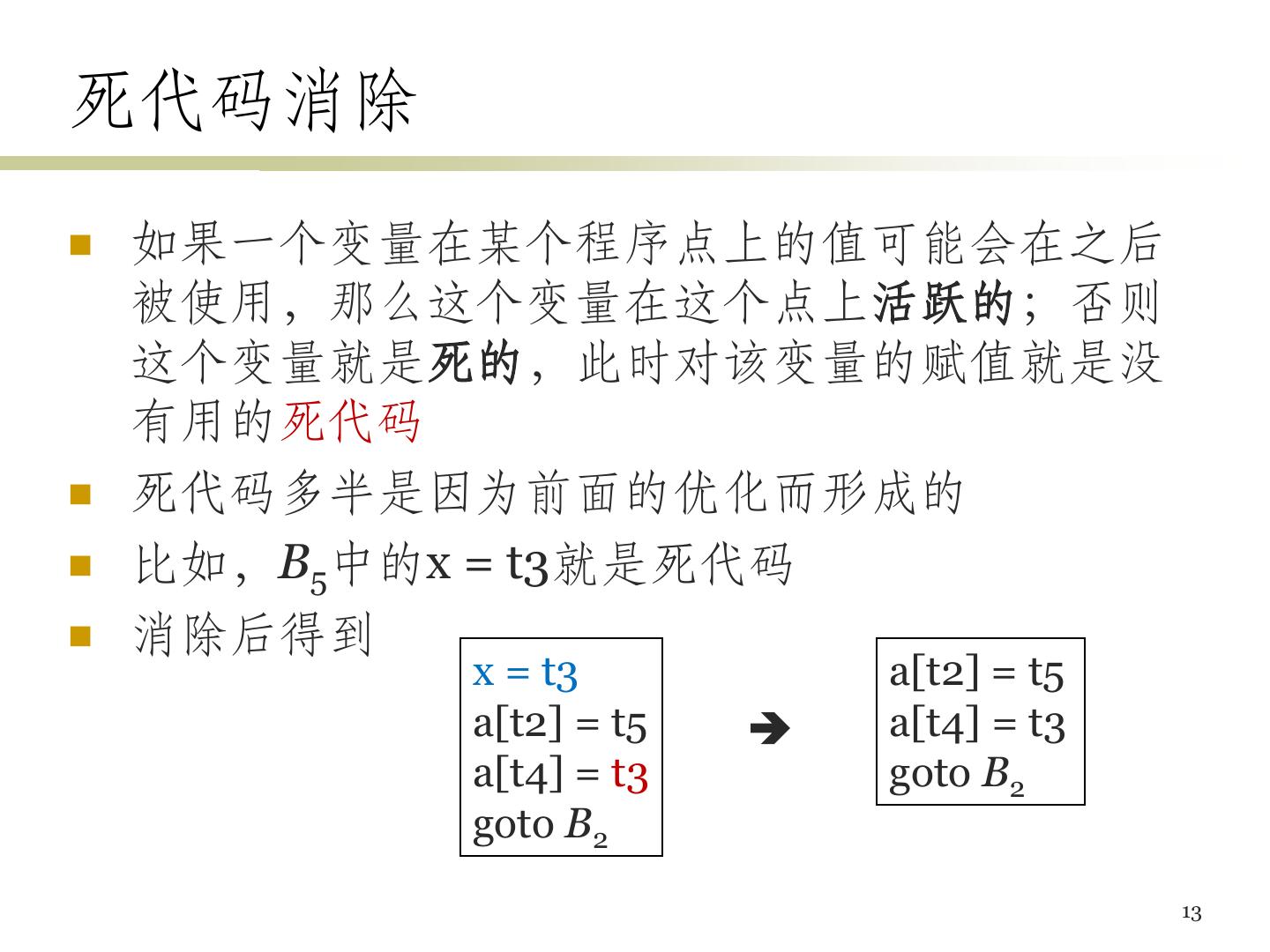
13 .死代码消除  如果一个变量在某个程序点上的值可能会在之后 被使用，那么这个变量在这个点上活跃的；否则 这个变量就是死的，此时对该变量的赋值就是没 有用的死代码  死代码多半是因为前面的优化而形成的  比如，B5中的x = t3就是死代码  消除后得到 x = t3 a[t2] = t5 a[t2] = t5  a[t4] = t3 a[t4] = t3 goto B2 goto B2 13 

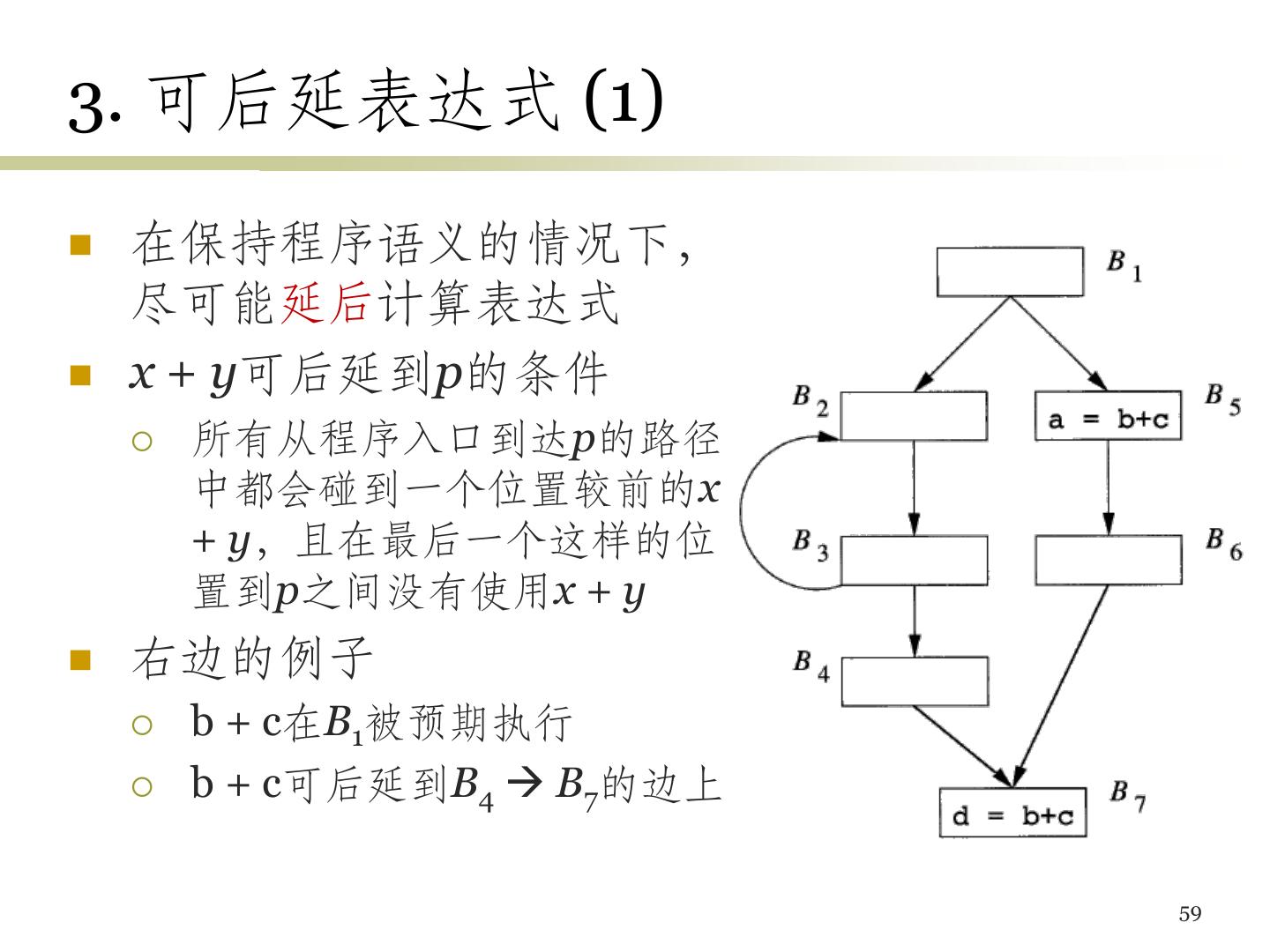
14 .代码移动  循环中的代码会被执行很多次  循环不变表达式：循环的同一次运行的不同迭代中， 表达式的值不变  把循环不变表达式移动到循环入口之前计算可以 提高效率  循环入口：进入循环的跳转都以这个入口为目标  while (i <= limit – 2) …  如果循环体不改变limit的值，可在循环外计算limit – 2 t = limit – 2 while (i <= t) … 14 

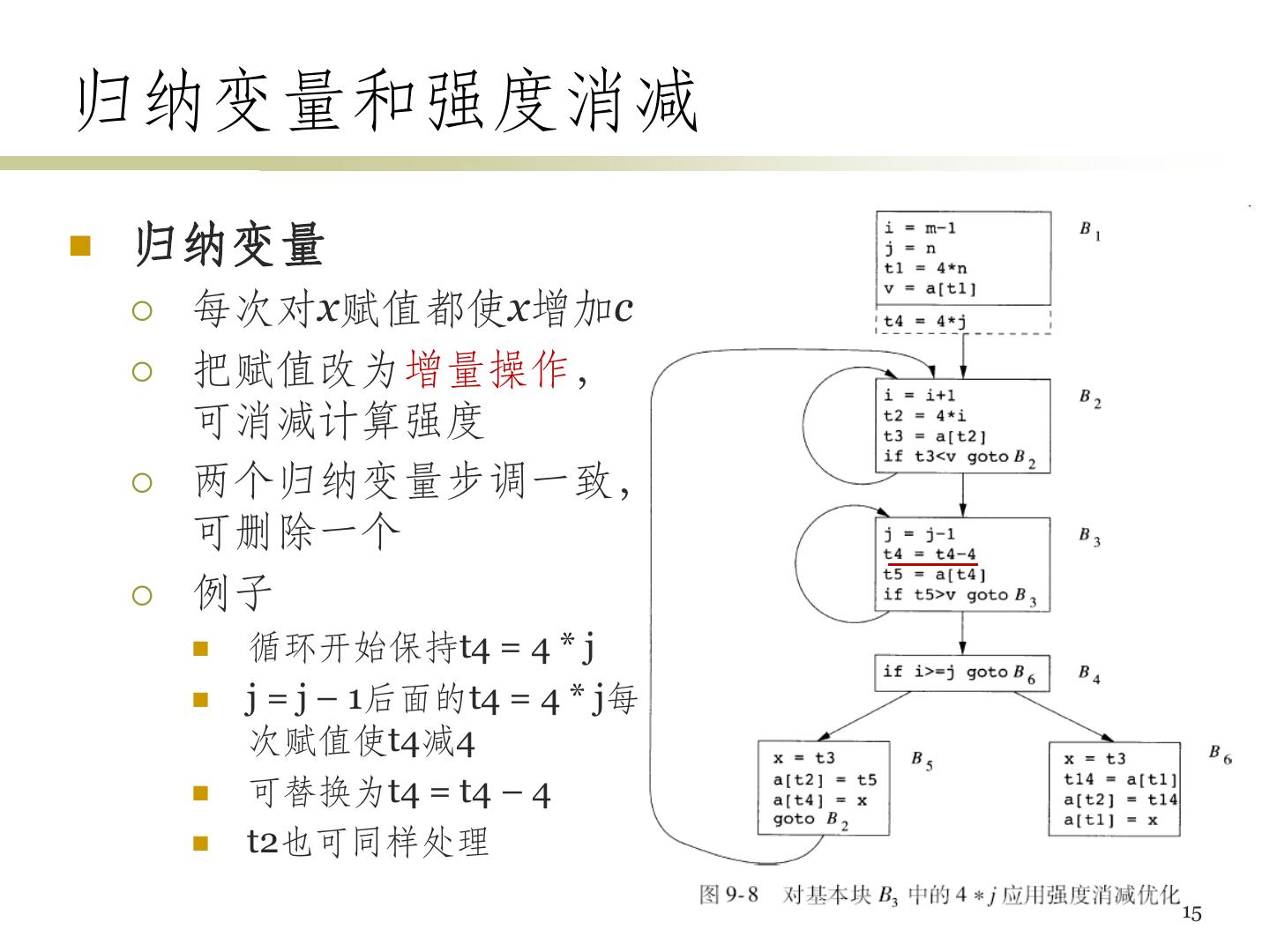
15 .归纳变量和强度消减  归纳变量  每次对x赋值都使x增加c  把赋值改为增量操作， 可消减计算强度  两个归纳变量步调一致， 可删除一个  例子  循环开始保持t4 = 4 * j  j = j – 1后面的t4 = 4 * j每 次赋值使t4减4  可替换为t4 = t4 – 4  t2也可同样处理 15 

16 .数据流分析  数据流分析  用于获取数据沿着程序执行路径流动信息的相关技术  是优化的基础  例如  两个表达式是否一定计算得到相同的值？(公共子表达 式)  一个语句的计算结果是否可能被后续语句使用？(死代 码消除) 16 

17 .数据流抽象 (1)  程序点  三地址语句之前或之后的位置  基本块内部：一个语句之后的程序点等于下一个语句 之前的程序点  如果流图中有B1到B2的边，那么B2的第一个语句之前 的点可能紧跟在B1的最后语句之后的点后面执行  从p1到pn的执行路径：p1, p2, …, pn  要么pi是一个语句之前的点，且pi+1是该语句之后的点  要么pi是某个基本块的结尾，且pi+1是该基本块的某个 后继的开头 17 

18 .数据流抽象 (2)  出现在某个程序点的程序状态  在某个运行时刻，当指令指针指向这个程序点时，各 个变量和动态内存中存放的值  指令指针可能多次指向同一个程序点，因此一个程序 点可能对应多个程序状态  数据流分析把可能出现在某个程序点上的程序状 态集合总结为一些特性  不管程序怎么运行，当它到达某个程序点时，程序状 态总是满足分析得到的特性  不同的分析技术关心不同的信息 18 

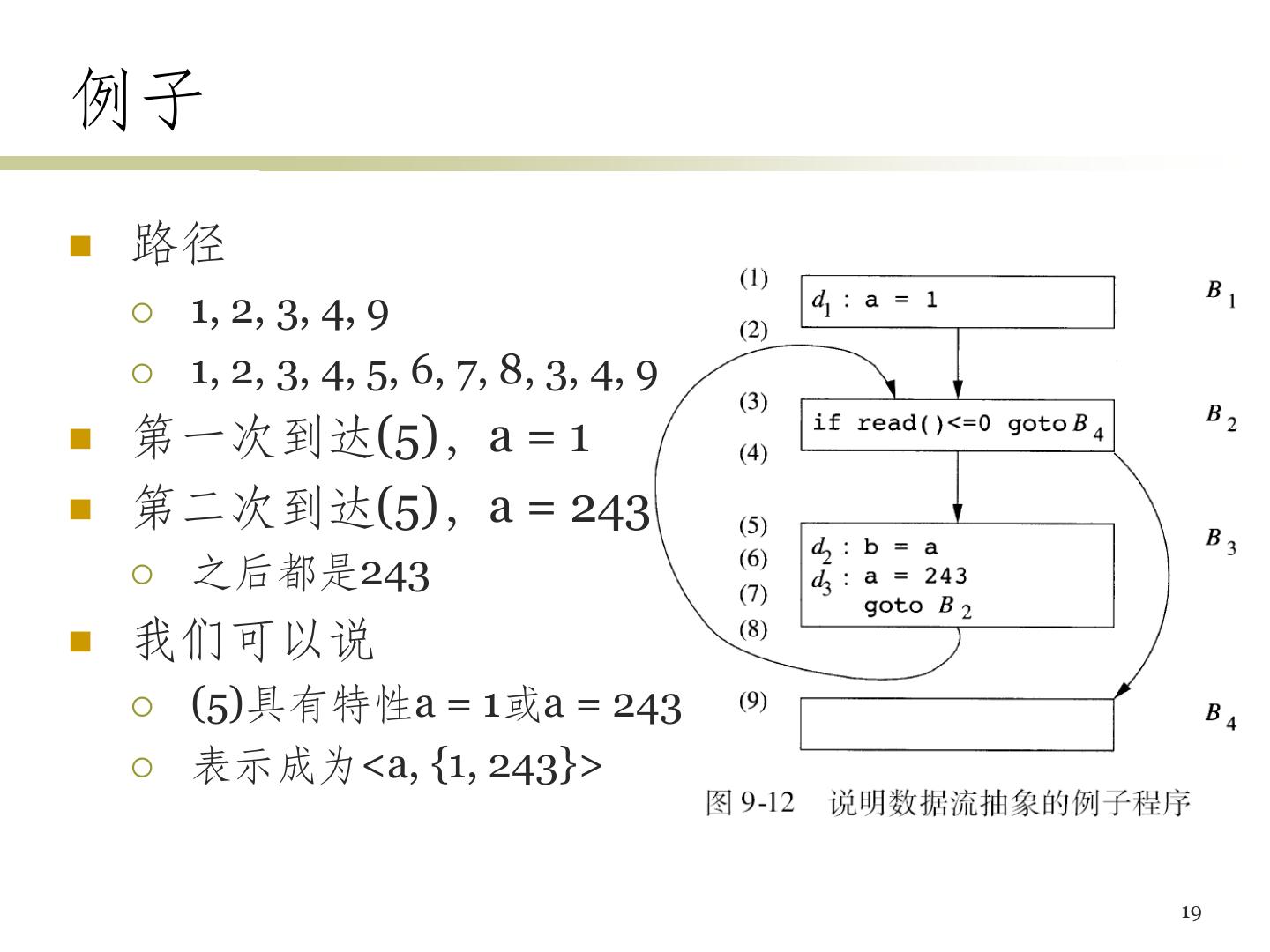
19 .例子  路径  1, 2, 3, 4, 9  1, 2, 3, 4, 5, 6, 7, 8, 3, 4, 9  第一次到达(5)，a = 1  第二次到达(5)，a = 243  之后都是243  我们可以说  (5)具有特性a = 1或a = 243  表示成为<a, {1, 243}> 19 

20 .性质和算法  根据不同的需要来设置不同的性质集合，然后设 计分析算法  程序点上的性质被表示成为数据流值，求解这些数据 流值实际上就是推导这些性质的过程  例子  如果要求出变量在某个点上的值可能在哪里定值，可 以使用到达定值 (Reaching Definition)  性质形式：x由d1定值  如果希望实现常量折叠优化，我们关心的是某个点上 变量x的值是否总是由某个常量赋值语句赋予  性质形式：x = c，以及x = NAC 20 

21 .数据流分析模式  数据流分析中，程序点和数据流值关联起来  数据流值表示了程序点具有的性质  和某个程序点关联的数据流值：程序运行中经过这个 点时必然满足的条件 (安全)  域  某个数据流所有可能值的集合称为该数据流值的域  不同的应用选用不同的域，比如到达定值  目标是分析在某个点上，各个变量的值由哪些语句定值  因此其数据流值是定值 (即三地址语句) 的集合 21 

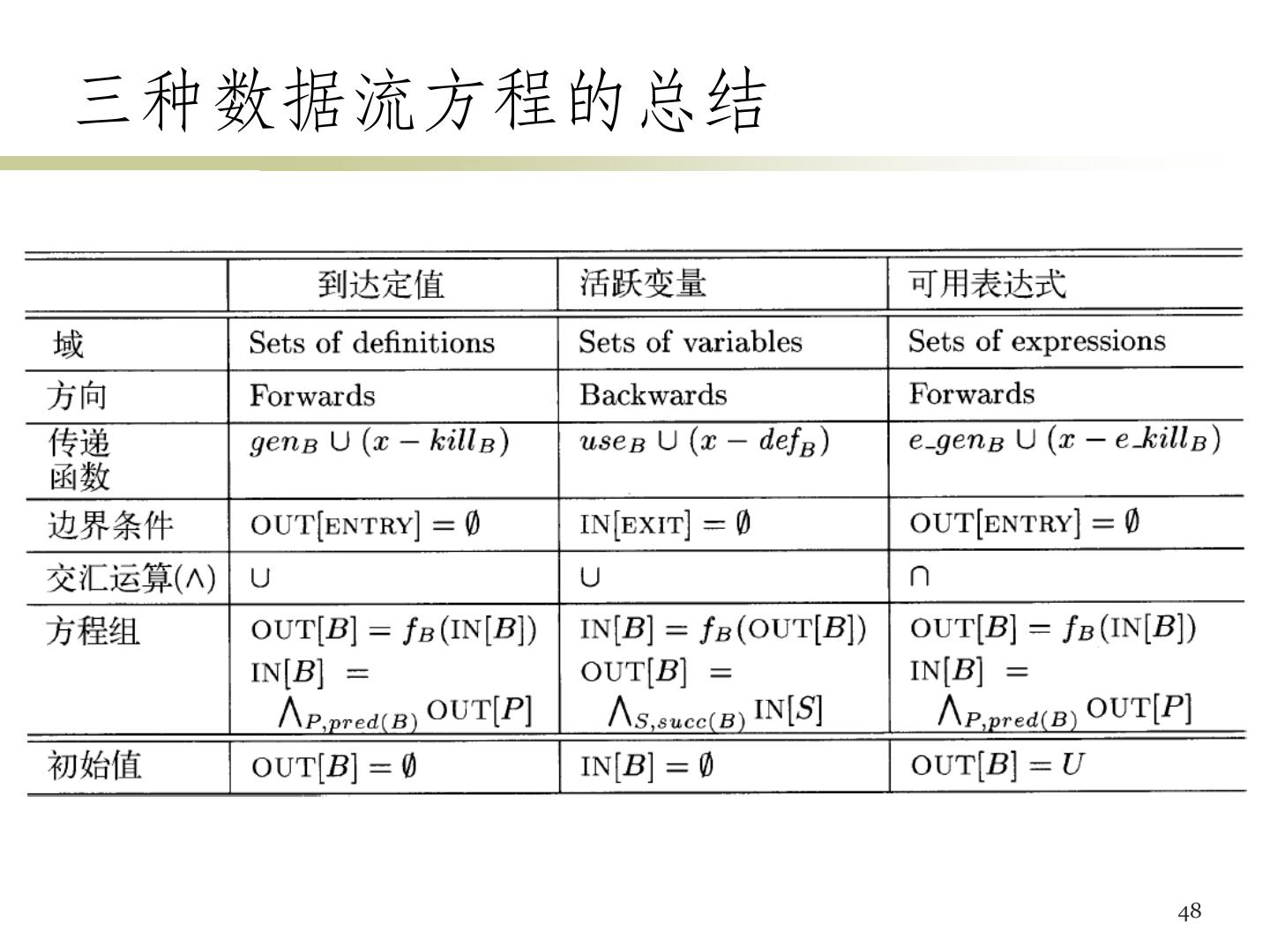
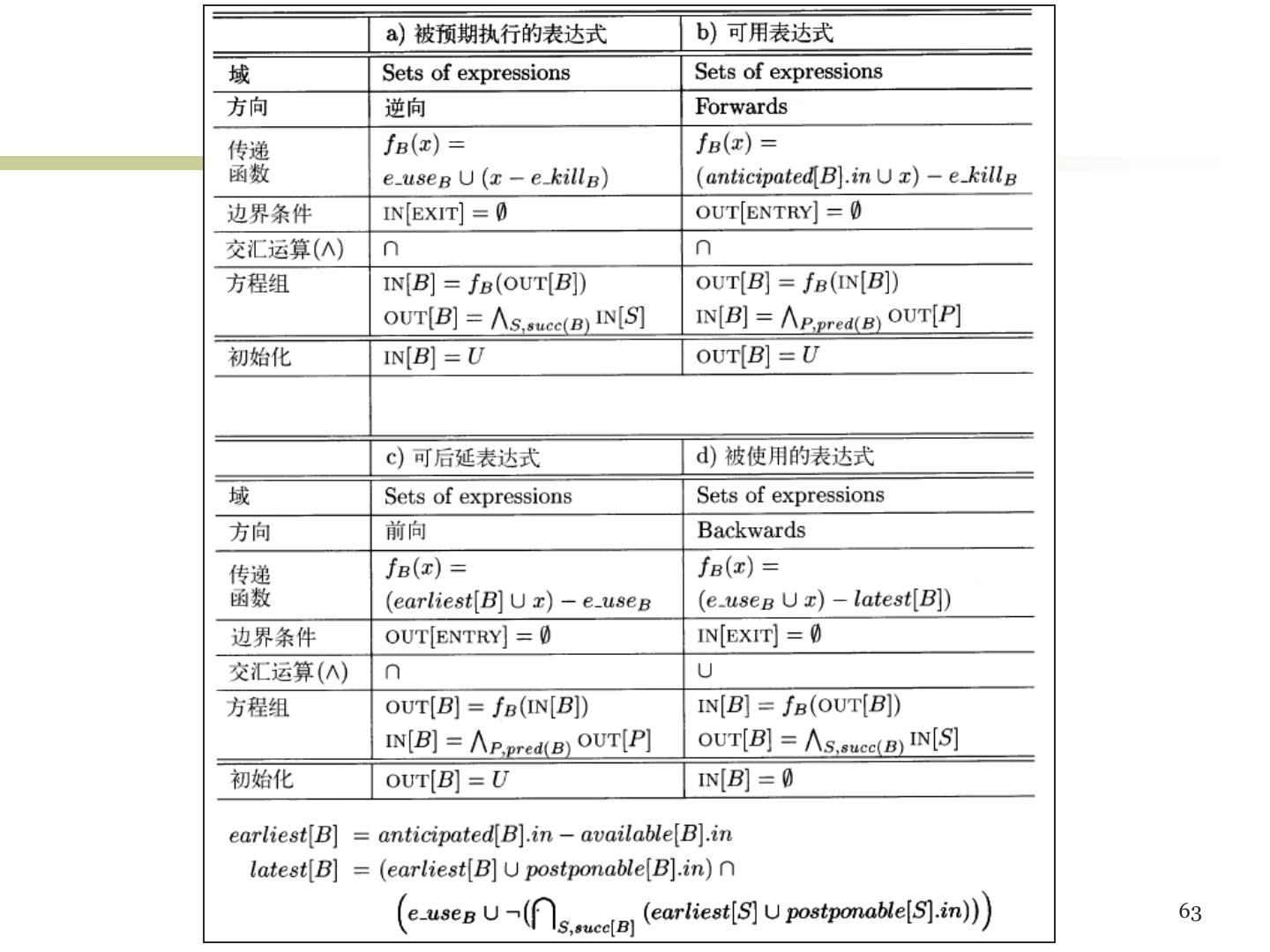
22 .数据流分析  对一组约束求解，得到各个点上的数据流值  两类约束：基于语句语义和基于控制流  基于语句语义的约束  一个语句之前和之后的数据流值受到其语义的约束  语句语义通常用传递函数表示，它把一个数据流值映 射为另一个数据流值  OUT[s] = fs(IN[s]) // 正向 IN[s] = fs(OUT[s]) // 逆向  基于控制流的约束  在基本块内部，一个语句的输出 = 下一语句的输入  流图的控制流边也对应新的约束 22 

23 .例子  考虑各个变量在某个程序点上是否为常量  s是语句x = 3  考虑变量x, y, z  如果IN[s]： x: NAC; y: 7; z: 3  那么OUT[s]： x: 3; y: 7; z: 3  如果  s是x = y + z，那么OUT[s]是？  s是x = x + y，那么OUT[s]是？ 23 

24 .基本块内的数据流模式  基本块内的控制流非常简单  从头到尾不会中断  没有分支  基本块的效果就是各个语句的效果的复合  可以预先处理基本块内部的数据流关系，给出基 本块对应的传递函数  OUT[B] = fB(IN[B]) 或 IN[B] = fB(OUT[B])  设基本块包含语句s1, s2, …, sn  fB = fsn ◦ … ◦ fs2 ◦ fs1 24 

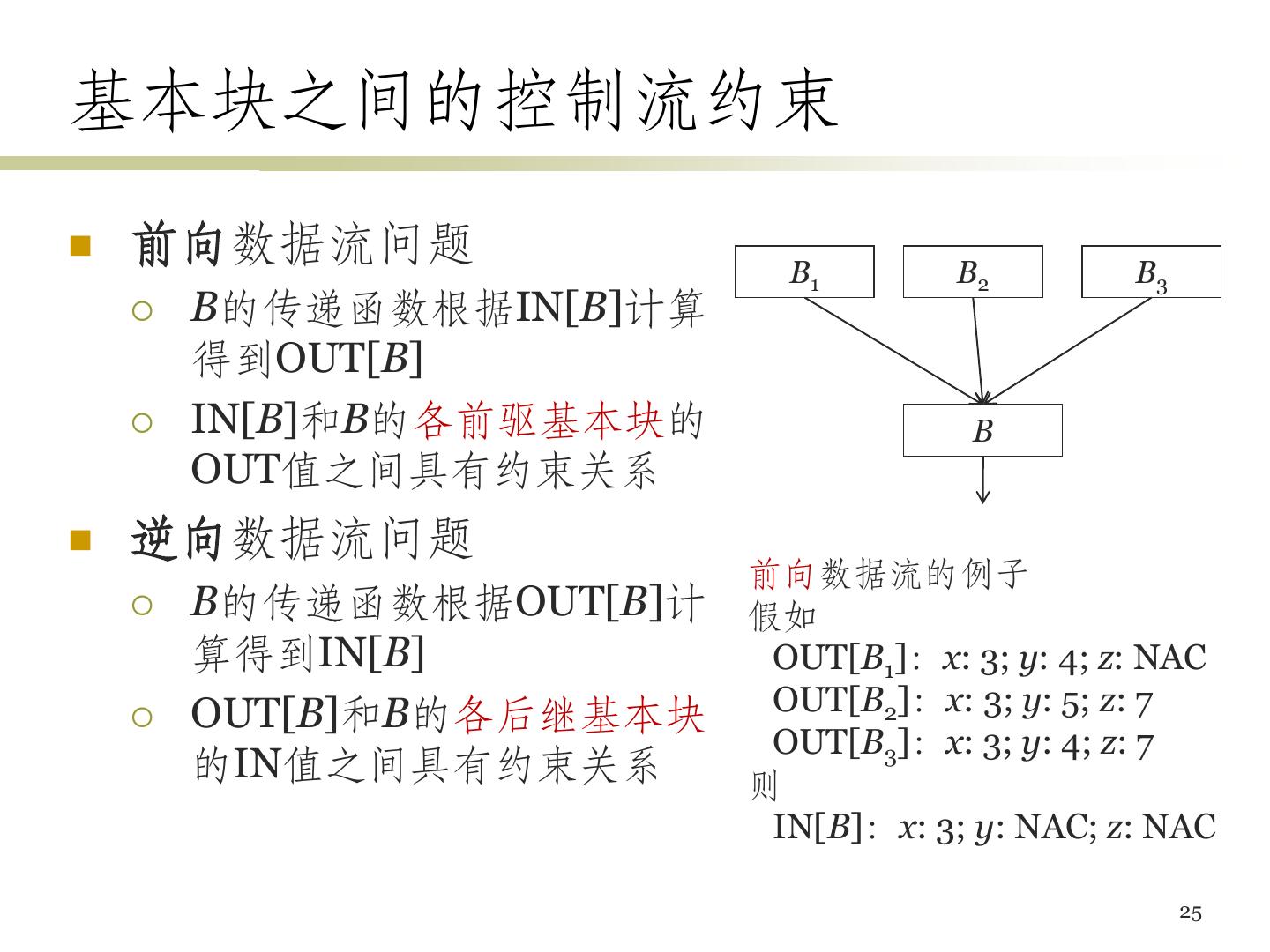
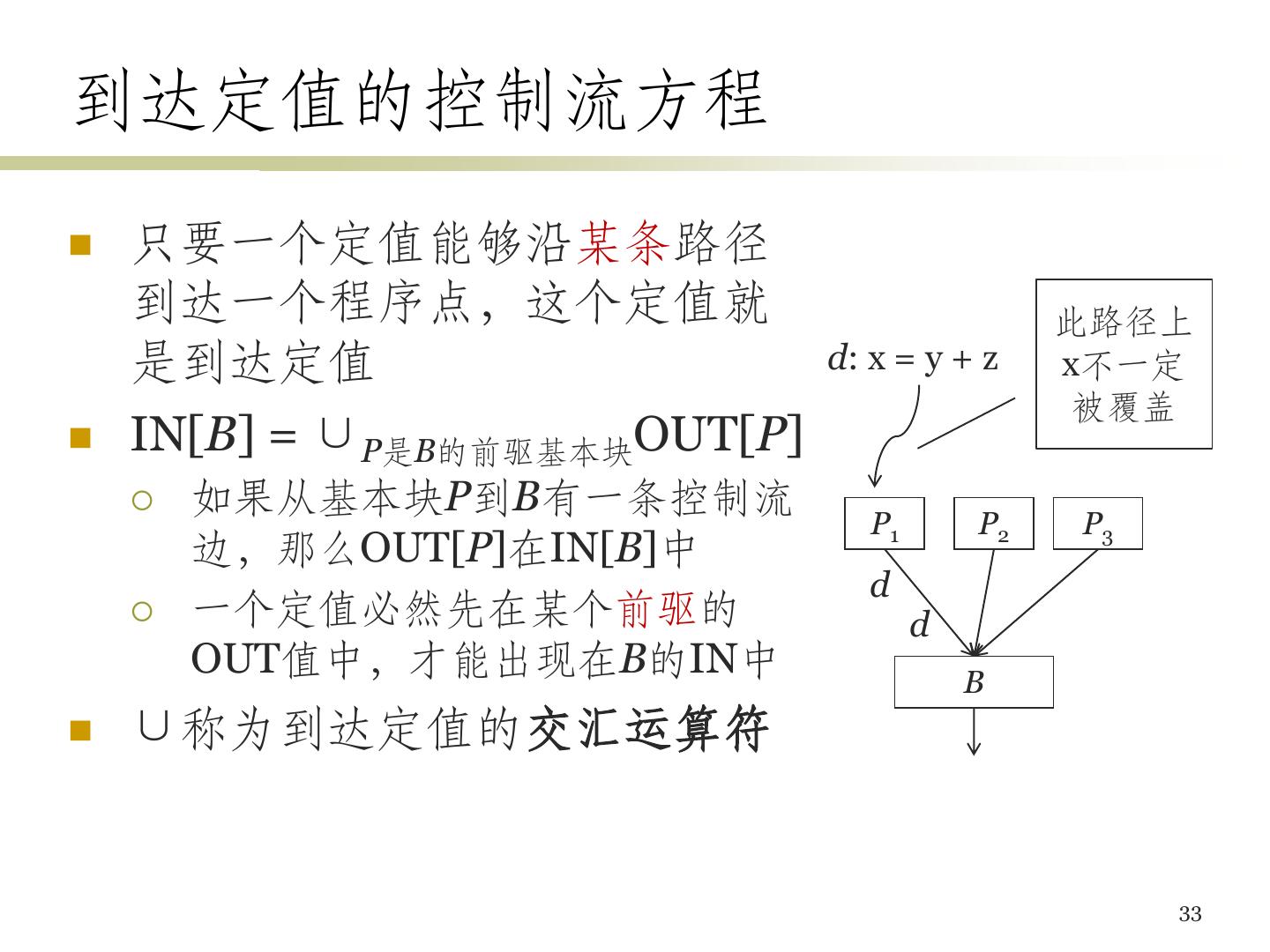
25 .基本块之间的控制流约束  前向数据流问题 B1 B2 B3  B的传递函数根据IN[B]计算 得到OUT[B]  IN[B]和B的各前驱基本块的 B OUT值之间具有约束关系  逆向数据流问题 前向数据流的例子  B的传递函数根据OUT[B]计 假如 算得到IN[B] OUT[B1]：x: 3; y: 4; z: NAC  OUT[B]和B的各后继基本块 OUT[B2]：x: 3; y: 5; z: 7 OUT[B3]：x: 3; y: 4; z: 7 的IN值之间具有约束关系 则 IN[B]：x: 3; y: NAC; z: NAC 25 

26 .数据流方程解的精确性和安全性  数据流方程通常没有唯一解  目标是寻找一个最“精确”且满足约束的解  精确：能够进行更多的改进  满足约束：根据分析结果来改进代码是安全的 26 

27 .到达定值 (1)  到达定值  假定x有定值d，如果存在一个路径，从紧随d的点到达 某点p，并且此路径上面没有x的其他定值点，则称x的 定值d到达p  如果在这条路径上有对x的其它定值，我们说变量x的 这个定值d被杀死了  如果某个变量x的一个定值d到达了点p，在p点使 用变量x的时候，x的值是由d最后定值的 27 

28 .到达定值 (2)  到达定值的解允许不精确，但必须是安全的  分析得到的到达定值可能实际上不会到达  但是实际到达的一定被分析出来，否则不安全  比如确定x在p点是否为常量  忽略实际的到达定值使得变化的值被误认为常量，将 这些值替换为常量会引起错误，不安全  过多估计则相反 28 

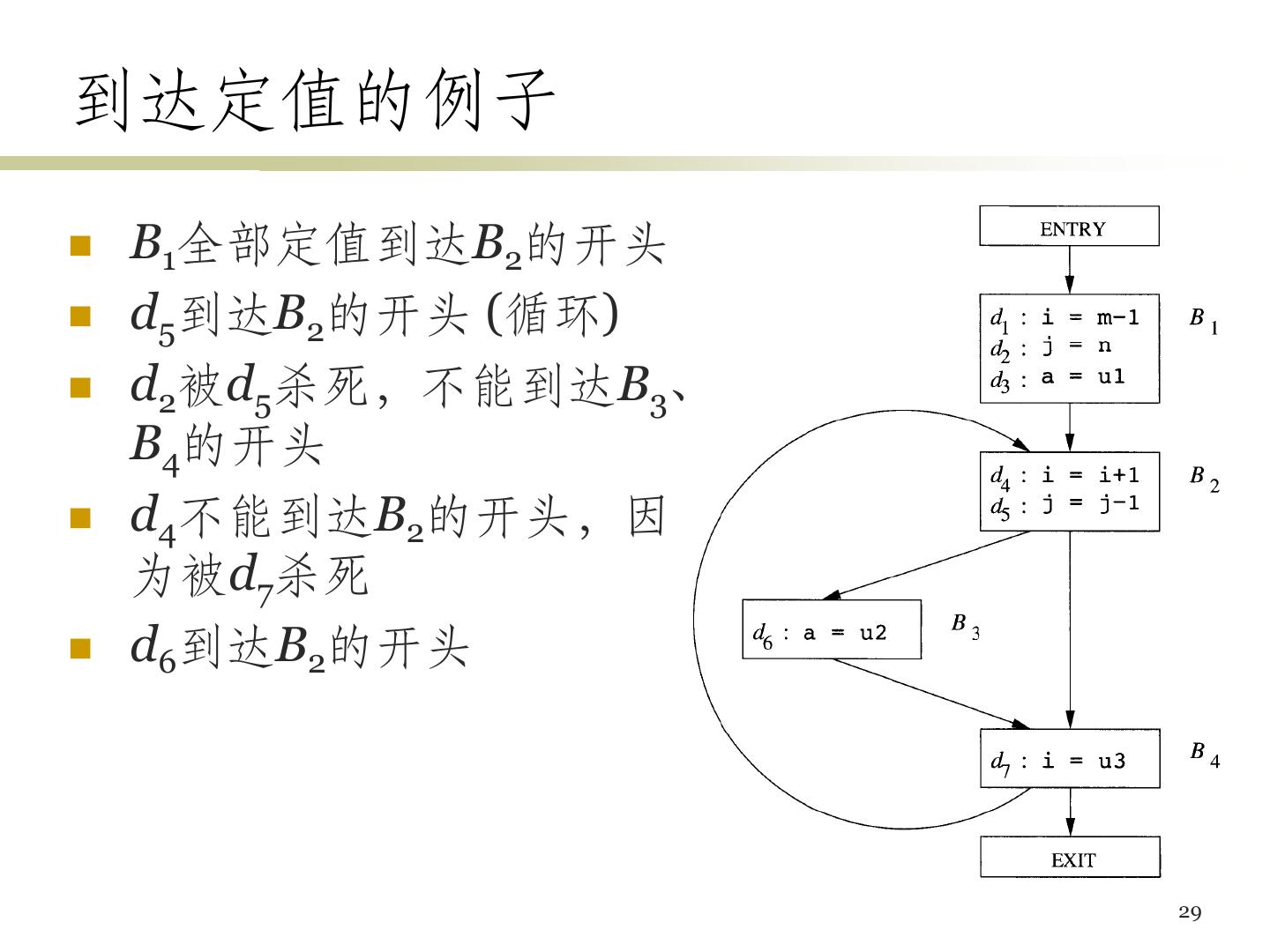
29 .到达定值的例子  B1全部定值到达B2的开头  d5到达B2的开头 (循环)  d2被d5杀死，不能到达B3、 B4的开头  d4不能到达B2的开头，因 为被d7杀死  d6到达B2的开头 29