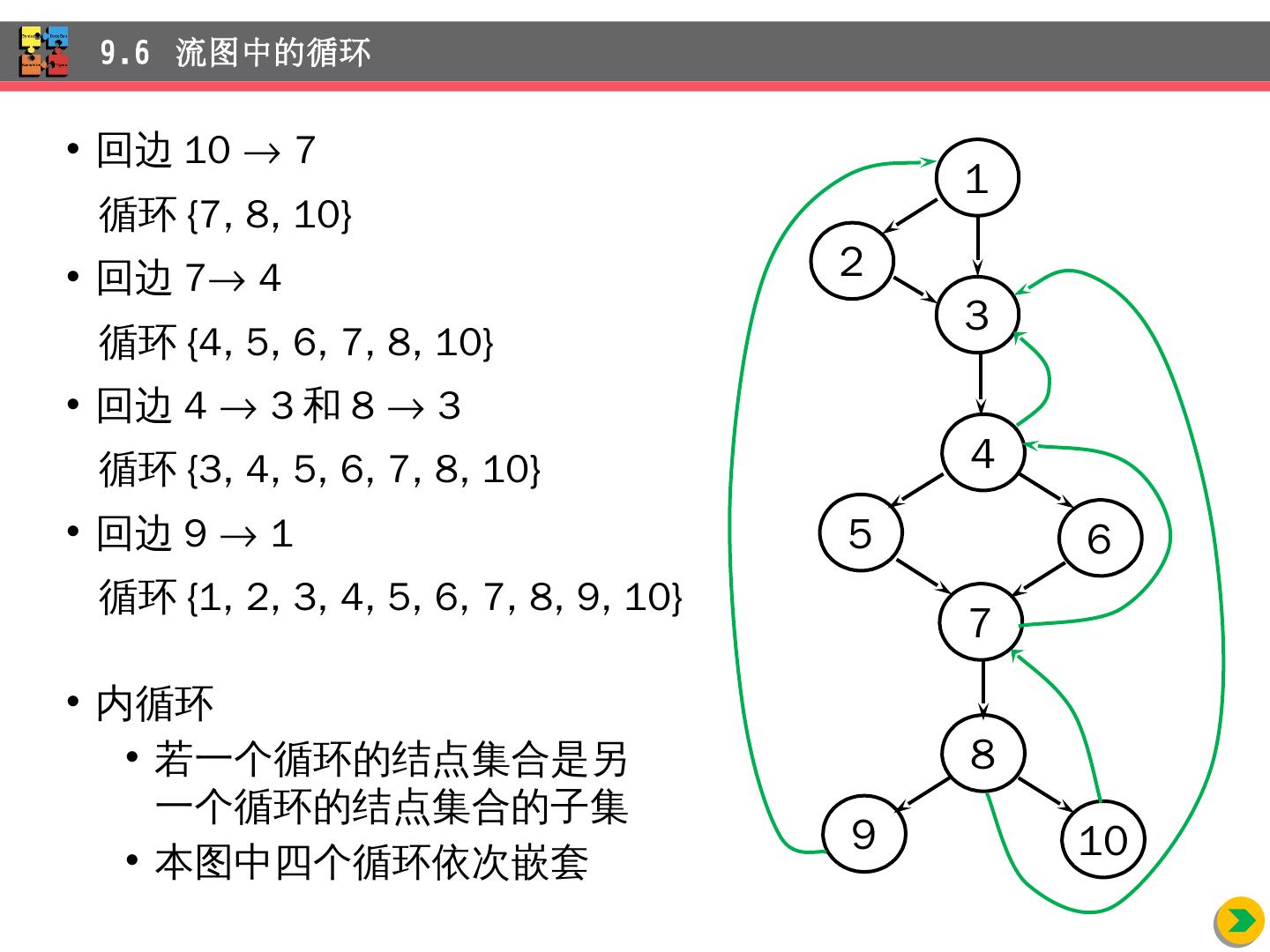
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
09 编译器原理与技术---独立于机器的优化
展开查看详情
1 .第 9 章 独立 于机器的优化 编译原理与技术
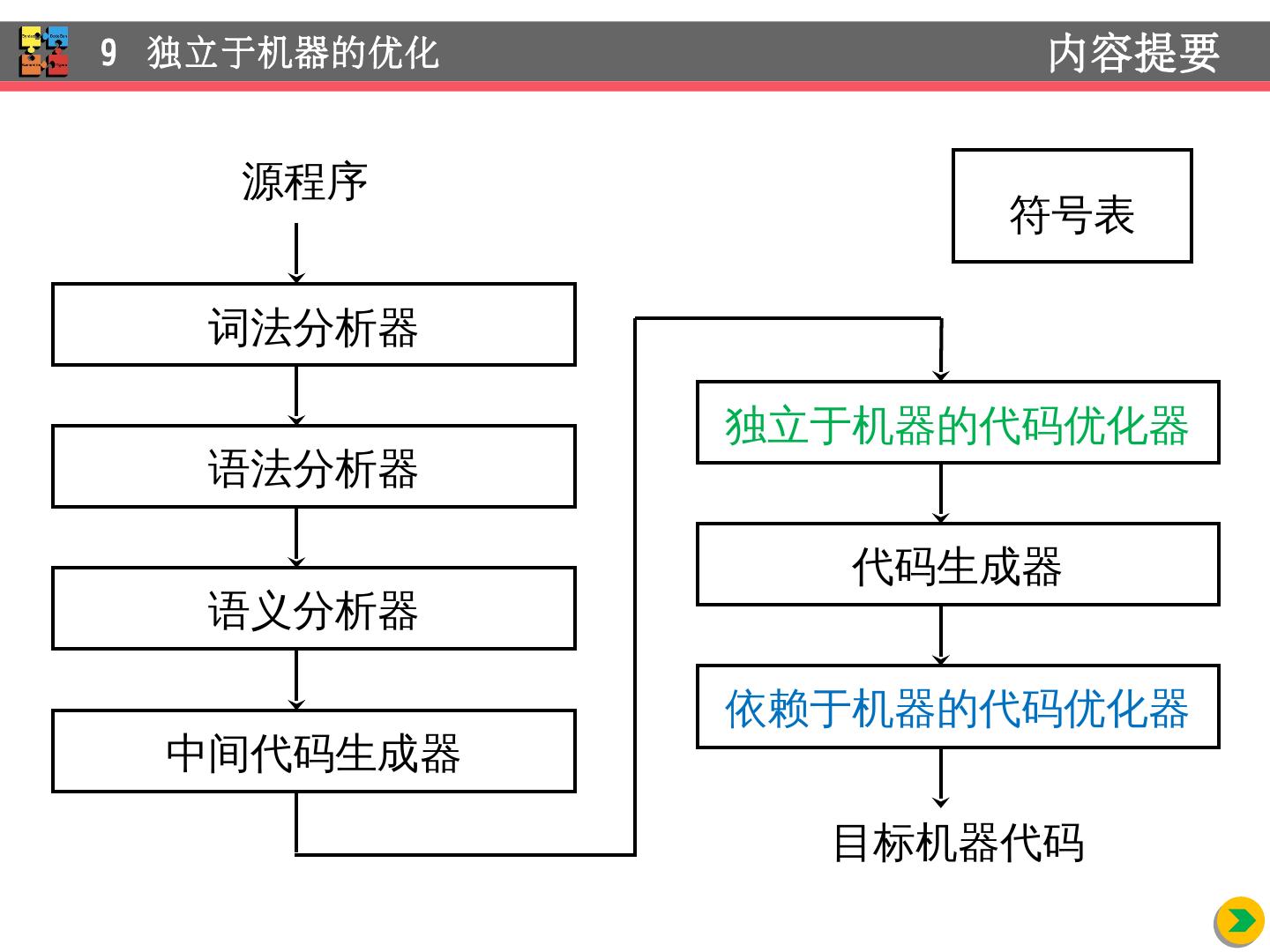
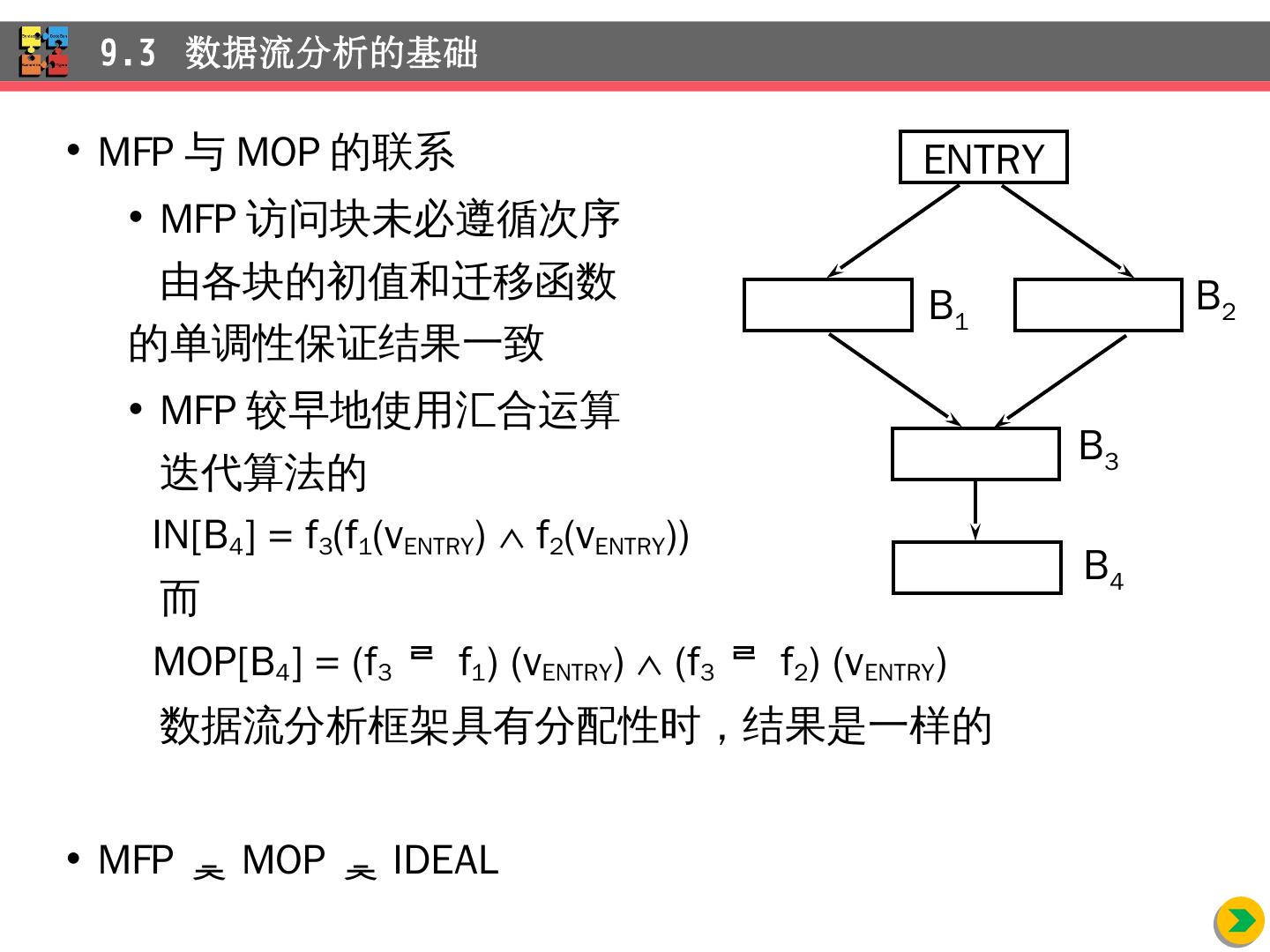
2 .9 独立 于机器的优化 内容提要 词法分析 器 语法分析 器 语义分析 器 源程序 中间代码 生成器 独立于机器的代码优化器 代码生成器 依赖于机器的代码优化器 目标机器代码 符号 表
3 .代码优化 通过程序变换(局部变换和全局变换)来改进程序,称为优化 代码 改进变换的标准 代码变换必须保程序的含义 采取安全稳妥的策略 变换减少程序的运行时间平均达到一个可度量的值 变换所作的努力是值得 的 9 独立 于机器的优化 内容提要
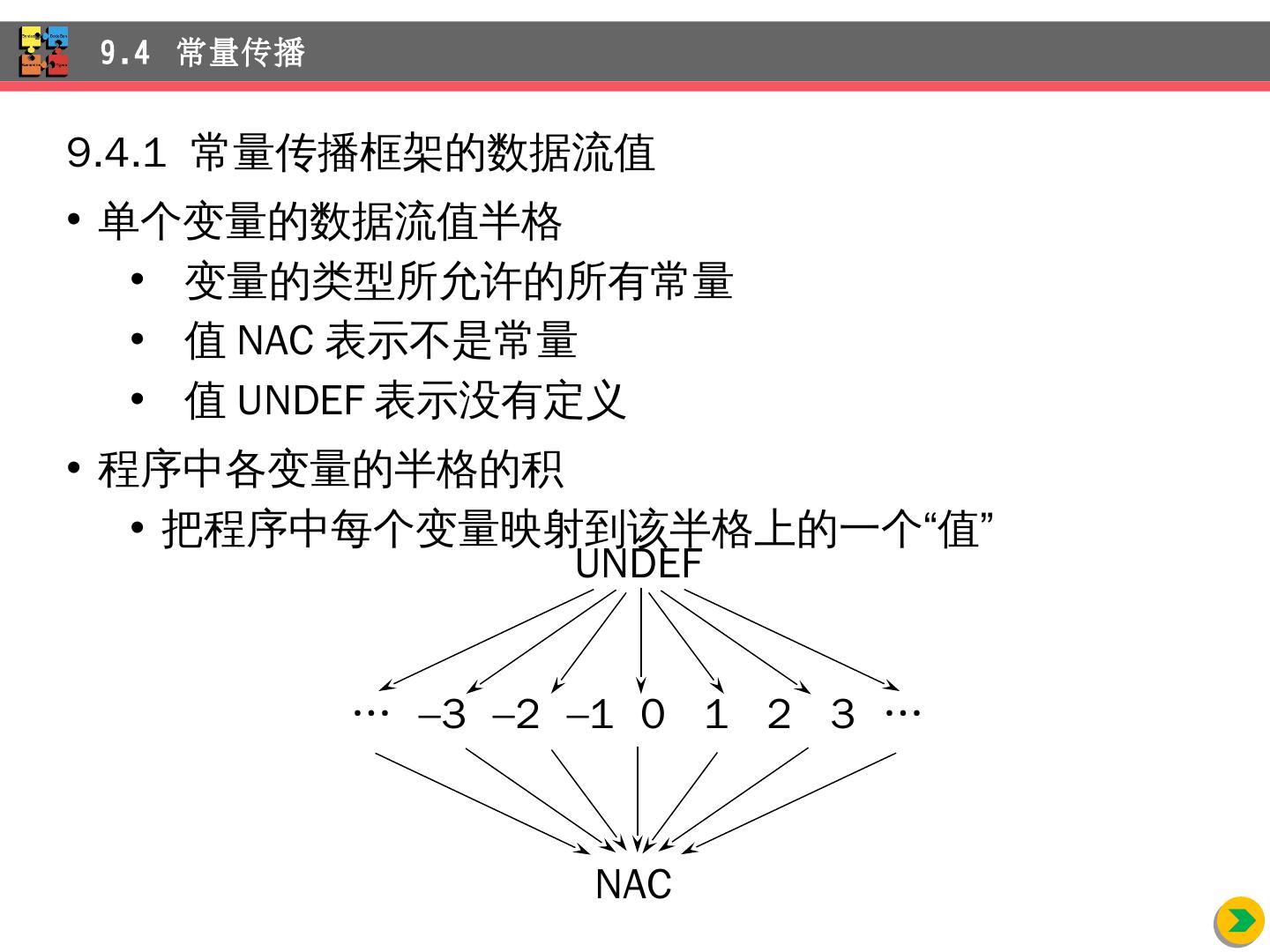
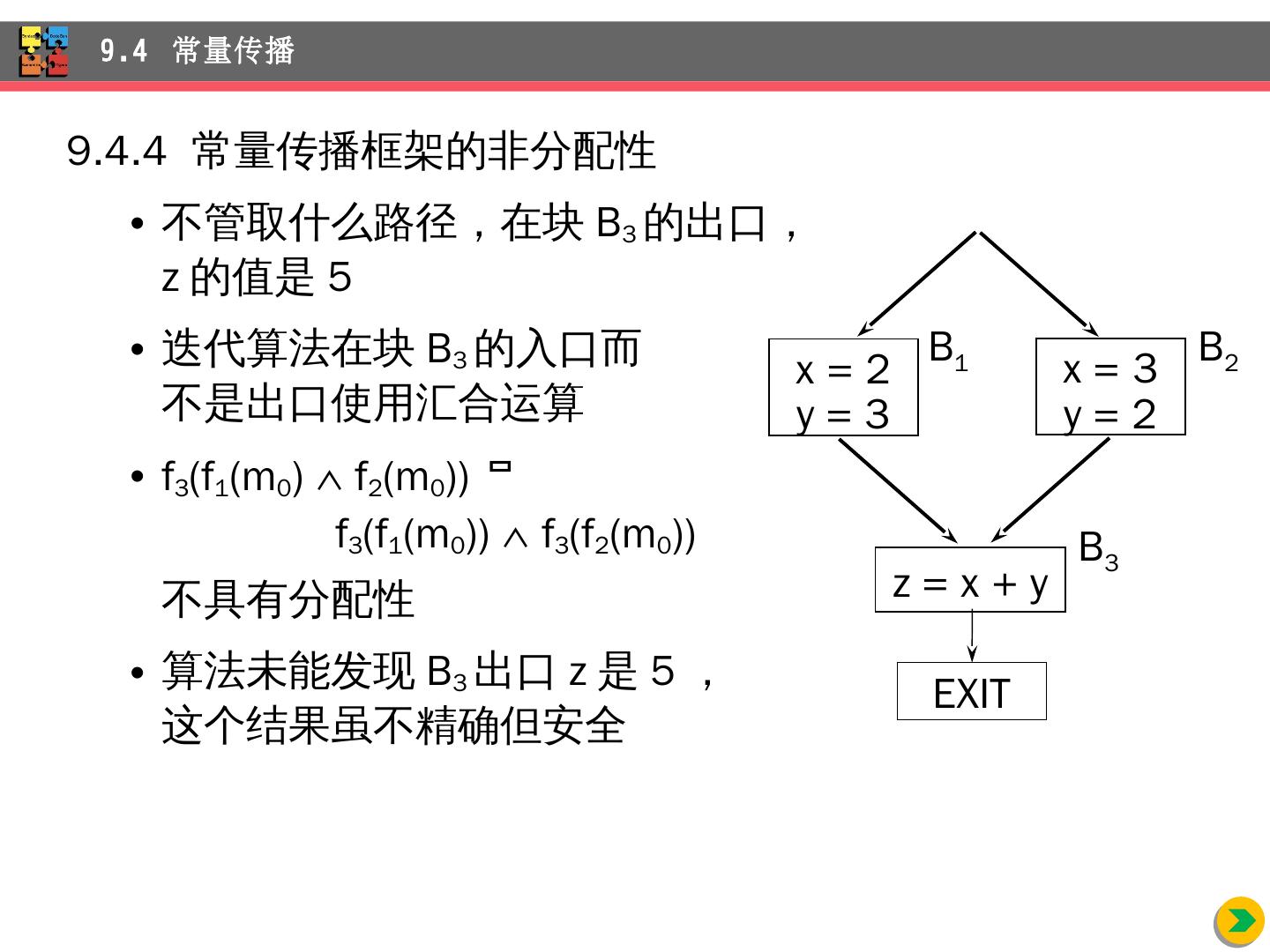
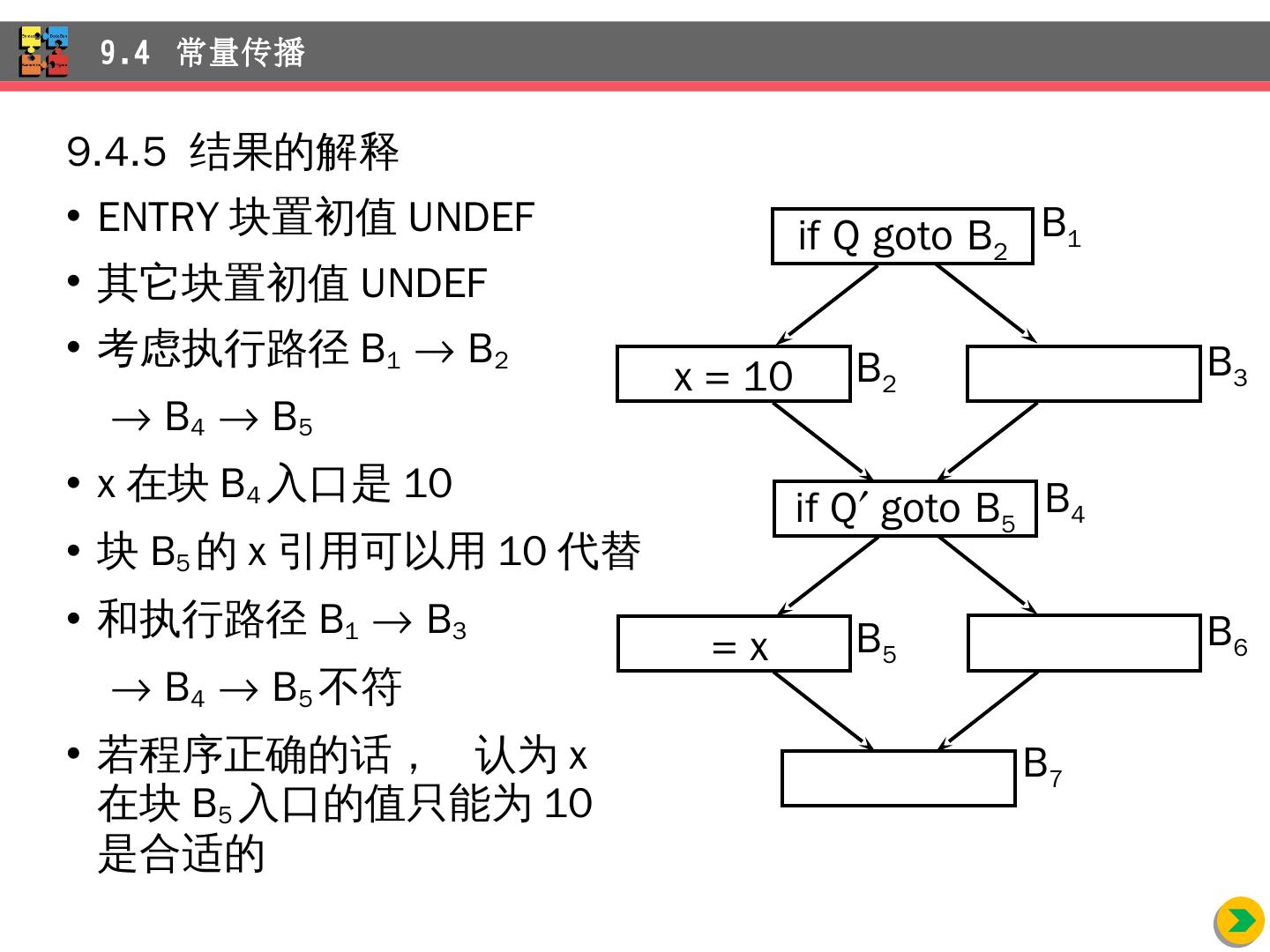
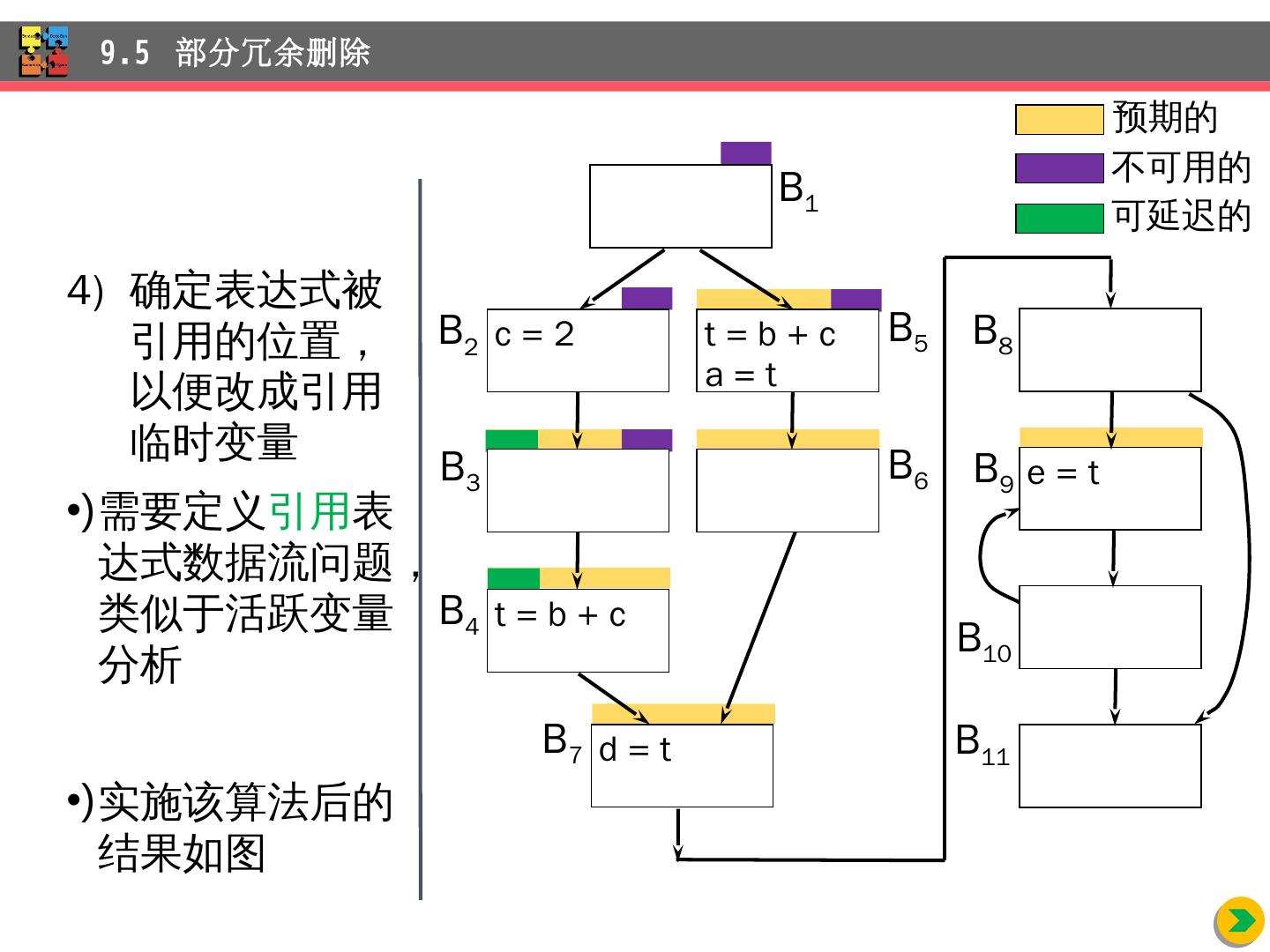
4 .介绍 独立于机器的优化,即不考虑任何 依赖 目标机器性质的优化变换 通过 实例来介绍代码改进的主要机会 数据流分析 包括的几类重要的全局收集的信息 数据流分析 的一般框架 和 一般框架有区别的常量传播 部分 冗余删除的优化技术 循环 的识别和分析 9 独立 于机器的优化 内容提要
5 .9.1 优化 的主要种类 第 9 章 独立 于机器的优化
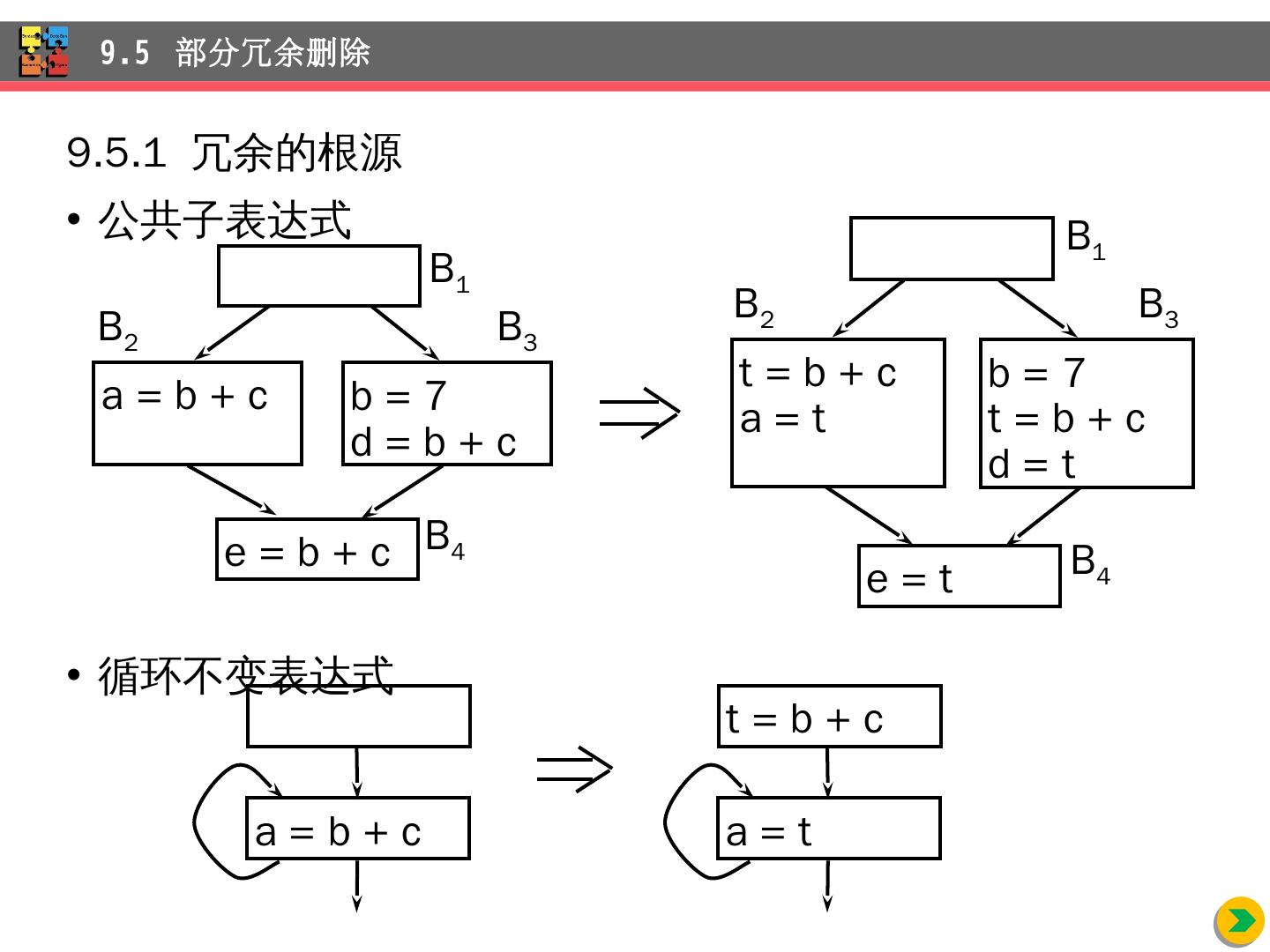
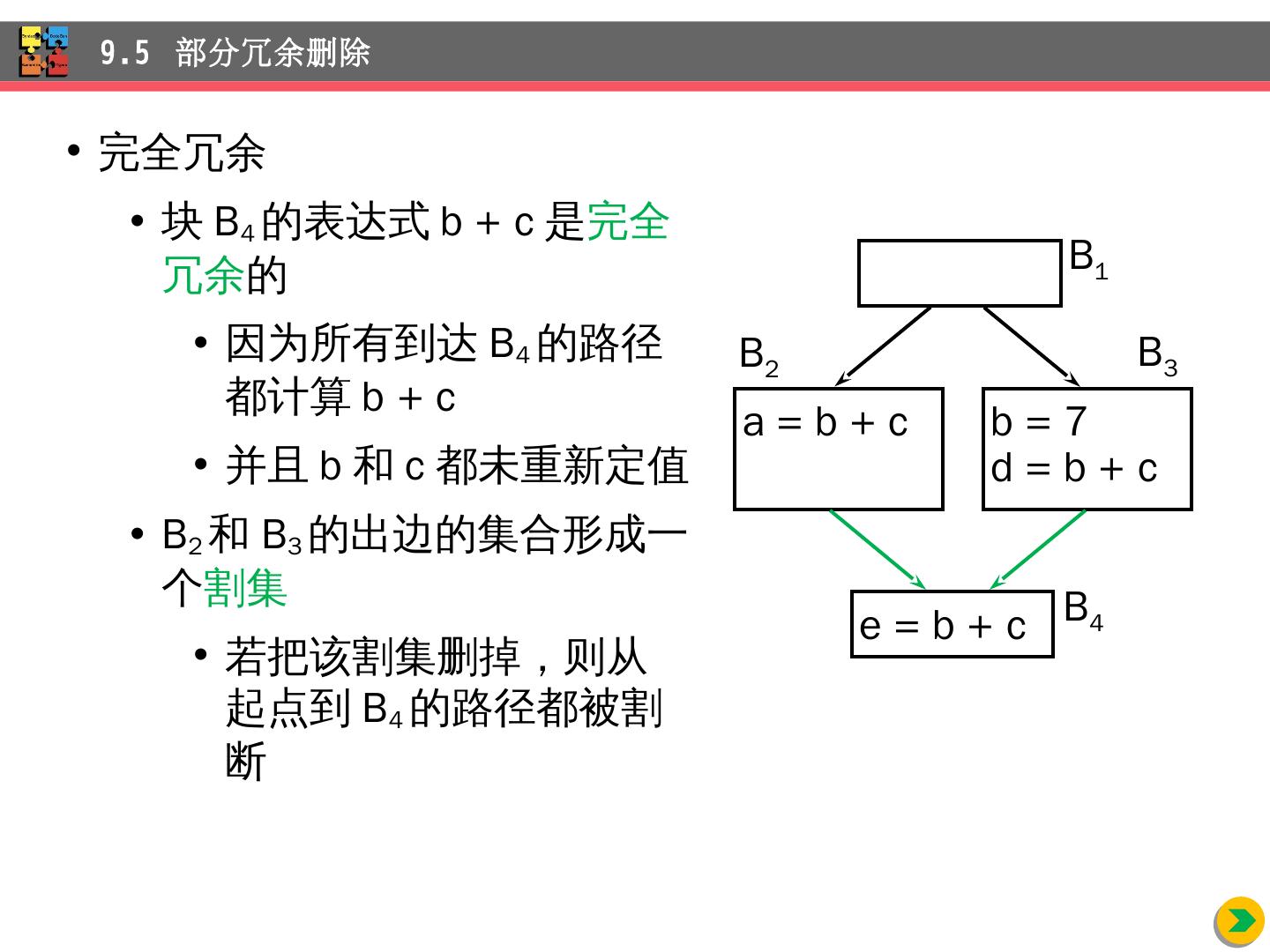
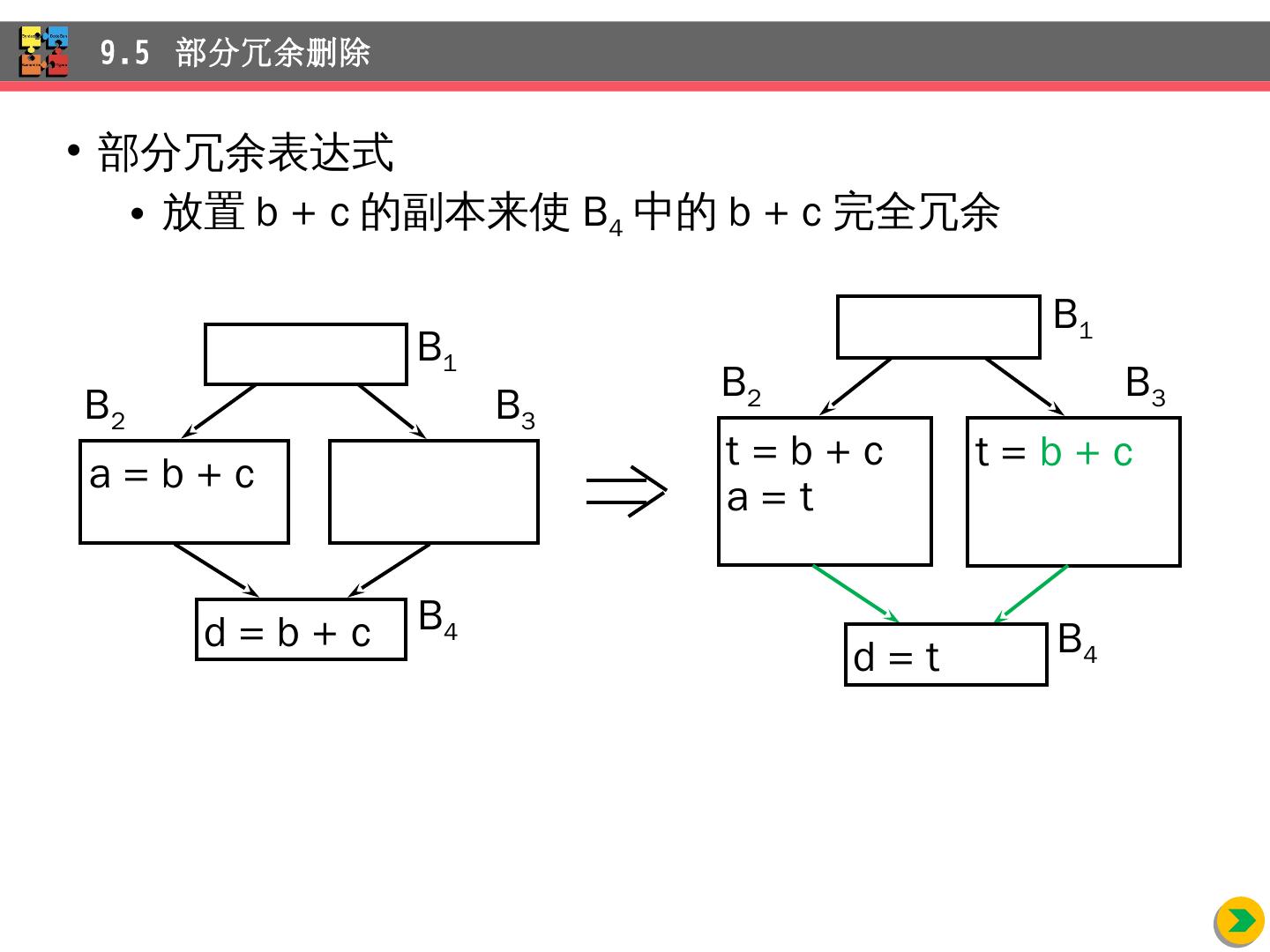
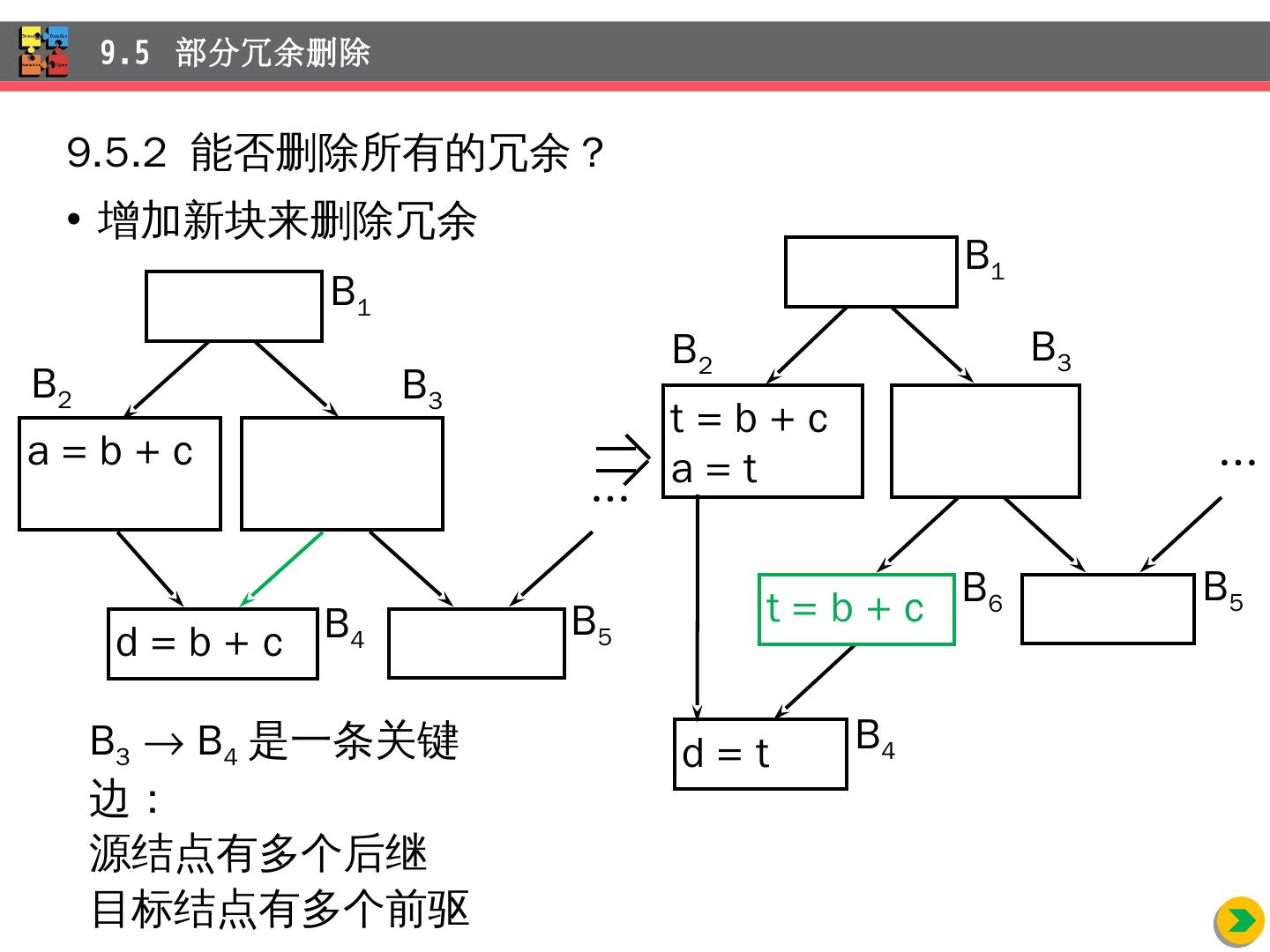
6 .9.1.1 优化的主要源头 程序中存在许多程序员无法避免的冗余运算 对于 A[ i ][j] 和 X.f1 这样访问数组元素和结构体的域的操作(例如, A[ i ][j] = A[ i ][j] + 10 ) 随着程序被编译,这些访问操作展开成多步低级算术运算 对同一个数据结构的多次访问导致许多公共的低级运算 程序员没有办法删除这些冗余 9.1 优化 的主要种类
7 .9.1.2 一个实例 i = m 1; j = n; v = a[n ]; ( 1) i = m 1 while (1) { ( 2) j = n do i = i +1; while(a[ i ]<v ); ( 3) t 1 = 4 n do j =j 1;while (a[j]>v ); ( 4) v = a[t 1 ] if ( i >= j) break ; ( 5) i = i + 1 x=a[ i ]; a[ i ]=a[j]; a[j]=x ; ( 6) t 2 = 4 i } ( 7) t 3 = a[t 2 ] x=a[ i ]; a[ i ]=a[n]; a[n]=x ; ( 8) if t 3 < v goto (5) 9.1 优化 的主要种类
8 .i = m 1; j = n; v = a[n ]; ( 9) j = j 1 while (1) { ( 10) t 4 = 4 j do i = i +1; while(a[ i ]<v ); ( 11) t 5 = a[t 4 ] do j =j 1;while (a[j]>v ); ( 12) if t 5 >v goto (9) if ( i >= j) break ; ( 13) if i >=j goto (23) x=a[ i ]; a[ i ]=a[j]; a[j]=x ; ( 14) t 6 = 4 i } ( 15 ) x = a[t 6 ] x=a[ i ]; a[ i ]=a[n]; a[n]=x ; . . . 9.1 优化 的主要种类
9 .程序流图 9.1 优化 的主要种类 i = m 1 j = n t 1 = 4 n v = a[t 1 ] i = i + 1 t 2 = 4 i t 3 = a[t 2 ] if t 3 < v goto B 2 B 1 B 2 j = j 1 t 4 = 4 j t 5 = a[t 4 ] if t 5 > v goto B 3 if i >= j goto B 6 B 4 B 3 B 5 B 6 t 6 = 4 i x = a[t 6 ] t 7 = 4 i t 8 = 4 j t 9 = a[t 8 ] a[t 7 ] = t 9 t 10 = 4 j a[t 10 ] = x goto B 2 t 11 = 4 i x = a[t 11 ] t 12 = 4 i t 13 = 4 n t 14 = a[t 13 ] a[t 12 ] = t 14 t 15 = 4 n a[t 15 ] = x
10 .9.1. 3 公共子表达式删除 B 5 x=a[ i ]; a[ i ]=a[j]; a[j]=x; 局部公共子表达式删除 , 复写传播 , 删除死代码 9.1 优化 的主要种类 t 6 = 4 i x = a[t 6 ] t 7 = 4 i t 8 = 4 j t 9 = a[t 8 ] a[ t 7 ] = t 9 t 10 = 4 j a[ t 10 ] = x goto B 2 t 6 = 4 i x = a[t 6 ] t 8 = 4 j t 9 = a[t 8 ] a[t 6 ] = t 9 a[t 8 ] = x goto B 2
11 .9.1 优化 的主要种类 i = m 1 j = n t 1 = 4 n v = a[t 1 ] i = i + 1 t 2 = 4 i t 3 = a[t 2 ] if t 3 < v goto B 2 B 1 B 2 j = j 1 t 4 = 4 j t 5 = a[t 4 ] if t 5 > v goto B 3 if i >= j goto B 6 B 4 B 3 B 5 B 6 t 6 = 4 i x = a[ t 6 ] t 8 = 4 j t 9 = a[ t 8 ] a[ t 6 ] = t 9 a[ t 8 ] = x goto B 2 B 5 全局公共子表达式删除 , 复写传播 , 删除死代码
12 .B 5 x=a[ i ]; a[ i ]=a[j]; a[j]=x; 9.1 优化 的主要种类 t 6 = 4 i x = a[t 6 ] t 7 = 4 i t 8 = 4 j t 9 = a[t 8 ] a[ t 7 ] = t 9 t 10 = 4 j a[ t 10 ] = x goto B 2 t 6 = 4 i x = a[ t 6 ] t 8 = 4 j t 9 = a[ t 8 ] a[t 6 ] = t 9 a[t 8 ] = x goto B 2 x = a[t 2 ] t 9 = a[t 4 ] a[t 2 ] = t 9 a[t 4 ] = x goto B 2
13 .9.1 优化 的主要种类 i = m 1 j = n t 1 = 4 n v = a[t 1 ] i = i + 1 t 2 = 4 i t 3 = a[t 2 ] if t 3 < v goto B 2 B 1 B 2 j = j 1 t 4 = 4 j t 5 = a[t 4 ] if t 5 > v goto B 3 if i >= j goto B 6 B 4 B 3 B 5 B 6 B 5 全局公共子表达式删除 , 复写传播 , 删除死代码 x = a[t 2 ] t 9 = a[t 4 ] a[t 2 ] = t 9 a[t 4 ] = x goto B 2
14 .B 5 x=a[ i ]; a[ i ]=a[j]; a[j]=x; 公共子表达式删除、复写传播、删除死 代码 9.1 优化 的主要种类 t 6 = 4 i x = a[t 6 ] t 7 = 4 i t 8 = 4 j t 9 = a[t 8 ] a[ t 7 ] = t 9 t 10 = 4 j a[ t 10 ] = x goto B 2 t 6 = 4 i x = a[ t 6 ] t 8 = 4 j t 9 = a[ t 8 ] a[t 6 ] = t 9 a[t 8 ] = x goto B 2 x = a[t 2 ] t 9 = a[t 4 ] a[t 2 ] = t 9 a[t 4 ] = x goto B 2 a[t 2 ] = t 5 a[t 4 ] = t 3 goto B 2
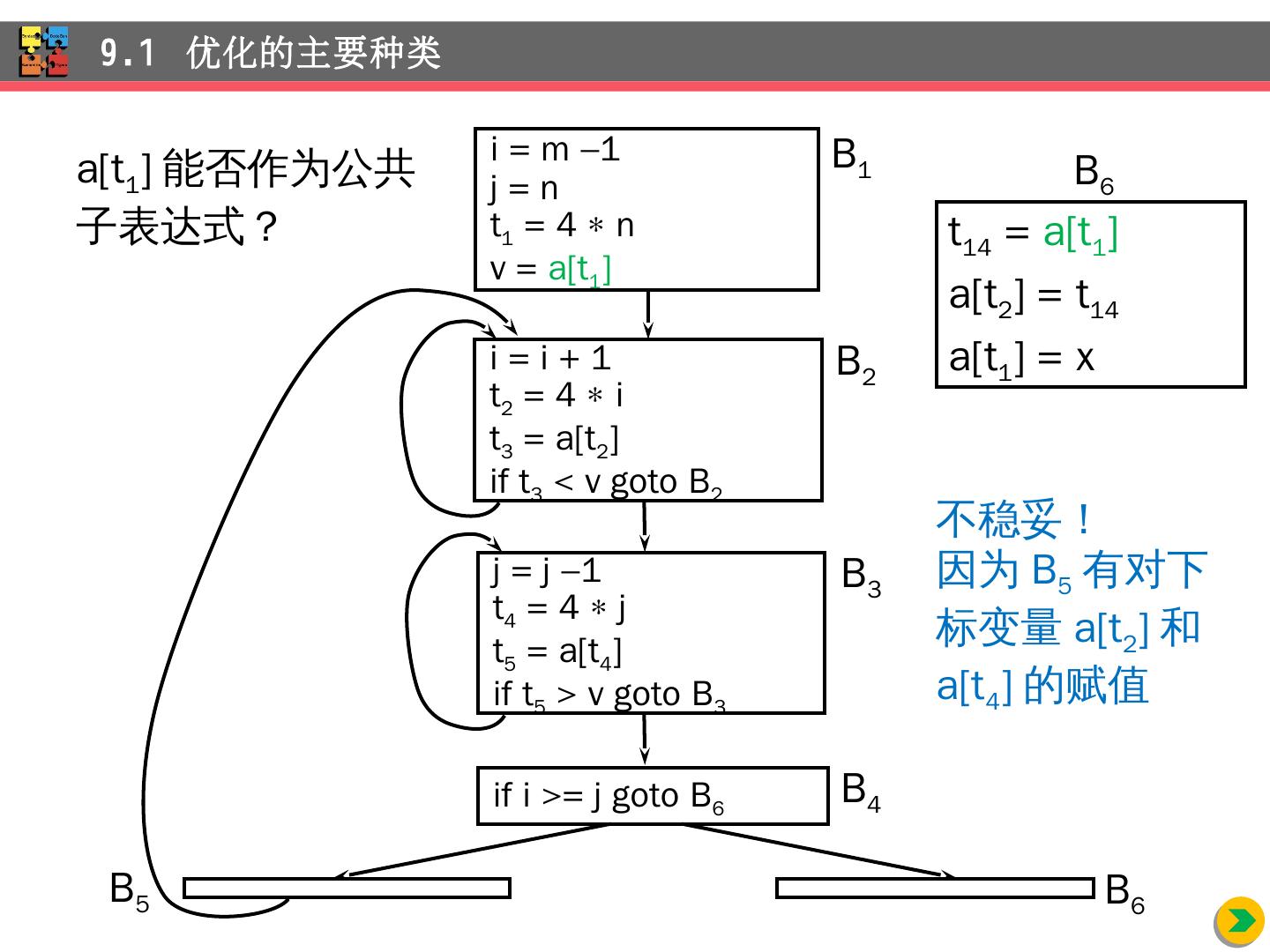
15 .B 6 x = a[ i ]; a[ i ] = a[n]; a[n] = x; a[t 1 ] 能否作为公共子表达式? 9.1 优化 的主要种类 t 11 = 4 i x = a[t 11 ] t 12 = 4 i t 13 = 4 n t 14 = a[t 13 ] a[ t 12 ] = t 14 t 15 = 4 n a[ t 15 ] = x t 14 = a[t 1 ] a[t 2 ] = t 14 a[t 1 ] = t 3 t 11 = 4 i x = a[ t 11 ] t 13 = 4 n t 14 = a[ t 13 ] a[t 11 ] = t 14 a[t 13 ] = x x = a[t 2 ] t 14 = a[t 1 ] a[t 2 ] = t 14 a[t 1 ] = x
16 .9.1 优化 的主要种类 i = m 1 j = n t 1 = 4 n v = a[t 1 ] i = i + 1 t 2 = 4 i t 3 = a[t 2 ] if t 3 < v goto B 2 B 1 B 2 j = j 1 t 4 = 4 j t 5 = a[t 4 ] if t 5 > v goto B 3 if i >= j goto B 6 B 4 B 3 B 5 B 6 B 6 a[t 1 ] 能否作为公共子表达式? t 14 = a[t 1 ] a[t 2 ] = t 14 a[t 1 ] = x 不稳妥! 因为 B 5 有对下标变量 a[t 2 ] 和 a[t 4 ] 的赋值
17 .9.1.4 复写传播 复写语句: 形式为 f = g 的赋值 优化过程中会大量引入复写 复写 传播变换的做法 是在 复写 语句 f = g 后, 尽可能 用 g 代表 f 复写 传播变换本身并不是优化 , 但 它给其它优化带来机会 常量合并(编译时可完成 的 计算 ) 死代码 删除 9.1 优化 的主要种类 删除局部公共 子表达式 期间 引进复写 t = d + e a = t t = d + e b = t c = t c = d + e b = d + e a = d + e x = t 3 a[t 2 ] = t 5 a[t 4 ] = t 3 goto B 2 x = t 3 a[t 2 ] = t 5 a[t 4 ] = x goto B 2 B 5
18 .9.1. 5 死代码删除 死代码是指计算的结果决不被引用的语句 例 :为 便于调试,可能在程序中加打印语句, 测试后 改成右边的 形式, 靠优化来保证目标代码中没有该条件语句部分 debug = true ; | debug = false; . . . | . . . if (debug) print … | if (debug) print … 一些 优化变换可能会引起死代码 例:复写传播可能会引起死代码 删除 9.1 优化 的主要种类 B 5 x = t 3 a[t 2 ] = t 5 a[t 4 ] = t 3 goto B 2 a[t 2 ] = t 5 a[t 4 ] = t 3 goto B 2 x = t 3 a[t 2 ] = t 5 a[t 4 ] = x goto B 2
19 .9.1. 6 代码外提 代码外提是 循环优化的一种 例: while ( i <= limit 2 ) … 代码外提后变换成 t = limit 2; while ( i <= t ) … 循环优化的其它重要技术 归纳变量删除 强度削弱 9.1 优化 的主要种类
20 .9.1. 7 强度削弱和归纳变量删除 j 和 t 4 的值步伐一致地变化 这样的变量叫做归纳变量 在循环中有多个归纳变量时 ,也许 只需 要留下一个 这个操作由归纳变量 删除过程 来 完 成 对本例可以先做强度 削弱,它 给 删 除 归纳变量创造机会 9.1 优化 的主要种类 j = j 1 t 4 = 4 j t 5 = a[t 4 ] if t 5 > v goto B 3 B 3
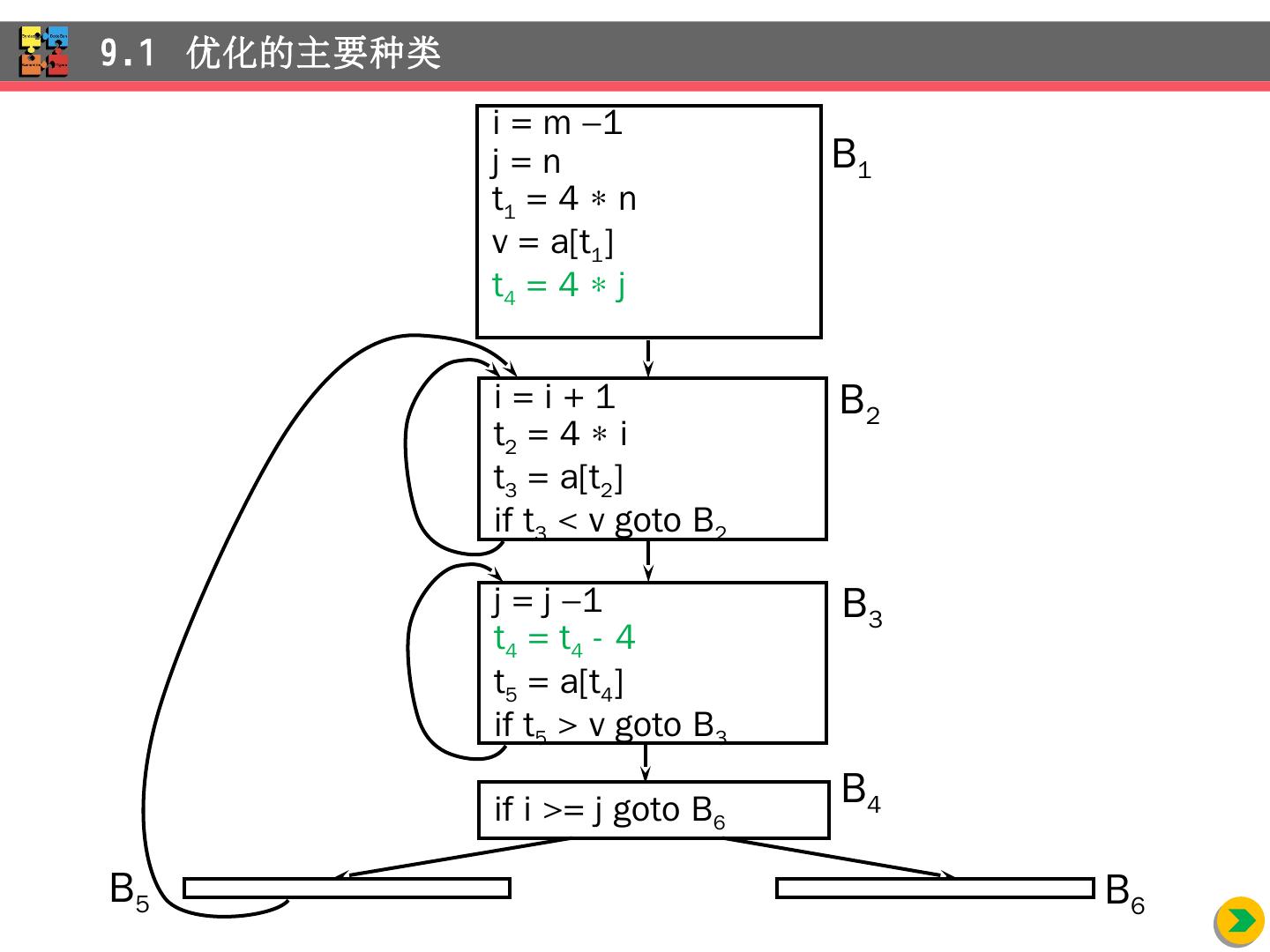
21 .9.1 优化 的主要种类 i = m 1 j = n t 1 = 4 n v = a[t 1 ] i = i + 1 t 2 = 4 i t 3 = a[t 2 ] if t 3 < v goto B 2 B 1 B 2 j = j 1 t 4 = 4 j t 5 = a[t 4 ] if t 5 > v goto B 3 if i >= j goto B 6 B 4 B 3 B 5 B 6 j = j 1 t 4 = 4 j t 5 = a[t 4 ] if t 5 > v goto B 3 B 3 除第一次外, t 4 = 4 j 在 B 3 的入口 一定保持 在 j = j 1 后, 关系 t 4 = 4 j + 4 也保持
22 .9.1 优化 的主要种类 i = m 1 j = n t 1 = 4 n v = a[t 1 ] t 4 = 4 j i = i + 1 t 2 = 4 i t 3 = a[t 2 ] if t 3 < v goto B 2 B 1 B 2 j = j 1 t 4 = t 4 - 4 t 5 = a[t 4 ] if t 5 > v goto B 3 if i >= j goto B 6 B 4 B 3 B 5 B 6
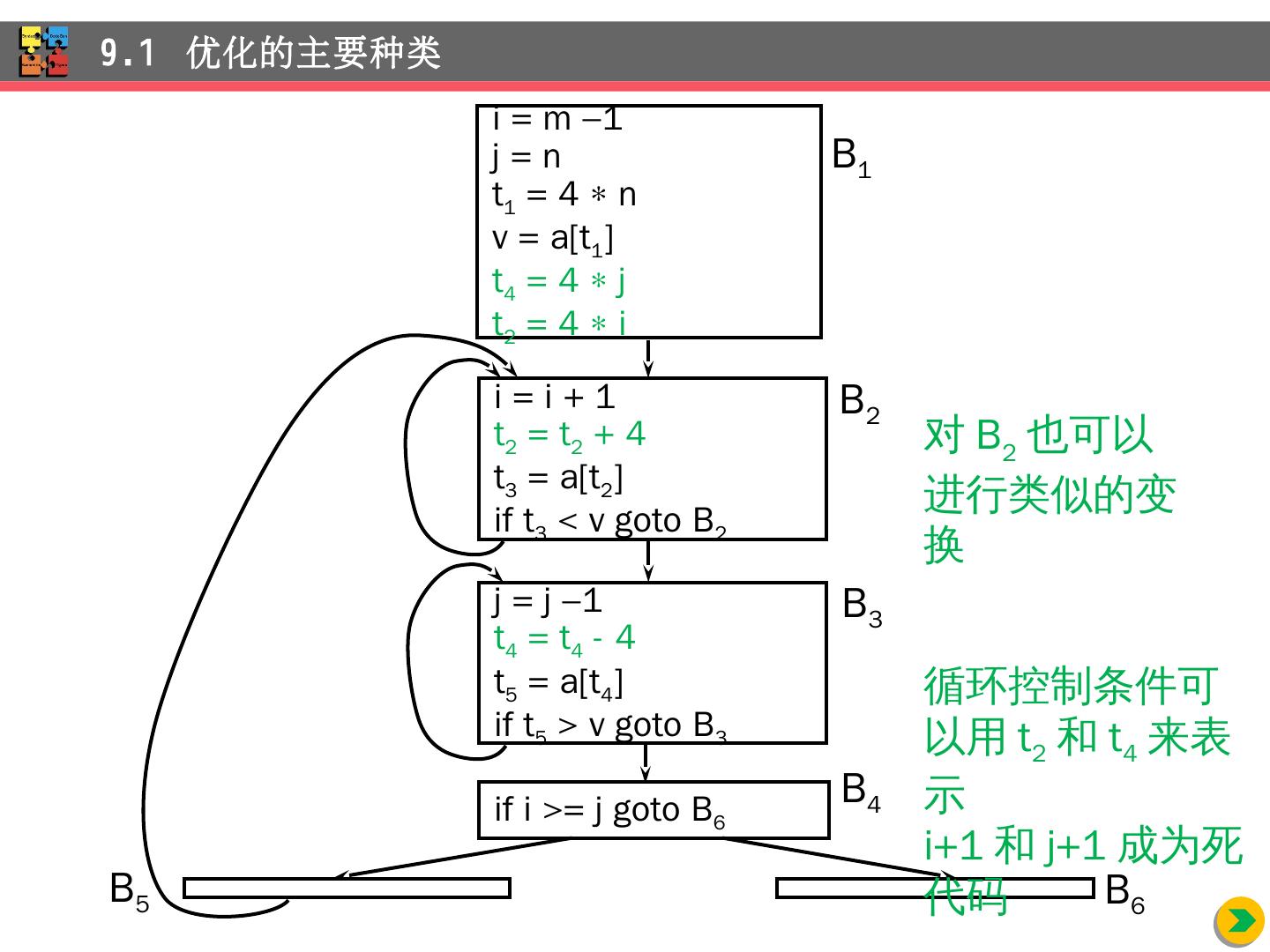
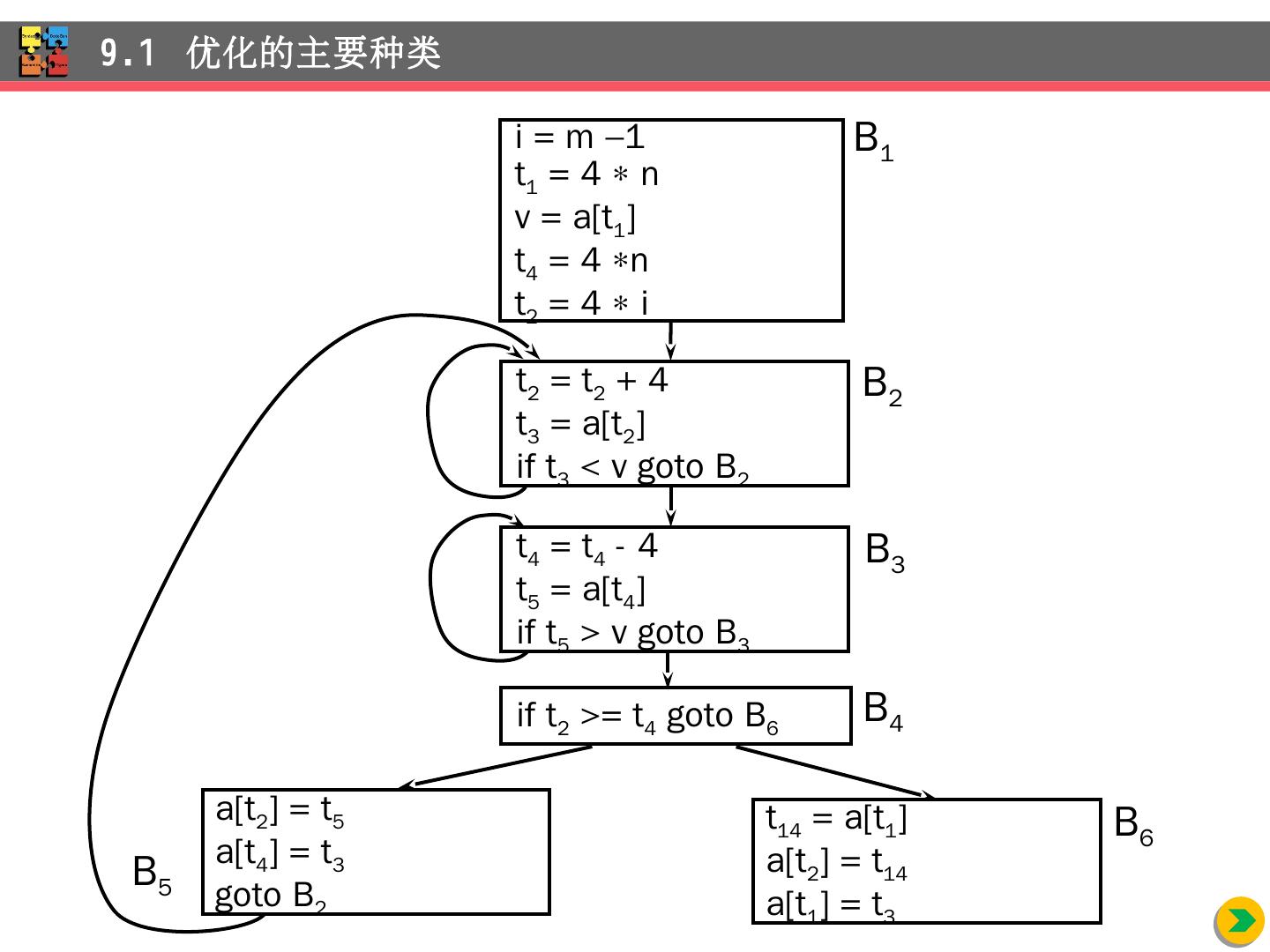
23 .9.1 优化 的主要种类 i = m 1 j = n t 1 = 4 n v = a[t 1 ] t 4 = 4 j t 2 = 4 i i = i + 1 t 2 = t 2 + 4 t 3 = a[t 2 ] if t 3 < v goto B 2 B 1 B 2 j = j 1 t 4 = t 4 - 4 t 5 = a[t 4 ] if t 5 > v goto B 3 if i >= j goto B 6 B 4 B 3 B 5 B 6 对 B 2 也可以进行类似的变换 循环控制条件可以用 t 2 和 t 4 来 表示 i+1 和 j+1 成为死代码
24 .9.1 优化 的主要种类 i = m 1 t 1 = 4 n v = a[t 1 ] t 4 = 4 n t 2 = 4 i t 2 = t 2 + 4 t 3 = a[t 2 ] if t 3 < v goto B 2 B 1 B 2 t 4 = t 4 - 4 t 5 = a[t 4 ] if t 5 > v goto B 3 if t 2 >= t 4 goto B 6 B 4 B 3 B 5 B 6 a[t 2 ] = t 5 a[t 4 ] = t 3 goto B 2 t 14 = a[t 1 ] a[t 2 ] = t 14 a[t 1 ] = t 3
25 .9.2 数据流分析 介绍 第 9 章 独立 于机器的优化
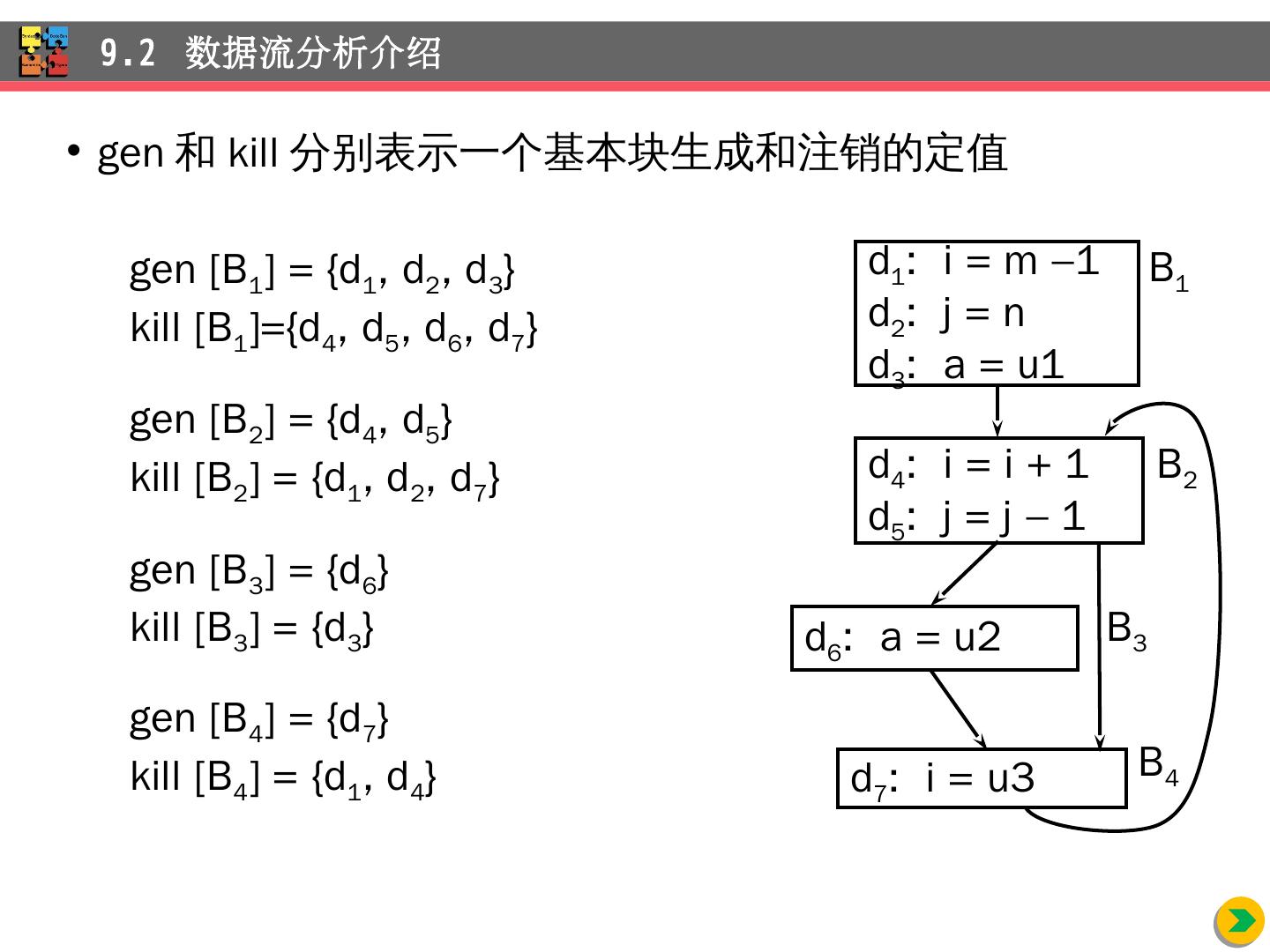
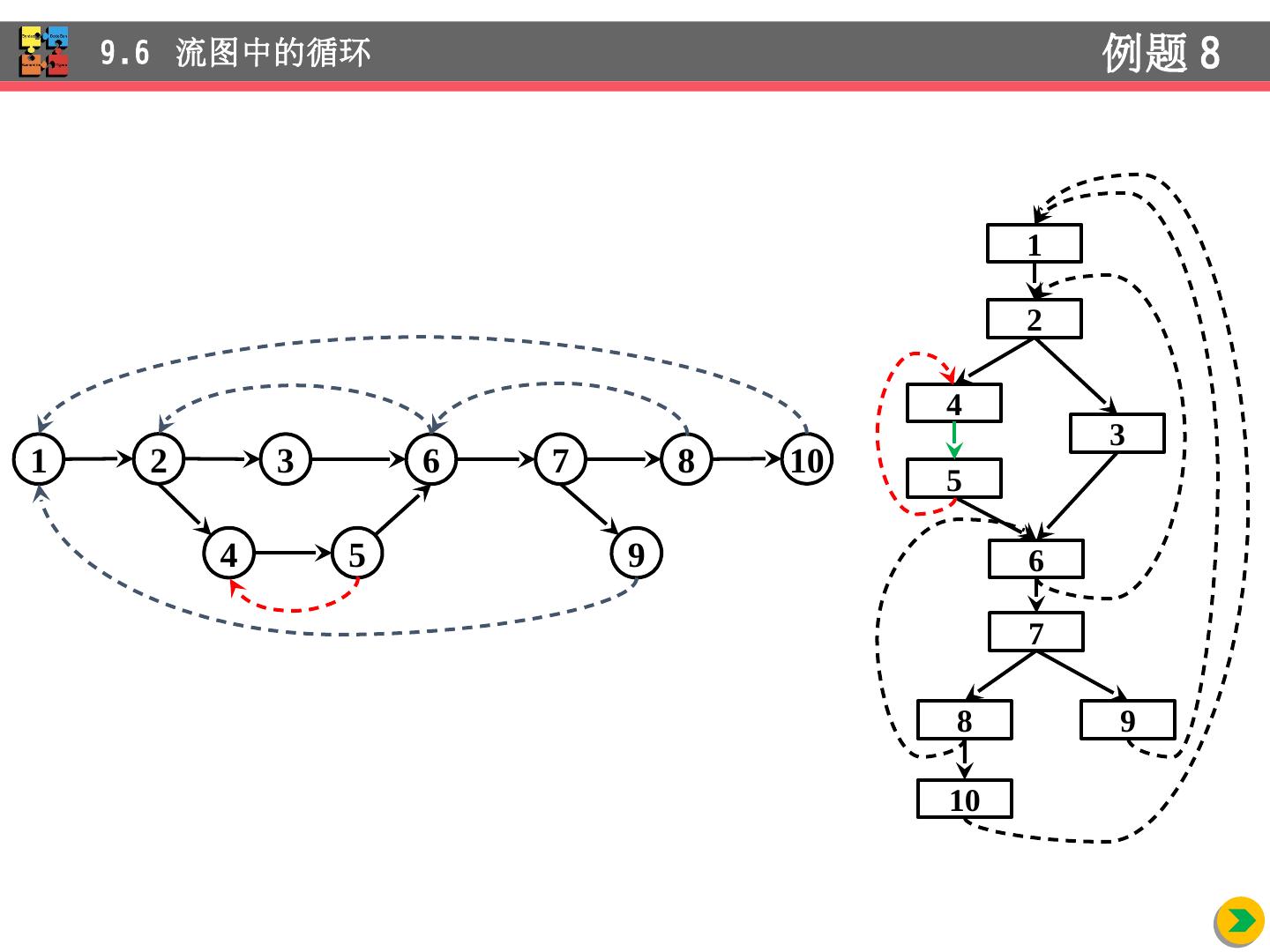
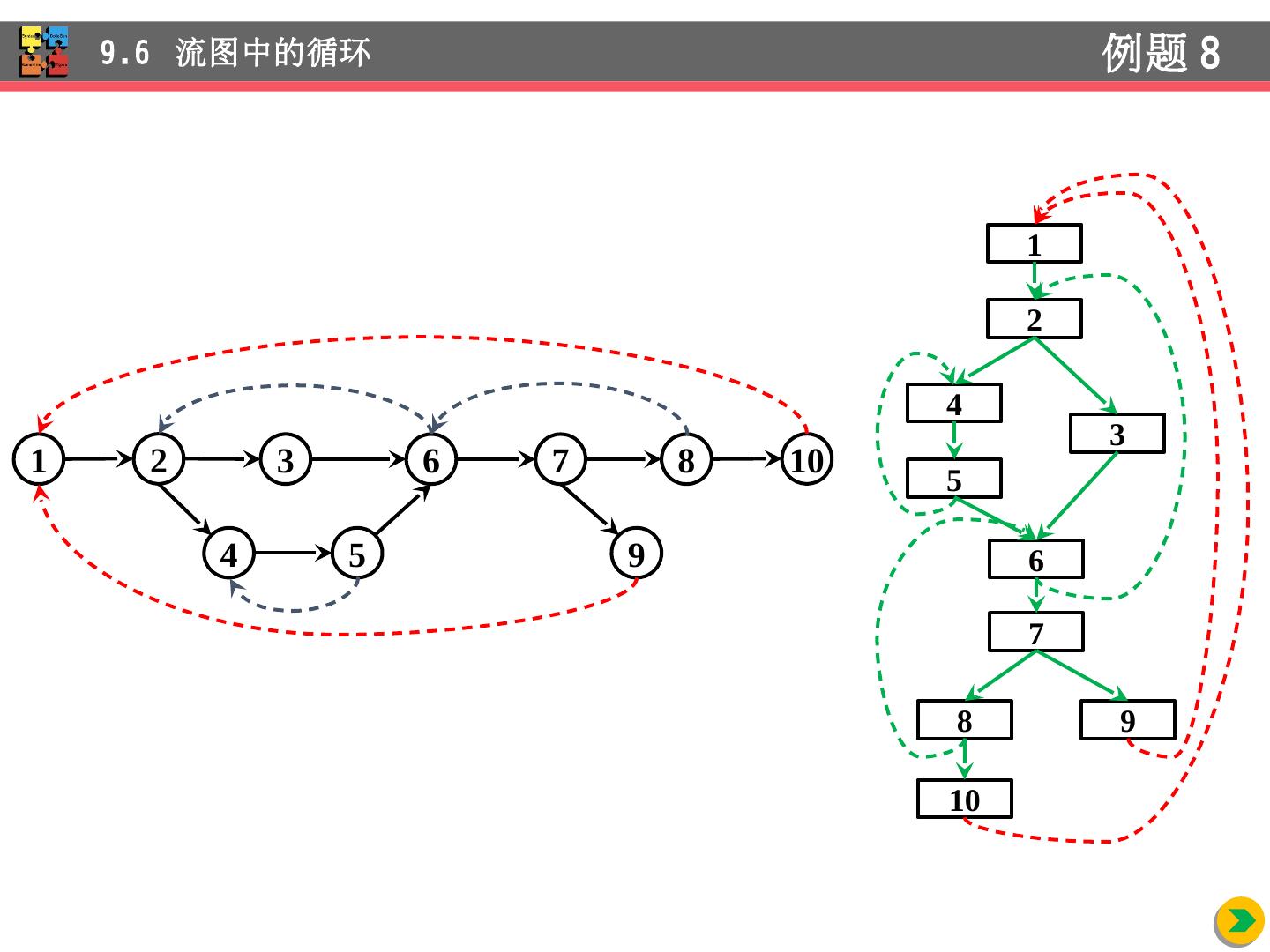
26 .9.2.1 数据流抽象 流图上的程序点 基本块中,两个相邻的语句之间为程序的一个 点 基本块的开始点和结束点 流 图上的路径 点序列 p 1 , p 2 , …, p n , 对 1 和 n - 1 间的每个 i , 满足 (1) p i 是先于一个语句的点, p i + 1 是同一块中位于该语句后的点,或者 (2) p i 是某块的结束点, p i + 1 是后继块的开始点 9.2 数据流分析 介绍 这 是针对顺序执行流图而言
27 .流 图上路径实例 - (1, 2, 3, 4, 9) - (1, 2, 3, 4, 5, 6, 7, 8, 3 , 4, 9) - (1, 2, 3, 4, 5, 6, 7, 8, 3 , 4, 5, 6, 7, 8, 3, 4, 9) - (1, 2, 3, 4, 5, 6, 7, 8, 3 , 4, 5, 6, 7, 8, 3 , 4, 5, 6, 7, 8, …) 路径长度无限 - 路径数无限 9.2 数据流分析 介绍 B 1 (1) d 2 : b = a d 3 : a = 243 goto B 3 B 4 B 2 B 3 if read()<=0 goto B 4 d 1 : a = 1 (2) (3) (4) (5) (6) (7) (8) (9)
28 .分析程序 的行为时, 必须 在 其流图上考虑 所有 的执 行 路径 (在调用或 返回语 句 被执行时,还需要 考虑 执行 路径在多个流图 之间 的 跳转) 通常 ,从流图得到的 程 序 执行路径数无限 , 且 执行 路径长度没有 有限 的上界 每个程序点的 不同 状态 数 也可能无限 程序状态 :存储单元 到 值 的映射 9.2 数据流分析 介绍 B 1 (1) d 2 : b = a d 3 : a = 243 goto B 3 B 4 B 2 B 3 if read()<=0 goto B 4 d 1 : a = 1 (2) (3) (4) (5) (6) (7) (8) (9)
29 .把握所有执行路径上的所有程序状态一般来说是不可能的 数据流分析 并不打算区分到达一个程序点的不同执行路径,也不试图掌握该点每个完整的状态 它 从这些状态中抽取解决特定数据流分析所需信息,以总结出用于该分析目的的一组有限的事实 并且 这组事实和到达这个程序点的路径无关,即从任何路径到达该程序点都有这样的事实 分析 的目的不同,从程序状态提炼的信息也不同 9.2 数据流分析 介绍