06 编译原理---中间代码生成

1 .第六章 中间代码生成 许畅 南京大学计算机系 2018年春季 

2 .本章内容  中间代码表示  表达式的有向无环图DAG  三地址代码：x = y op z  类型检查  类型、类型检查、表达式的翻译  中间代码生成  控制流、回填 2 

3 .编译器前端的逻辑结构  前端是对源语言进行分析并产生中间表示  处理与源语言相关的细节，与目标机器无关  前端后端分开的好处：不同的源语言、不同的机 器可以得到不同的编译器组合 3 

4 .中间代码表示及其好处  形式  多种中间表示，不同层次  抽象语法树  三地址代码  重定位  为新的机器建编译器，只需要做从中间代码到新的目 标代码的翻译器 (前端独立)  高层次的优化  优化与源语言和目标机器都无关 4 

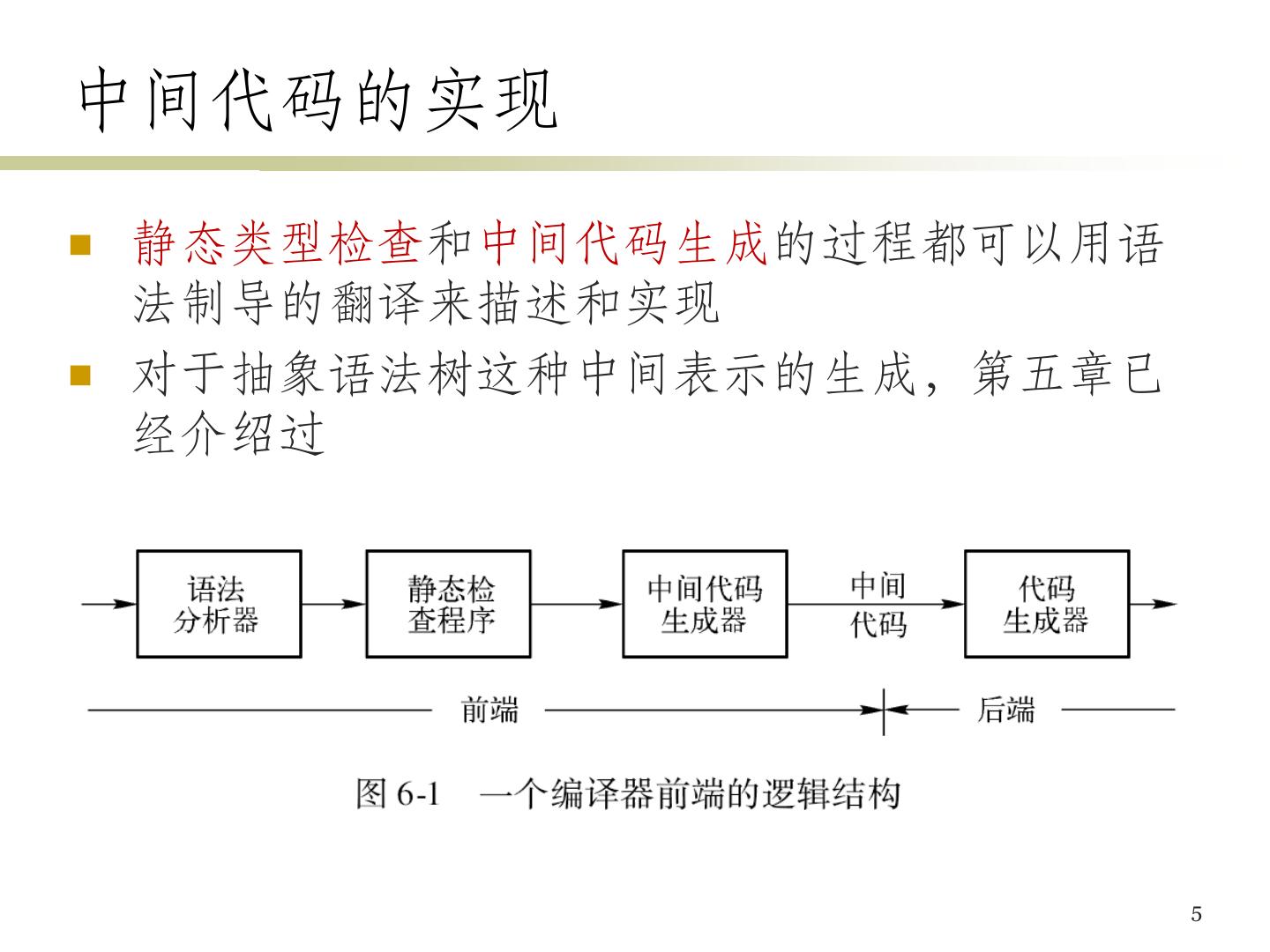
5 .中间代码的实现  静态类型检查和中间代码生成的过程都可以用语 法制导的翻译来描述和实现  对于抽象语法树这种中间表示的生成，第五章已 经介绍过 5 

6 .生成抽象语法树的语法制导定义  a + a * (b – c) + (b – c) * d的抽象语法树 6 

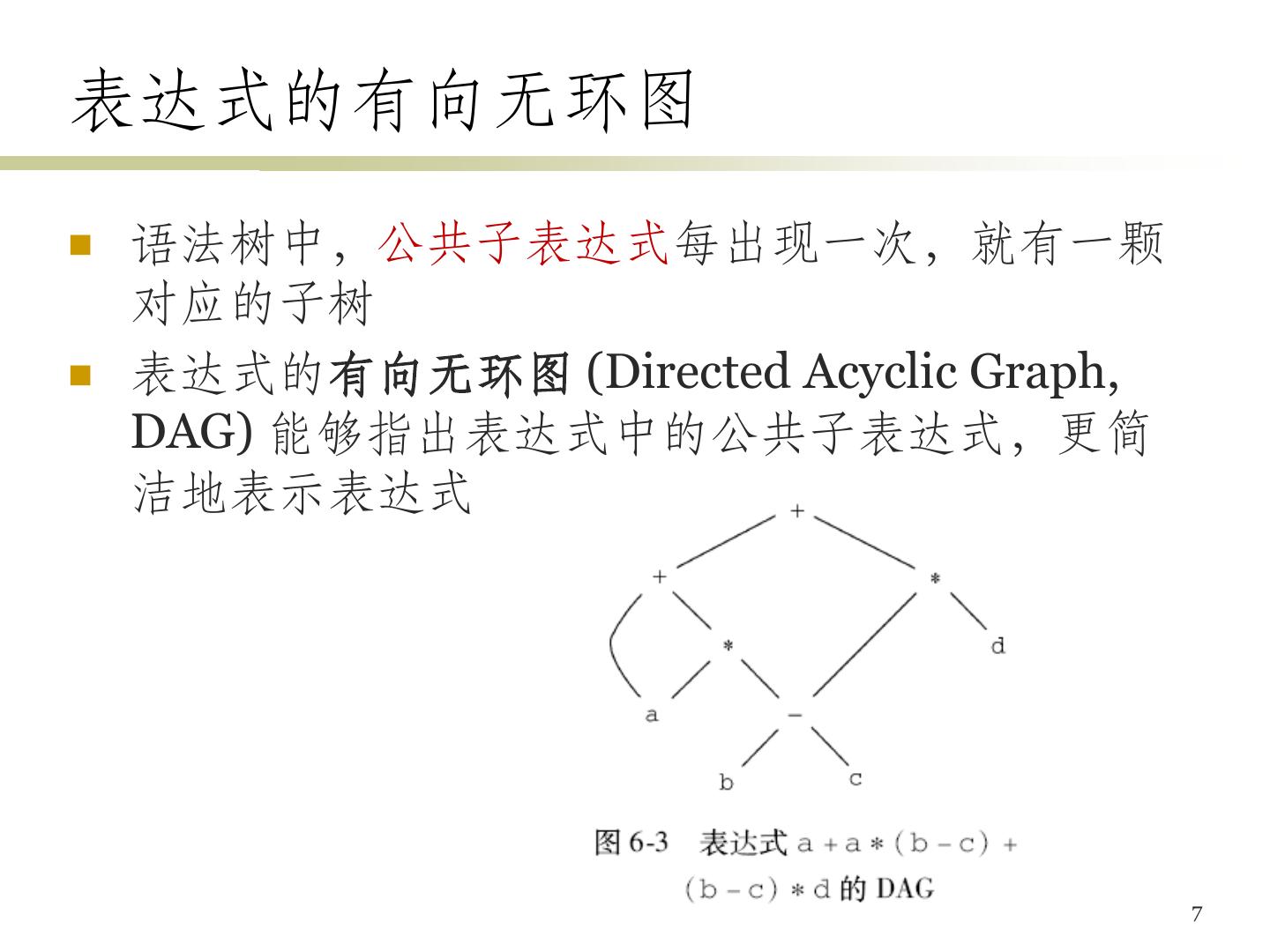
7 .表达式的有向无环图  语法树中，公共子表达式每出现一次，就有一颗 对应的子树  表达式的有向无环图 (Directed Acyclic Graph, DAG) 能够指出表达式中的公共子表达式，更简 洁地表示表达式 7 

8 .DAG构造  可以用和构造抽象语法树一样的SDD来构造  不同的处理  在函数Leaf和Node每次被调用时，构造新节点前先检 查是否已存在同样的节点，如果已经存在，则返回这 个已有的节点  构造过程示例 8 

9 .三地址代码 (1)  每条指令右侧最多有一个运算符  一般情况可以写成x = y op z  允许的运算分量  名字：源程序中的名字作为三地址代码的地址  常量：源程序中出现或生成的常量  编译器生成的临时变量 9 

10 .三地址代码 (2)  指令集合 (1)  运算/赋值指令： x = y op z x = op y  复制指令： x=y  无条件转移指令： goto L  条件转移指令： if x goto L if False x goto L  条件转移指令： if x relop y goto L 10 

11 .三地址代码 (3) • 指令集合 (2) – 过程调用/返回 • param x1 // 设置参数 • param x2 • … • param xn • call p, n // 调用子过程p，n为参数个数 – 带下标的复制指令：x = y[i] x[i] = y • 注意：i表示离开数组位置第i个字节，而不是数组的第i个元素 – 地址/指针赋值指令 • x = &y x = *y *x = y 11 

12 .例子  语句  do i = i + 1; while (a[i] < v); 12 

13 .三地址指令的四元式表示方法 • 在实现时，可使用四元式/三元式/间接三元式/静 态单赋值来表示三地址指令 • 四元式：可以实现为记录 (或结构) – 格式 (字段) ： op arg1 arg2 result – op：运算符的内部编码 – arg1, arg2, result是地址 – x=y+z + y z x • 单目运算符不使用arg2 • param运算不使用arg2和result • 条件转移/非条件转移将目标标号放在result字段 13 

14 .四元式的例子  赋值语句：a = b *  c + b *  c 14 

15 .三元式表示 • 三元式 (Triple) ： op arg1 arg2 • 使用三元式的位置来引用三元式的运算结果 • x = y op z需要拆分为 (?是编号) – ? op y z – = x (?) • x[i] = y需要拆分为两个三元式 – 求x[i]的地址，然后再赋值 • 优化时经常需要移动/删除/添加三元式，导致三 元式的移动 15 

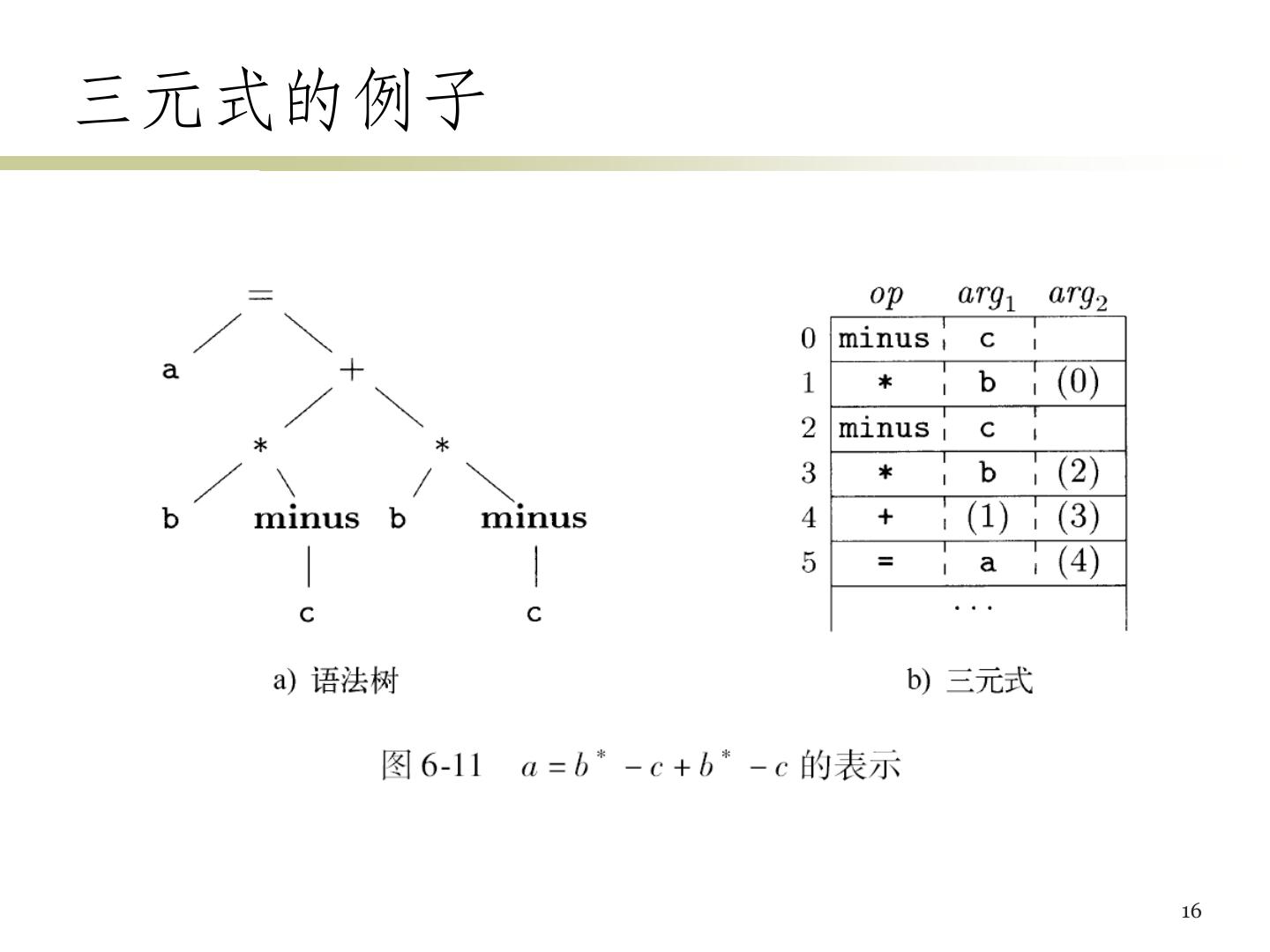
16 .三元式的例子 16 

17 .间接三元式  包含了一个指向三元式的指针的列表  可以对这个列表进行操作，完成优化功能，操作 时不需要修改三元式中的参数 17 

18 .静态单赋值 (SSA)  Static Single Assignment (SSA) 中的所有赋值都 是针对不同名的变量  对于同一个变量在不同路径中定值的情况，可以 使用φ函数来合并不同的定值  if (flag) x = 1; else x = 1; y = x * a;  if (flag) x1 = 1; else x2 = 1; x3 = φ(x1, x2); y = x3 * a; 18 

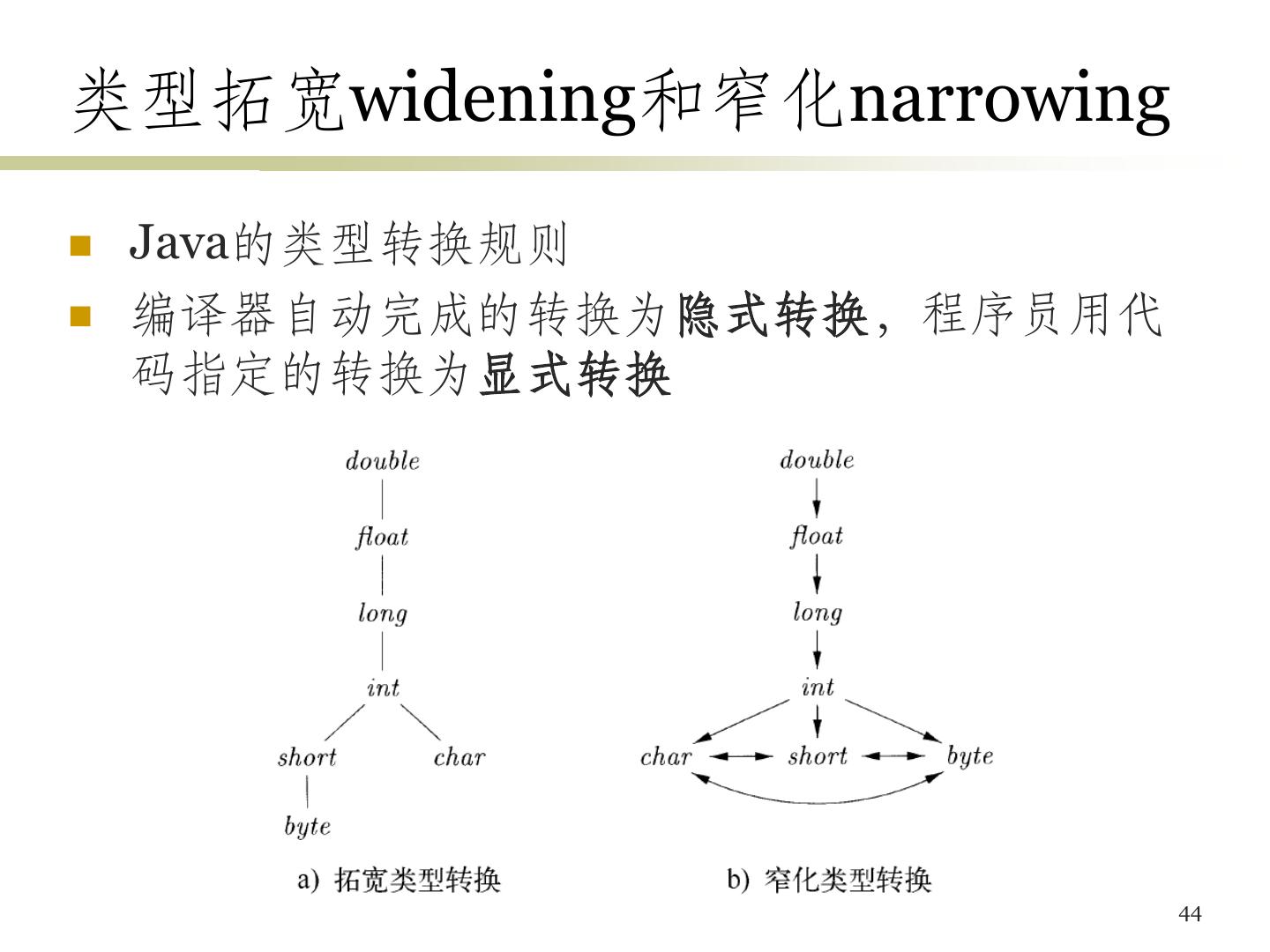
19 .类型和声明 • 类型检查 (Type checking) – 利用一组规则来检查运算分量的类型和运算符的预期 类型是否匹配 • 类型信息的用途 – 查错、确定名字需要的内存空间、计算数组元素的地 址、类型转换、选择正确的运算符 • 本节的内容 – 确定名字的类型 – 变量的存储空间布局 (相对地址) 19 

20 .类型表达式 • 类型表达式 (Type expression)：表示类型的结构 – 可能是基本类型 – 也可能通过类型构造算子作用于类型表达式而得到 • 如int [2][3]，表示由两层数组组成的数组  array(2, array(3, integer))  array是类型构造算子，有两个参数：数字和类型 20 

21 .类型表达式的定义  基本类型 (或类型名) 是类型表达式  如：boolean, char, integer, float, void, …  类型构造算子array作用于数字和类型表达式得到 类型表达式，record作用于字段名和相应的类型 得到类型表达式  类型构造算子→可得到函数类型的类型表达式  如果s, t是类型表达式，其笛卡尔积s  t也是类型 表达式  如：struct { int a[10]; float f; } st;  对应于：record((a  array(0..9, int))  (f  real)) 21 

22 .类型等价  不同的语言有不同的类型等价的定义  结构等价  它们是相同的基本类型，或  由相同的构造算子作用于结构等价的类型而得到，或  一个类型是另一个类型表达式的名字  名等价  类型名仅代表自身 (仅有前两个条件) 22 

23 .类型的声明 • 处理基本类型、数组类型或记录类型的文法 – D  T id; D | ε – T  B C | record '{' D '}' – B  int | float – C  ε | [num] C • 应用该文法及其对应的语法制导定义，除了得到 类型表达式之外，还得进行各种类型的存储布局 23 

24 .局部变量的存储布局  变量的类型可以确定变量需要的内存  即类型的宽度 (该类型一个对象所需的存储单元的数量)  可变大小的数据结构只需要考虑指针  函数的局部变量总是分配在连续的区间  因此给每个变量分配一个相对于这个区间开始处的相 对地址  变量的类型信息保存在符号表中 24 

25 .计算T的类型和宽度的SDT • 综合属性：type, width • 全局变量t和w用于将类型和宽度信息从B传递到C  ε • 相当于C的继承属性 (也可以把t和w替换为C.t和C.w) { { ;} 25 

26 .SDT运行的例子  输入：int [2][3] 26 

27 .声明序列的SDT (1) • 在处理一个过程/函数时，局部变量应该放到单独 的符号表中去 • 这些变量的内存布局独立 – 相对地址从0开始，变量的放置和声明的顺序相同 • SDT的处理方法 – 变量offset记录当前可用的相对地址 – 每分配一个变量，offset增加相应的值 (加宽度) • top.put(id.lexeme, T.type, offset) – 在符号表中创建条目，记录标识符的类型和偏移量 27 

28 .声明序列的SDT (2) • 可以把offset看作D的继承属性 – D.offset表示D中第一个变量的相对地址 – P  { D.offset = 0; } D – D  T id; { D1.offset = D.offset + T.width; } D1 28 

29 .记录和类中的字段 (1)  记录变量声明的翻译方案  约定  一个记录中各个字段的名字必须互不相同  字段名的偏移量 (相对地址)，是相对于该记录的数据 区字段而言的  记录类型使用一个专用的符号表，对其各个字段 的类型和相对地址进行单独编码  记录类型record(t)：record是类型构造算子，t是 符号表对象，保存该记录类型各个字段的信息 29