07 编译器原理与技术---中间代码生成

1 .第 7 章 中间代码生成 编译原理与技术

2 .介绍 几种常用的中间表示 ： 后缀 表示、图形表示和三地址代码 用语法制导定义和翻译方案来说明源语言的各种构造怎样被翻译成中间形式 7 中间代码生成 内容提要 分析器 静态 检查器 中间 代码 生成器 中间 代码 记号流 代码 生成器

3 .7.1 中间语言 第 7 章 中间代码生成

4 .7.1.1 后缀表示 E  E op E | uop E | ( E) | id | num 表达式 E 的后缀表示可以如下归纳定义： 表达式 E 后缀 式 E  id id num num E 1 op E 2 E 1  E 2  op uop E E  uop ( E ) E  7.1 中间语言

5 .后缀表示不需要括号 (8 - 5) + 2 的后缀表示是8 5 - 2 + 后缀 表示的最大优点是便于计算机处理表达式 计算 栈 输入 串 8 5 - 2 + 8 5 - 2 + 8 5 - 2 + 3 2 + 3 2 + 5 后缀 表示也可以拓广到表示赋值语句和控制语句，但很难用栈来描述控制语句的 计算 7.1 中间语言

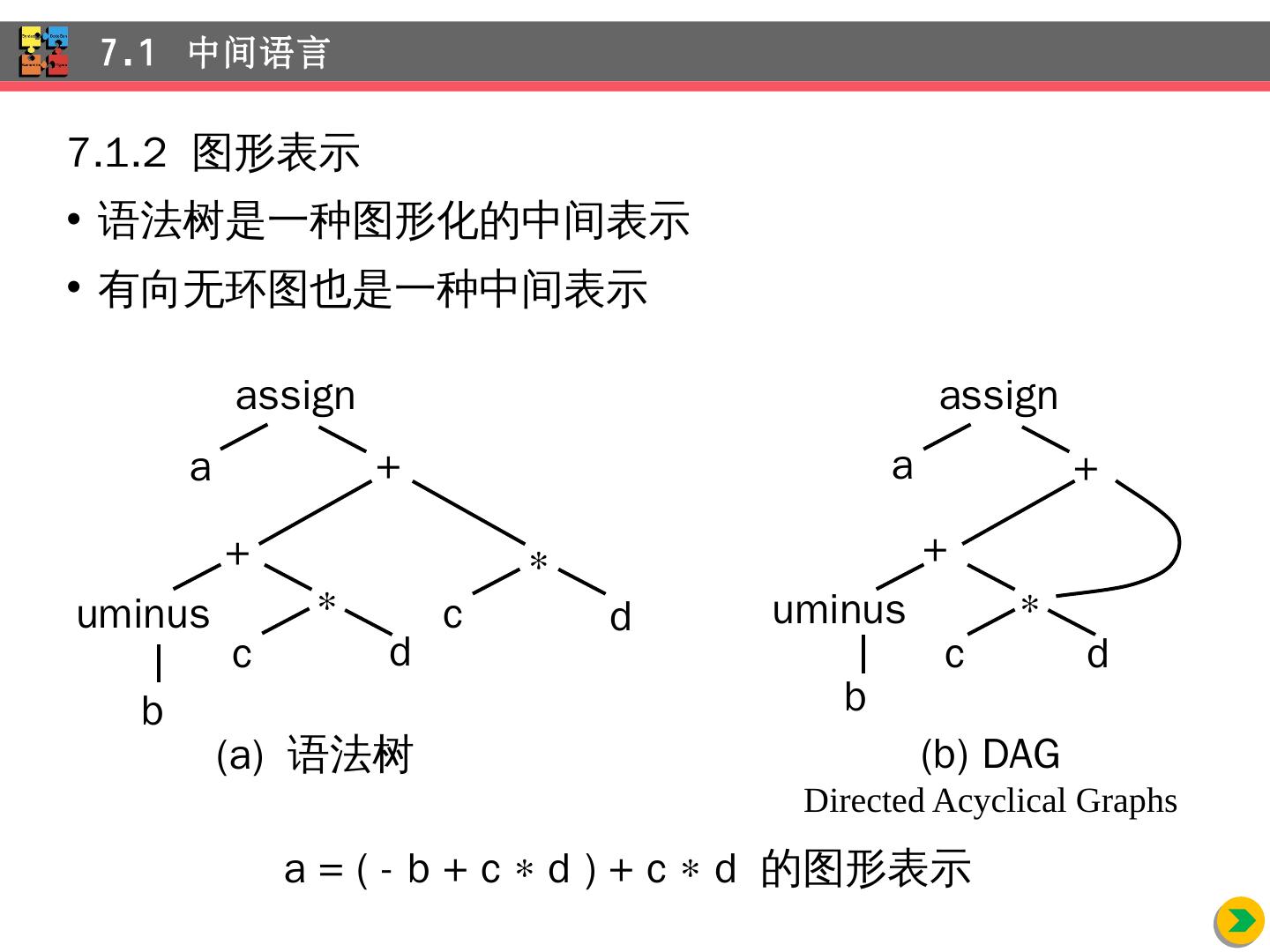
6 .7.1.2 图形表示 语法树是一种图形化的中间表示 有向无环图 也是一种中间 表示 7.1 中间语言 assign a + +  b c d uminus ( b) DAG Directed Acyclical Graphs assign a + +   b c d c d uminus ( a) 语法树 a = ( - b + c  d ) + c  d 的 图形表示

7 .构造赋值语句语法树的语法制导定义 修改构造结点的函数可生成有向无环图 7.1 中间语言 产 生 式 语 义 规 则 S  id = E S.nptr = mkNode ( assign, mkLeaf (id, id.entry ), E.nptr ) E  E 1 + E 2 E.nptr = mkNode ( +, E 1 .nptr, E 2 .nptr) E  E 1  E 2 E.nptr = mkNode (  , E 1 .nptr, E 2 .nptr) E  - E 1 E.nptr = mkUNode ( uminus , E 1 .nptr) E  (E 1 ) E.nptr = E 1 .nptr F  id E.nptr = mkLeaf (id, id.entry )

8 .7.1.3 三地址代码 一般形式： x = y op z 例 表达式 x + y  z 翻译成的三地址语句序列是 t 1 = y  z t 2 = x + t 1 7.1 中间语言

9 .三地址代码是语法树或 DAG 的一种线性表示 例 a = ( - b + c  d ) + c  d 语法树的代码 t 1 = - b t 2 = c  d t 3 = t 1 + t 2 t 4 = c  d t 5 = t 3 + t 4 a = t 5 7.1 中间语言 assign a + +   b c d c d uminus DAG 的代码 t 1 = - b t 2 = c  d t 3 = t 1 + t 2 t 4 = t 3 + t 2 a = t 4 assign a + +  b c d uminus

10 .本书常用的三地址语句 赋值 语句 x = y op z ， x = op y ， x = y 无条件转移 goto L 条件转移 if x relop y goto L 过程调用 param x 和 call p , n 过程返回 return y 索引 赋值 x = y[ i ] 和 x[ i ] = y 地址和指针 赋值 x = & y，x =  y 和  x = y 7.1 中间语言

11 .7.1. 4 静态单赋值形式 一种便于某些代码优化的中间表示 和三地址代码的主要区别 所有 赋值指令都是对不同名字的变量的赋值 三地址代码 静态 单赋值形式 p = a +b p 1 = a +b q = p - c q 1 = p 1 - c p = q  d p 2 = q 1  d p = e - p p 3 = e - p 2 q = p + q q 2 = p 3 + q 1 7.1 中间语言

12 .一个变量在不同路径上都定值的解决办法 if (flag) x =  1; else x = 1; y = x  a; 改成 if (flag) x 1 =  1; else x 2 = 1; x 3 =  (x 1 , x 2 ); // 由 flag 的值决定用 x 1 还是 x 2 y = x  x 3 ; 7.1 中间语言

13 .7.2 声明语句 第 7 章 中间代码生成

14 .本节介绍 为局部名字建立符号表条目 为它分配存储单元 符号表中包含名字的类型和分配给它的存储单元的相对地址等信息 7.2 声明 语句

15 .7.2.1 过程中的声明 计算 被声明名字的类型和相对地址 P  { offset = 0 } D ; S D  D ; D D  id : T { enter ( id.lexeme , T.type , offset); offset = offset + T.width } T  integer { T.type = integer; T.width = 4 } T  real { T.type = real; T.width = 8 } T  array [ num ] of T 1 { T.type = array ( num.val , T 1 .type); T.width = num.val  T 1 .width} T   T 1 { T.type = pointer (T 1 .type); T.width = 4 } 7.2 声明 语句

16 .7.2.2 作用域信息的保存 所讨论语言的文法 P  D; S D  D ; D | id : T | proc id ; D ; S 7.2 声明 语句 sort var a:…; x:…; readarray var i:…; exchange quicksort var k, v:…; partition var i , j:…; 图 6.14 的 程序参数 被略去

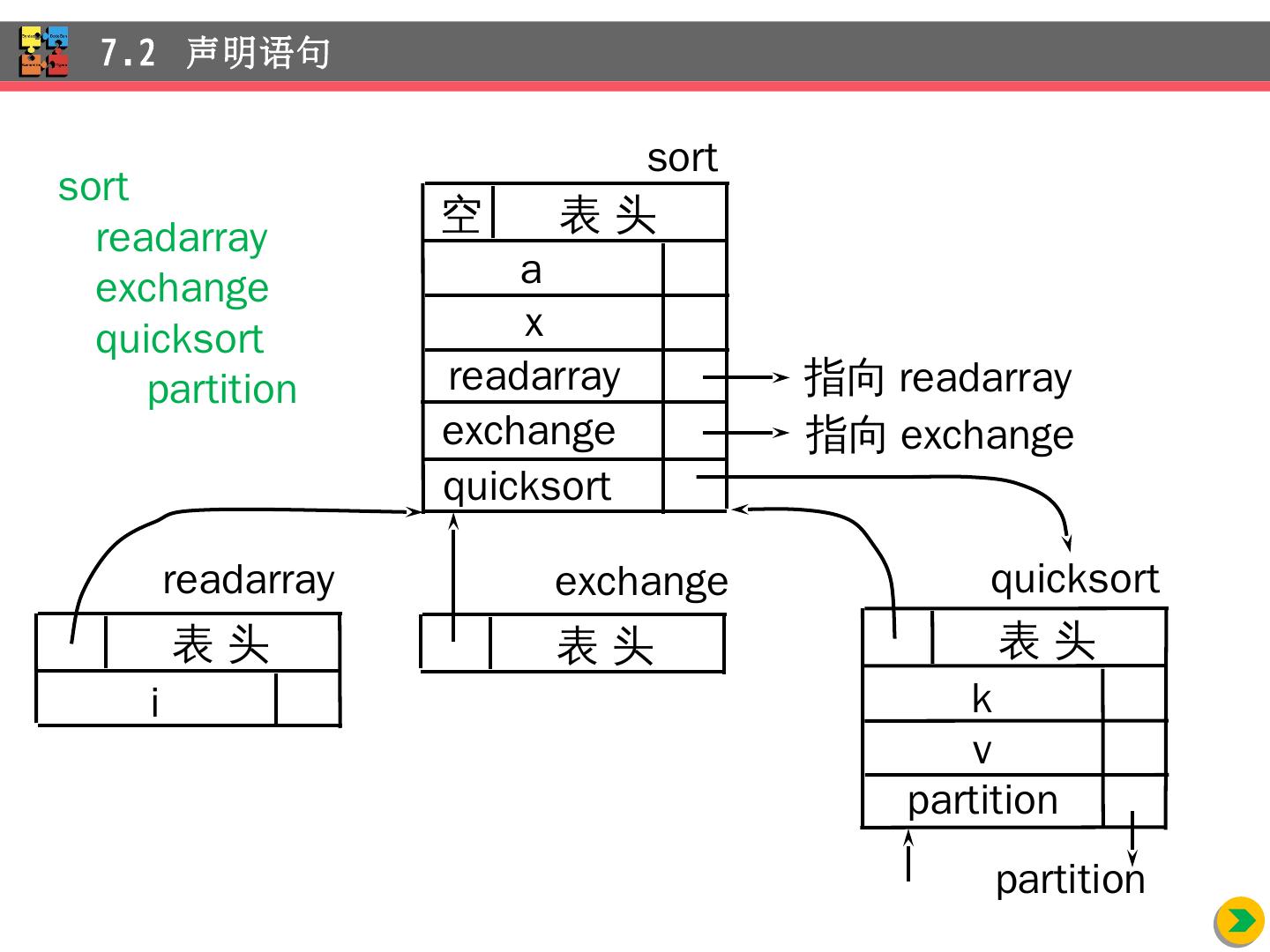
17 .7.2 声明 语句 exchange readarray x a 表 头 空 sort quicksort 指向 readarray partition v k 表 头 quicksort readarray i 表 头 exchange 表 头 指向 exchange partition sort readarray exchange quicksort partition

18 .符号表的特点 各过程有各自的符号表 符号表之间有双向链 构造符号表时需要符号表栈 构造符号表需要偏移记录 栈 语义动作用到的函数 mkTable (previous ) // 创立新表 enter(table, name, type, offset ) // 增加新的 id 条目 addWidth (table, width ) // 将表大小写入表中 enterProc (table, name, newtable ) // 添加新的表条目 7.2 声明 语句

19 .P  M D ; S { addWidth (top ( tblptr ), top (offset)); pop( tblptr ); pop (offset) } M   { t = mkTable (nil); push(t , tblprt ); push (0, offset) } D  D 1 ; D 2 D  proc id ; N D 1 ; S { t = top( tblptr ); addWidth (t , top(offset) ); pop( tblptr ); pop(offset); enterProc (top( tblptr ), id.lexeme , t) } D  id : T { enter(top( tblptr ), id.lexeme , T.type , top(offset)); top(offset ) = top(offset) + T.width } N   { t = mkTable (top( tblptr ) ); push(t , tblptr ); push(0, offset) } 7.2 声明 语句

20 .7.2.3 记录的域名 T  record D end 记录 类型单独建符号表，作为类型表达式 的主要 部分，域的相对地址从 0 开始 T  record L D end { T.type = record (top( tblptr ) ); T.width = top(offset); pop( tblptr ); pop(offset) } L   { t = mkTable (nil); push(t , tblprt ); push(0, offset) } 7.2 声明 语句 record a : … ; r : record i : … ; . . . end ; k : … ; end

21 .7.3 赋值语句 第 7 章 中间代码生成

22 .7.3.1 符号表中的名字 S  id := E { p = lookup( id.lexeme ); if p != nil then emit ( p, = , E.place ) else error } E  E 1 + E 2 { E.place = newTemp (); emit ( E.place , = , E 1 .place, + , E 2 .place) } E  - E 1 { E.place = newTemp (); emit ( E.place , = , uminus , E 1 .place) } E  (E 1 ) { E.place = E 1 .place } E  id { p = lookup( id.lexeme ); if p != nil then E.place = p else error } 7.3 赋值语句

23 .7.3. 2 数组元素的地址计算 一维数组 A 的第 i 个元素的地址计算 base + ( i - low )  w 变换成 i  w + (base - low  w) 减少了运行时的计算 7.3 赋值语句

24 .二维数组 A: array[1..2, 1..3] of T 列为主 A[1, 1], A[2, 1], A[1, 2], A[2, 2], A[1, 3], A[2, 3] 行 为主 A[1, 1], A[1, 2], A[1, 3], A[2, 1], A[2, 2], A[2, 3] A[i 1 , i 2 ] 的 地址： base + ((i 1 - low 1 )  n 2 + (i 2 - low 2 ))  w ( 其中 n 2 =high 2 - low 2 +1 ) 变换成 (( i 1  n 2 )+i 2 )  w + base - ((low 1  n 2 )+low 2 )  w 7.3 赋值语句 A[1, 1] A[1 , 2] A[1, 3] A[2, 1] A[2, 2] A[2, 3] i 1  i 2  A[1, 1] A[1 , 2] … A[2, 1] A[2, 2] … … … …

25 .多维数组下标变量 A[i 1 , i 2 , ..., i k ] 的地址表达式 ( (… ( ( i 1  n 2 +i 2 )  n 3 +i 3 ) … )  n k +i k )  w + base  ((…((low 1  n 2 +low 2 )  n 3 +low 3 ) … )  n k +low k )  w 7.3 赋值语句

26 .7.3. 3 数组元素地址计算的翻译方案 下标变量访问的产生式 L  id [ Elist ] | id Elist  Elist , E | E 不 便于在处理下标表达式时到符号表取信息 为便于写语义动作，改成等价的 L  Elist ] | id Elist  Elist , E | id [E 7.3 赋值语句

27 .所有产生式 S  L := E E  E + E E  (E ) E  L L  Elist ] L  id Elist  Elist , E Elist  id [ E 7.3 赋值语句

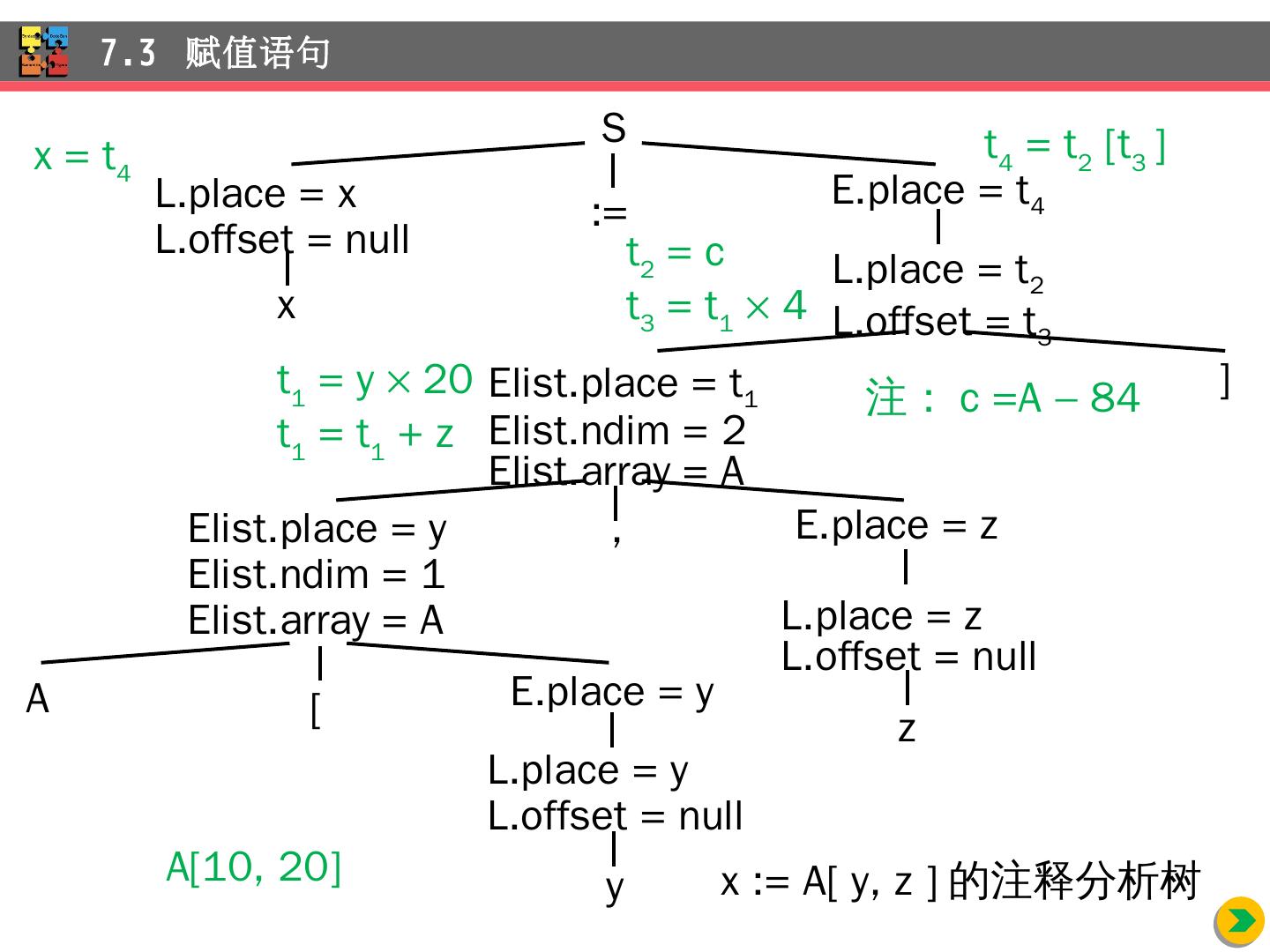
28 .L  id { L.place = id.place ; L.offset = null; } Elist  id [ E { Elist.place = E.place ; Elist.ndim = 1; Elist.array = id.place ; } Elist  Elist 1 , E { t = newTemp (); m = Elist 1 .ndim + 1; emit (t, =, Elist 1 .place,  , limit(Elist 1 .array, m ); ); emit (t, =, t, +, E.place ); Elist.array = Elist 1 .array; Elist.place = t; Elist.ndim = m; } L  Elist ] { L.place = newTemp (); emit ( L.place , =, base( Elist.array ), -, invariant( Elist.array )); L.offset = newTemp (); emit ( L.offset , =, Elist.place ,  , width( Elist.array )); } 7.3 赋值语句

29 .E  L { if L.offset == null then /  L 是简单变量  / E.place = L.place ; else { E.place = newTemp (); emit ( E.place , =, L.place , [, L.offset , ]); } } E  E 1 + E 2 { E.place = newTemp (); emit ( E.place , =, E 1 .place , +, E 2 .place ); } E  ( E 1 ) { E.place = E 1 .place; } S  L := E { if L.offset == null then /  L 是简单变量  / emit ( L.place , =, E.place ); else emit ( L.place , [, L.offset , ], =, E.place ); } 7.3 赋值语句