05 编译原理---语法制导的翻译

1 .第五章 语法制导的翻译 许畅 南京大学计算机系 2018年春季 

2 .介绍  使用上下文无关文法引导语言的翻译  CFG的非终结符号代表了语言的某个构造  程序设计语言的构造由更小的构造组合而成  一个构造的语义可以由小构造的含义综合而来  比如：表达式x + y的类型由x、y的类型和运算符+决定  也可以从附近的构造继承而来  比如：声明int x中x的类型由它左边的类型表达式决定 2 

3 .语法制导定义和语法制导翻译 • 语法制导定义 – 将文法符号和某些属性相关联，并通过语义规则来描 述如何计算属性的值 – E  E1 + T E.code = E1.code || T.code || '+' – 属性code代表表达式的逆波兰表示，规则说明加法表 达式的逆波兰表示由两个分量的逆波兰表示并置，然 后加上'+'得到 • 语法制导翻译 – 在产生式体中加入语义动作，并在适当时候执行动作 – E  E1 + T { print '+'; } 3 

4 .语法制导的定义 (SDD) • Syntax-Directed Definition (SDD) 是上下文 无关文法和属性/规则的结合 – 属性和文法符号相关联，按照需要来确定各个文法符 号需要哪些属性 – 规则和产生式相关联 • 对于文法符号X和属性a，我们用X.a表示分析树 中某个标号为X的结点的值 • 一个分析树结点和它的分支对应于一个产生式规 则，而对应的语义规则确定了这些结点上的属性 的取值和计算 4 

5 .分析树和属性值 (1) • 假设我们需要知道一个表达式的类型，以及对应 代码将它的值存放的内存地址 • 我们需要两个属性：type, place • 产生式规则：E  E1 + T – 假设只有int/float类型 – E.type = if (E1.type == T.type) T.type else float; – E.place = newTempPlace(); // 返回一个新的内存位置 • 产生式规则：F  id – F.type = lookupIDTable(id.lexValue)->type; – F.place = lookupIDTable(id.lexValue)->address; 5 

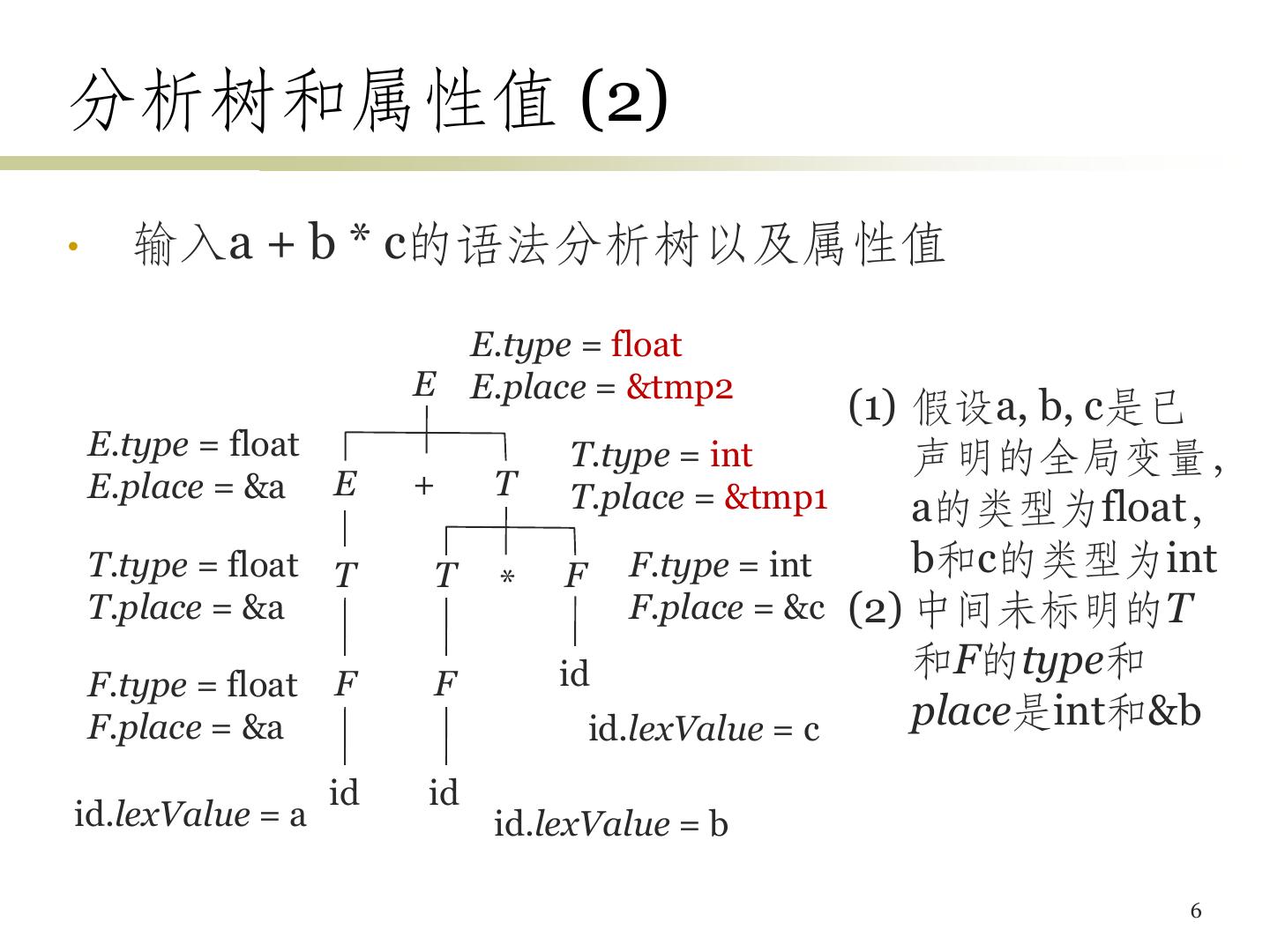
6 .分析树和属性值 (2) • 输入a + b * c的语法分析树以及属性值 E.type = float E E.place = &tmp2 (1) 假设a, b, c是已 E.type = float T.type = int 声明的全局变量， E.place = &a E + T T.place = &tmp1 a的类型为float， T.type = float T T F F.type = int b和c的类型为int * T.place = &a F.place = &c (2) 中间未标明的T id 和F的type和 F.type = float F F F.place = &a id.lexValue = c place是int和&b id id id.lexValue = a id.lexValue = b 6 

7 .综合属性和继承属性 • 综合属性 (Synthesized Attribute) • 结点N的属性值由N的产生式所关联的语义规则来定义 • 通过N的子结点或N本身的属性值来定义 • 继承属性 (Inherited Attribute) • 结点N的属性值由N的父结点所关联的语义规则来定义 • 依赖于N的父结点、N本身和N的兄弟结点上的属性值 • 几条约束 • 不允许N的继承属性通过N的子结点上的属性来定义， 但允许N的综合属性依赖于N本身的继承属性 • 终结符号有综合属性 (来自词法分析)，但无继承属性 7 

8 .SDD的例子 • 计算表达式行L的值 (属性val) • 计算L的val值需要E的val值，E的val值又依赖于 E1和T的val值… • 终结符号digit有综合属性lexval 8 

9 .S属性的SDD • 只包含综合属性的SDD称为S属性的SDD – 每个语义规则都根据产生式体中的属性值来计算头部 非终结符号的属性值 • S属性的SDD可以和LR语法分析器一起实现 – 栈中的状态/文法符号可以附加相应的属性值 – 归约时，按照语义规则计算归约得到的符号的属性值 • 语义规则不应该有复杂的副作用 – 要求副作用不影响其它属性的求值 – 没有副作用的SDD称为属性文法 9 

10 .语法分析树上的SDD求值 (1) • 实践中很少先构造语法分析树再进行SDD求值， 但在分析树上求值有助于翻译方案的可视化，便 于理解 • 注释语法分析树 – 包含了各个结点的各属性值的语法分析树 • 步骤 – 对于任意的输入串，首先构造出相应的分析树 – 给各个结点 (根据其文法符号) 加上相应的属性 – 按照语义规则计算这些属性的值 10 

11 .语法分析树上的SDD求值 (2) • 按照分析树中的分支对应的文法产生式，应用相 应的语义规则计算属性值 • 计算顺序 – 如果某个结点N的属性a为f(N1.b1, N2.b2, …, Nk.bk)，那 么我们需要先算出N1.b1, N2.b2, …, Nk.bk的值 • 如果可以给各个属性值排出计算顺序，那么这个 注释分析树就可以计算得到 – S属性的SDD一定可以按照自底向上的方式求值 • 下面的SDD不能计算 – AB A.s = B.i B.i = A.s + 1 11 

12 .注释分析树的例子 3*5+4n 12 

13 .适用于自顶向下分析的SDD (1)  前面的文法存在左递归，我们无法用自顶向下的 分析方法进行处理  但消除左递归之后，我们无法直接使用属性val进 行处理  比如规则：T  F T ' T'*FT'|  T对应的项中，第一个因子对应F，而运算符却在T '中  需要用继承属性来完成这样的计算 比较T  T * F | F 13 

14 .适用于自顶向下分析的SDD (2) 比较T  T * F | F T '的属性inh实际上继承了相应的*号的左运算分量 14 

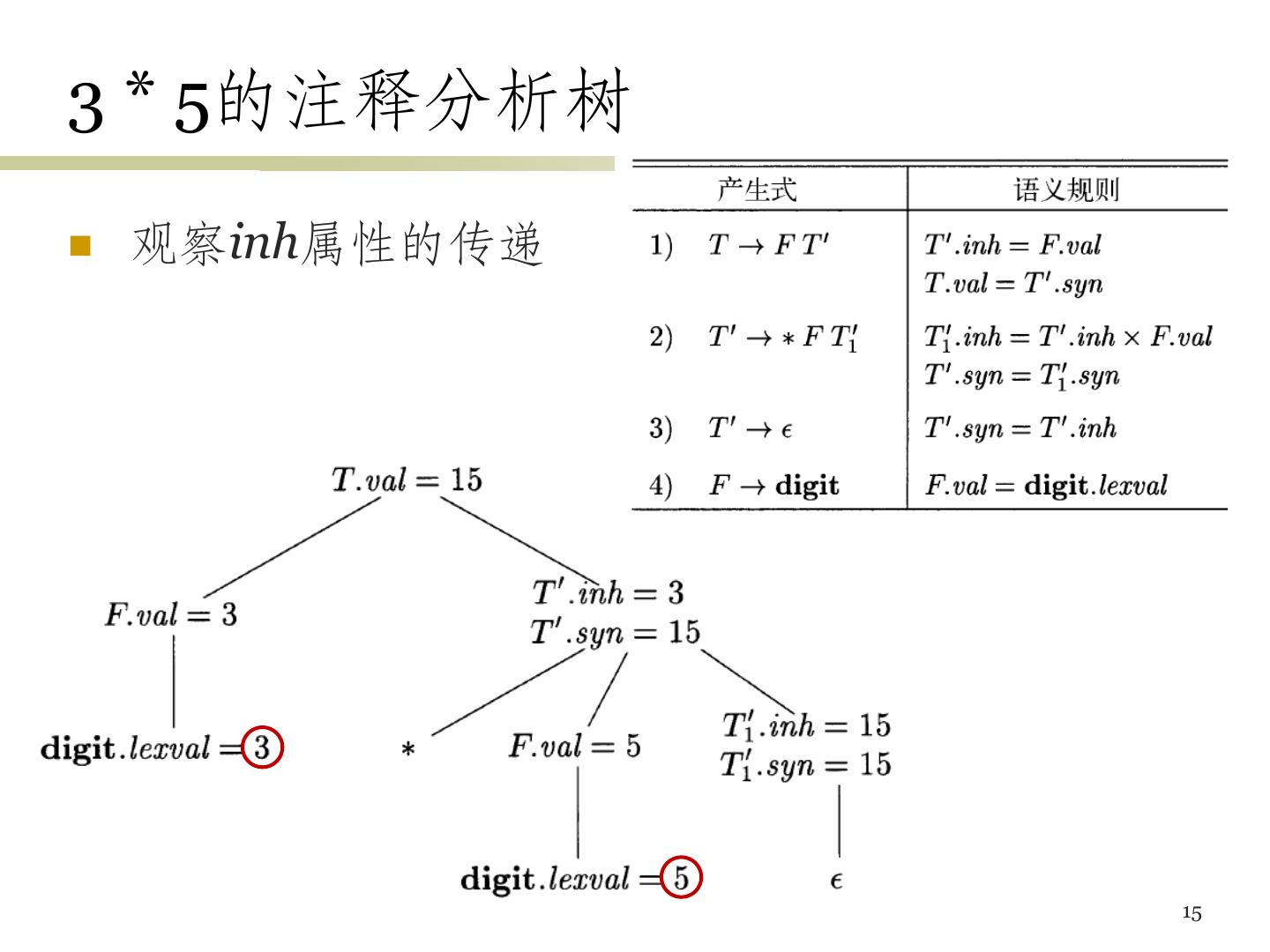
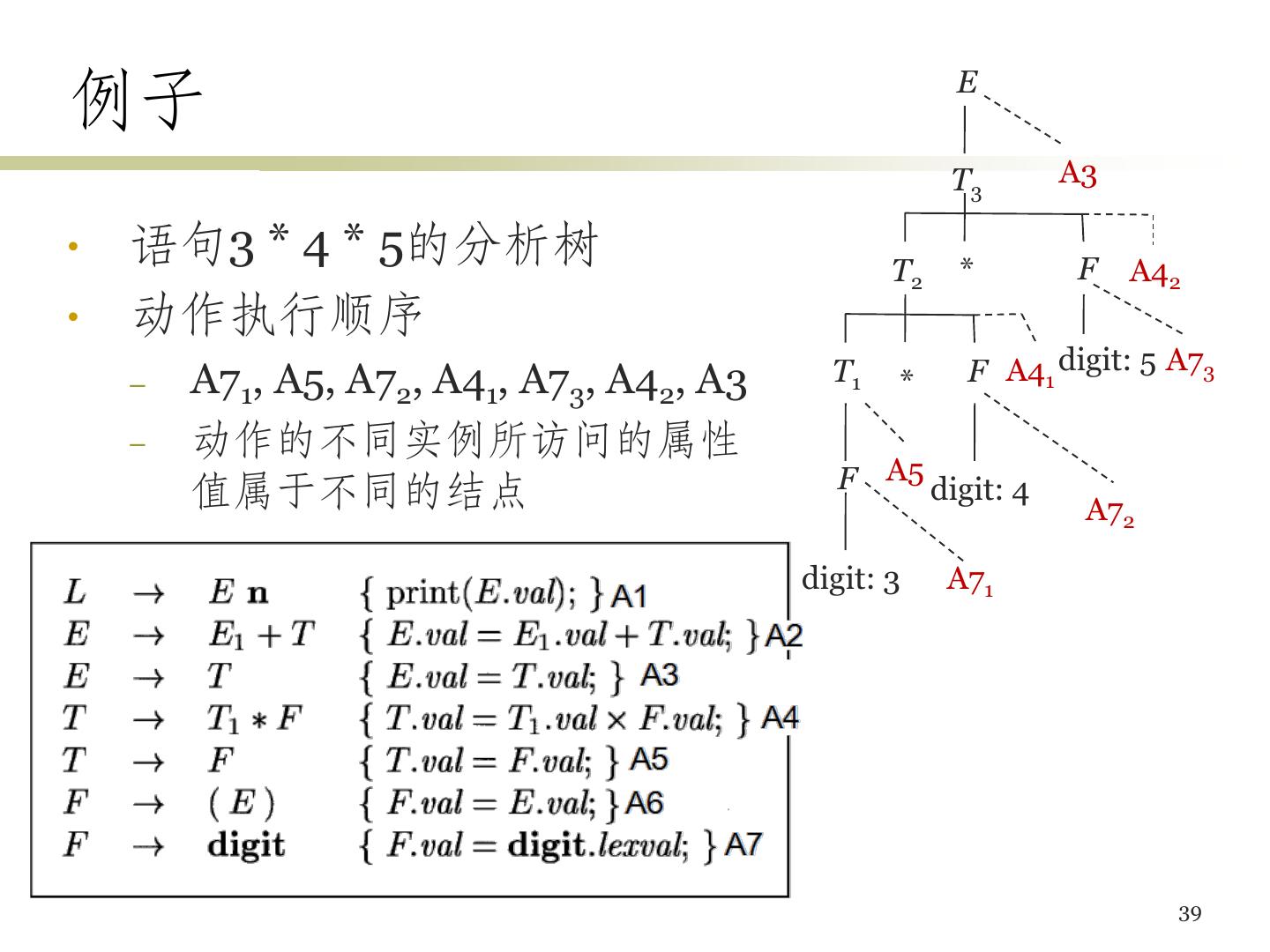
15 .3 * 5的注释分析树  观察inh属性的传递 15 

16 .消除直接左递归时语义规则的处理 • 假设 – A  A1 Y A.a = g(A1.a, Y.y) – AX A.a = f(X.x) • 那么 – AXR R.i = f(X.x); A.a = R.s – R  Y R1 R1.i = g(R.i, Y.y); R.s = R1.s – Rε R.s = R.i R即是我们以前消除左递归时引入的A' 16 

17 .SDD的求值顺序  在对SDD的求值过程中  如果结点N的属性a依赖于结点M1的属性a1，M2的属性 a2，…那么我们必须先计算出Mi的属性ai，才能计算N 的属性a  使用依赖图来表示计算顺序  这些值的计算顺序形成一个偏序关系，如果依赖图中 出现了环，表示属性值无法计算 17 

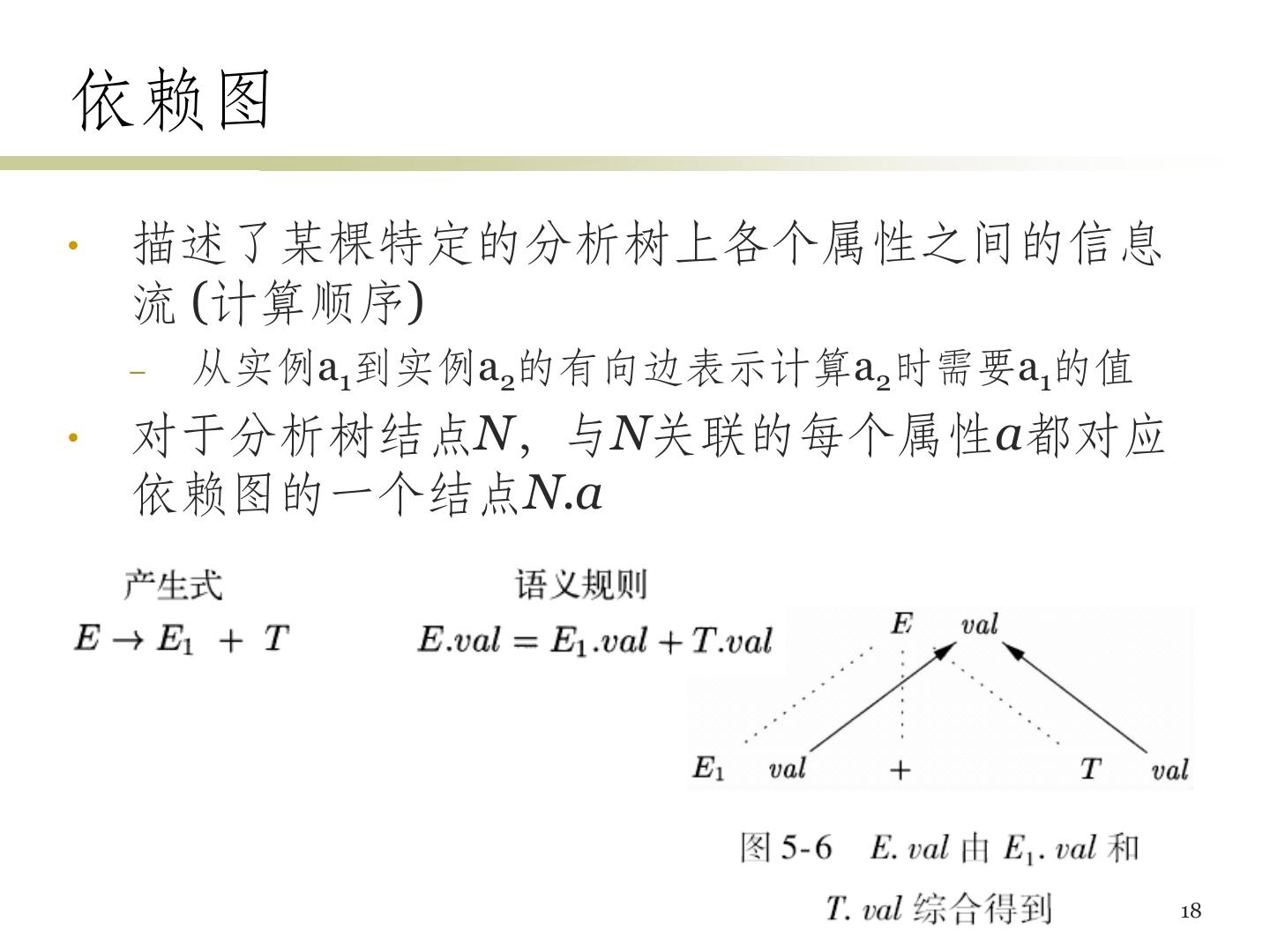
18 .依赖图 • 描述了某棵特定的分析树上各个属性之间的信息 流 (计算顺序) – 从实例a1到实例a2的有向边表示计算a2时需要a1的值 • 对于分析树结点N，与N关联的每个属性a都对应 依赖图的一个结点N.a 18 

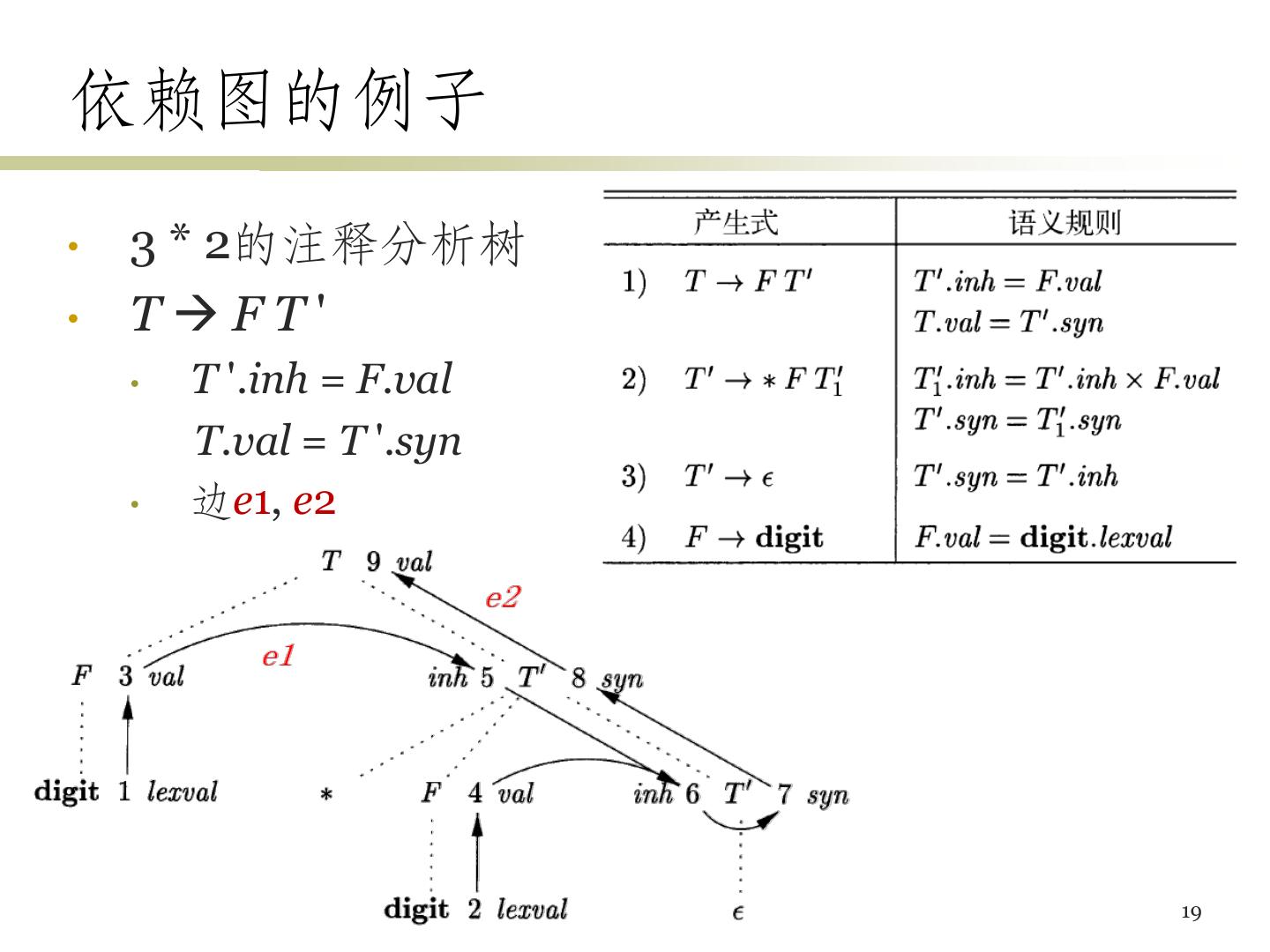
19 .依赖图的例子 • 3 * 2的注释分析树 • TFT' • T '.inh = F.val T.val = T '.syn • 边e1, e2 19 

20 .属性值的计算顺序 • 各个属性值需要按照依赖图的拓扑顺序计算 – 如果依赖图中存在环，则属性计算无法进行 • 给定一个SDD，很难判定是否存在一棵分析树， 其对应的依赖图包含环 • 但是特定类型的SDD一定不包含环，且有固定的 计算顺序 – 如：S属性的SDD，L属性的SDD 20 

21 .S属性的SDD • 每个属性都是综合属性，都是根据子构造的属性 计算出父构造的属性 • 在依赖图中，总是通过子结点的属性值来计算父 结点的属性值，可以和自底向上或自顶向下的语 法分析过程一起计算 – 自底向上 • 在构造分析树结点的同时计算相关的属性 (此时其子结点的属 性必然已经计算完毕) – 自顶向下 • 在递归子程序法中，在过程A()的最后计算A的属性 (此时A调 用的其他过程 (对应于其子结构) 已经调用完毕) 21 

22 .在分析树上计算SDD • 按照后序遍历的顺序计算属性值即可 postorder(N) { for (从左边开始，对N的每个子结点C) postorder(C); // 递归调用返回时，各子结点的属性已计算完毕 对N的各个属性求值; } • 在LR分析过程中，我们实际上不需要构造分析树 的结点 22 

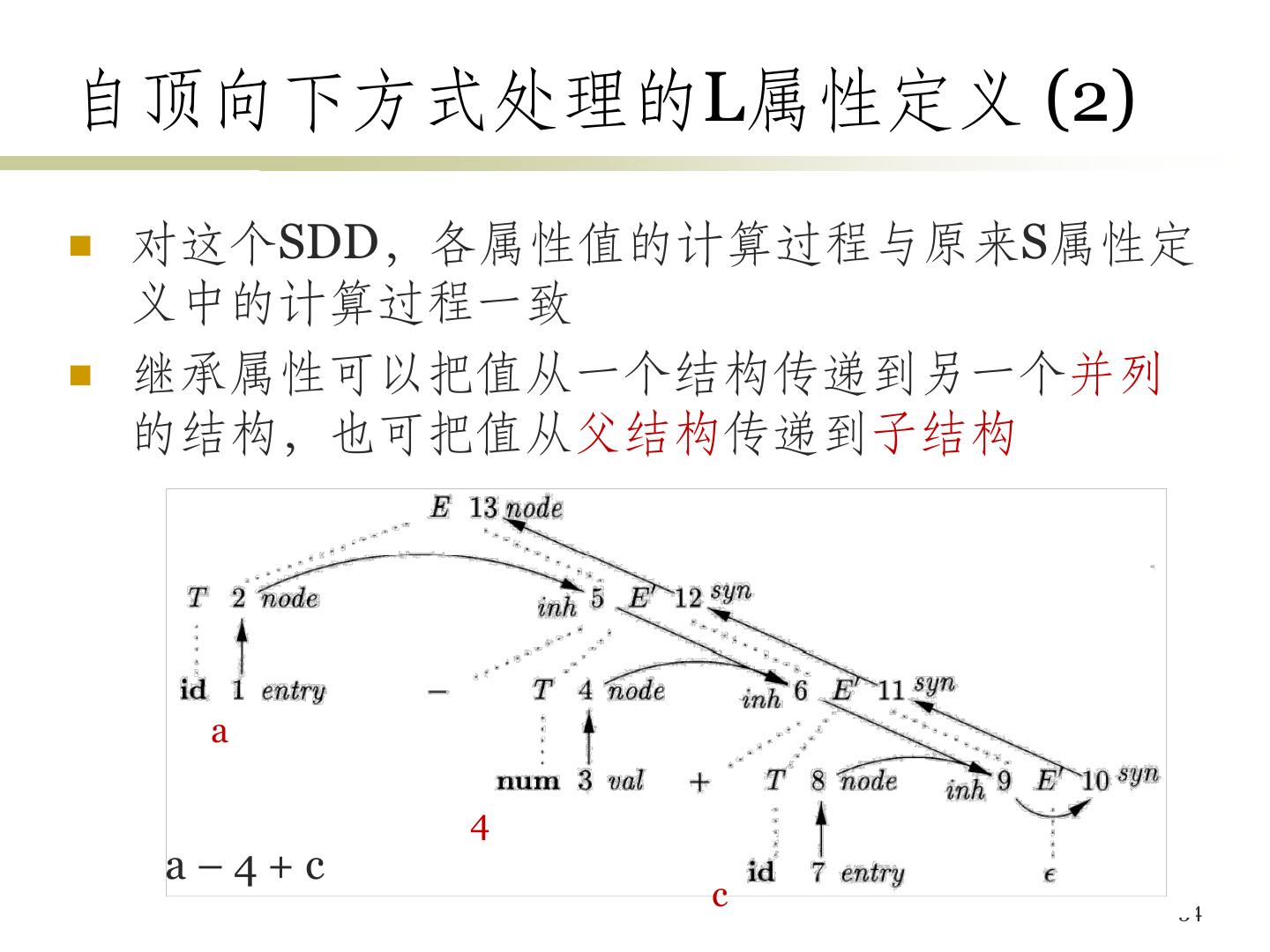
23 .L属性的SDD • 每个属性 – 是综合属性，或 – 是继承属性，且A  X1X2…Xn中计算Xi.a的规则只能用 • A的继承属性，或 • Xi左边的文法符号Xj的继承属性或综合属性，或 • Xi自身的继承或综合属性 (这些属性间的依赖关系不形成环) • 特点 – 依赖图中的边 • 综合属性从下到上 • 继承属性从上到下，或从左到右 – 计算一个属性值时，它所依赖的属性值都已计算完毕 23 

24 .L属性SDD和自顶向下语法分析 (1)  在递归子程序法中实现L属性  对于每个非终结符号A，其所对应过程的参数为继承属 性，返回值为综合属性  在处理规则A  X1X2…Xn时  在调用Xi()之前计算Xi的继承属性值，然后以它们为参 数调用Xi()  在该产生式对应代码的最后计算A的综合属性  如果所有文法符号的属性计算按上面的方式进行，计 算顺序必然和依赖关系一致 24 

25 .L属性SDD和自顶向下语法分析 (2) • L属性SDD其属性总可以按如下方式计算 L_dfvisit(n) { for m = 从左到右n的每个子节点 do { 计算m的继承属性; L_dfvisit(m); } 计算n的综合属性; } 25 

26 .L属性SDD的例子及反例  非L属性的例子  A  BC A.s = B.b; B.i = f(C.c, A.s)  L属性的例子 26 

27 .具有受控副作用的语义规则 • 属性文法没有副作用，但增加了描述的复杂度 – 比如语法分析时，如果没有副作用，标识符表就必须 作为属性传递 – 可以把标识符表作为全局变量，然后通过函数来添加 新的标识符 • 受控的副作用 – 不会对属性求值产生约束，即可以按照任何拓扑顺序 求值，不会影响最终结果 – 或者对求值过程添加简单的约束 27 

28 .受控副作用的例子 • L  E n { print(E.val); } – 通过副作用打印出E的值 – 总在最后执行，不影响其它属性的求值 • 变量声明SDD中的副作用 – addType将标识符的类型信息加入标识符表中 – 只要标识符不被重复声明，其类型信息总是正确的 28 

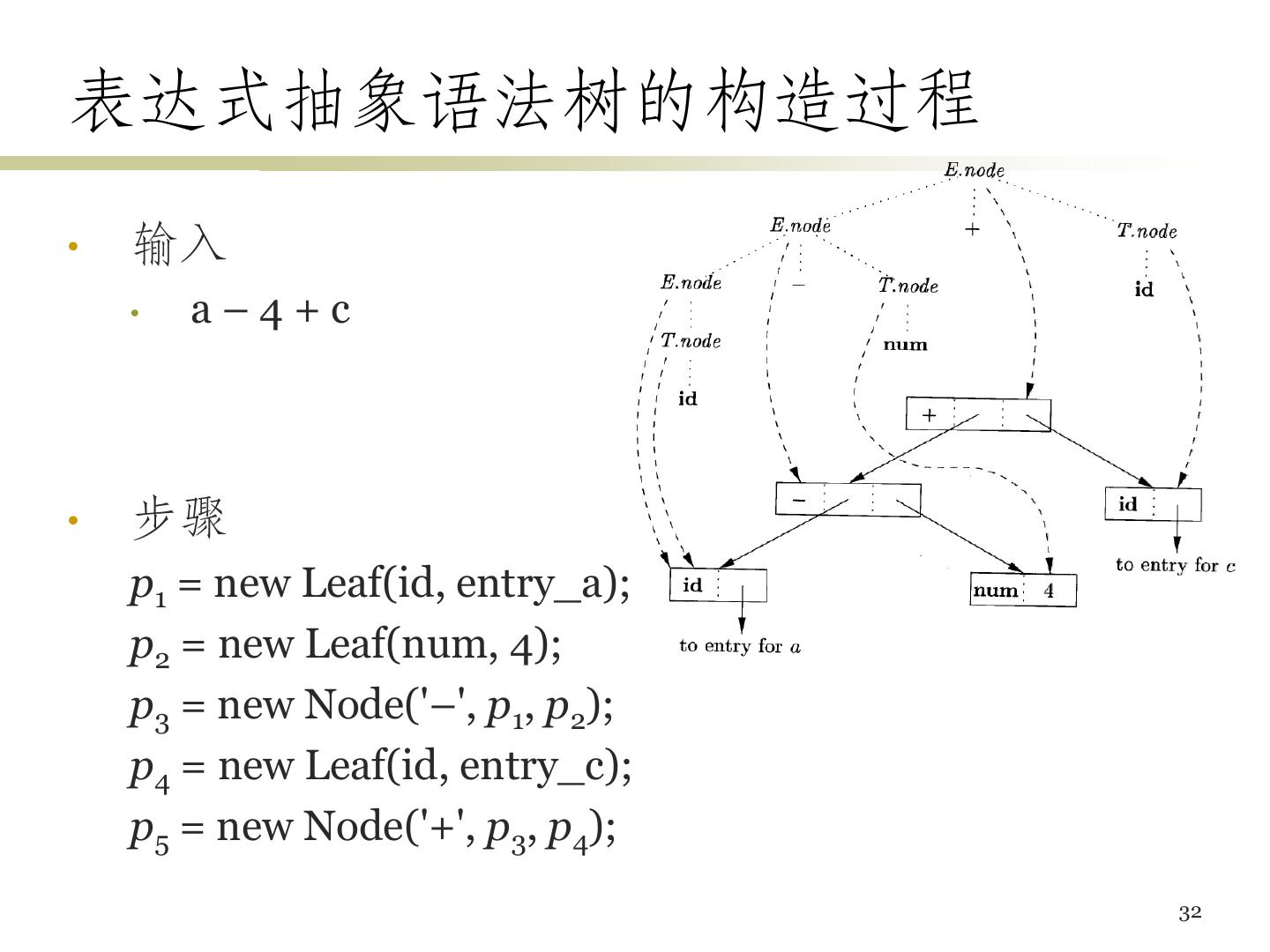
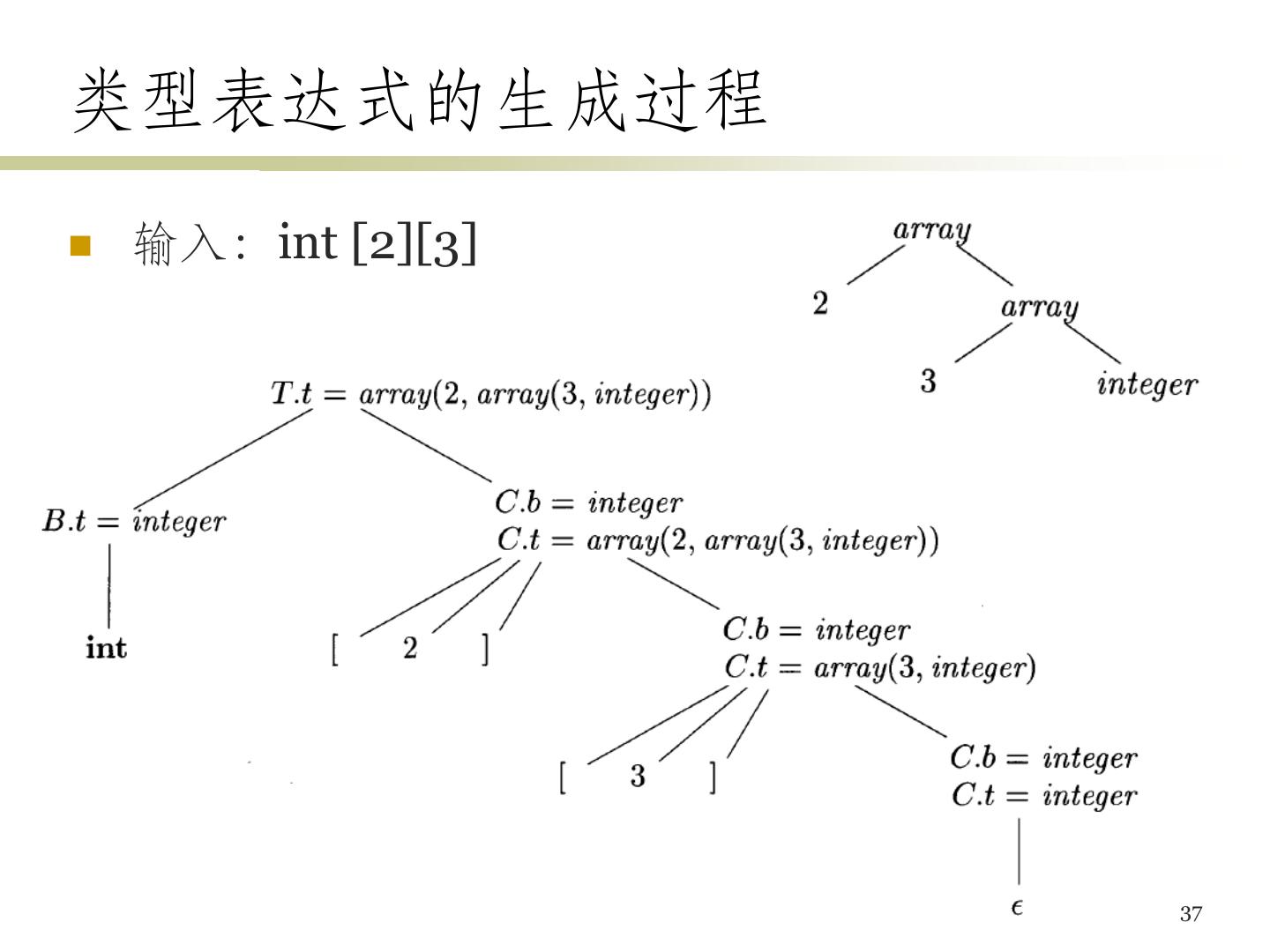
29 .SDD的应用例子  抽象语法树的构造  基本类型和数组类型的L属性定义 29