04 编译原理---语法分析

1 .第四章 语法分析 许畅 南京大学计算机系 2018年春季 

2 .概要  语法分析器  上下文无关文法  语法分析技术  自顶向下  自底向上  语法分析器生成工具 2 

3 .程序设计语言构造的描述  程序设计语言构造的语法可使用上下文无关文法 (CFG) 或BNF表示法来描述  文法可给出精确易懂的语法规则  可以自动构造出某些类型的文法的语法分析器  文法指出了语言的结构，有助于进一步的语义处理/代 码生成  支持语言的演化和迭代 3 

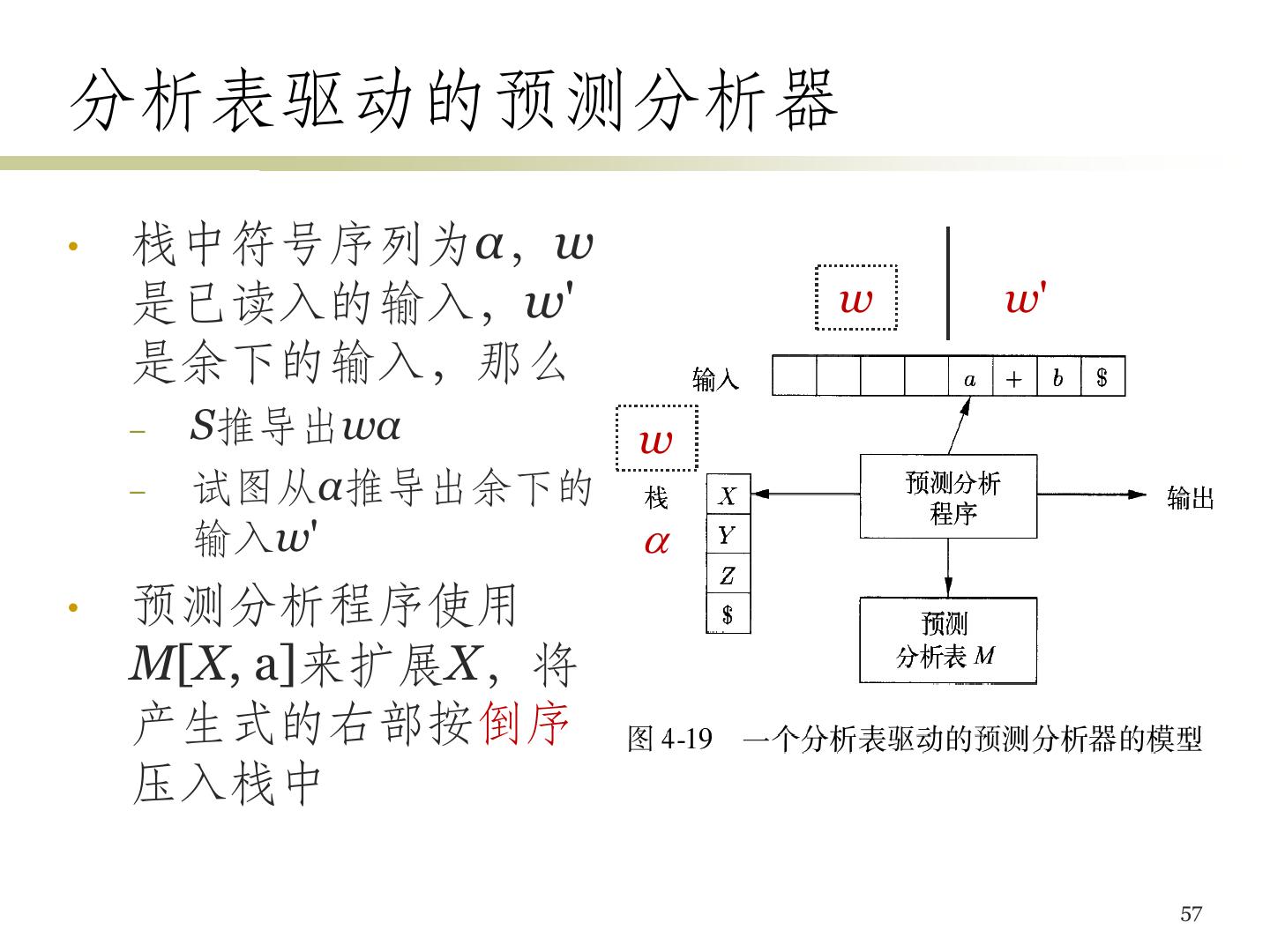
4 .语法分析器的作用 • 基本作用 – 从词法分析器获得词法单元的序列，确认该序列是否 可以由语言的文法生成 – 对于语法错误的程序，报告错误信息 – 对于语法正确的程序，生成语法分析树 (简称语法树) • 通常并不真的产生这棵语法分析树 4 

5 .语法分析器的分类 • 通用语法分析器 – 可以对任意文法进行语法分析 – 效率很低，不适合用于编译器 • 自顶向下语法分析器 (通常用于处理LL文法) – 从语法分析树的根部开始构造语法分析树 • 自底向上语法分析器 (通常用于处理LR文法) – 从语法分析树的叶子开始构造语法分析树 • 后两种方法 – 总是从左到右、逐个扫描词法单元 – 只能处理特定类型的文法，但足以描述程序设计语言 5 

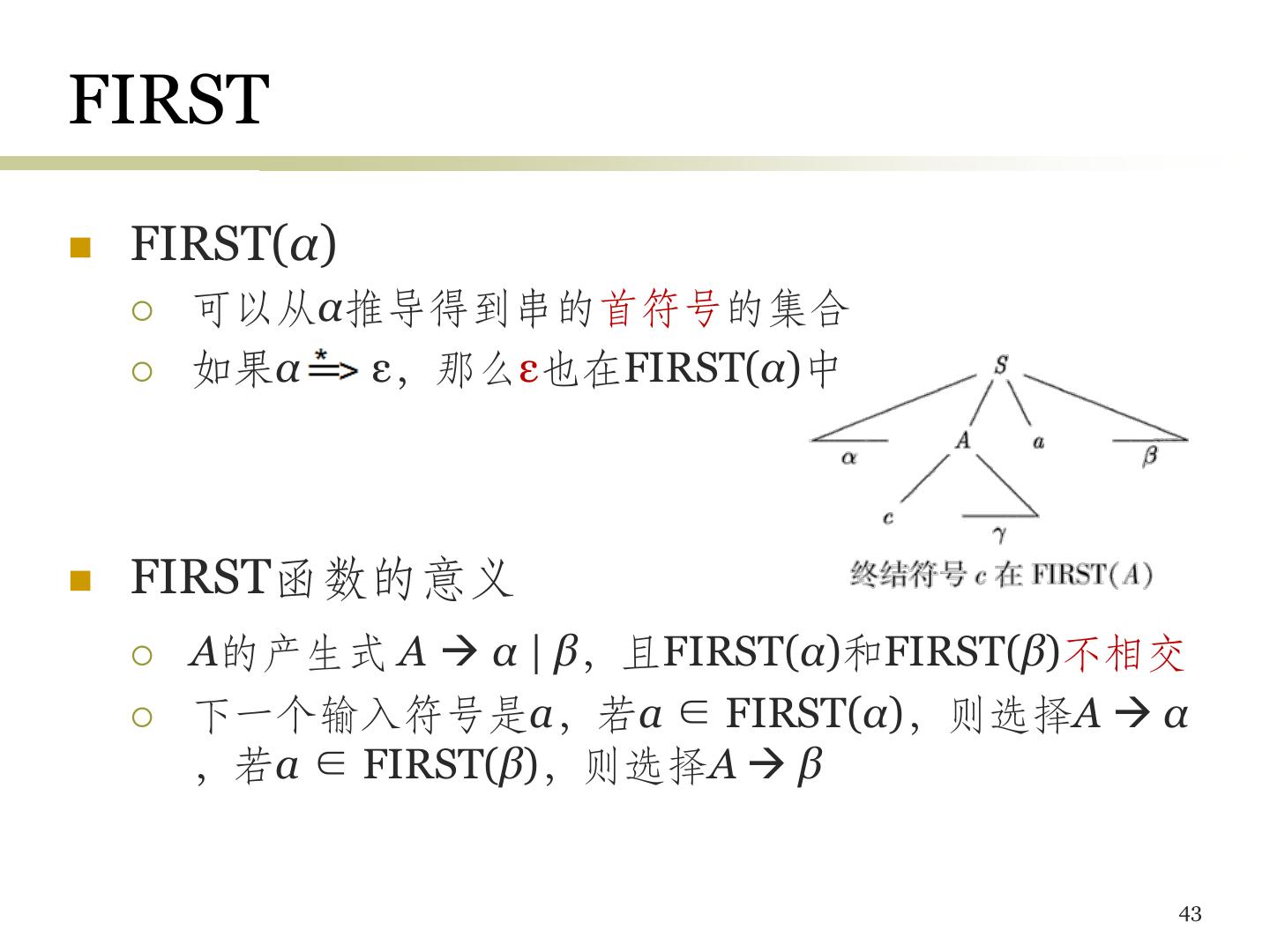
6 .上下文无关文法 • 一个上下文无关文法 (CFG) 包含四个部分 – 终结符号：组成串的基本符号 (词法单元名字) – 非终结符号：表示串的集合的语法变量 • 在程序设计语言中通常对应于某个程序构造，比如stmt (语句) – 开始符号：某个被指定的非终结符号 • 它对应的串的集合就是文法的语言 – 产生式：描述将终结符号和非终结符号组成串的方法 • 形式：头 (左) 部  体 (右) 部 • 头部是一个非终结符号，右部是一个符号串 • 例子：expression  expression + term 6 

7 .上下文无关文法的例子 • 简单算术表达式的文法 – 终结符号：id, +, –, *, /, (, ) – 非终结符号：expression, term, factor – 开始符号：expression – 产生式集合 expression  expression + term expression  expression – term expression  term term  term * factor term  term / factor term  factor factor  ( expression ) factor  id 7 

8 .文法简单形式的例子 EE+T|E–T|T TT*F|T/F|F F  ( E ) | id  注意  | 是元符号 (即文法描述中的符号，而不是文法符号)  这里的 ( 和 ) 不是元符号 9 

9 .推导 (1)  推导  将待处理的串中的某个非终结符号替换为这个非终结 符号的某个产生式的体  从开始符号出发，不断进行上面的替换，就可以得到 文法的不同句型  例子  文法：E  – E | E + E | E * E | ( E ) | id  推导序列：E => – E => – ( E ) => – ( id ) 10 

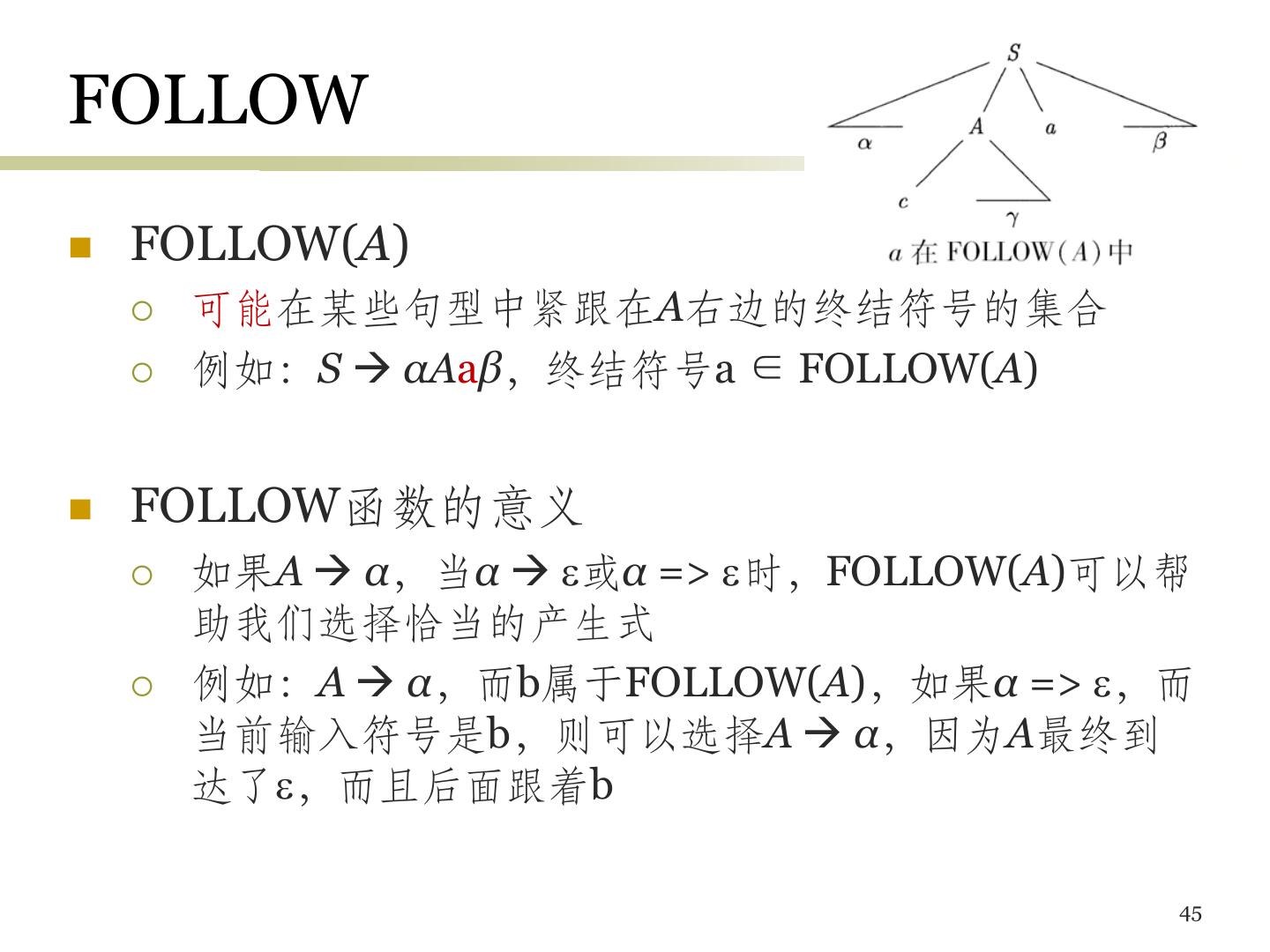
10 .推导 (2) • 推导的正式定义 – 如果A  γ是一个产生式，那么αAβ => αγβ – 最左 (右) 推导：α(β) 中不包含非终结符号 • 符号： • 经过零步或者多步推导出： – 对于任何串α α – 如果α β且β => γ，那么α γ • 经过一步或者多步推导出： – α β等价于α β且α不等于β 11 

11 .句型/句子/语言 • 句型 (Sentential form) – 如果S α，那么α就是文法S的句型 – 可能既包含非终结符号，又包含终结符号，也可以是 空串 • 句子 (Sentence) – 文法的句子就是不包含非终结符号的句型 • 语言 – 文法G的语言就是G的句子的集合，记为L(G) – w在L(G)中当且仅当w是G的句子，即S w 12 

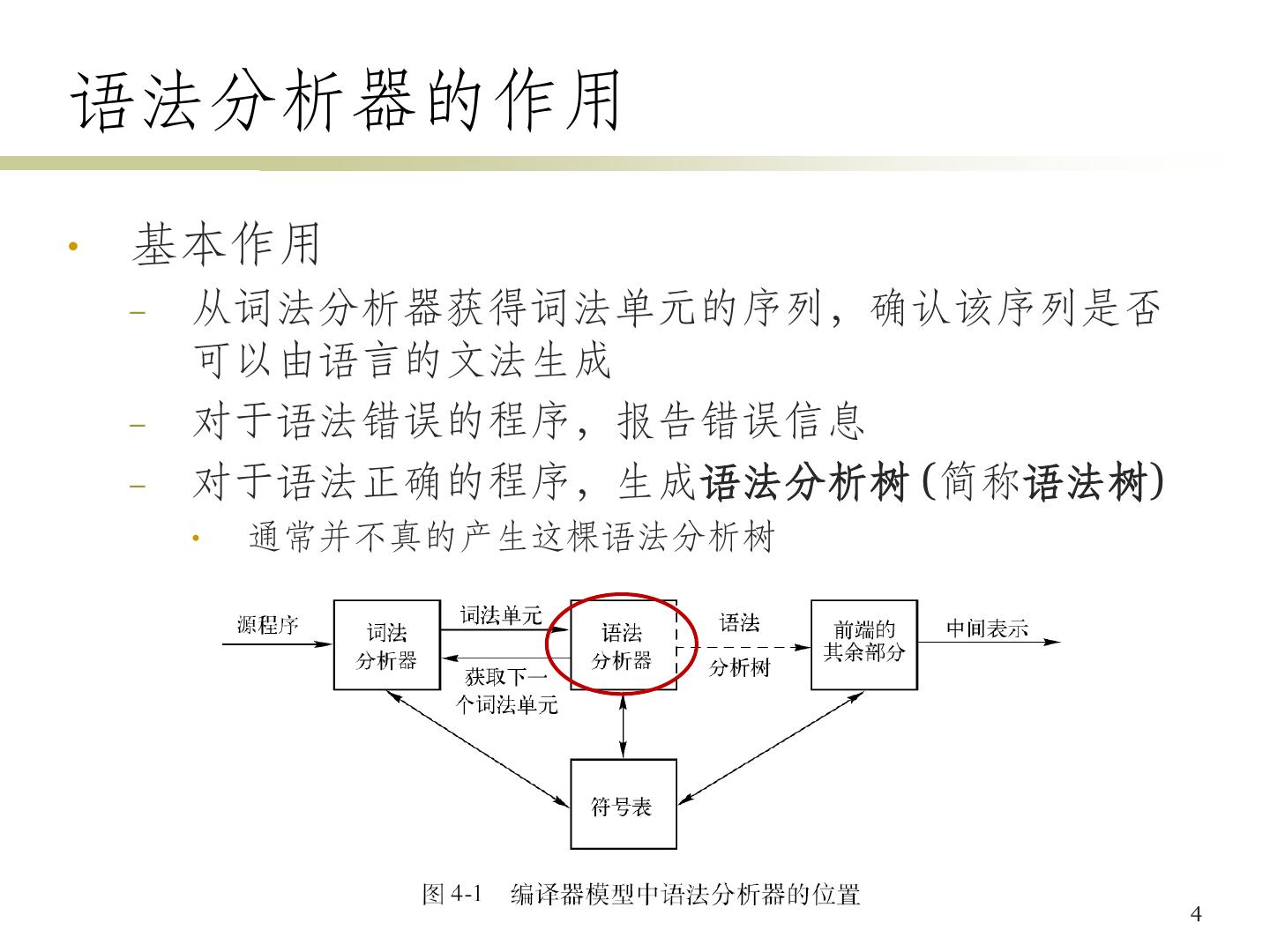
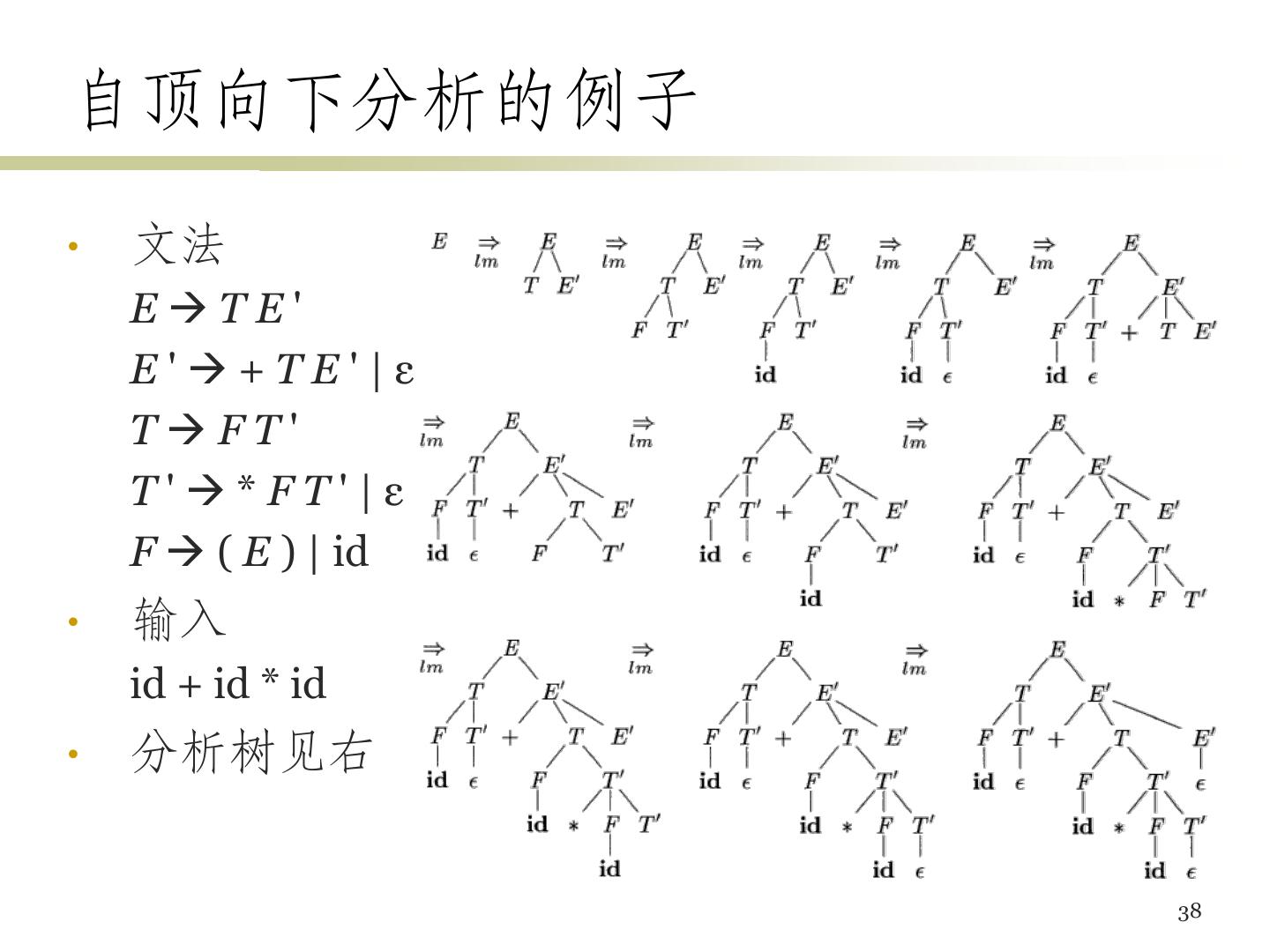
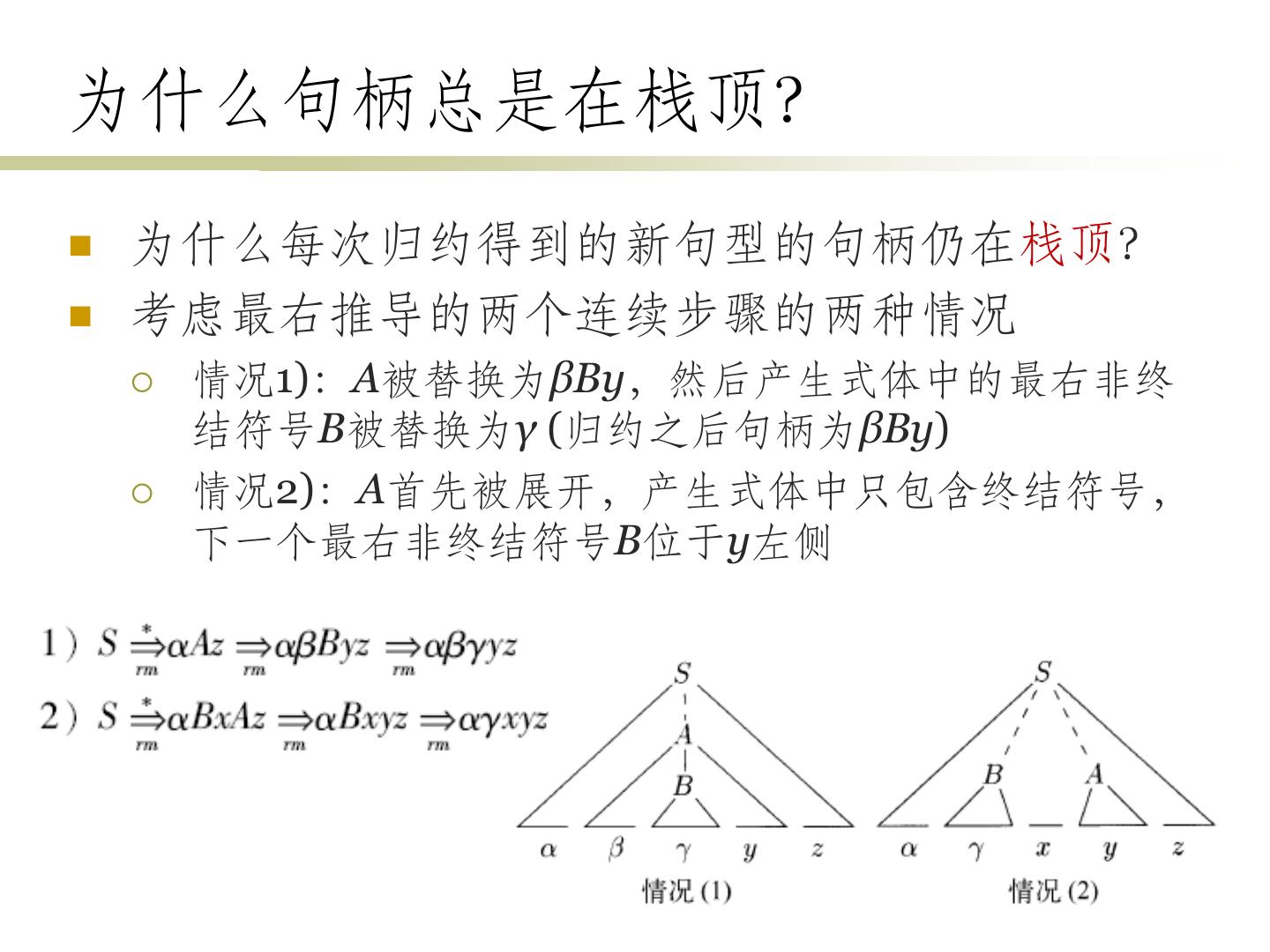
12 .语法分析树 • 推导的图形表示形式 – 根结点的标号是文法的开始符号 – 每个叶子结点的标号是非终结符号、终结符号或ε – 每个内部结点的标号是非终结符号 – 每个内部结点表示某个产生式的一次应用 • 结点的标号为产生式头，其子结点从左到右是产生式的体 • 树的叶子组成的序列是根的文法符号的一个句型 • 一棵语法分析树可对应多个推导序列 • 但只有唯一的最左推导及最右推导 13 

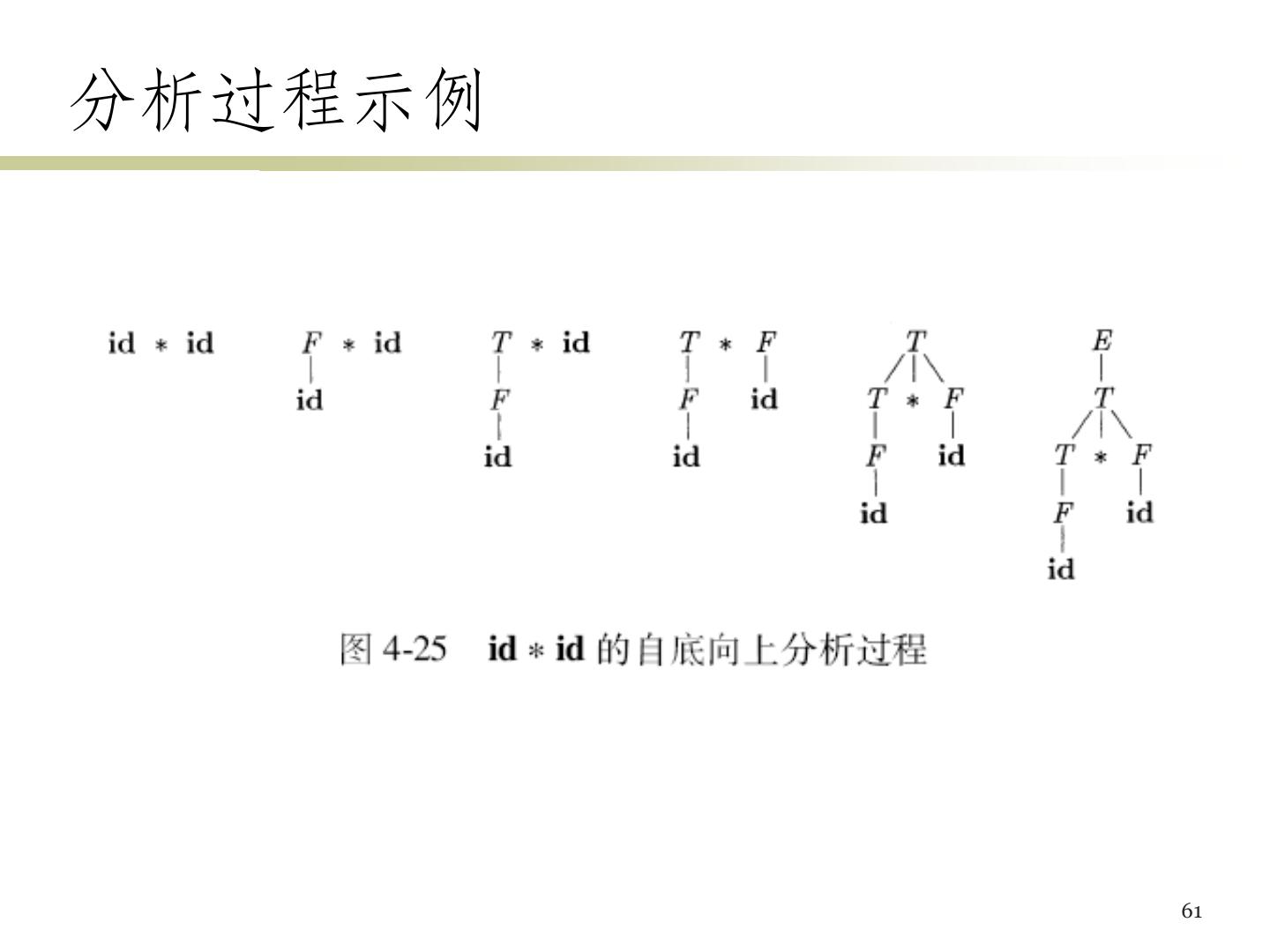
13 .语法分析树的例子  文法：E  – E | E + E | E * E | ( E ) | id  句子：– ( id + id ) 14 

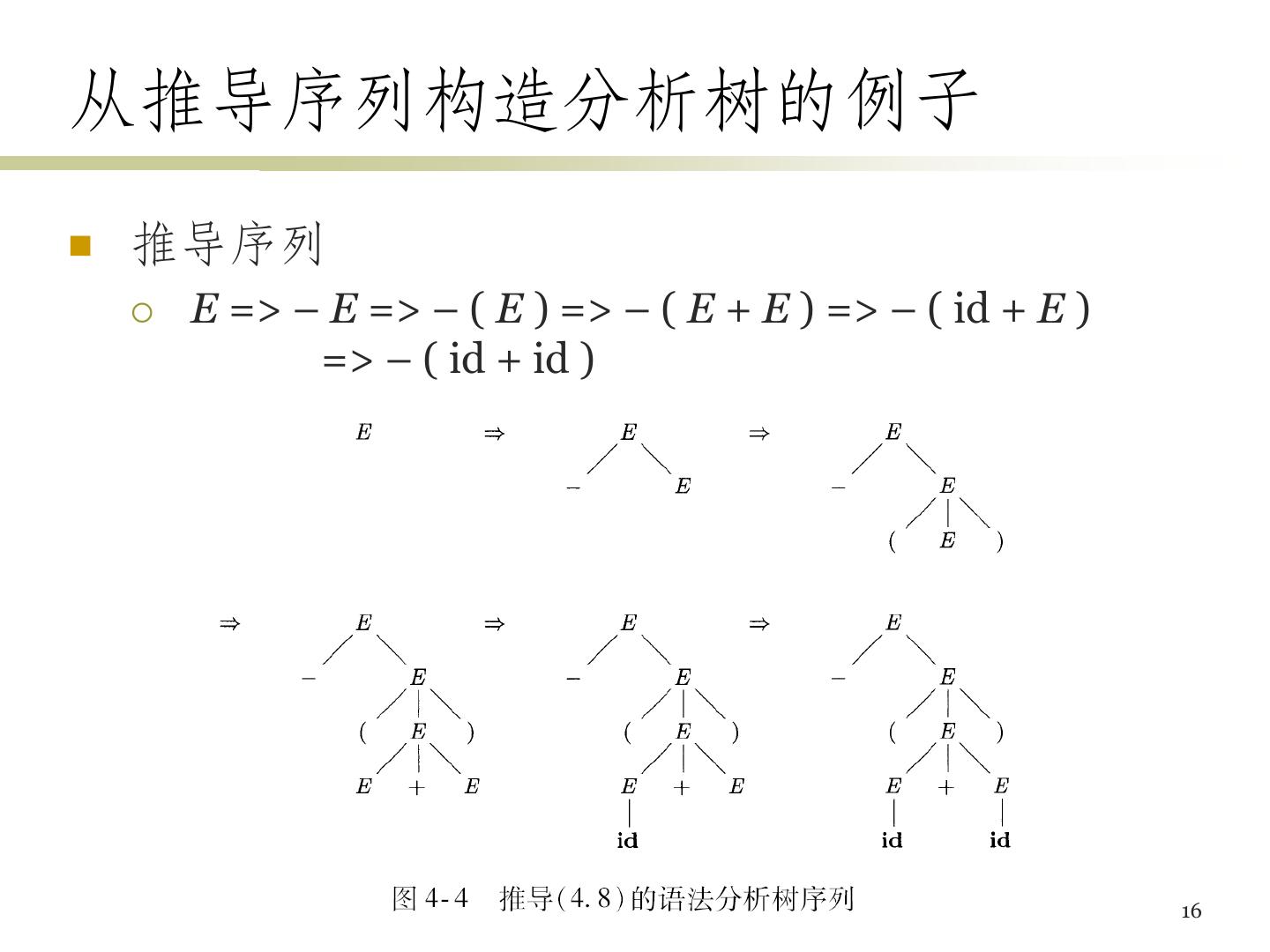
14 .从推导序列构造分析树的例子  推导序列  E => – E => – ( E ) => – ( E + E ) => – ( id + E ) => – ( id + id ) 16 

15 .二义性 (1) • 二义性 (Ambiguity)：如果一个文法可以为某个句 子生成多棵语法分析树，这个文法就是二义的 • 例子 – E => E + E => id + E => id + E * E => id + id * E => id + id * id – E => E * E => E + E * E => id + E * E => id + id * E => id + id * id 都是最左推导 17 

16 .二义性 (2) • 程序设计语言的文法通常是无二义的 – 否则就会导致一个程序有多种“正确”的解释 – 如文法 E  – E | E + E | E * E | ( E ) | id 应对句子 a + b*c时 • 有些二义性的情况可以方便文法或语法分析器的 设计 – 但需要消二义性规则来剔除不要的语法分析树 – 比如：先乘除后加减 18 

17 .词法分析和语法分析的比较 阶段 输入 输出 描述体系 词法分析 源程序符号串 词法单元序列 正则表达式 语法分析 词法单元序列 语法分析树 上下文无关文法 19 

18 .上下文无关文法和正则表达式 (1) • 上下文无关文法比正则表达式的能力更强 – 所有的正则语言都可以使用文法描述 – 但有一些用文法描述的语言不能用正则表达式描述 • 证明 – 首先S  aSb | ab描述了语言L {anbn | n > 0}，但这个 语言无法用DFA识别 • 假设有DFA识别此语言L，且这个DFA有k个状态。那么在识 别ak+1…的输入串时，必然两次到达同一个状态。假设自动机 在第i个和第j个a时进入同一个状态，那么：因为DFA识别L， ajbj必然到达接受状态，因此aibj必然也到达接受状态。 • 直观地讲：有穷自动机不能计数 20 

19 .上下文无关文法和正则表达式 (2) • 证明 (续) – 任何正则语言都可以表示为上下文无关文法的语言 – 任何正则语言都必然有一个NFA，对于该NFA构造如 下的上下文无关文法 • 对NFA的每个状态i，创建非终结符号Ai • 如果有i在输入a上到达j的转换，增加产生式Ai  aAj • 如果i在输入ε上到达j，那么增加产生式Ai  Aj • 如果i是一个接受状态，增加产生式Ai  ε • 如果i是开始状态，令Ai为所得文法的开始符号 21 

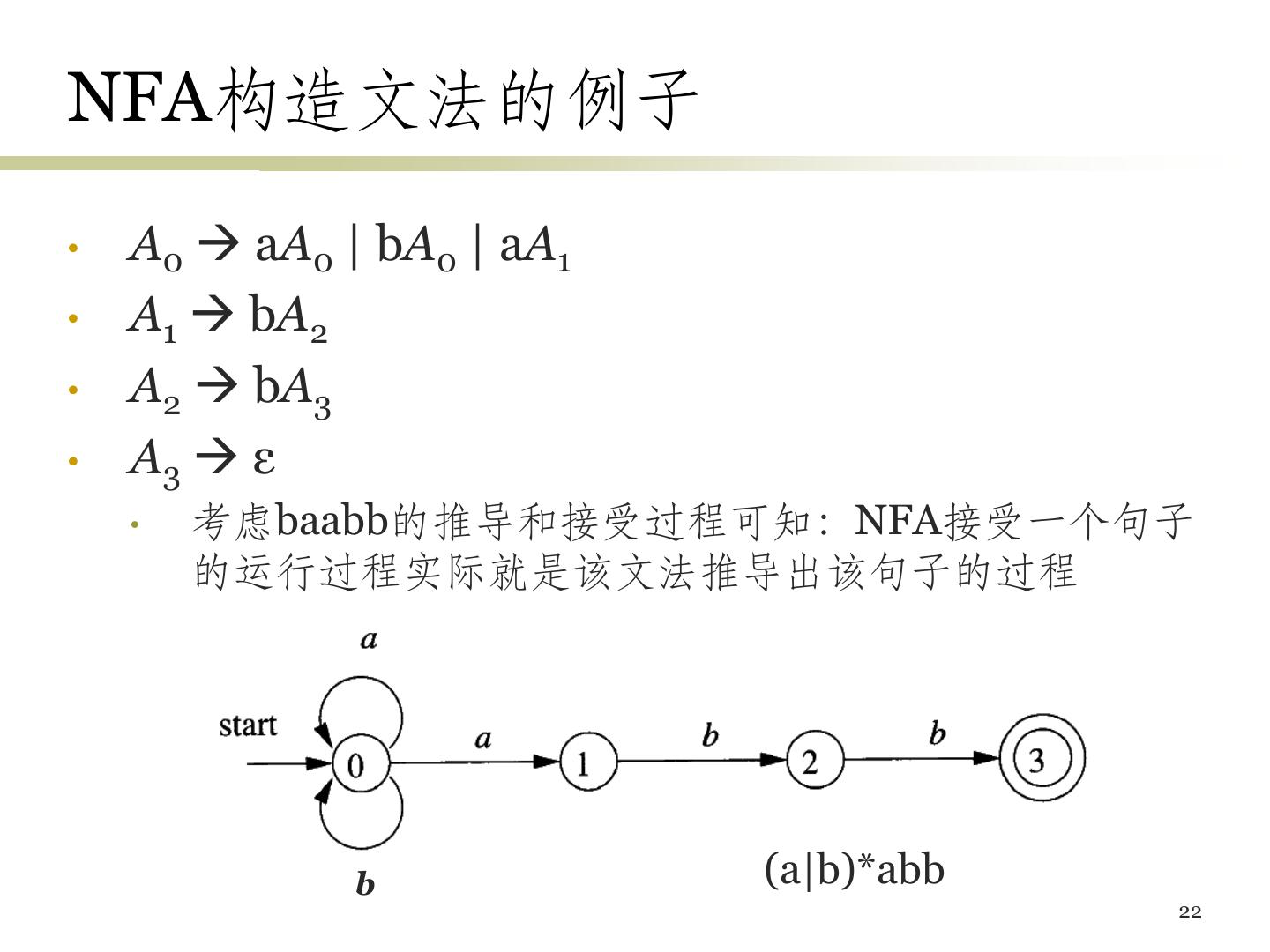
20 .NFA构造文法的例子 • A0  aA0 | bA0 | aA1 • A1  bA2 • A2  bA3 • A3  ε • 考虑baabb的推导和接受过程可知：NFA接受一个句子 的运行过程实际就是该文法推导出该句子的过程 b (a|b)*abb 22 

21 .文法及其生成的语言  语言是从文法的开始符号出发，能推导得到的所 有句子的集合  文法G：S  aS | a | b，L(G) = { ai(a|b), i >= 0 }  文法G：S  aSb | ab，L(G) = { anbn, n >= 1 }  文法G：S  (S)S | ε，L(G) = { 所有具有对称括号对的 串}  如何验证文法G所确定的语言L  证明G生成的每个串都在L中  证明L中的每个串都能被G生成 23 

22 .设计文法 (1)  文法能够描述程序设计语言的大部分语法  但不是全部，比如，标识符的先声明后使用则无法用 上下文无关文法描述  因此语法分析器接受的语言是程序设计语言的超集； 必须通过语义分析来剔除一些符合文法、但不合法的 程序 24 

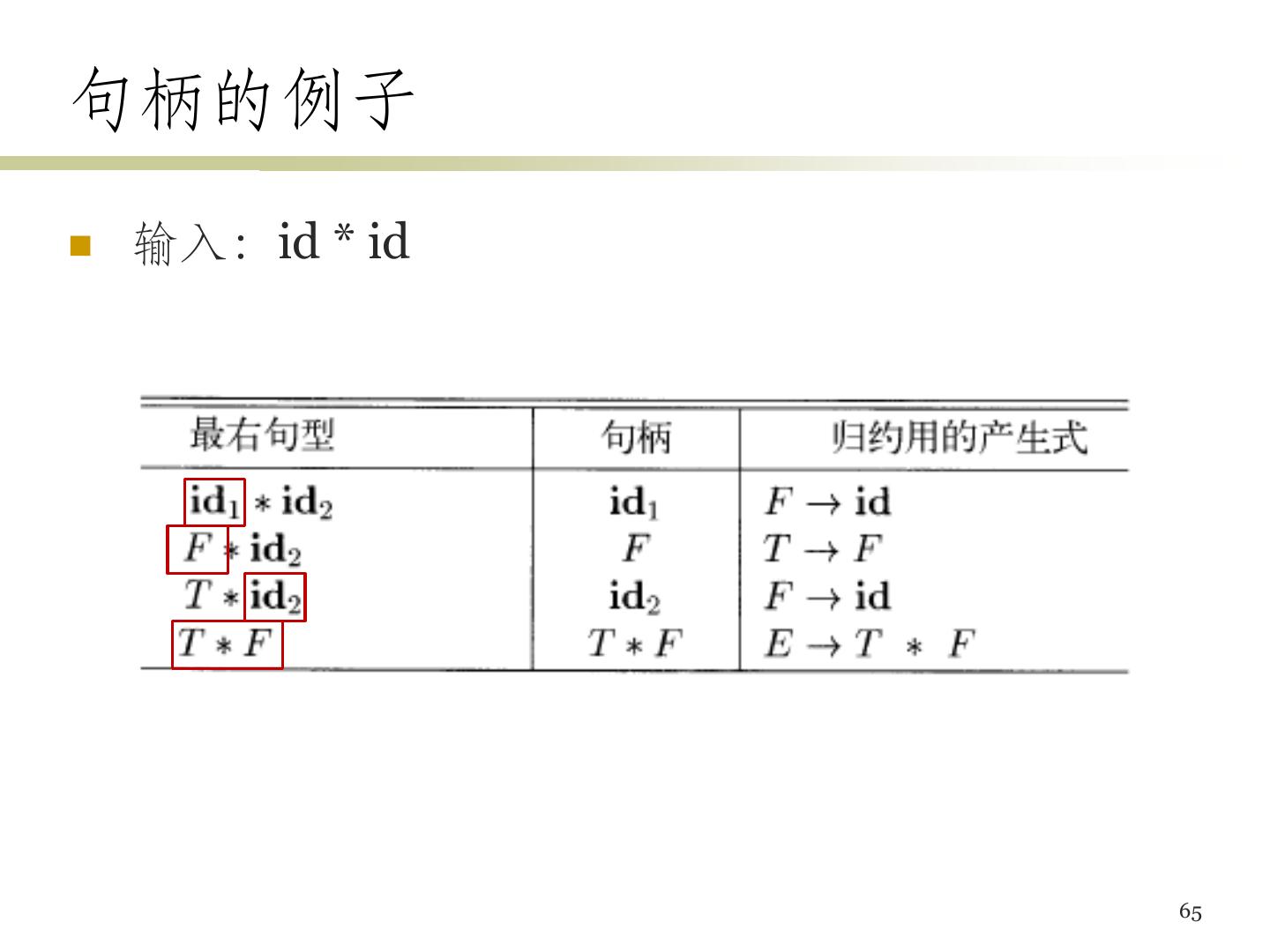
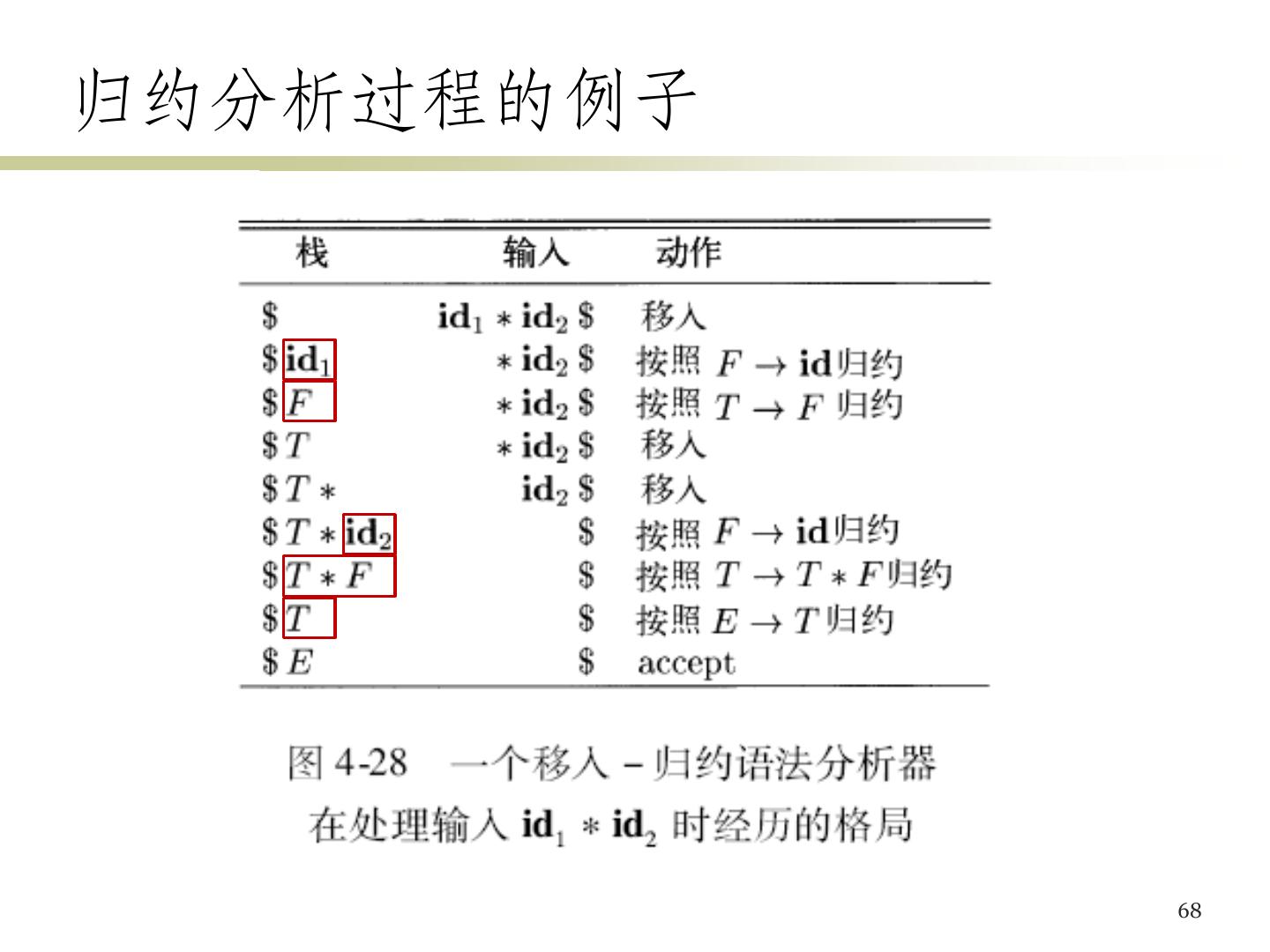
23 .设计文法 (2)  在进行高效的语法分析之前，需要对文法做以下 处理  消除二义性  二义性：文法可以为一个句子生成多颗不同的分析树  消除左递归  左递归：文法中一个非终结符号A使得对某个串α，存在一个 推导 A Aα，则称这个文法是左递归的  提取左公因子 25 

24 .二义性的消除 (1) • 一些二义性文法可被改成等价的无二义性的文法 • 例子 stmt  if expr then stmt | if expr then stmt else stmt | other • if E1 then if E2 then S1 else S2的两棵语法树 26 

25 .二义性的消除 (2) • 保证else和最近未匹配的then匹配 • 要求在then和 else之间出现的语句必须是匹配好的 • 引入matched_stmt表示匹配好的语句 stmt  matched_stmt | open_stmt matched_stmt  if expr then matched_stmt else matched_stmt | other open_stmt  if expr then stmt | if expr then matched_stmt else open_stmt • 二义性的消除方法没有规律可循 27 

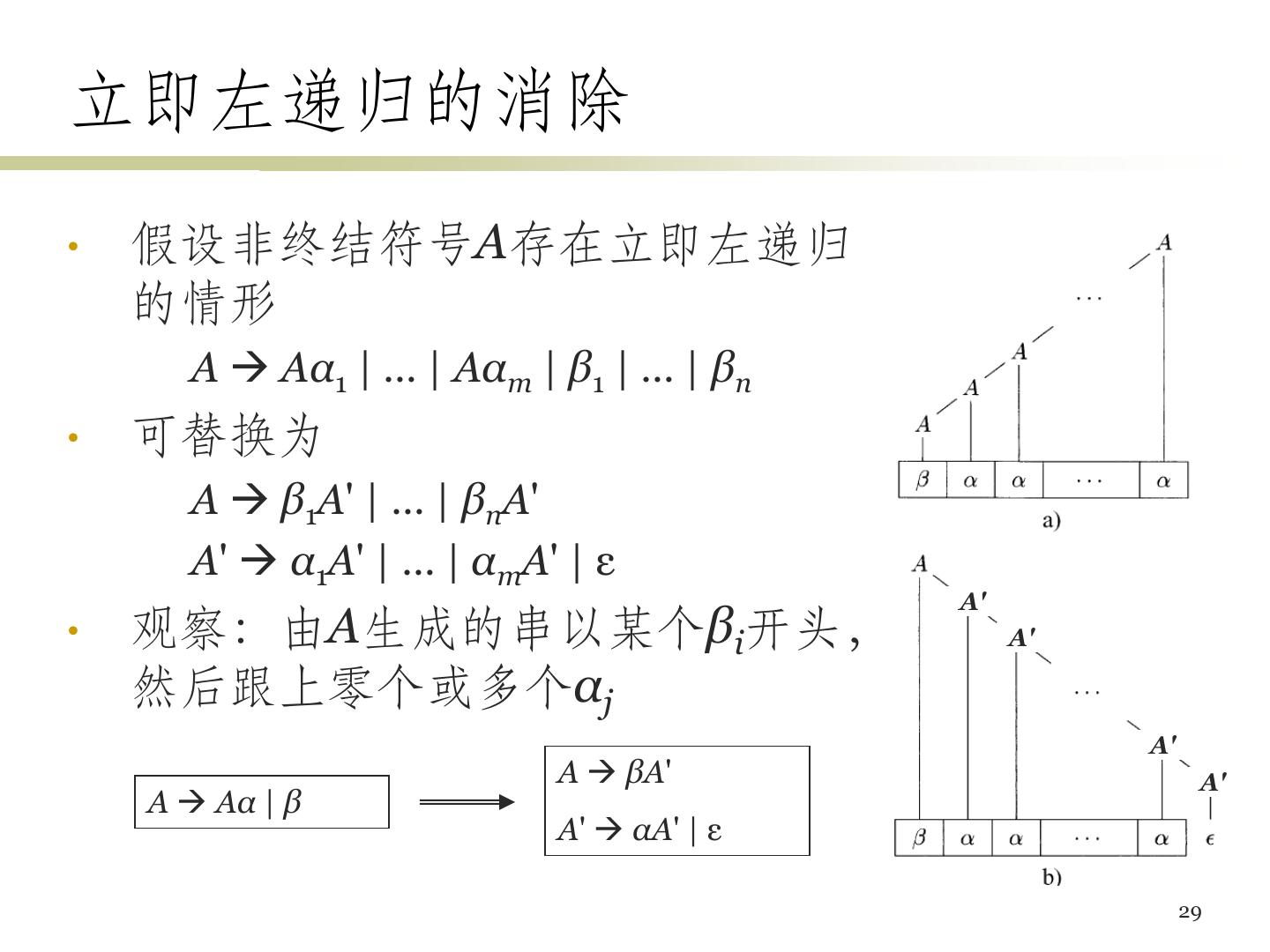
26 .左递归的消除  左递归的定义  如果一个文法中有非终结符号A使得A Aα，那么这 个文法就是左递归的  立即左递归 (规则左递归)  文法中存在一个形如A  Aα的产生式  自顶向下的语法分析技术不能处理左递归的情况， 因此需要消除左递归，但是自底向上的技术可以 处理左递归 28 

27 .立即左递归的消除 • 假设非终结符号A存在立即左递归 的情形 A  Aα1 | … | Aαm | β1 | … | βn • 可替换为 A  β1A' | … | βnA' A'  α1A' | … | αmA' | ε A' • 观察：由A生成的串以某个βi开头， A' 然后跟上零个或多个αj A' A  βA' A' A  Aα | β A'  αA' | ε 29 

28 .立即左递归消除示例 30 

29 .消除多步左递归  消除立即左递归的方法并不能消除因为多步推导 而产生的左递归  文法：S  Aa | b A  Ac | Sd | ε  S => Aa => Sda  如何消除？ 31