- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Naive Bayesian Document Classification
展开查看详情
1 .Naive Bayesian Classification Abel Sanchez, John R Williams
2 .Stunningly Simple The mathematics of Bayes Theorem are stunningly simple. In its most basic form, it is just an equation with three known variables and one unknown one. This simple formula can lead to surprising predictive insights.
3 .Bayes and Laplace The intimate connection between probability, prediction, and scientific progress was thus well understood by Bayes and Laplace in the eighteenth century— the period when human societies were beginning to take the explosion of information that had become available with the invention of the printing press several centuries earlier, and finally translate it into sustained scientific, technological, and economic progress.
4 .Conditional Probability Bayes’s theorem is concerned with conditional probability. That is, it tells us the probability that a hypothesis is true if some event has happened.
5 .Bayes Theorem P(A) and P(B) are the probabilities of A and B independent of each other P(A|B) a conditional probability, is the probability of A given that B is true P(B|A) is the probability of B given that A is true
6 .Example
7 .Probability that your partner is cheating on you, given an event Event: you come home from a business trip to discover a strange pair of underwear. Condition: you have found the underwear Hypothesis: probability that you are being cheated on
8 .p( u/c ) - The probability of underwear u given cheating c Probability of underwear appearing, conditional on his cheating 50%
9 .p(u) - The probability of the underwear u appearing if NO cheating Probability of the underwear’s appearing conditional on the hypothesis being false . 5%
10 .p(u ) - The probability of cheating c What is the probability you would have assigned to him cheating on you before you found the underwear? 4 %
11 .p(u ) - The probability of cheating c What is the probability you would have assigned to him cheating on you before you found the underwear? 4 %
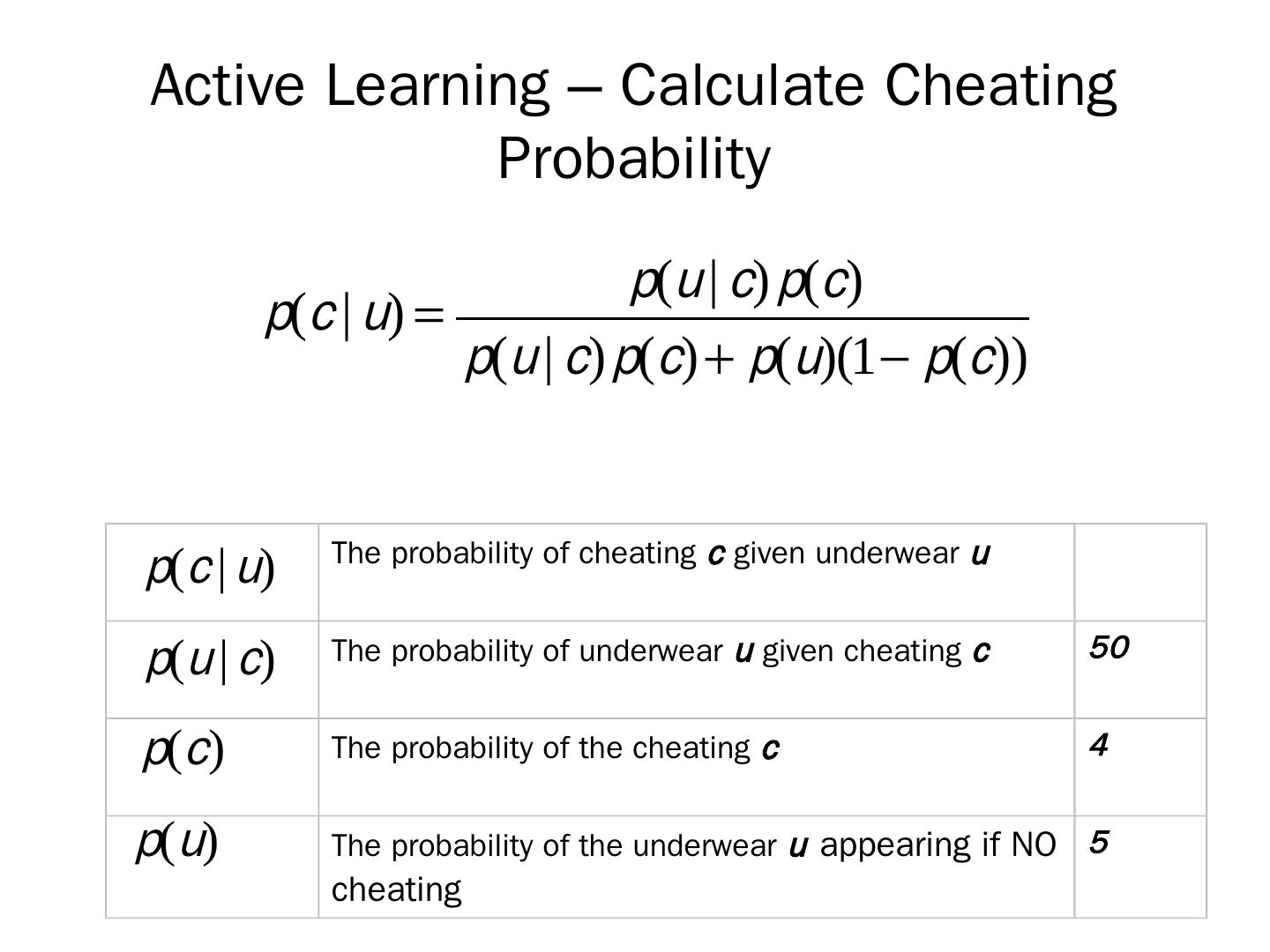
12 .Active Learning
13 .Active Learning – Calculate Cheating Probability T he probability of cheating c given underwear u The probability of underwear u given cheating c 50 The probability of the cheating c 4 The probability of the underwear u appearing if NO cheating 5
14 .Classification of Drew
15 .Example: classification of Drew We have two classes: c 1 =male, and c 2 =female Classifying drew as male or female is equivalent to asking is it more probable that drew is male or female. probability of being called “drew” given that you are a male? Probability of being a male? probability of being named “drew”?
16 .Using Data Name Gender Drew Male Claudia Female Drew Female Drew Female Alberto Male Karin Female Nina Female Sergio Male p(male|drew) = 1/3 x 3/8 = 0.125 3/8 3/8 p(female|drew) = 2/5 x 5/8 = 0.250 3/8 3/8 probability of being called “drew” given that you are a male? Probability of being a male? probability of being named “drew”?
17 .Bayesian Approach Posterior p robability based on prior probability plus a new event
18 .Classification of Documents
19 .Questions We Can Answer Is this spam? Who wrote which Federalist papers ? Positive or negative movie review ? What is the subject of this article?
20 .Text Classification Assigning subject categories, topics, or genres Authorship identification Age/gender identification Language Identification Sentiment analysis …
21 .Bayes Theorem a conditional probability, is the probability of class c given document d is the probability of document d given class c the probability of the class c the probability of the document d For a document d and a class c
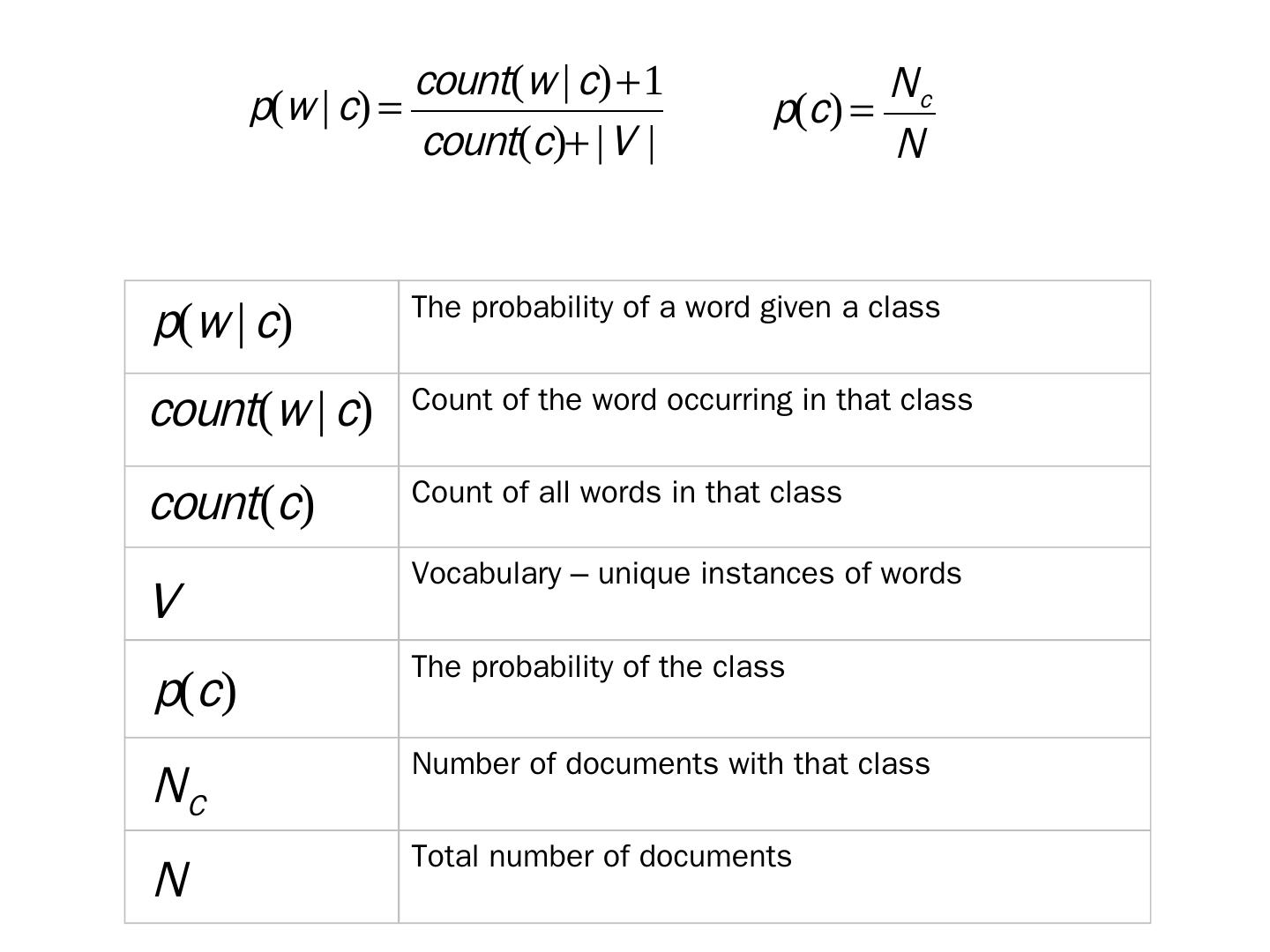
22 .The probability of a word given a class Count of the word occurring in that class Count of all words in that class Vocabulary – unique instances of words The probability of the class Number of documents with that class Total number of documents
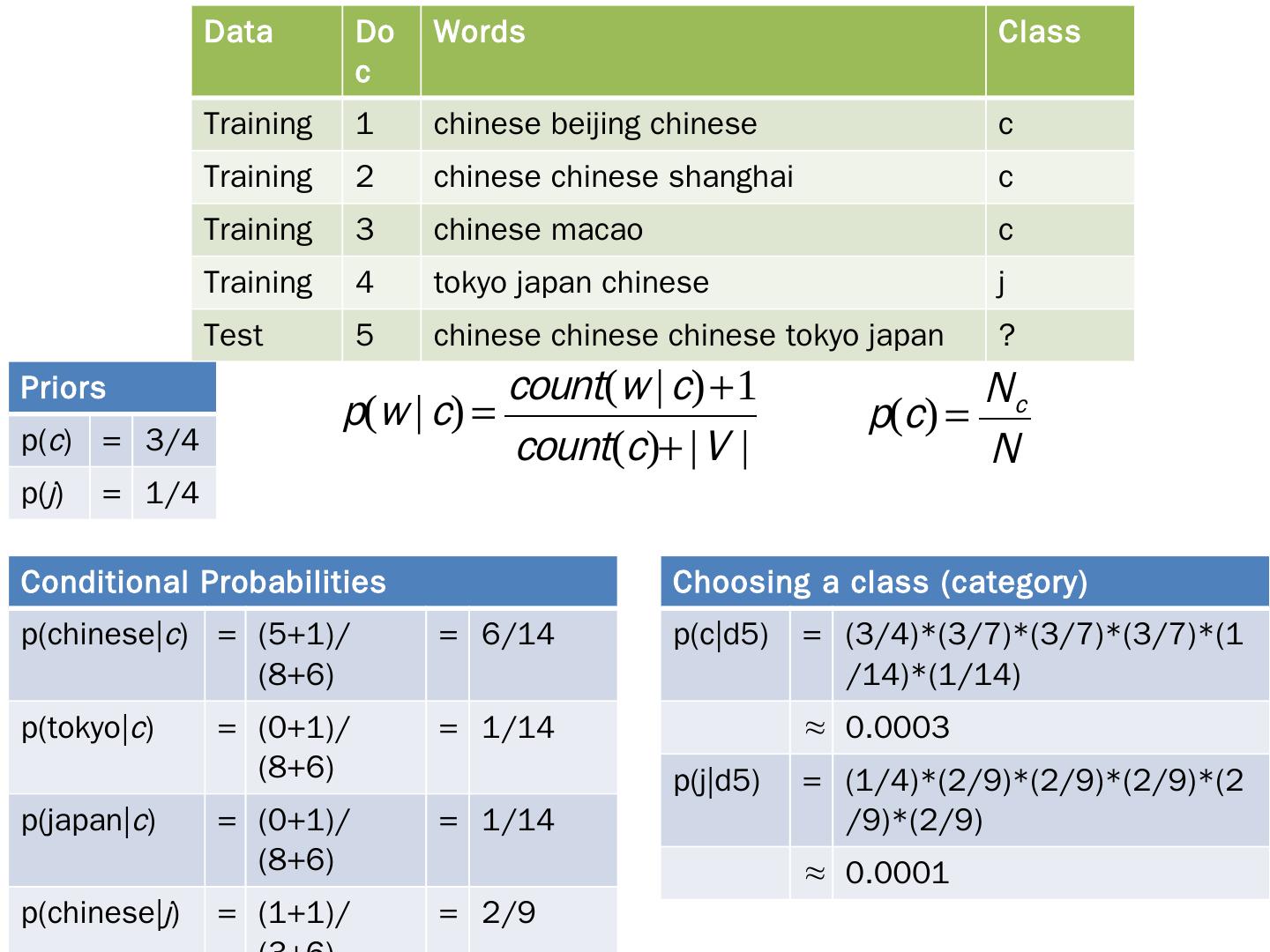
23 .Data Doc Words Class Training 1 chinese beijing chinese c Training 2 chinese chinese shanghai c Training 3 chinese macao c Training 4 tokyo japan chinese j Test 5 chinese chinese chinese tokyo japan ? Conditional Probabilities p(chinese| c ) = (5+1)/(8+6) = 6/14 p(tokyo| c ) = (0+1)/(8+6) = 1/14 p(japan| c ) = (0+1)/(8+6) = 1/14 p(chinese| j ) = (1+1)/(3+6) = 2/9 p(tokyo| j ) = (1+1)/(3+6) = 2/9 p(japan| j ) = (1+1)/(3+6) = 2/9 Priors p( c ) = 3/4 p( j ) = 1/4 Choosing a class (category) p(c| d5 ) = (3/4)*(3/7)*(3/7)*(3/7)*(1/14)*(1/14) ≈ 0.0003 p(j| d5 ) = (1/4)*(2/9)*(2/9)*(2/9)*(2/9)*(2/9) ≈ 0.0001
24 .For homework we will use*: probability of language given word Probability that word is in language Probability that word is not in language * http://en.wikipedia.org/wiki/Naive_Bayes_spam_filtering
25 .Calculating Probabilities // probability that word shows up in a language // probability that word is not in language
26 .Underflow Prevention Multiplying lots of probabilities can result in floating-point underflow. Since log( xy ) = log(x) + log(y ); better to sum logs of probabilities instead of multiplying probabilities . Add probability of words (per language) using: In JavaScript ln is Math.log , and e is Math.exp At completion of each language: