- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
naive Bayes
展开查看详情
1 .Why does it work? We have not addressed the question of why does this classifier performs well, given that the assumptions are unlikely to be satisfied. The linear form of the classifiers provides some hints. 1
2 .In the case of two classes we have that: but since We get (plug in (2) in (1); some algebra): Which is simply the logistic (sigmoid) function Naïve Bayes: Two Classes We have: A = 1-B; Log(B/A) = -C. Then: Exp (-C) = B/A = = (1-A)/A = 1/A – 1 = + Exp ( -C) = 1/A A = 1/(1+Exp(-C)) 2
3 .3 Why Does it Work? Learning Theory Probabilistic predictions are done via Linear [Statistical Queries] Models [Roth’99] The low expressivity explains Generalization + Robustness Expressivity (1: Methodology) Why is it possible to (approximately) fit the data with these models? Is there a reason to believe that these hypotheses minimize the empirical error? In General, No. ( Unless it some probabilistic assumptions happen to hold ). But: if the hypothesis does not fit the training data, augment set of features But now, you actually follow the Learning Theory Protocol: Try to learn a hypothesis that is consistent with the data Generalization will be a function of the low expressivity Expressivity (2: Theory) [ Garg&Roth (ECML’01 )]: Product distributions are “dense” in the space of all distributions. Consequently, for most generating distributions the resulting predictor’s error is close to optimal classifier (that is, given the correct distribution)
4 .4 What’s Next? (1) If probabilistic hypotheses are actually like other linear functions, can we interpret the outcome of other linear learning algorithms probabilistically? Yes (2) If probabilistic hypotheses are actually like other linear functions, can you train them similarly (that is, discriminatively)? Yes. Classification : Logistics regression/Max Entropy HMM: can be learned as a linear model, e.g., with a version of Perceptron (Structured Models class)
5 .Recall: Naïve Bayes, Two Classes 5 In the case of two classes we have: but since We get (plug in (2) in (1); some algebra): Which is simply the logistic (sigmoid) function used in the neural network representation.
6 .Conditional Probabilities (1) If probabilistic hypotheses are actually like other linear functions, can we interpret the outcome of other linear learning algorithms probabilistically? Yes General recipe Train a classifier f using your favorite algorithm (Perceptron, SVM, Winnow, etc ). Then: Use Sigmoid1/1+exp{-( Aw T x + B)} to get an estimate for P(y | x) A, B can be tuned using a held out that was not used for training. Done in LBJava , for example 6
7 .(2) If probabilistic hypotheses are actually like other linear functions, can you actually train them similarly (that is, discriminatively)? The logistic regression model assumes the following model: P(y= +/-1 | x,w )= [1+exp(-y( w T x + b)] -1 This is the same model we derived for naïve Bayes, only that now we will not assume any independence assumption. We will directly find the best w. Therefore training will be more difficult. However, the weight vector derived will be more expressive. It can be shown that the naïve Bayes algorithm cannot represent all linear threshold functions. On the other hand, NB converges to its performance faster. Logistic Regression 7 How?
8 .Logistic Regression (2) Given the model: P(y = +/-1 | x,w )= [1+exp(-y(w T x + b)] -1 The goal is to find the ( w, b) that maximizes the log likelihood of the data: {x 1 ,x 2 … x m }. We are looking for ( w,b ) that minimizes the negative log-likelihood min w,b 1 m log P(y = +/-1 | x,w )= min w,b 1 m log[1+exp(-y i (w T x i + b )] This optimization problem is called Logistics Regression Logistic Regression is sometimes called the Maximum Entropy model in the NLP community (since the resulting distribution is the one that has the largest entropy among all those that activate the same features). 8
9 .Logistic Regression (3) Using the standard mapping to linear separators through the origin, we would like to minimize: min w 1 m log P(y= +/-1 | x,w )= min w , 1 m log[1+exp (-y i (w T x i )] To get good generalization, it is common to add a regularization term , and the regularized logistics regression then becomes: min w f(w) = ½ w T w + C 1 m log[1+exp (-y i (w T x i )], Where C is a user selected parameter that balances the two terms. 9 Empirical loss Regularization term
10 .Comments on discriminative Learning min w f(w) = ½ w T w + C 1 m log[1+exp (- y i w T x i )], Where C is a user selected parameter that balances the two terms. Since the second term is t he loss function Therefore , regularized logistic regression can be related to other learning methods, e.g., SVMs. L 1 SVM solves the following optimization problem: min w f 1 (w) = ½ w T w + C 1 m max(0,1-y i ( w T x i ) L 2 SVM solves the following optimization problem: min w f 2 (w ) = ½ w T w + C 1 m (max(0,1-y i w T x i )) 2 10 Empirical loss Regularization term
11 .Optimization: How to Solve 11 All methods are iterative methods, that generate a sequence w k that converges to the optimal solution of the optimization problem above. Many options within this category: Iterative scaling: Low cost per iteration, slow convergence, updates each w component at a time Newton methods: High cost per iteration, faster convergence non-linear conjugate gradient; quasi-Newton methods ; truncated Newton methods; trust-region newton method. Limited memory BFGS is very popular Stochastic Gradient Decent methods The runtime does not depend on n =#(examples); advantage when n is very large. Stopping criteria is a problem: method tends to be too aggressive at the beginning and reaches a moderate accuracy quite fast, but it’s convergence becomes slow if we are interested in more accurate solutions .
12 .Summary (1) If probabilistic hypotheses are actually like other linear functions, can we interpret the outcome of other linear learning algorithms probabilistically? Yes (2) If probabilistic hypotheses are actually like other linear functions, can you train them similarly (that is, discriminatively)? Yes. Classification : Logistic regression/Max Entropy HMM: can be trained via Perceptron (Structured Learning Class: Spring 2016) 12
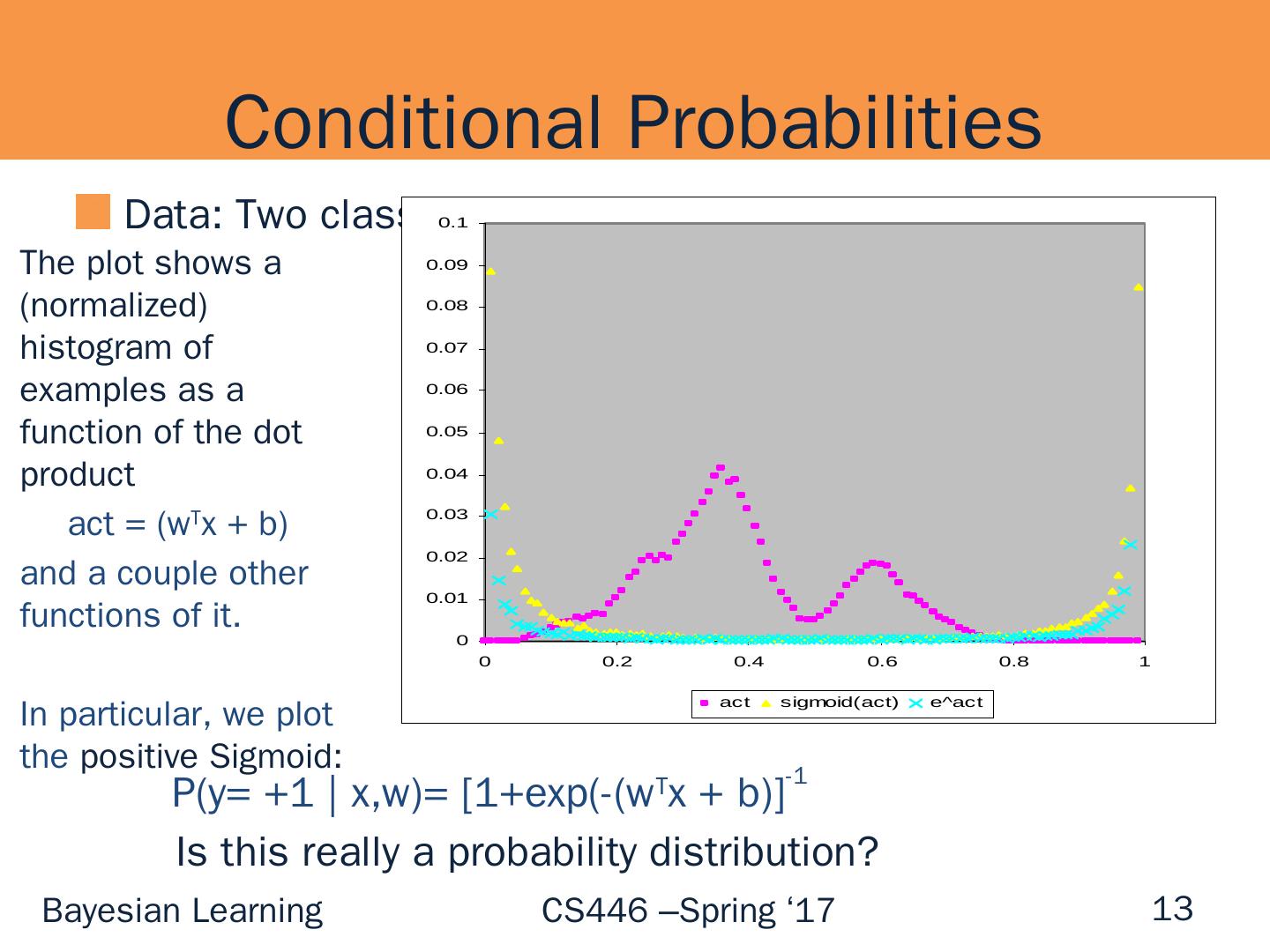
13 .Conditional Probabilities Data: Two class (Open/ NotOpen Classifier) 13 The plot shows a (normalized) histogram of examples as a function of the dot product act = ( w T x + b) and a couple other functions of it. In particular, we plot the positive Sigmoid: P(y = +1 | x,w )= [1+exp (-( w T x + b)] -1 Is this really a probability distribution?
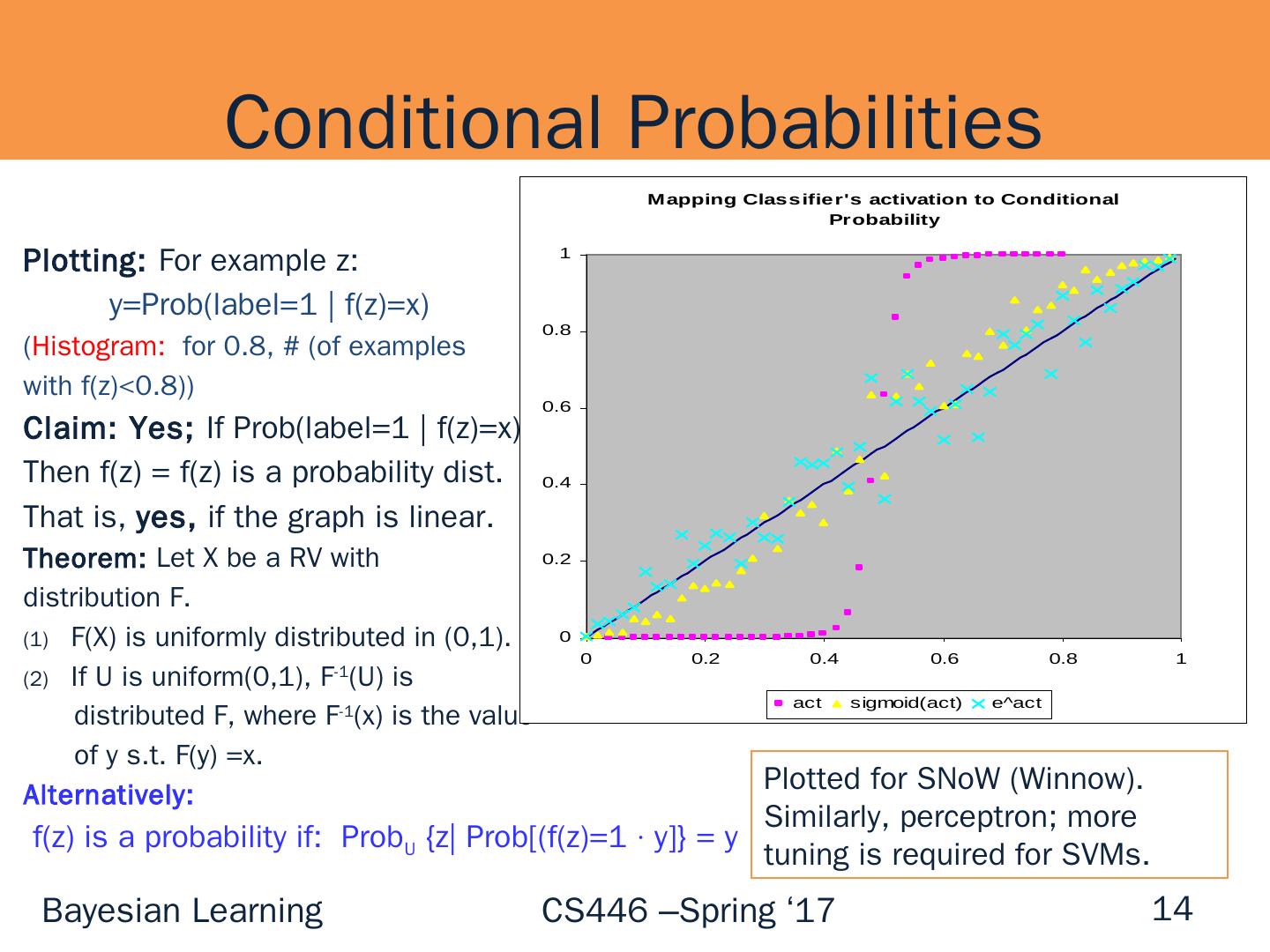
14 .Plotting: For example z: y= Prob (label=1 | f(z)=x ) ( Histogram: for 0.8, # (of examples with f(z)<0.8)) Claim: Yes; If Prob (label=1 | f(z)=x) = x Then f(z) = f(z) is a probability dist. That is, yes, if the graph is linear. Theorem : Let X be a RV with distribution F. F(X ) is uniformly distributed in (0,1). If U is uniform(0,1 ), F -1 (U) is distributed F, where F -1 (x) is the value of y s.t. F(y) =x. Alternatively: f(z) is a probability if: Prob U {z| Prob [ (f(z)=1 · y]} = y Conditional Probabilities 14 Plotted for SNoW (Winnow). Similarly, perceptron; more tuning is required for SVMs.