14 .CIS 700-004: Lecture 4M Deep vs. shallow learning 02/04/19
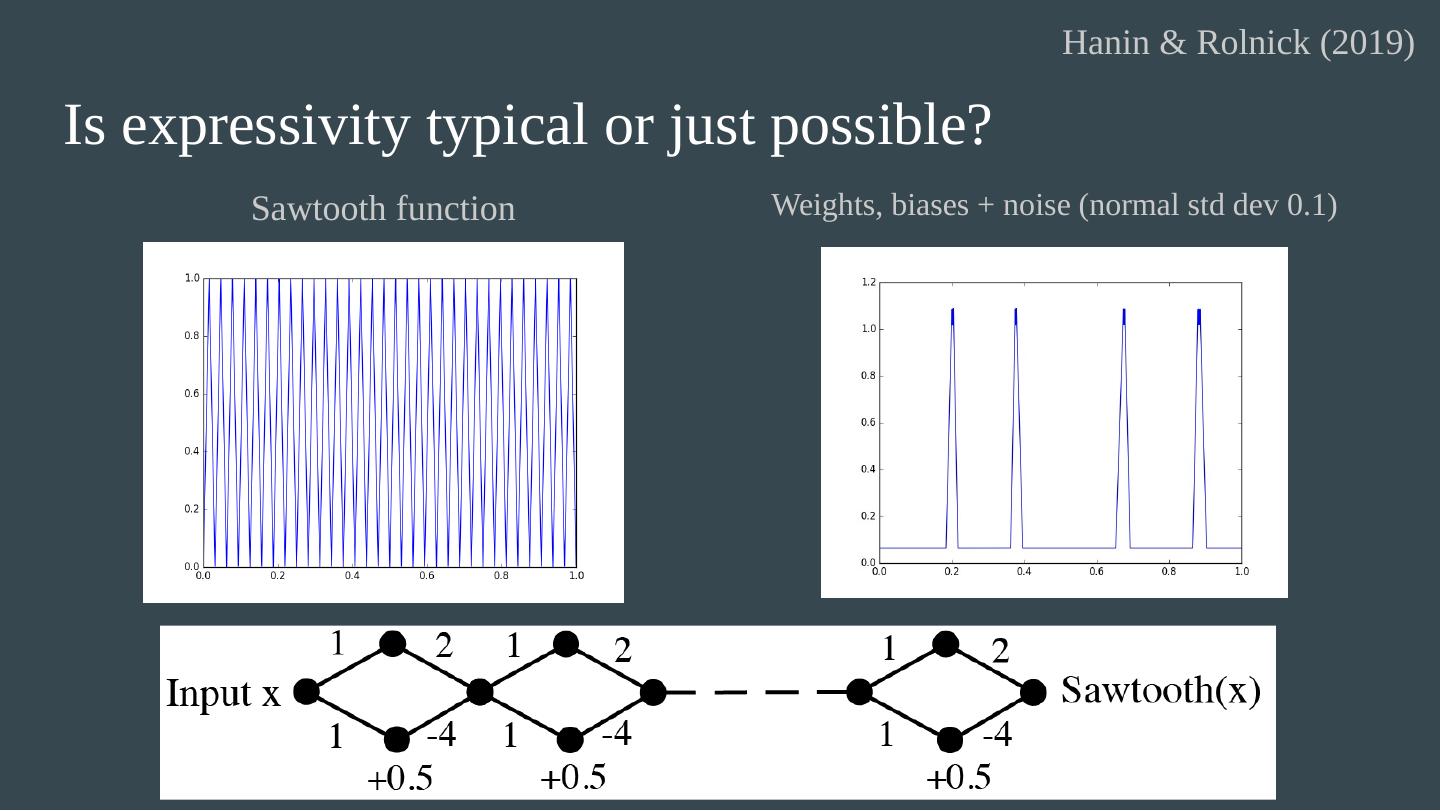
15 .Expressivity We know even shallow neural nets (=1 hidden layer) are universal approximators under various assumptions. That could require huge width. Given a particular architecture, we can looks at its expressivity , or the set of functions it can approximate. Why do we need to look at approximation here?
16 .What is a ResNet? He et al. (2016)
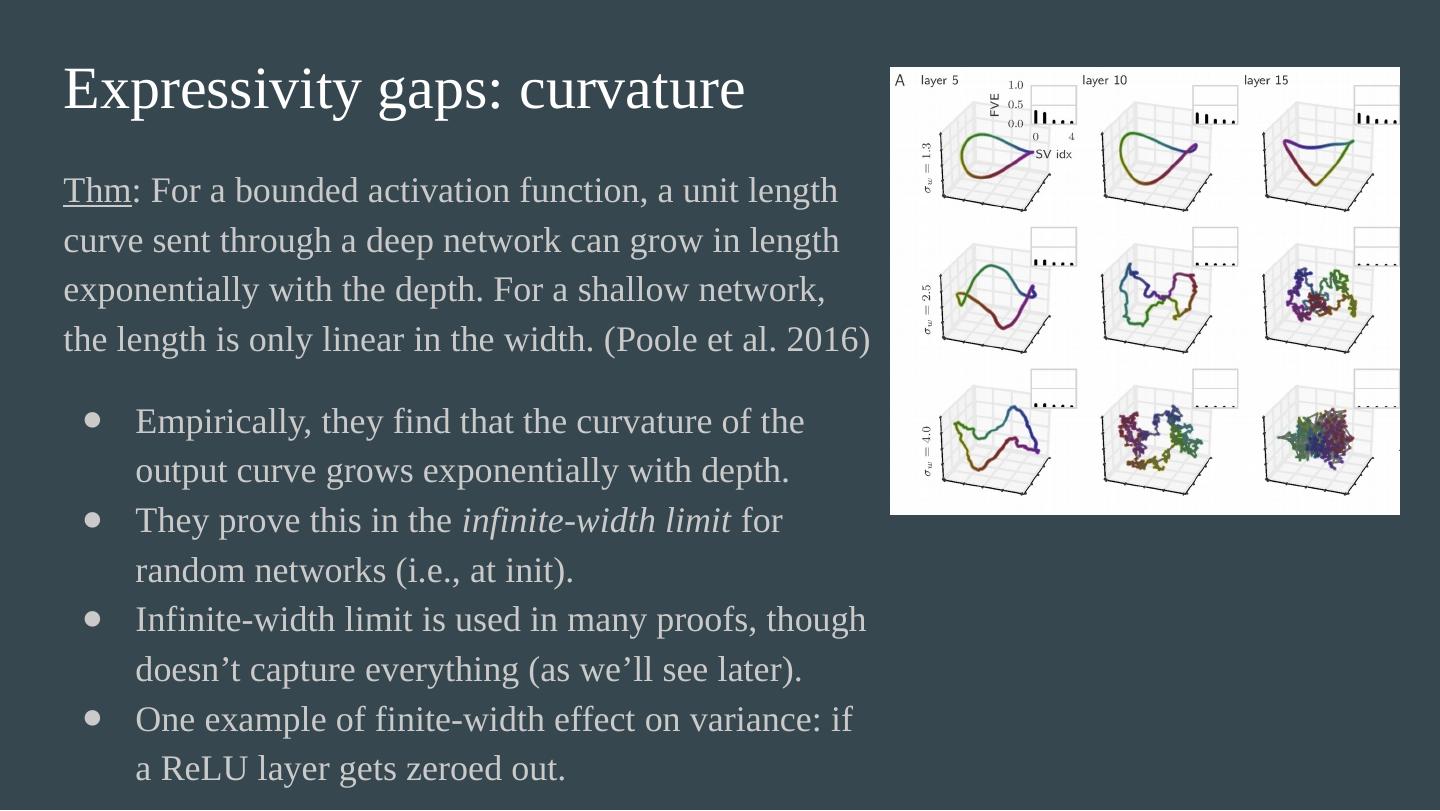
17 .Expressivity gaps: curvature Thm : For a bounded activation function, a unit length curve sent through a deep network can grow in length exponentially with the depth. For a shallow network, the length is only linear in the width. (Poole et al. 2016)
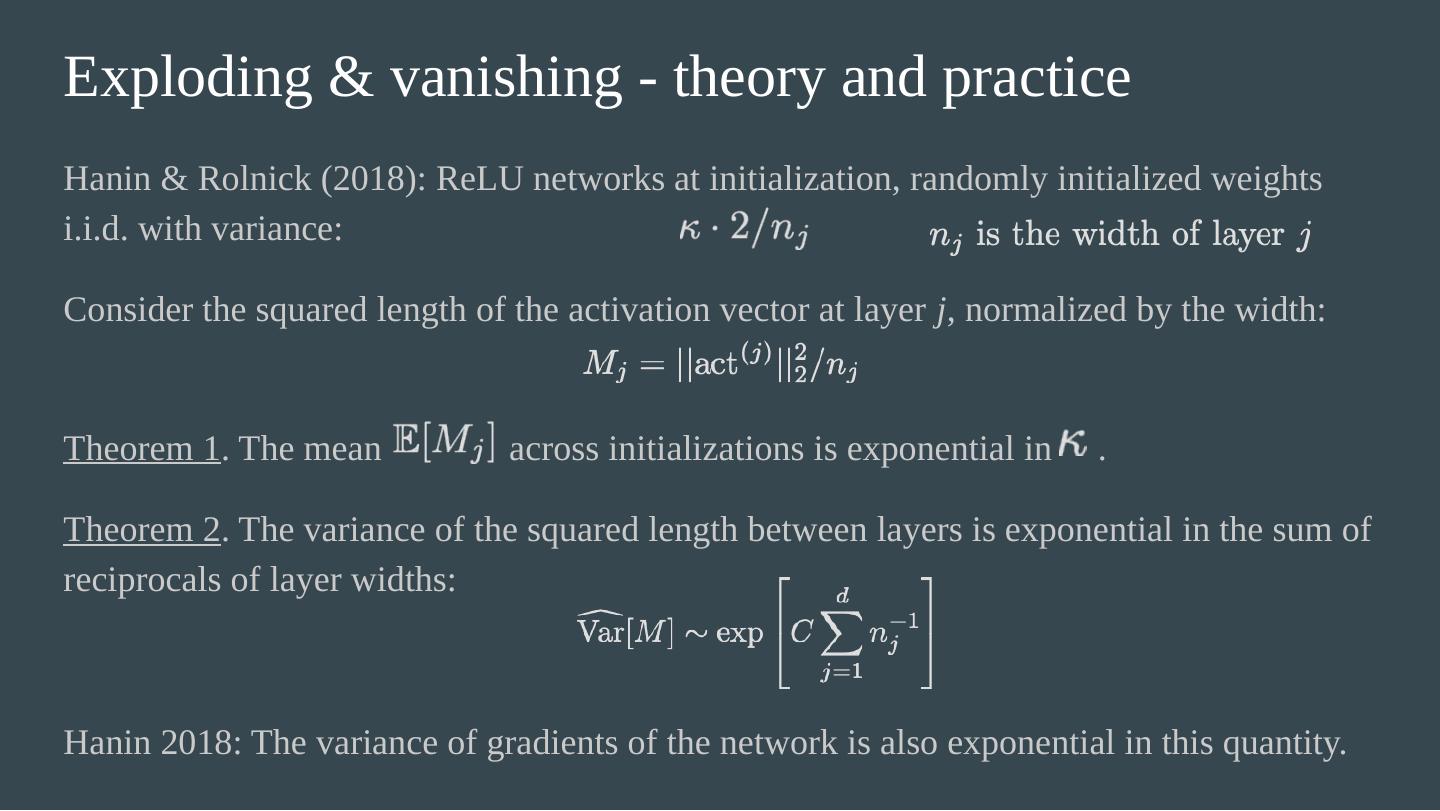
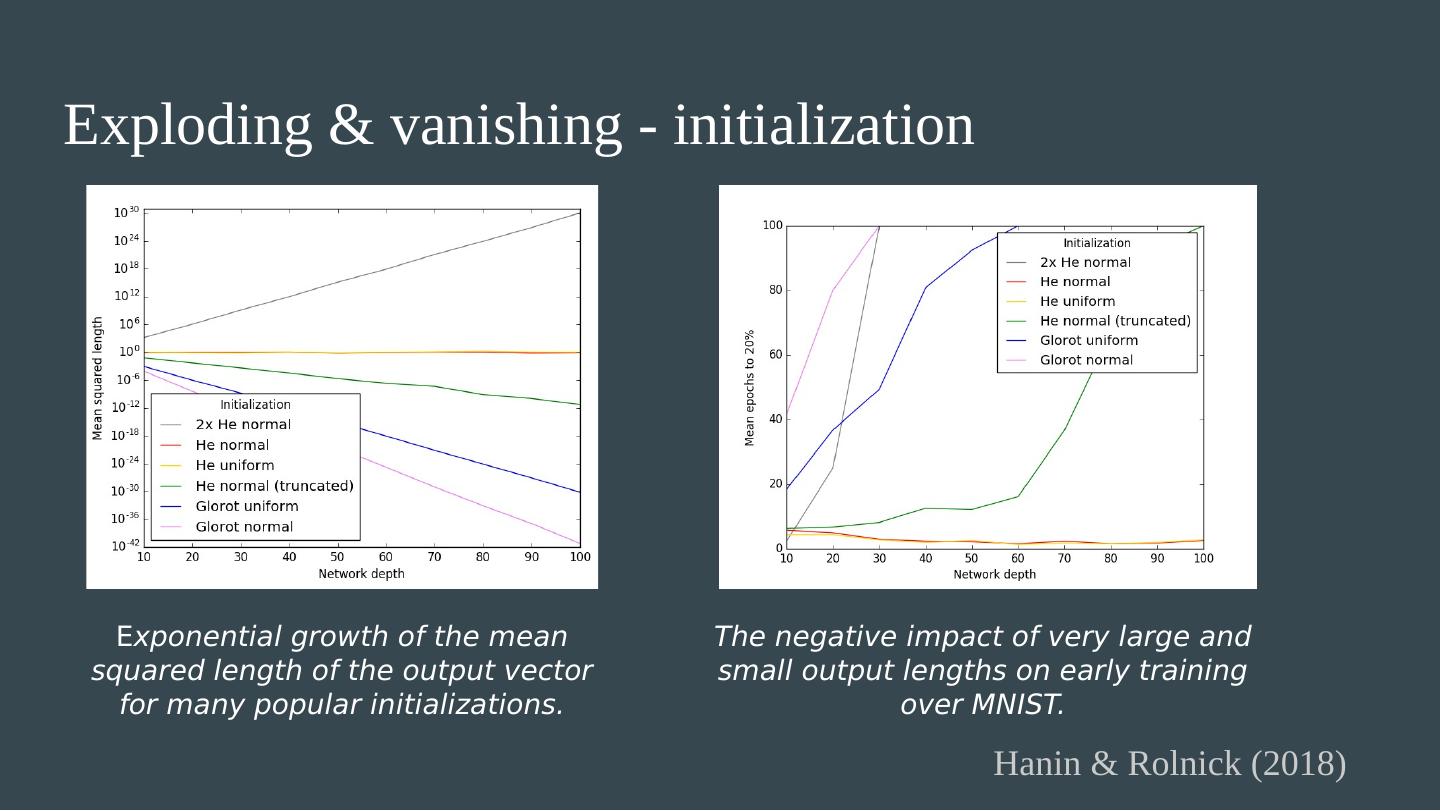
18 .Exploding & vanishing - theory and practice Hanin & Rolnick (2018): ReLU networks at initialization, randomly initialized weights i.i.d. with variance: Consider the squared length of the activation vector at layer j , normalized by the width: Theorem 1 . The mean across initializations is exponential in . Theorem 2 . The variance of the squared length between layers is exponential in the sum of reciprocals of layer widths: Hanin 2018: The variance of gradients of the network is also exponential in this quantity.
19 .DenseNets
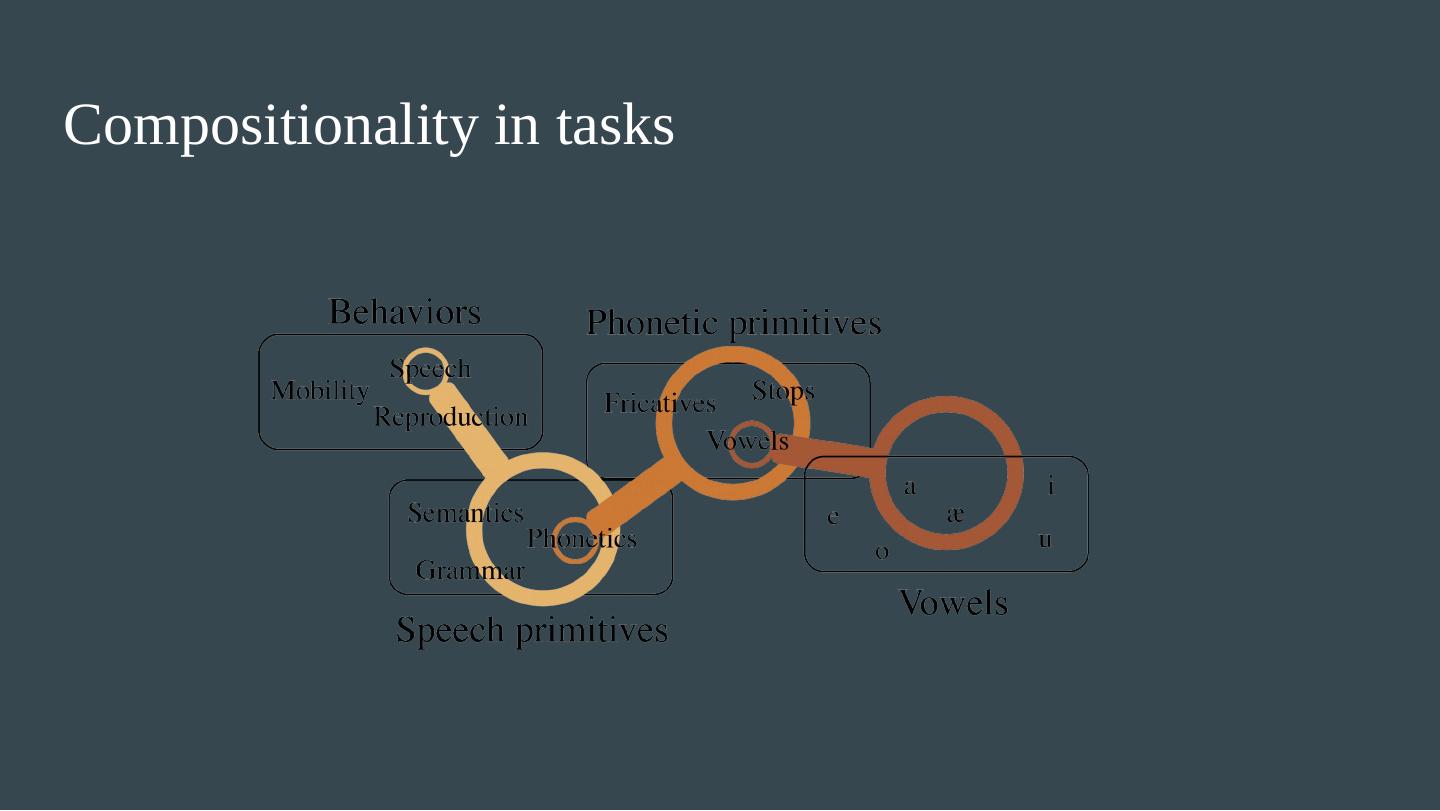
20 .Compositionality in tasks
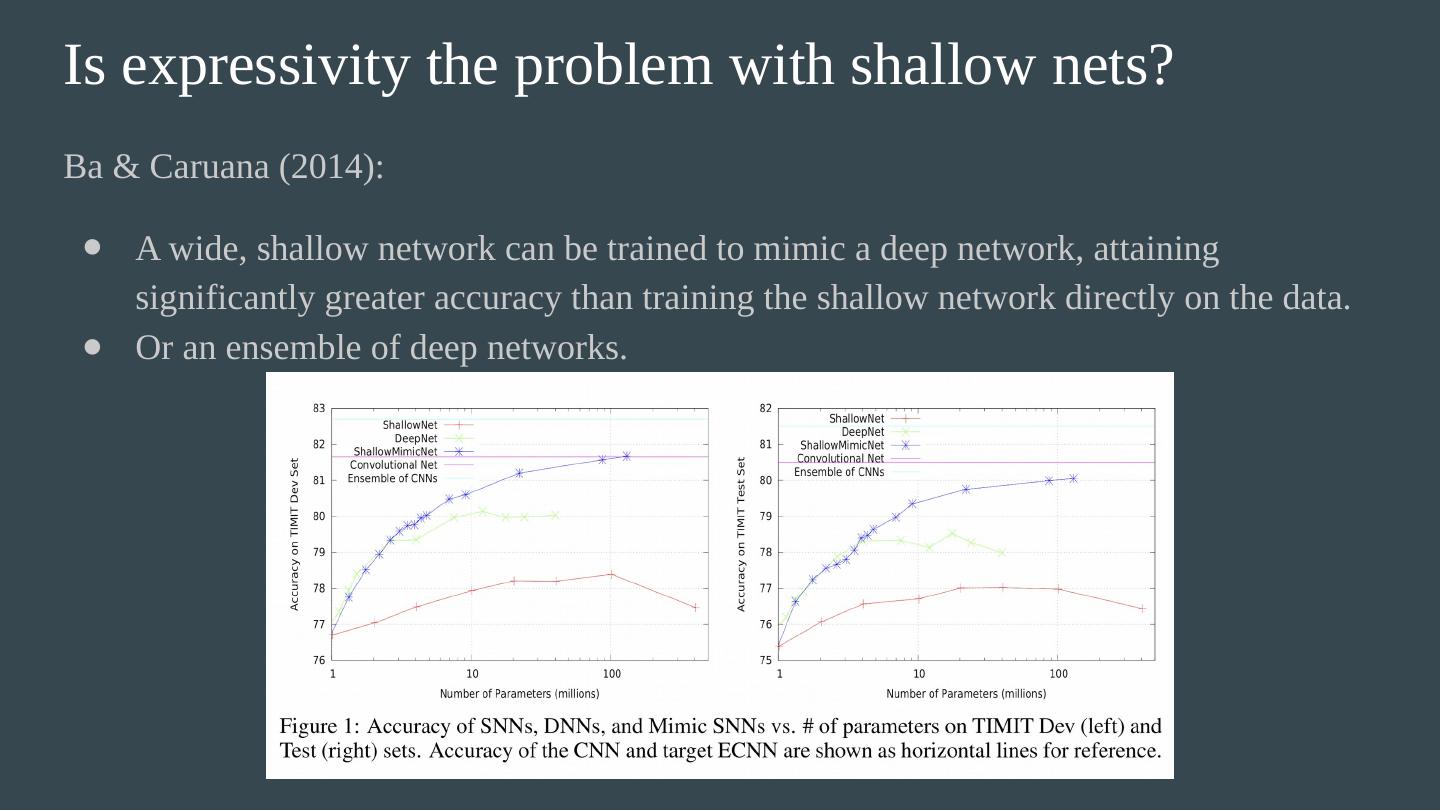
21 .Is expressivity the problem with shallow nets? Ba & Caruana (2014): A wide, shallow network can be trained to mimic a deep network, attaining significantly greater accuracy than training the shallow network directly on the data. Or an ensemble of deep networks. The mimic networks output the pre-softmax output of the teach networks. Why is there more information here than simply training on the raw data? Learnability of deeper networks may be more important than expressivity in practice.
22 .The intuitive benefits of depth
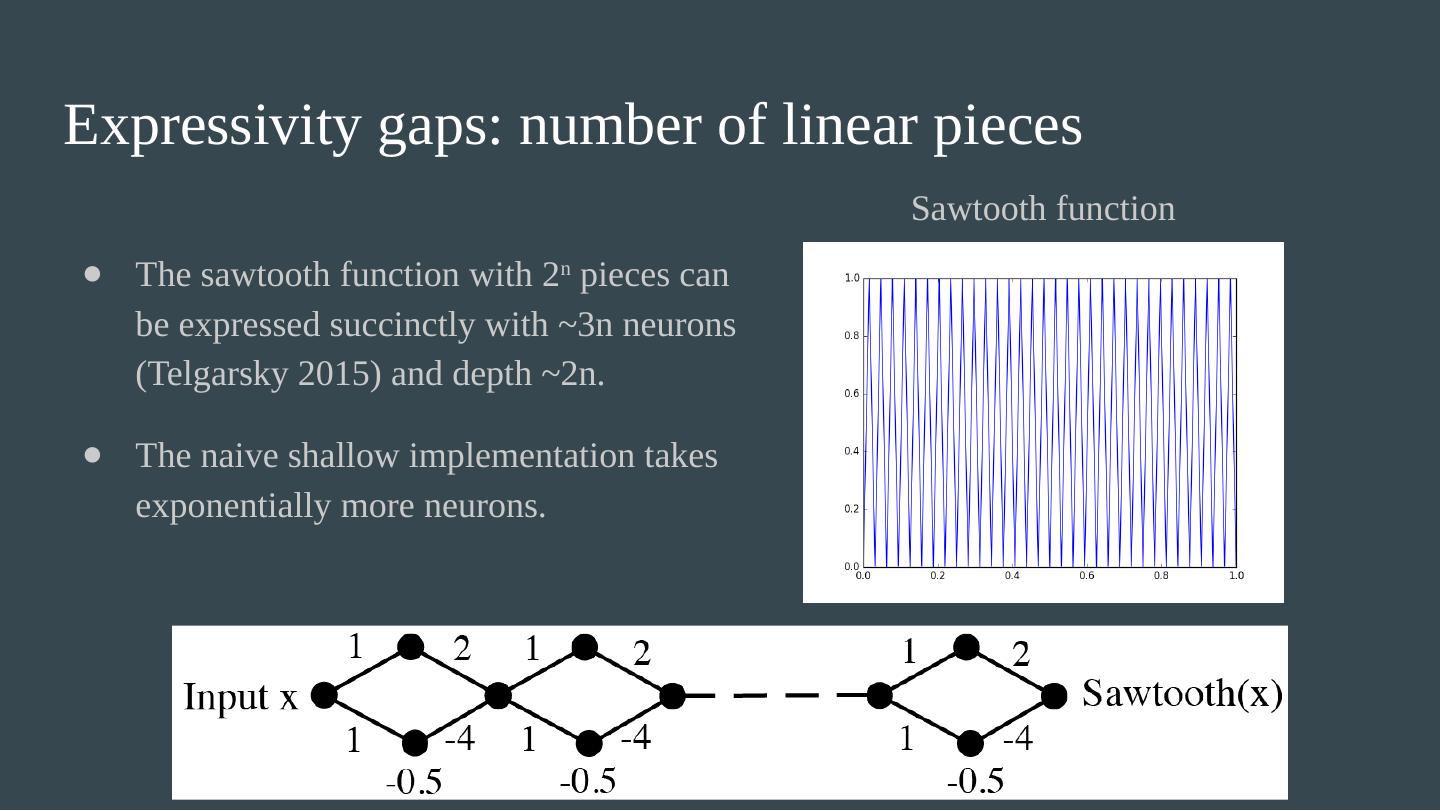
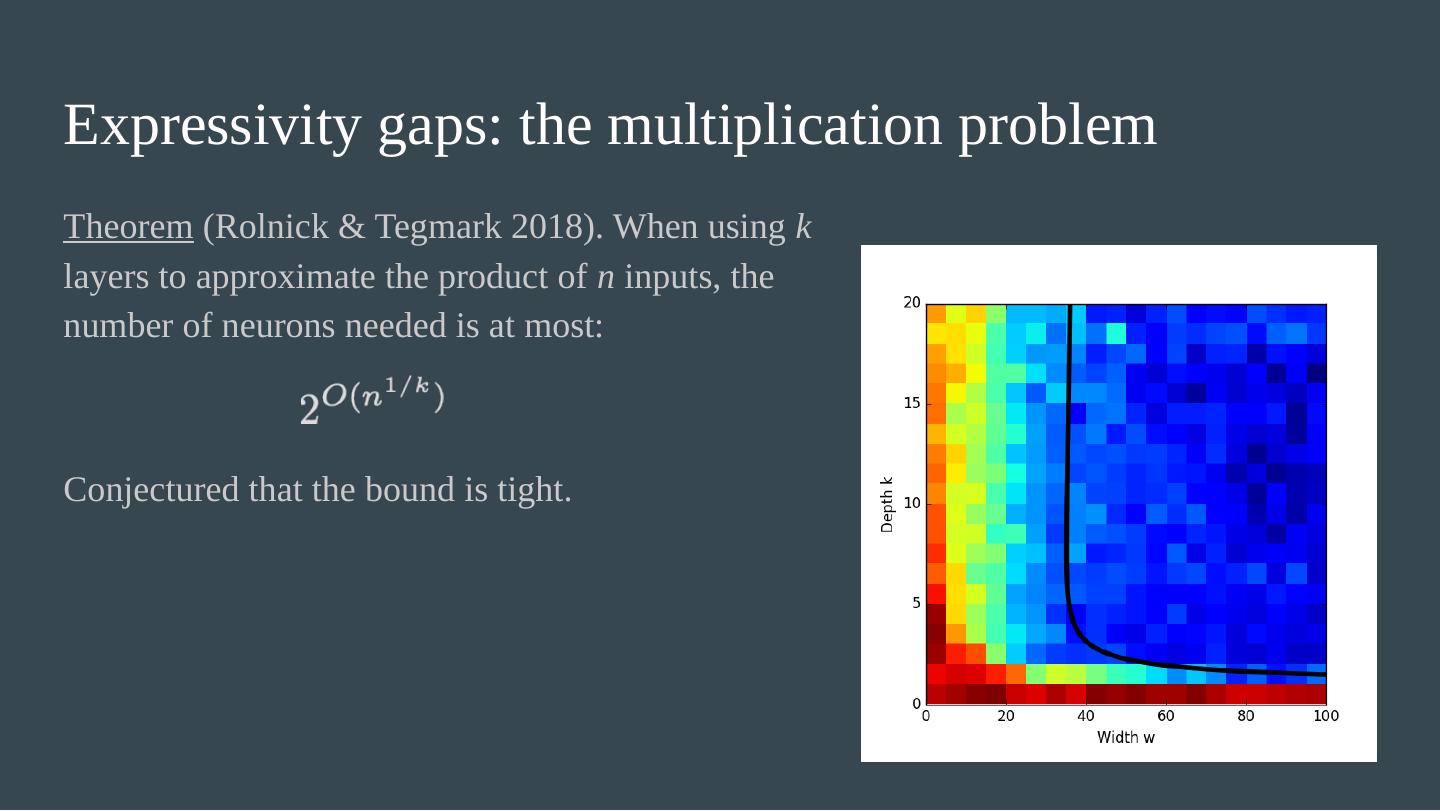
23 .Expressivity gaps: the multiplication problem Theorem ( Rolnick & Tegmark 2018). When using k layers to approximate the product of n inputs, the number of neurons needed is at most: Conjectured that the bound is tight.
24 .Exploding & vanishing - takeaways Poor initialization and poor architecture both stop networks from learning. Initialization: Use i.i.d. weights with variance 2/fan-in (e.g. He normal / He uniform). Watch out for truncated normals! Architecture: Width (or #features in ConvNets) should grow with depth. Even a single narrow layer makes training hard.
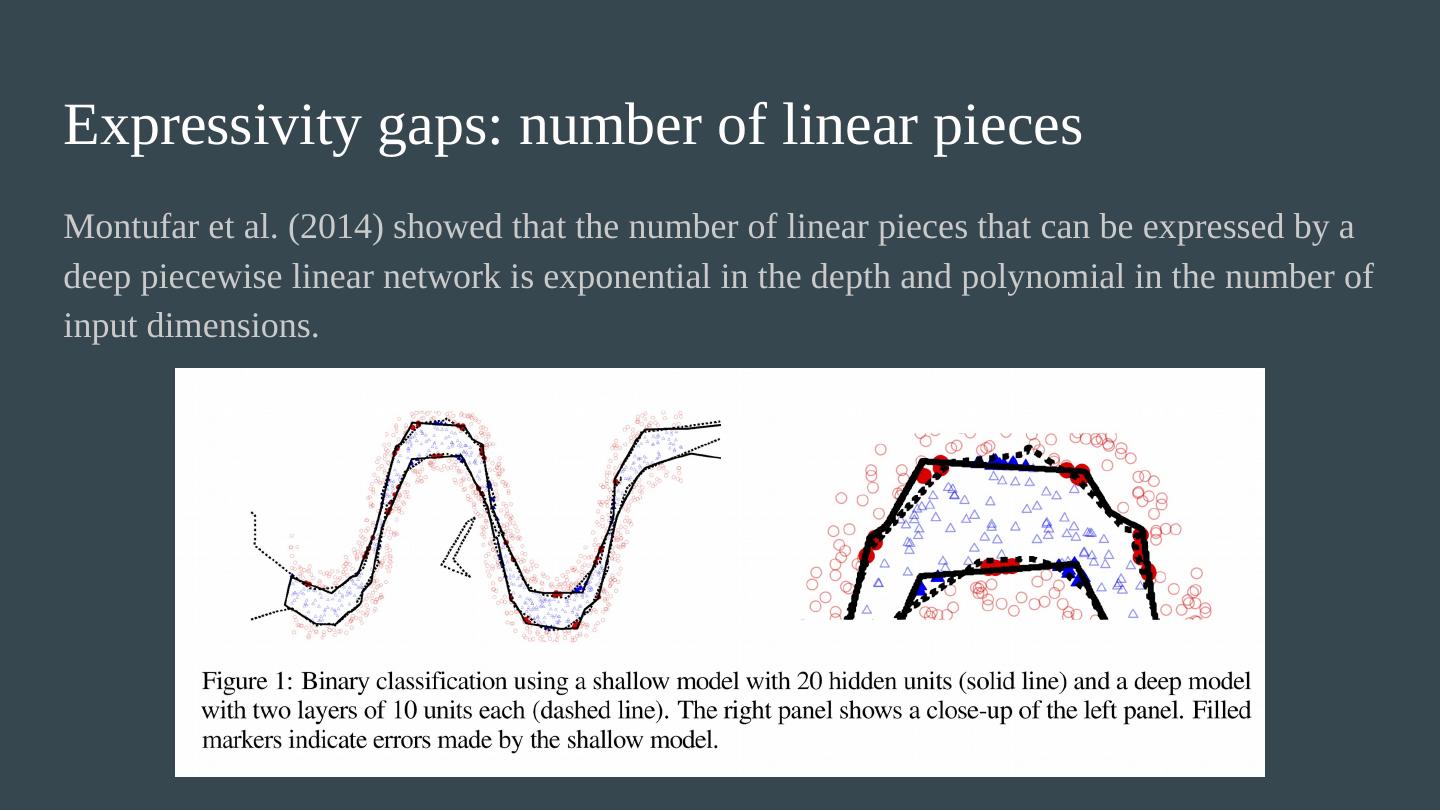
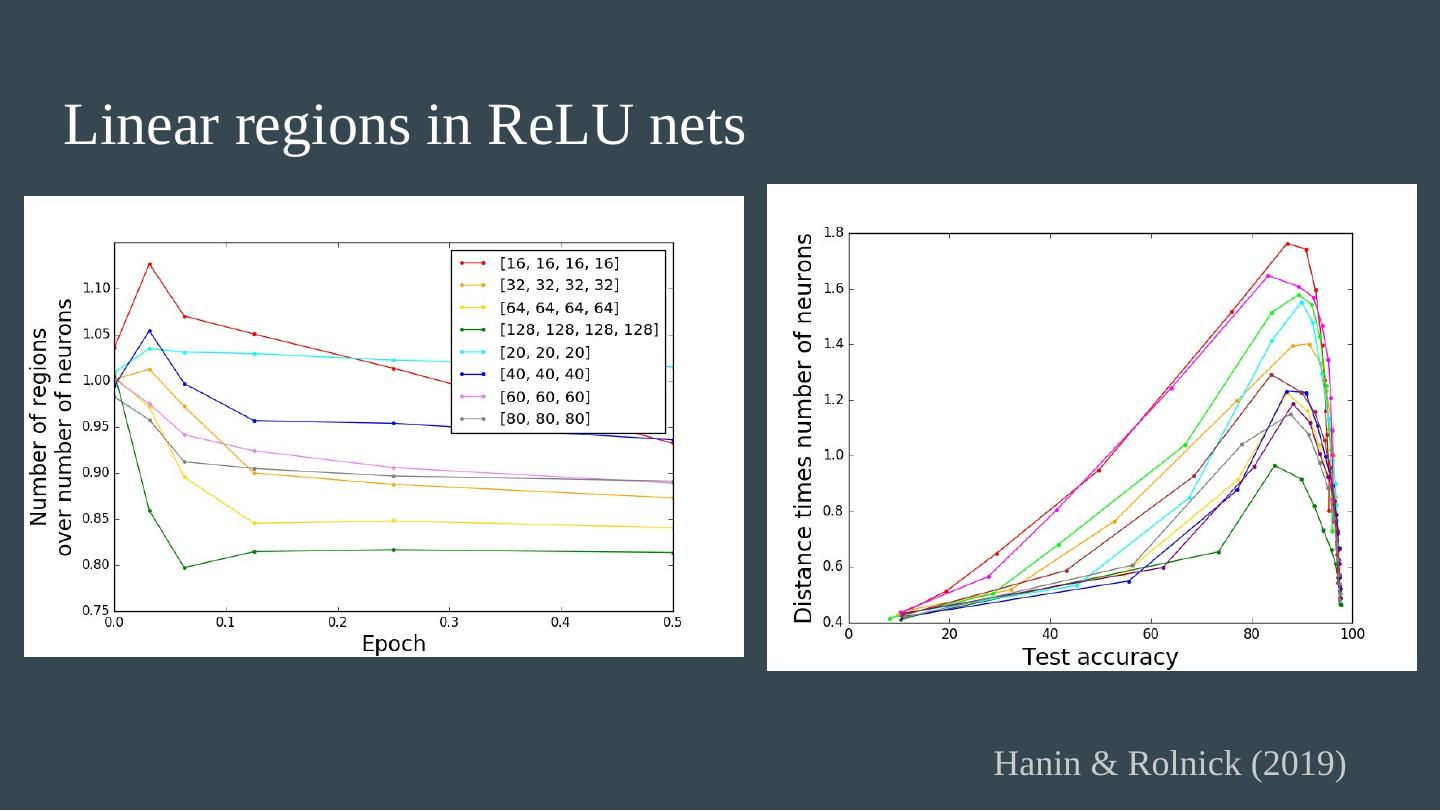
25 .Linear regions in ReLU nets The number of linear regions in a ReLU network (which is piecewise linear) can be exponential in the depth. (Montufar et al. 2014) Hanin & Rolnick (2019) - the regions for a typical ReLU net at initialization. Theorem 1 : The expected number of regions that intersect any 1D trajectory (e.g. a line) per unit length is linear in N , the total number of neurons. Theorem 2 : The expected surface area of the total boundary between regions, per unit volume, is linear in N . Theorem 3 : The expected distance to the nearest region boundary scales as 1/N . For n -dimensional input, number of regions conjectured to grow as (depth) n .
26 .Loss landscapes of neural networks The loss landscape refers to how the loss changes over parameter space. The dimension of parameter space is very high (potentially millions). Learning aims to find a global minimum. On right is a surface plot with z = loss and xy = a 2D projection of params. The individual directions in the projection are normalized by the network weights. Li et al. (2018)
热门城市
