- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- <iframe src="https://www.slidestalk.com/u181/VT_Computer_Vision_13_ImageStitching?embed" frame border="0" width="640" height="360" scrolling="no" allowfullscreen="true">复制
- 微信扫一扫分享
图像拼接
展开查看详情
1 .Image Stitching Computer Vision Jia-Bin Huang, Virginia Tech Many slides from S. Seitz and D. Hoiem Add example
2 .Administrative stuffs HW 3 is out due 11:59 PM Oct 17 Please start early. D eadlines are firm. N o emails requesting extensions Getting help? *Five* free late days without penalty Piazza Office hours No free late dates for final projects
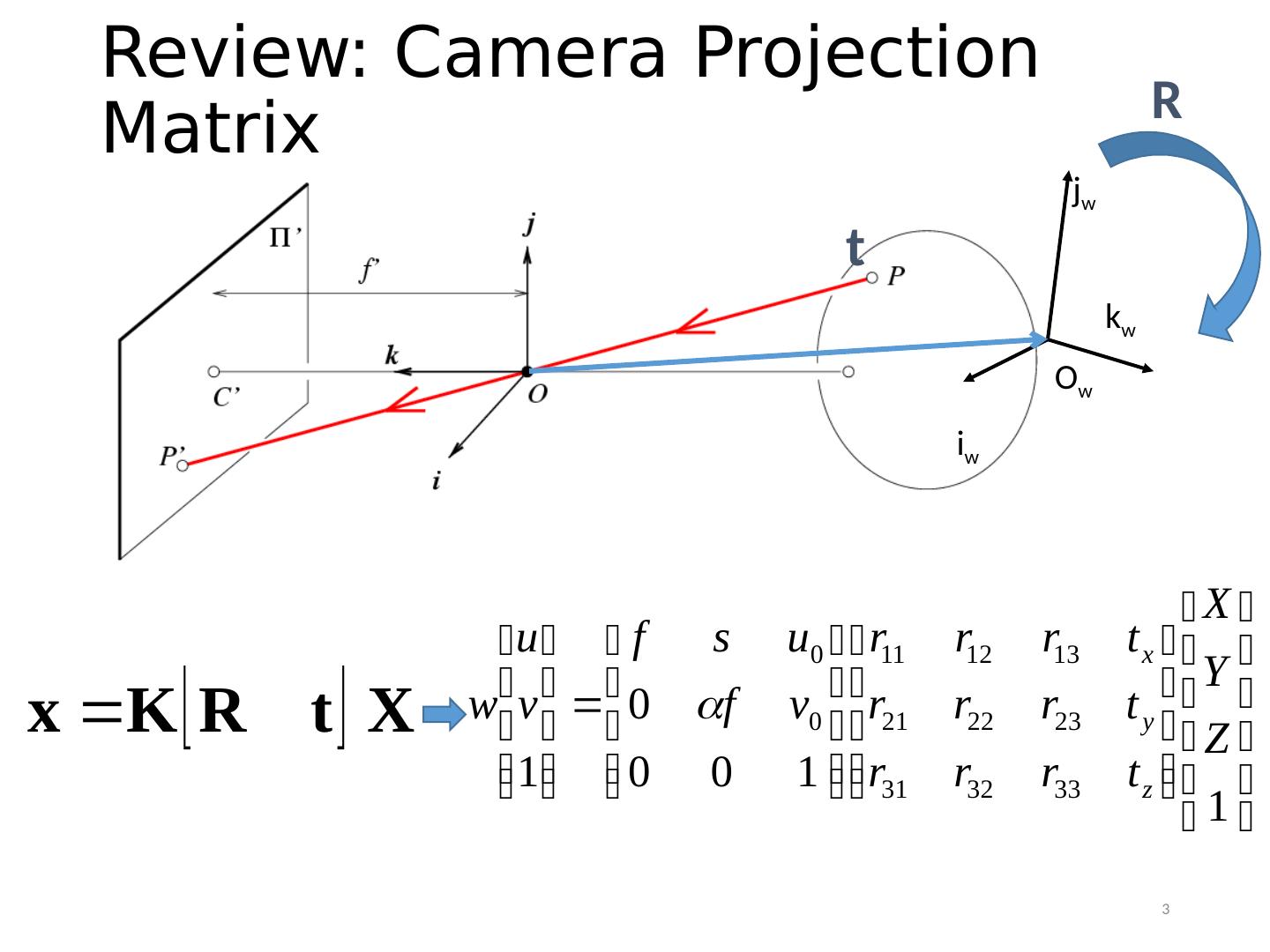
3 .Review: Camera Projection Matrix O w i w k w j w t R 3
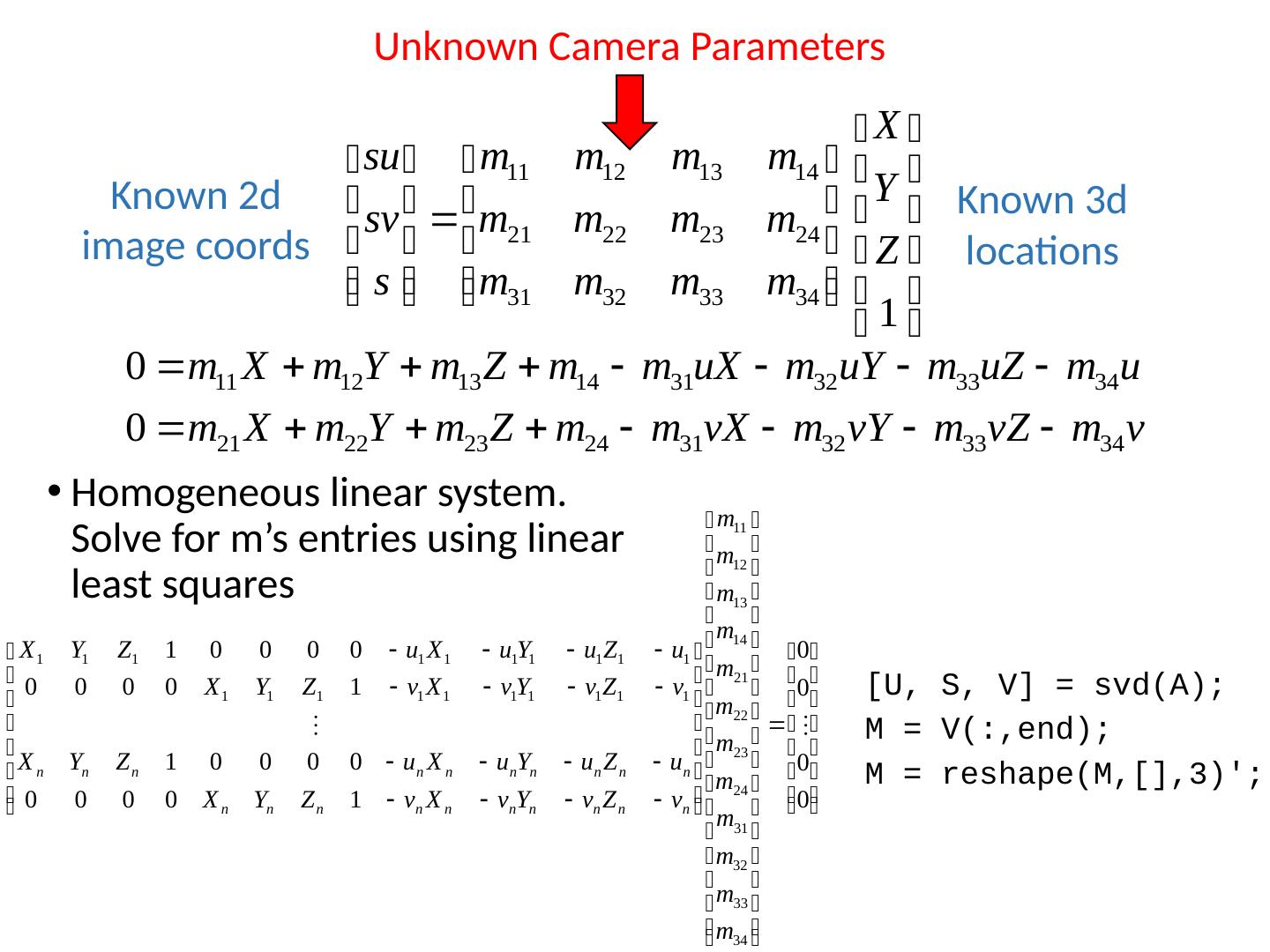
4 .Review: Camera Calibration Method 1: Use an object (calibration grid) with known geometry Correspond image points to 3d points Get least squares solution (or non-linear solution) 4 Known 3d locations Known 2d image coordinates Unknown Camera Parameters
5 .Review: Camera Calibration Method 1: Use an object (calibration grid) with known geometry Correspond image points to 3d points Get least squares solution (or non-linear solution) 4 Known 3d locations Known 2d image coordinates Unknown Camera Parameters
6 .Constraints for , Review: Calibration by vanishing points Orthogonality constraints VP (2D) VP (3D) Unknown c amera parameters = 0 = 0 = 0 … Eqn (1) … Eqn (2) … Eqn (3) Eqn (1 ) – Eqn (2) Eqn (2) – Eqn ( 3 ) Solve for
7 .Rotation matrix Set directions of vanishing points Review: Calibration by vanishing points Unknown c amera parameters Special properties of R inv ( R )= R T Each row and column of R has unit length
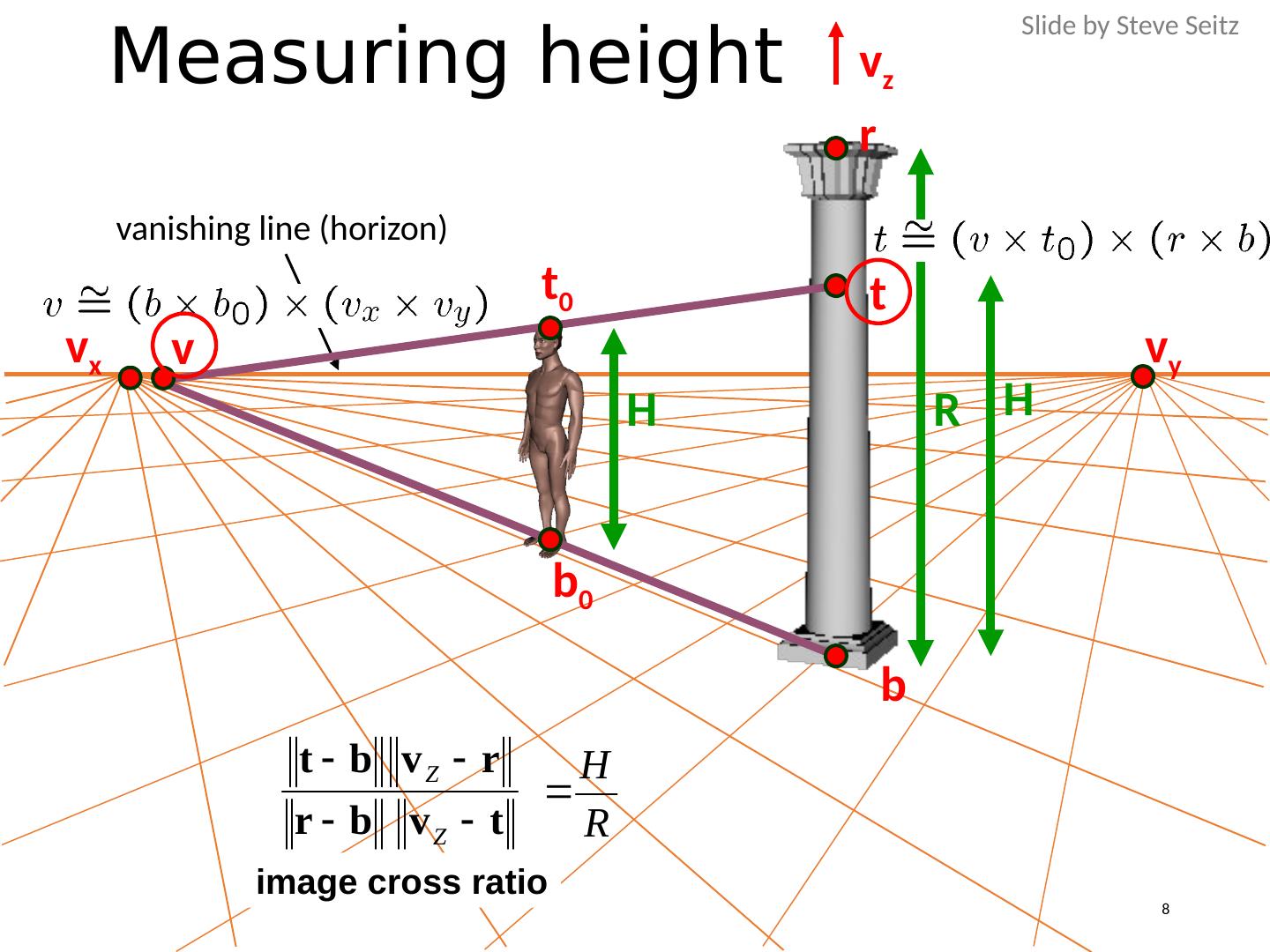
8 .Measuring height R H v z r b t H b 0 t 0 v v x v y vanishing line (horizon) image cross ratio Slide by Steve Seitz 8
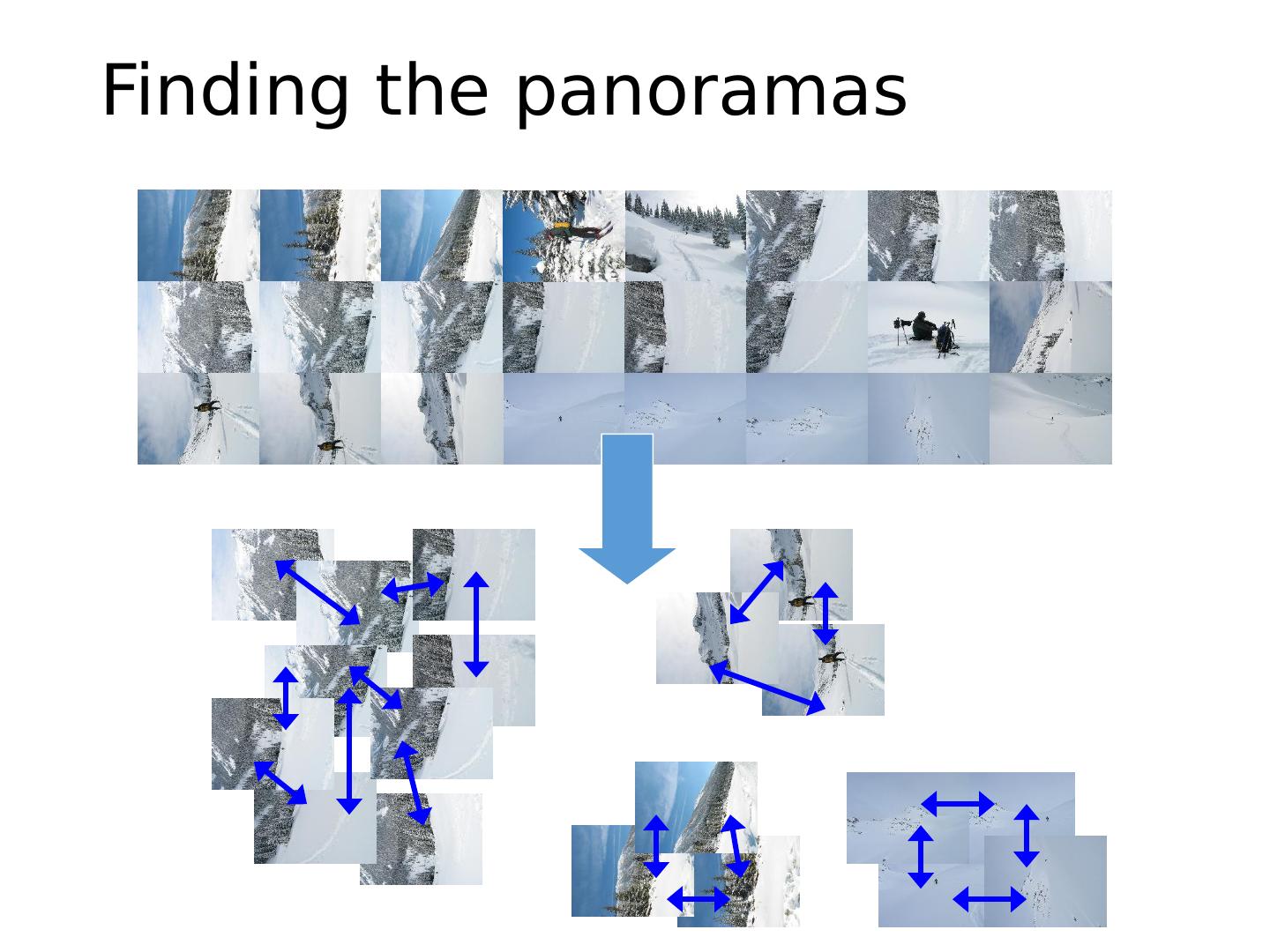
9 .This class: Image Stitching Combine two or more overlapping images to make one larger image Add example Slide credit: Vaibhav Vaish
10 .Concepts introduced/reviewed in today’s lecture Camera model Homographies Solving homogeneous systems of linear equations Keypoint -based alignment RANSAC Blending How the iphone stitcher works
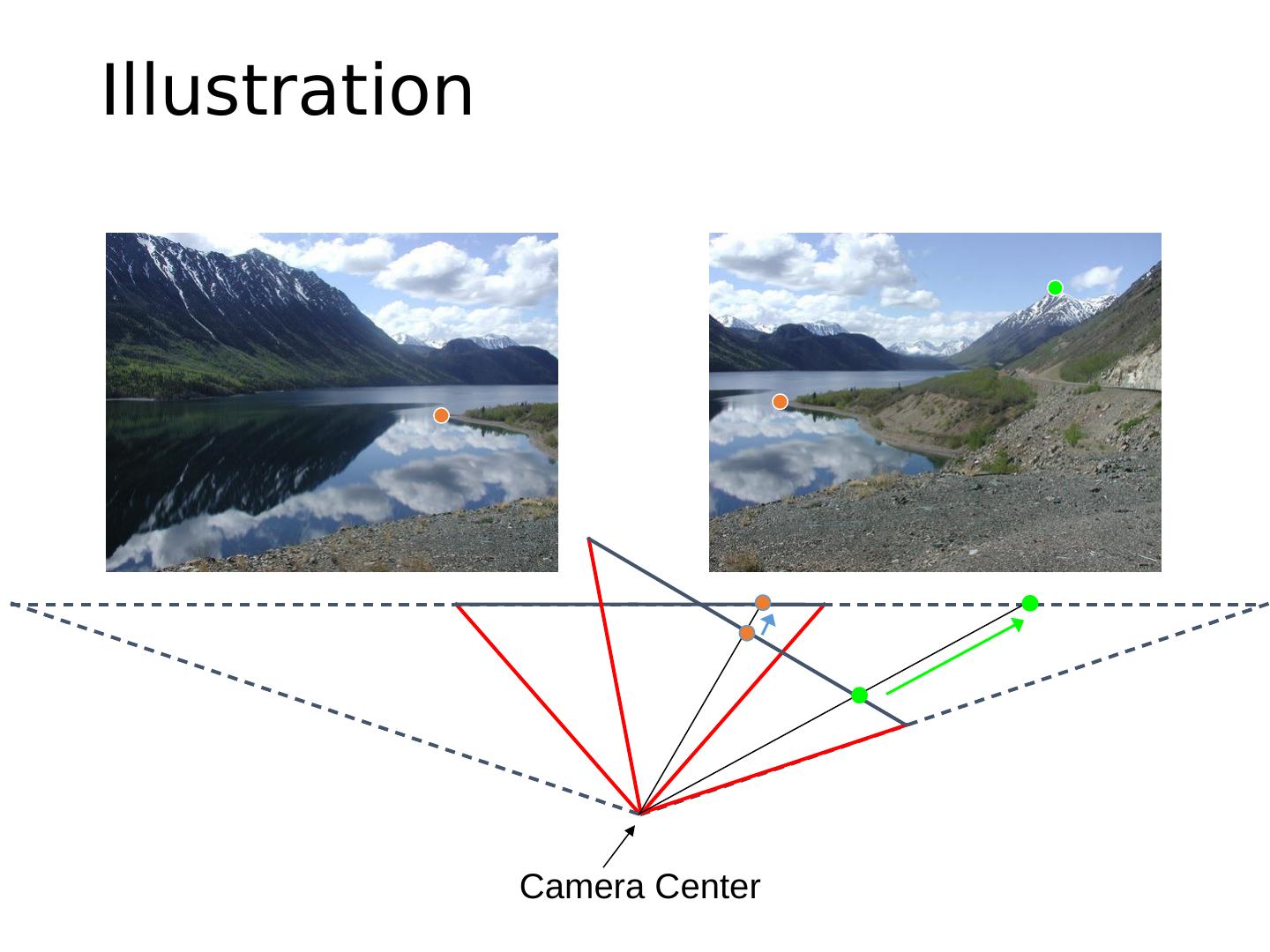
11 .Illustration Camera Center
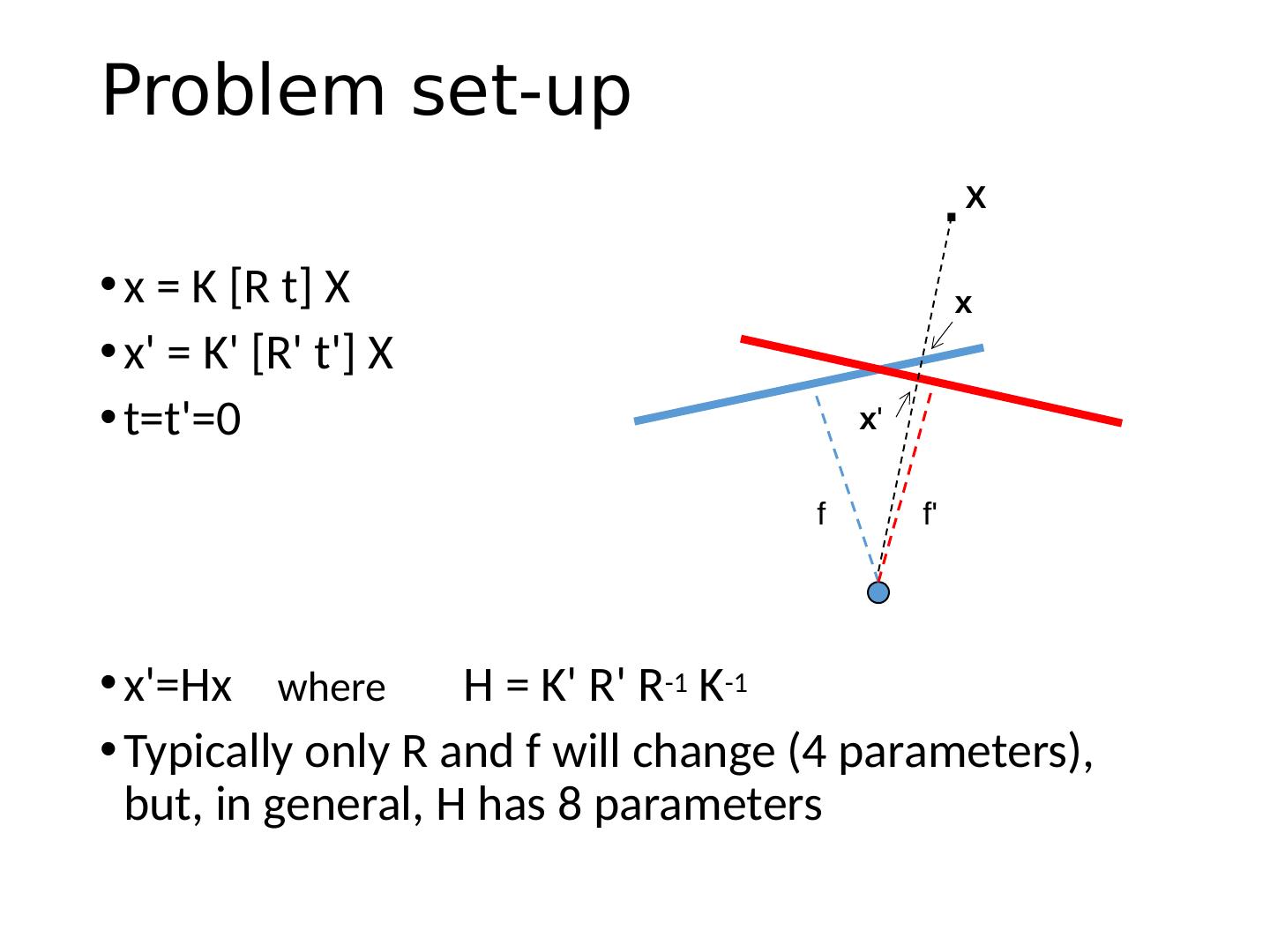
12 .Problem set-up x = K [R t] X x = K [R t] X t=t=0 x= Hx where H = K R R -1 K -1 Typically only R and f will change (4 parameters), but, in general, H has 8 parameters f f . x x X
13 .Homography Definition General mathematics: homography = projective linear transformation Vision (most common usage): homography = linear transformation between two image planes Examples Project 3D surface into frontal view Relate two views that differ only by rotation
14 .Homography example: Image rectification To unwarp (rectify) an image solve for homography H given p and p ’ : w p ’=Hp p p’
15 .Homography example: Planar mapping Freedom HP Commercial
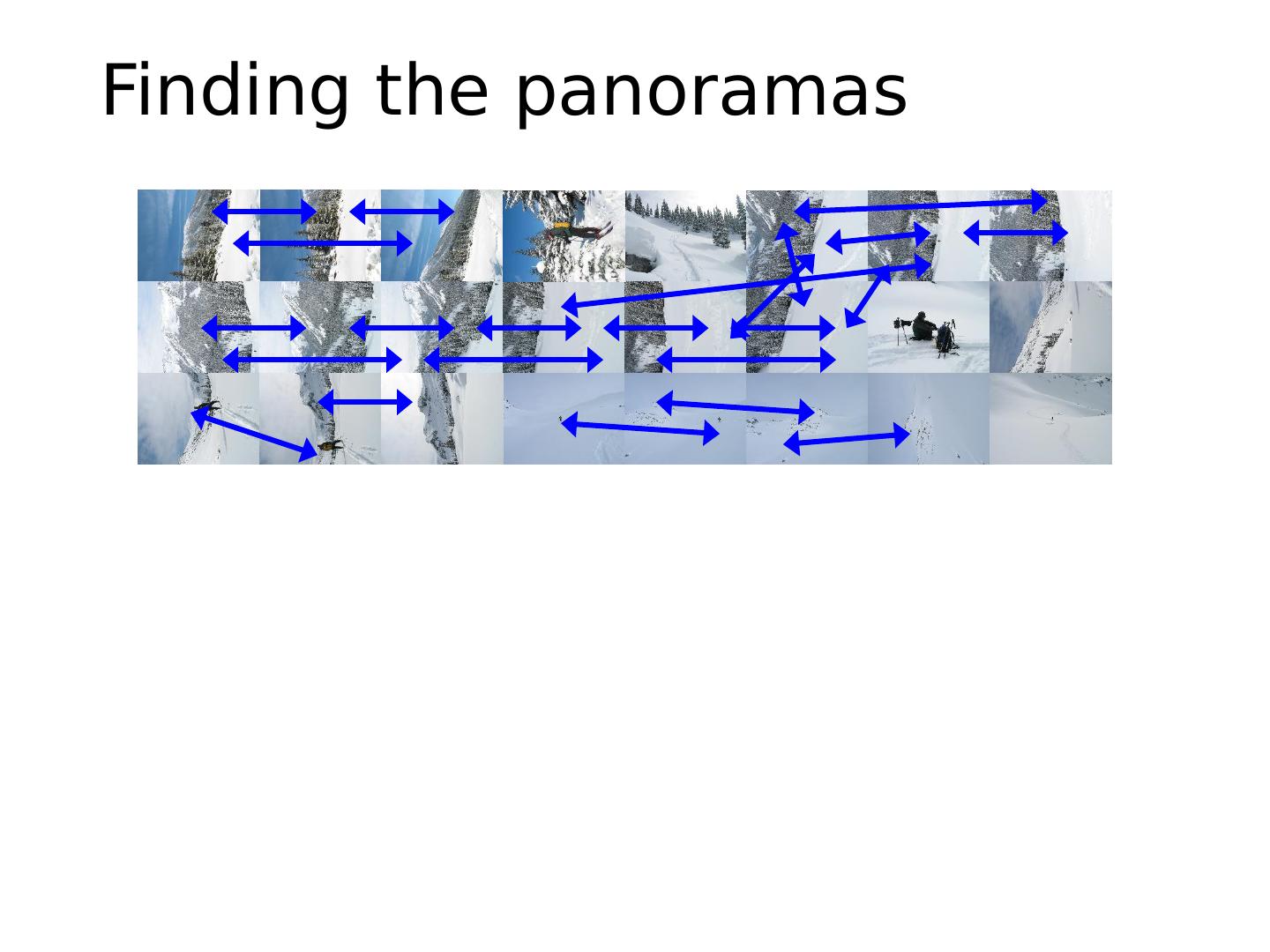
16 .Image Stitching Algorithm Overview Detect keypoints (e.g., SIFT) Match keypoints (e.g., 1 st /2 nd NN < thresh) Estimate homography with four matched keypoints (using RANSAC) Combine images
17 .Computing homography Assume we have four matched points: How do we compute homography H ? Direct Linear Transformation (DLT)
18 .Computing homography Direct Linear Transform Apply SVD: UDV T = A h = V smallest (column of V corr. to smallest singular value) Matlab [U, S, V] = svd(A); h = V(:, end); Explanations of SVD and solving homogeneous linear systems
19 .Computing homography Assume we have four matched points: How do we compute homography H ? Normalized DLT Normalize coordinates for each image Translate for zero mean Scale so that average distance to origin is ~ sqrt (2) This makes problem better behaved numerically (see HZ p. 107-108) Compute using DLT in normalized coordinates Unnormalize :
20 .Computing homography Assume we have matched points with outliers: How do we compute homography H ? Automatic Homography Estimation with RANSAC Choose number of samples N HZ Tutorial ‘99
21 .Computing homography Assume we have matched points with outliers: How do we compute homography H ? Automatic Homography Estimation with RANSAC Choose number of samples N Choose 4 random potential matches Compute H using normalized DLT Project points from x to x ’ for each potentially matching pair: Count points with projected distance < t E.g., t = 3 pixels Repeat steps 2-5 N times Choose H with most inliers HZ Tutorial ‘99
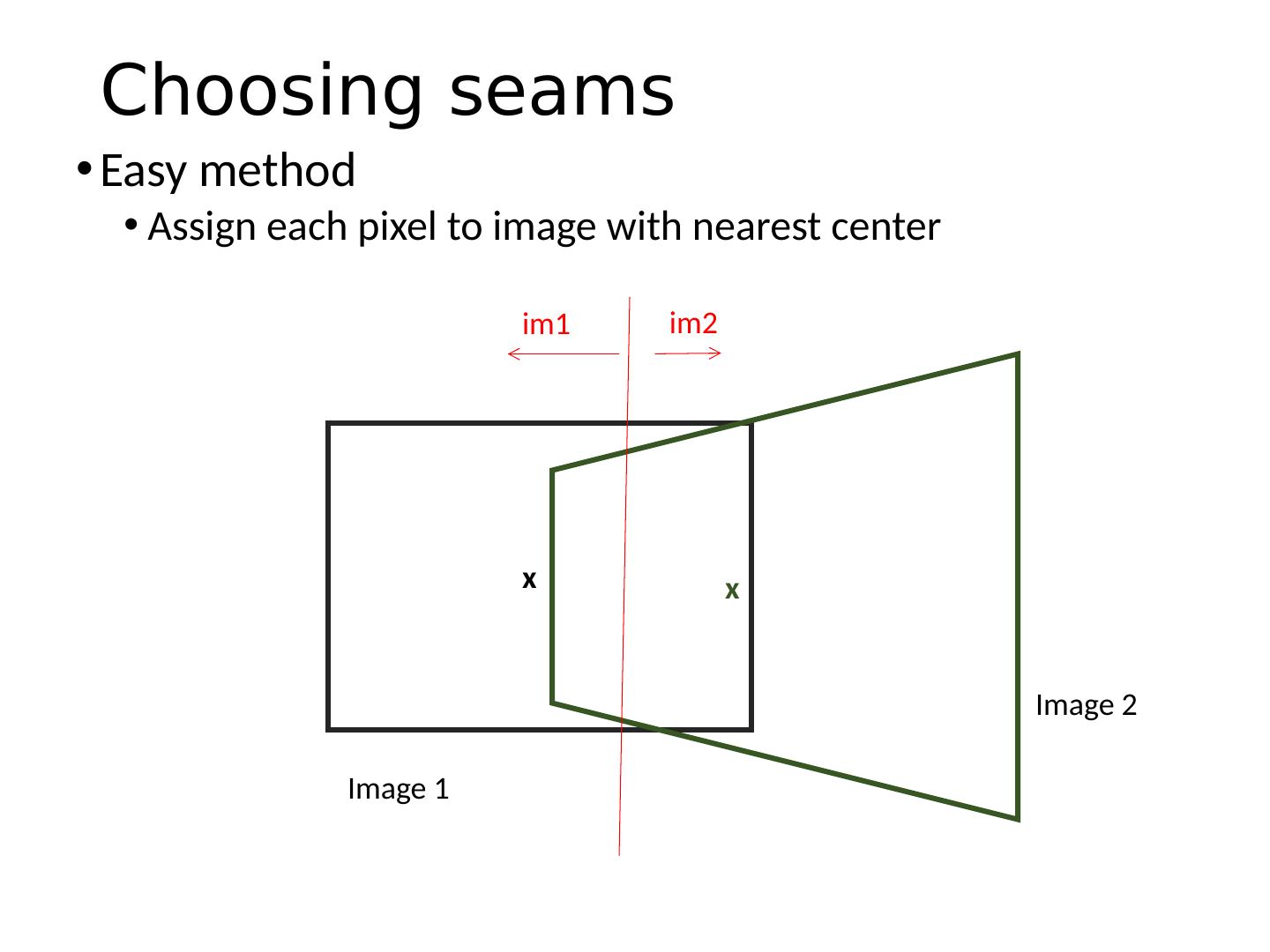
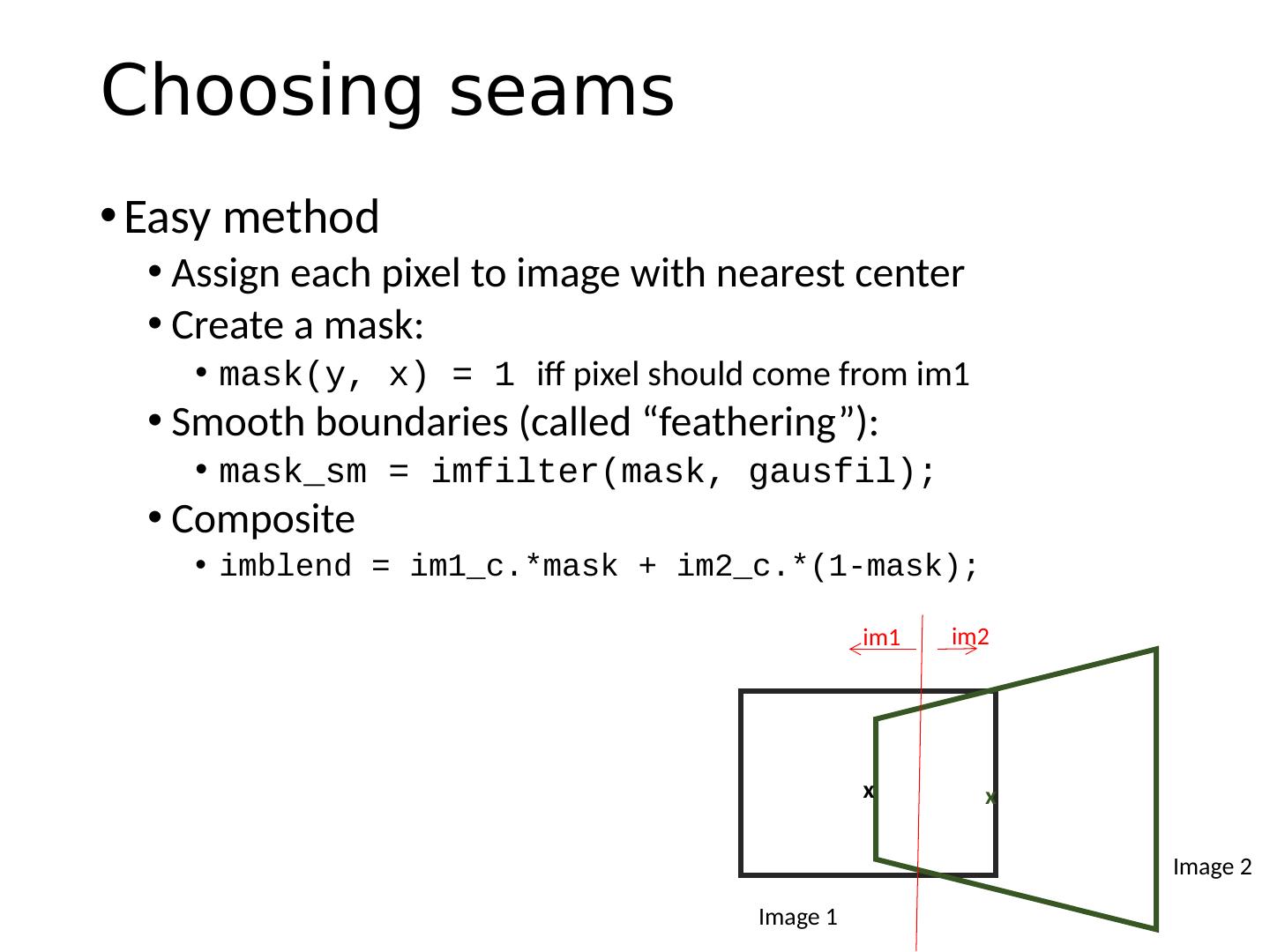
22 .Automatic Image Stitching Compute interest points on each image Find candidate matches Estimate homography H using matched points and RANSAC with normalized DLT Project each image onto the same surface and blend Matlab : maketform , imtransform
23 .RANSAC for Homography Initial Matched Points
24 .RANSAC for Homography Final Matched Points
25 .Verification
26 .RANSAC for Homography
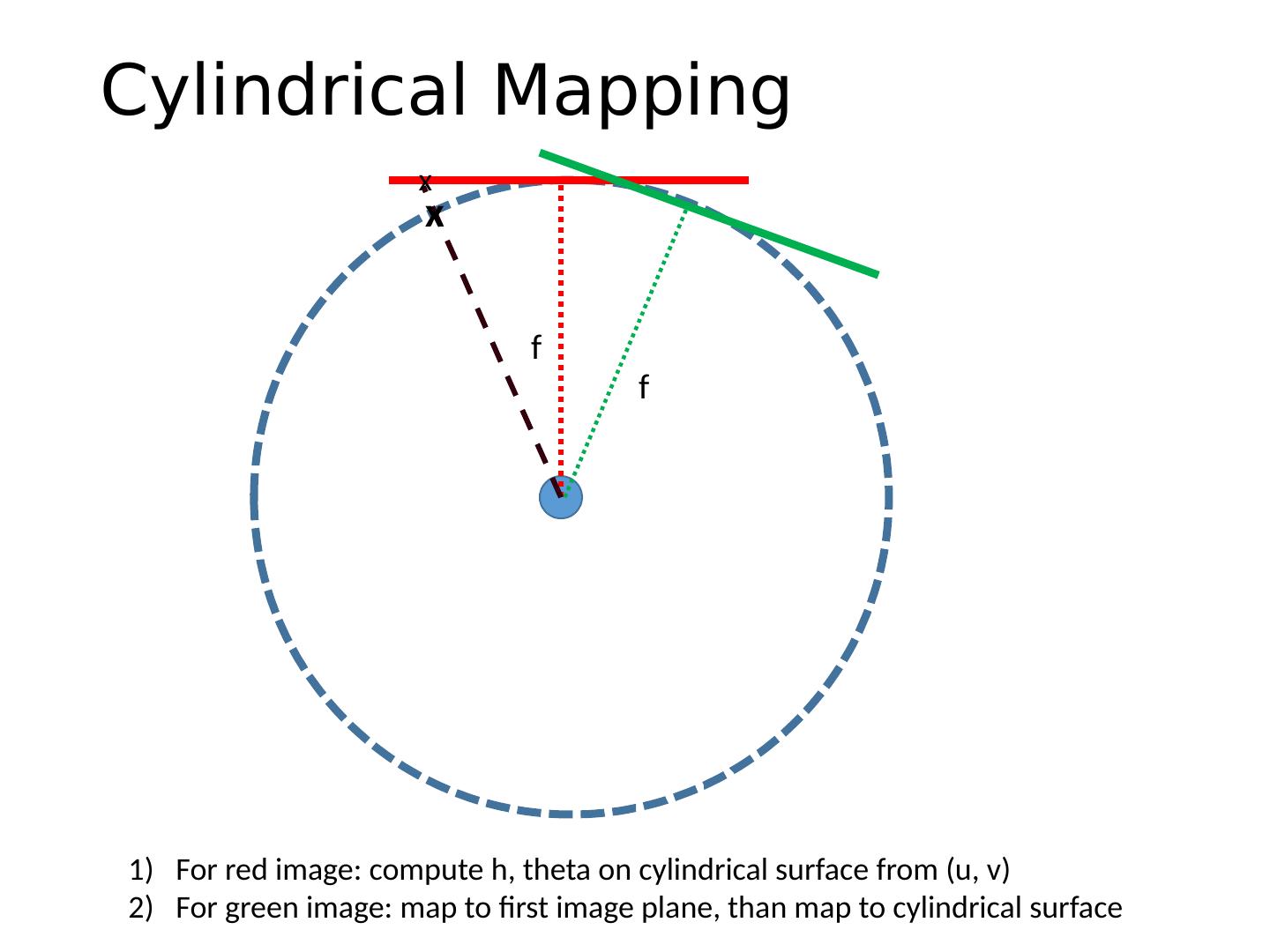
27 .Choosing a Projection Surface Many to choose: planar, cylindrical, spherical, cubic, etc.
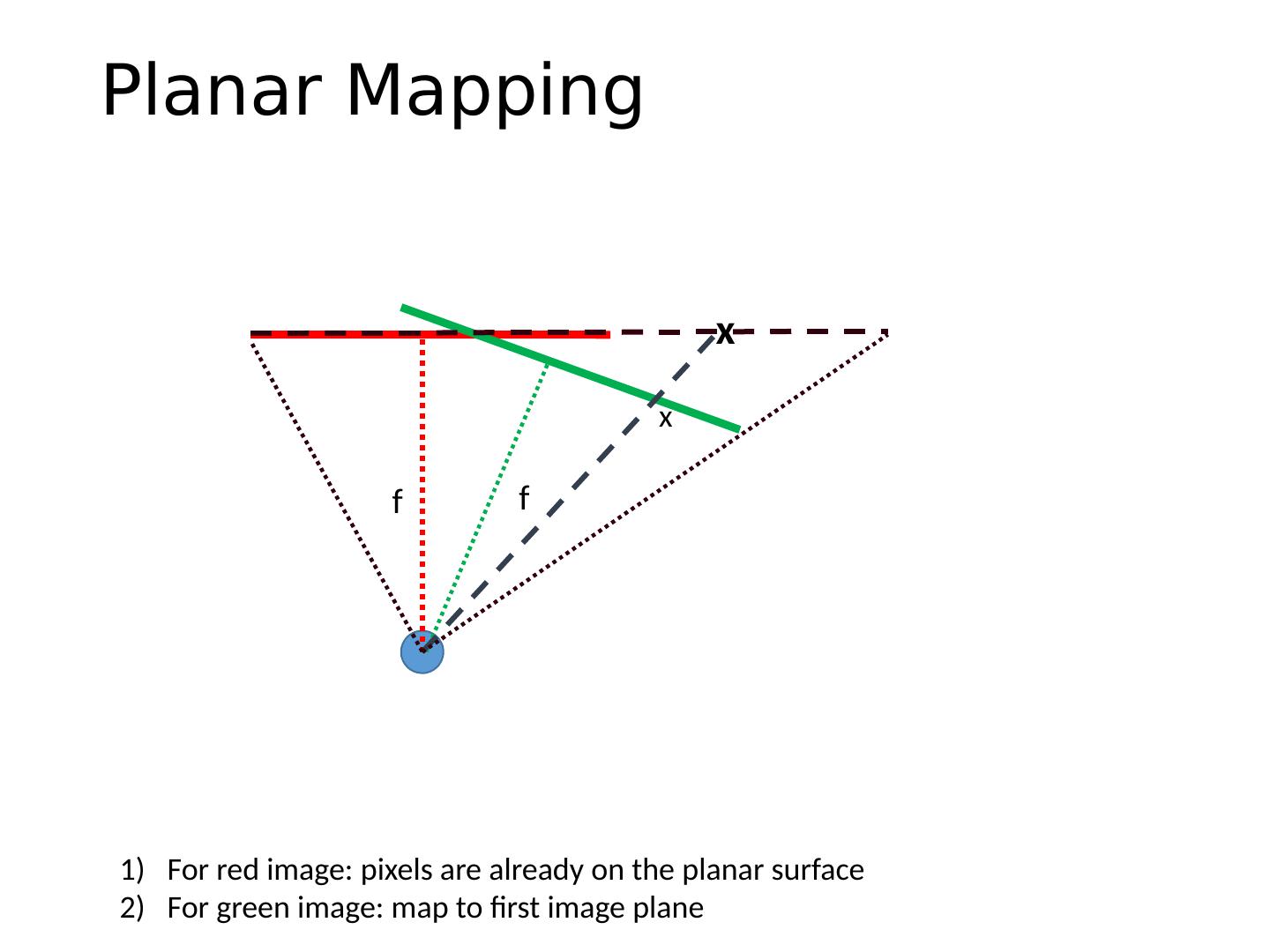
28 .Planar Mapping f f x x For red image: pixels are already on the planar surface For green image: map to first image plane
29 .Planar Projection Planar Photos by Russ Hewett