- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
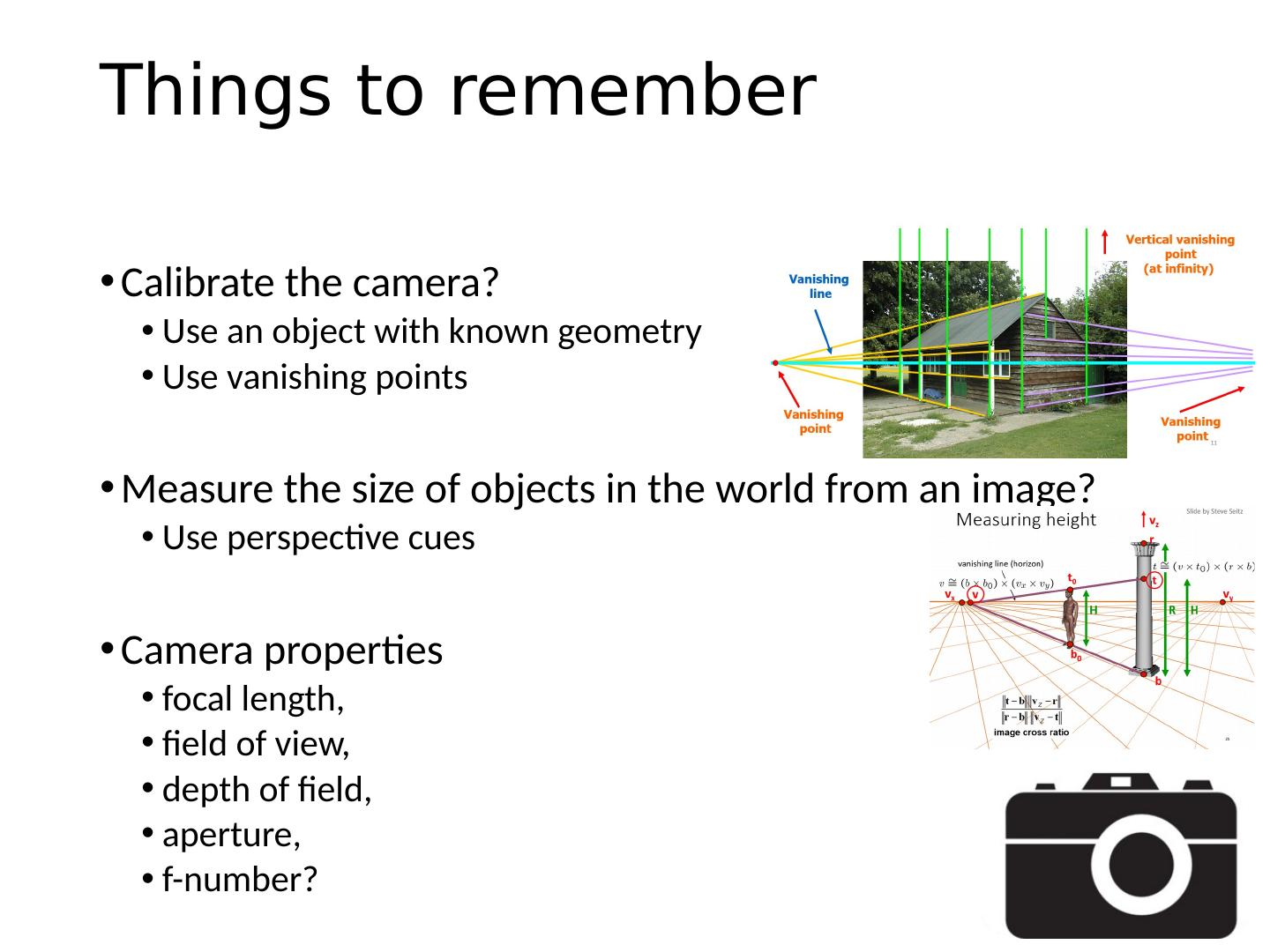
单视图计量和摄像机校准
展开查看详情
1 .Single-view Metrology and Camera Calibration Computer Vision Jia-Bin Huang, Virginia Tech Many slides from S. Seitz and D. Hoiem
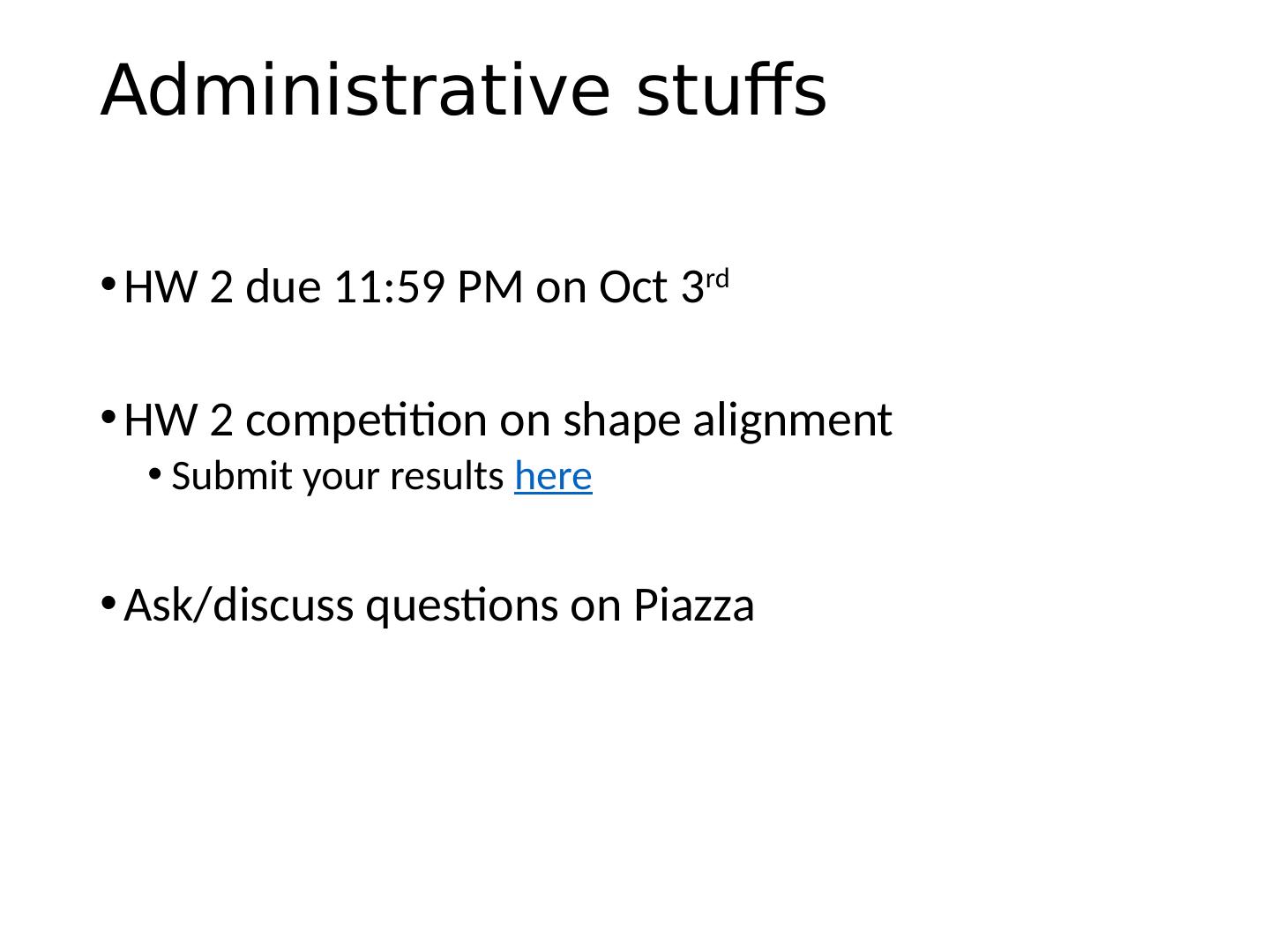
2 .Administrative stuffs HW 2 due 11:59 PM on Oct 3 rd HW 2 competition on shape alignment Submit your results here Ask/discuss questions on Piazza
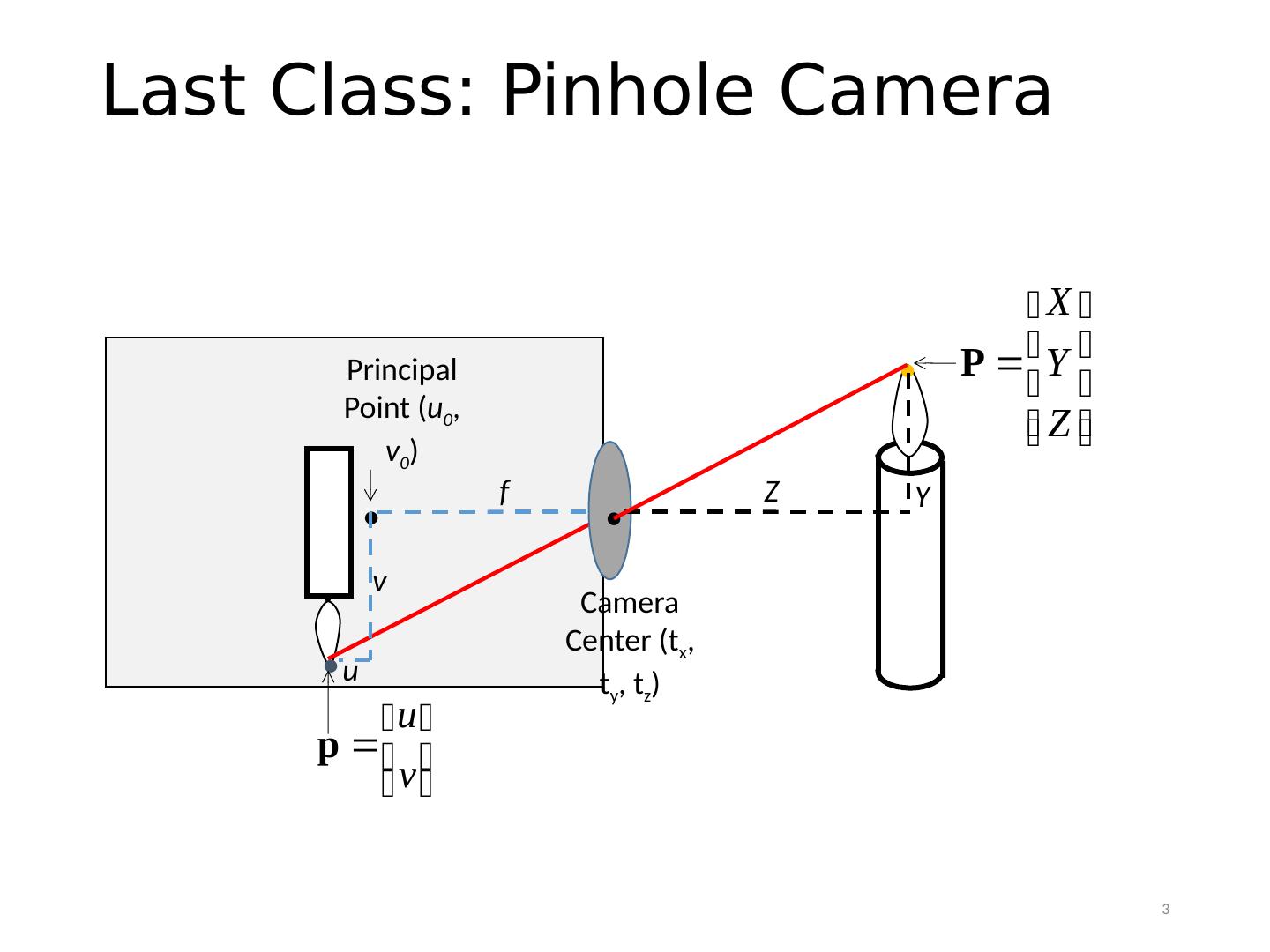
3 .Last Class: Pinhole Camera Camera Center ( t x , t y , t z ) . . . f Z Y . Principal Point ( u 0 , v 0 ) v u 3
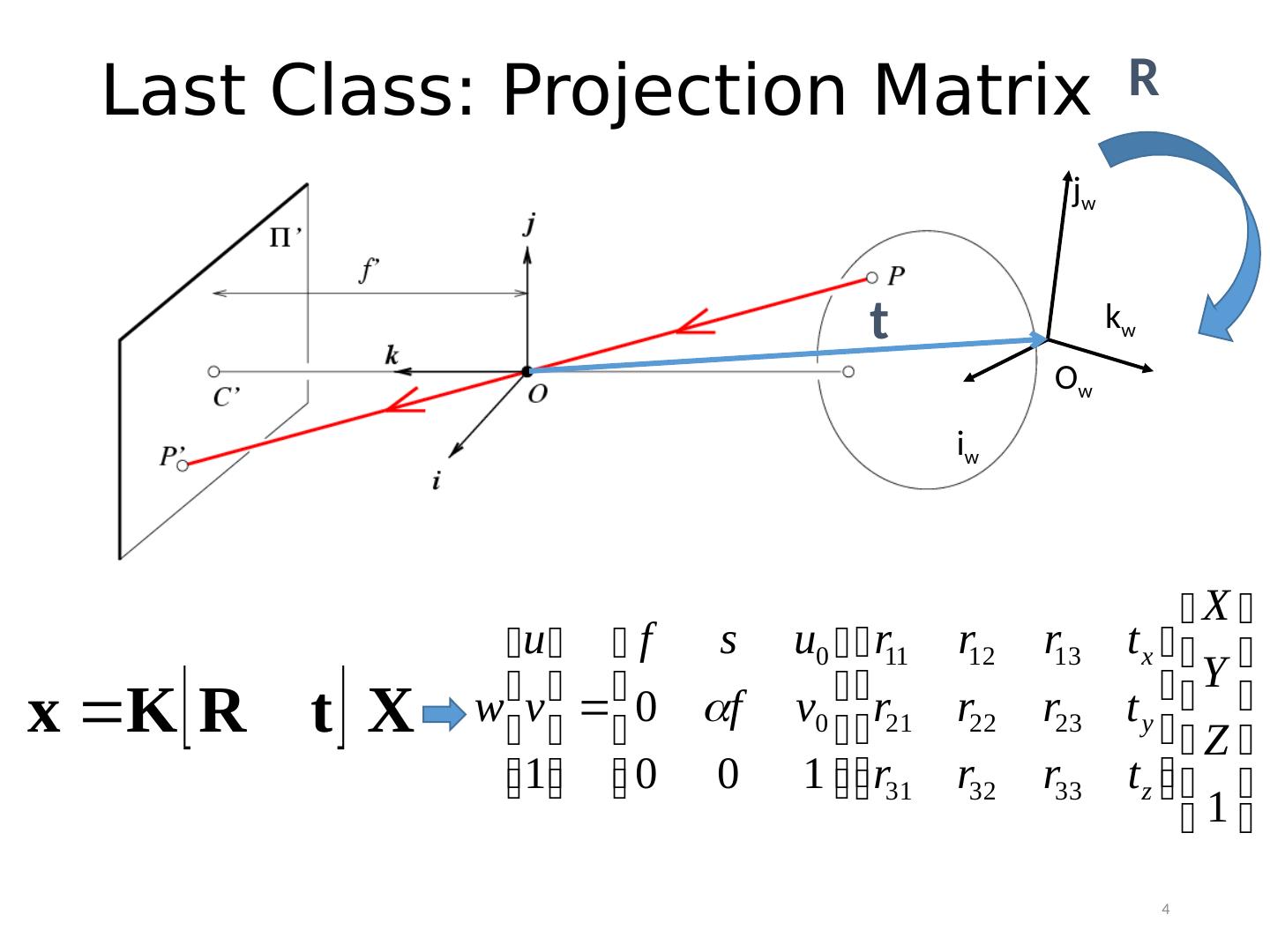
4 .Last Class: Projection Matrix O w i w k w j w t R 4
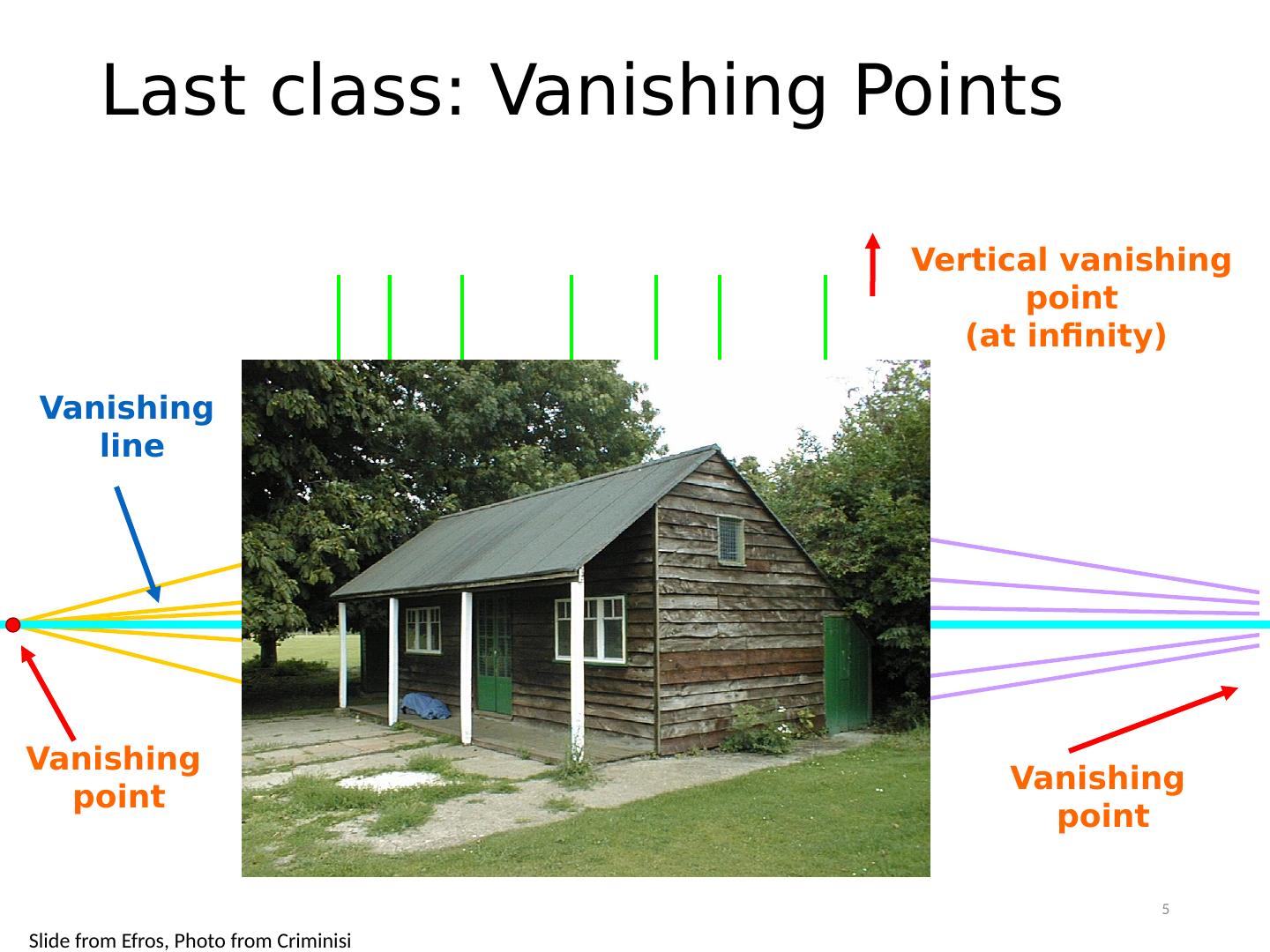
5 .Last class: Vanishing Points Vanishing point Vanishing line Vanishing point Vertical vanishing point (at infinity) Slide from Efros, Photo from Criminisi 5
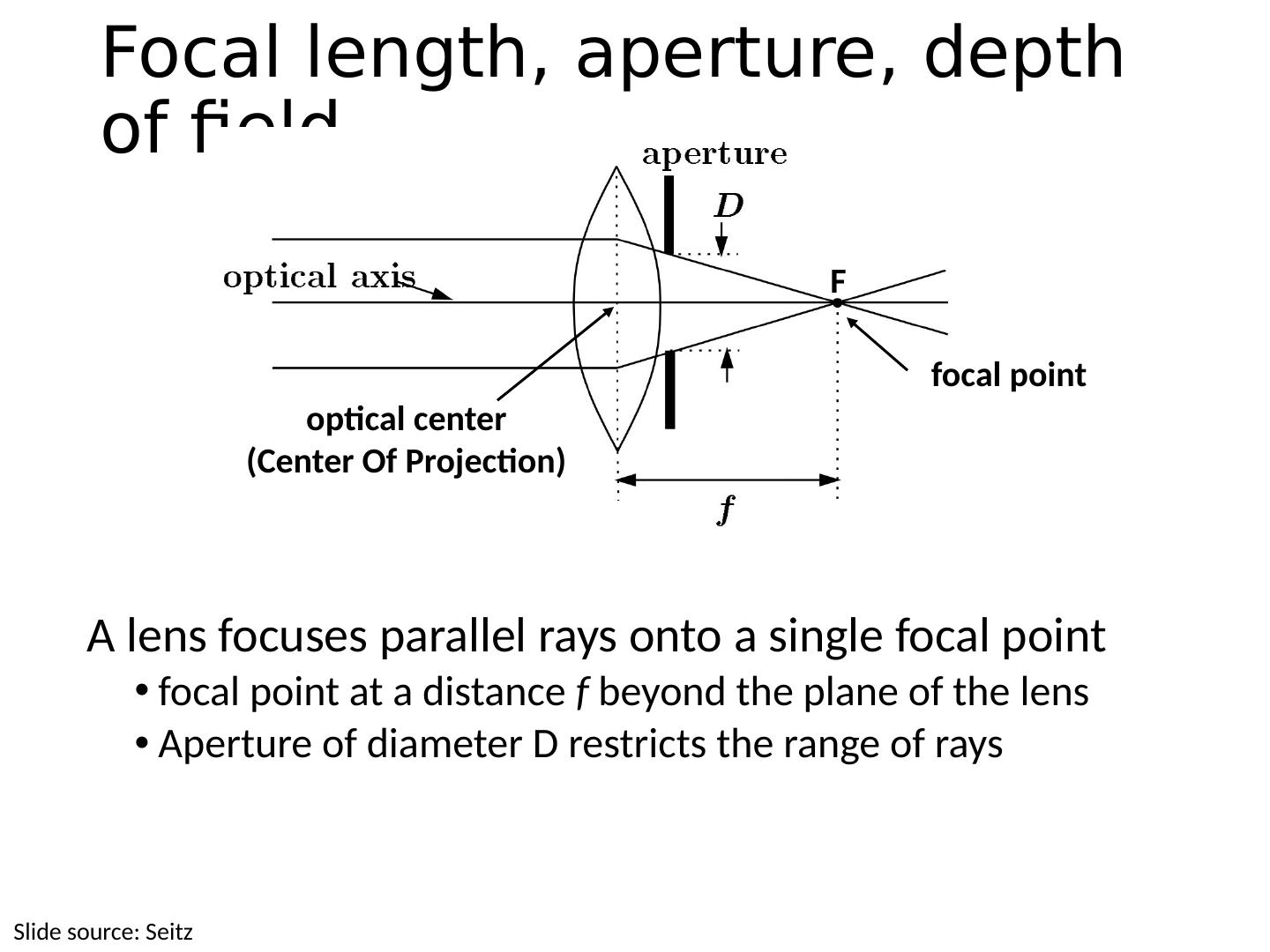
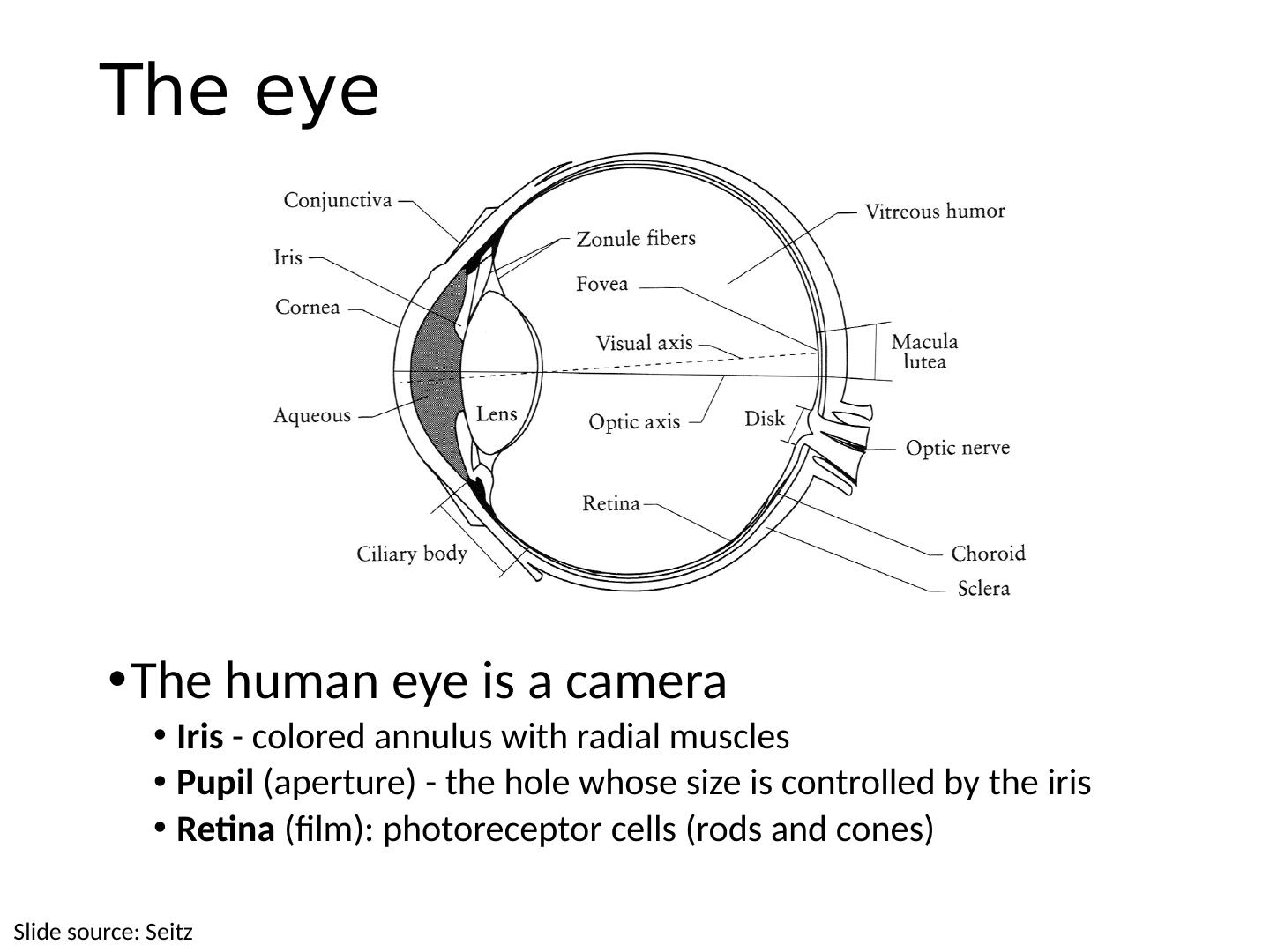
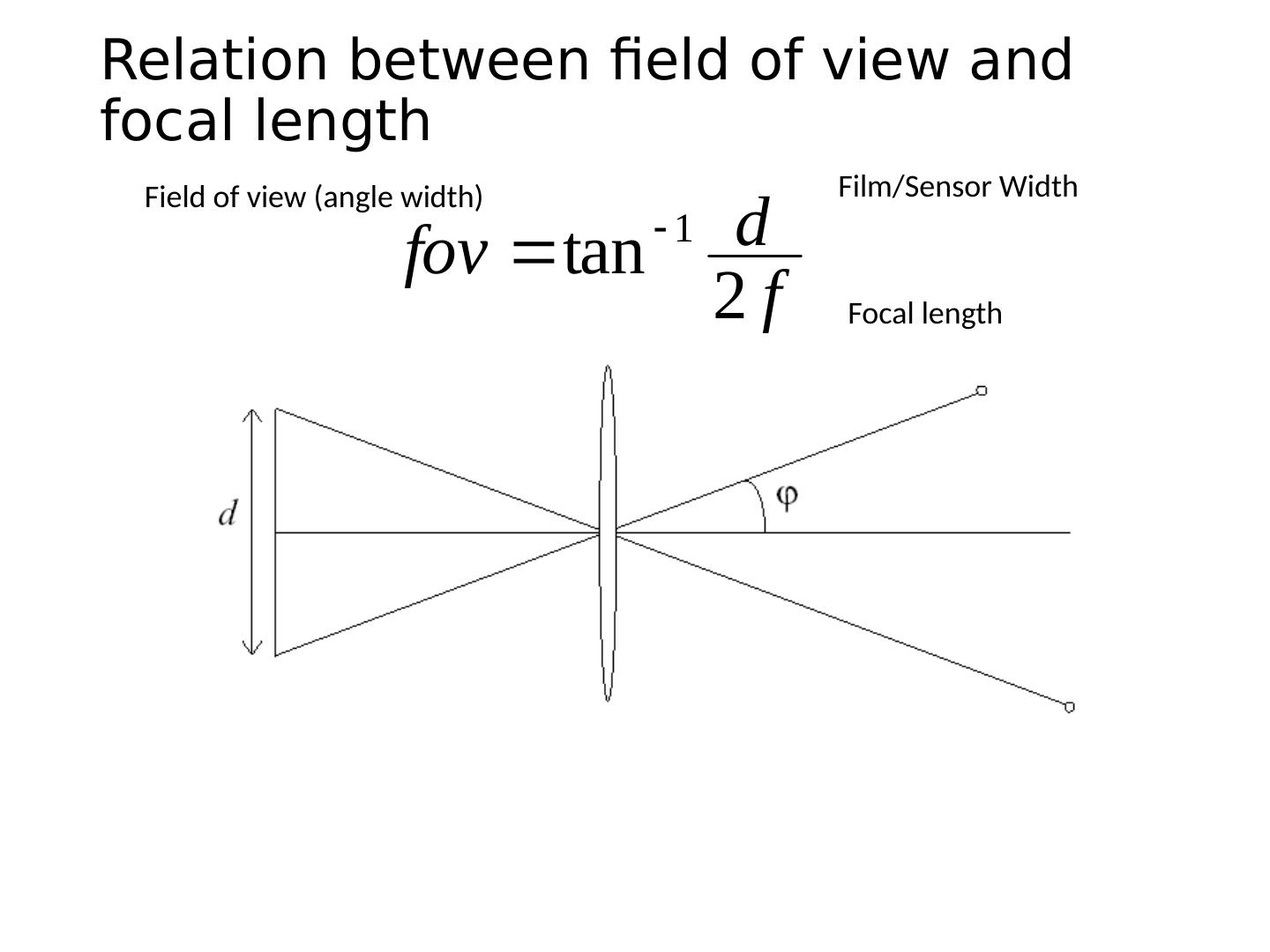
6 .This class How can we calibrate the camera? How can we measure the size of objects in the world from an image? What about other camera properties: focal length, field of view, depth of field, aperture, f-number? 6
7 .How to calibrate the camera? 7
8 .Calibrating the Camera Method 1: Use an object (calibration grid) with known geometry Correspond image points to 3d points Get least squares solution (or non-linear solution) 8 Known 3d locations Known 2d image coordinates Unknown Camera Parameters
9 .Known 3d locations Known 2d image coords Unknown Camera Parameters
10 .Known 3d locations Known 2d image coords Unknown Camera Parameters
11 .Known 3d locations Known 2d image coords Unknown Camera Parameters
12 .Calibration with linear method Advantages Easy to formulate and solve Provides initialization for non-linear methods Disadvantages Doesn’t directly give you camera parameters Doesn’t model radial distortion Can’t impose constraints, such as known focal length Doesn’t minimize projection error Non-linear methods are preferred Define error as difference between projected points and measured points Minimize error using Newton’s method or other non-linear optimization 12
13 .Can we factorize M back to K [R | T]? Yes! You can use RQ factorization (note – not the more familiar QR factorization). R (right diagonal) is K, and Q (orthogonal basis) is R. T, the last column of [R | T], is inv (K) * last column of M. But you need to do a bit of post-processing to make sure that the matrices are valid. See http://ksimek.github.io/2012/08/14/decompose/ Slide credit: J. Hays
14 .Calibrating the Camera Method 2: Use vanishing points Find vanishing points corresponding to orthogonal directions Vanishing point Vanishing line Vanishing point Vertical vanishing point (at infinity) 14
15 .Calibration by orthogonal vanishing points Intrinsic camera matrix Use orthogonality as a constraint Model K with only f , u 0 , v 0 What if you don’t have three finite vanishing points? Two finite VP: solve f , get valid u 0 , v 0 closest to image center One finite VP: u 0 , v 0 is at vanishing point; can’t solve for f For vanishing points 15
16 .Calibration by vanishing points Intrinsic camera matrix Rotation matrix Set directions of vanishing points e.g., X 1 = [1, 0, 0] Each VP provides one column of R Special properties of R inv( R )= R T Each row and column of R has unit length 16
17 .How can we measure the size of 3D objects from an image? Slide by Steve Seitz 17
18 .Perspective cues Slide by Steve Seitz 18
19 .Perspective cues Slide by Steve Seitz 19
20 .Perspective cues Slide by Steve Seitz 20
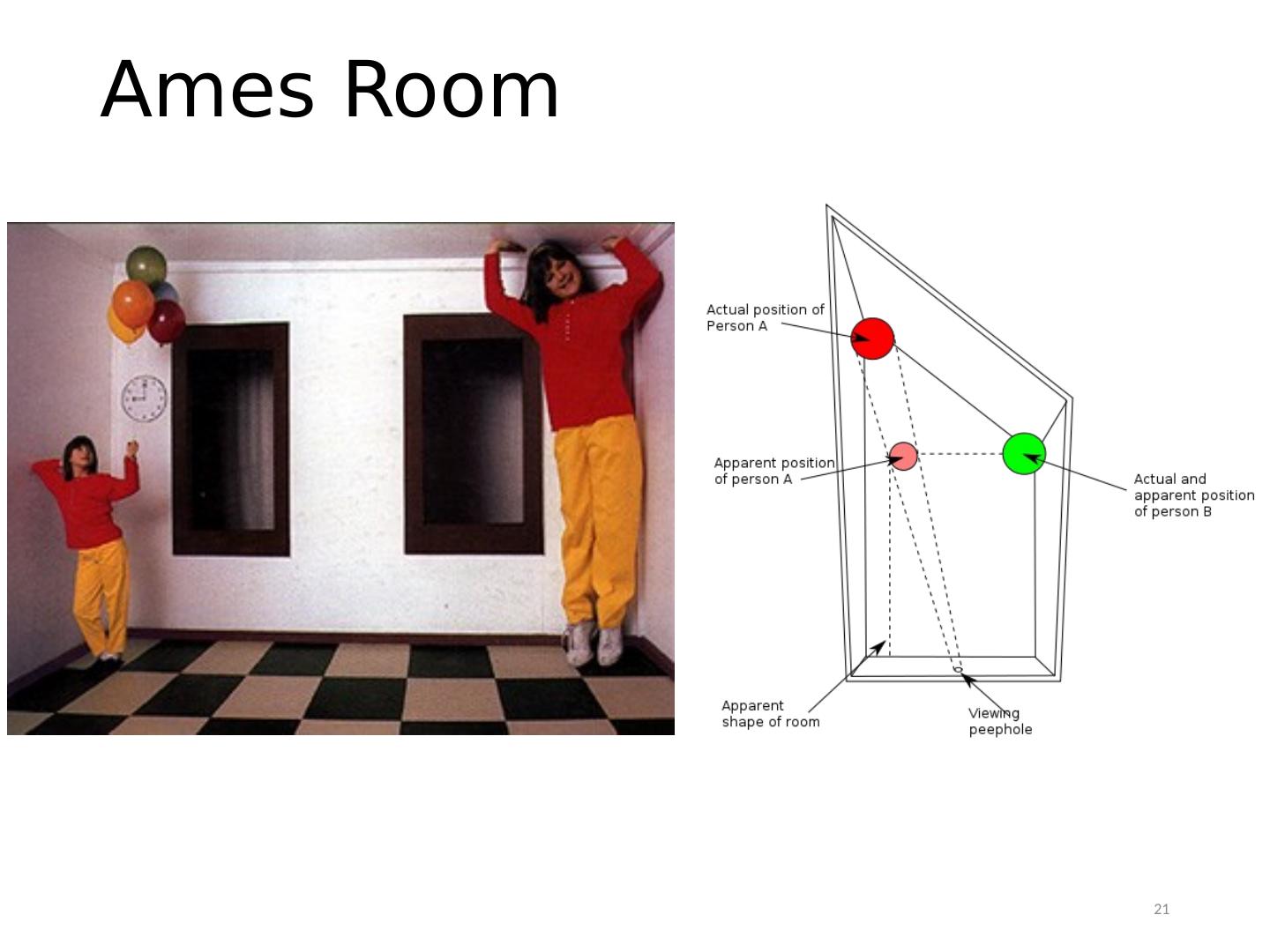
21 .Ames Room 21
22 .
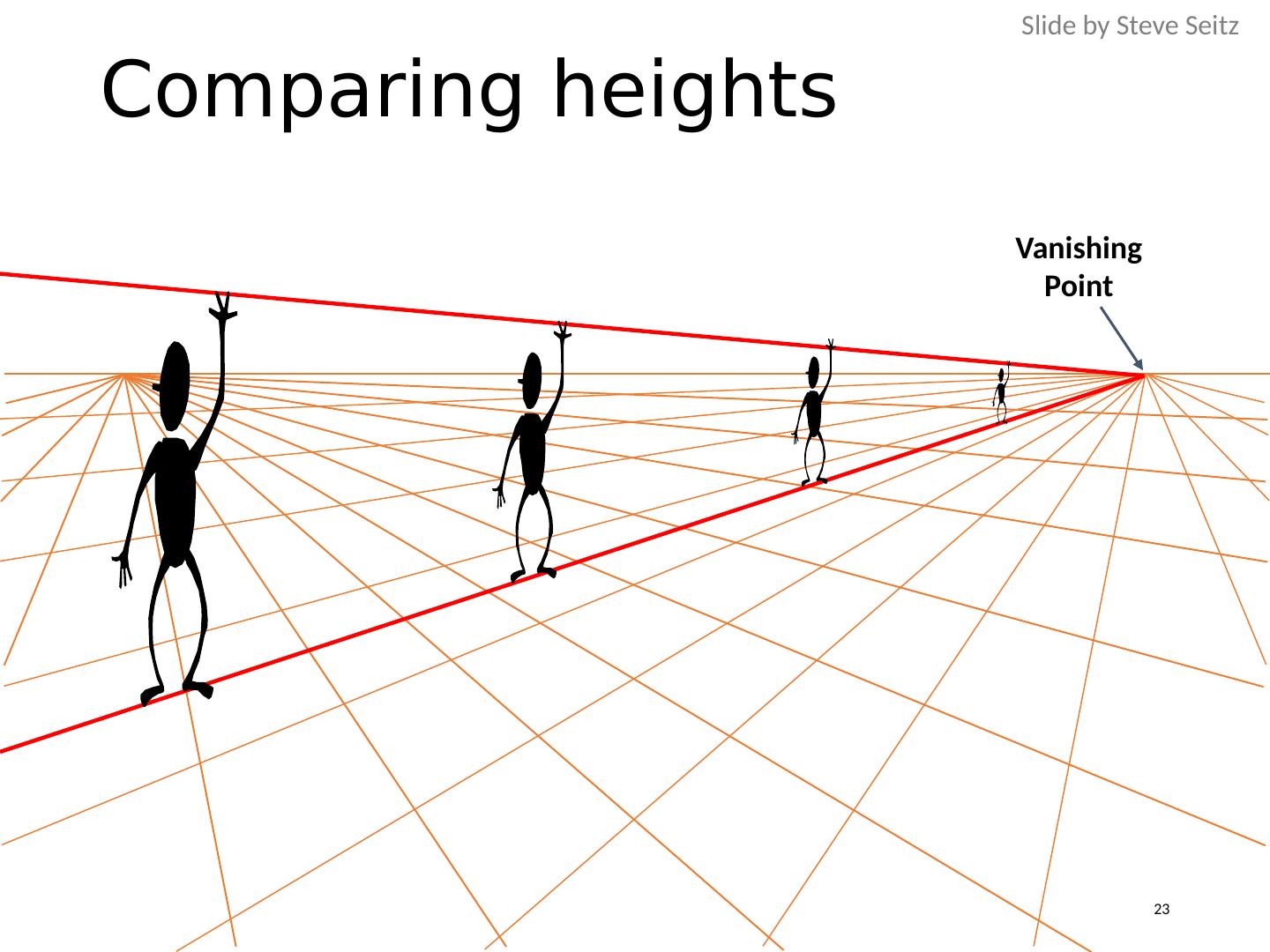
23 .Comparing heights Vanishing Point Slide by Steve Seitz 23
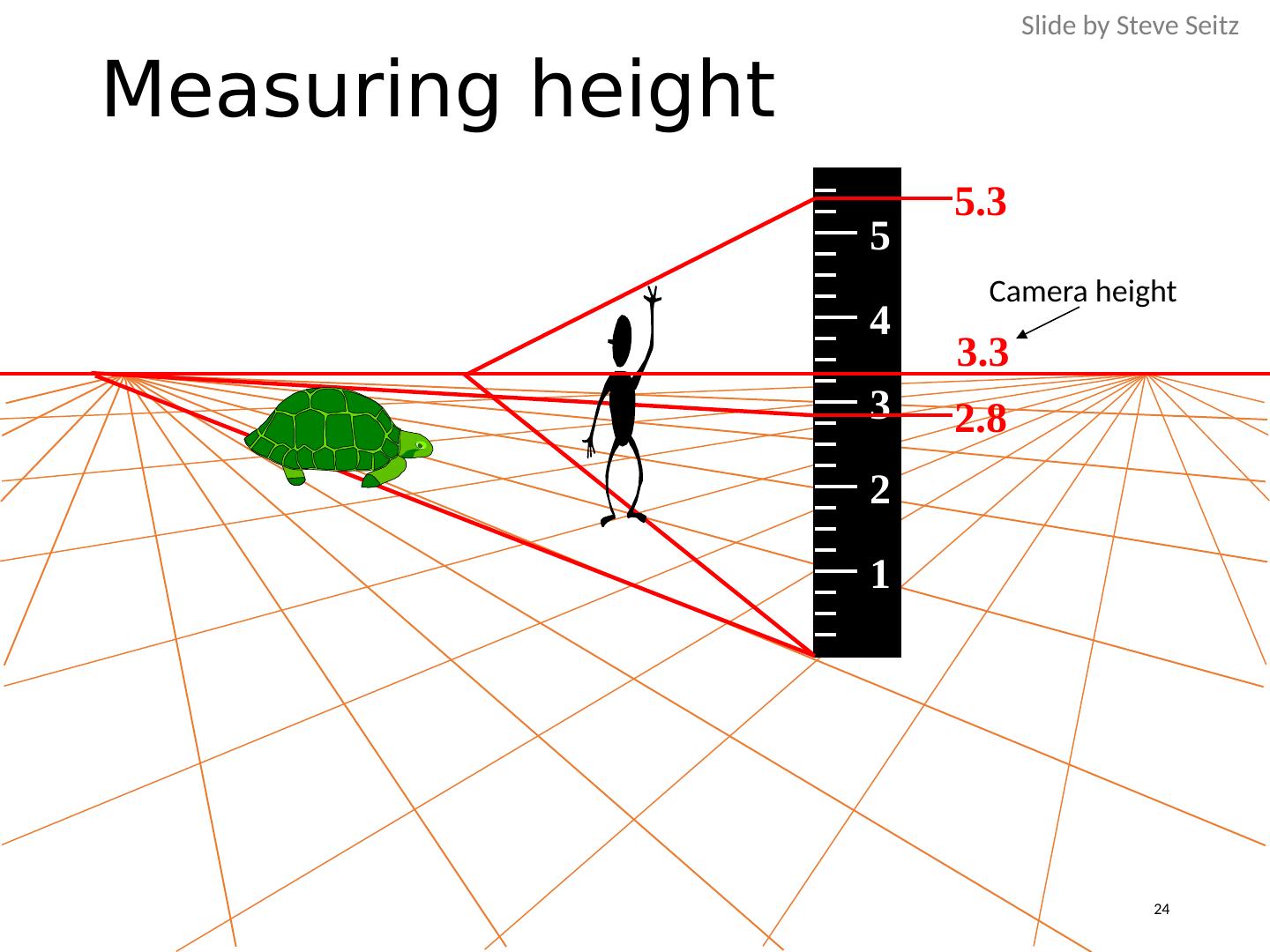
24 .Measuring height 1 2 3 4 5 5.3 2.8 3.3 Camera height Slide by Steve Seitz 24
25 . Which is higher – the camera or the man in the parachute? 25
26 .The cross ratio A Projective Invariant Something that does not change under projective transformations (including perspective projection) P 1 P 2 P 3 P 4 The cross-ratio of 4 collinear points Can permute the point ordering 4! = 24 different orders (but only 6 distinct values) This is the fundamental invariant of projective geometry Slide by Steve Seitz 26
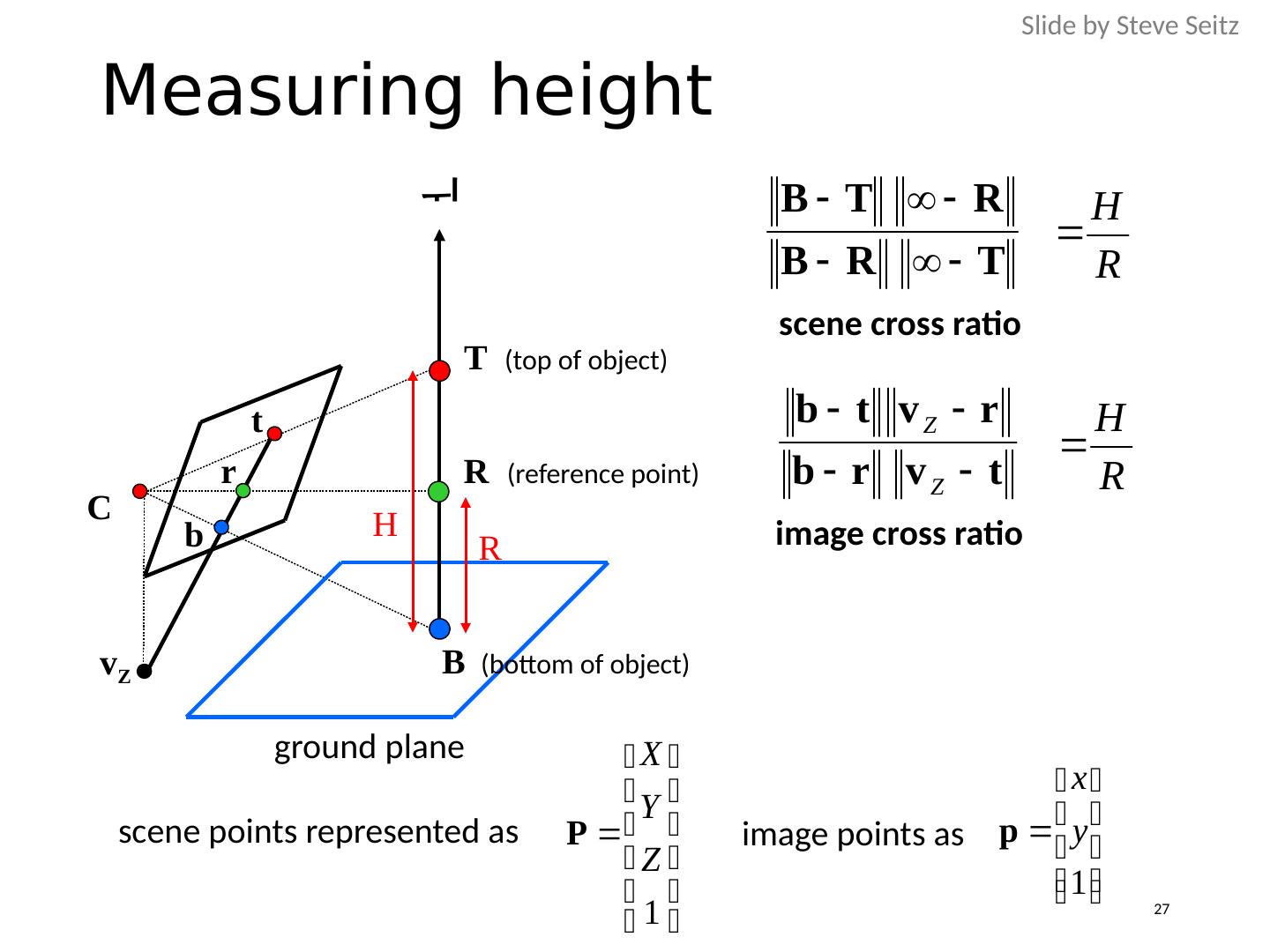
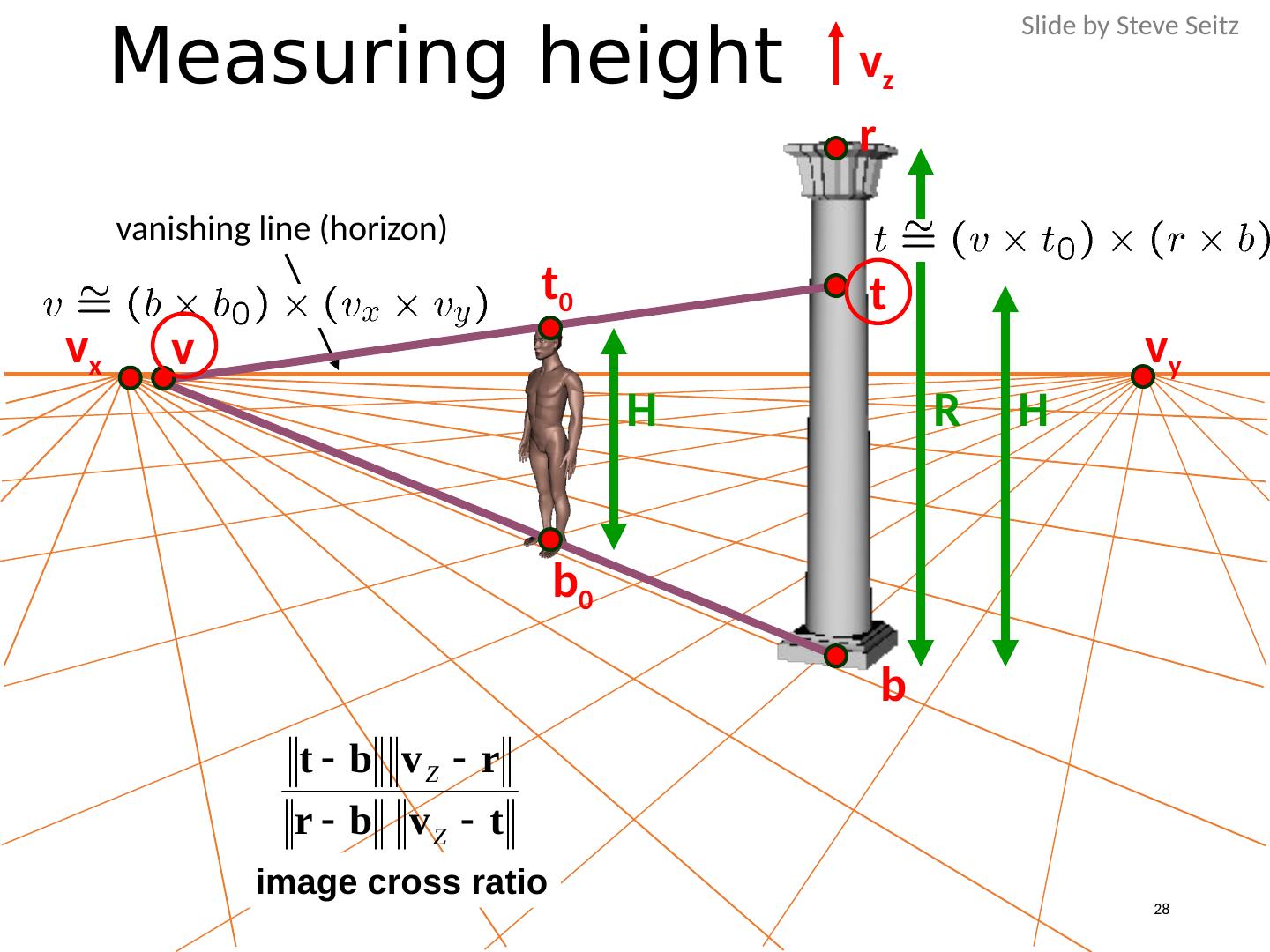
27 .v Z r t b image cross ratio Measuring height B (bottom of object) T (top of object) R (reference point) ground plane H C scene cross ratio scene points represented as image points as R Slide by Steve Seitz 27
28 .Measuring height R H v z r b t H b 0 t 0 v v x v y vanishing line (horizon) image cross ratio Slide by Steve Seitz 28
29 .Measuring height v z r b t 0 v x v y vanishing line (horizon) v t 0 m 0 What if the point on the ground plane b 0 is not known? Here the guy is standing on the box, height of box is known Use one side of the box to help find b 0 as shown above b 0 t 1 b 1 Slide by Steve Seitz 29