- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
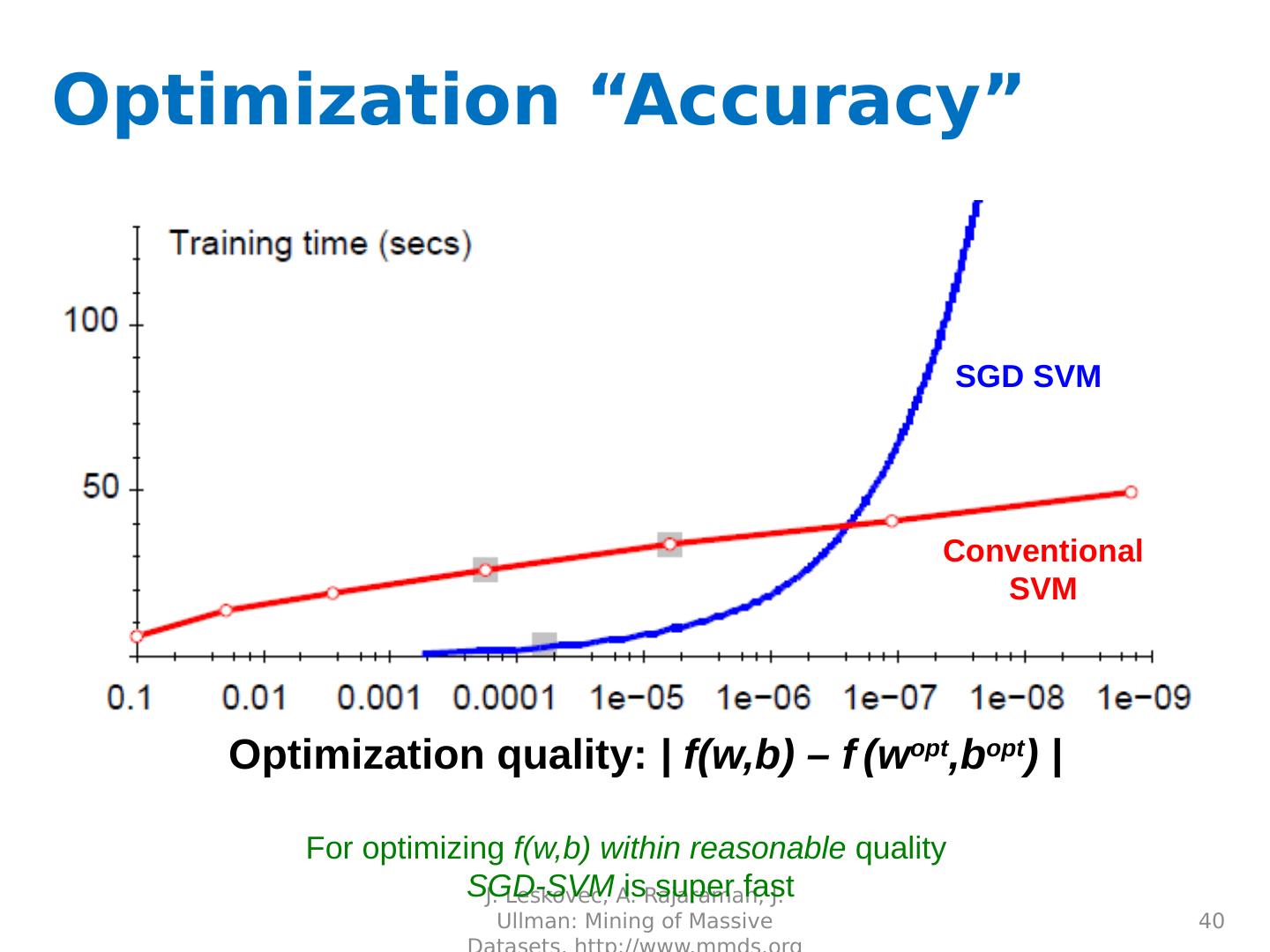
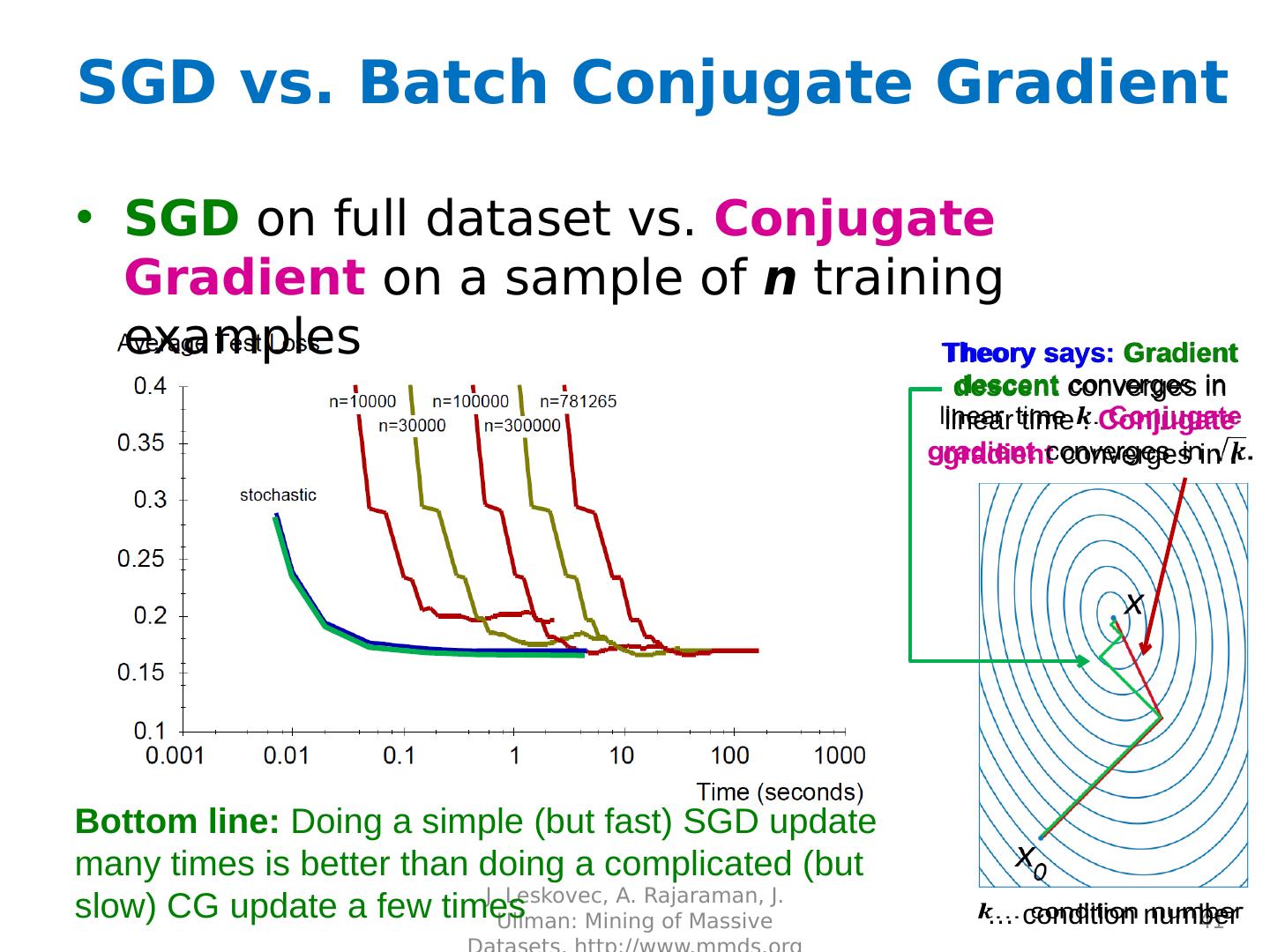
Large-scale Classification and Regression
展开查看详情
1 .Large-scale Classification and Regression Shannon Quinn (with thanks to J. Leskovec , A. Rajaraman , J. Ullman: Mining of Massive Datasets, http:// www.mmds.org )
2 .Supervised Learning Would like to do prediction : estimate a function f(x) so that y = f(x) Where y can be: Real number : Regression Categorical : Classification Complex object: Ranking of items, Parse tree, etc. Data is labeled : Have many pairs {(x, y)} x … vector of binary, categorical, real valued features y … class ({+1, -1}, or a real number) J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 2 X Y X’ Y’ Training and test set Estimate y = f(x ) on X,Y. Hope that the same f(x) also works on unseen X’, Y’
3 .Large Scale Machine Learning We will talk about the following methods: k -Nearest Neighbor (Instance based learning) Perceptron (neural networks) Support Vector Machines Decision trees Main question: How to efficiently train (build a model/find model parameters) ? J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 3
4 .Instance Based Learning Instance based learning Example: Nearest neighbor Keep the whole training dataset: {(x, y)} A query example (vector) q comes Find closest example(s) x * Predict y * Works both for regression and classification Collaborative filtering is an example of k-NN classifier Find k most similar people to user x that have rated movie y Predict rating y x of x as an average of y k J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 4
5 .1-Nearest Neighbor To make Nearest Neighbor work we need 4 things: Distance metric: Euclidean How many neighbors to look at? One Weighting function (optional): Unused How to fit with the local points? Just predict the same output as the nearest neighbor J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 5
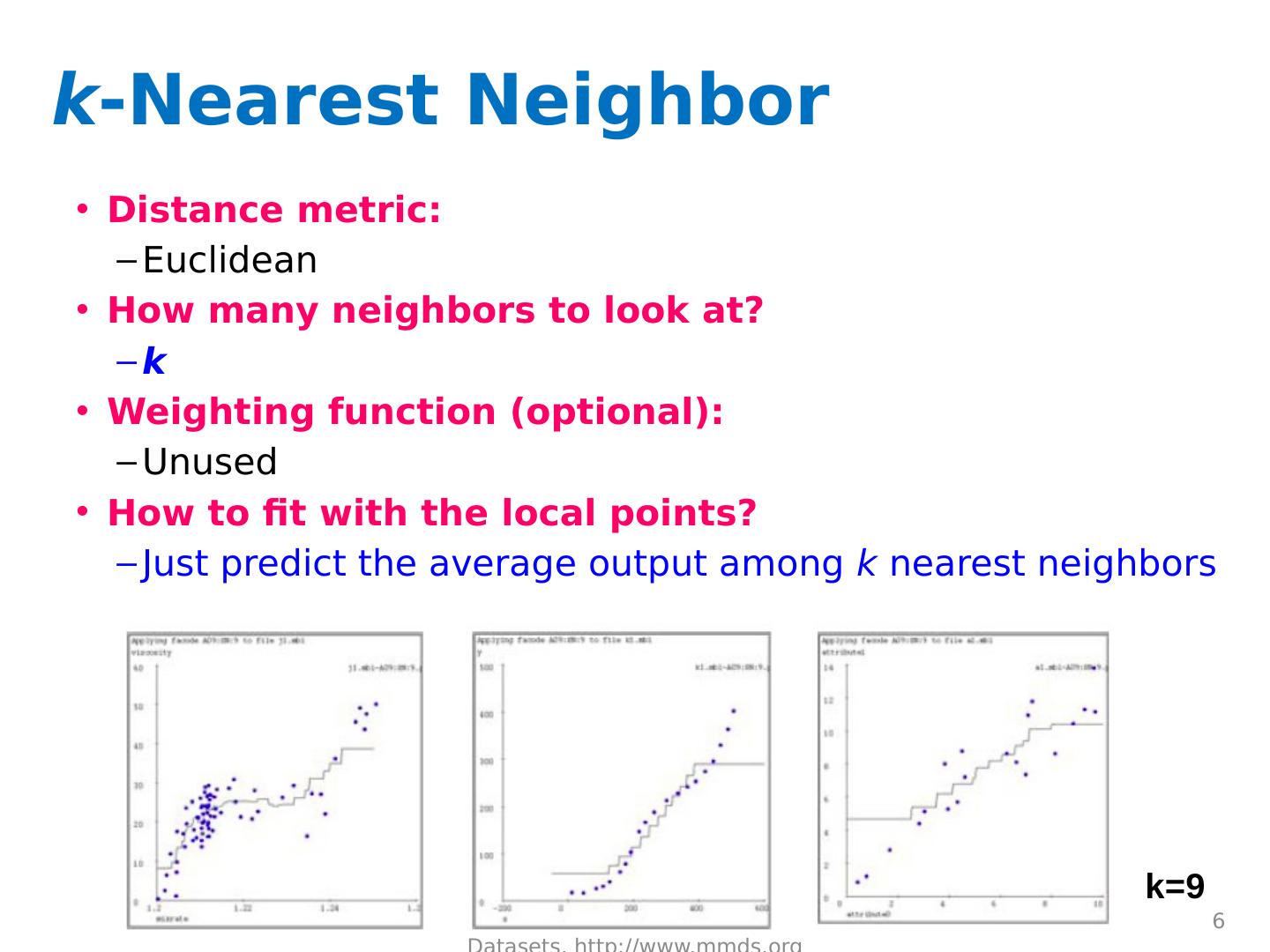
6 .k -Nearest Neighbor Distance metric: Euclidean How many neighbors to look at? k Weighting function (optional): Unused How to fit with the local points? Just predict the average output among k nearest neighbors J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 6 k=9
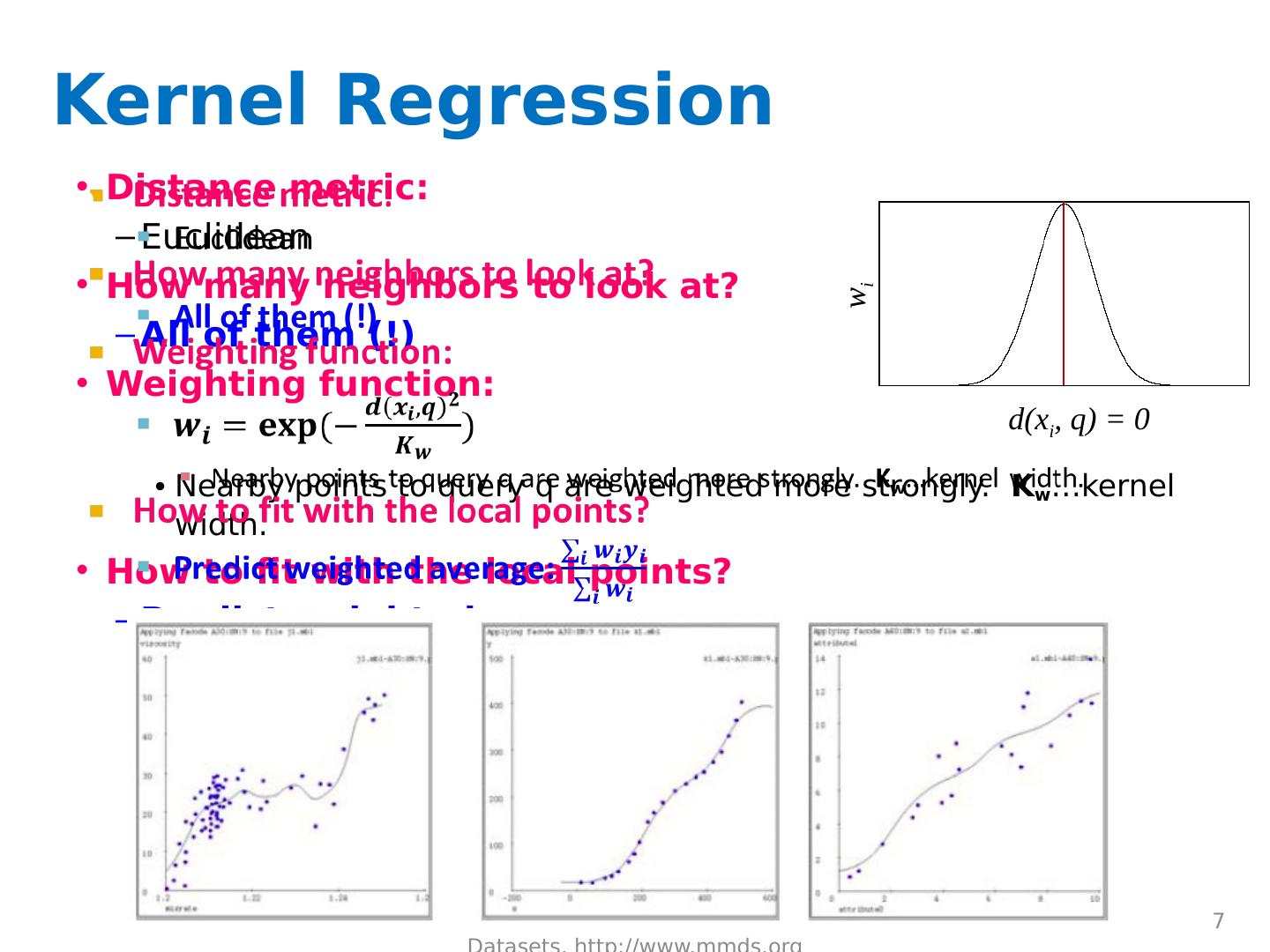
7 .Kernel Regression Distance metric: Euclidean How many neighbors to look at? All of them (!) Weighting function: Nearby points to query q are weighted more strongly. K w …kernel width. How to fit with the local points? Predict weighted average: J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 7 K w =10 K w =20 K w =80 d(x i , q) = 0 w i
8 .How to find nearest neighbors? Given: a set P of n points in R d Goal: Given a query point q NN: Find the nearest neighbor p of q in P Range search: Find one/all points in P within distance r from q J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 8 q p
9 .Algorithms for NN Main memory: Linear scan Tree based: Quadtree kd -tree Hashing: Locality-Sensitive Hashing J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 9
10 .Perceptron
11 .Linear models: Perceptron Example: Spam filtering Instance space x X (| X |= n data points) Binary or real-valued feature vector x of word occurrences d features (words + other things, d ~100,000) Class y Y y : Spam (+1), Ham (-1) J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 11
12 .Linear models for classification Binary classification: Input: Vectors x (j) and labels y (j) Vectors x (j ) are real valued where Goal: Find vector w = (w 1 , w 2 ,... , w d ) Each w i is a real number J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 12 f ( x ) = +1 if w 1 x 1 + w 2 x 2 +. . . w d x d -1 o therwise { w x = 0 - - - - - - - - - - - - - - - w x = Note: Decision boundary is linear w
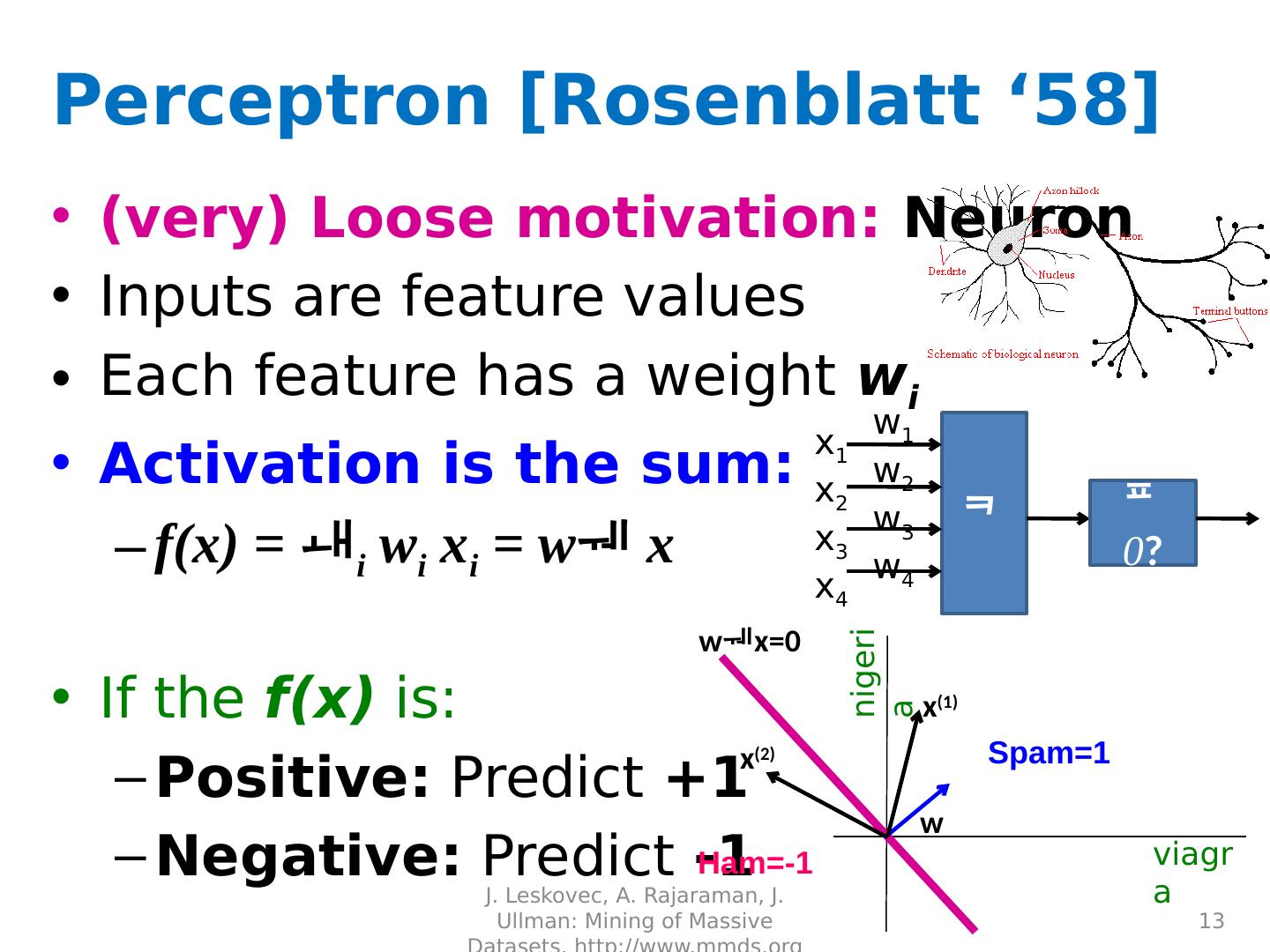
13 .Perceptron [Rosenblatt ‘58] (very) Loose motivation: Neuron Inputs are feature values Each feature has a weight w i Activation is the sum: f(x) = i w i x i = w x If the f(x) is: Positive: Predict +1 Negative: Predict -1 J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 13 x 1 x 2 x 3 x 4 0 ? w 1 w 2 w 3 w 4 viagra nigeria Spam=1 Ham=-1 w x (1) x (2) wx =0
14 .Perceptron : Estimating w Perceptron : y’ = sign(w x) How to find parameters w ? Start with w 0 = 0 Pick training examples x (t) one by one (from disk) Predict class of x (t) using current weights y’ = sign(w (t) x (t) ) If y’ is correct (i.e., y t = y’ ) No change: w (t+1) = w (t ) If y’ is wrong: adjust w (t ) w (t+1) = w (t) + y (t) x (t) is the learning rate parameter x (t) is the t- th training example y (t) is true t- th class label ({+1, -1}) J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 14 w (t) y (t) x (t) x (t) , y (t) =1 w (t+1) Note that the Perceptron is a conservative algorithm: it ignores samples that it classifies correctly.
15 .Perceptron Convergence Perceptron Convergence Theorem: If there exist a set of weights that are consistent (i.e., the data is linearly separable) the Perceptron learning algorithm will converge How long would it take to converge? Perceptron Cycling Theorem: If the training data is not linearly separable the Perceptron learning algorithm will eventually repeat the same set of weights and therefore enter an infinite loop How to provide robustness, more expressivity? J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 15
16 .Properties of Perceptron Separability: S ome parameters get training set perfectly Convergence: If training set is separable, perceptron will converge (Training) Mistake bound: Number of mistakes where and Note we assume x Euclidean length 1 , then γ is the minimum distance of any example to plane u J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 16
17 .Updating the Learning Rate Perceptron will oscillate and won’t converge When to stop learning? (1) Slowly decrease the learning rate A classic way is to: = c 1 /(t + c 2 ) But, we also need to determine constants c 1 and c 2 (2) Stop when the training error stops chaining (3) Have a small test dataset and stop when the test set error stops decreasing (4) Stop when we reached some maximum number of passes over the data J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 17
18 .Multiclass Perceptron What if more than 2 classes? Weight vector w c for each class c Train one class vs. the rest: Example: 3-way classification y = {A, B, C} Train 3 classifiers: w A : A vs. B,C; w B : B vs. A,C; w C : C vs. A,B Calculate activation for each class f( x,c ) = i w c,i x i = w c x Highest activation wins c = arg max c f( x,c ) J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 18 w A w C w B w A x biggest w C x biggest w B x biggest
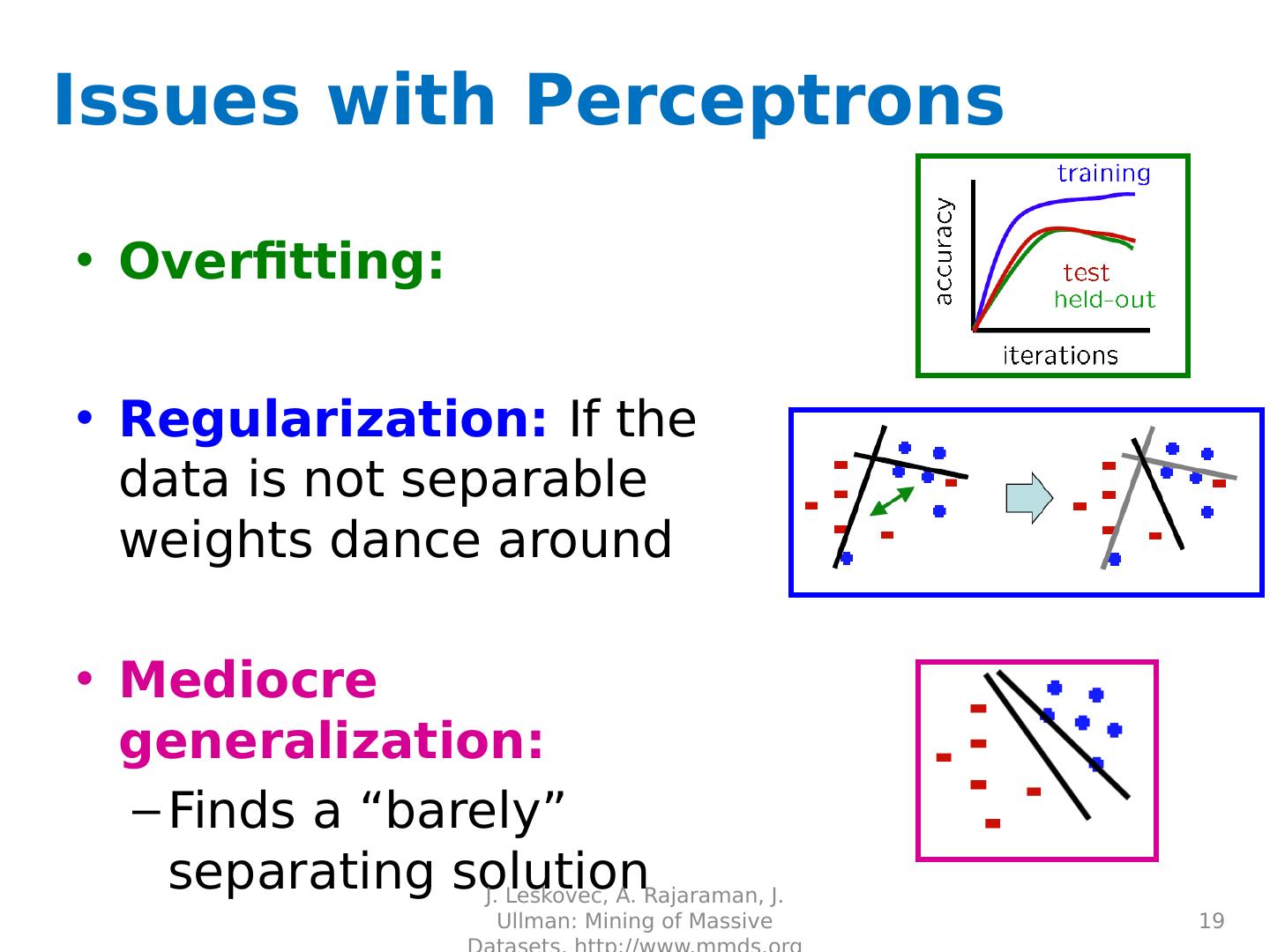
19 .Issues with Perceptrons Overfitting : Regularization: If the data is not separable weights dance around Mediocre generalization: Finds a “barely” separating solution J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 19
20 .Support Vector Machines Want to separate “+” from “-” using a line J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 20 Data: Training e xamples: (x 1 , y 1 ) … ( x n , y n ) Each example i : x i = ( x i (1) ,… , x i (d) ) x i (j) is real valued y i { -1, +1 } Inner product: + + + + + + - - - - - - - Which is best linear separator (defined by w )?
21 .+ + + + + + + + + - - - - - - - - - A B C Largest Margin Distance from the separating hyperplane corresponds to the “confidence” of prediction Example: We are more sure about the class of A and B than of C J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 21
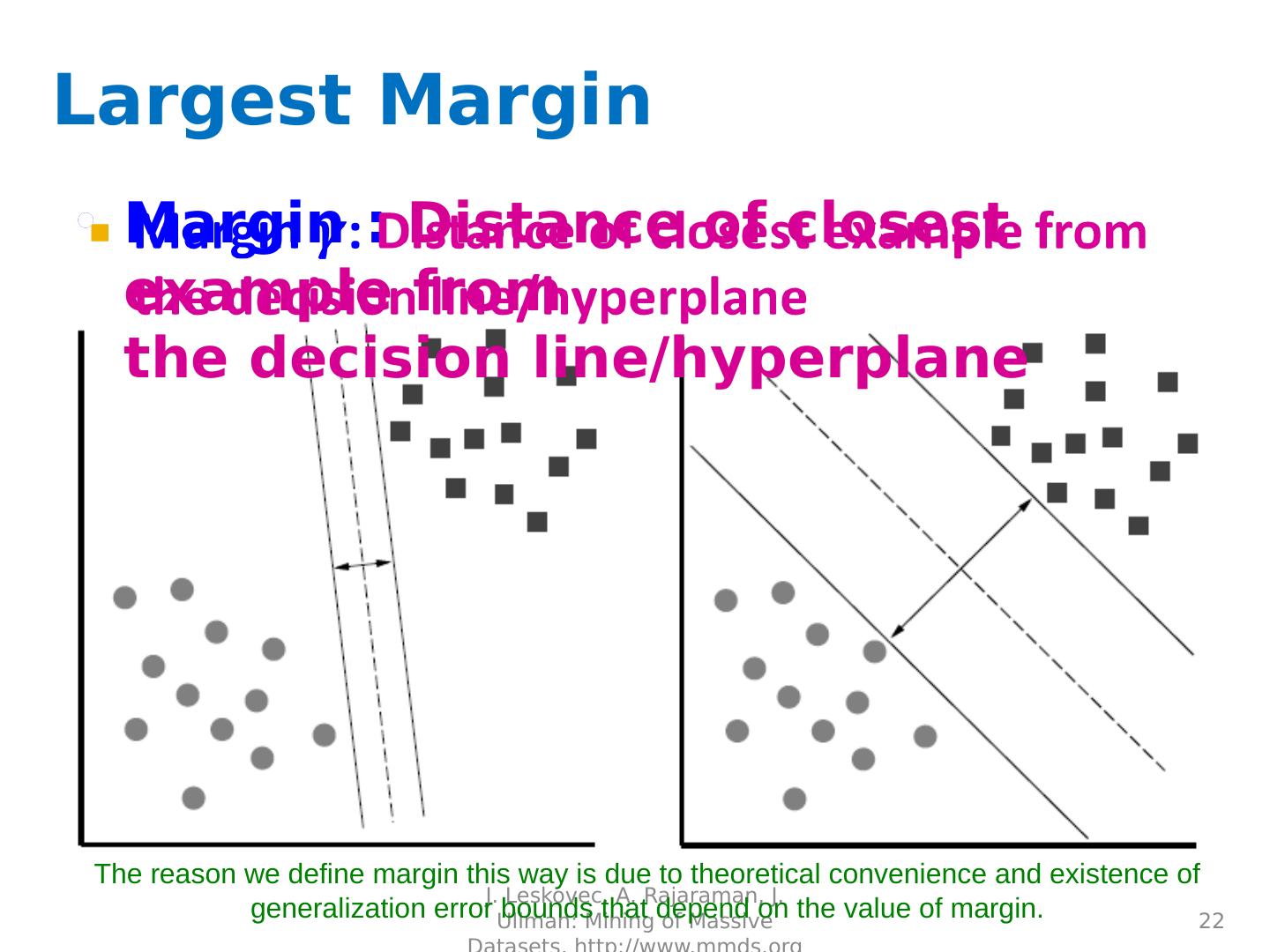
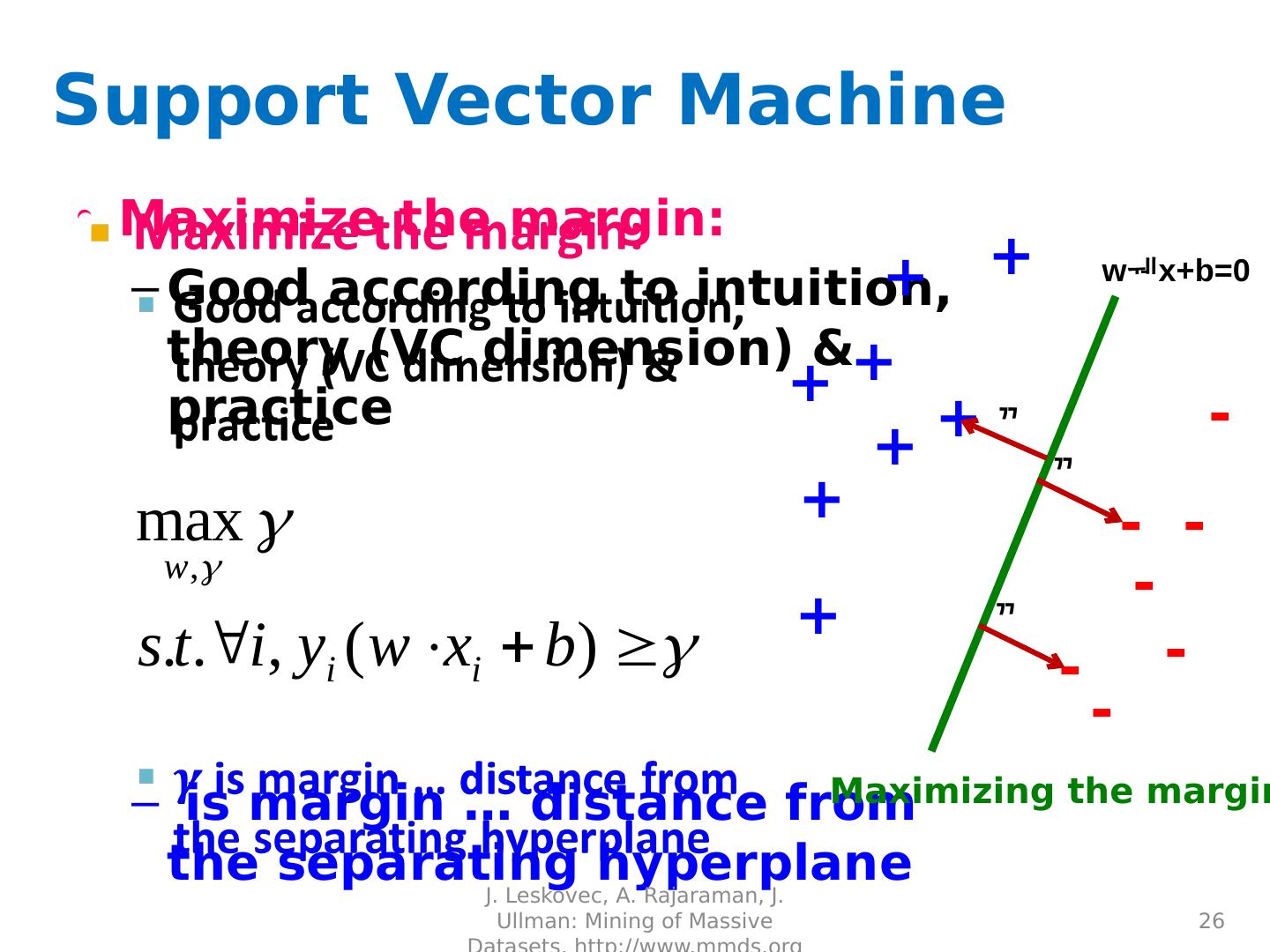
22 .Largest Margin Margin : Distance of closest example from the decision line/ hyperplane J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 22 The reason we define margin this way is due to theoretical convenience and existence of generalization error bounds that depend on the value of margin.
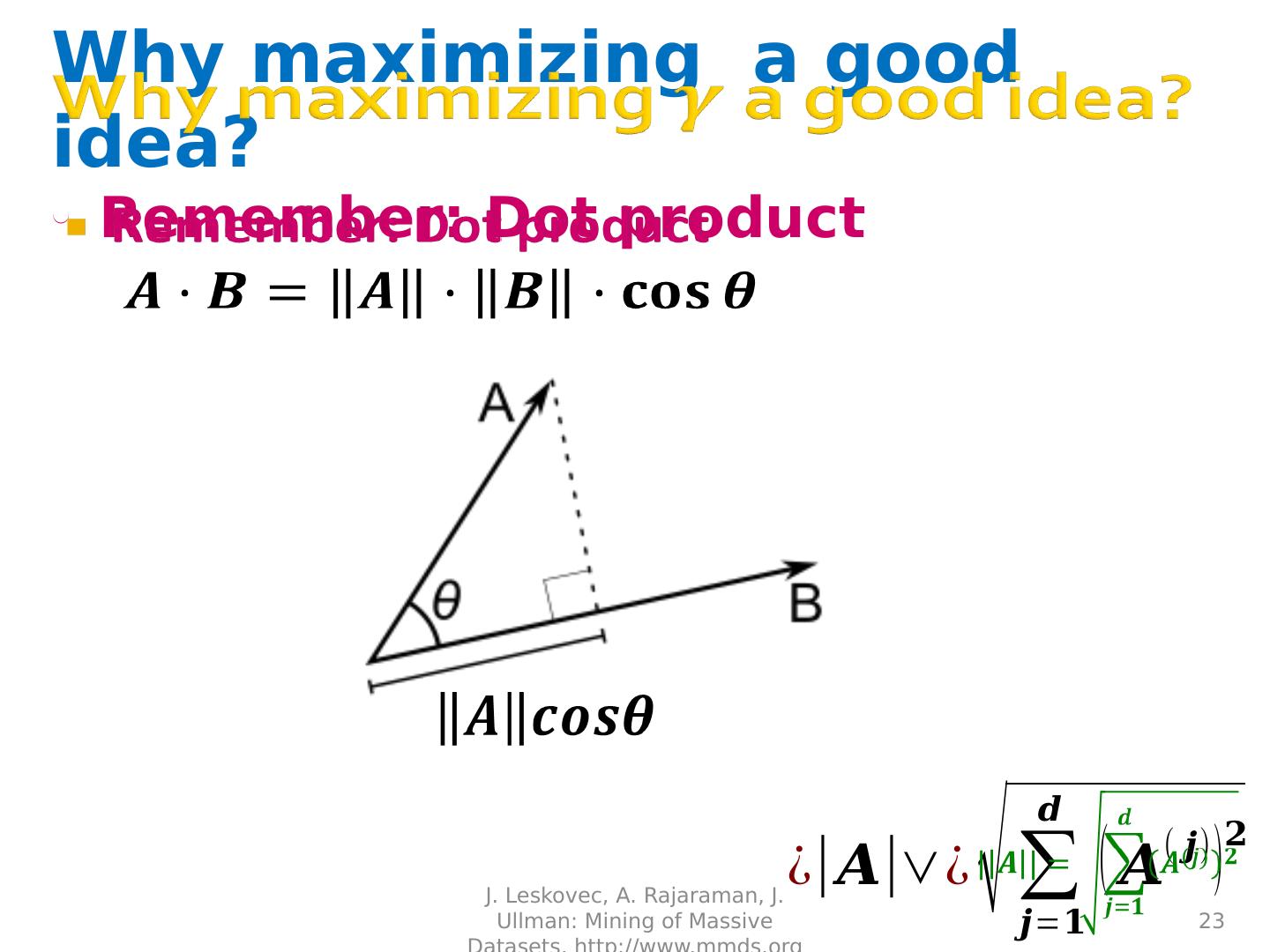
23 .Why maximizing a good idea? Remember: Dot product J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 23
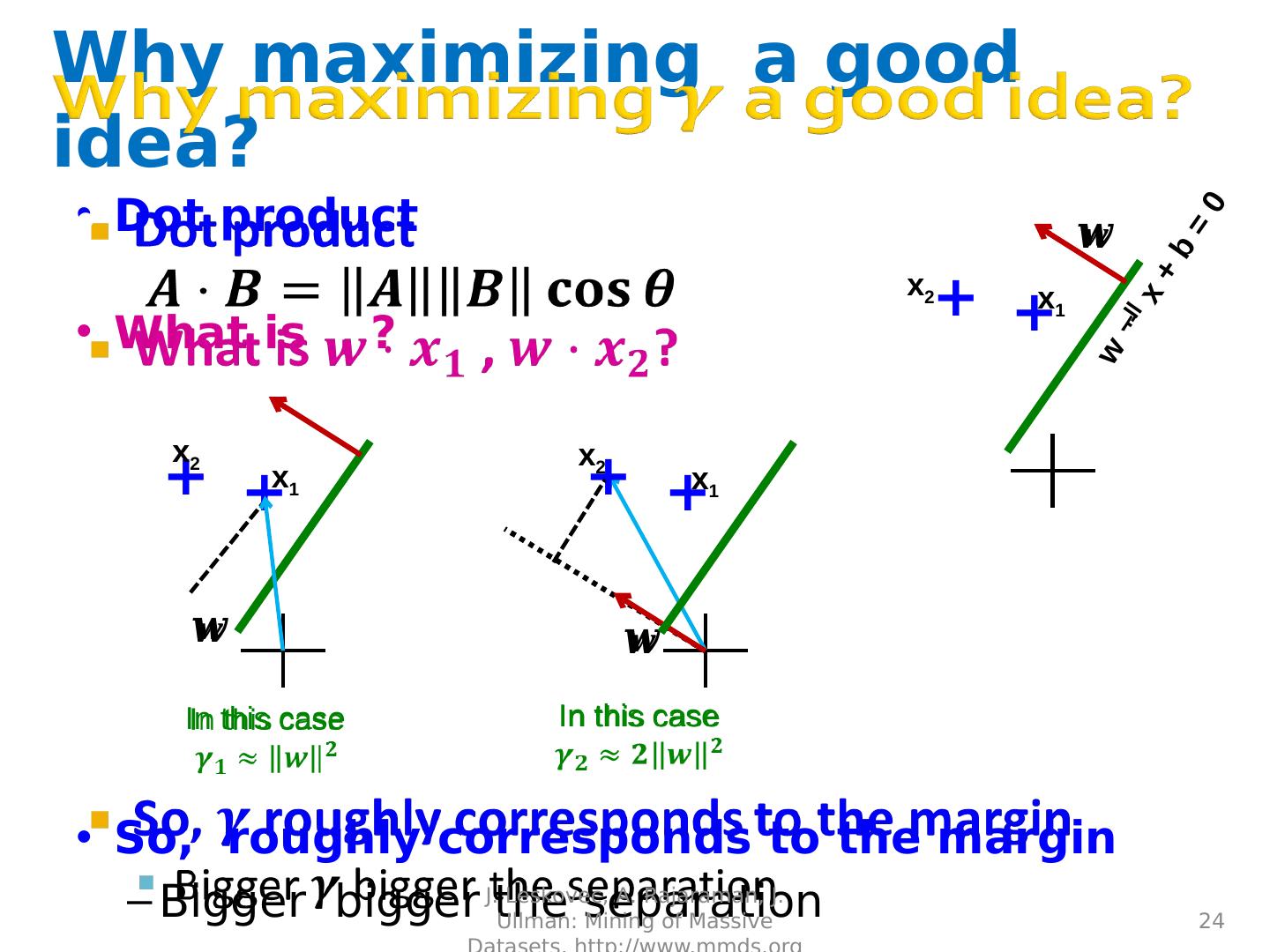
24 .Why maximizing a good idea? Dot product What is , ? So, roughly corresponds to the margin Bigger bigger the separation J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 24 w x + b = 0 + + x 2 x 1 In this case + x 1 + x 2 + x 2 In this case + x 1
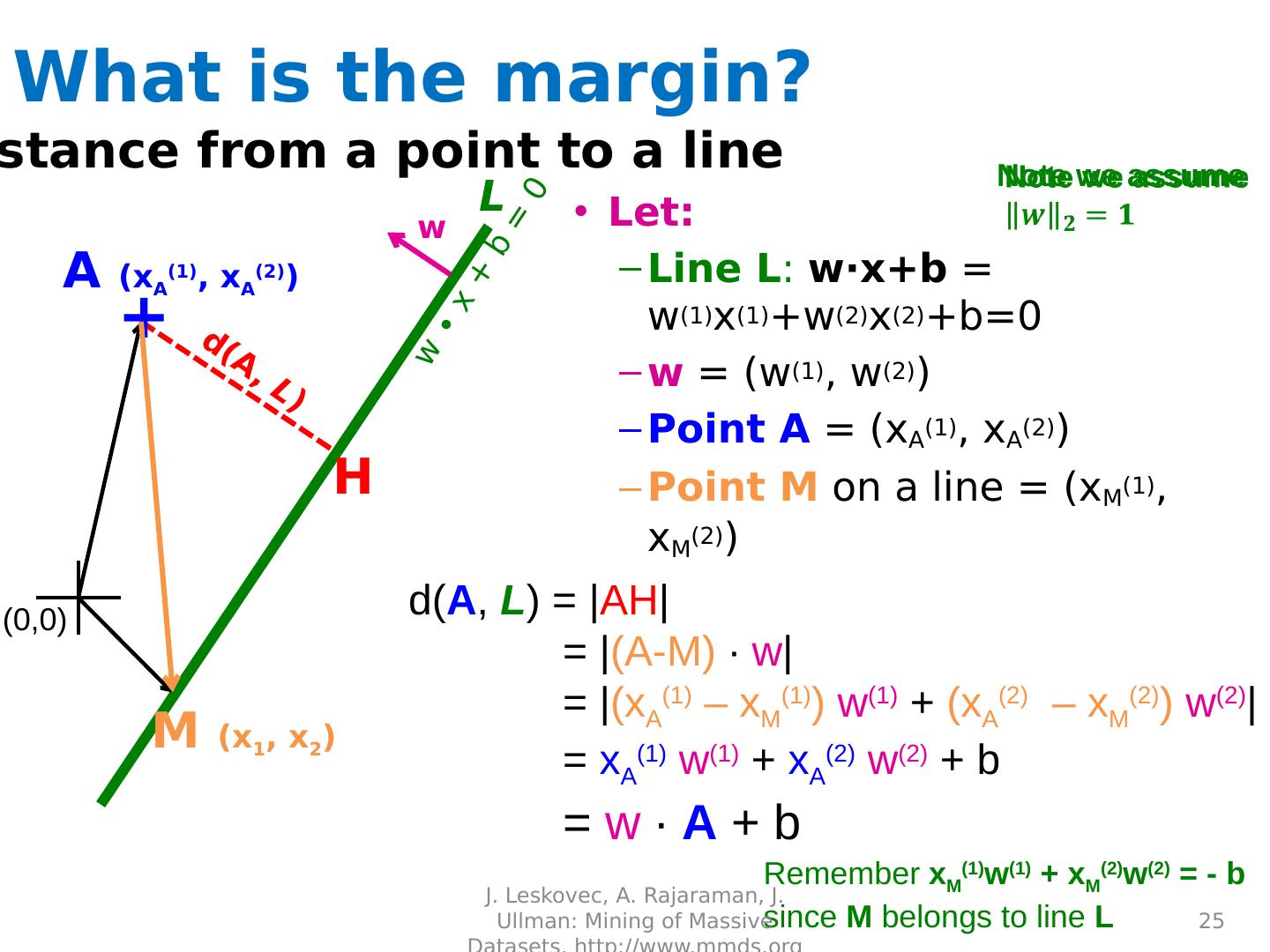
25 .w ∙ x + b = 0 Distance from a point to a line A ( x A (1) , x A (2) ) M ( x 1 , x 2 ) H d( A , L ) = | AH | = | (A-M) ∙ w | = | ( x A (1) – x M (1) ) w (1) + ( x A (2) – x M (2) ) w (2) | = x A (1) w (1) + x A (2) w (2) + b = w ∙ A + b Remember x M (1) w (1) + x M (2) w (2 ) = - b since M belongs to line L w d(A, L ) L + What is the margin? Let: Line L : w∙x+b = w (1) x (1) +w (2) x (2) +b=0 w = ( w (1) , w (2) ) Point A = ( x A (1) , x A (2) ) Point M on a line = ( x M (1) , x M (2 ) ) (0,0) J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 25 Note we assume
26 .Support Vector Machine Maximize the margin: Good according to intuition, theory (VC dimension) & practice is margin … distance from the separating hyperplane J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 26 + + + + + + + + - - - - - - - w x+b =0 Maximizing the margin
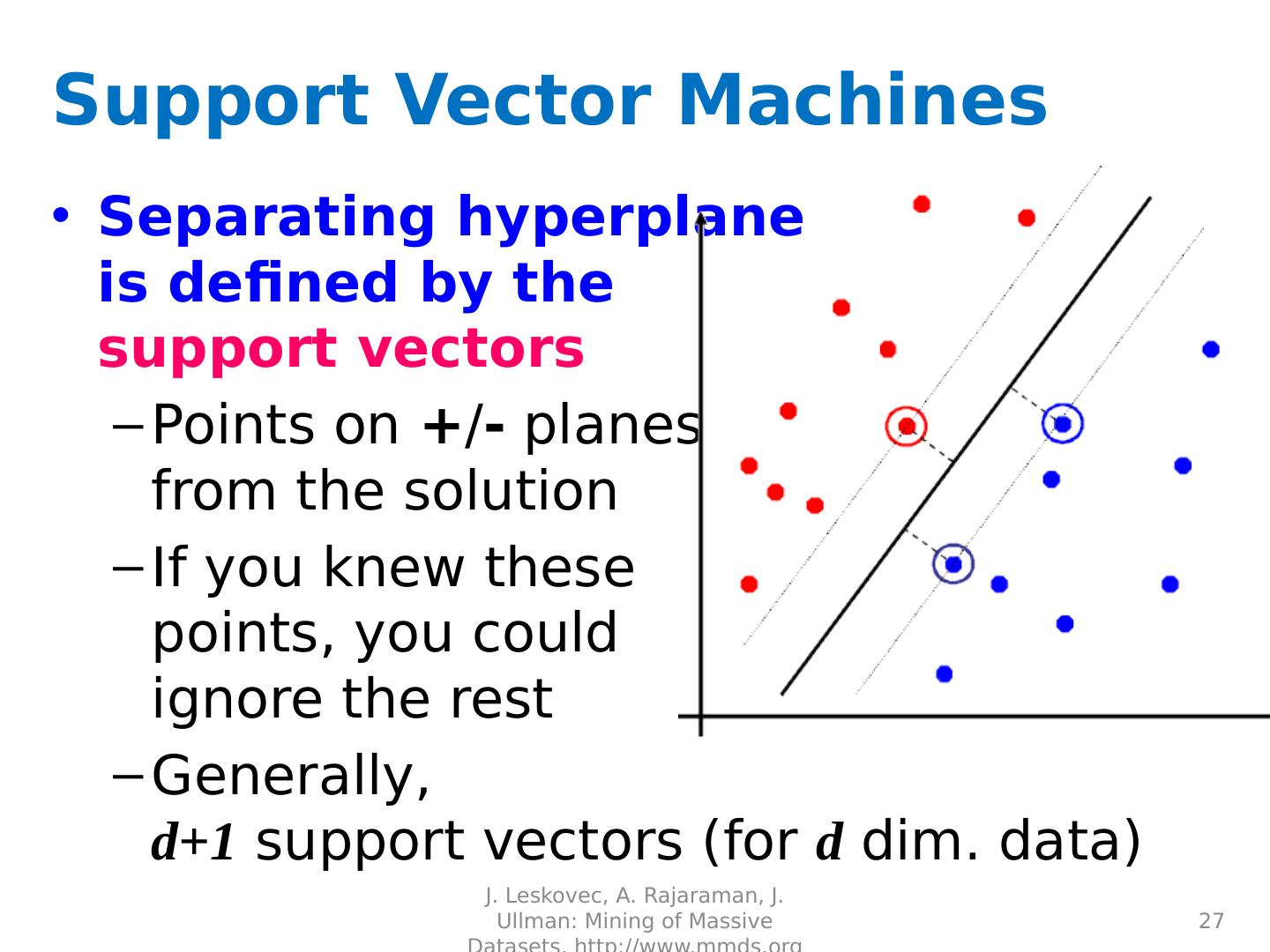
27 .Support Vector Machines Separating hyperplane is defined by the support vectors Points on + / - planes from the solution If you knew these points, you could ignore the rest Generally, d+1 support vectors (for d dim. data) J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 27
28 .Non-linearly Separable Data If data is not separable introduce penalty : Minimize ǁwǁ 2 plus the number of training mistakes Set C using cross validation How to penalize mistakes? All mistakes are not equally bad! J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 28 + + + + + + + - - - - - - - w x+b =0 + - -
29 .Support Vector Machines Introduce slack variables i If point x i is on the wrong side of the margin then get penalty i J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 29 + + + + + + + - - - - - w x+b =0 For each data point: If margin 1, don’t care If margin < 1, pay linear penalty + j - i