- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Graphs
展开查看详情
1 .Graphs (Part I) Shannon Quinn (with thanks to William Cohen of CMU and Jure Leskovec , Anand Rajaraman , and Jeff Ullman of Stanford University)
2 .Why I’m talking about graphs Lots of large data is graphs Facebook, Twitter, citation data, and other social networks The web, the blogosphere, the semantic web, Freebase, W ikipedia, Twitter, and other information networks Text corpora (like RCV1), large datasets with discrete feature values, and other bipartite networks nodes = documents or words links connect document word or word document Computer networks, biological networks (proteins, ecosystems, brains, …), … Heterogeneous networks with multiple types of nodes people, groups, documents
3 .Properties of Graphs Descriptive Statistics Number of connected components Diameter Degree distribution … Models of Growth/Formation Erdos-Renyi Preferential attachment Stochastic block models …. Let’s look at some examples of graphs … but first, why are these statistics important?
4 .An important question How do you explore a dataset? compute statistics (e.g., feature histograms, conditional feature histograms, correlation coefficients, …) sample and inspect run a bunch of small-scale experiments How do you explore a graph? compute statistics (degree distribution, …) sample and inspect how do you sample?
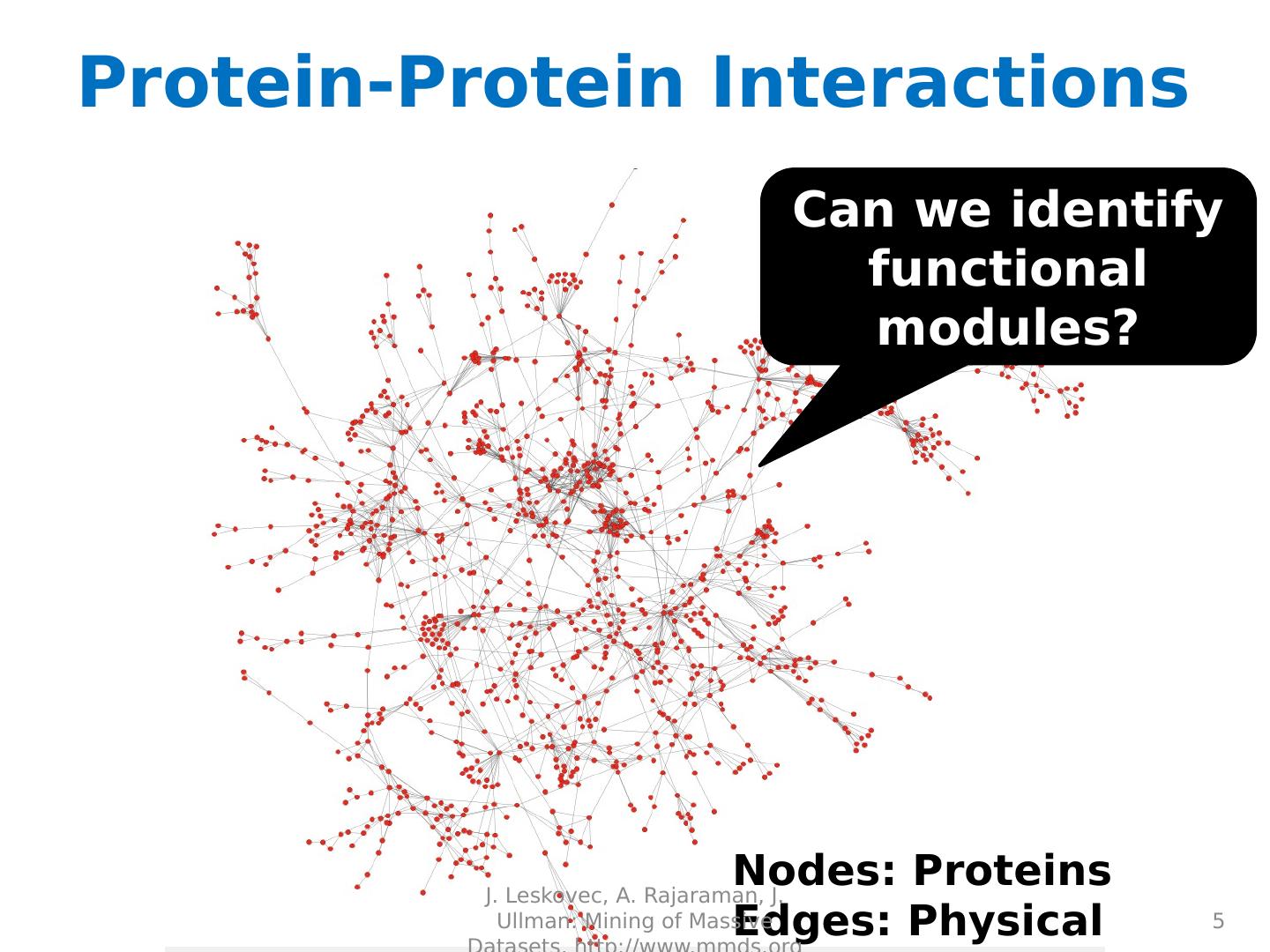
5 .Protein-Protein Interactions 5 Can we identify functional modules? Nodes: Proteins Edges: Physical interactions J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org
6 .Protein-Protein Interactions 6 Functional modules Nodes: Proteins Edges: Physical interactions J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org
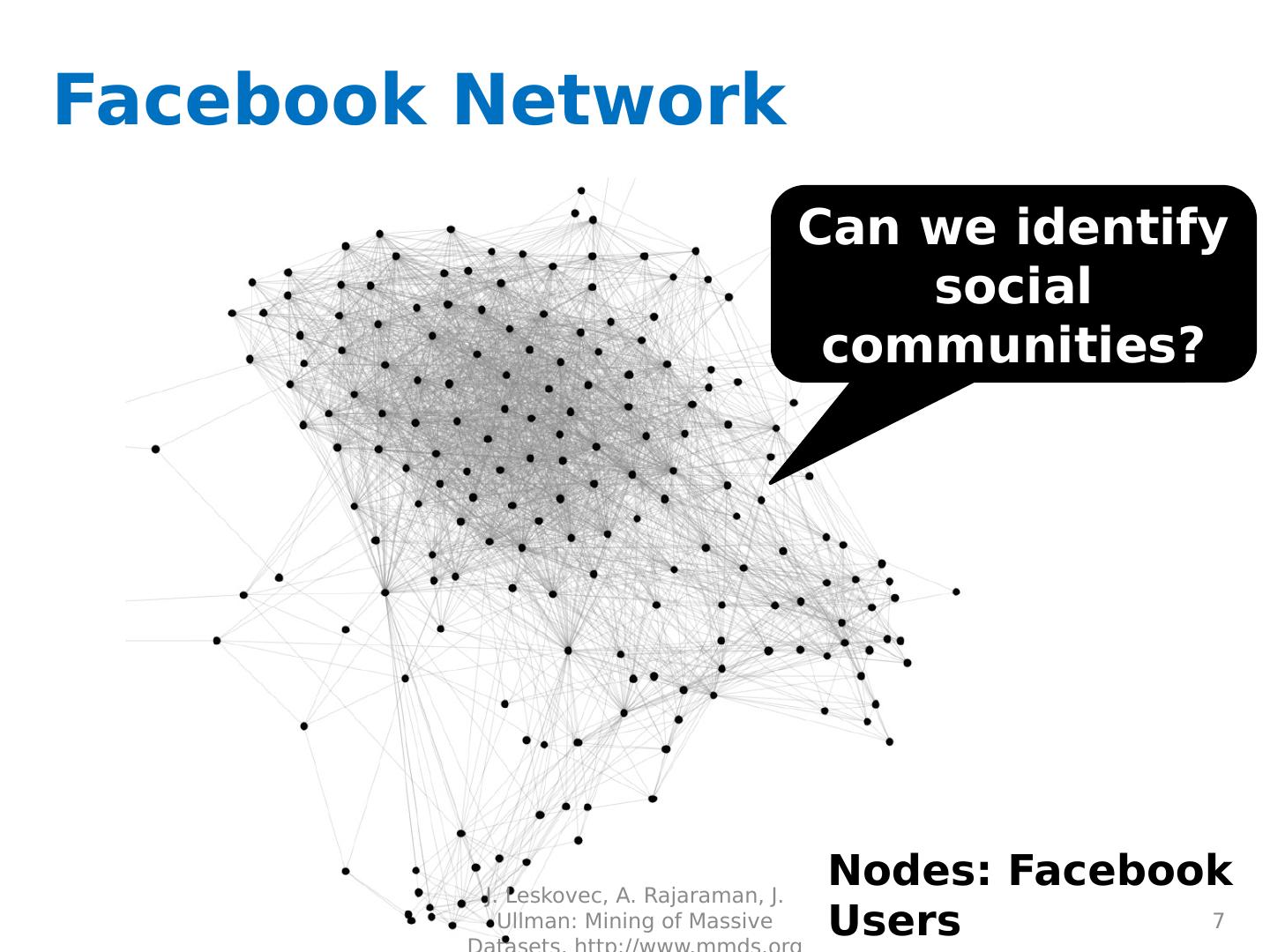
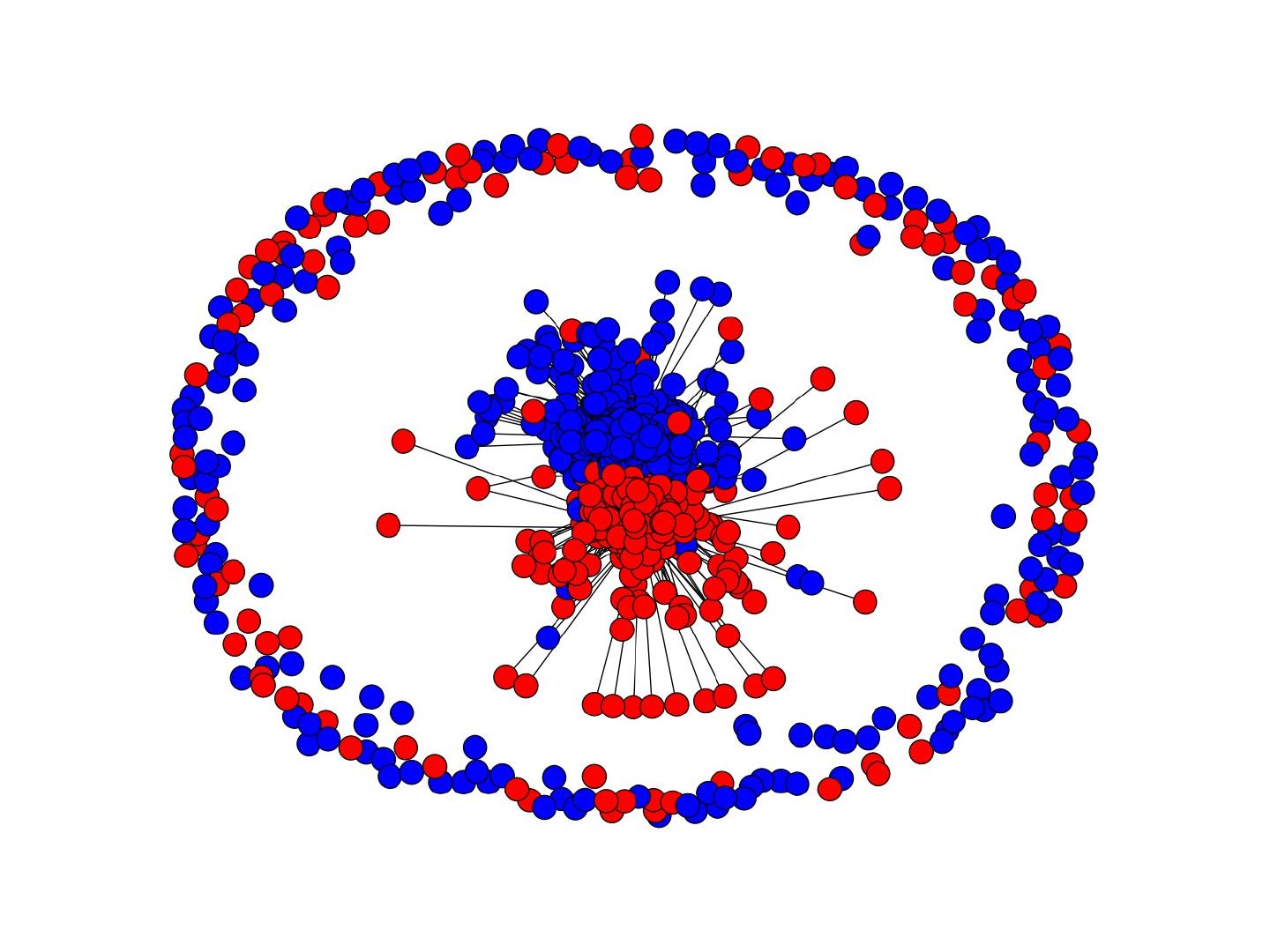
7 .Facebook N etwork 7 Can we identify social communities? Nodes: Facebook Users Edges: Friendships J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org
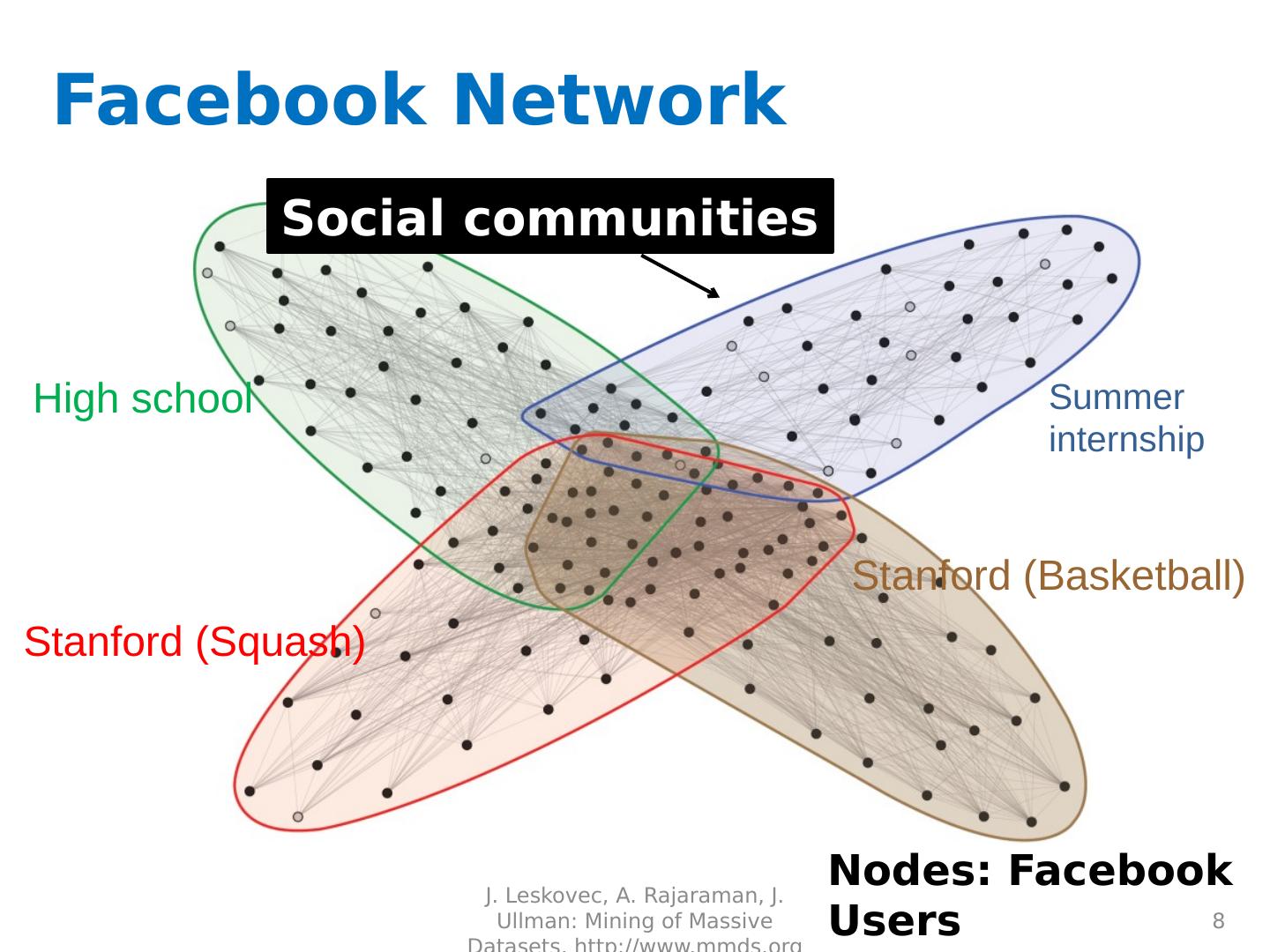
8 .Facebook Network 8 High school Summer internship Stanford (Squash) Stanford (Basketball) Social communities Nodes: Facebook Users Edges: Friendships J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org
9 .Blogs
10 .Citations
11 .Citations
12 .Citations
13 .How do you model graphs?
14 .What are we trying to do? Normal curve: Data to fit Underlying process that “explains” the data Closed-form parametric form Only models a small part of the data
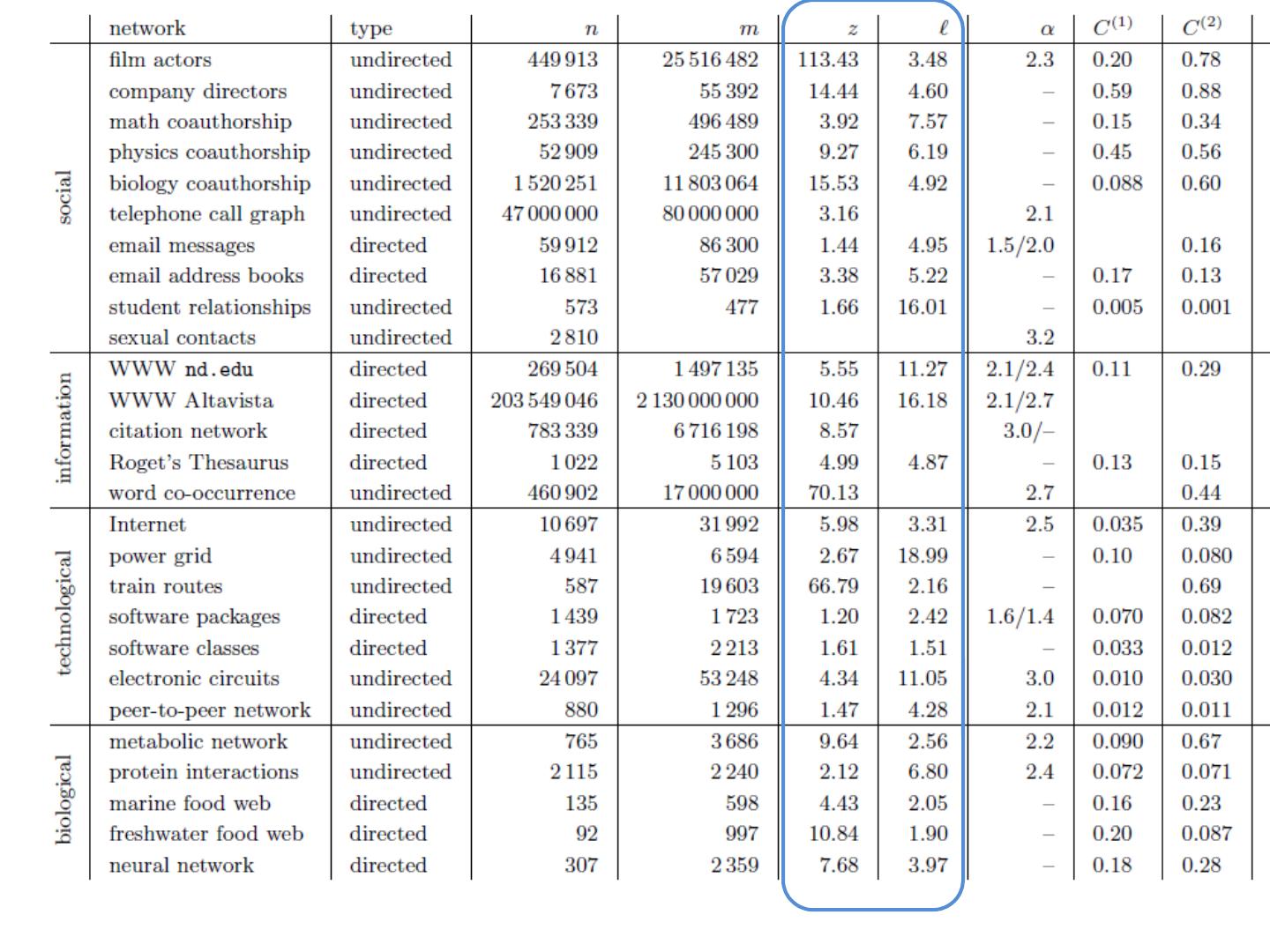
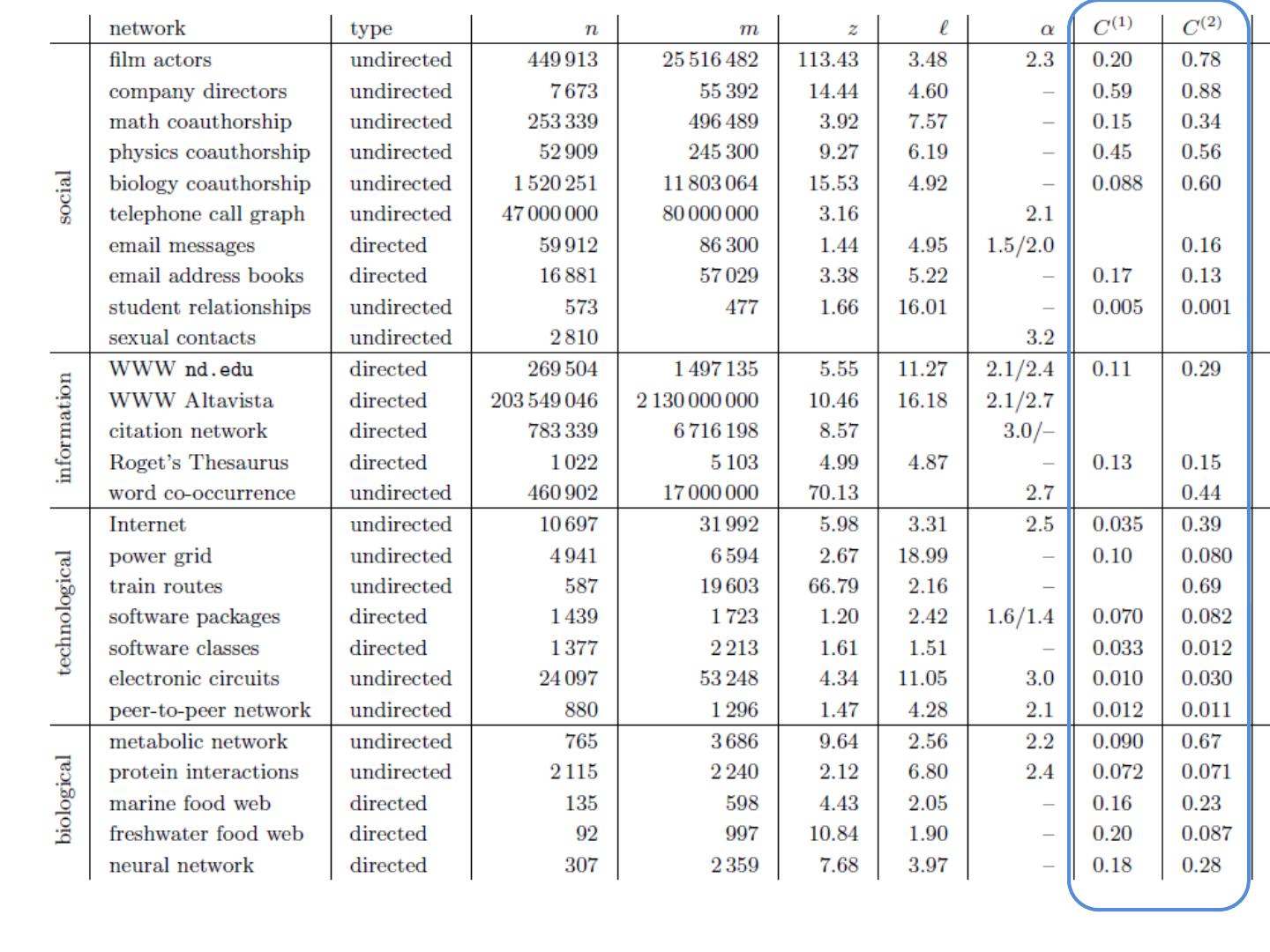
15 .Graphs Set V of vertices/nodes v1,… , set E of edges ( u,v ),…. Edges might be directed and/or weighted and/or labeled Degree of v is #edges touching v Indegree and Outdegree for directed graphs Path is sequence of edges (v0,v1),(v1,v2),…. Geodesic path between u and v is shortest path connecting them Diameter is max u,v in V {length of geodesic between u,v } Effective diameter is 90 th percentile Mean diameter is over connected pairs (Connected) component is subset of nodes that are all pairwise connected via paths Clique is subset of nodes that are all pairwise connected via edges Triangle is a clique of size three
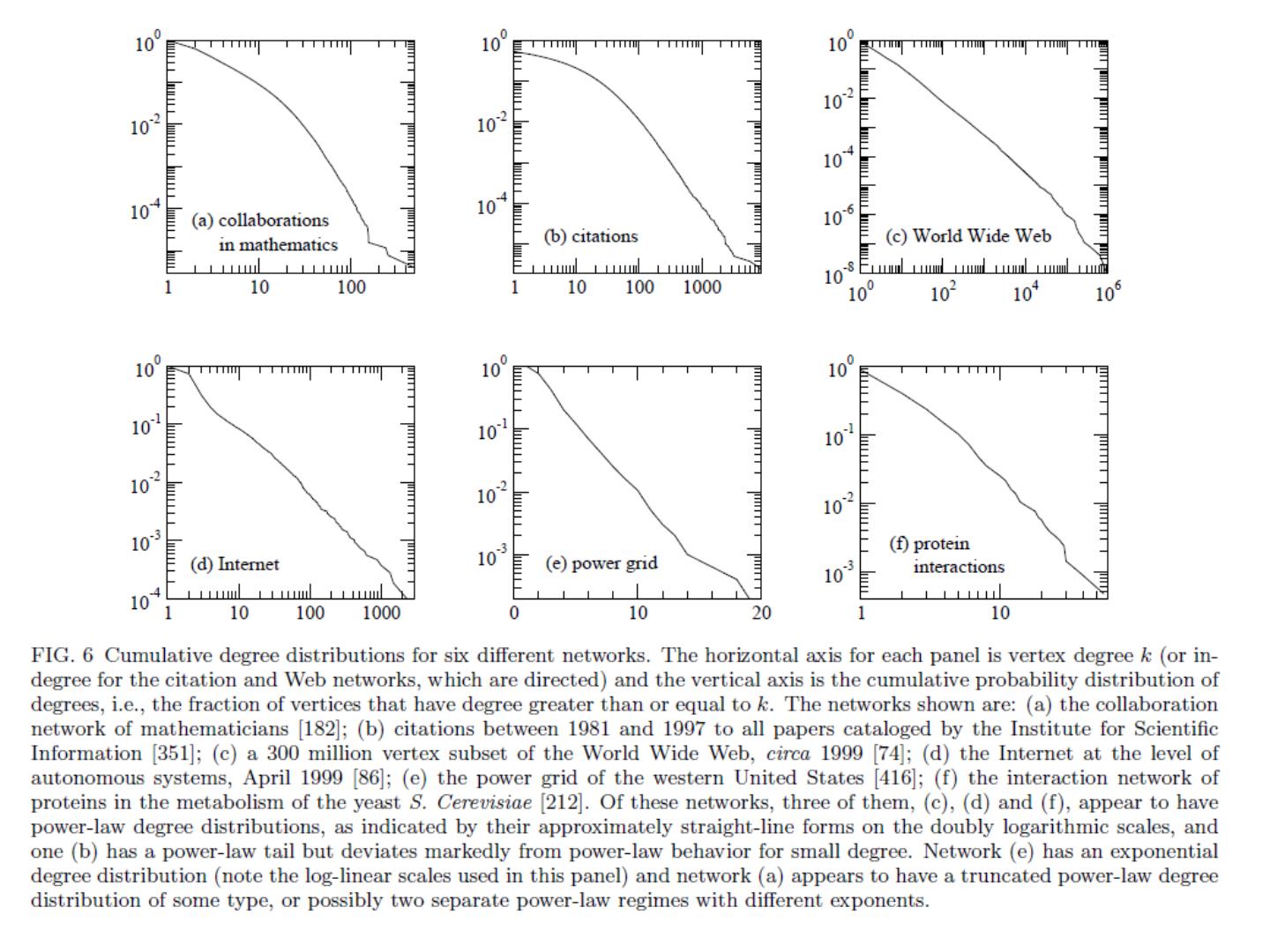
16 .Graphs Some common properties of graphs: Distribution of node degrees Distribution of cliques (e.g., triangles) Distribution of paths Diameter (max shortest-path) Effective diameter (90 th percentile) Connected components … Some types of graphs to consider: Real graphs (social & otherwise) Generated graphs: Erdos-Renyi “Bernoulli” or “Poisson” Watts- Strogatz “small world” graphs Barbosi -Albert “preferential attachment” …
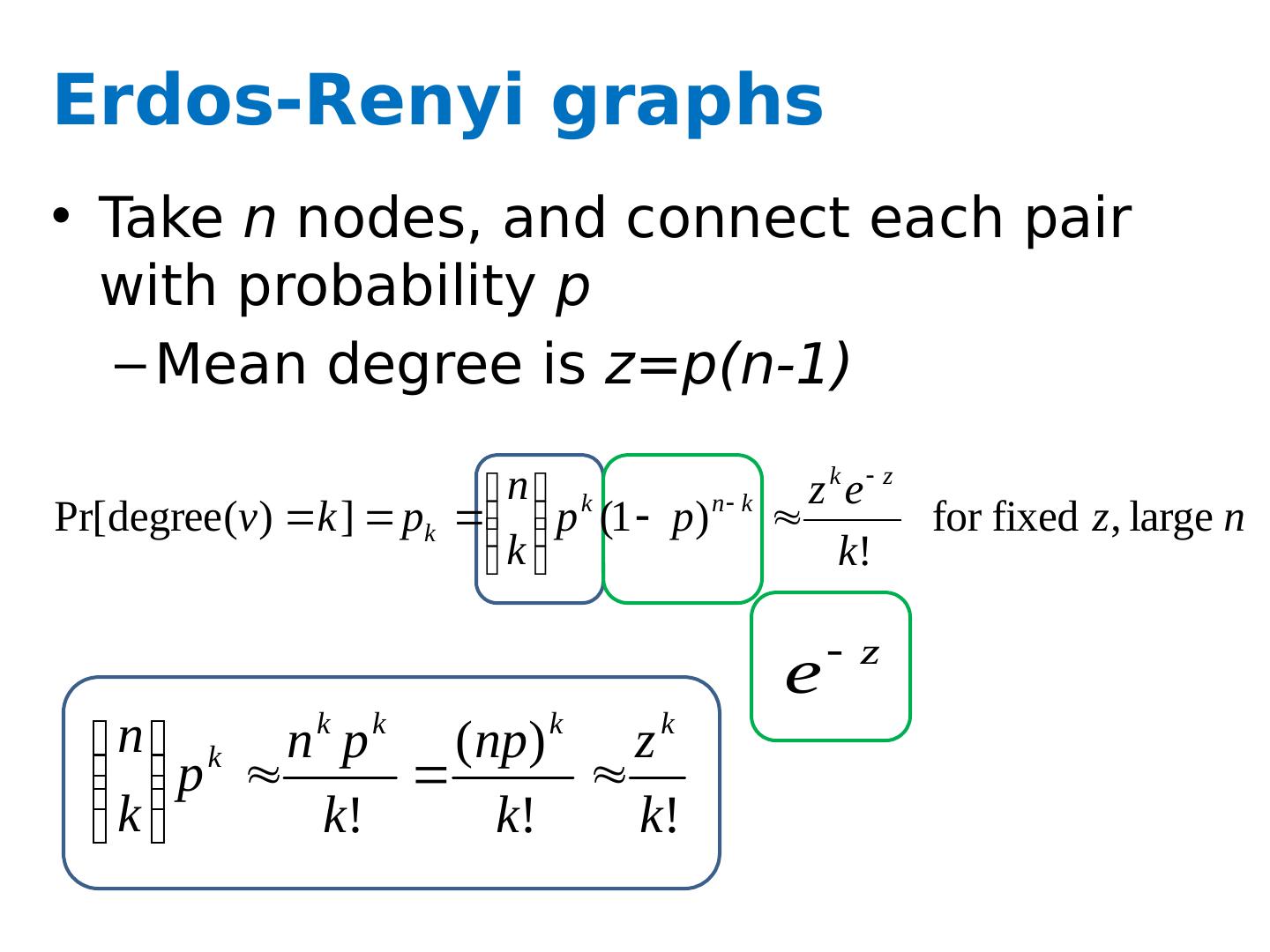
17 .Erdos-Renyi graphs Take n nodes, and connect each pair with probability p Mean degree is z = p(n-1)
18 .Erdos-Renyi graphs Take n nodes, and connect each pair with probability p Mean degree is z = p(n-1) Mean number of neighbors distance d from v is z d How large does d need to be so that z d >=n ? If z>1, d = log(n)/log(z) If z<1, you can’t do it So: There tend to be either many small components (z<1) or one large one ( z>1 ) giant connected component) Another intuition: If there are a two large connected components, then with high probability a few random edges will link them up.
19 .
20 .
21 .Erdos-Renyi graphs Take n nodes, and connect each pair with probability p Mean degree is z = p(n-1) Mean number of neighbors distance d from v is z d How large does d need to be so that z d >=n ? If z>1, d = log(n)/log(z) If z<1, you can’t do it So: If z>1, diameters tend to be small (relative to n)
22 .Sociometry , Vol. 32, No. 4. (Dec., 1969), pp. 425-443. 64 of 296 chains succeed, avg chain length is 6.2
23 .Illustrations of the Small World Millgram’s experiment Erdős numbers http://www.ams.org/mathscinet/searchauthors.html Bacon numbers http://oracleofbacon.org/ LinkedIn http://www.linkedin.com/ Privacy issues: the whole network is not visible to all
24 .Illustrations of the Small World Millgram’s experiment Erdős numbers http://www.ams.org/mathscinet/searchauthors.html Bacon numbers http://oracleofbacon.org/ LinkedIn http://www.linkedin.com/ Privacy issues: the whole network is not visible to all
25 .Illustrations of the Small World Millgram’s experiment Erdős numbers http://www.ams.org/mathscinet/searchauthors.html Bacon numbers http://oracleofbacon.org/ LinkedIn http://www.linkedin.com/ Privacy issues: the whole network is not visible to all
26 .Erdos-Renyi graphs Take n nodes, and connect each pair with probability p Mean degree is z = p(n-1) This is usually not a good model of degree distribution in natural networks
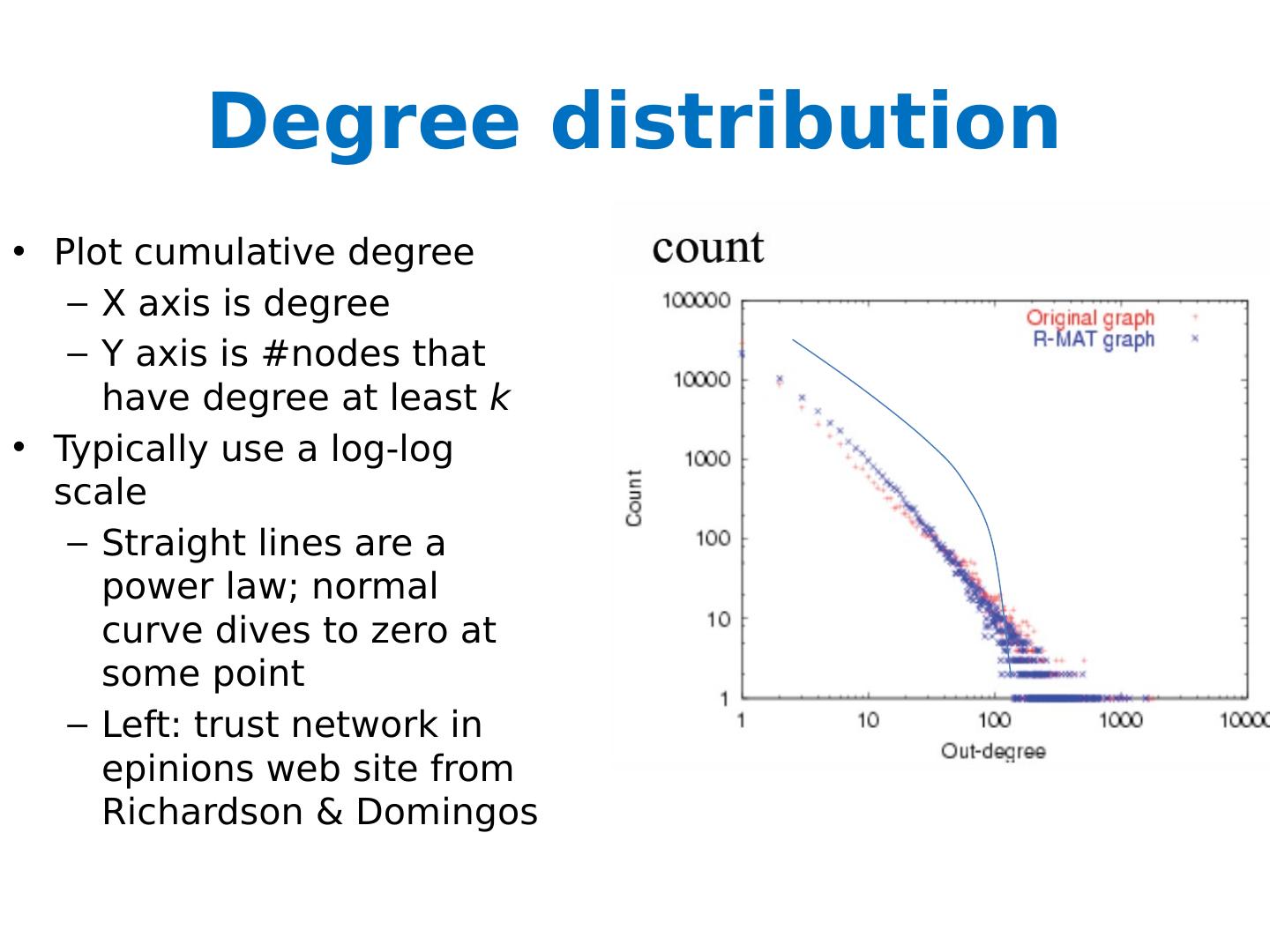
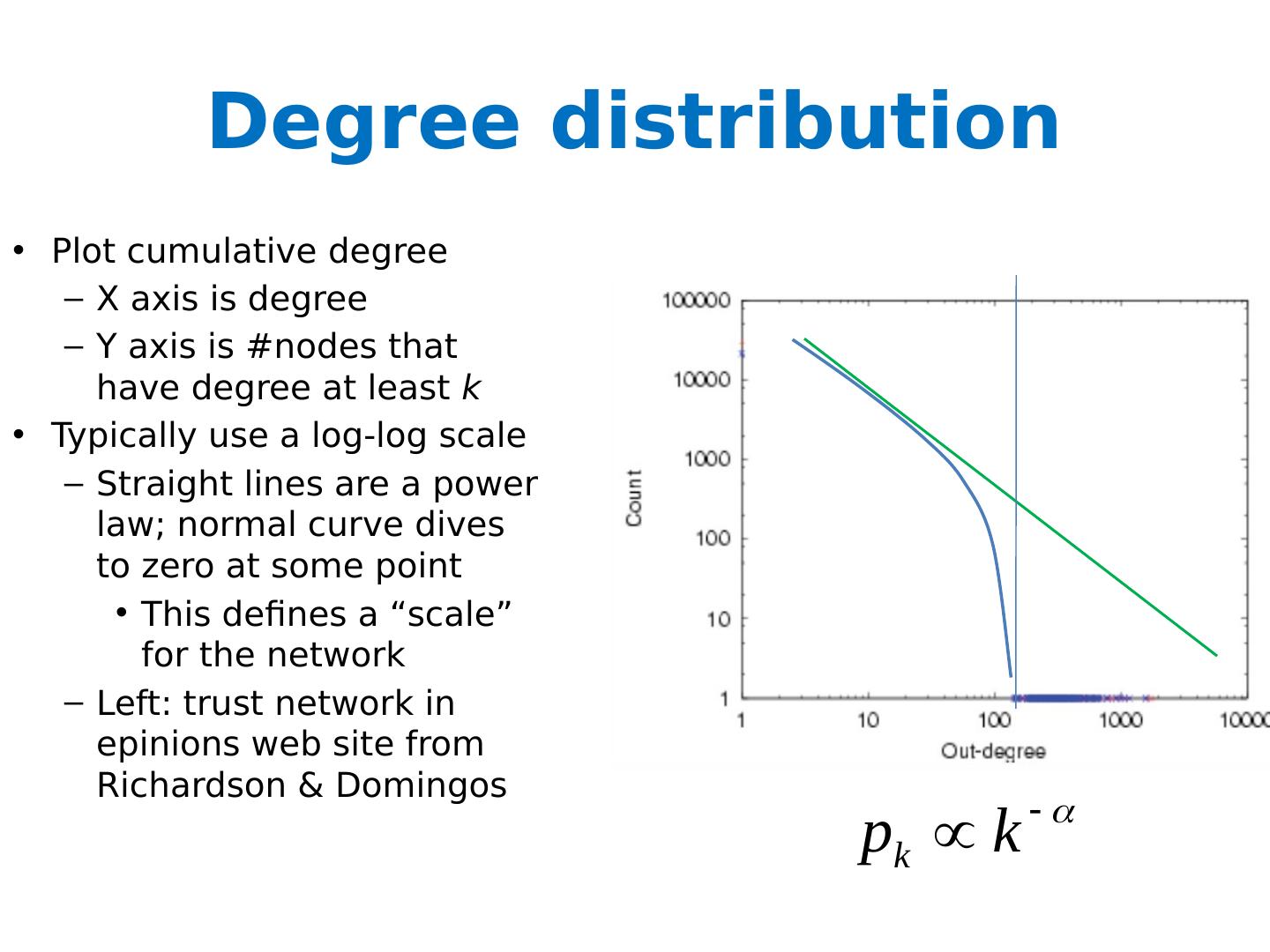
27 .Degree distribution Plot cumulative degree X axis is degree Y axis is #nodes that have degree at least k Typically use a log-log scale Straight lines are a power law; normal curve dives to zero at some point Left: trust network in epinions web site from Richardson & Domingos
28 .Degree distribution Plot cumulative degree X axis is degree Y axis is #nodes that have degree at least k Typically use a log-log scale Straight lines are a power law; normal curve dives to zero at some point This defines a “scale” for the network Left: trust network in epinions web site from Richardson & Domingos
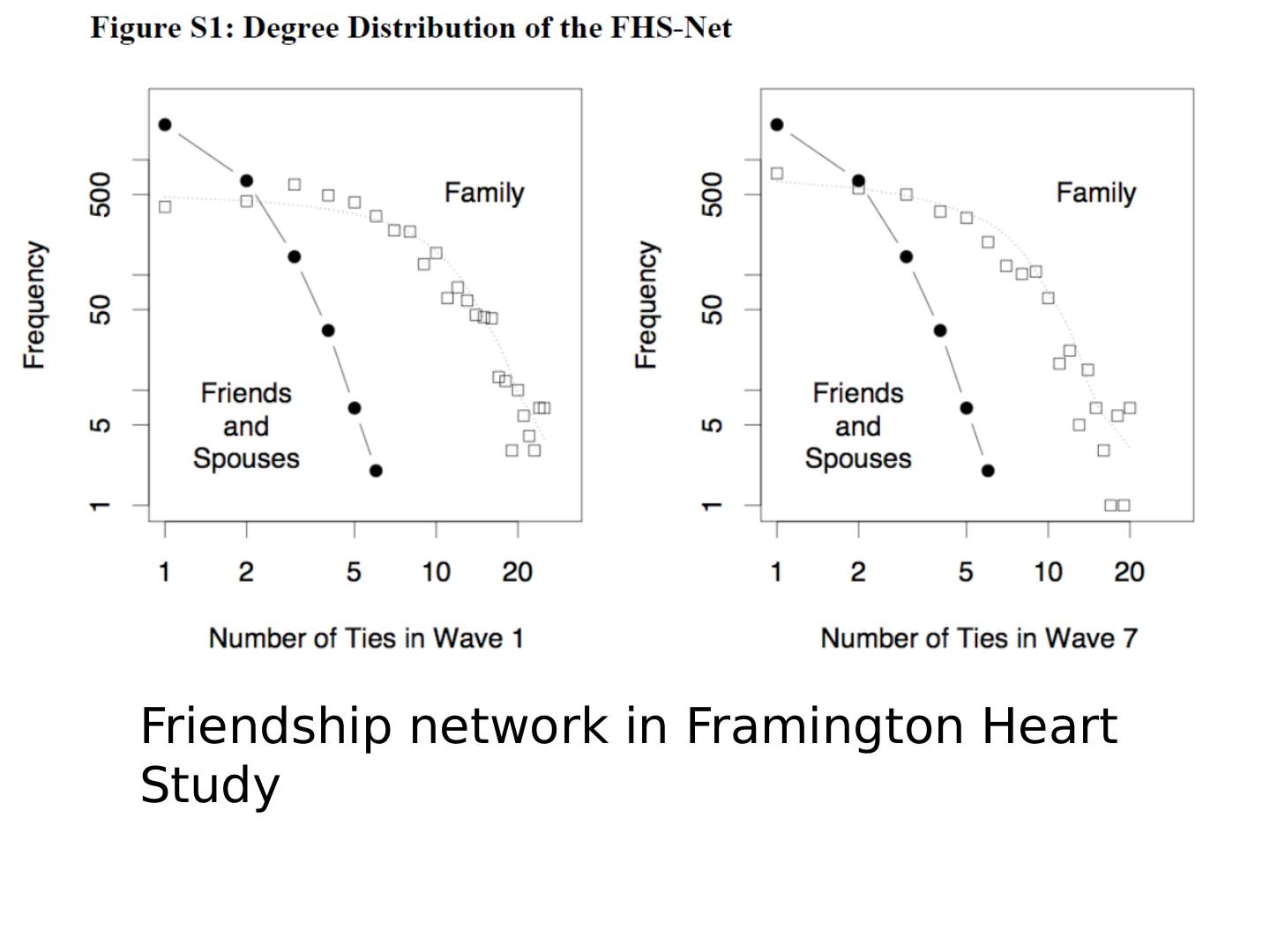
29 .Friendship network in Framington Heart Study