- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Dijkstra's Algorithm
展开查看详情
1 .CSE 373: Data Structures & Algorithms Graph Traversals: Dijkstra’s Riley Porter Winter 2017 CSE373: Data Structures & Algorithms 1
2 .Course Logistics HW4 out graphs! Topic Summary on Graphs coming out by tomorrow evening. We’ll add more after we finish Graphs next week. Grade computation guide (as best we can) out tonight. 2 CSE373: Data Structures & Algorithms
3 .Review: Graph Traversals For an arbitrary graph and a starting node v , find all nodes reachable from v (i.e., there exists a path from v ) Basic idea of traversal: Keep following nodes But “mark” nodes after visiting them, so the traversal terminates and processes each reachable node exactly once 3 CSE373: Data Structures & Algorithms
4 .Review: DFS 4 CSE373: Data Structures & Algorithms A B D E C F H G DFS ( Node start) { initialize stack s to hold start mark start as visited while(s is not empty) { next = s.pop () // and “process” for each node u adjacent to next if(u is not marked) mark u and push onto s } } A, C, F , H, G, B, E, D A different but perfectly fine depth traversal
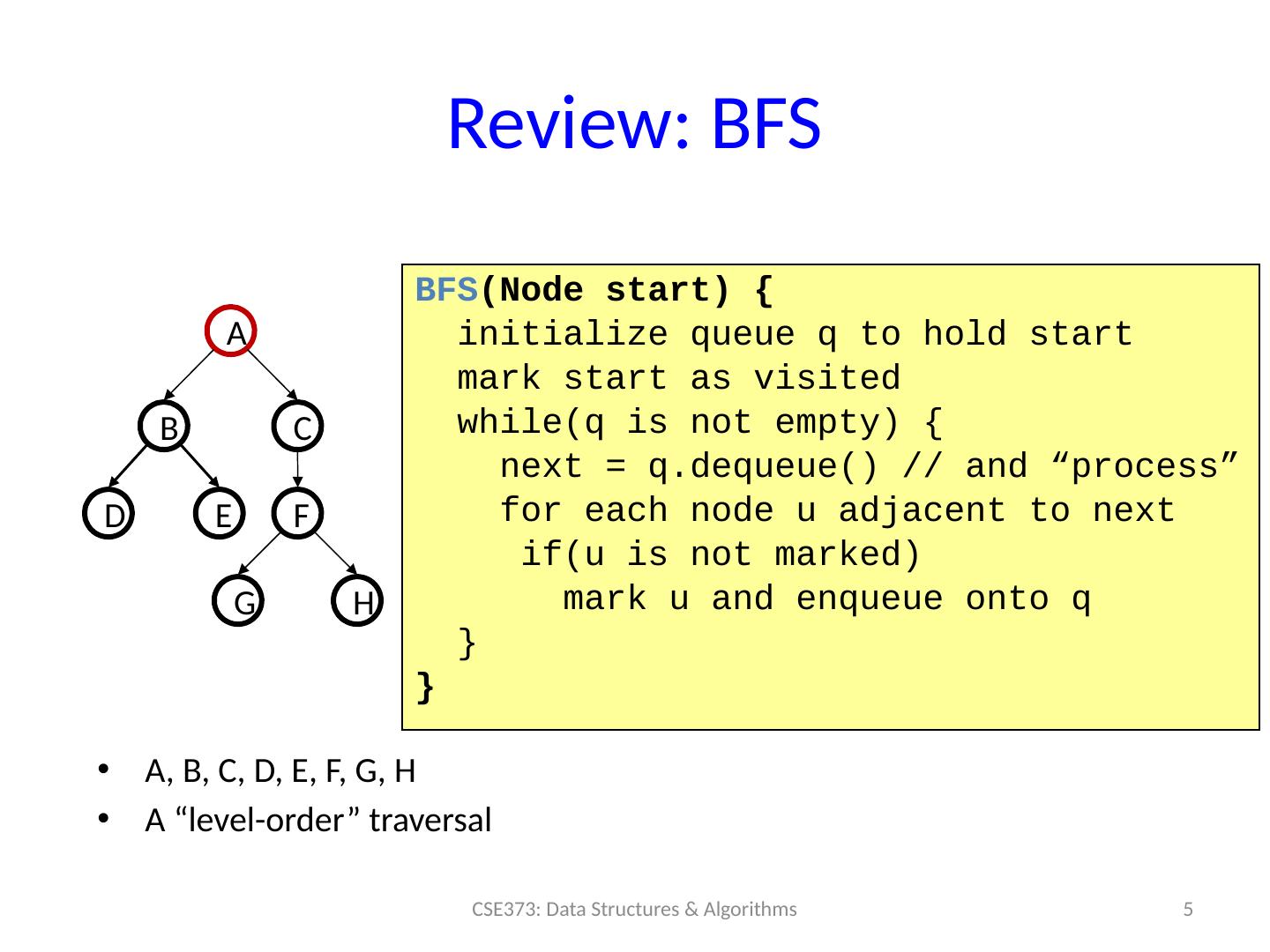
5 .Review: BFS 5 CSE373: Data Structures & Algorithms A B D E C F H G BFS (Node start) { initialize queue q to hold start mark start as visited while(q is not empty) { next = q.dequeue () // and “process” for each node u adjacent to next if(u is not marked) mark u and enqueue onto q } } A, B, C, D, E, F, G, H A “level-order” traversal
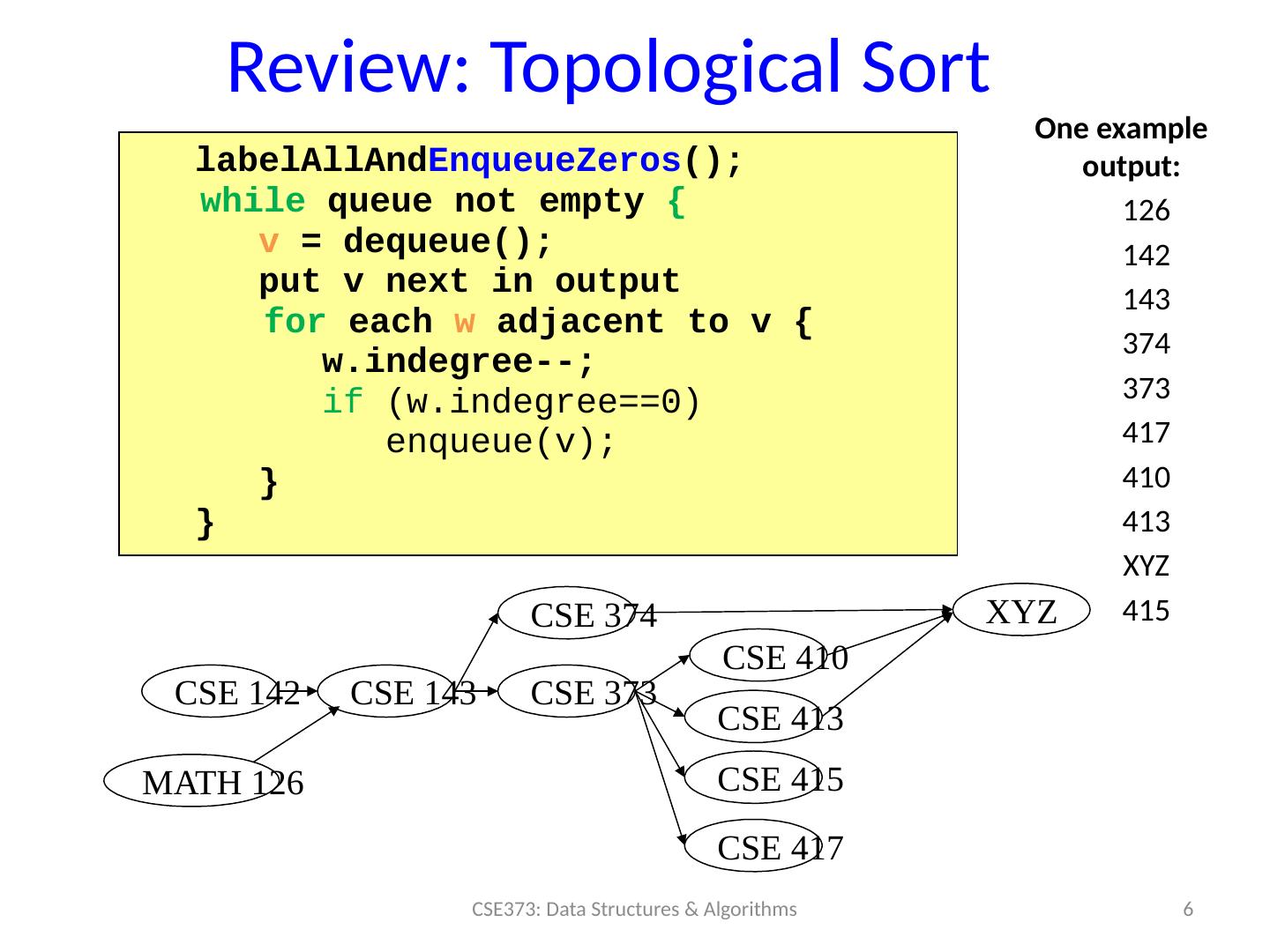
6 .Review: Topological Sort One example output: 126 142 143 374 373 417 410 413 XYZ 415 6 CSE373: Data Structures & Algorithms CSE 142 CSE 143 CSE 374 CSE 373 CSE 410 MATH 126 CSE 417 CSE 415 CSE 413 XYZ labelAllAnd EnqueueZeros (); while queue not empty { v = dequeue (); put v next in output for each w adjacent to v { w.indegree --; if ( w.indegree ==0) enqueue (v); } }
7 .Today: Shortest COST Path 7 CSE373: Data Structures & Algorithms
8 .Single source shortest paths Done: BFS to find the minimum path length from v to u in O (|E|+|V|) Actually, can find the minimum path length from v to every node Still O (|E|+|V|) No faster way for a “distinguished” destination in the worst-case Now: Weighted graphs Given a weighted graph and node v , find the minimum-cost path from v to every node As before, asymptotically no harder than for one destination Unlike before, BFS will not work -> only looks at path length. 8 CSE373: Data Structures & Algorithms
9 .Shortest Path: Applications Driving directions Cheap flight itineraries Network routing Critical paths in project management 9 CSE373: Data Structures & Algorithms
10 .Not as easy Why BFS won’t work: Shortest path may not have the fewest edges Annoying when this happens with costs of flights 10 CSE373: Data Structures & Algorithms 500 100 100 100 100 We will assume there are no negative weights Problem is ill-defined if there are negative-cost cycles Today’s algorithm is wrong if edges can be negative There are other, slower (but not terrible) algorithms 7 10 5 -11 A B
11 .Dijkstra : an important CS “founder” Algorithm named after its inventor Edsger Dijkstra (1930-2002 ) A good Dijkstra quote: “computer science is no more about computers than astronomy is about telescopes ” My favorite Dijkstra joke: “Well, obviously he had to go into computer science, he has ijk in his name! He’s basically built for writing loops” 11 CSE373: Data Structures & Algorithms
12 .Dijkstra’s algorithm The idea: reminiscent of BFS, but adapted to handle weights Grow the set of nodes whose shortest distance has been computed Nodes not processed yet will have a “best distance so far” A priority queue will turn out to be useful for efficiency 12 CSE373: Data Structures & Algorithms
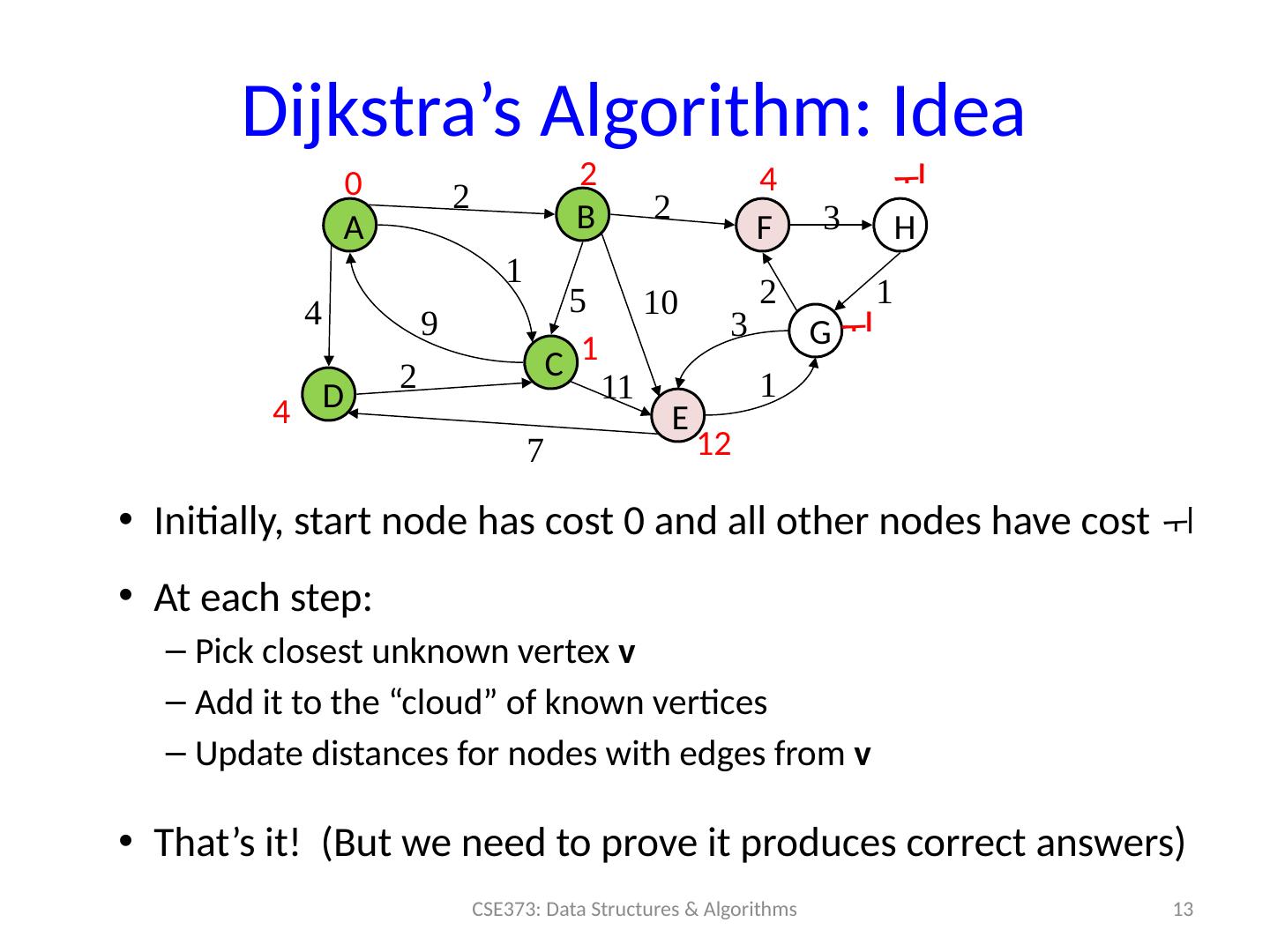
13 .Dijkstra’s Algorithm: Idea 13 CSE373: Data Structures & Algorithms Initially, start node has cost 0 and all other nodes have cost At each step: Pick closest unknown vertex v Add it to the “cloud” of known vertices Update distances for nodes with edges from v That’s it! (But we need to prove it produces correct answers) A B D C F H E G 0 2 4 4 1 12 2 2 3 1 10 2 3 1 11 7 1 9 2 4 5
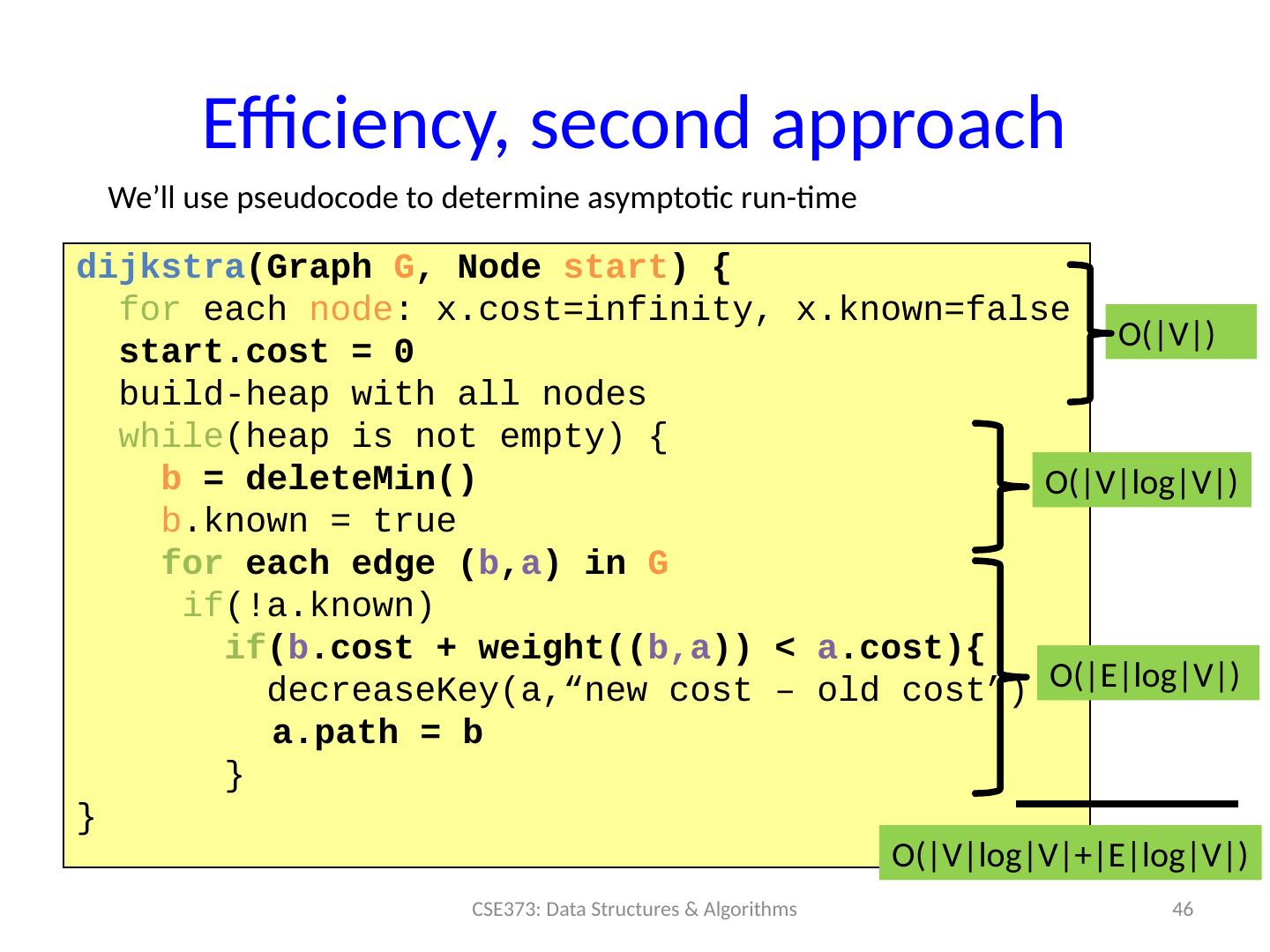
14 .The Algorithm For each node v , set v.cost = and v.known = false Set source.cost = 0 While there are unknown nodes in the graph Select the unknown node v with lowest cost Mark v as known For each edge ( v,u ) with weight w , c1 = v.cost + w // cost of best path through v to u c2 = u.cost // cost of best path to u previously known if(c1 < c2){ // if the path through v is better u.cost = c1 u.path = v // for computing actual paths } 14 CSE373: Data Structures & Algorithms
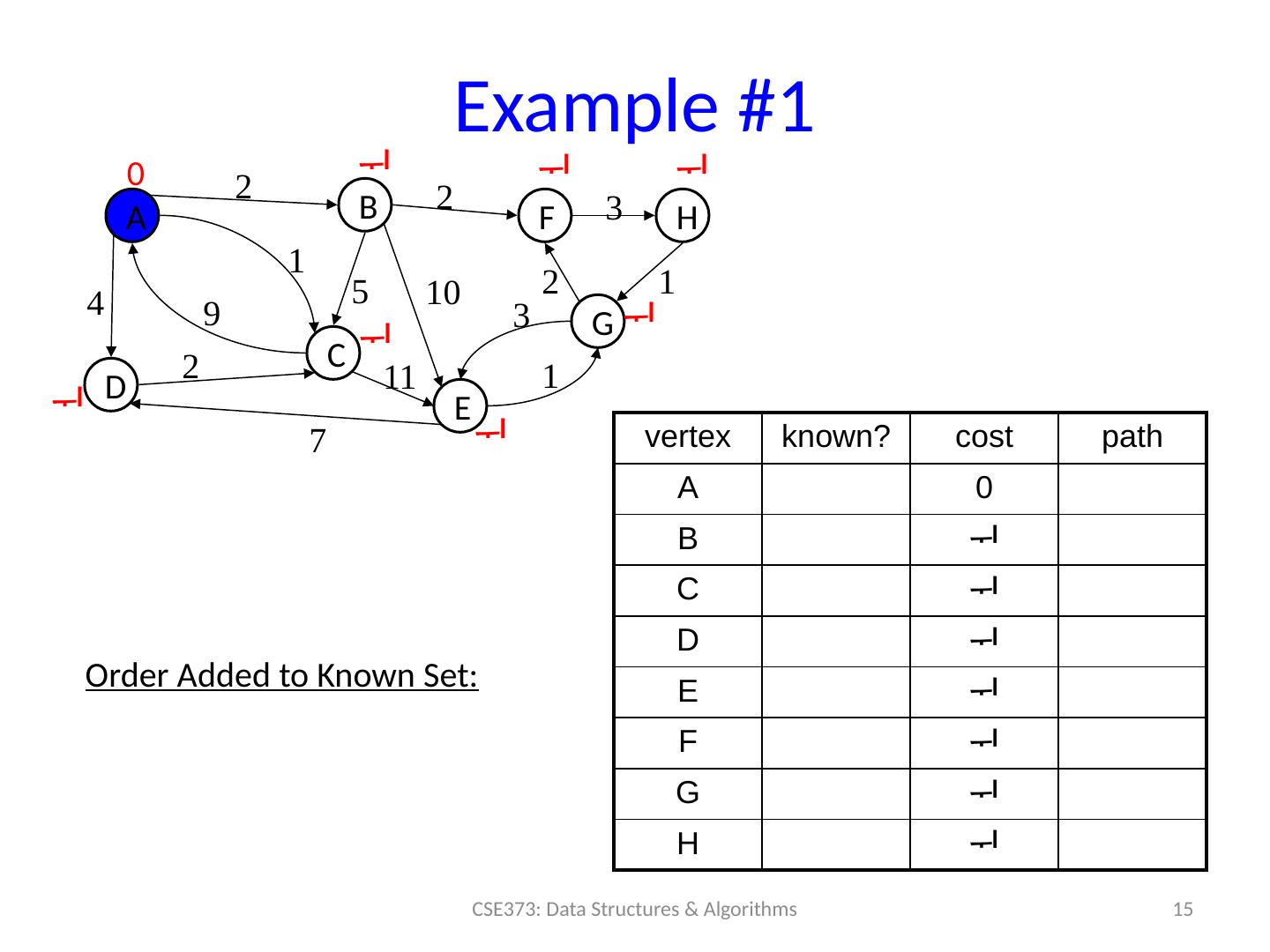
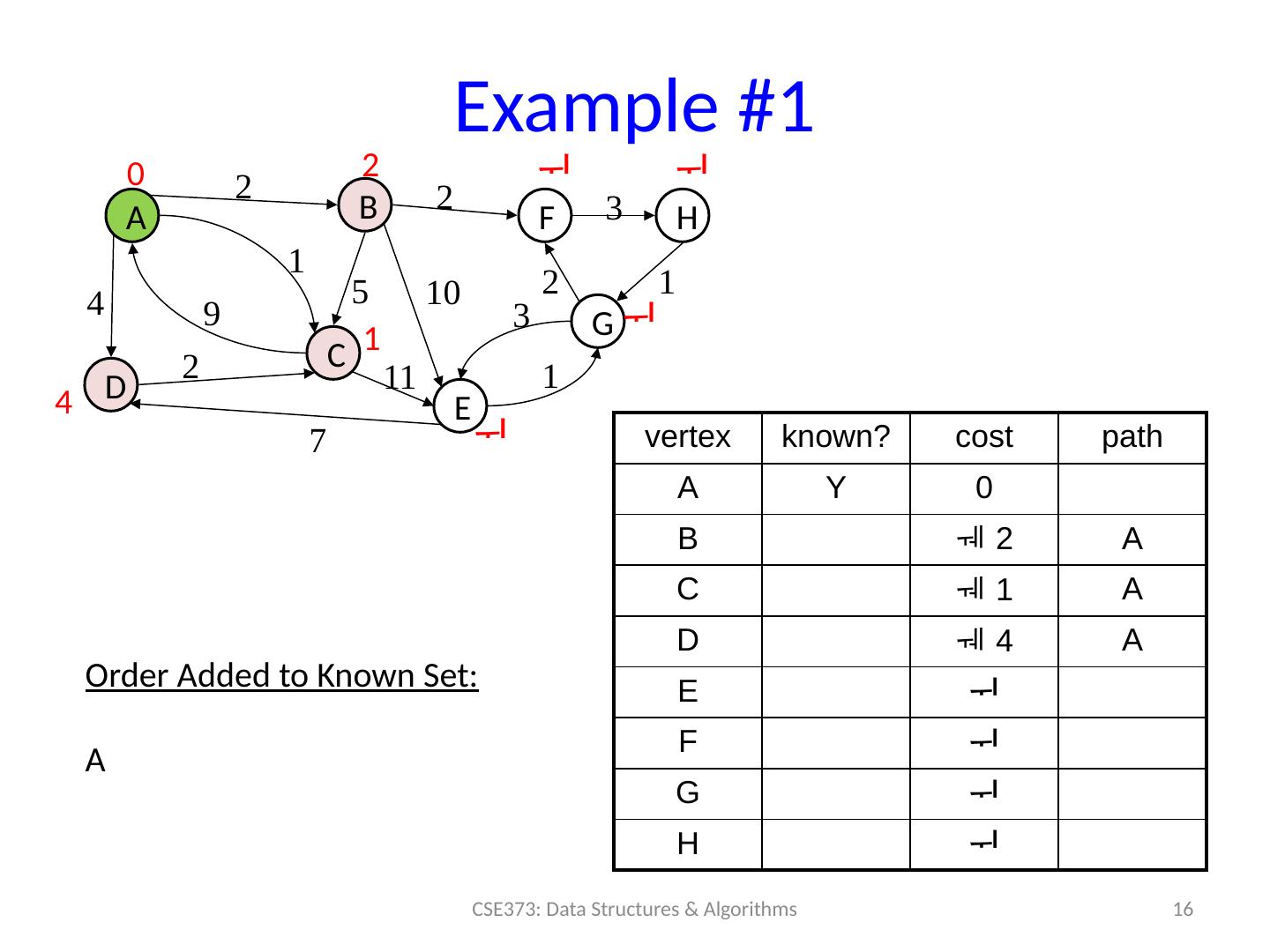
15 .Example #1 15 CSE373: Data Structures & Algorithms A B D C F H E G 0 2 2 3 1 10 2 3 1 11 7 1 9 2 4 vertex known? cost path A 0 B C D E F G H 5 Order Added to Known Set :
16 .Example #1 16 CSE373: Data Structures & Algorithms A B D C F H E G 0 2 4 1 2 2 3 1 10 2 3 1 11 7 1 9 2 4 vertex known? cost path A Y 0 B 2 A C 1 A D 4 A E F G H 5 Order Added to Known Set : A
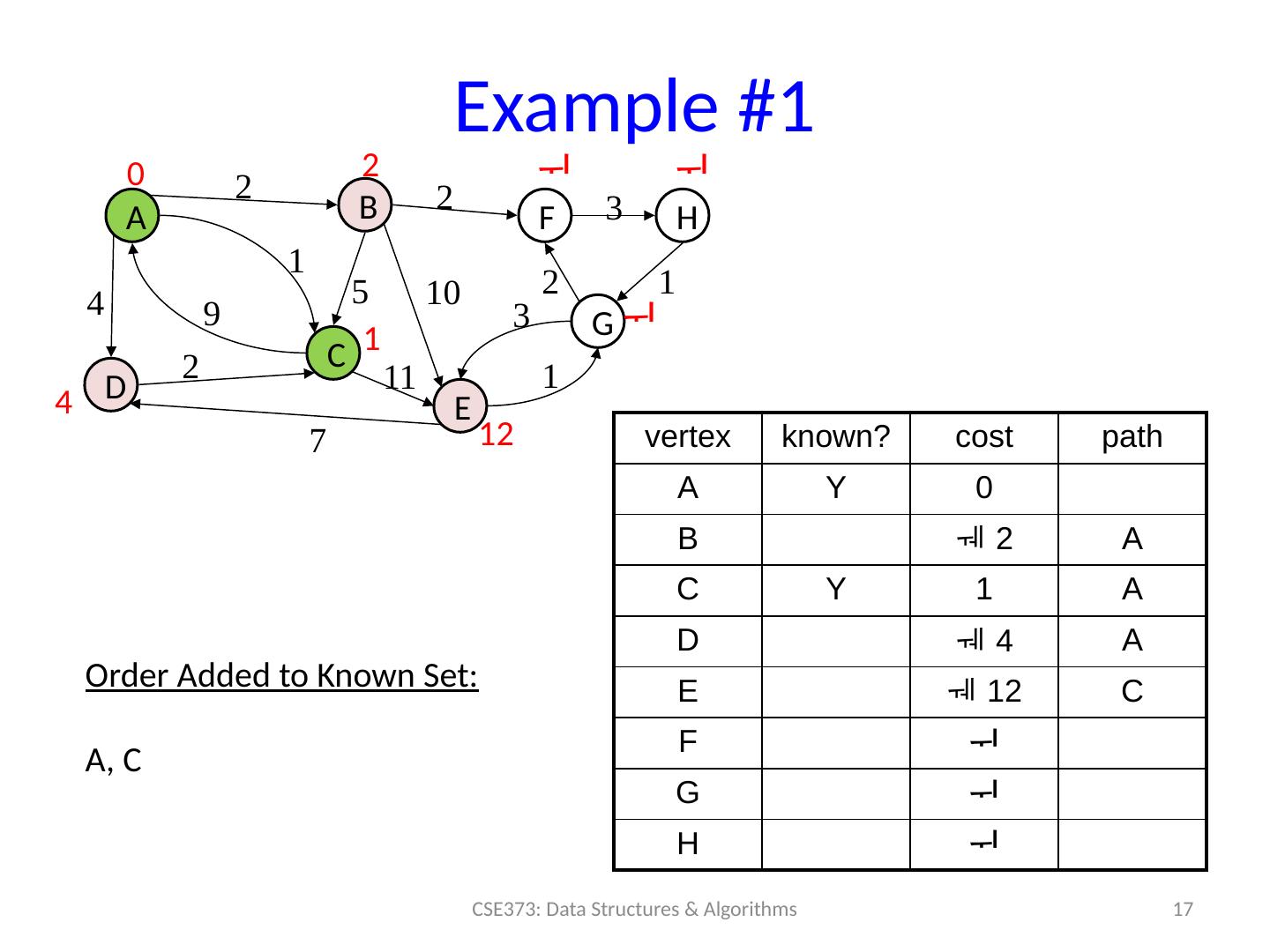
17 .Example #1 17 CSE373: Data Structures & Algorithms A B D C F H E G 0 2 4 1 12 2 2 3 1 10 2 3 1 11 7 1 9 2 4 vertex known? cost path A Y 0 B 2 A C Y 1 A D 4 A E 12 C F G H 5 Order Added to Known Set : A, C
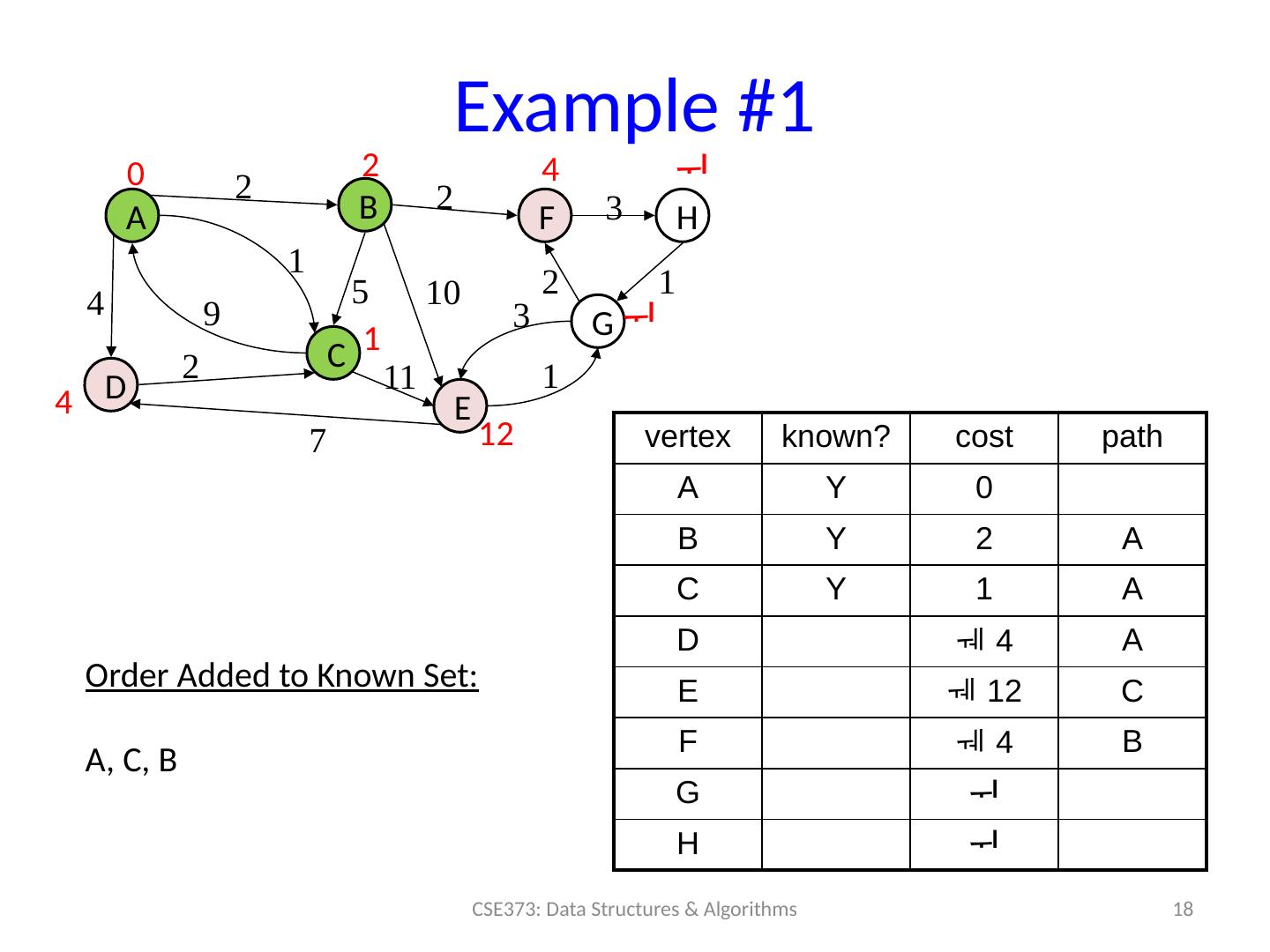
18 .Example #1 18 CSE373: Data Structures & Algorithms A B D C F H E G 0 2 4 4 1 12 2 2 3 1 10 2 3 1 11 7 1 9 2 4 vertex known? cost path A Y 0 B Y 2 A C Y 1 A D 4 A E 12 C F 4 B G H 5 Order Added to Known Set : A, C, B
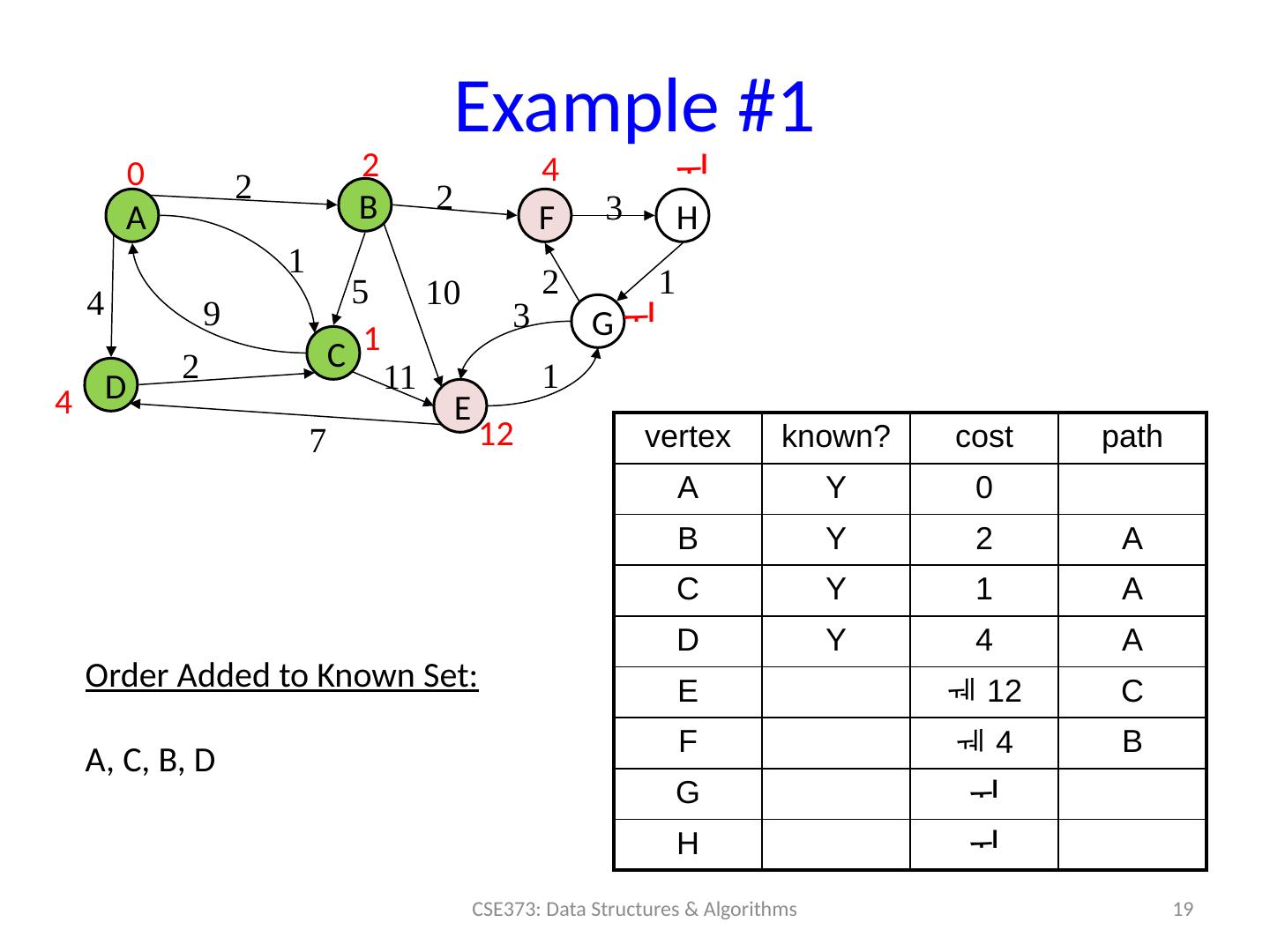
19 .Example #1 19 CSE373: Data Structures & Algorithms A B D C F H E G 0 2 4 4 1 12 2 2 3 1 10 2 3 1 11 7 1 9 2 4 vertex known? cost path A Y 0 B Y 2 A C Y 1 A D Y 4 A E 12 C F 4 B G H 5 Order Added to Known Set : A, C, B, D
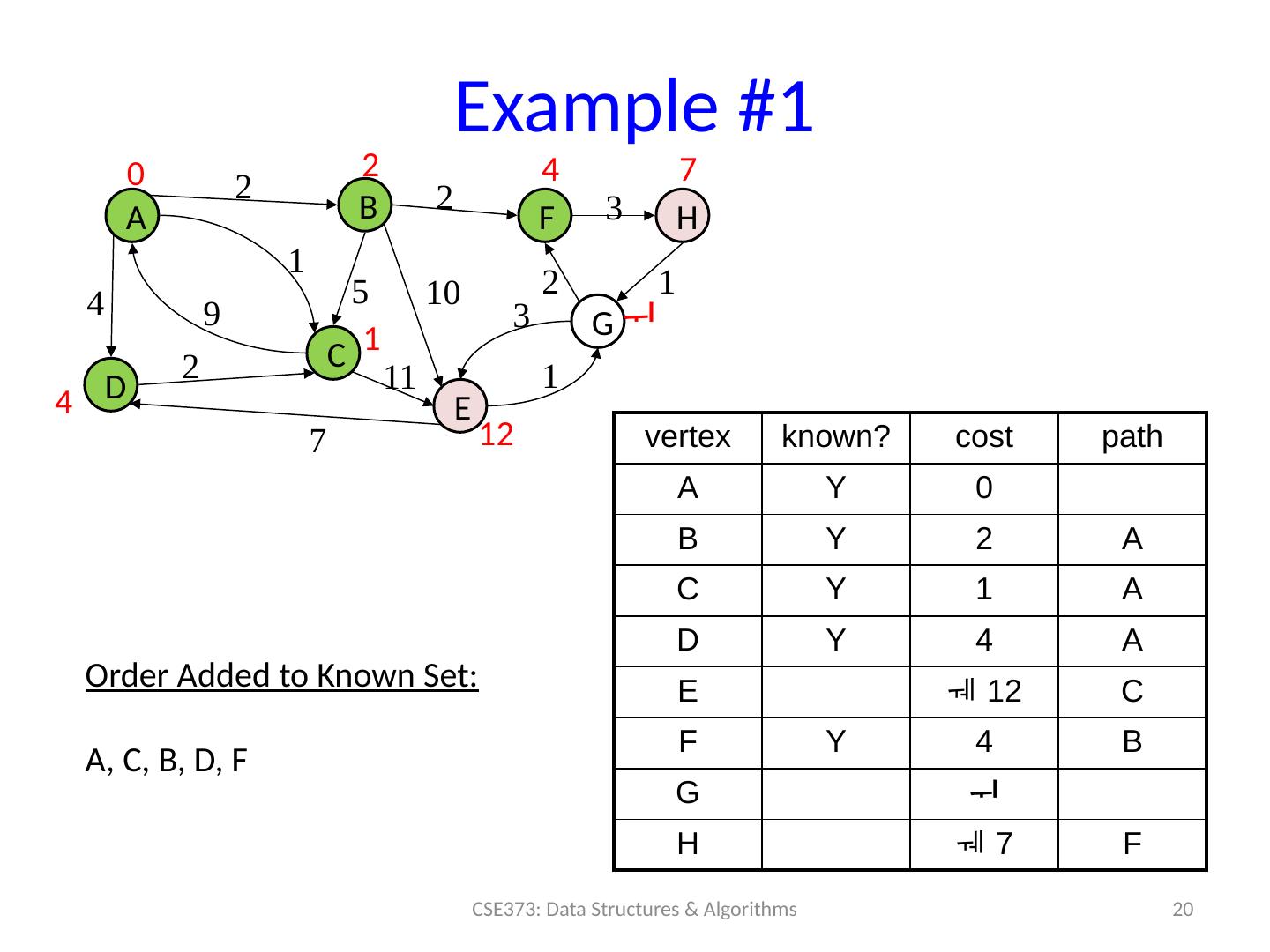
20 .Example #1 20 CSE373: Data Structures & Algorithms A B D C F H E G 0 2 4 7 4 1 12 2 2 3 1 10 2 3 1 11 7 1 9 2 4 vertex known? cost path A Y 0 B Y 2 A C Y 1 A D Y 4 A E 12 C F Y 4 B G H 7 F 5 Order Added to Known Set : A, C, B, D, F
21 .Example #1 21 CSE373: Data Structures & Algorithms A B D C F H E G 0 2 4 7 4 1 12 8 2 2 3 1 10 2 3 1 11 7 1 9 2 4 vertex known? cost path A Y 0 B Y 2 A C Y 1 A D Y 4 A E 12 C F Y 4 B G 8 H H Y 7 F 5 Order Added to Known Set : A, C, B, D, F, H
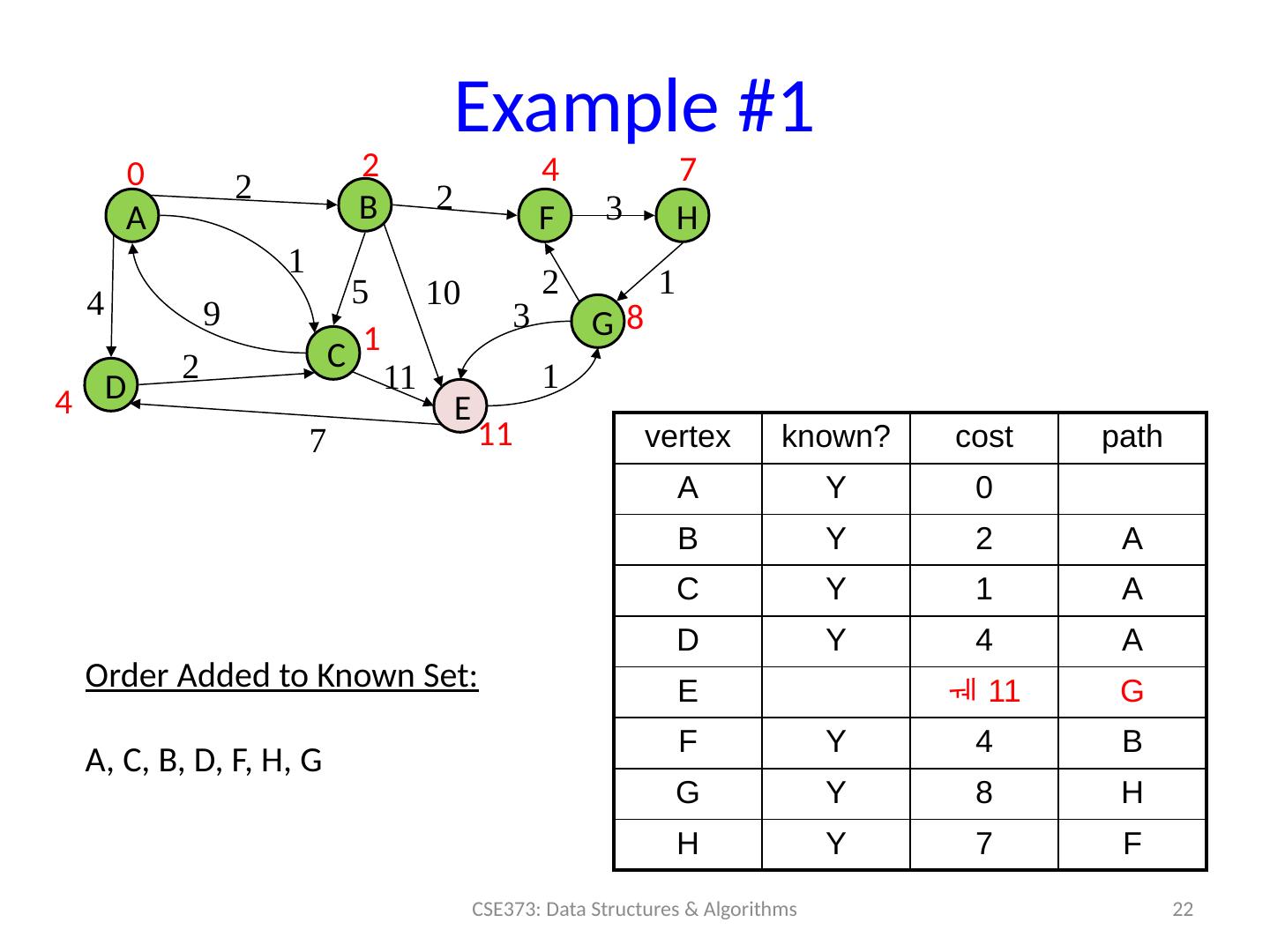
22 .Example #1 22 CSE373: Data Structures & Algorithms A B D C F H E G 0 2 4 7 4 1 11 8 2 2 3 1 10 2 3 1 11 7 1 9 2 4 vertex known? cost path A Y 0 B Y 2 A C Y 1 A D Y 4 A E 11 G F Y 4 B G Y 8 H H Y 7 F 5 Order Added to Known Set : A, C, B, D, F, H, G
23 .Example #1 23 CSE373: Data Structures & Algorithms A B D C F H E G 0 2 4 7 4 1 11 8 2 2 3 1 10 2 3 1 11 7 1 9 2 4 vertex known? cost path A Y 0 B Y 2 A C Y 1 A D Y 4 A E Y 11 G F Y 4 B G Y 8 H H Y 7 F 5 Order Added to Known Set : A, C, B, D, F, H, G, E
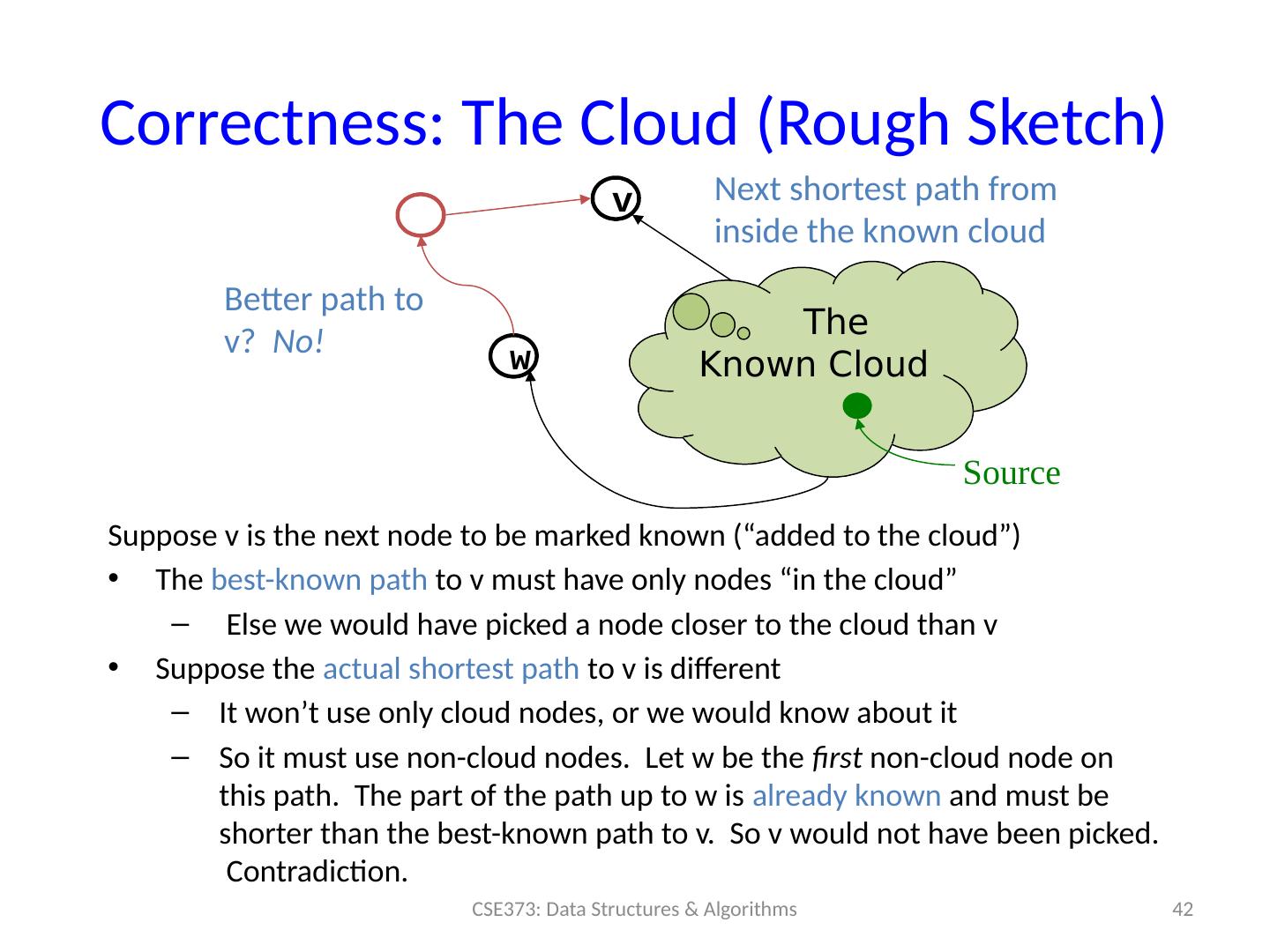
24 .Features When a vertex is marked known, the cost of the shortest path to that node is known The path is also known by following back-pointers While a vertex is still not known, another shorter path to it might still be found Note: The “Order Added to Known Set” is not important A detail about how the algorithm works (client doesn’t care) Not used by the algorithm (implementation doesn’t care) It is sorted by path-cost, resolving ties in some way Helps give intuition of why the algorithm works CSE373: Data Structures & Algorithms 24
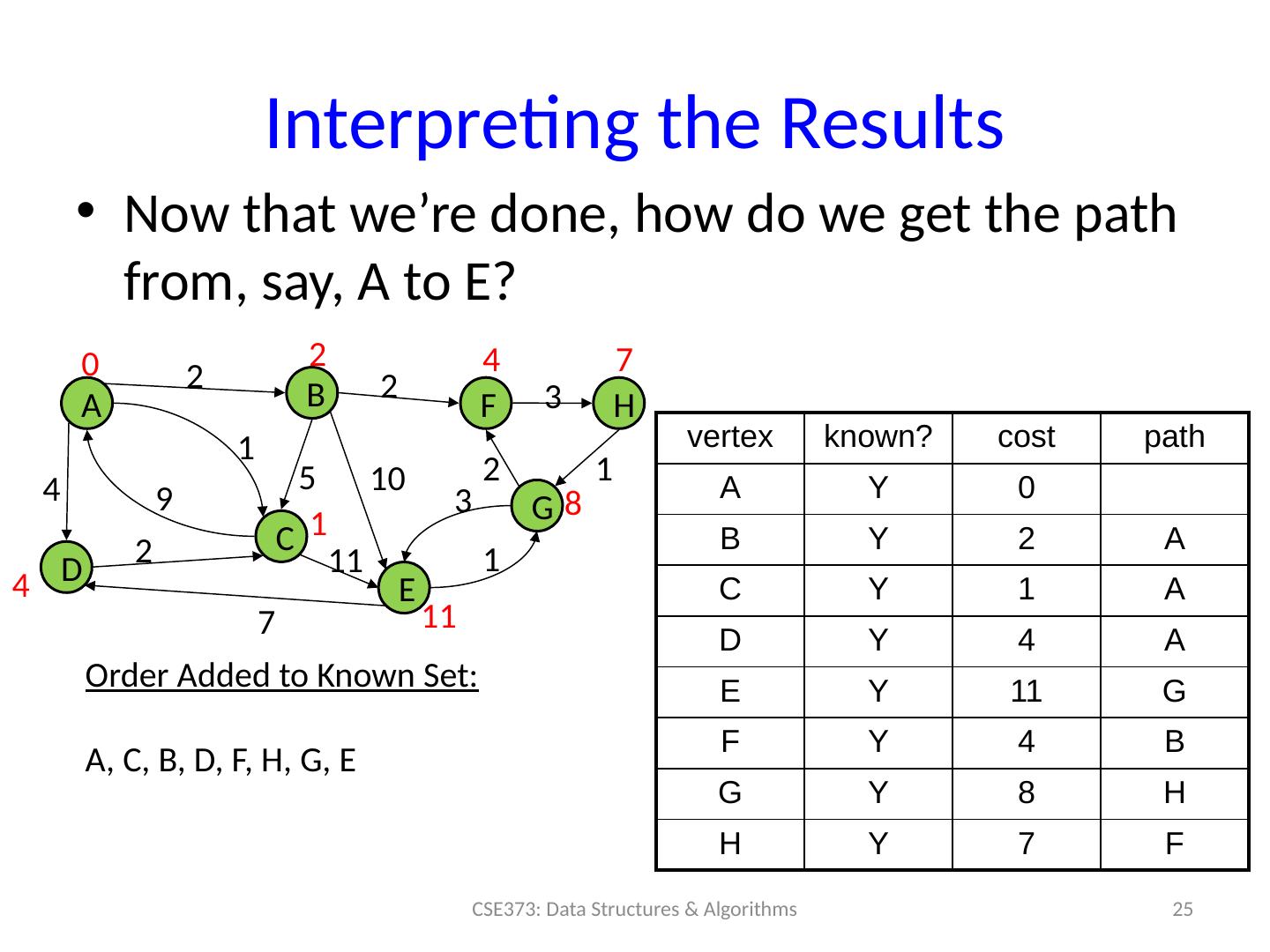
25 .Interpreting the Results Now that we’re done, how do we get the path from, say, A to E? A B D C F H E G 0 2 4 7 4 1 11 8 2 2 3 1 10 2 3 1 11 7 1 9 2 4 5 vertex known? cost path A Y 0 B Y 2 A C Y 1 A D Y 4 A E Y 11 G F Y 4 B G Y 8 H H Y 7 F Order Added to Known Set : A, C, B, D, F, H, G, E CSE373: Data Structures & Algorithms 25
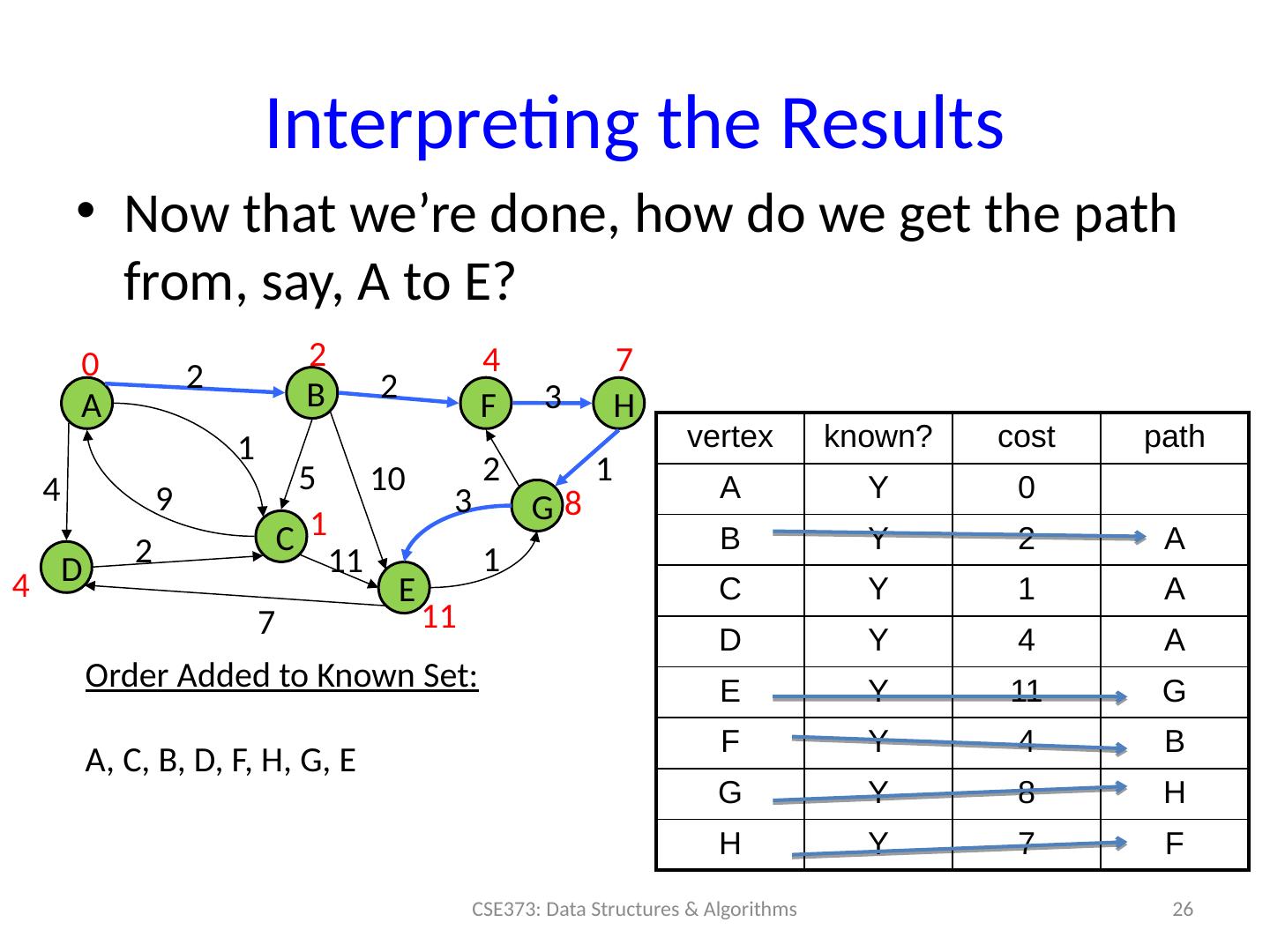
26 .Interpreting the Results Now that we’re done, how do we get the path from, say, A to E? A B D C F H E G 0 2 4 7 4 1 11 8 2 2 3 1 10 2 3 1 11 7 1 9 2 4 5 vertex known? cost path A Y 0 B Y 2 A C Y 1 A D Y 4 A E Y 11 G F Y 4 B G Y 8 H H Y 7 F Order Added to Known Set : A, C, B, D, F, H, G, E CSE373: Data Structures & Algorithms 26
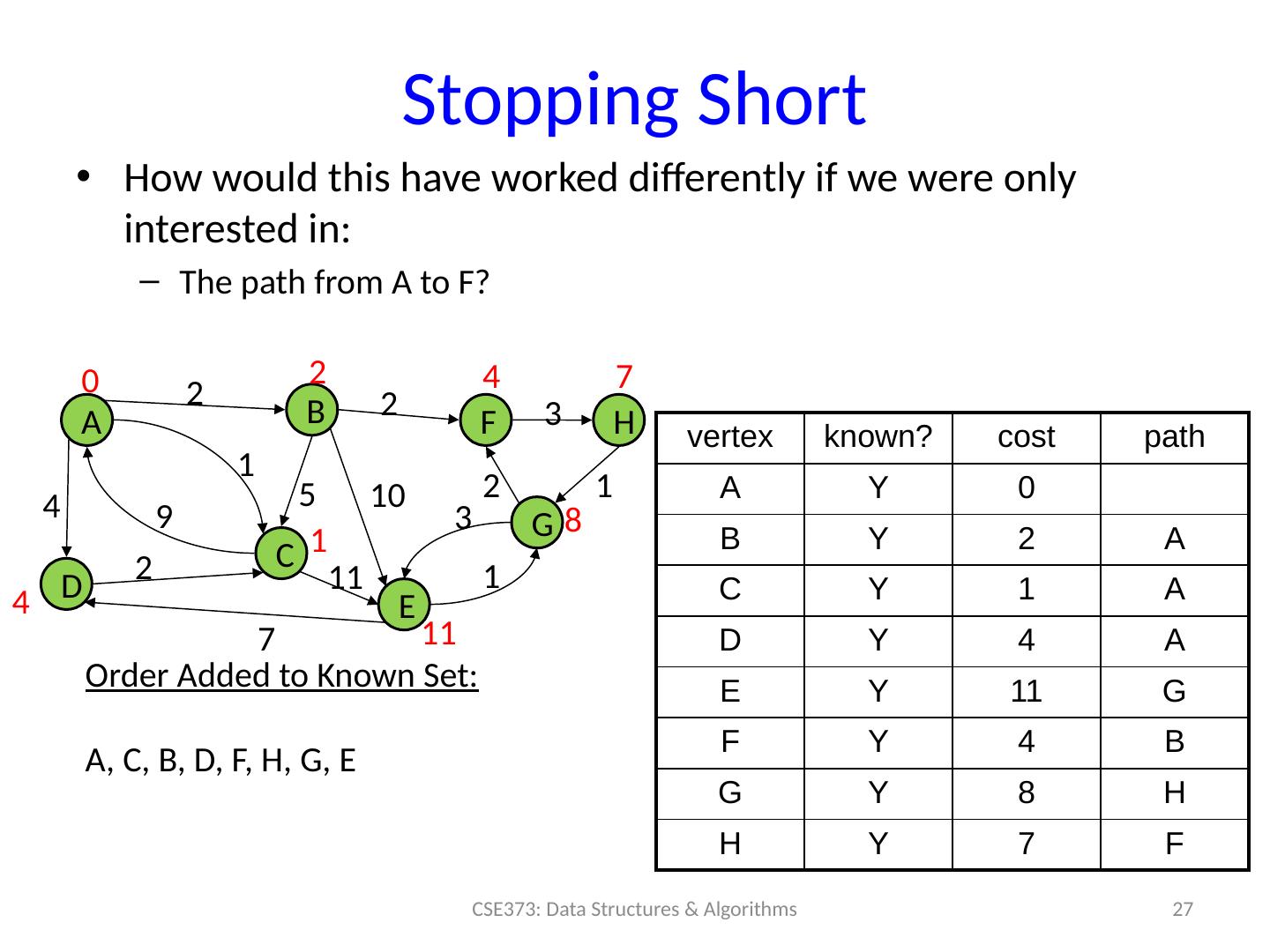
27 .Stopping Short How would this have worked differently if we were only interested in: The path from A to F? A B D C F H E G 0 2 4 7 4 1 11 8 2 2 3 1 10 2 3 1 11 7 1 9 2 4 5 vertex known? cost path A Y 0 B Y 2 A C Y 1 A D Y 4 A E Y 11 G F Y 4 B G Y 8 H H Y 7 F Order Added to Known Set : A, C, B, D, F, H, G, E CSE373: Data Structures & Algorithms 27
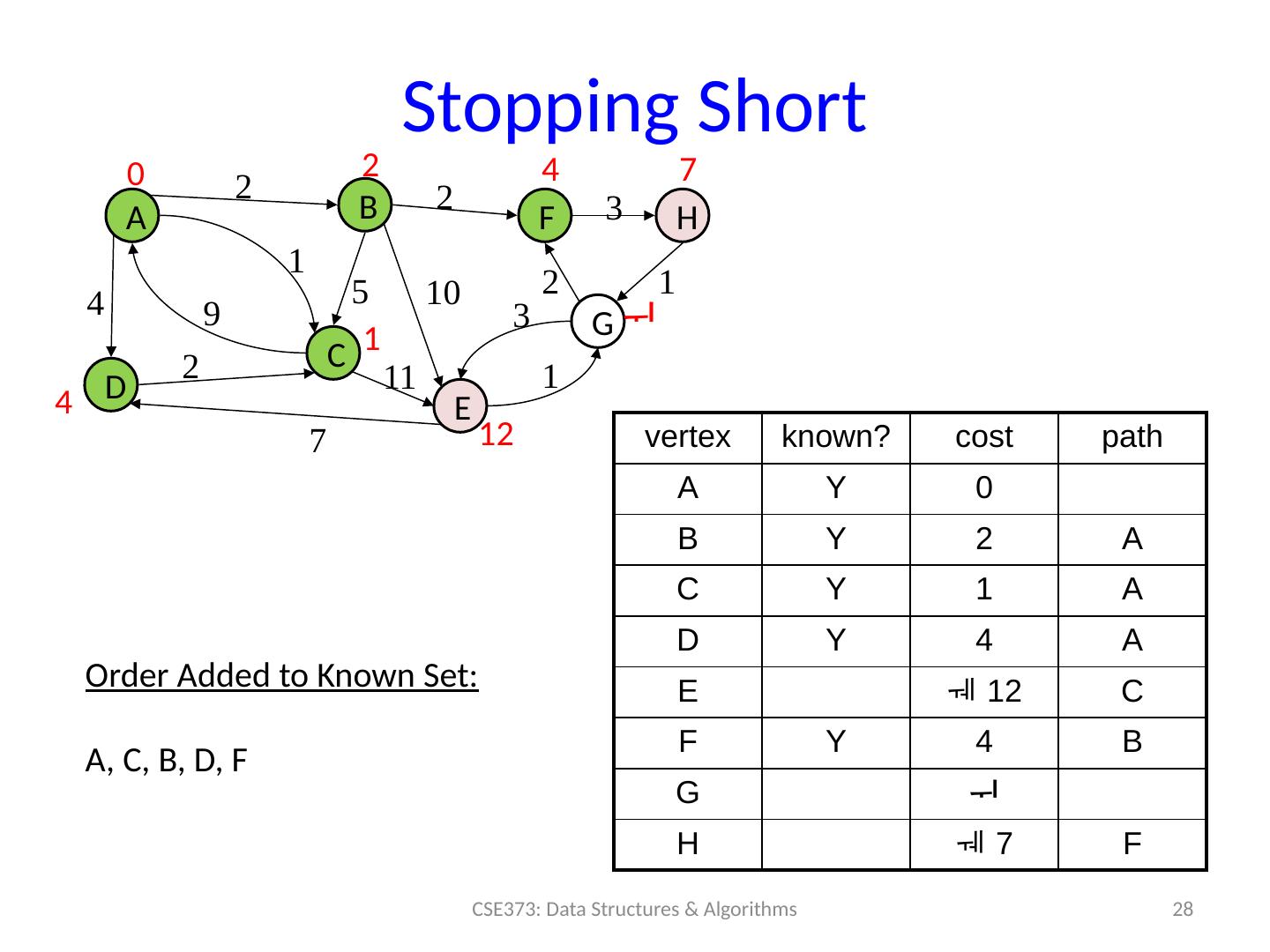
28 .Stopping Short 28 CSE373: Data Structures & Algorithms A B D C F H E G 0 2 4 7 4 1 12 2 2 3 1 10 2 3 1 11 7 1 9 2 4 vertex known? cost path A Y 0 B Y 2 A C Y 1 A D Y 4 A E 12 C F Y 4 B G H 7 F 5 Order Added to Known Set : A, C, B, D, F
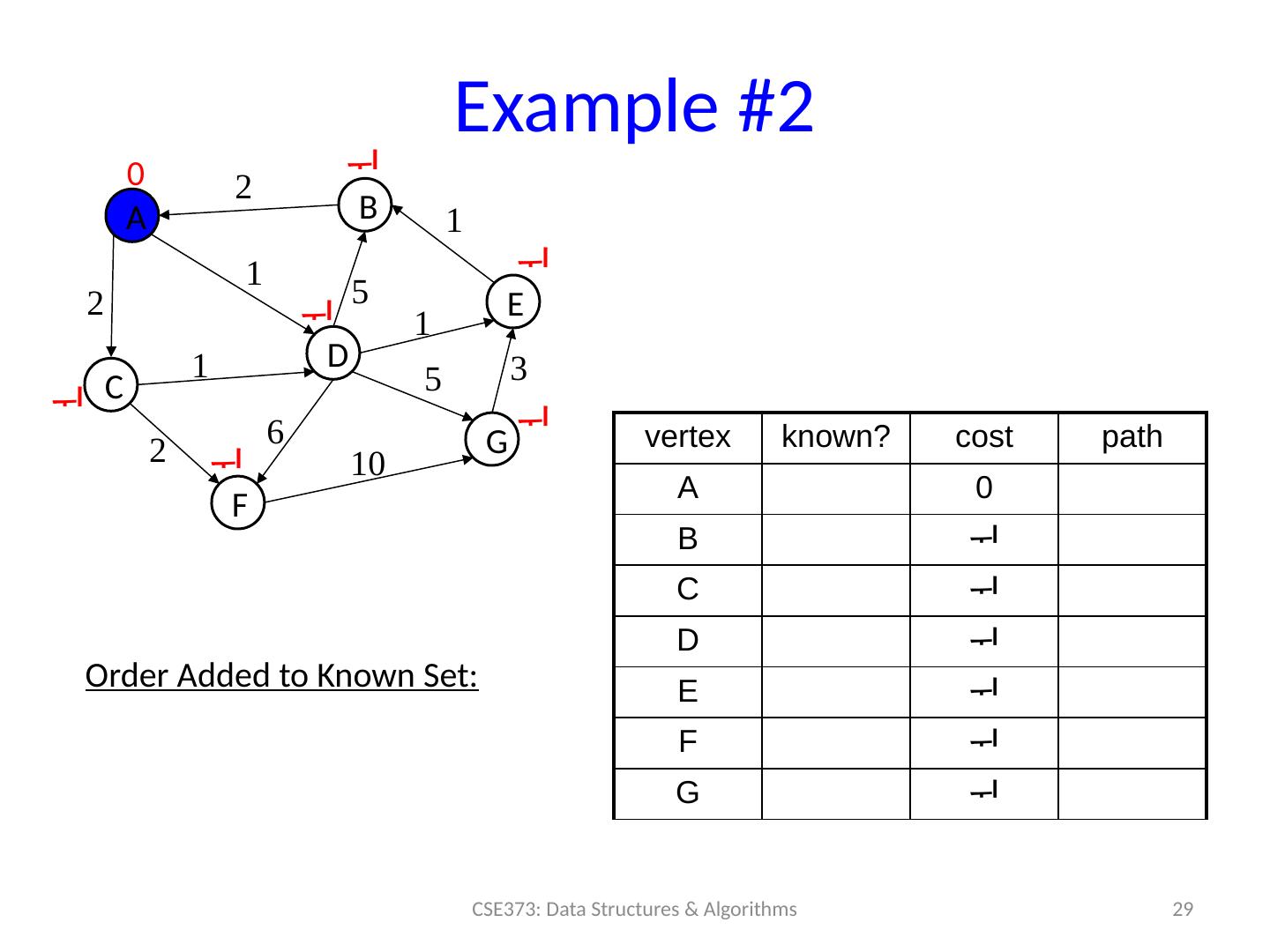
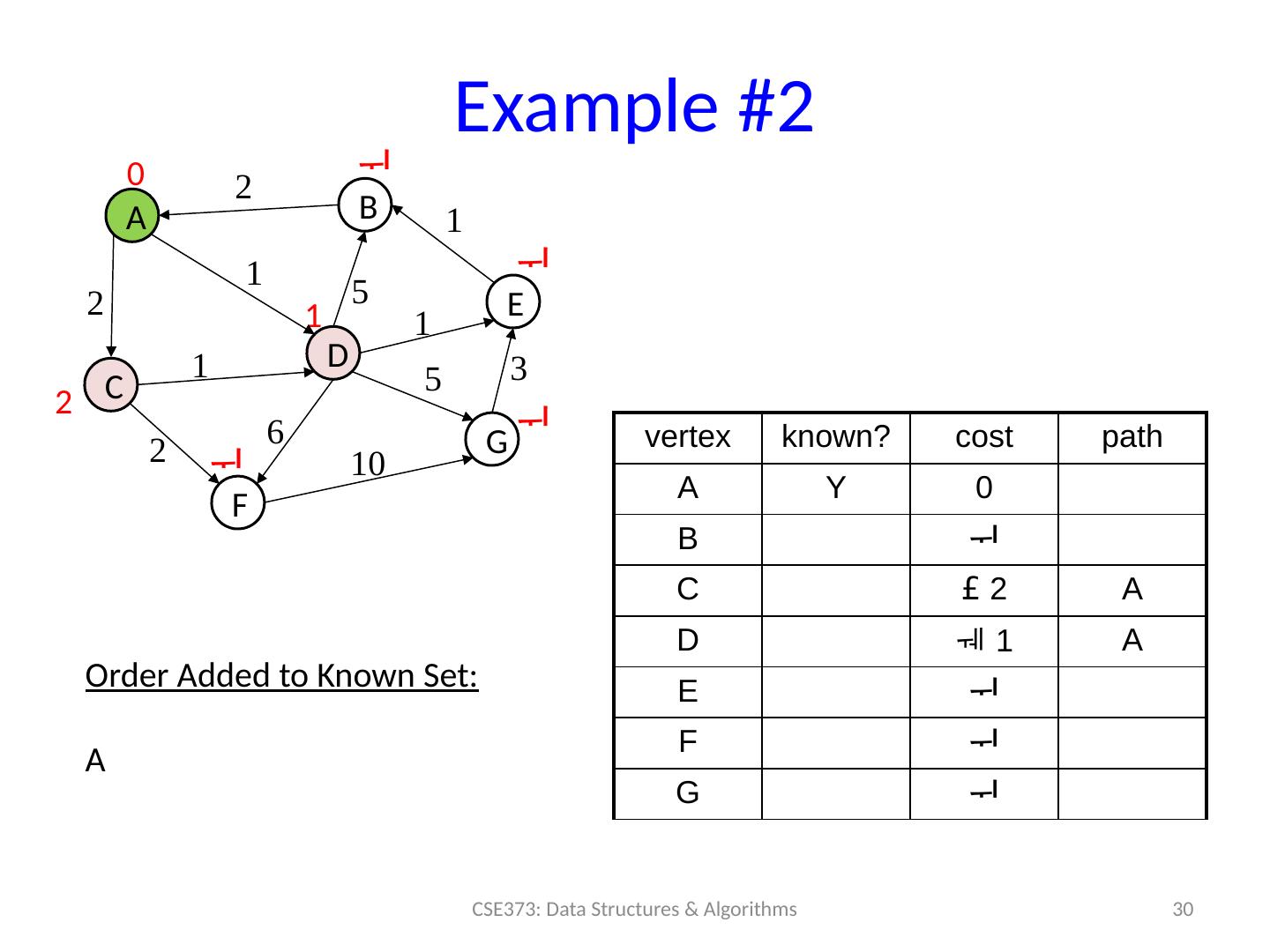
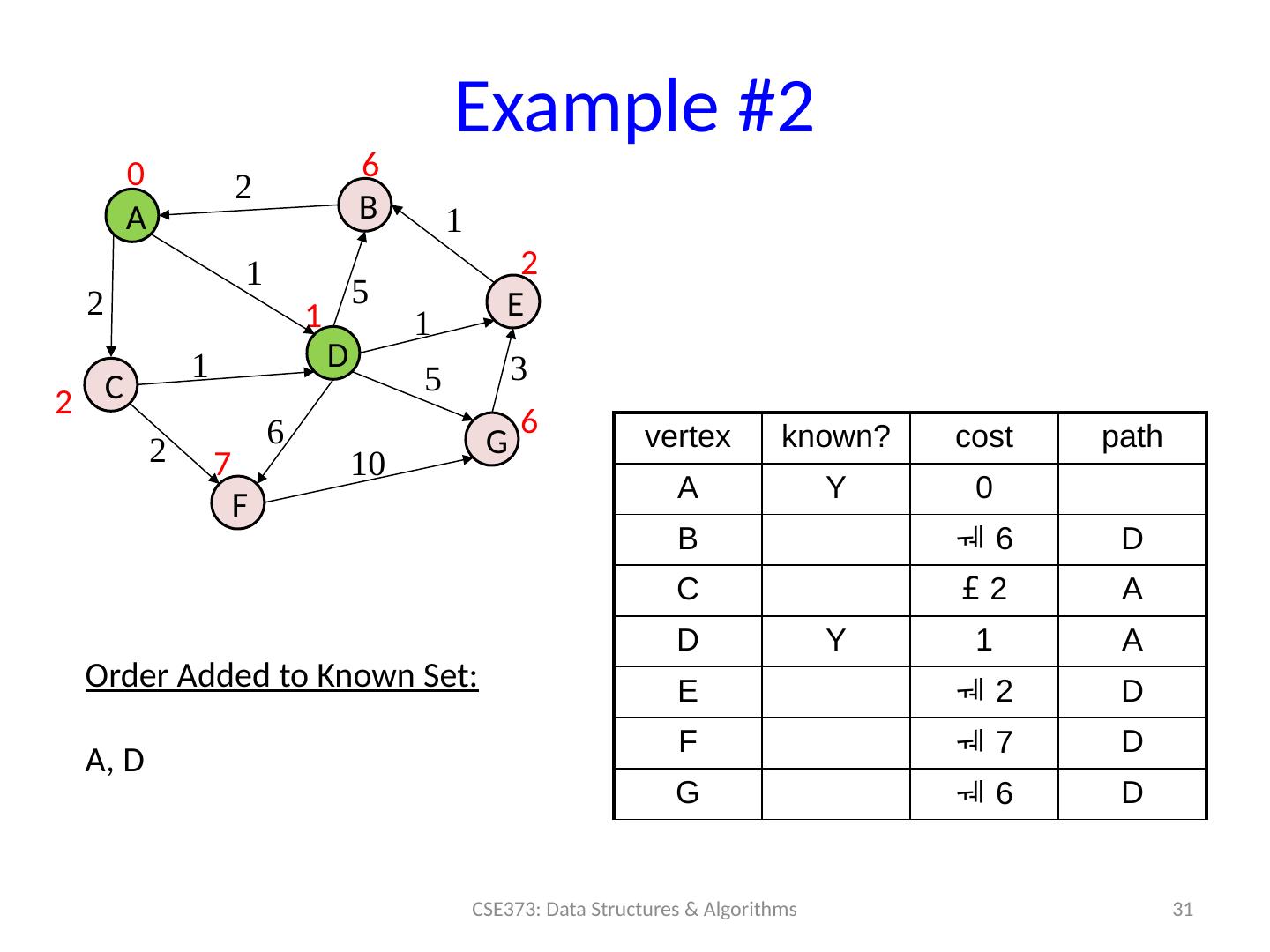
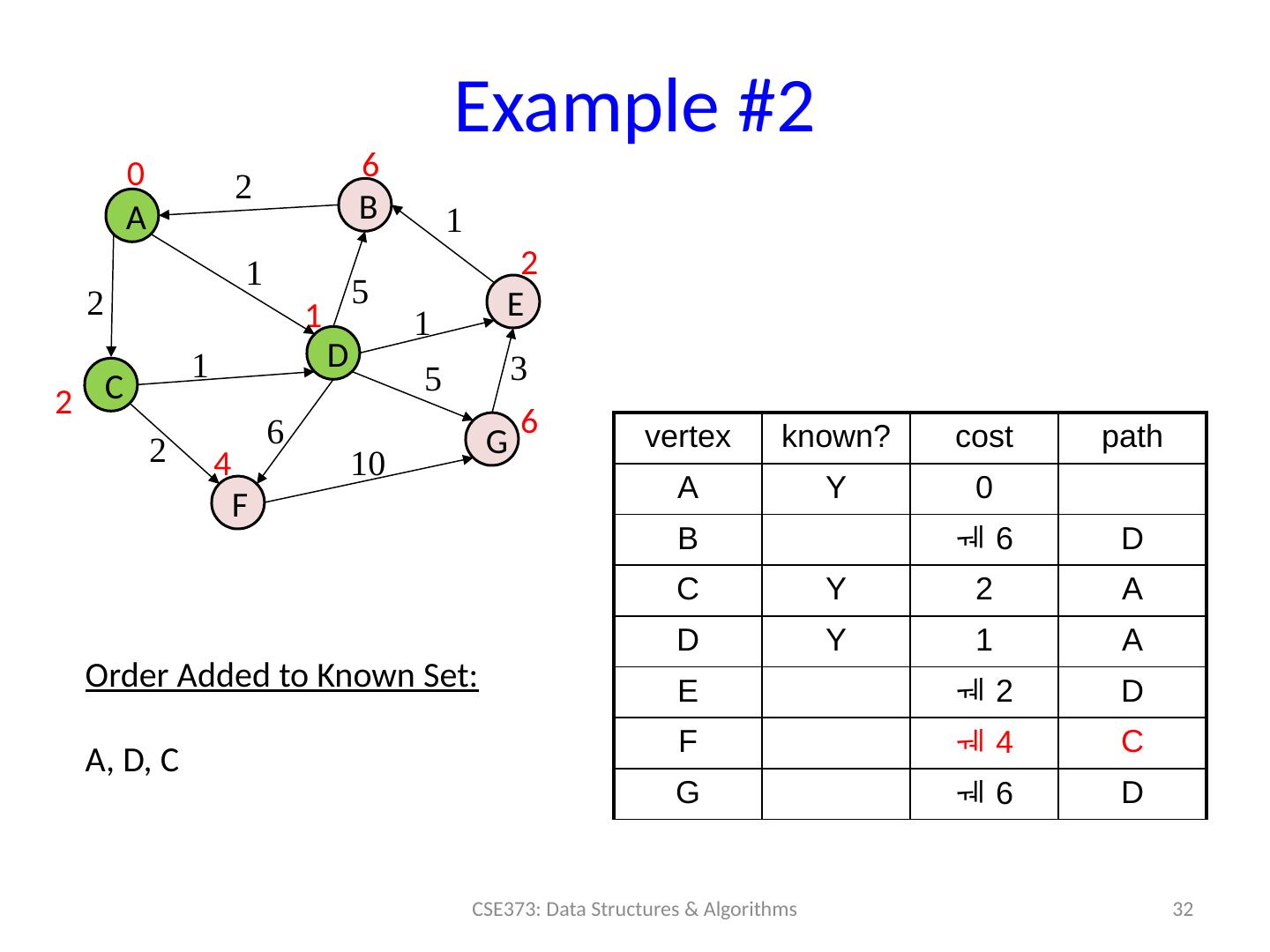
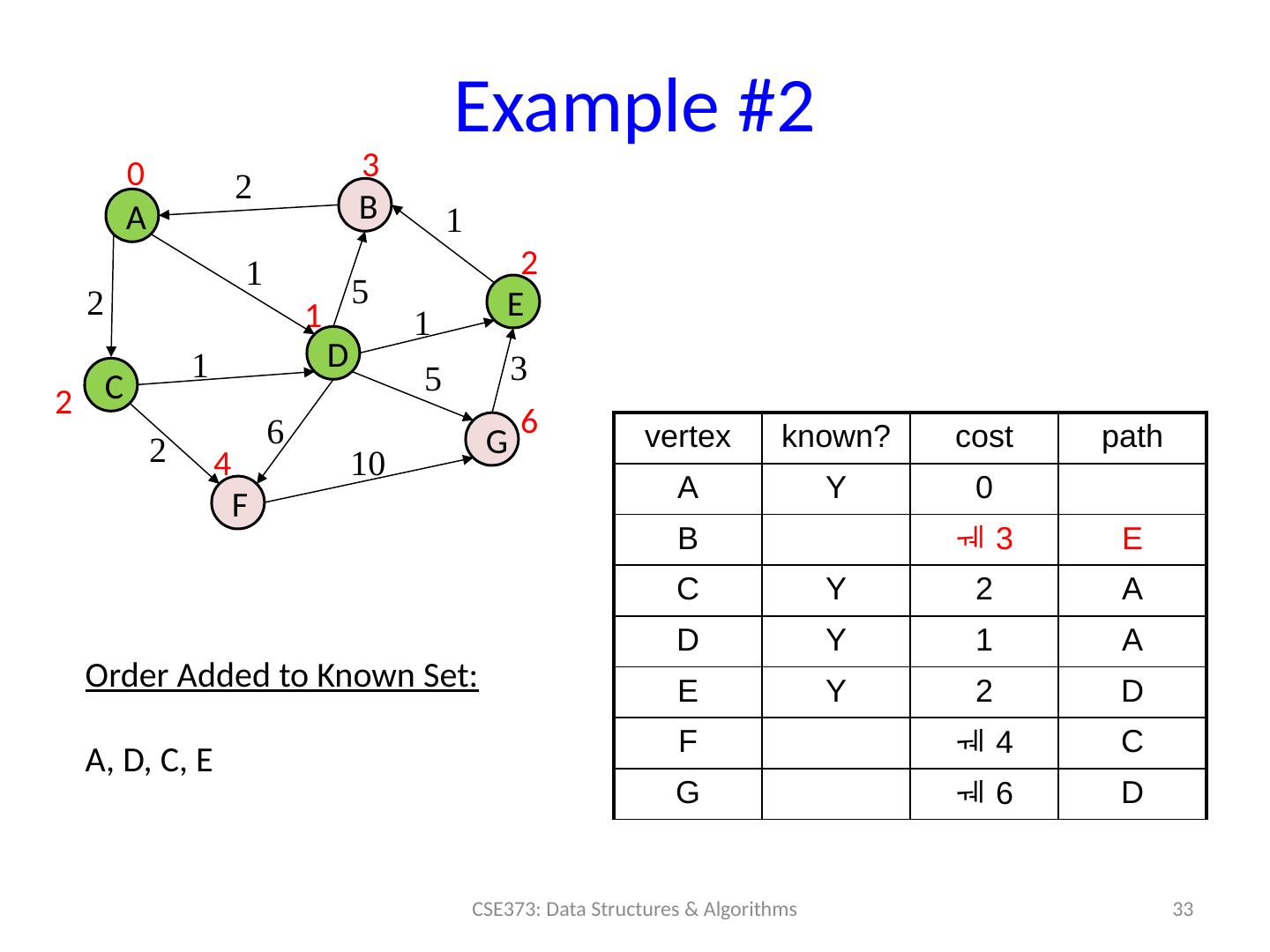
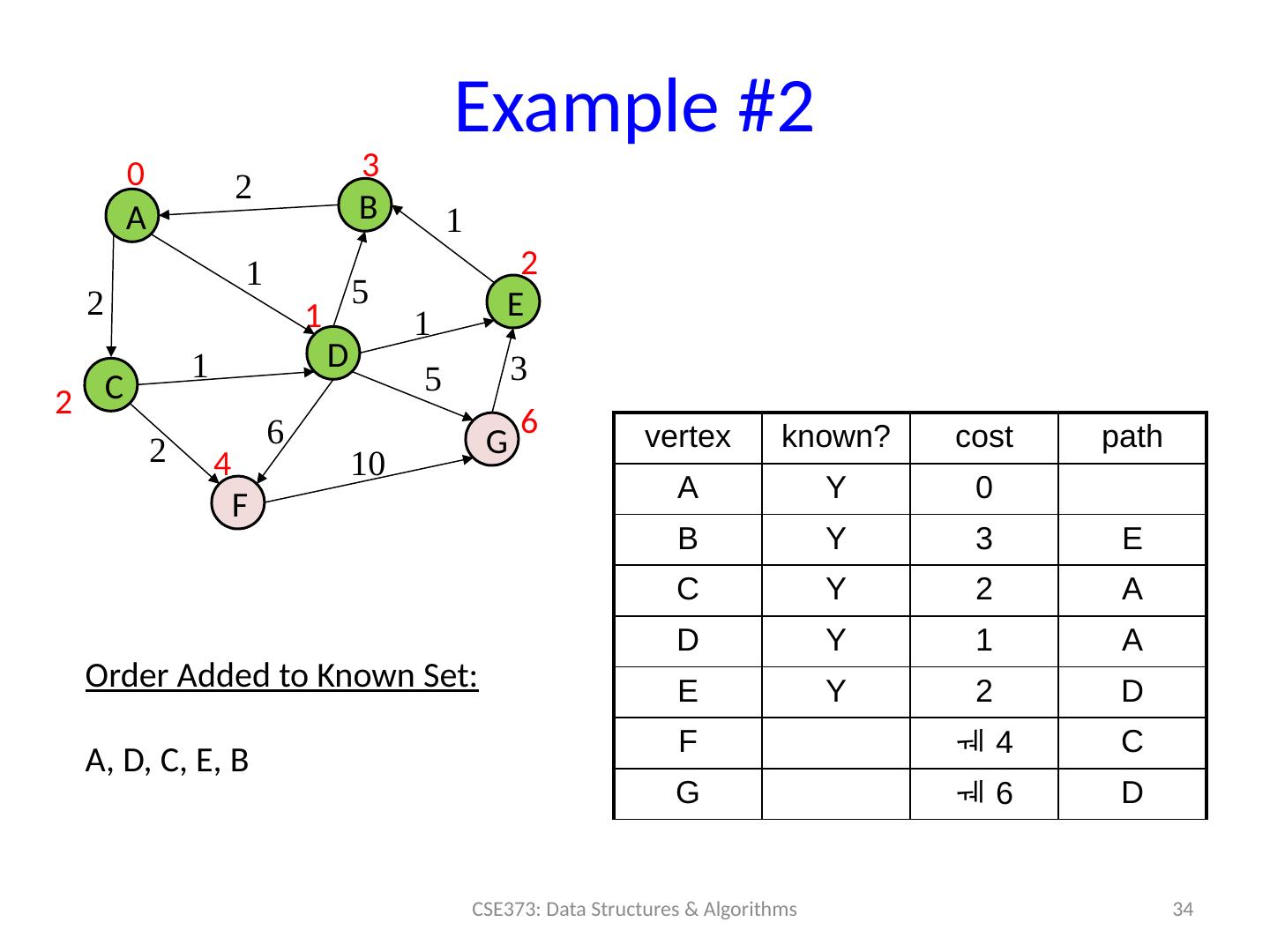
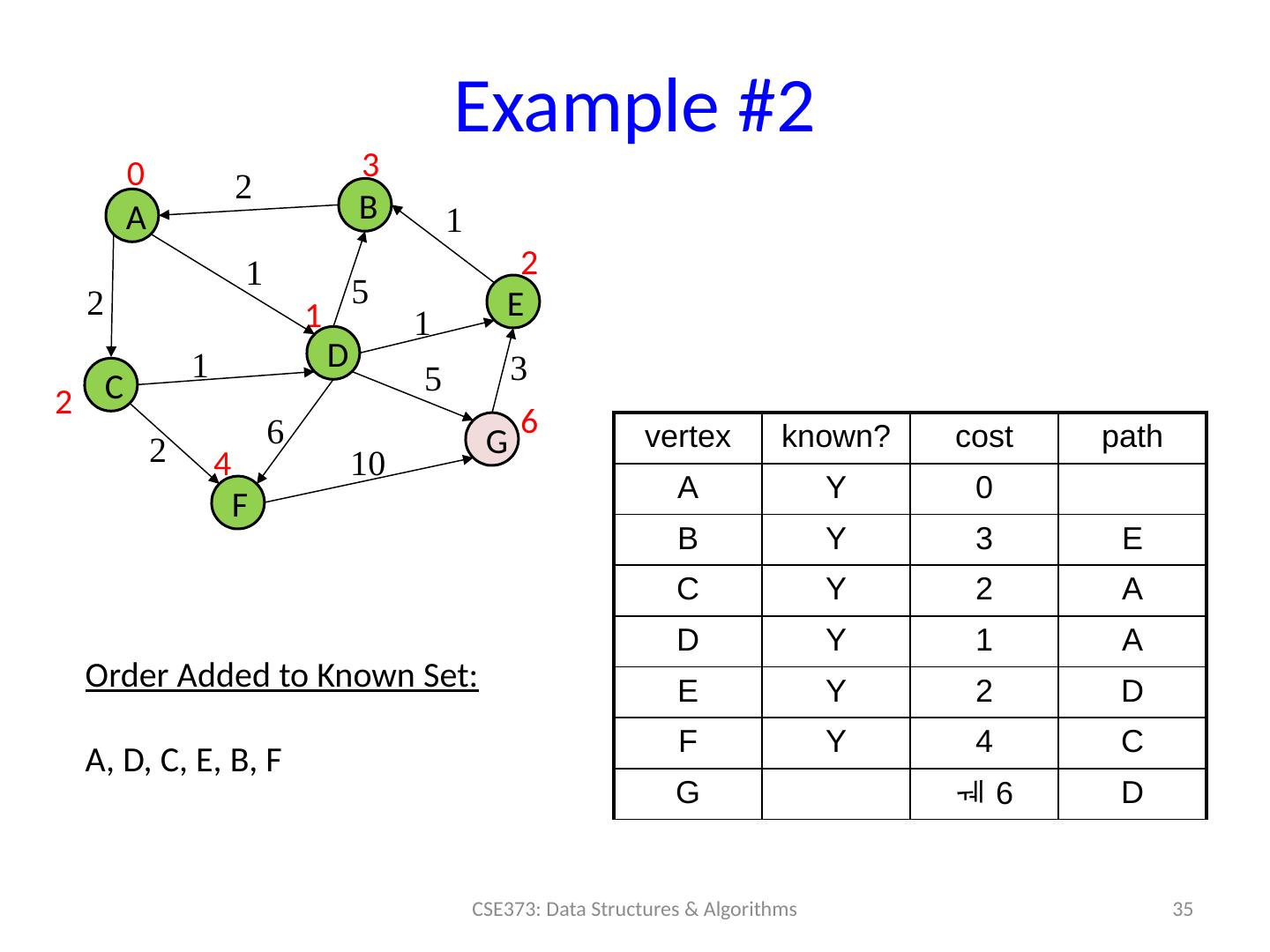
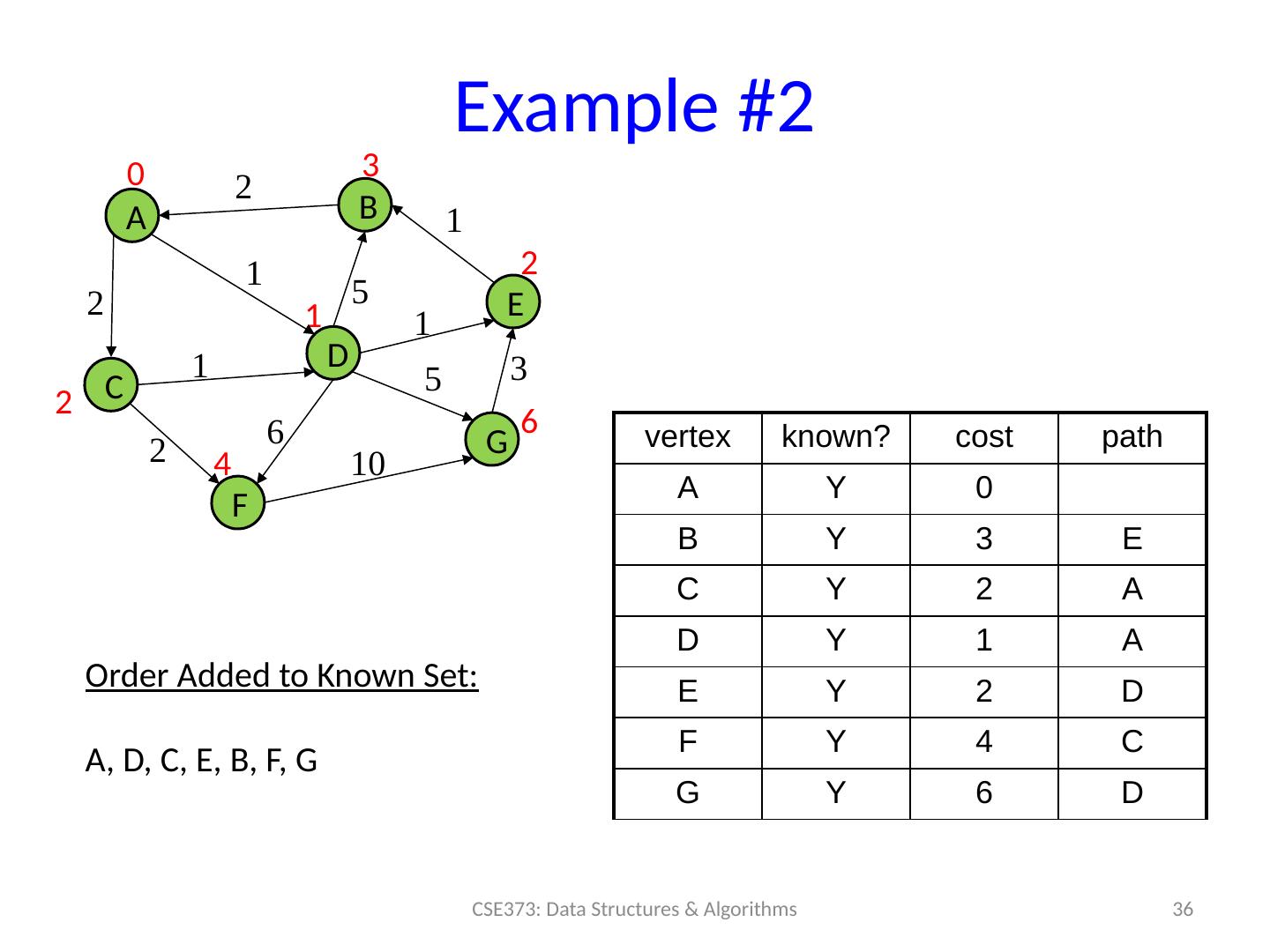
29 .Example #2 29 CSE373: Data Structures & Algorithms A B C D F E G 0 2 1 2 vertex known? cost path A 0 B C D E F G 5 1 1 1 2 6 5 3 10 Order Added to Known Set :