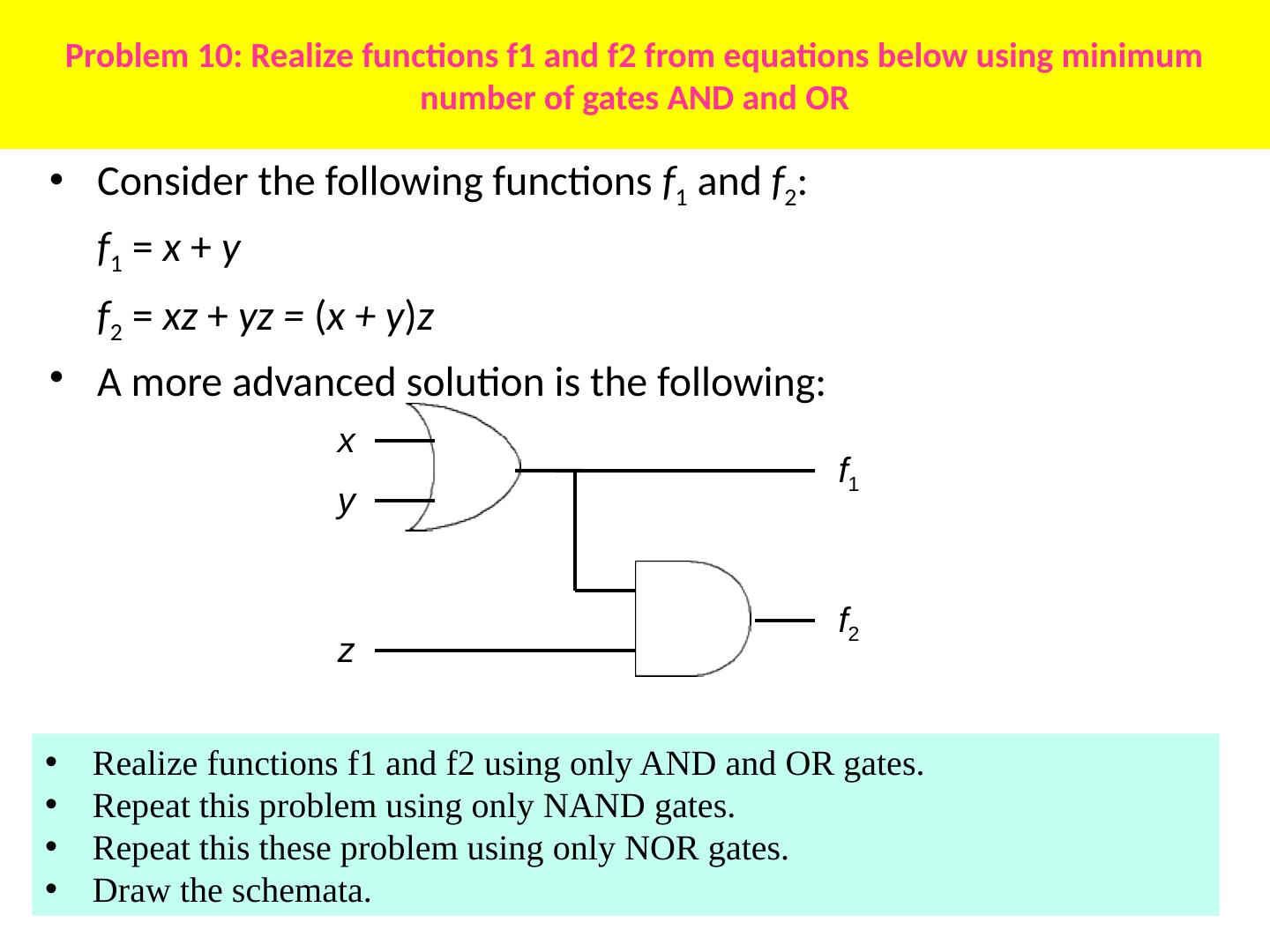
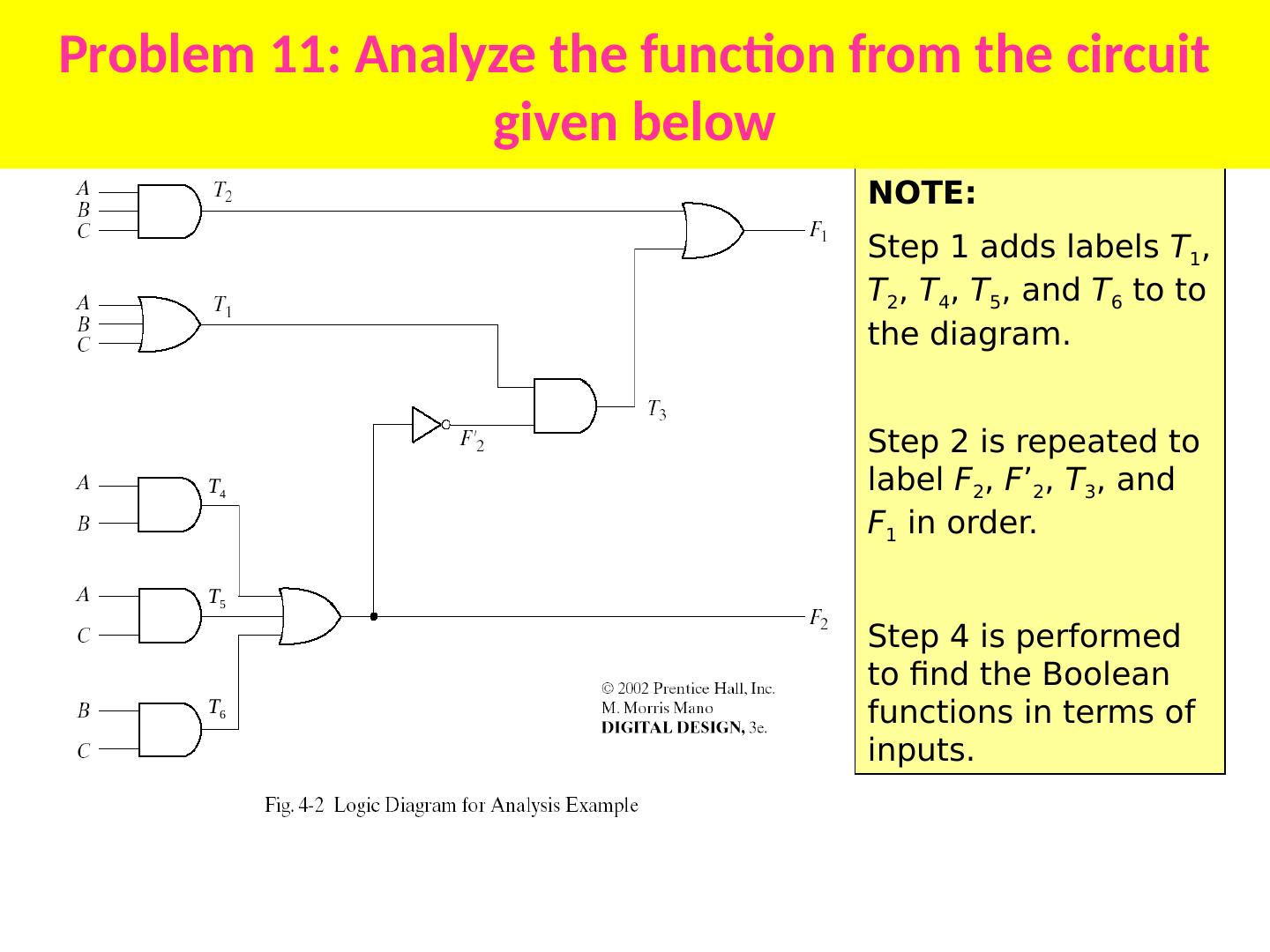
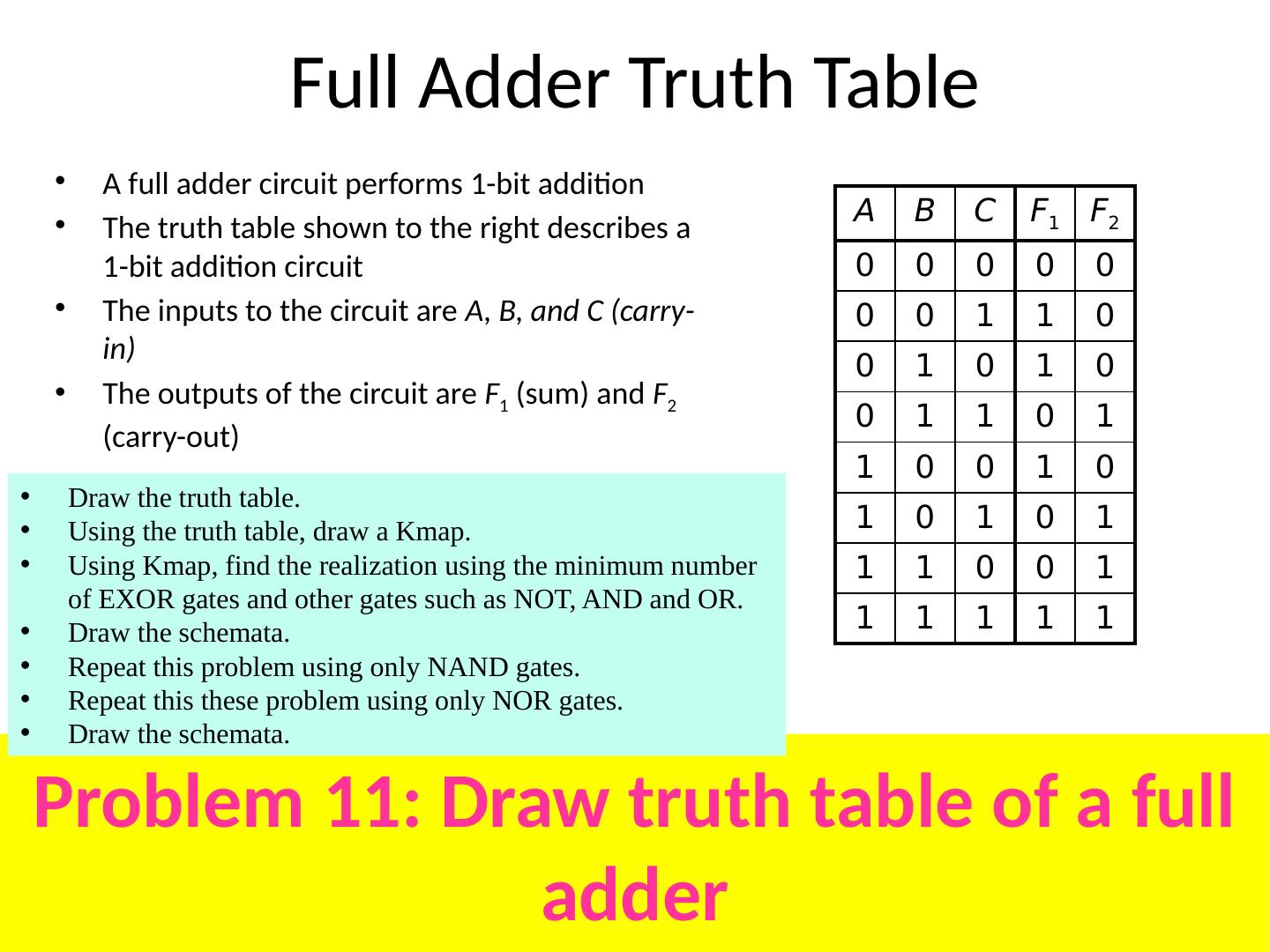
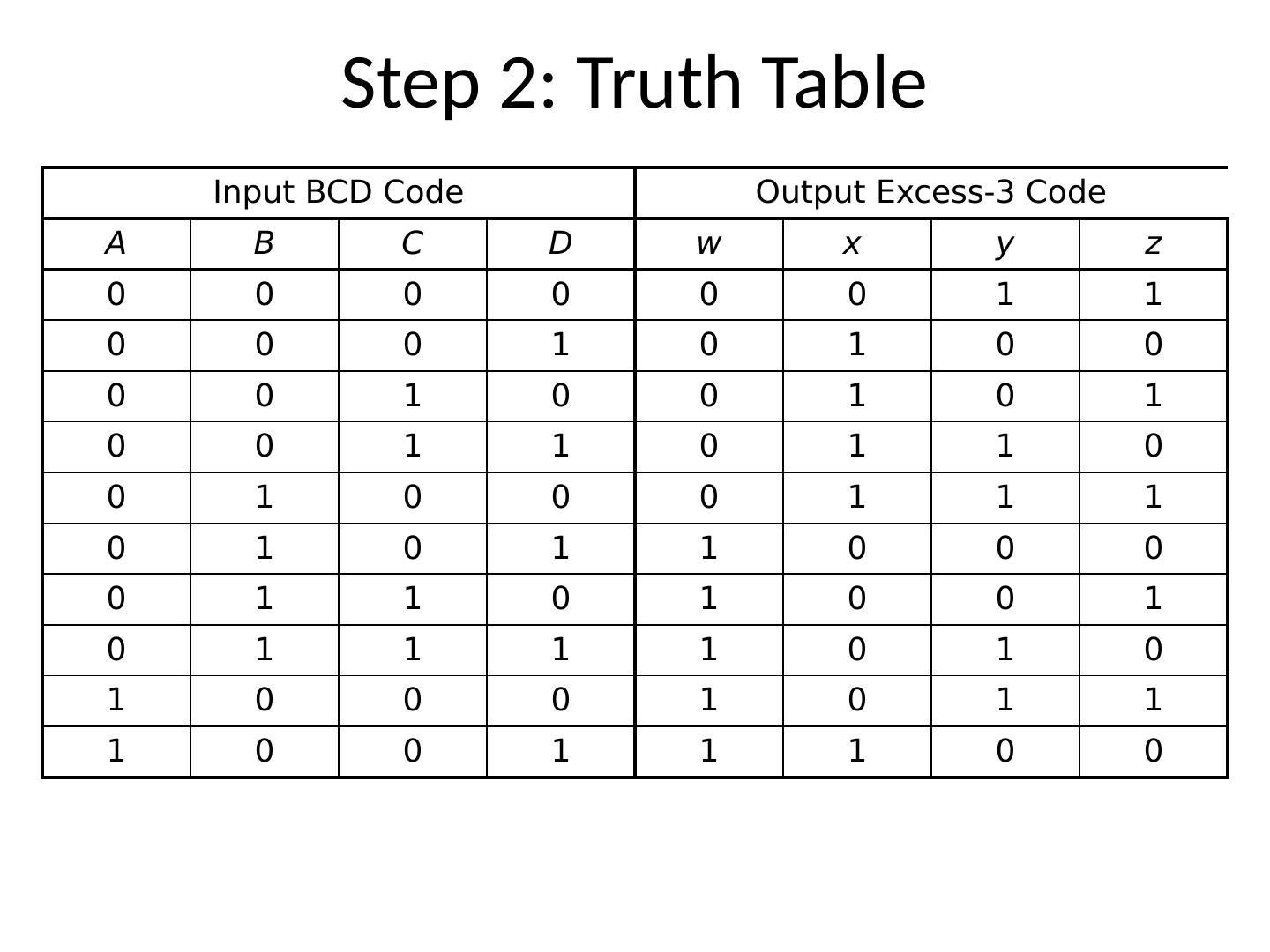
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
05 Boolean Equations and KMaps NN
展开查看详情
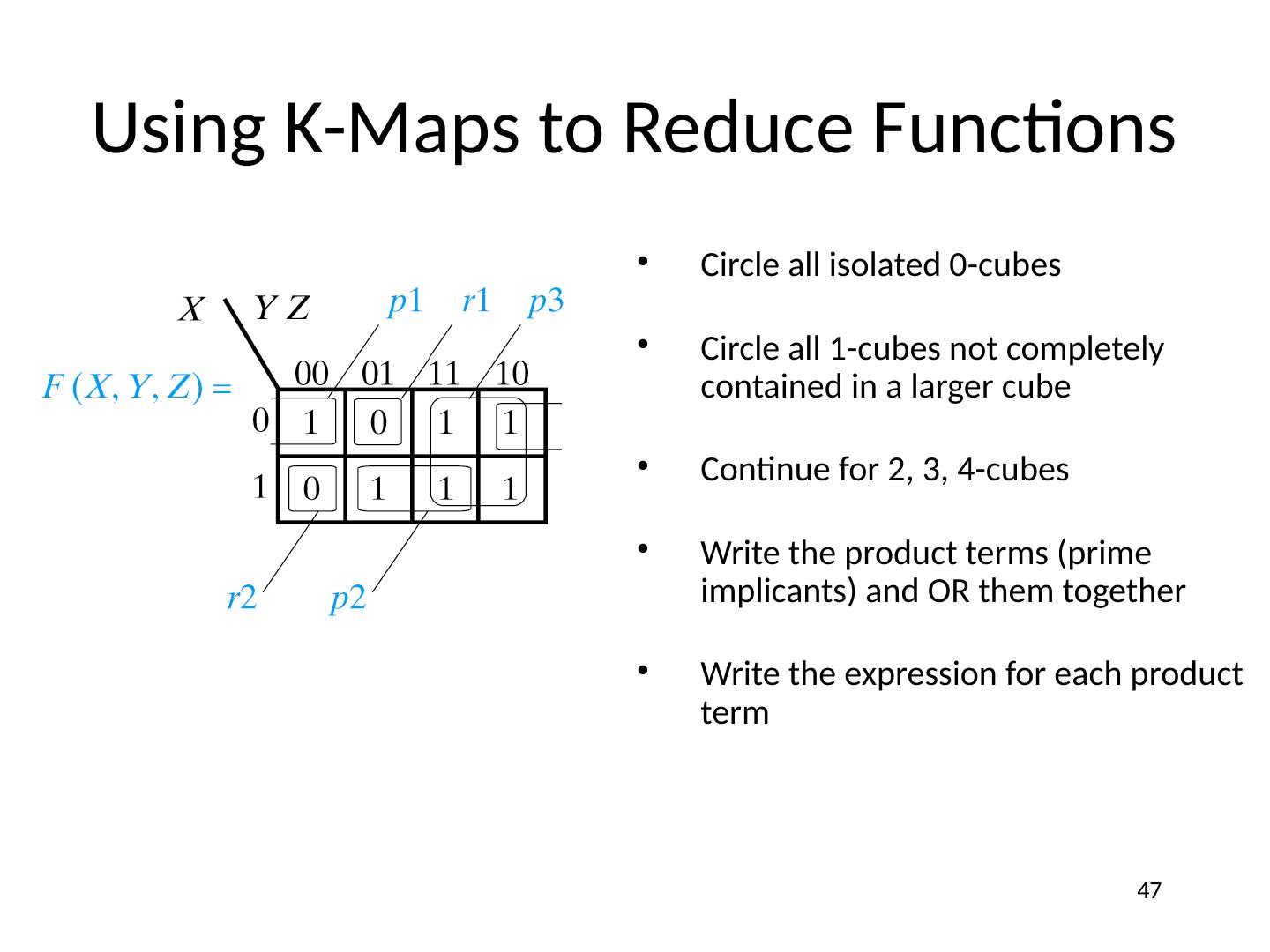
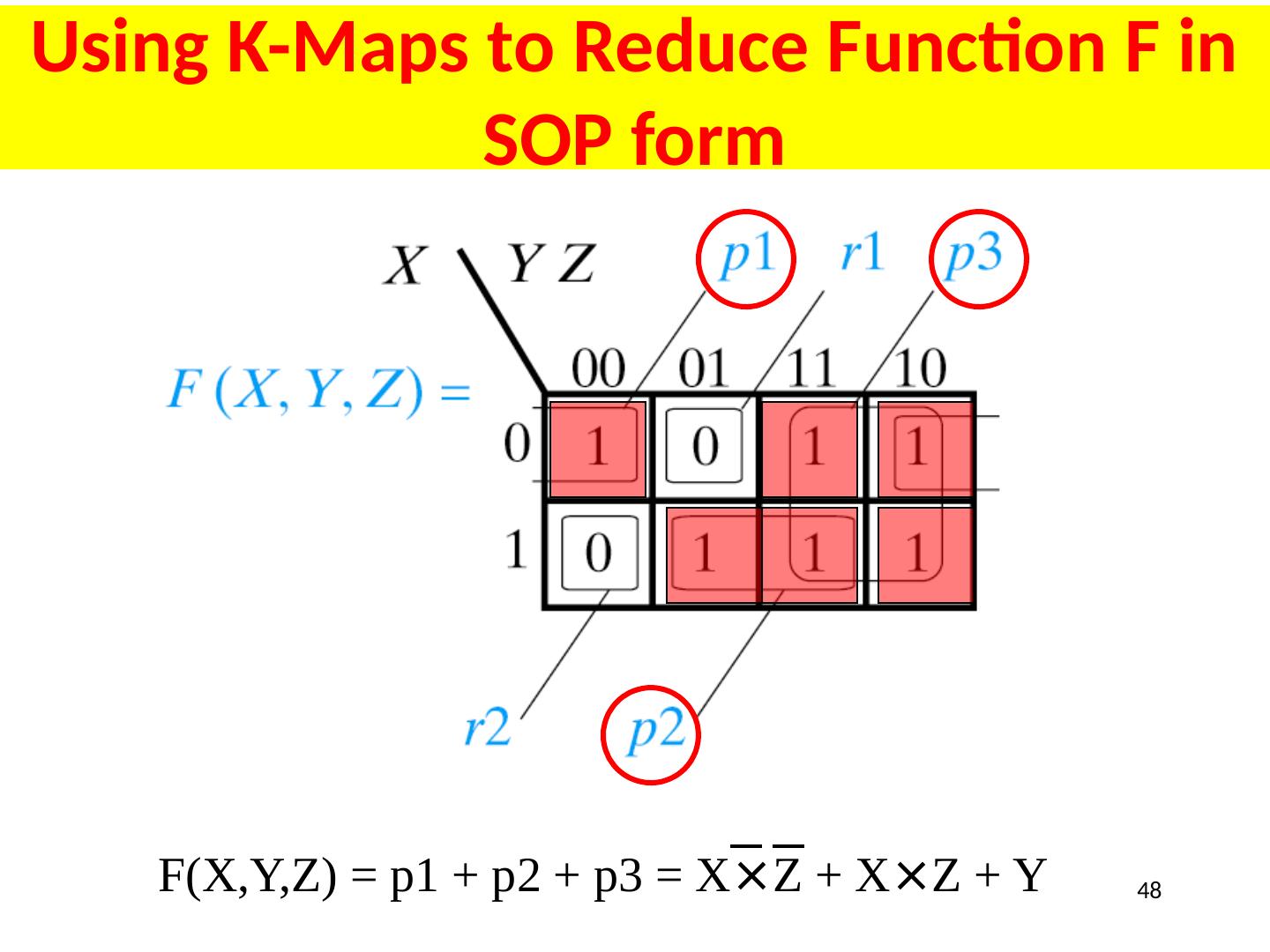
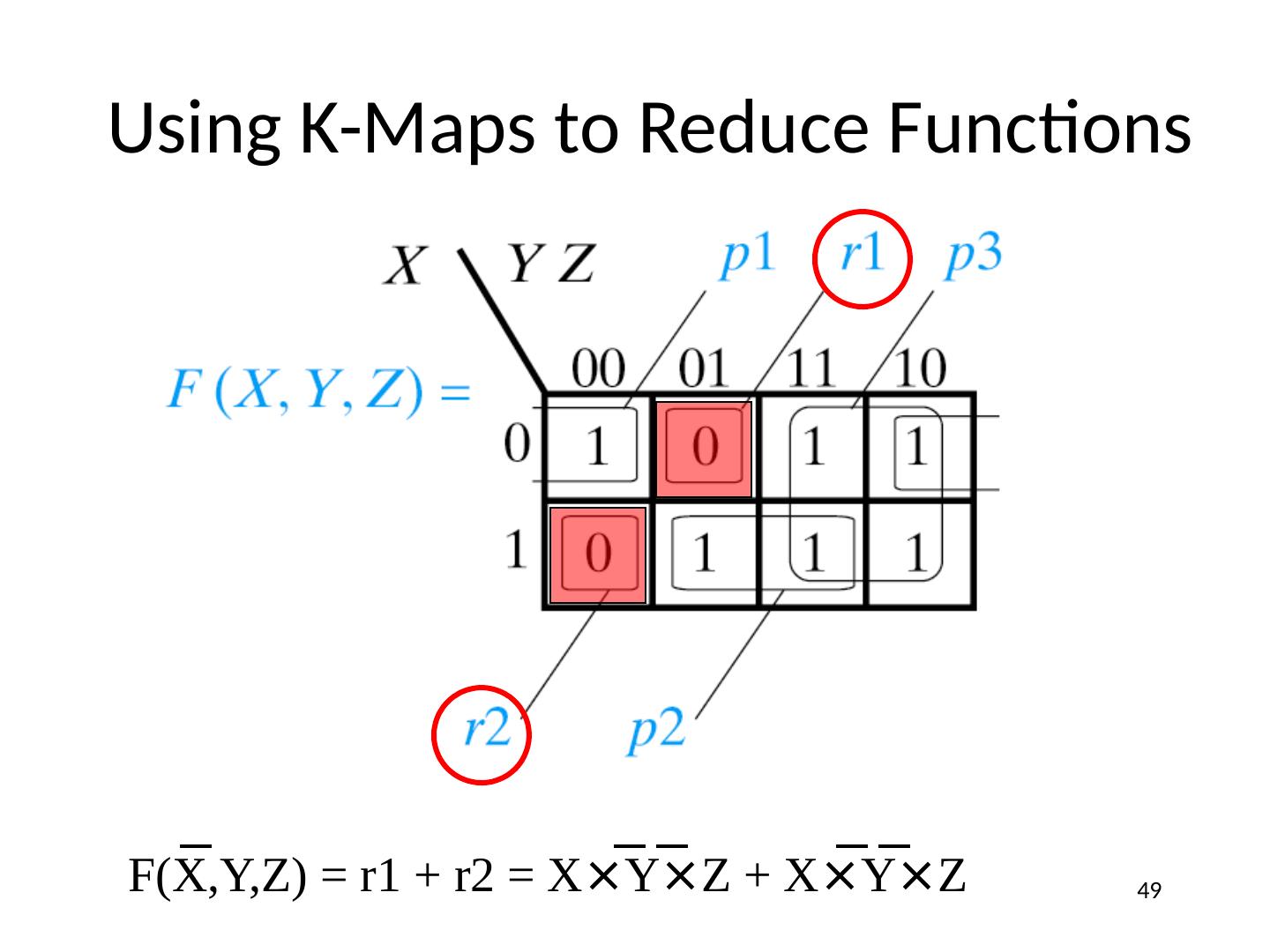
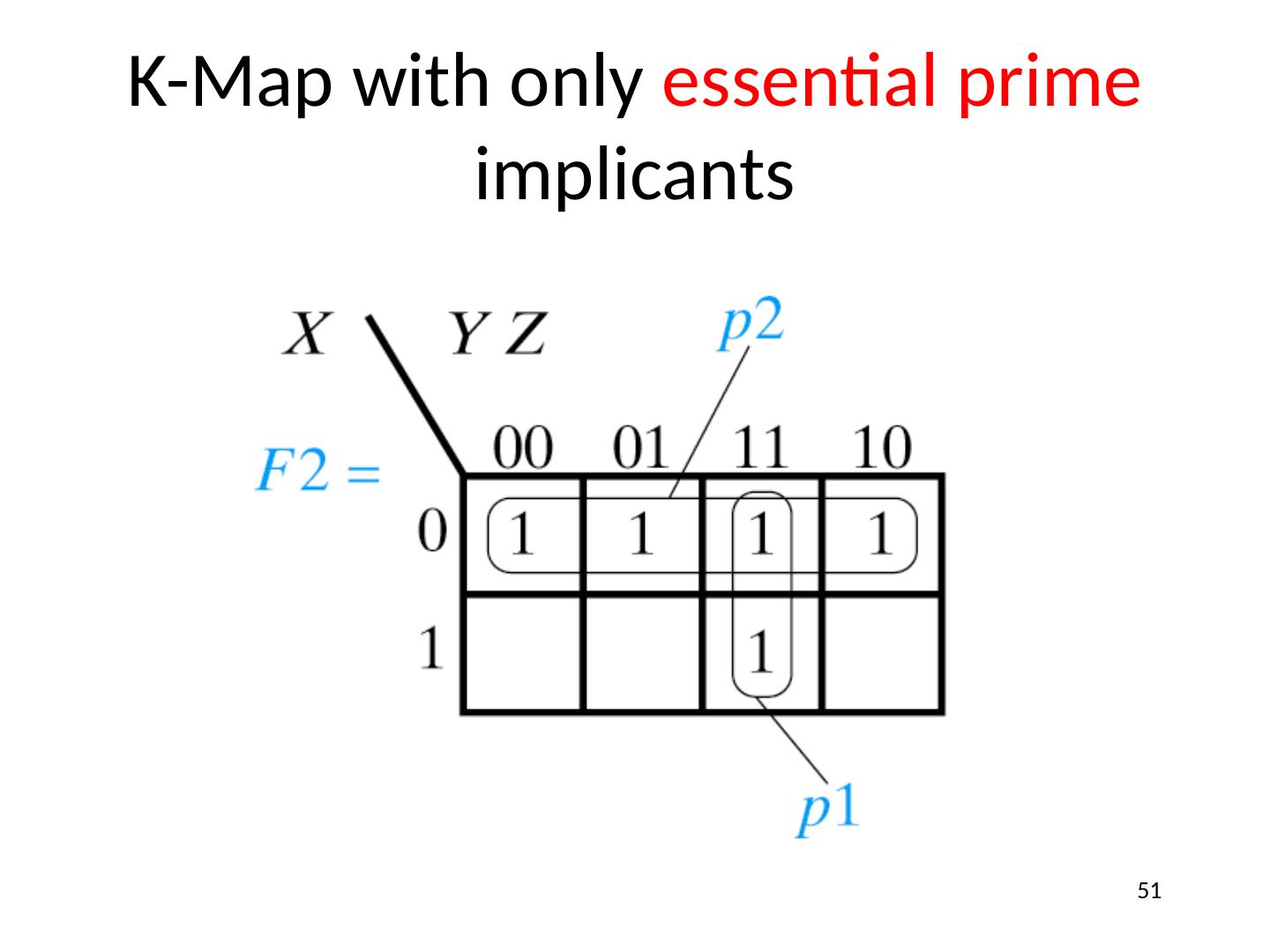
1 .Lecture 5 Topics Canonical or Standard Forms of Functions SOP (Sum of Products) form POS (Product of Sums) form Relationship Between MinTerms and MaxTerms Converting Between Compact Forms of Functions Minimizing (Reducing) Functions Karnaugh Maps (K-maps) Product term sharing 1
2 .Boolean Equations
3 .Obtaining a Boolean Equation In Ecotopia it’s generally illegal to use a car pool lane during weekdays if the car doesn’t have at least two occupants. However, hybrid vehicles can use the lanes any time regardless of the number of occupants. SUVs (even with two or more occupants) are never allowed to use the car pool lanes (unless they are also hybrids). Write a Boolean expression in SOP form for F(W, O, S, H) which is 1 if the car is permitted to use the car pool lane today. W is 1 if today is a weekday. O is 1 if there are two or more occupants, S is 1 if the vehicle is an SUV, H is 1 if the vehicle is a hybrid. W O S H F ---------- 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0 0 0 1 1 1 0 1 0 0 1 0 1 0 1 1 0 1 1 0 0 0 1 1 1 1 1 0 0 0 0 1 0 0 1 1 1 0 1 0 0 1 0 1 1 1 1 1 0 0 1 1 1 0 1 1 1 1 1 0 0 1 1 1 1 1 ECOTOPIA EXAMPLE
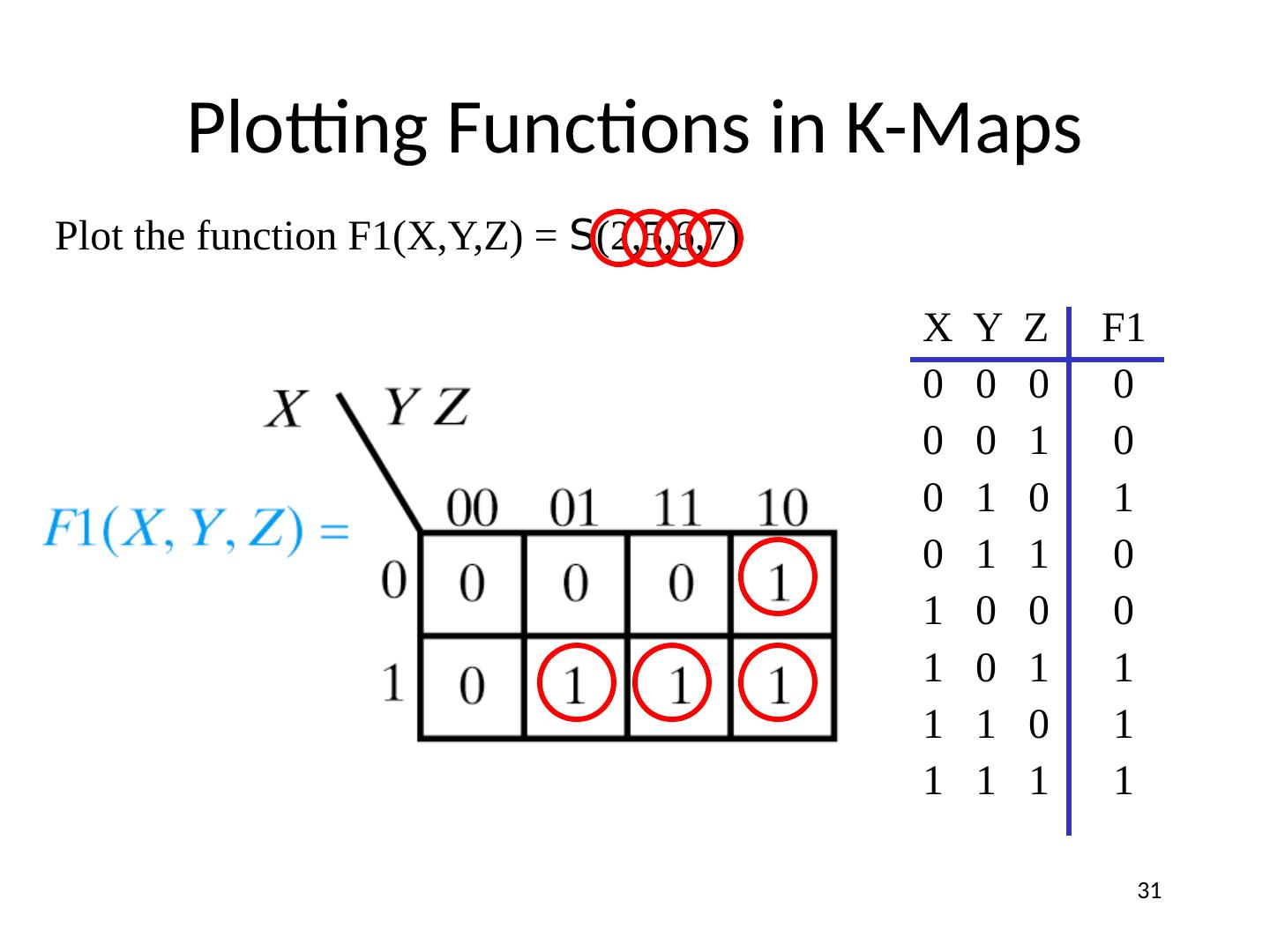
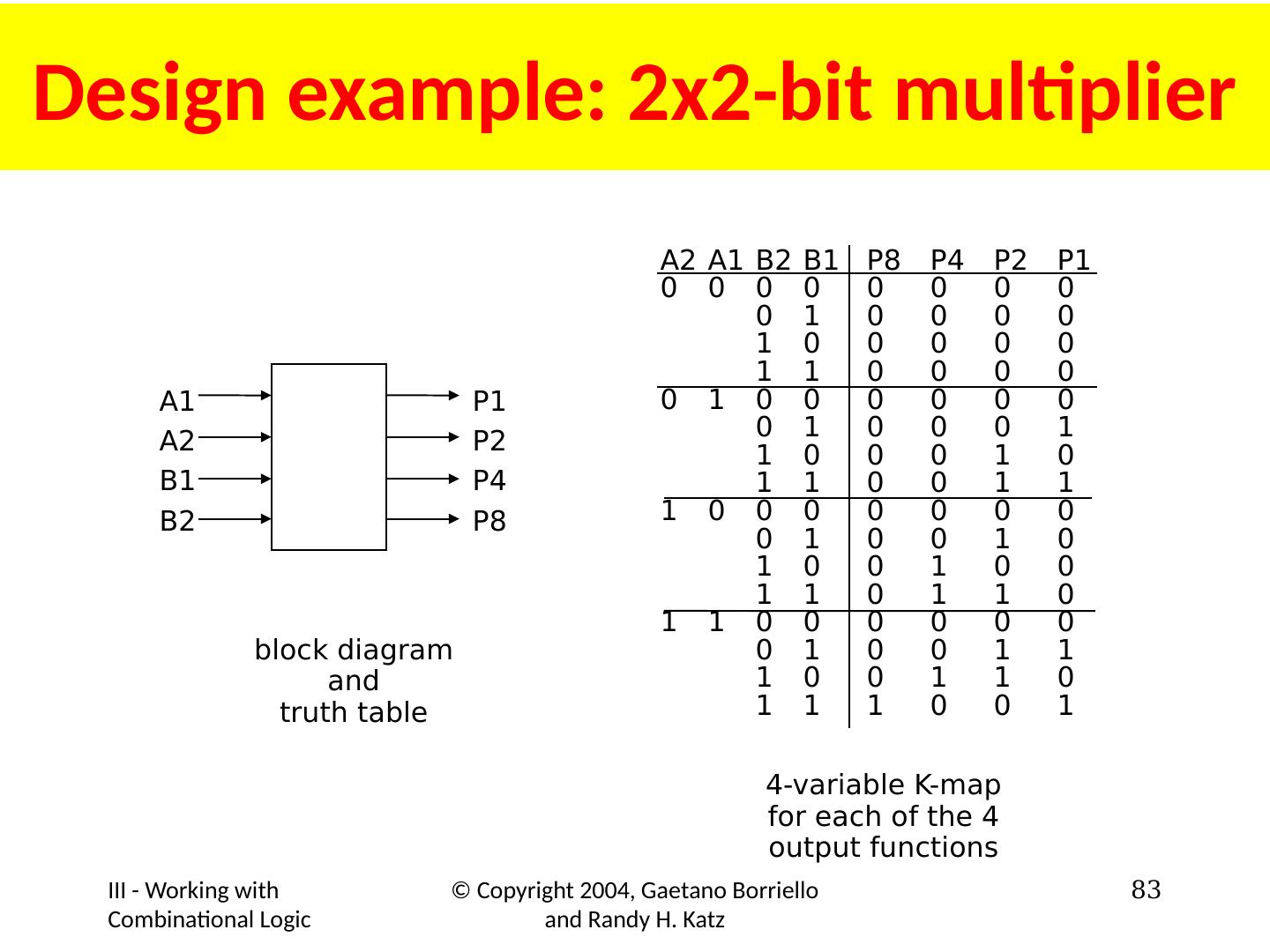
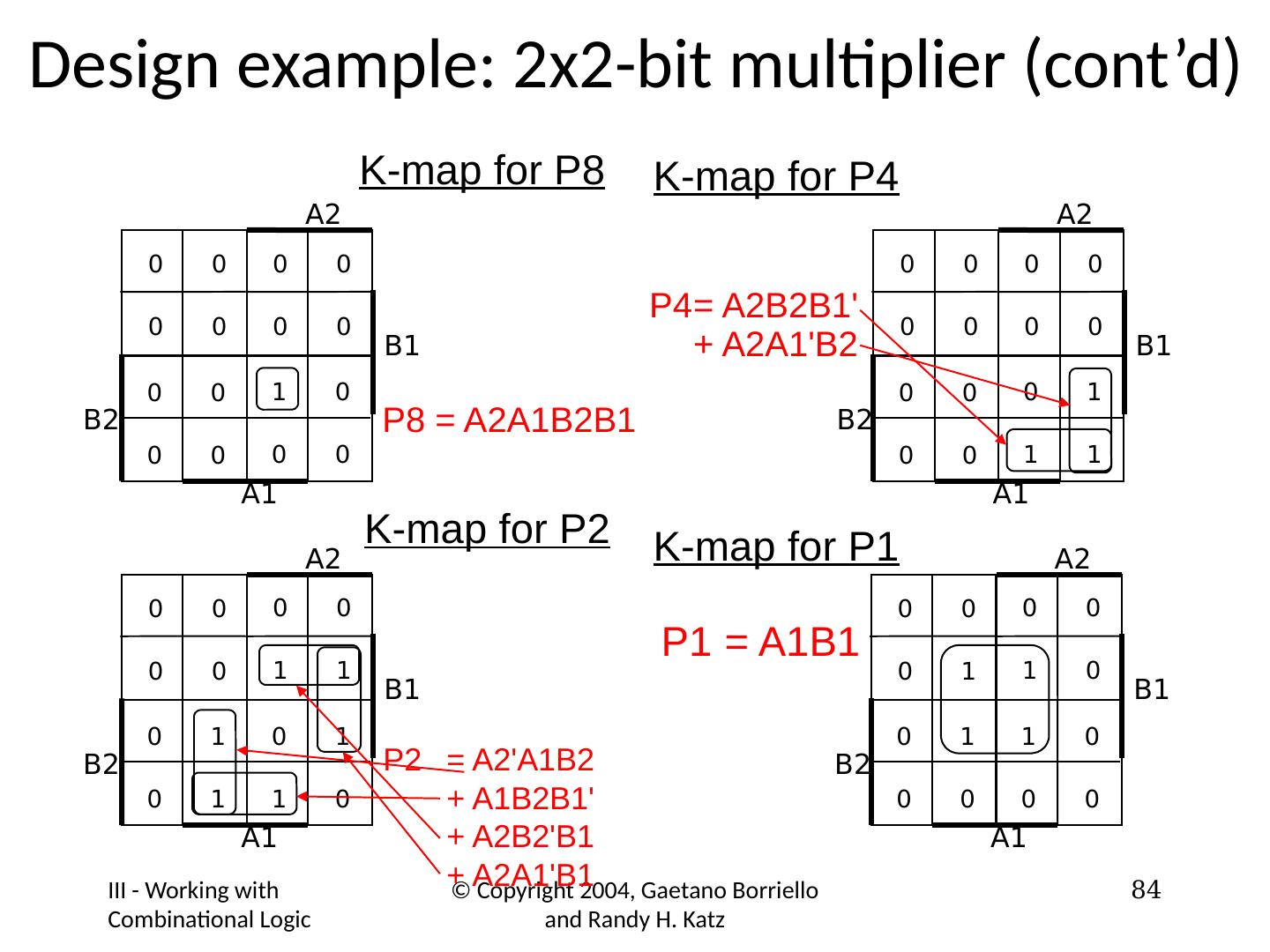
4 .Another Example: Deriving Boolean Equations A truth table is a complete, unambiguous definition of a Boolean function… But how do we get a Boolean expression from a truth table? SOP or POS X Y Z F 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 0 1 1 0 1 1 1 1 0 F = X × Y × Z + X × Y × Z + X × Y × Z 4
5 .F(A,B) = F(0,0) × A × B + F(0,1) × A × B + F(1,0) × A × B + F(1,1) × A × B = 0 × A × B + 1 × A × B + 1 × A × B + 1 × A × B = 0 + A × B + A × B + A × B = A × B + A × B + A × B Another Example: Obtaining SOP Forms of Functions OR truth table A B F(A,B) 0 0 0 = F(0,0) 0 1 1 = F(0,1) 1 0 1 = F(1,0) 1 1 1 = F(1,1) Reduced Form Canonical or Standard SOP Form Standard Product Term (Minterm) A + B 5
6 .Minterms and Maxterms
7 .Minterms 7
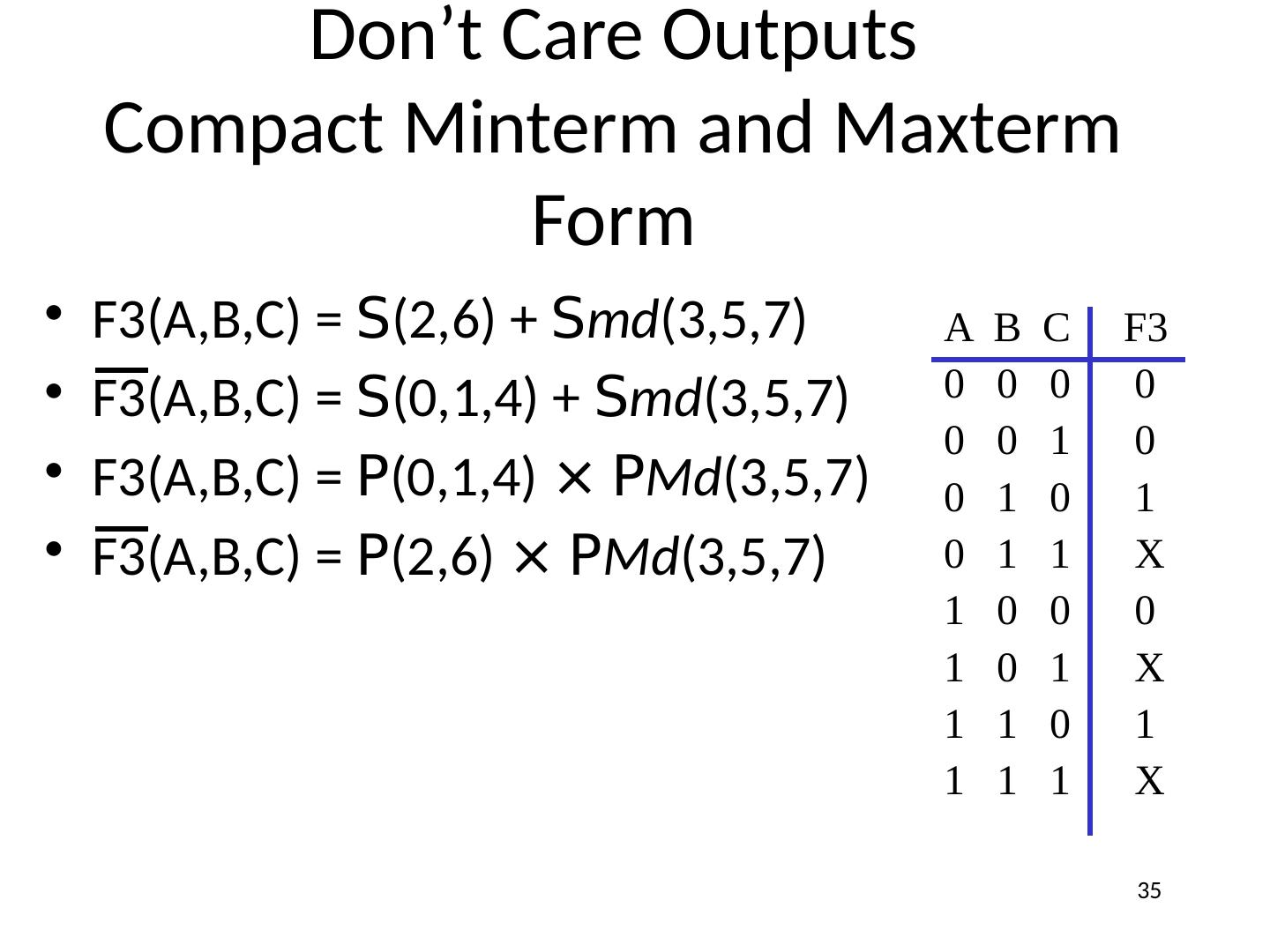
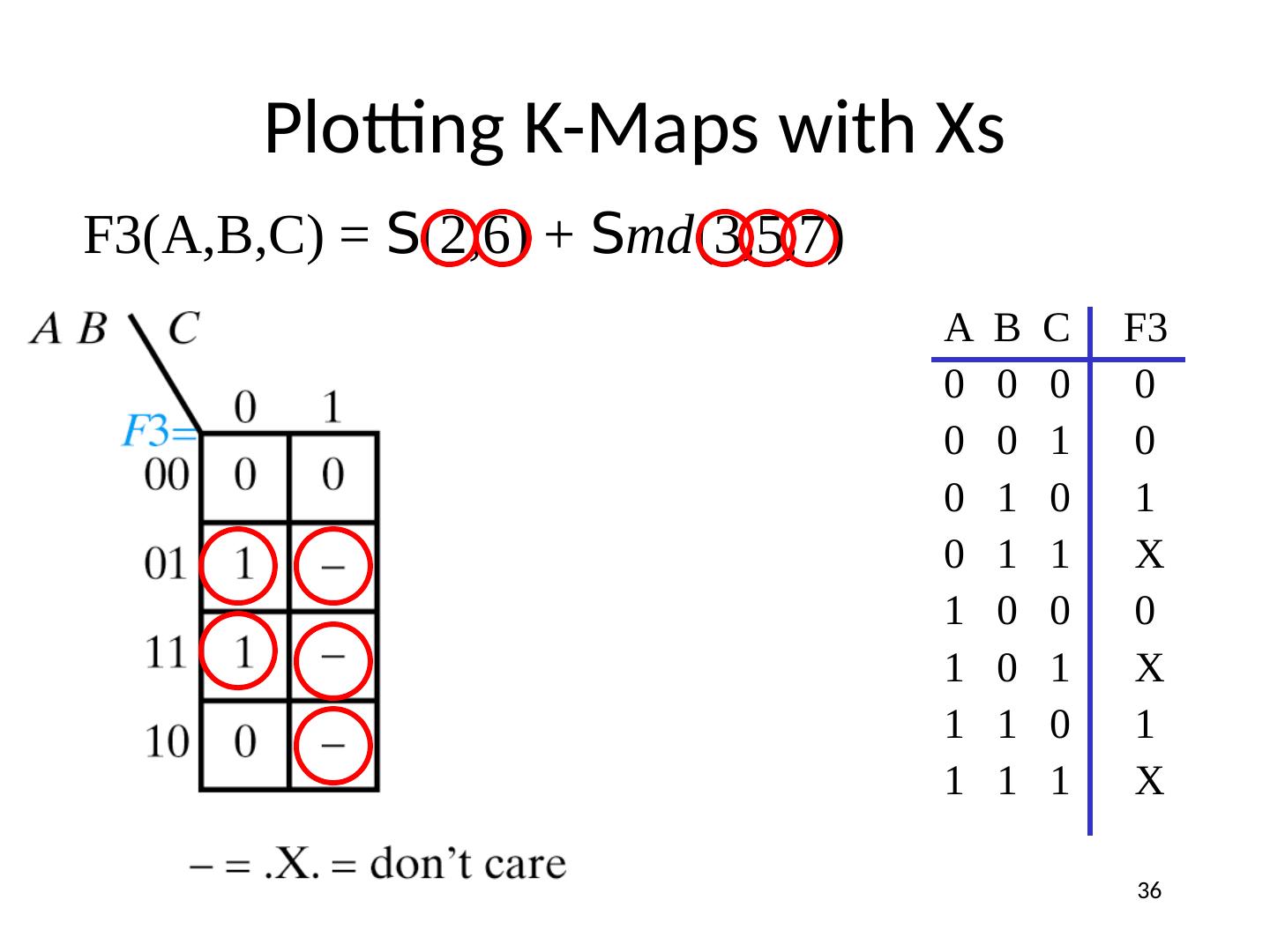
8 .F(A,B) = F(0,0) × A × B + F(0,1) × A × B + F(1,0) × A × B + F(1,1) × A × B = S 3 i=0 (F i × m i ) = 0 × m 0 + 1 × m 1 + 1 × m 2 + 1 × m 3 = m 1 + m 2 + m 3 = S m(1,2,3) = S (1,2,3) Compact Minterm Form OR truth table A B F(A,B) 0 0 0 = F(0,0) 0 1 1 = F(0,1) 1 0 1 = F(1,0) 1 1 1 = F(1,1) 8
9 .Minterms S (3,5,6,7) 9
10 .Generalized Compact Minterm Form F(X 1 , X 2 ,… X n ) = S ( minterms for 1s of the function) F(X 1 , X 2 ,… X n ) = S (minterms for 0s of the function) 10 Pay attention, this is negation of function F
11 .F(A,B) = (F(0,0) + A + B) × ( F(0,1) + A + B) × (F(1,0) + A + B) × (F(1,1) + A + B) = (0 + A + B) × (0 + A + B) × (0 + A + B) × (1 + A + B) = (A + B) × (A + B) × (A + B) × (1) = (A + B) × (A + B) × (A + B) Obtaining POS Forms of Functions AND truth table A B F(A,B) 0 0 0 = F(0,0) 0 1 0 = F(0,1) 1 0 0 = F(1,0) 1 1 1 = F(1,1) Standard Sum Term (Maxterm) Canonical or Standard POS Form Reduced Form A × B 11
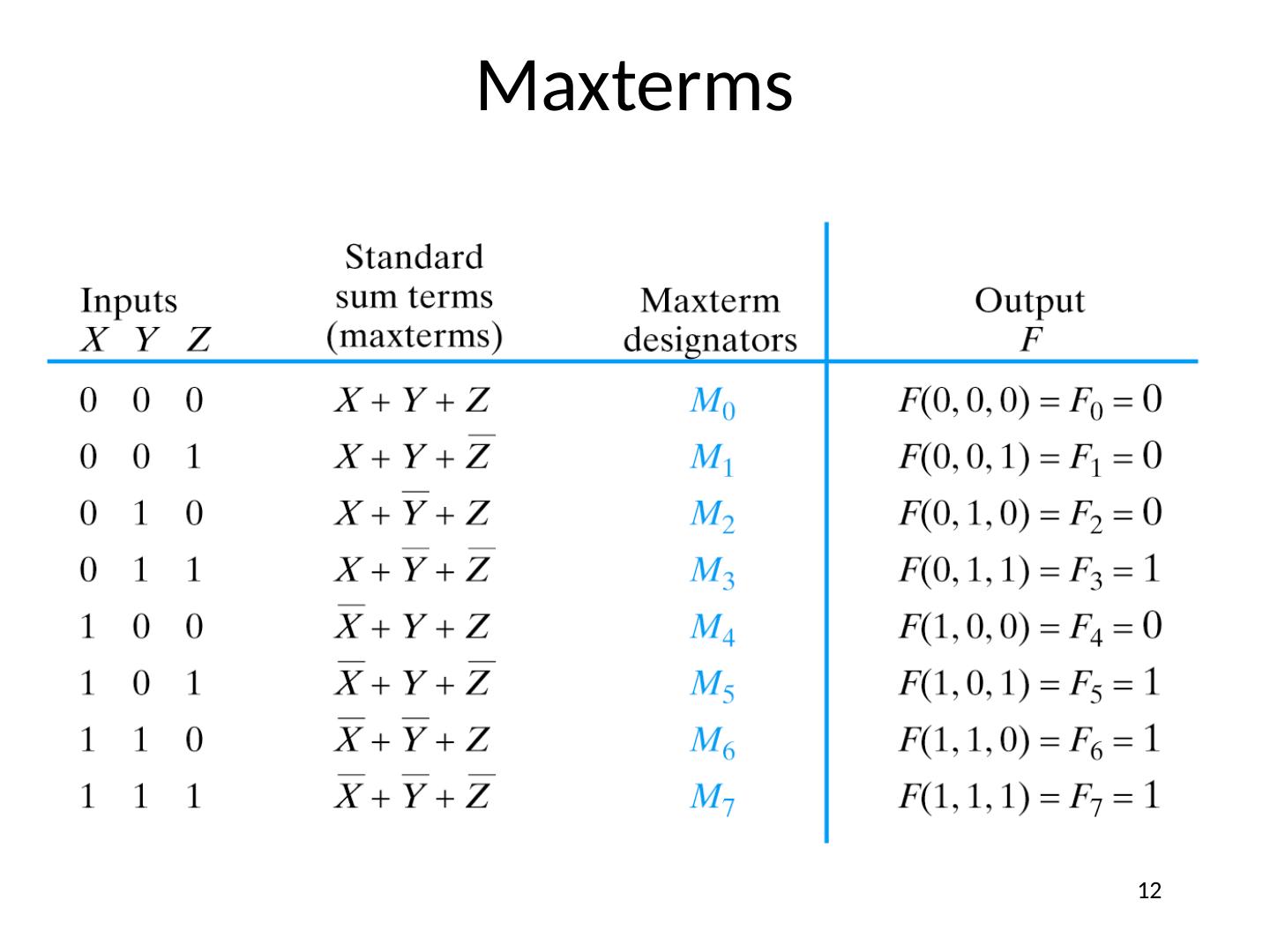
12 .Maxterms 12
13 .F(A,B) = (F(0,0) + A + B ) × ( F(0,1) + A + B ) × (F(1,0) + A + B ) × (F(1,1) + A + B ) = P 3 i=0 ( F i + M i ) = (0 + M 0 ) × (0 + M 1 ) × (0 + M 2 ) × (1 + M 3 ) = M 0 × M 1 × M 2 = P M(0,1,2) = P (0,1,2) Compact Maxterm Form AND truth table A B F(A,B) 0 0 0 = F(0,0) 0 1 0 = F(0,1) 1 0 0 = F(1,0) 1 1 1 = F(1,1) 13
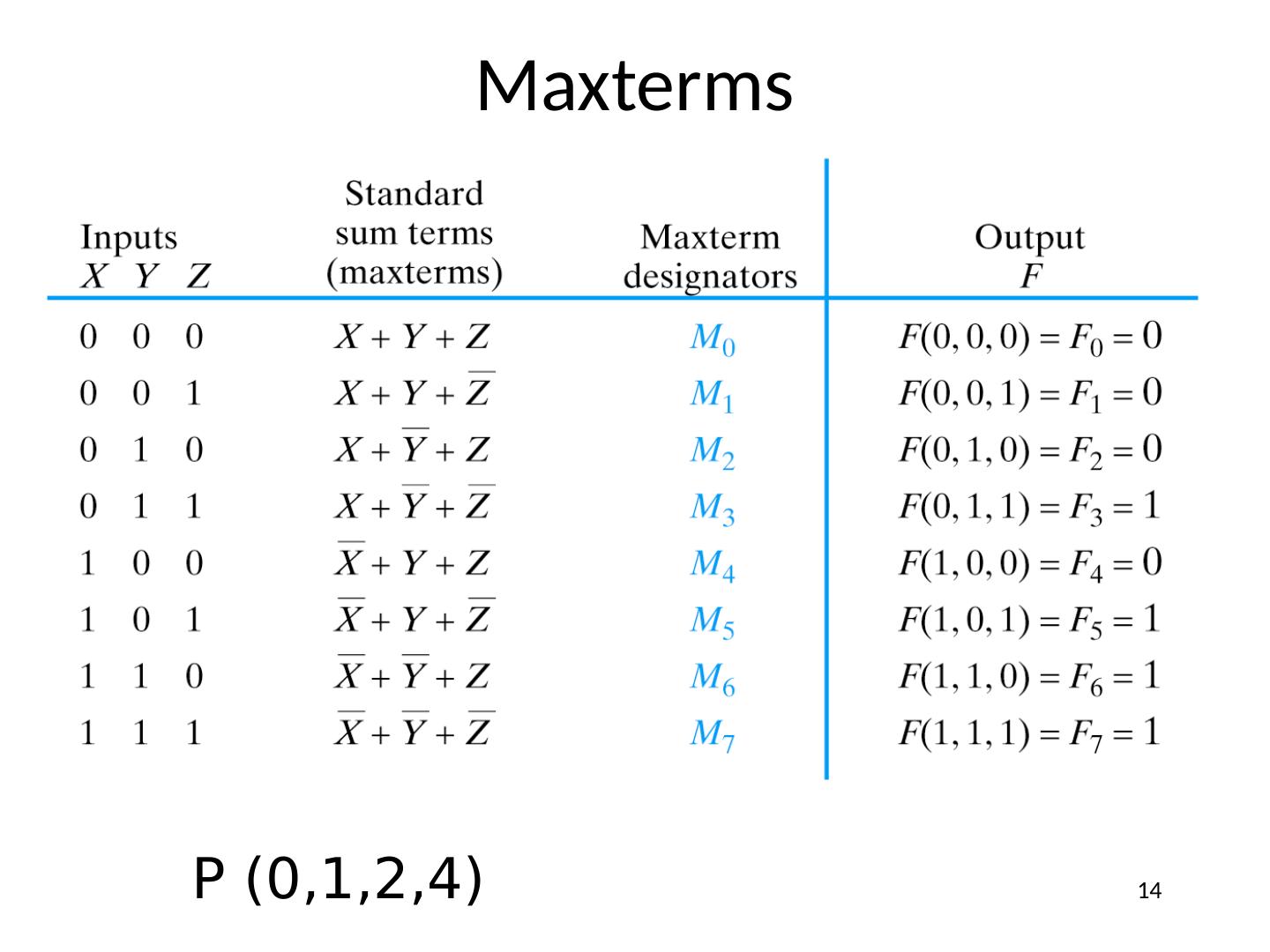
14 .Maxterms P (0,1,2,4) 14
15 .Generalized Compact Maxterm Form F(X 1 , X 2 ,… X n ) = P ( maxterms for 0s of the function) F(X 1 , X 2 ,… X n ) = P ( maxterms for 1s of the function) 15 Canonical SOP Canonical POS negation
16 .Relationship Between Minterms and Maxterms m i = M i , M i = m i S = P , P = S 16
17 .Canonical SOP and POS forms using minterms and maxterms
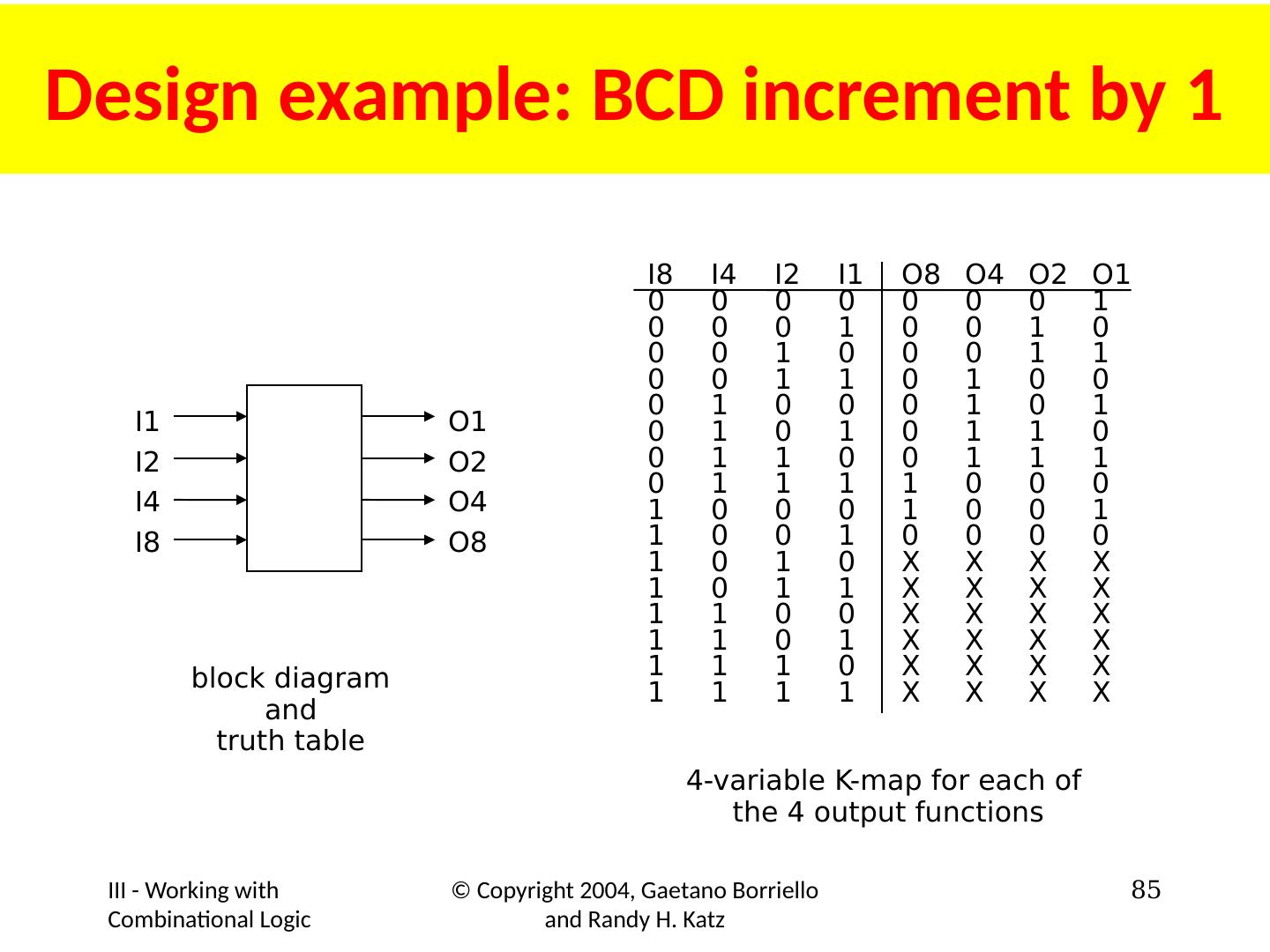
18 .An example : Given the accompanying truth table, write the compact minterm form for F for its 1s and 0s. Write the standard SOP form for each . X Y Z F 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 0 1 1 0 1 1 1 1 0 F = S (3,4,6) Compact minterm form 1s : Compact minterm form 0s : Corresponding SOP form: Corresponding SOP form: F = X × Y × Z + X × Y × Z + X × Y × Z F = S (0,1,2,5,7) F = X × Y × Z + X × Y × Z + X × Y × Z + X × Y × Z + X × Y × Z 18 This is example problem 15, page 85. Solution on page 107.
19 .An example: Given the accompanying truth table, write the compact maxterm form for F for its 1s and 0s. Write the standard POS form for each. X Y Z F 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 0 1 1 0 1 1 1 1 0 Compact maxterm form 1s: Compact maxterm form 0s: Corresponding POS form: Corresponding POS form: F = P (0,1,2,5,7) F = P (3,4,6) F = (X + Y + Z) × (X + Y + Z) × (X + Y + Z) F = (X + Y + Z) × (X + Y + Z) × (X + Y + Z) × (X + Y + Z) × (X + Y + Z) 19 This uses the same truthtable as the preceding problem but asks for maxterms
20 .Function Minimization : Reduce Number of Literals and Terms Simplify for Comprehension Reduce Number of Components Reduce Amount of Wiring/Routing Smaller Circuit/Board Area Lower Cost Higher Reliability 20
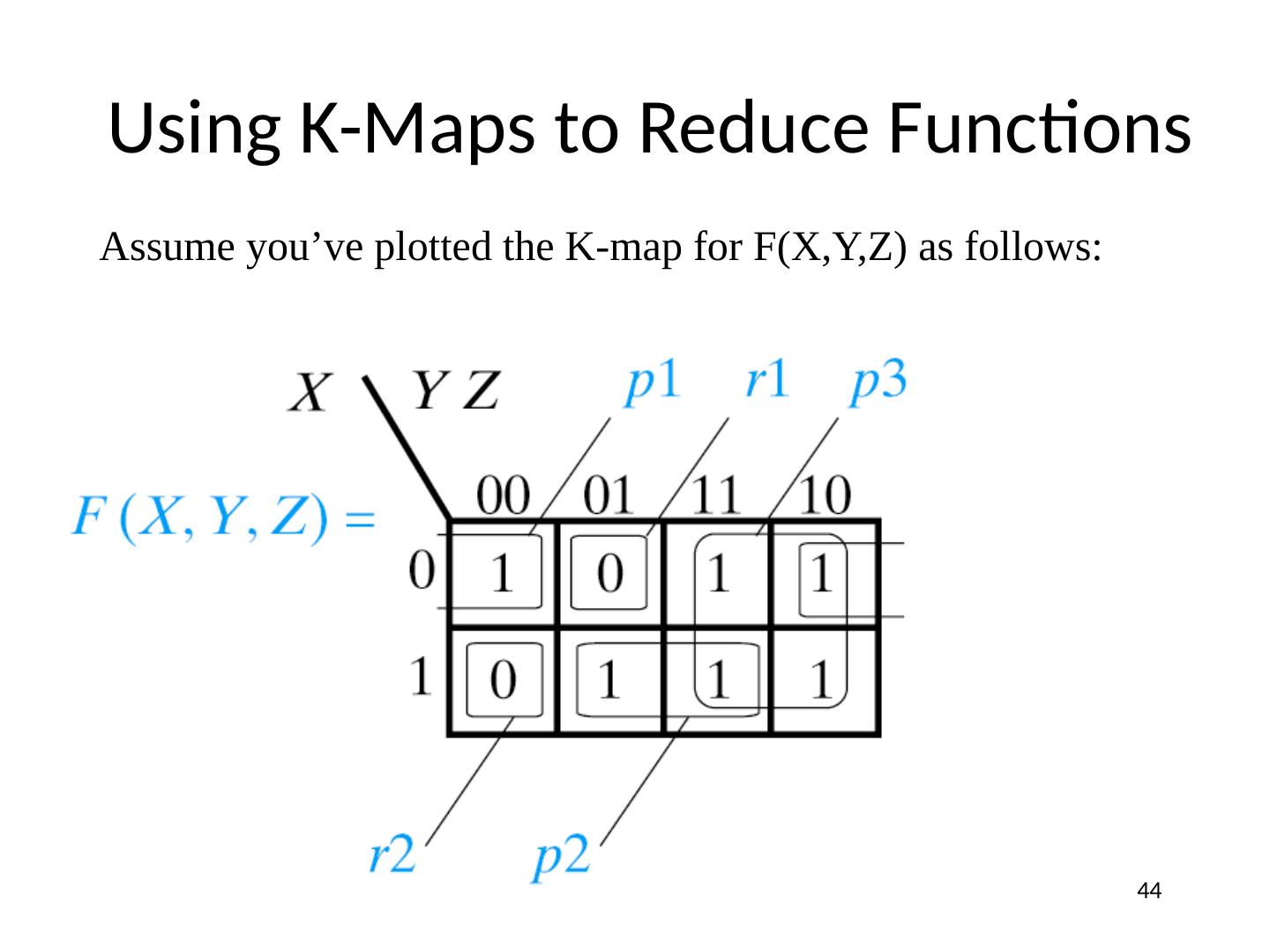
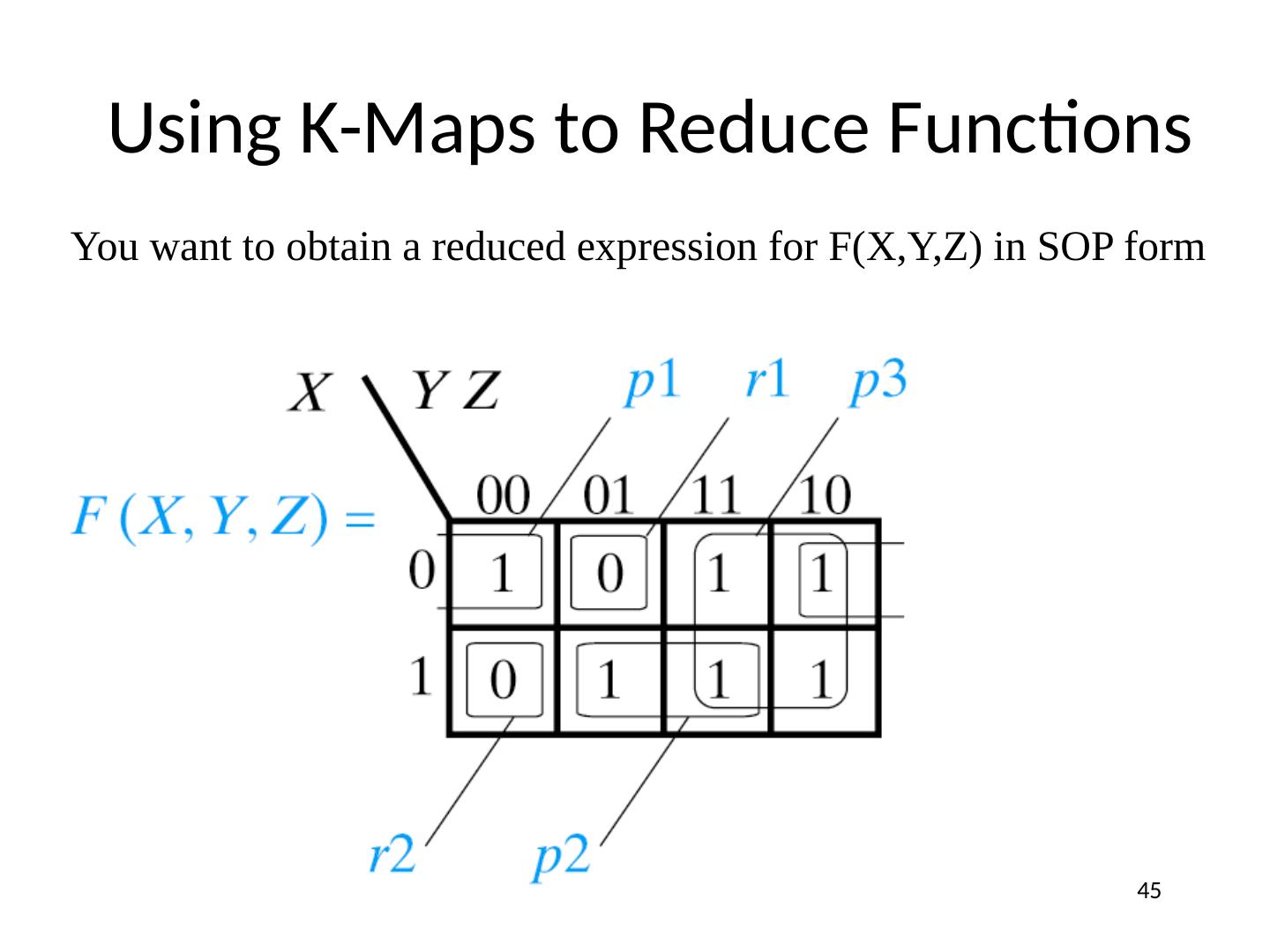
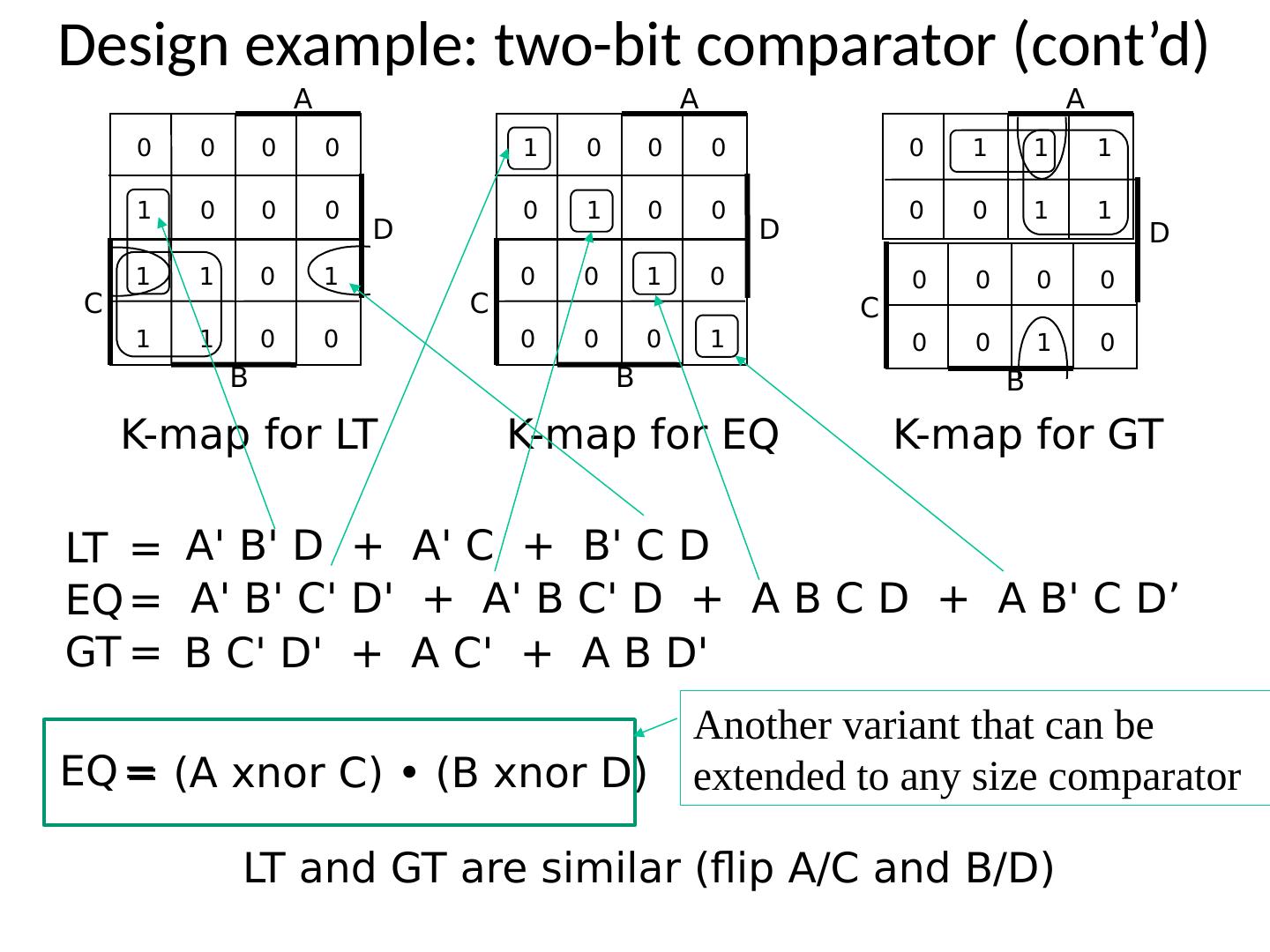
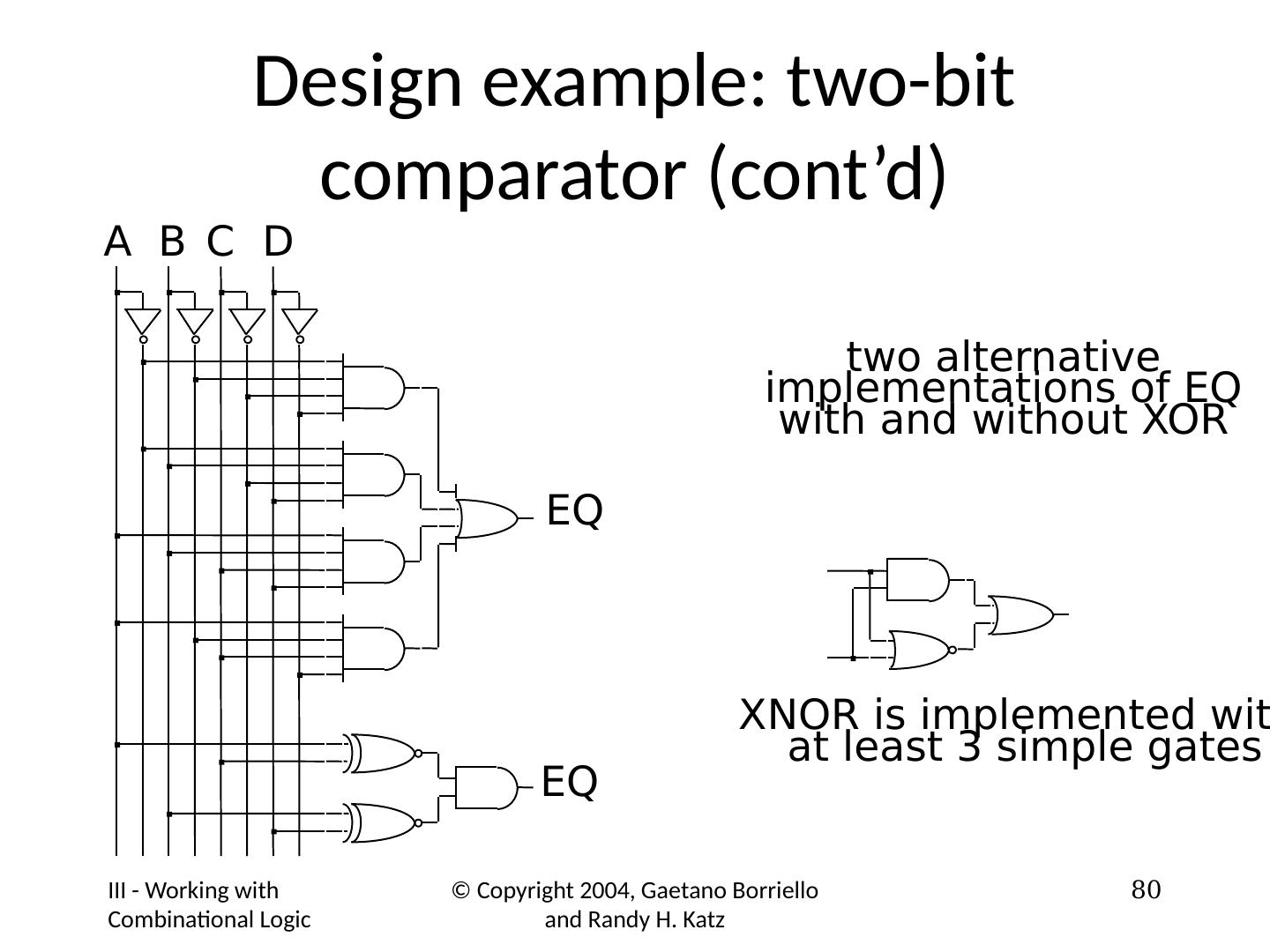
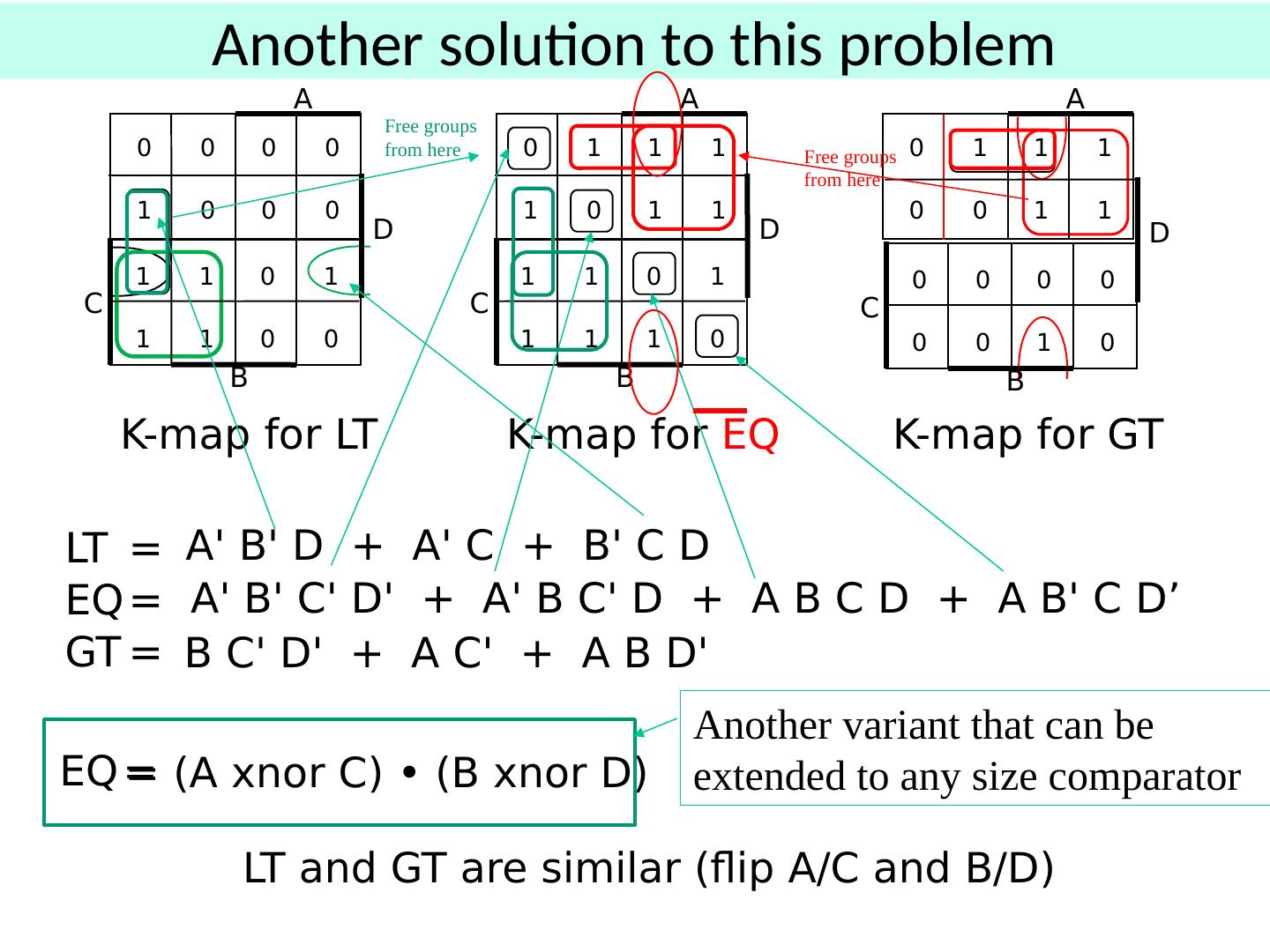
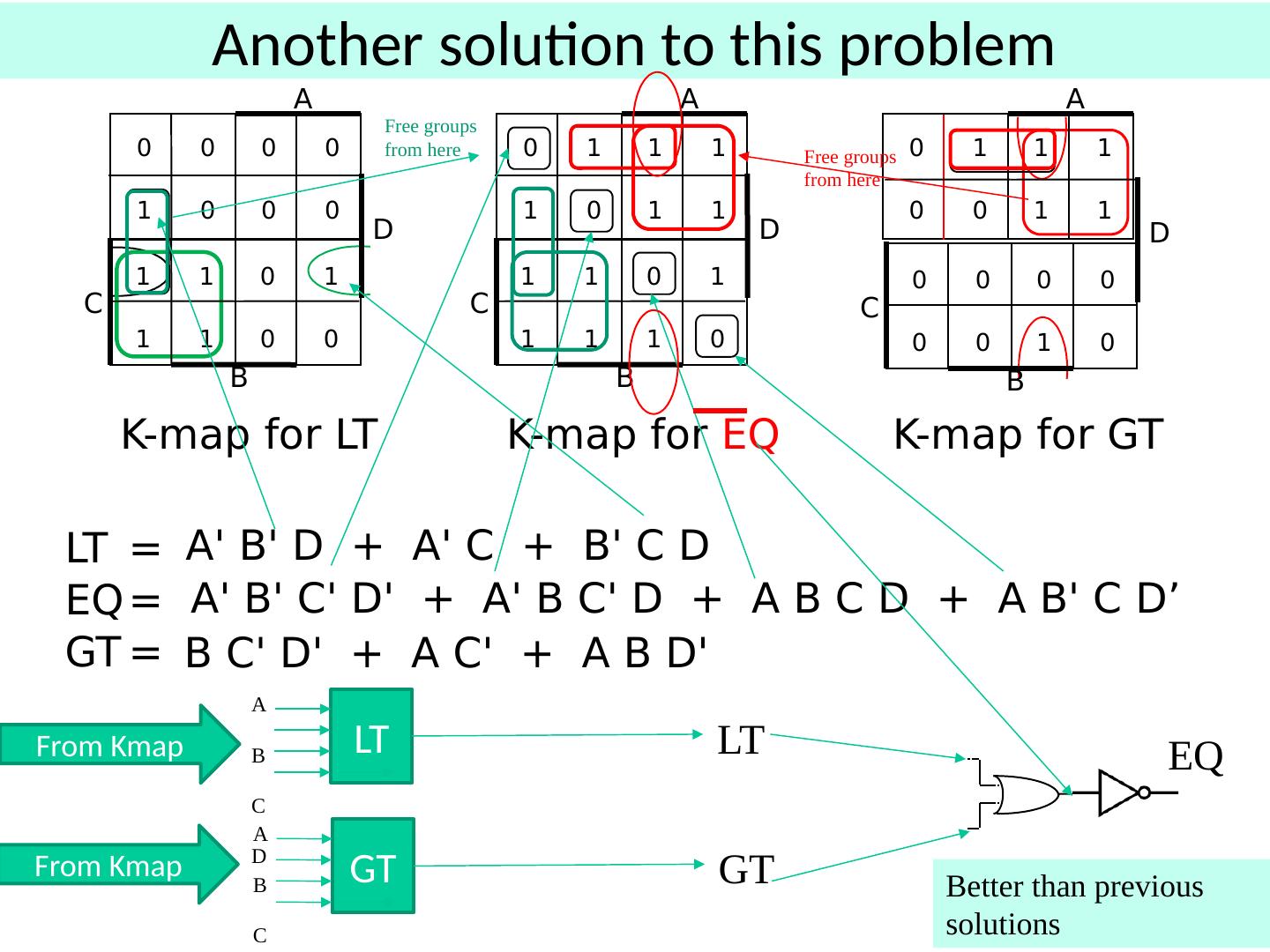
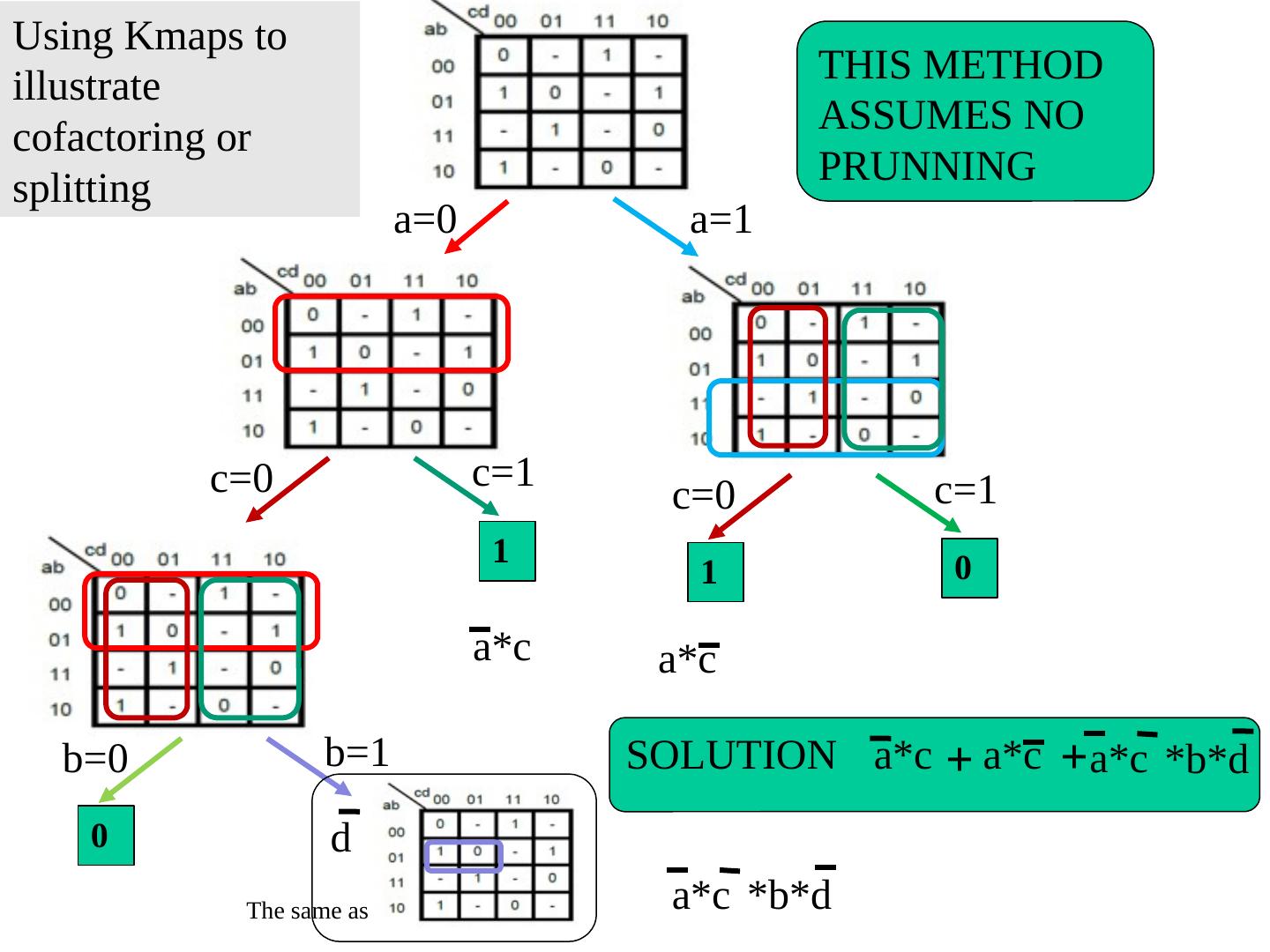
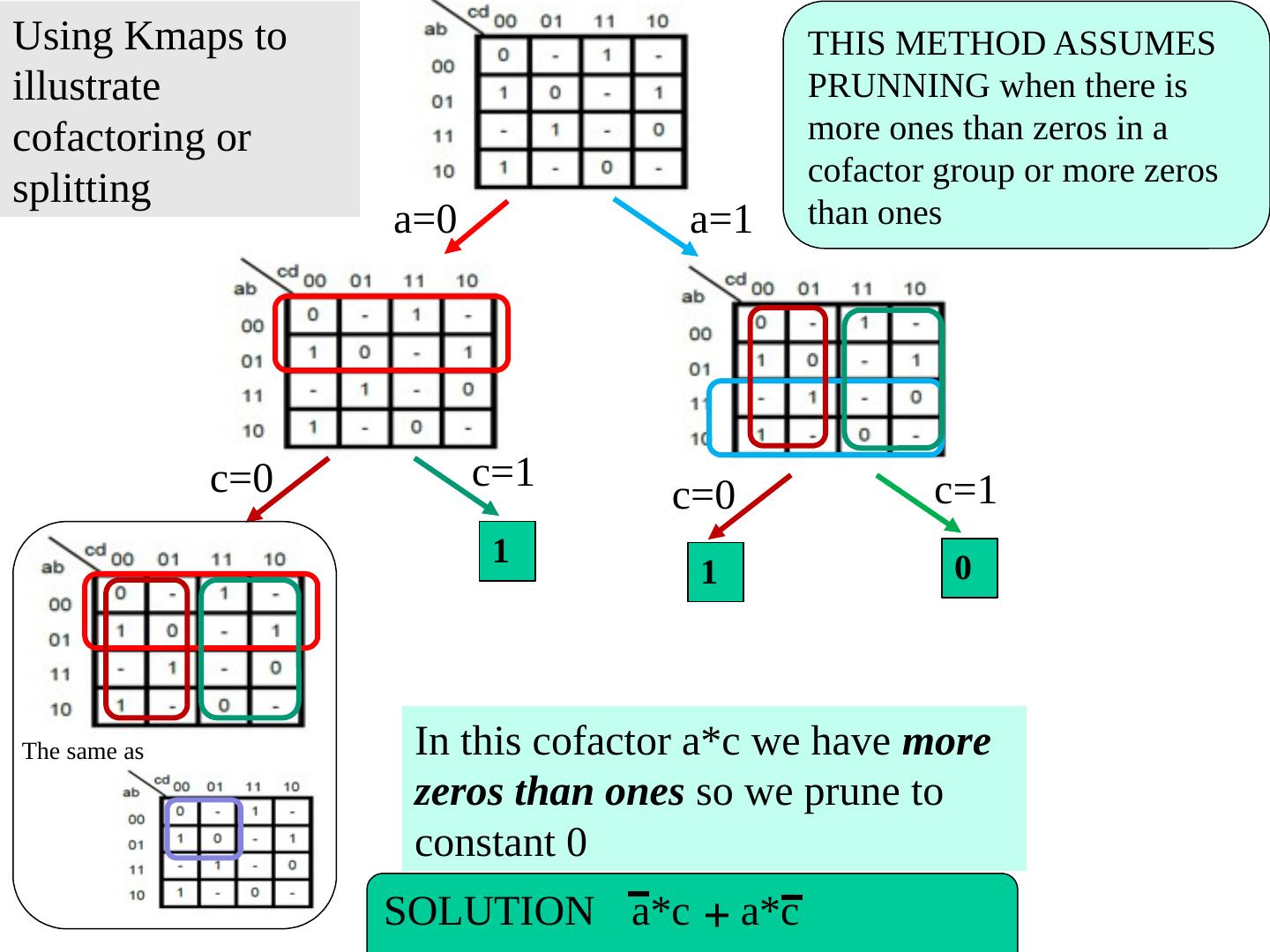
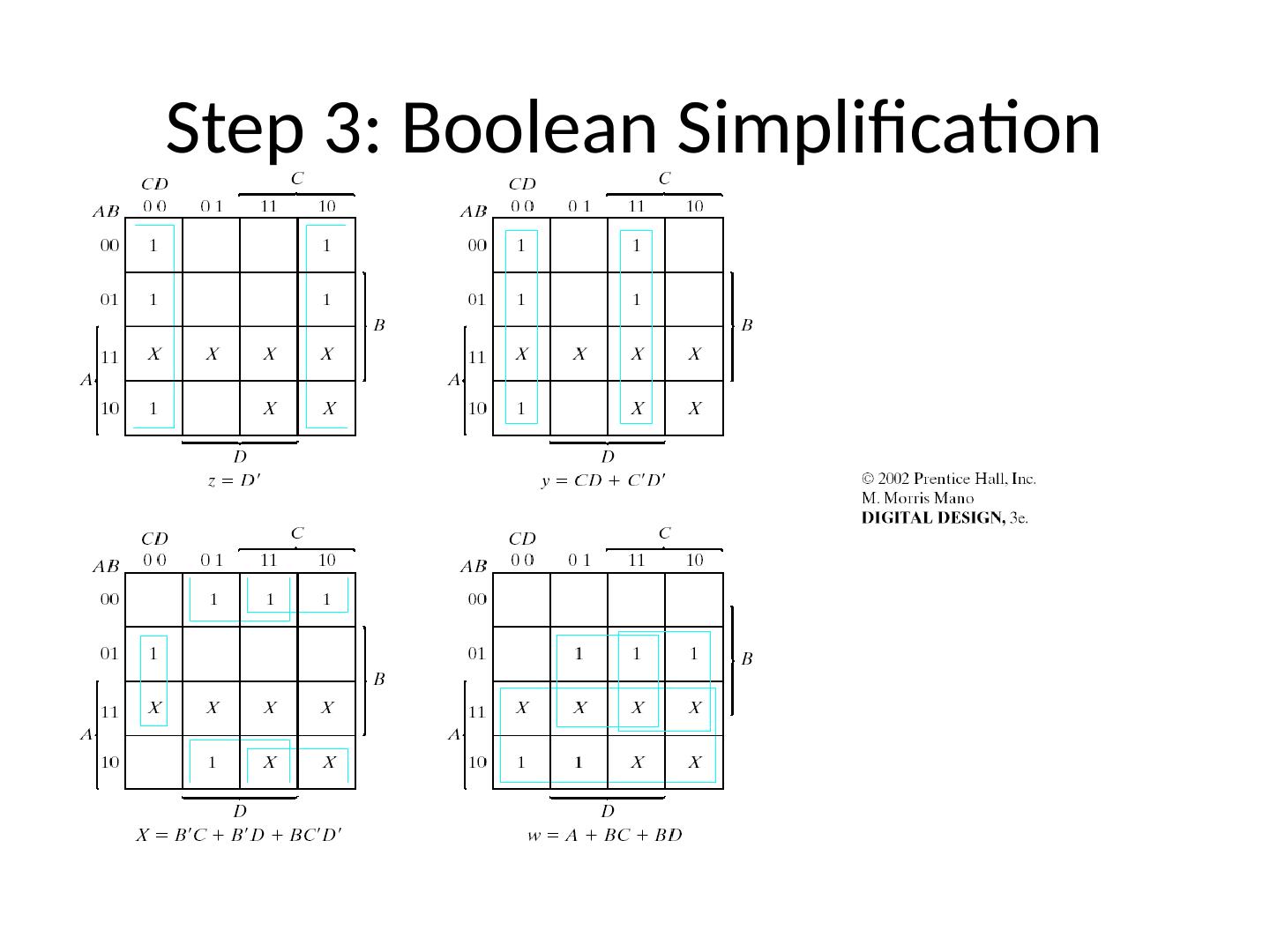
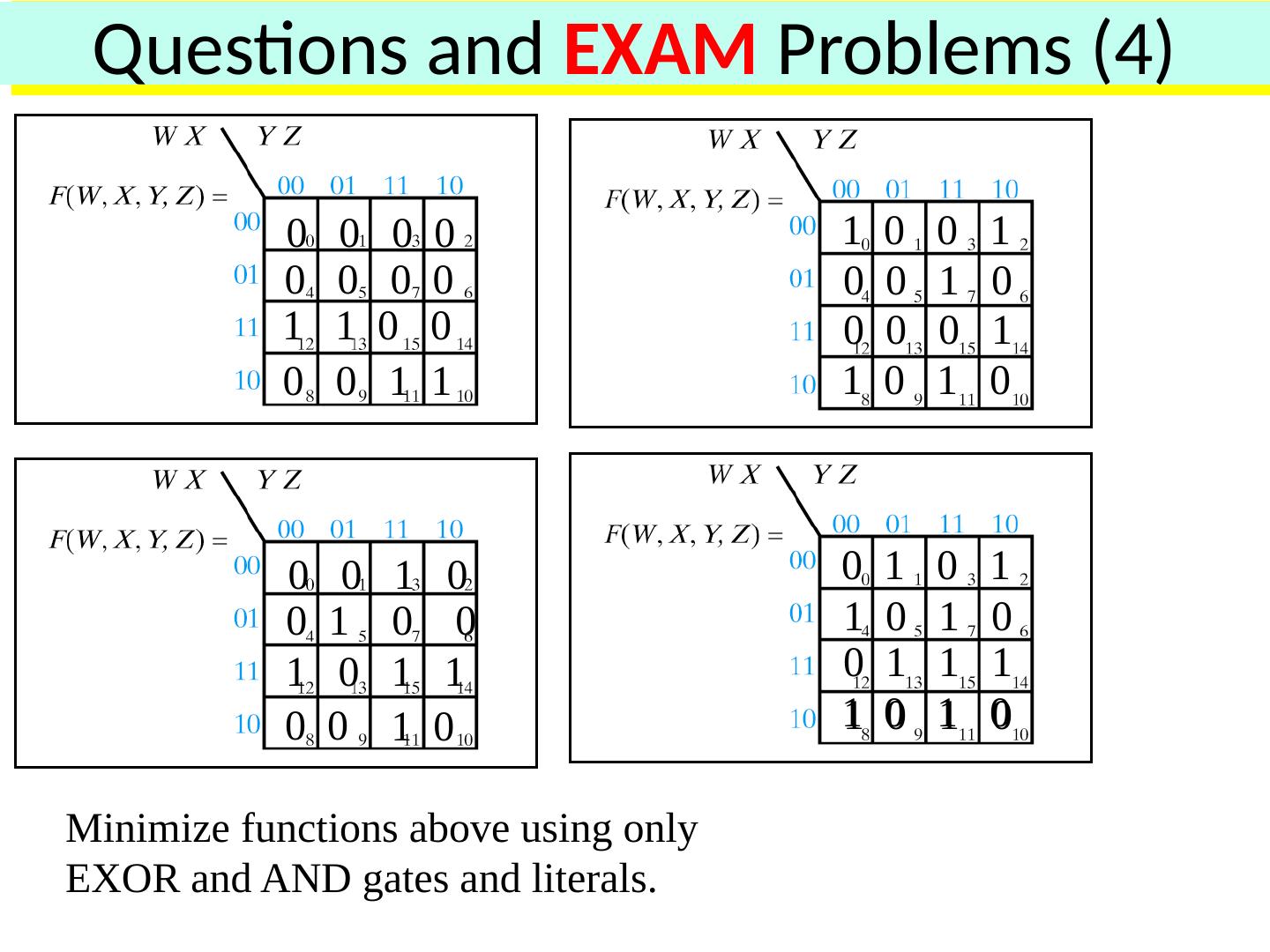
21 .Function Minimization: Reduce Number of Literals and Terms Apply Boolean Algebra Employ Computer Algorithm Quine-McCluskey tabular algorithm Boozer McBoole Espresso and Espresso/Exact (CAD packages) Systematic Algebraic Reduction (SAR) Karnaugh Maps (K-Maps) 21
22 .Karnaugh Maps
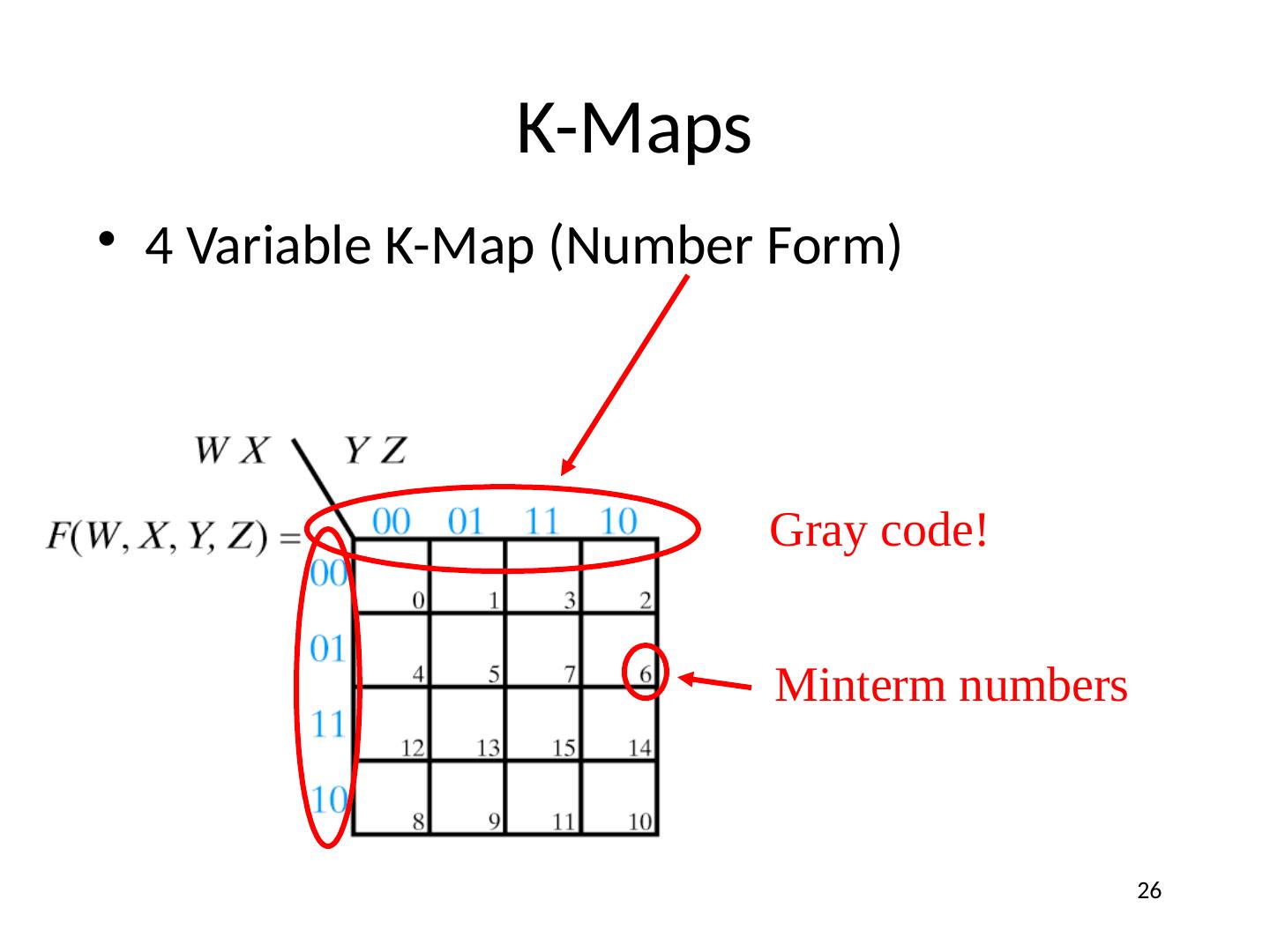
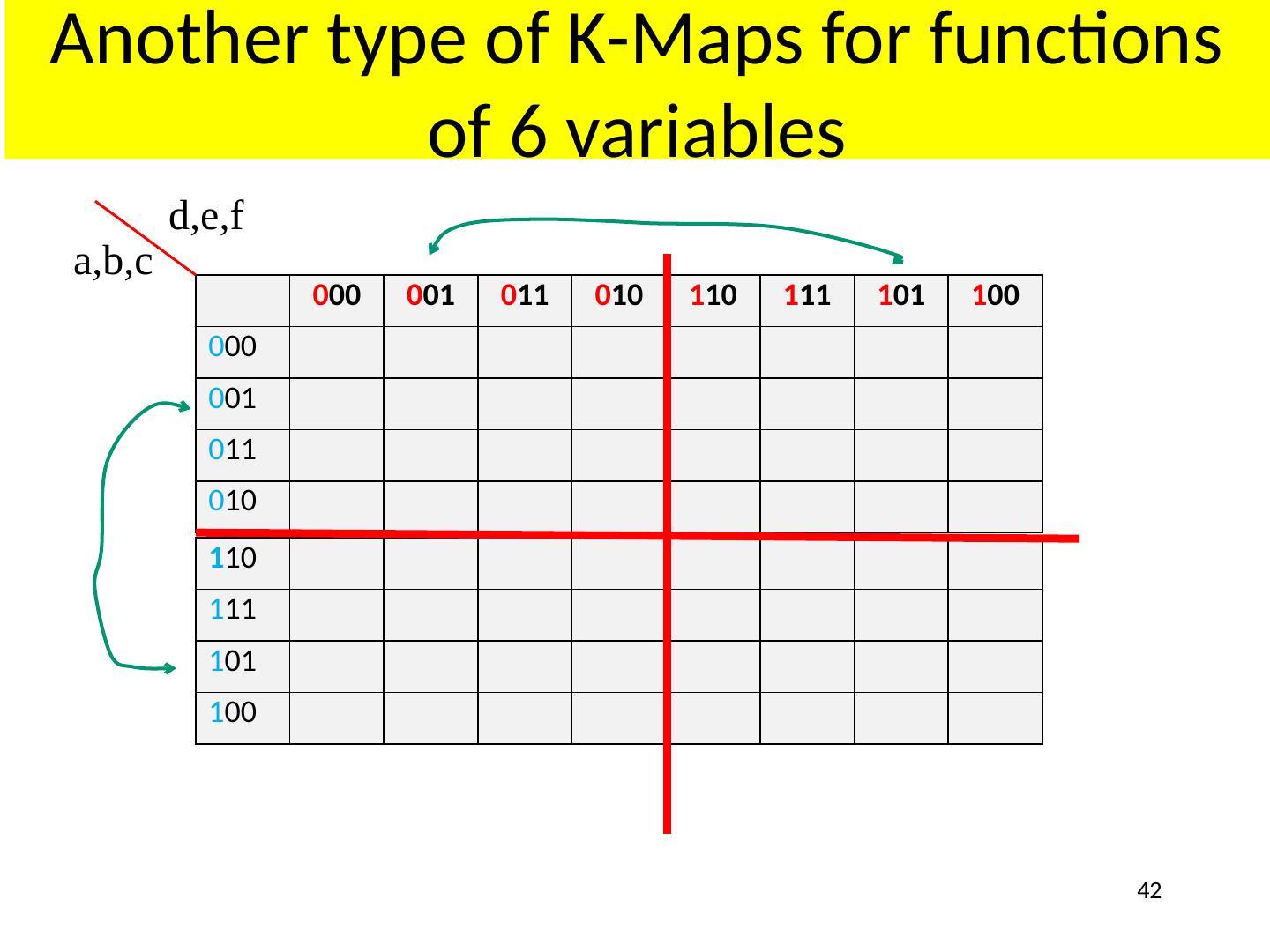
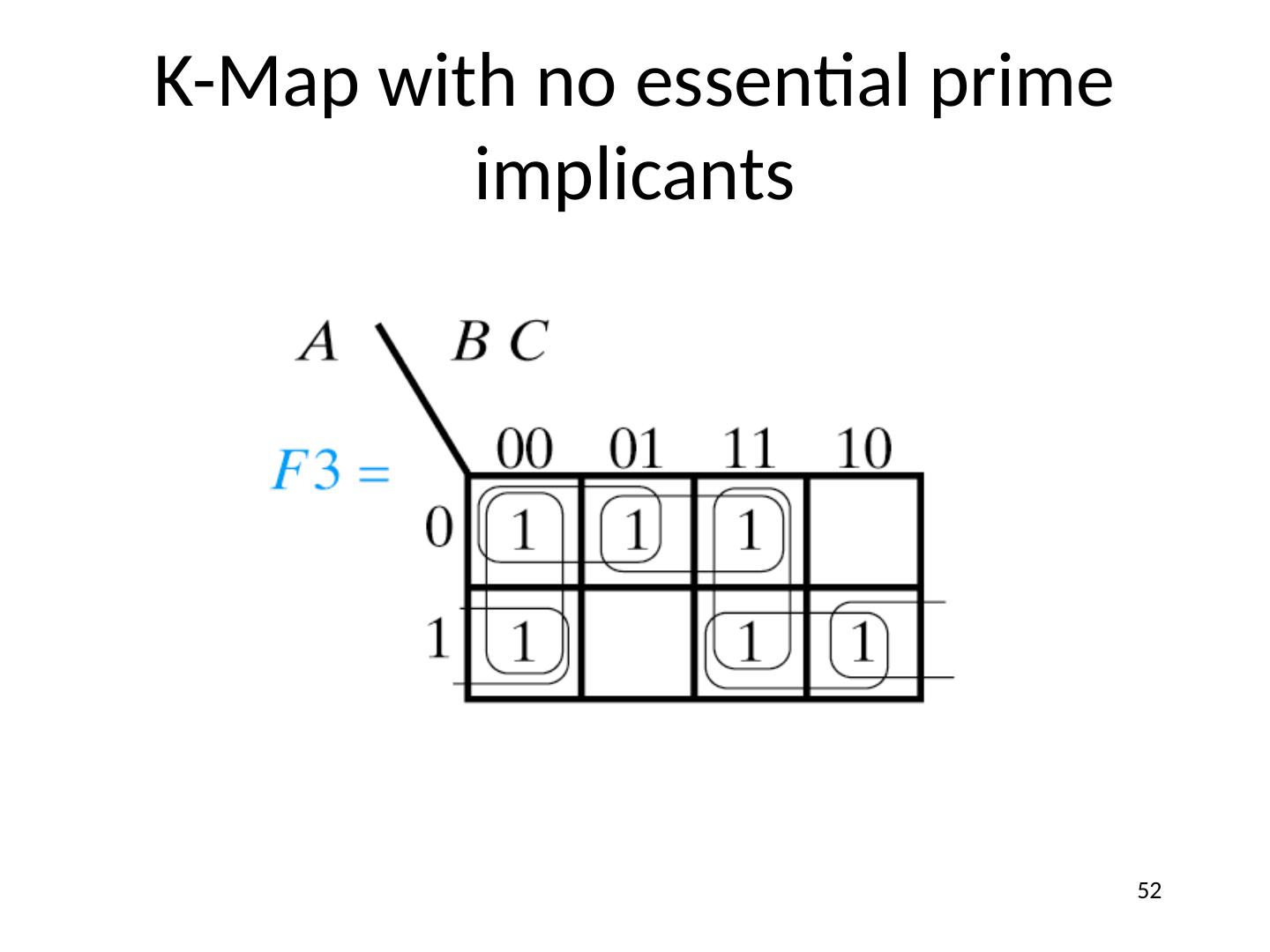
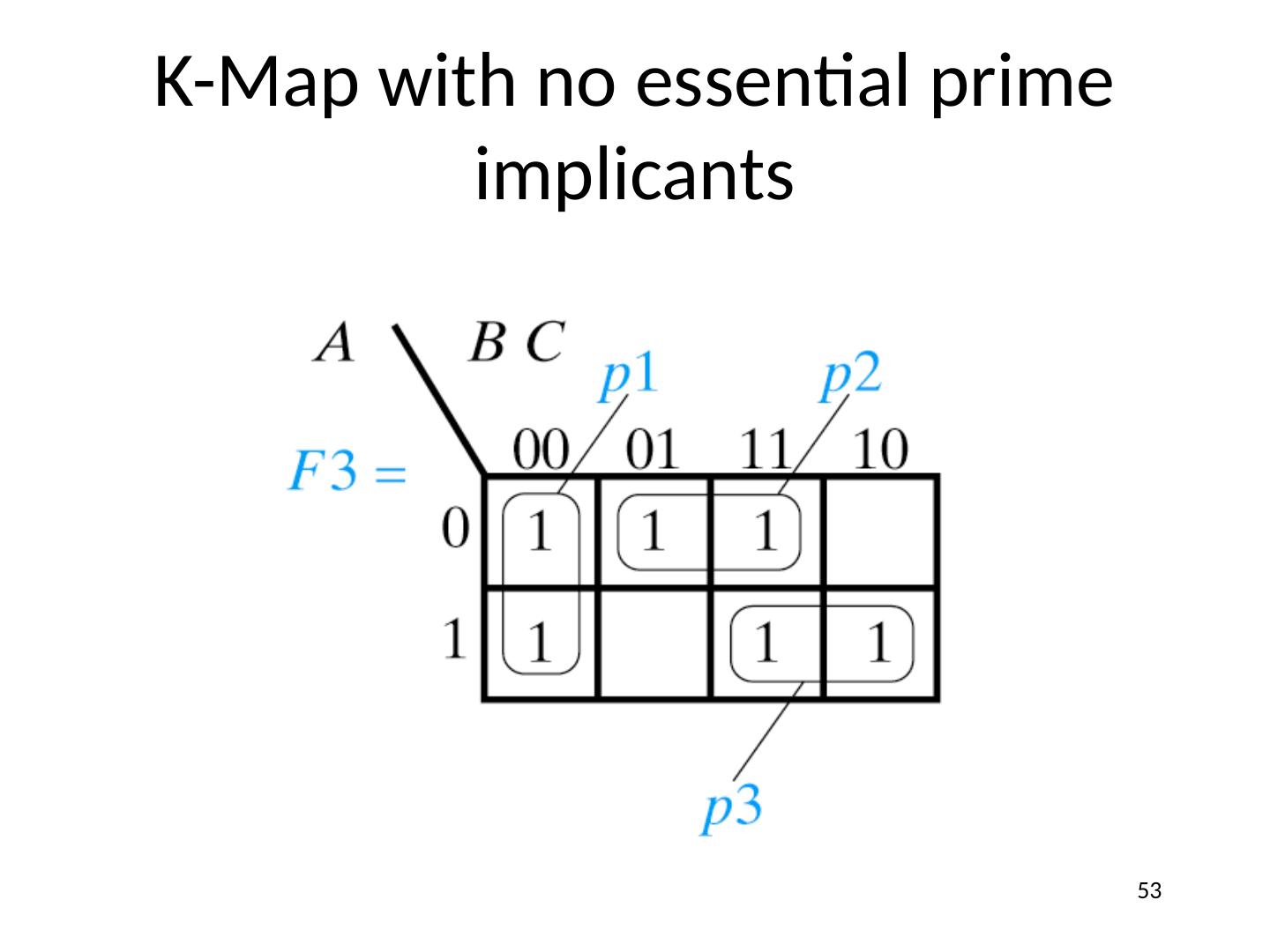
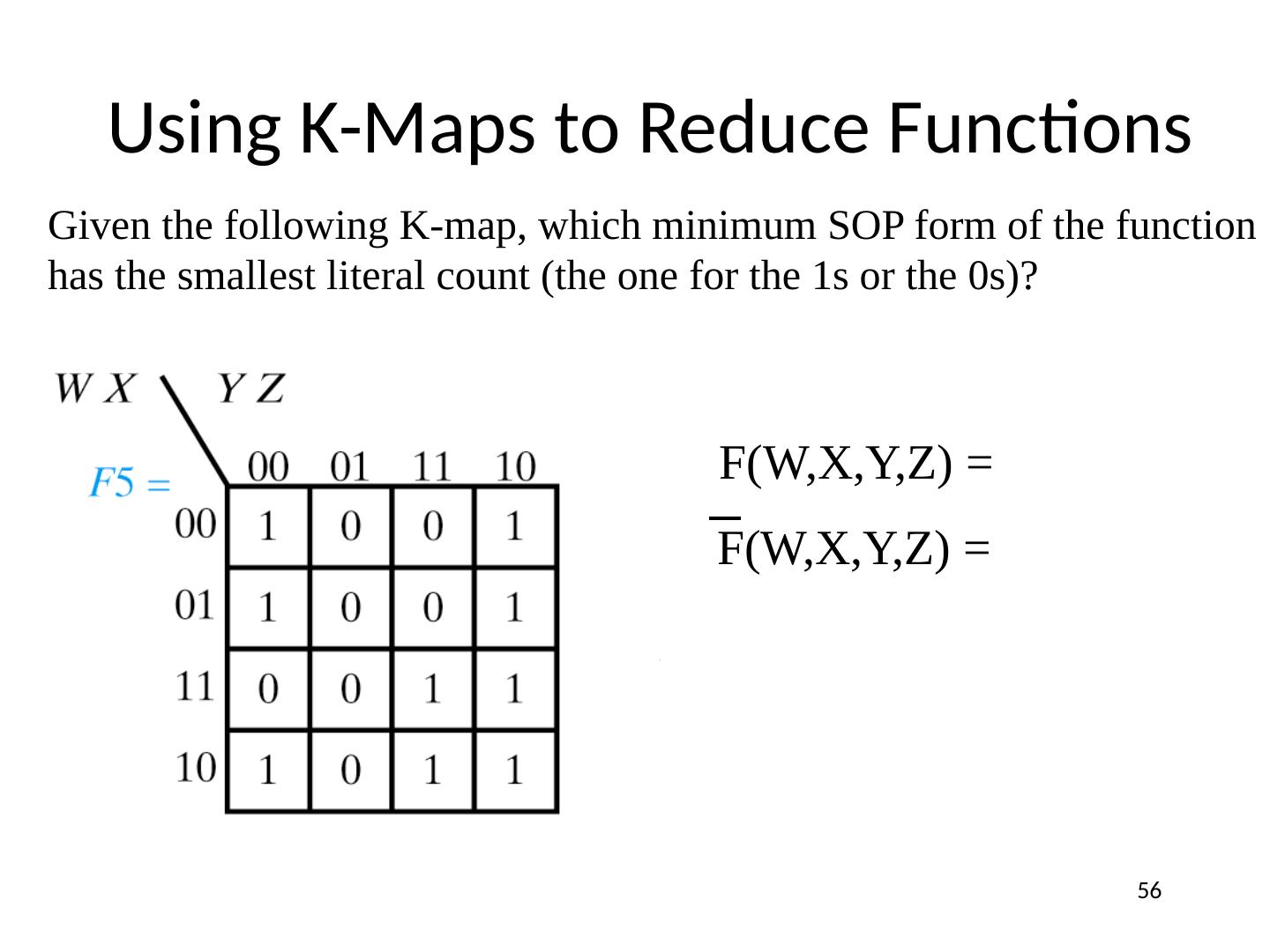
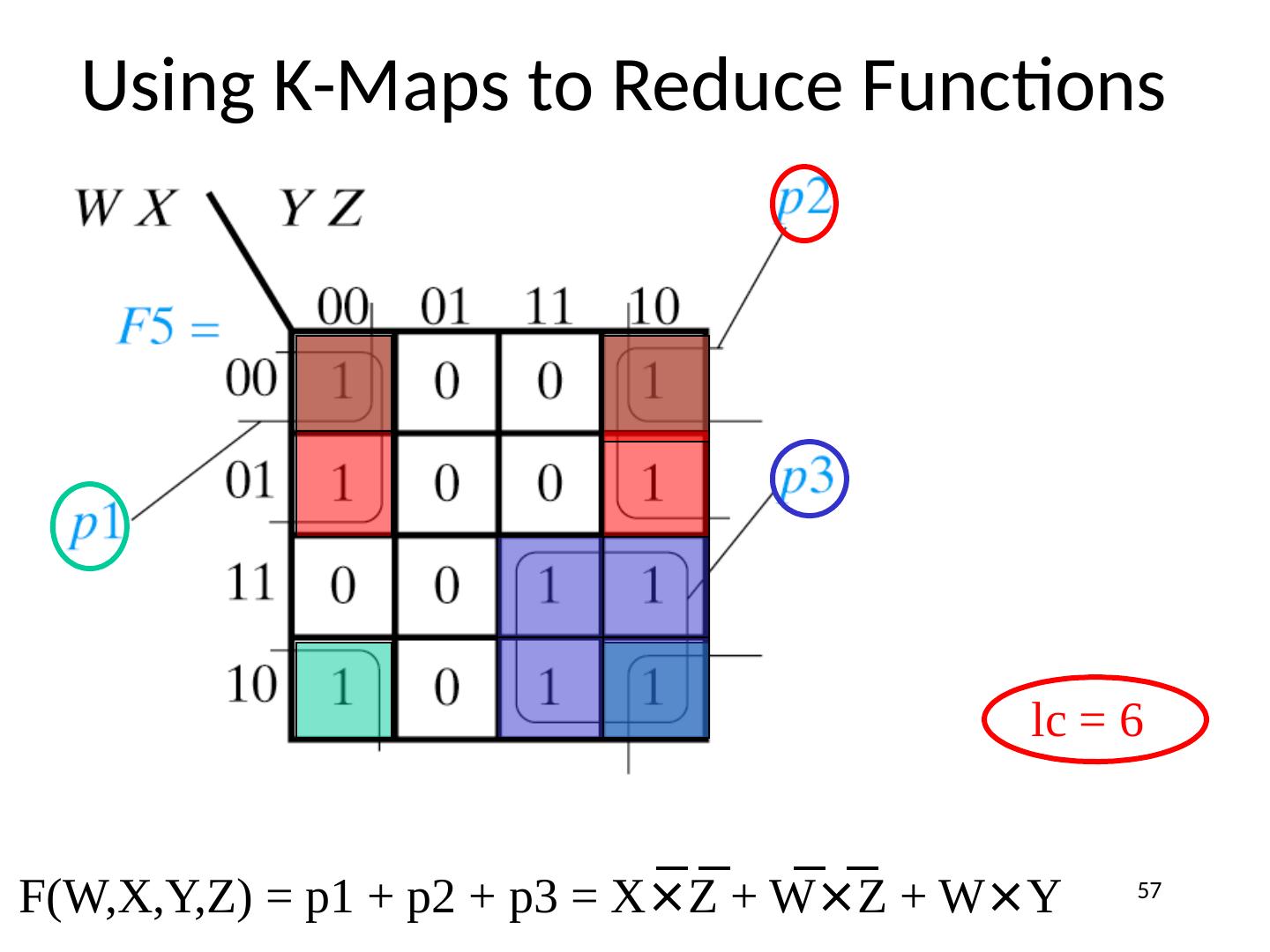
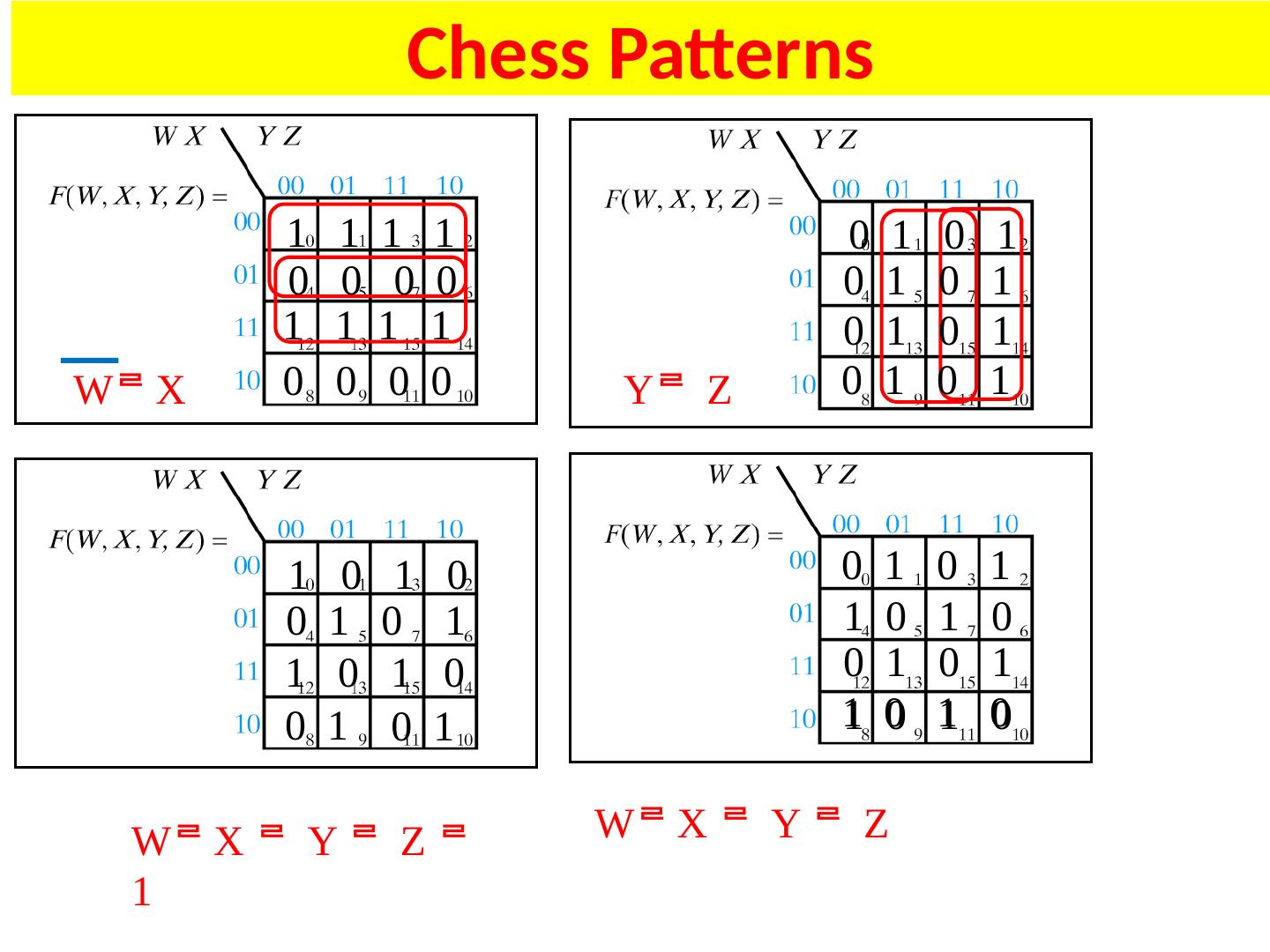
23 .Karnaugh (K) Maps A graphical representation of Boolean function Easy to perform functional reduction Relies on adjacency (Gray code) of minterms Adjacent (horizontal/vertical & wrap around) cells differ in only one variable (complement) Number form and Variable form 23
24 .K-Maps 2 Variable K-Map (Number Form) Gray code! Minterm numbers 24
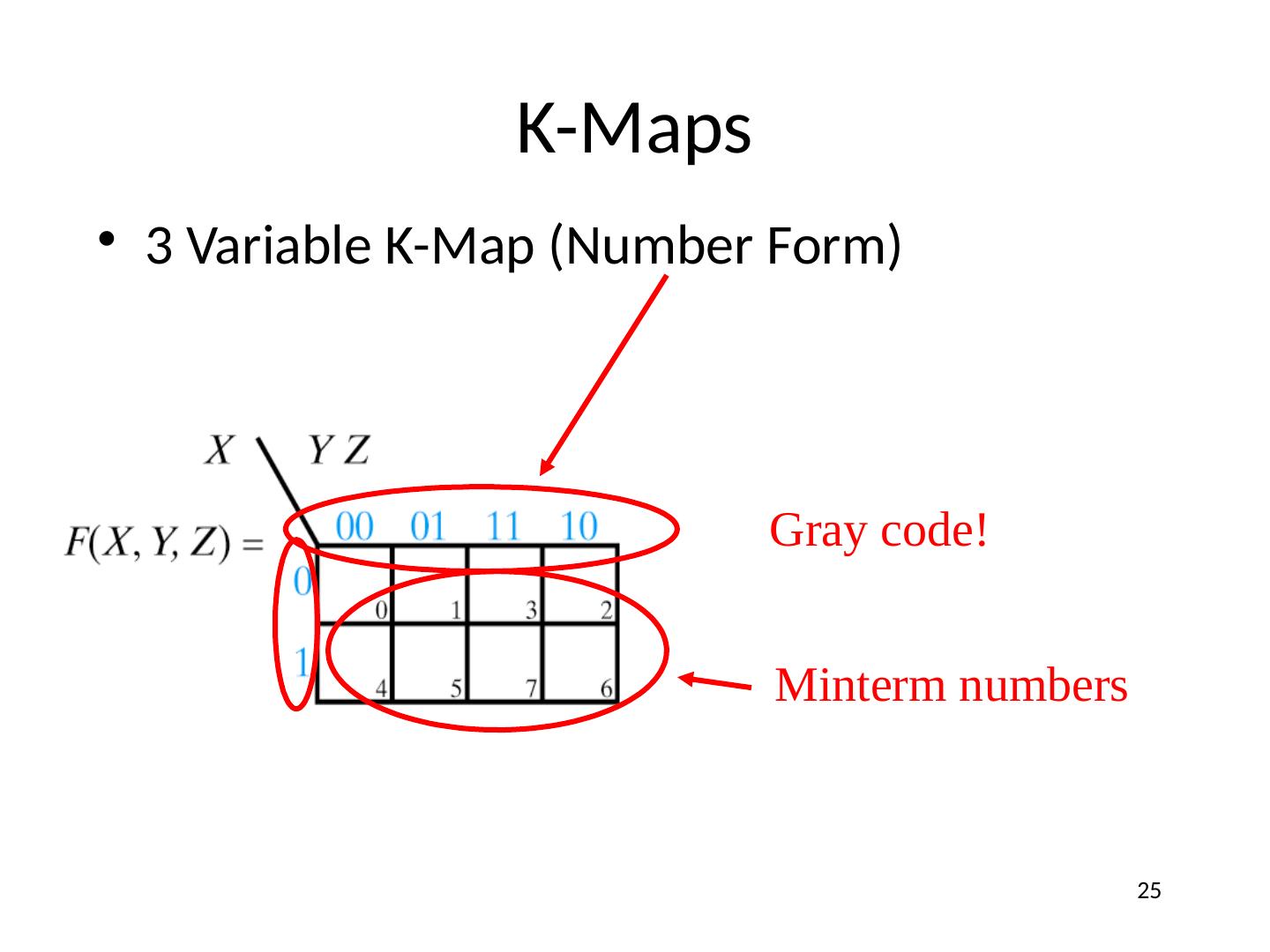
25 .K-Maps 3 Variable K-Map (Number Form) Gray code! Minterm numbers 25
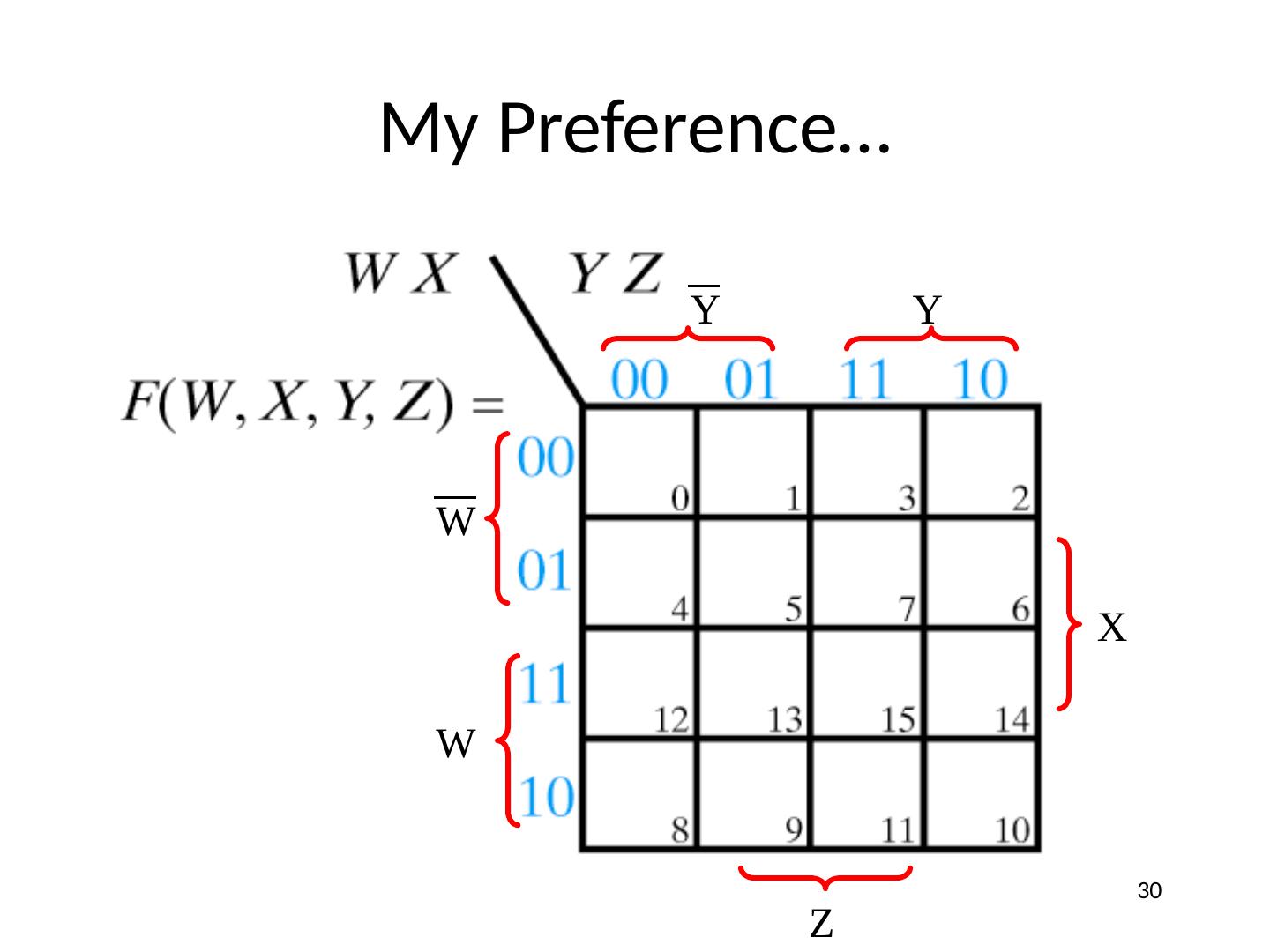
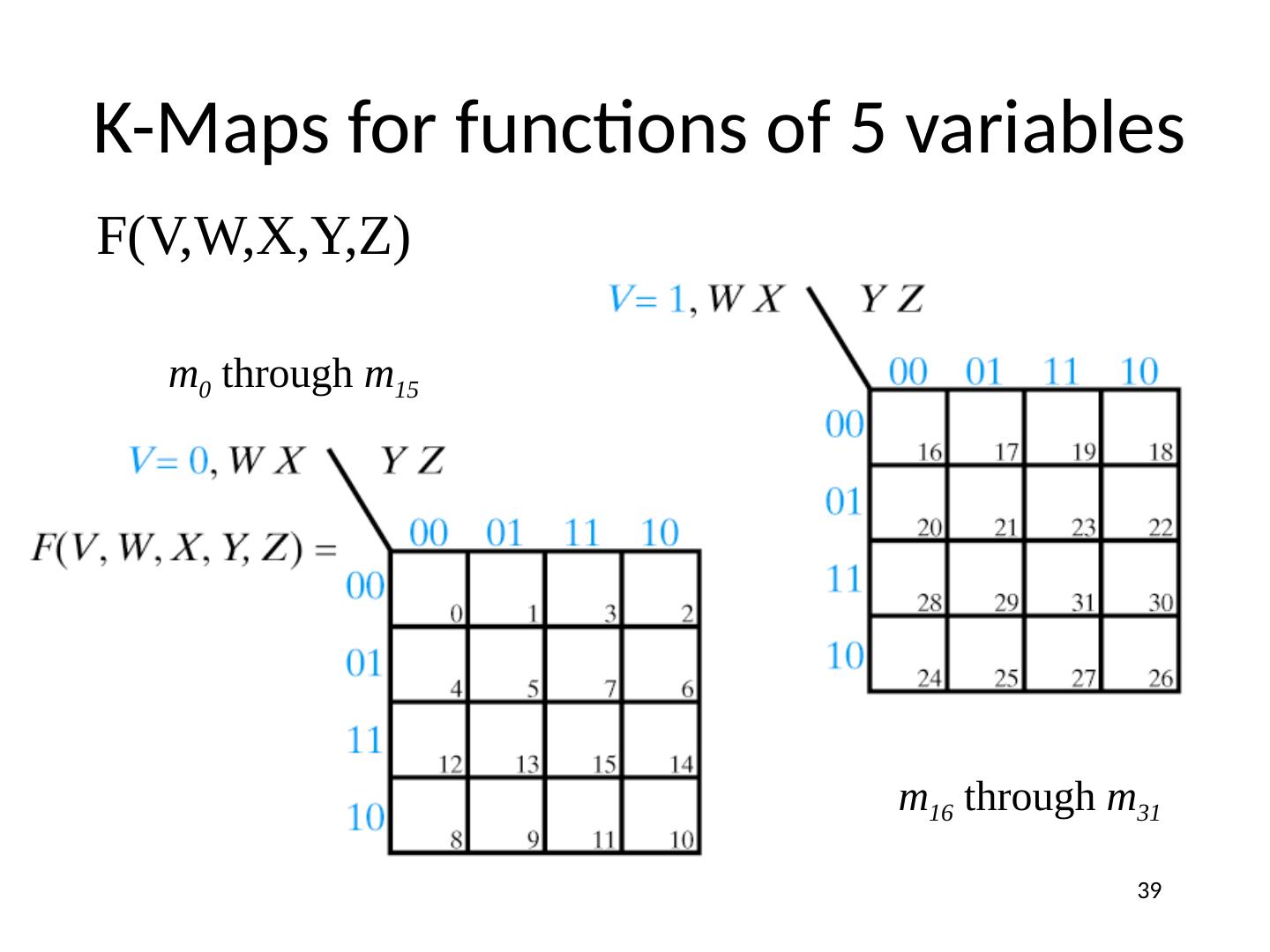
26 .K-Maps 4 Variable K-Map (Number Form) Gray code! Minterm numbers 26
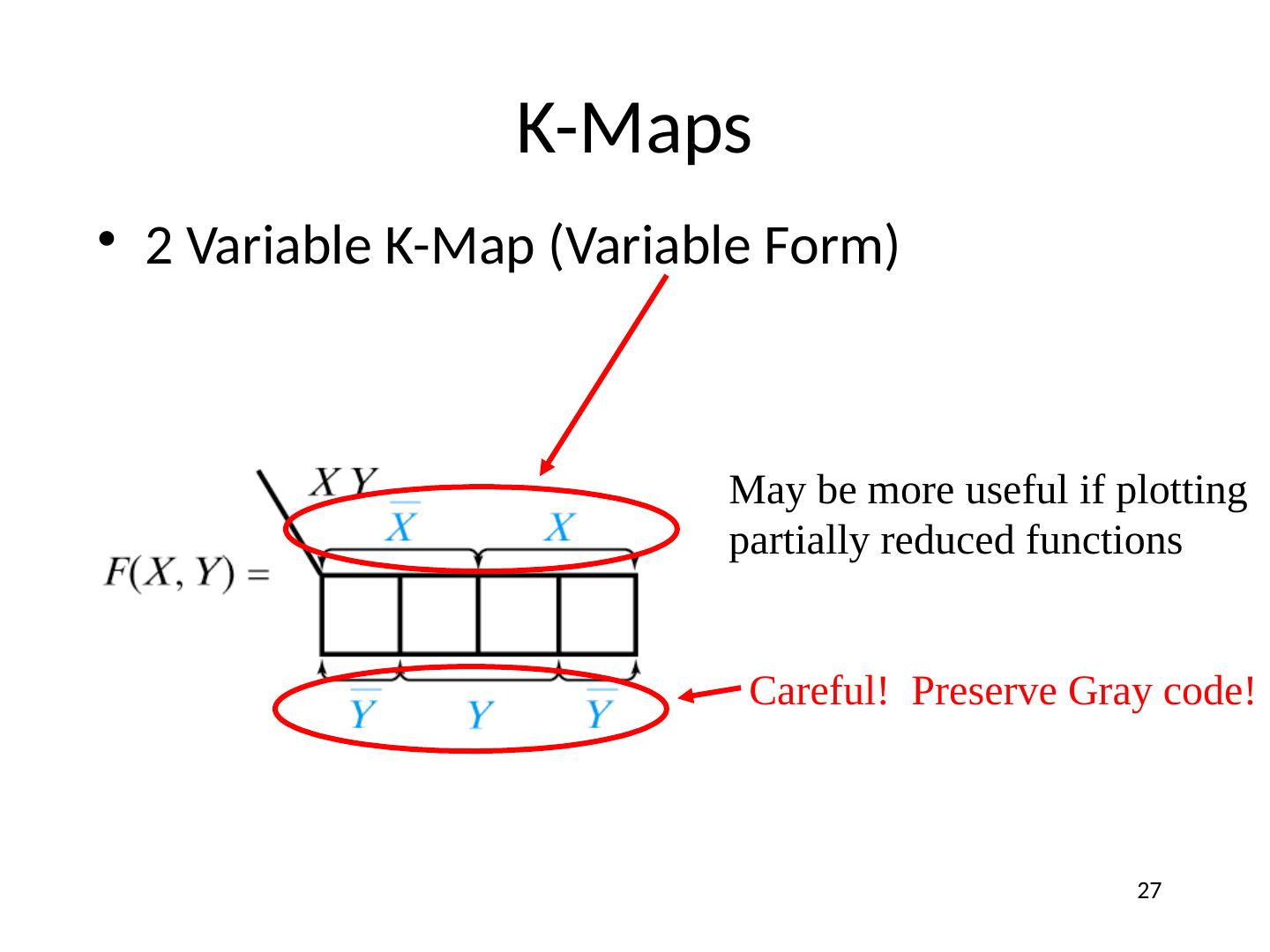
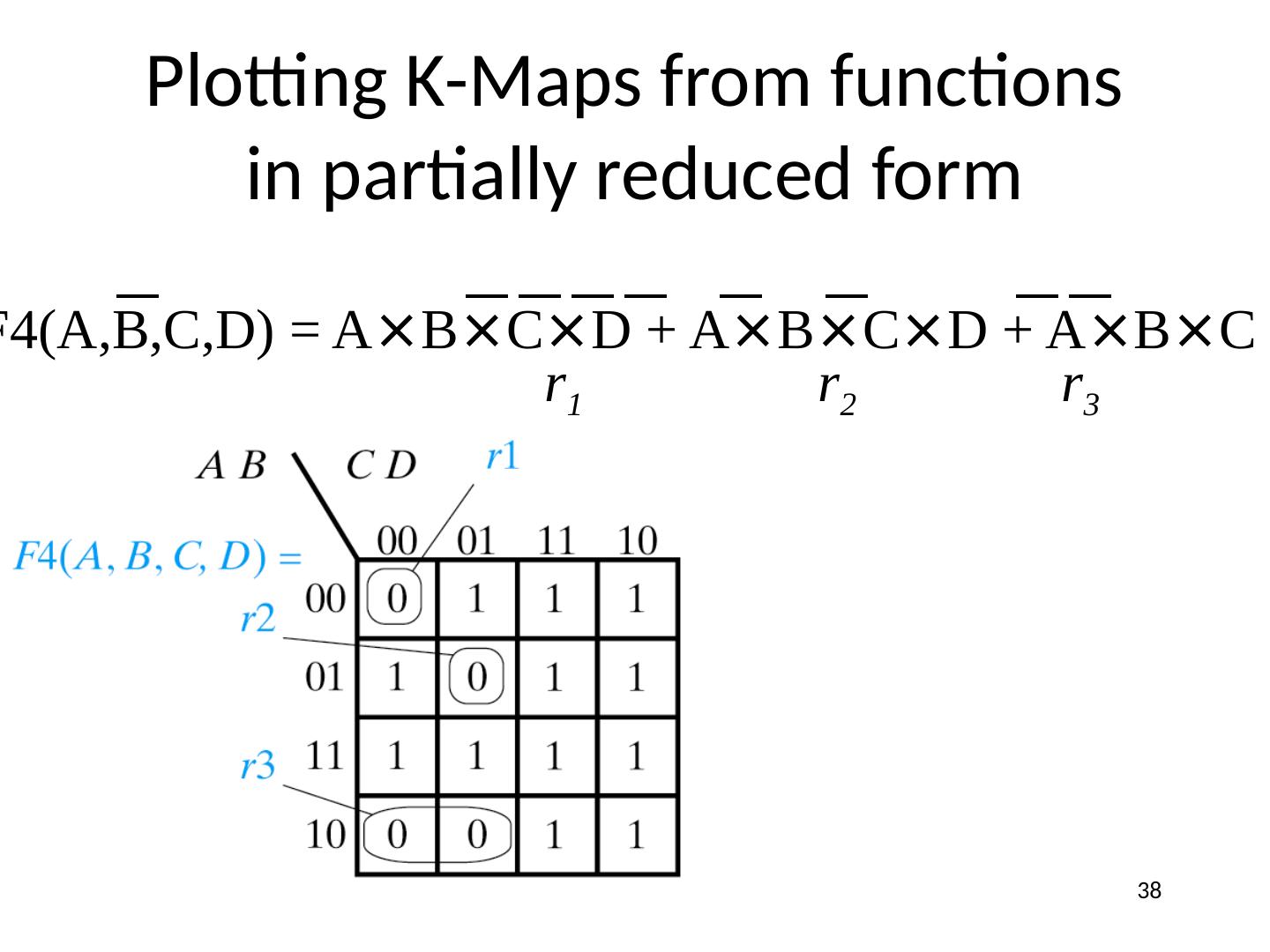
27 .K-Maps 2 Variable K-Map (Variable Form) May be more useful if plotting partially reduced functions Careful! Preserve Gray code! 27
28 .K-Maps 3 Variable K-Map (Variable Form) 28
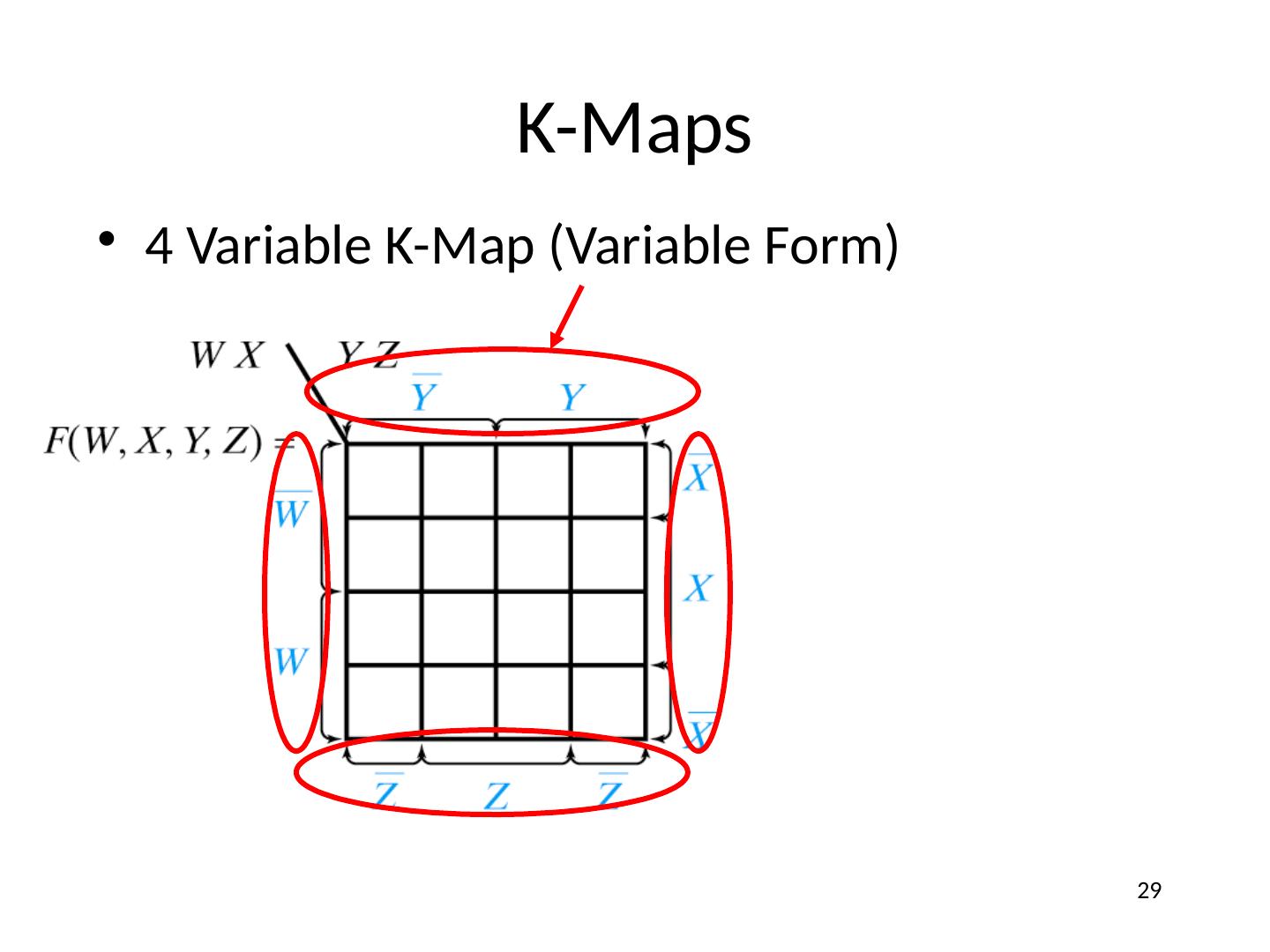
29 .K-Maps 4 Variable K-Map (Variable Form) 29