Classical Distributed Algorithms with DDS

1 . Classical Distributed Algorithms with DDS Sara Tucci-Piergiovanni, PhD Angelo Corsaro, PhD Researcher Chief Technology Officer CEA LIST PrismTech 

2 . Outline •  DDS and QoS, properties of streams and local caches •  Advanced properties on local caches: the eventual queue •  Implementation of the eventual queue based on Lamport’s distributed mutual exclusion algorithm •  Dealing with failures, mutual exclusion implemented as a Paxos-like algorithm •  Concluding Remarks 

3 .DDS and QoS, properties of streams and local caches 

4 . DDS streams •  DDS let multiple writers/readers produce and consume streams of data, like this: w (1) w (2) w(3) dataWriter r ():1 r ():2 r() :3 dataReader 

5 . QoS: properties on streams (1/3) •  legal stream of reads Reliability Policy = Best Effort w (1) w (2) w(3) dataWriter r(): 1 r (): nil r (): nil dataReader Proactive read, only new values Non-blocking write 

6 . QoS properties on streams (2/3) •  legal stream of reads if Reliable Policy = Reliable à the last value is eventually read w (1) w (2) w(3) dataWriter r ( ; 1) r () : nil r ( ; 3) dataReader 

7 . QoS properties on streams (3/3) •  legal stream of reads if Reliable Policy = Reliable, History = keepAllà all the values are eventually read w (1) w (2) w(3) dataWriter r (): 1 r () : nil r(): [2,3] dataReader History defines how many ‘samples’ to keep in the local cache 

8 . Local Caches and Message Arrivals w (1) w (2) w(3) dataWriter r (): 1 r () : nil r(): [2,3] dReader1 1 The update arrives after 1 the read 2 3 r (): 1 r () : 2 r():3 dReader2 1 1 1 2 2 3 

9 . Local Caches and Message Arrivals •  Writer crash - eventual semantics is not guaranteed: dReader2 misses 3 w (1) w (2) w(3) dataWriter r (): 1 r () : nil r(): [2,3] dReader1 1 The update arrives after 1 the read 2 3 r (): 1 r () : 2 r():nil dReader2 1 1 1 2 2 

10 . Fault-Tolerant Reliable Multicast •  First useful abstraction to guarantee eventual consistency in case of writer failure •  Many possible implementations ranging from deterministic flooding to epidemic diffusion. §  History= = KeepLast(1) q  Possible Implementation: Push with Failure Detectors: each process (data reader) relays the last message when it suspects the writer to be failed (optimizations are possible). §  History = keep all q  Sending the last value does not suffice, local caches should be synchronized from time to time •  Let us remark that different protocols could be implemented. Depending on the history QoS setting the best suited protocol will be employed. •  However, FT Reliable Multicast is best implemented as an extension of the DDSI/RTPS wire protocol. Some DDS implementations, such as OpenSplice, provide FT Reliable Multicast as yet another level of Reliability Policy •  In the context of this presentation we focused on user-level mechanisms 

11 . DDS Caches’ Properties Local Caches benefit of eventual consistency in absence of failures DDS provides an eventual consistency model where W=0 (number of acks expected before completing a write) and R=1 (number of « replicas » accessed to retrieve data). This means that data is eventually written on all « destinations » but is only read locally With failures, eventual consistency only implementing a fault-tolerant reliable multicast What about stronger properties on caches? Let’s try to implement a global queue producers consumers 

12 .Advanced properties on local caches: the eventual queue 

13 . Properties on caches Local Caches benefits of eventual consistency in absence of failures With failures, eventual consistency only implementing a fault-tolerant reliable multicast What about stronger properties on caches? Let’s try to implement a global queue .enq( ) 

14 . Properties on caches Local Caches benefits of eventual consistency in absence of failures With failures, eventual consistency only implementing a fault-tolerant reliable multicast What about stronger properties on caches? Let’s try to implement a global queue .enq( ) 

15 . Properties on caches Local Caches benefits of eventual consistency in absence of failures With failures, eventual consistency only implementing a fault-tolerant reliable multicast What about stronger properties on caches? Let’s try to implement a global queue .enq( ) 

16 . Properties on caches Local Caches benefits of eventual consistency in absence of failures With failures, eventual consistency only implementing a fault-tolerant reliable multicast What about stronger properties on caches? Let’s try to implement a global queue .deq( ) 

17 . Properties on caches Local Caches benefits of eventual consistency in absence of failures With failures, eventual consistency only implementing a fault-tolerant reliable multicast What about stronger properties on caches? Let’s try to implement a global queue .deq( ) 

18 . Properties on caches Local Caches benefits of eventual consistency in absence of failures With failures, eventual consistency only implementing a fault-tolerant reliable multicast What about stronger properties on caches? Let’s try to implement a global queue .deq( ) 

19 . Eventual Consistent Queue We are not interested in guaranteeing one-copy serializability: §  If a process performs enq(a) at some point t and the queue is empty, the subsequent deq() will get a. §  If a process performs deq(a), no other process will perform deq(a) Serializability would seriously limit concurrency We propose a weaker, but still useful, semantics for the queue: Eventual Queue §  (Eventual Dequeue) if a process performs an enq(a), and there exists an infinite number of subsequent deq(), eventually some process will perform deq(a). §  (Unique Dequeue) If a correct* process performs deq(a), no other process will perform deq(a) *correct process=process that never crashes 

20 . Eventual Dequeue .enq( ) .enq( ) (Eventual Dequeue) if a process performs an enq(a), and there exists an infinite numbers of subsequente deq(), eventually some process will perform deq(a). 

21 . Eventual Dequeue .deq( ) .deq( )… .deq( ) (Eventual Dequeue) if a process performs an enq(a), and there exists an infinite numbers of subsequente deq(), eventually some process will perform deq(a). The order in which values are de-queued is not guaranteed to be the order in which they have been enqueued. Some value enqueued after could be de-queued before , but eventually each value will be de-queued. 

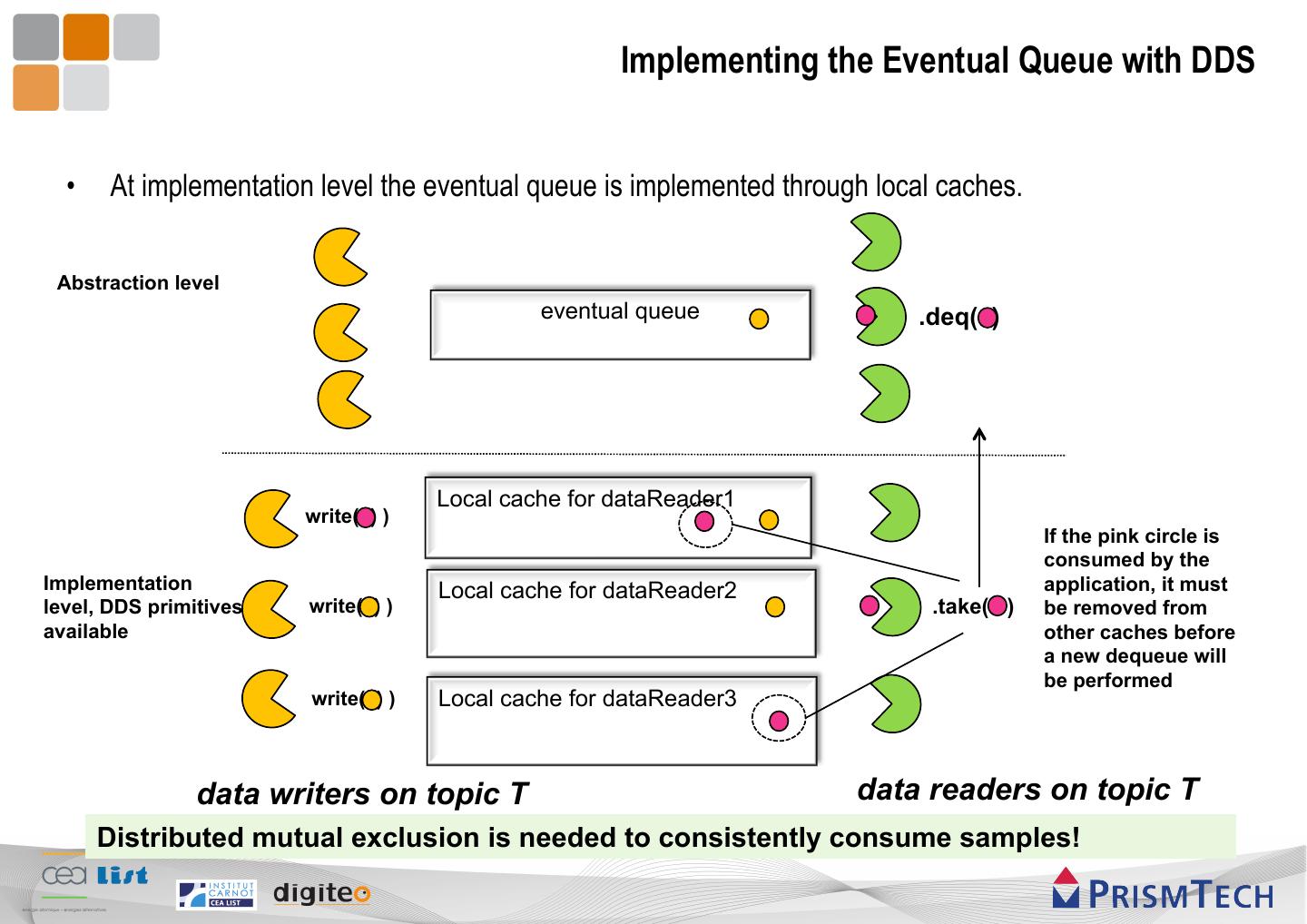
22 . Implementing the Eventual Queue with DDS •  At implementation level the eventual queue is implemented through local caches. Abstraction level eventual queue .deq( ) Local cache for dataReader1 write( ) ) If the pink circle is consumed by the Implementation Local cache for dataReader2 application, it must level, DDS primitives write( ) ) .take( ) be removed from available other caches before a new dequeue will be performed write( ) ) Local cache for dataReader3 data writers on topic T data readers on topic T Distributed mutual exclusion is needed to consistently consume samples! 

23 . Queue Abstract Interface •  In terms of programming API our distributed Queue implementation is specified as follows: 1 abstract class Queue[T] {! 2! 3 def enqueue(t: T)! 4! 5 def dequeue(): Option[T]! 6! 7 def sdequeue(): Option[T]! 8! 9 def length: Int! 10! 11 def isEmpty: Boolean = length == 0! 12! 13 }! •  The operation above have exactly the same semantics of the eventual queue formally specified a few slides back 

24 .Implementing the Distributed Queue in DDS 

25 . A Distributed Mutual Exclusion Based Distributed-Queue •  Different distributed algorithms can be used to implement the specification of our Eventual Queue •  In a first instance we’ll investigate an extension of Lamport’s Distributed Mutual Exclusion for implementing an Eventual Distributed Queue •  In these case the enqueue and the dequeue operations are implemented by the following protocol: enqueue(): dequeue(): •  Do a DDS write §  If the the “local” cache is empty then return “None” §  Otherwise start the Distributed Mutual Exclusion Algorithm §  Once entered on the critical section, pick an item from the queue §  Ask all other group members to POP this element from their “local” cache §  Exit the critical section and ACK other member if necessary §  Return the data to the application 

26 . A Distributed Mutual Exclusion Based Distributed-Queue •  Data readers will issue a request to perform a take on their own local cache (set of requesters) •  The same set of data readers will acknowledge the access to the local cache (set of acceptors) Assumptions •  We need to know the group of requesters/acceptors in advance, a total order on their IDs must be defined •  FIFO channels between data readers •  No synchronization between clocks, no assumptions on bounds for message delays: the algorithm is based on logical clocks 

27 . Implementation 1 -A possible run deq():a (1,1) (1,1) (3,2) app 1 (1,2) 1 1 2 3 3 4 a, ts req {ts, (1,1)} ack {ts,(4,2)} b, ts’ b pop{ts, (1,3)} deq():b req {ts, (1,2)} ack {ts,(2,2)} req{ts’(3,2)} pop{ts, (1,3)} app 2 (1,2) (1,1) 1 (1,2) 2 3 1 a, ts b, ts’ b 

28 . In DDS Terms.. •  To implement this algorithm it is required that §  DEQUEUE/ACK/POP messages are FIFO §  POPs issued by a member are received before its ACKs that release control •  This leads to use a single topic/topic type for all commands and a single data-writer for writing them •  The queue implementation uses only two topics defined as follows: §  Topic(name = QueueElement, type = TQueueElement, QoS = {Reliability.Reliable, History.KeepAll}) §  Topic(name = QueueCommand, type = TQueueCommand, QoS = {Reliability.Reliable, History.KeepAll}) 9 enum TCommandKind {! 1 typedef sequence<octet> TData;! 10 DEQUEUE,! 2 struct TQueueElement {! 11 ACK,! 3 TLogicalClock ts;! 12 POP! 4 TData data;! 13 };! 5 };! 14 ! 6 #pragma keylist TQueueElement! 15 struct TQueueCommand {! ! 16 TCommandKind kind;! 17 long mid;! 18 TLogicalClock ts;! 19 };! 20 #pragma keylist TQueueCommand! ! 

29 . Sample Application •  Let’s see what it would take to create a multi-writer multi-reader distributed queue where writers enqueue messages that should be consumed by one and only one reader .enq( ) .enq( )