Lessons in Linear Algebra at Scale with Apache Spark

1 .WIFI SSID:SparkAISummit | Password: UnifiedAnalytics 

2 .Lessons In Linear Algebra At Scale With Apache Spark Let’s make the sparse details a bit more dense Anna Holschuh, Target #UnifiedAnalytics #SparkAISummit 

3 .What This Talk is About • A journey in building a text-based similarity engine • Brief Basic Linear Algebra Refresher • Linear Algebra at Scale in Spark • Focus on Scala with code examples #UnifiedAnalytics #SparkAISummit 3 

4 .Who am I • Lead Data Engineer/Scientist at Target since 2016 • Deep love of all things Target • Other Spark Summit talks: o 2018: Extending Apache Spark APIs Without Going Near Spark Source Or A Compiler o 2019: Parallelizing With Apache Spark In Unexpected Ways #UnifiedAnalytics #SparkAISummit 4 

5 .Agenda • Motivation • A Similarity Engine • Linear Algebra in Spark • Lessons Learned #UnifiedAnalytics #SparkAISummit 5 

6 .Agenda • Motivation • A Similarity Engine • Linear Algebra in Spark • Lessons Learned #UnifiedAnalytics #SparkAISummit 6 

7 .Motivation Neighbors The • For a core object with rich text-based attributes, we slow wanted to create a system that would return the N brown most similar objects for a given input object at scale. fox Score: 0.75 • The goal was to first produce the raw data and then Input build a configurable component that could be pulled The The into other computation engines. quick quick brown orange • The question of similarity is foundational and is addressed in a variety of ways across many fox cat disciplines: Text Mining, Information Retrieval, Entity Score: 0.50 Resolution, Recommendation Engines, etc. A slow • scikit-learn and pyspark were first used to implement KNN in an MVP. This first pass struggled to scale brown and this is where Spark and Scala were introduced. dog Score: 0.25 #UnifiedAnalytics #SparkAISummit 7 

8 .Agenda • Motivation • A Similarity Engine • Linear Algebra in Spark • Lessons Learned #UnifiedAnalytics #SparkAISummit 8 

9 .A Similarity Engine Neighbors The GOALS slow brown • For an input object, the system should return the Input fox N most similar objects in the system Score: 0.75 The The • It should work off of a corpus of 40k total objects quick quick brown orange • It should support a vocabulary that has 15k fox cat tokens Score: 0.50 • It should be able to compute pairwise scores A slow across the entire corpus brown dog • It should perform in a reasonable amount of time Score: 0.25 (on the order of minutes) #UnifiedAnalytics #SparkAISummit 9 

10 .A Similarity Engine K-Nearest Neighbors (KNN) Brute Force Cosine Similarity • The most naïve approach • A pairwise scoring approach to compute one number between 0 and 1 • Unsupervised learning method representing the similarity of two vectors • Data is represented in a Vector/Matrix format • Computes pairwise scores between all pairs of points in the Dataset. For N samples and D dimensions, the scale of this method is O[DN2] #UnifiedAnalytics #SparkAISummit 10 

11 .A Similarity Engine Bag of Words Representation How do we represent our features in such a system? Represent Features in a Collect Raw Features Build a Feature Vocab Matrix the,quick,brown,fox,slow,orange,cat,a,dog The quick brown fox 1 1 1 1 0 0 0 0 0 1 1 1 1 0 0 0 0 0 The slow brown fox 1 0 1 1 1 0 0 0 0 1 0 1 1 1 0 0 0 0 1 1 0 0 0 1 1 0 0 The quick orange cat 1 1 0 0 0 1 1 0 0 0 0 1 0 1 0 0 1 1 A slow brown dog 0 0 1 0 1 0 0 1 1 #UnifiedAnalytics #SparkAISummit 11 

12 .A Similarity Engine Cosine Similarity • A measure of similarity between two vectors that measures the cosine of the angle between them • The cosine function is periodic and ranges from -1 to 1 • Vectors that are relatively close to one another cos(x) x2 will have a score that approaches 1. Vectors that are orthogonal will have a score of 0. Vectors that are diametrically opposed will have a score of -1 • Cosine similarity is often used to generate scores in the positive space from 0 to 1. x1 • This measurement handles sparse data well as only non-zero dimensions are considered. References: Wolfram Alpha, Wikipedia #UnifiedAnalytics #SparkAISummit 12 

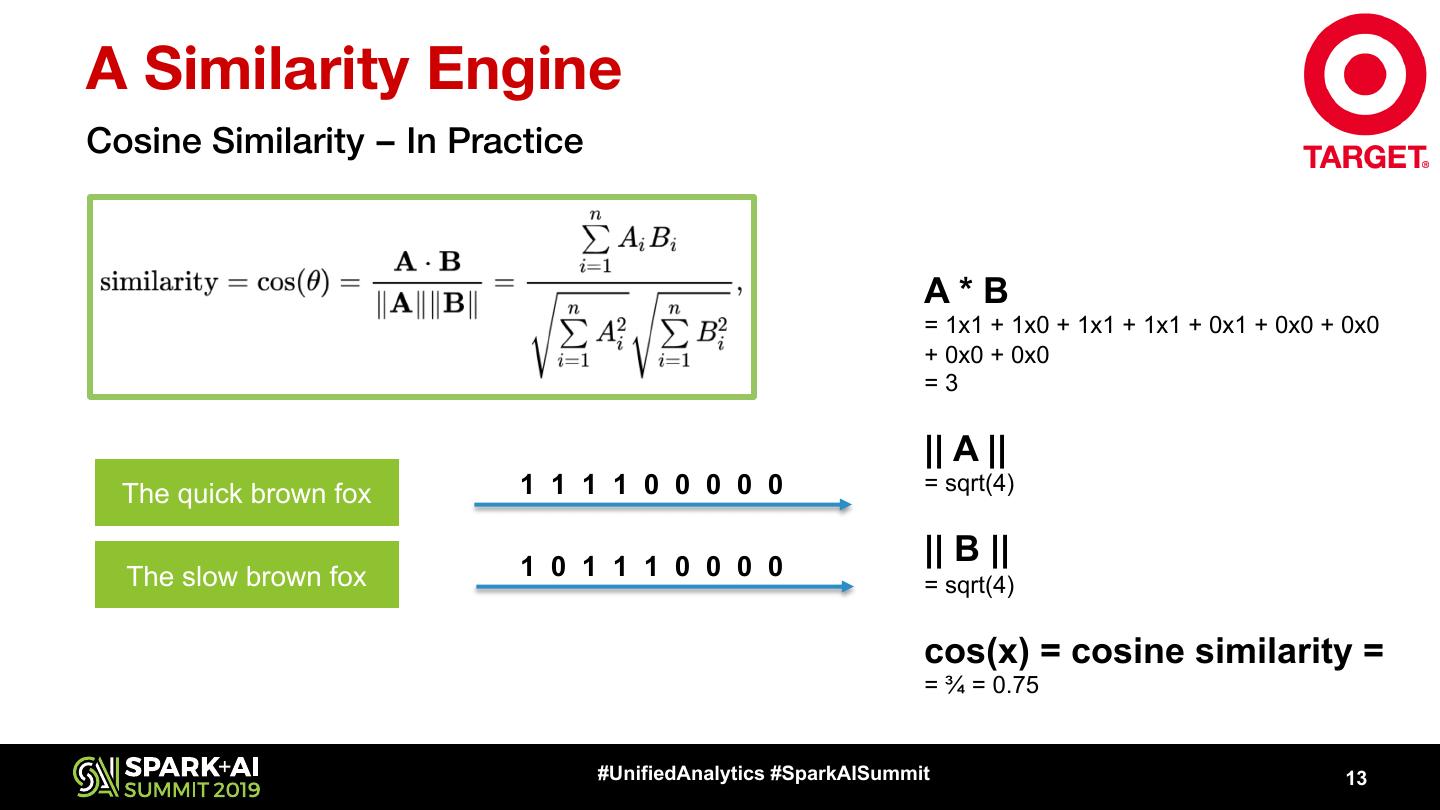
13 .A Similarity Engine Cosine Similarity – In Practice A*B = 1x1 + 1x0 + 1x1 + 1x1 + 0x1 + 0x0 + 0x0 + 0x0 + 0x0 =3 || A || The quick brown fox 1 1 1 1 0 0 0 0 0 = sqrt(4) 1 0 1 1 1 0 0 0 0 || B || The slow brown fox = sqrt(4) cos(x) = cosine similarity = = ¾ = 0.75 #UnifiedAnalytics #SparkAISummit 13 

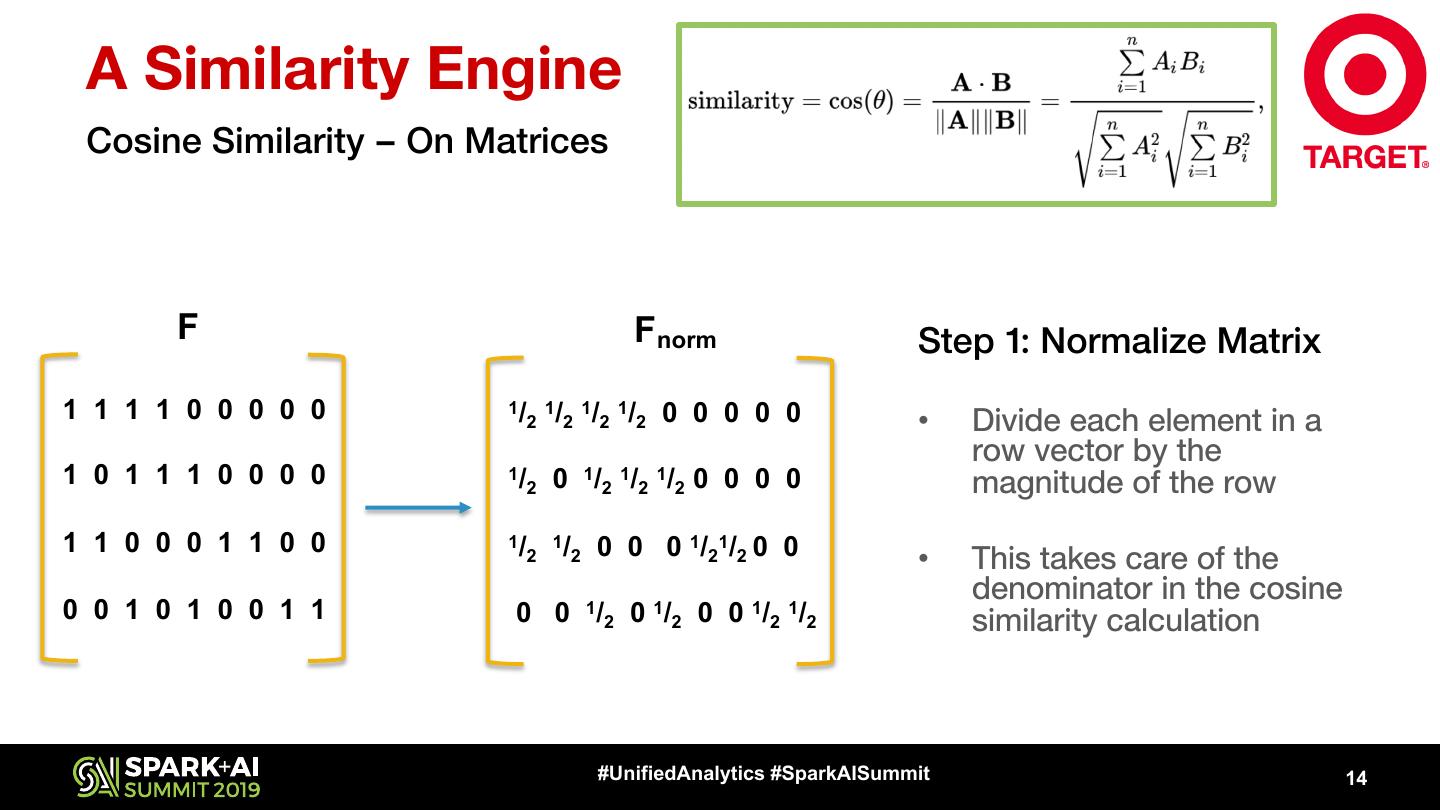
14 . A Similarity Engine Cosine Similarity – On Matrices F Fnorm Step 1: Normalize Matrix 1 1 1 1 0 0 0 0 0 1/ 1/ 1/ 1/ 2 2 2 2 0 0 0 0 0 • Divide each element in a row vector by the 1 0 1 1 1 0 0 0 0 1/ 2 0 1/2 1/2 1/2 0 0 0 0 magnitude of the row 1 1 0 0 0 1 1 0 0 1/ 1/ 0 0 0 1/21/2 0 0 2 2 • This takes care of the denominator in the cosine 0 0 1 0 1 0 0 1 1 0 0 1/2 0 1/2 0 0 1/2 1/2 similarity calculation #UnifiedAnalytics #SparkAISummit 14 

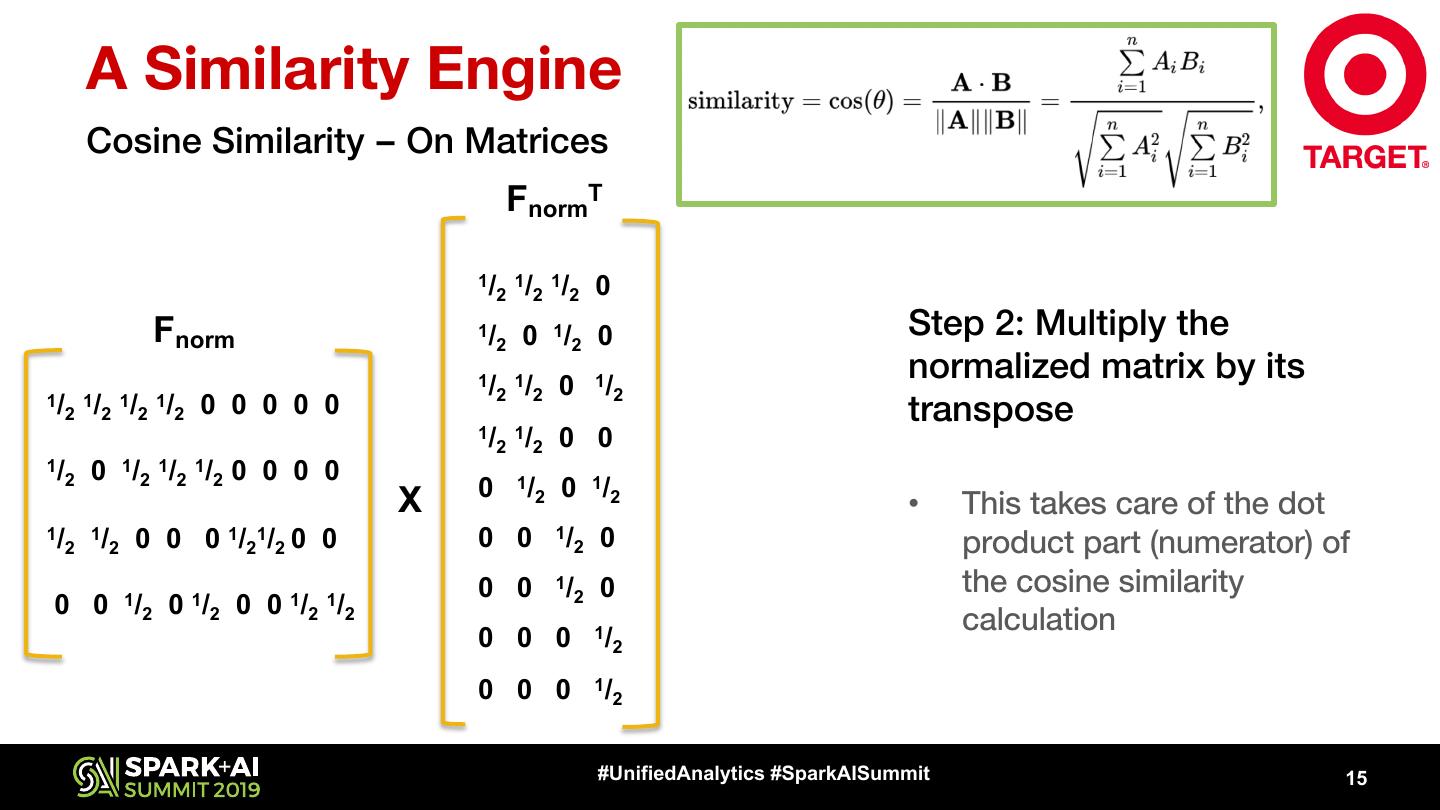
15 . A Similarity Engine Cosine Similarity – On Matrices FnormT 1/ 1/ 1/ 0 2 2 2 Fnorm 1/ 2 0 1/2 0 Step 2: Multiply the 1/ 1/ 0 1/ normalized matrix by its 2 2 2 1/ 1/ 1/ 1/ 2 2 2 2 0 0 0 0 0 1/ 1/ transpose 2 2 0 0 1/ 0 1/2 1/2 1/2 0 0 0 0 2 0 1/ 0 1/2 X 2 • This takes care of the dot 1/ 1/ 2 2 0 0 0 1/ 1/ 2 2 0 0 0 0 1/ 2 0 product part (numerator) of 0 0 1/ 2 0 the cosine similarity 0 0 1/2 0 1/2 0 0 1/2 1/2 calculation 0 0 0 1/ 2 0 0 0 1/ 2 #UnifiedAnalytics #SparkAISummit 15 

16 . A Similarity Engine Pairwise Scoring Fnorm X FnormT = Scores 4x9 9x4 4x4 Pairwise Scoring The quick brown fox • Produces a square, 1 3/ 4 1/ 1/ 2 4 symmetric matrix 3/ 4 1 1/ 1/ 4 2 The slow brown fox 1/ 1/ • The diagonal is always 2 4 1 0 ones, representing that a The quick orange cat 1/ 1/ 0 1 feature is perfectly similar 4 2 with itself A slow brown dog • Rows can be read to find the indices of objects that are the best match #UnifiedAnalytics #SparkAISummit 16 

17 .A Similarity Engine Putting it all together Moving to Spark • We want to leverage this same exact approach at scale • Instead of dealing with 4 features with 9 vocabulary words, we want to deal with upwards of 40k features with upwards of 15k vocabulary words • We want to be able to distribute this large scale computation across a cluster • We want this to be performant and reliable #UnifiedAnalytics #SparkAISummit 17 

18 .Agenda • Motivation • A Similarity Engine • Linear Algebra in Spark • Lessons Learned #UnifiedAnalytics #SparkAISummit 18 

19 .Linear Algebra in Spark Getting Started • Completed this work using Spark 2.2 • There is no Spark MLlib KNN implementation available • That’s ok, because we know how to carry out this computation at a low level with Linear Algebra concepts • The next step is to dig into Spark’s APIs for Linear Algebra #UnifiedAnalytics #SparkAISummit 19 

20 .Linear Algebra in Spark Local Vector • Int, 0-based indices, double-typed • Able to be stored on a single values machine • Sparse and Dense • Building block for local and distributed matrices in Spark References: https://spark.apache.org/docs/2.2.0/mllib-data-types.html #UnifiedAnalytics #SparkAISummit 20 

21 .Linear Algebra in Spark Distributed Matrix APIs RowMatrix CoordinateMatrix • Each entry is a tuple of (i: Long, j: Long, • Row-oriented matrix represented by an value: Double) RDD[Vector] • Should only be used when both • No meaningful indices dimensions of the matrix are huge and the matrix is sparse IndexedRowMatrix BlockMatrix • Row-oriented matrix represented by an • A distributed matrix backed by an RDD of RDD[IndexedRow] MatrixBlocks • A MatrixBlock is a tuple of [(Int,Int),Matrix] References: https://spark.apache.org/docs/2.2.0/mllib-data-types.html #UnifiedAnalytics #SparkAISummit 21 

22 .Linear Algebra in Spark Feature Generation • We need to convert our Dataset of Articles into useful features to carry out similarity calculations on • We first need to tokenize the text contained in the article and can use Spark’s RegexTokenizer • We then need to turn a collection of tokens per article into vector bag of words representations across the entire vocabulary corpus • We use the CountVectorizer, although there are other options available • This works great! No problems here. #UnifiedAnalytics #SparkAISummit 22 

23 .Linear Algebra in Spark Feature Generation, continued • We also need to normalize our features before we carry out matrix multiplication to generate scores • We can use Spark’s Normalizer to carry this out • Again, this works great! No problems here. #UnifiedAnalytics #SparkAISummit 23 

24 .Linear Algebra in Spark Pairwise Scoring – Attempt 1 • THIS CODE DOES NOT WORK • We need to generate a feature set of bag of words vectors and multiply this matrix by itself to generate cosine similarity scores • Working in the IndexedRowMatrix API seems most intuitive for what we’re trying to accomplish #UnifiedAnalytics #SparkAISummit 24 

25 .Linear Algebra in Spark Lessons Learned • Transpose is only available on the BlockMatrix and CoordinateMatrix APIs • Multiply is only available when both matrices are distributed on the BlockMatrix API • (Multiplying by a local Matrix is available on the RowMatrix and IndexedRowMatrix APIs) • BlockMatrix API it is… #UnifiedAnalytics #SparkAISummit 25 

26 .Linear Algebra in Spark Pairwise Scoring – Attempt 2 • THIS CODE DOES NOT WORK • We attempt to work in the BlockMatrix API instead to make use of transpose and multiply. • Converting back and forth between different Distributed matrix APIs can be expensive, so if this works, we’d go back and start out in that API. • This code compiles • This code blows up on a relatively hefty cluster with OOM errors #UnifiedAnalytics #SparkAISummit 26 

27 .Linear Algebra in Spark Lessons Learned • BlockMatrix is the only Distributed Matrix API that supports multiplying two distributed matrices • It accomplishes its multiply on SparseMatrices by converting them to DenseMatrices • One can configure the number of rows and columns contained in a block, so the tradeoff can be made between alleviating memory pressure during the toDense operation and increasing the number of operations involved in the multiply with more blocks #UnifiedAnalytics #SparkAISummit 27 

28 .Linear Algebra in Spark Back to the drawing board • It would be ideal to keep things in a Sparse representation throughout the multiply operation • Idea 1: Use the CoordinateMatrix API to manually manage the transpose and multiplication based on coordinates o This seems like it would generate a lot of shuffle activity • Idea 2: Go back to IndexedRowMatrix and broadcast smaller chunks of the matrix to be used in local multiplication on executors. o Digging through the source code also shows these matrices are converted to dense • Idea 3: Wrap SparseVectors in a Dataset/RDD to be distributed and broadcast smaller chunks of Vectors to be locally assembled into matrices for multiplication. #UnifiedAnalytics #SparkAISummit 28 

29 .Linear Algebra in Spark Pairwise Scoring – Attempt 3 • Going with Idea 3 • THIS CODE DOES NOT WORK • We would like to wrap a SparseVector to pass around in a Dataset for manually managing the multiplication #UnifiedAnalytics #SparkAISummit 29