Learning to Optimize Join Queries With Deep Reinforcement Learni

1 . Learning to Optimize Join Queries With Deep Reinforcement Learning Sanjay Krishnan1,2 , Zongheng Yang1 , Ken Goldberg1 , Joseph M. Hellerstein1 , Ion Stoica1 1 RISELab, UC Berkeley 2 Computer Science, University of Chicago skr@cs.uchicago.edu {zongheng, goldberg, hellerstein, istoica}@berkeley.edu ABSTRACT 1 INTRODUCTION Exhaustive enumeration of all possible join orders is often Join optimization has been studied for more than four avoided, and most optimizers leverage heuristics to prune the decades [44] and continues to be an active area of re- search space. The design and implementation of heuristics search [33, 40, 49]. The problem’s combinatorial complexity are well-understood when the cost model is roughly linear, leads to the ubiquitous use of heuristics. For example, clas- and we find that these heuristics can be significantly subop- sical System R-style dynamic programs often restrict their timal when there are non-linearities in cost. Ideally, instead search space to certain shapes (e.g., “left-deep” plans). Query of a fixed heuristic, we would want a strategy to guide the optimizers sometimes apply further heuristics to large join search space in a more data-driven way—tailoring the search queries using genetic [4] or randomized [40] algorithms. In to a specific dataset and query workload. Recognizing the edge cases, these heuristics can break down (by definition), link between classical Dynamic Programming enumeration which results in poor plans [29]. methods and recent results in Reinforcement Learning (RL), In light of recent advances in machine learning, a new we propose a new method for learning optimized join search trend in database research explores replacing programmed strategies. We present our RL-based DQ optimizer, which cur- heuristics with learned ones [11, 25, 26, 32–34, 37, 41]. In- rently optimizes select-project-join blocks. We implement spired by these results, this paper explores the natural ques- three versions of DQ to illustrate the ease of integration tion of synthesizing dataset-specific join search strategies into existing DBMSes: (1) A version built on top of Apache using learning. Assuming a given cost model and plan space, Calcite, (2) a version integrated into PostgreSQL, and (3) a can we optimize the search over all possible join plans for version integrated into SparkSQL. Our extensive evaluation a particular dataset? The hope is to learn tailored search shows that DQ achieves plans with optimization costs and strategies from the outcomes of previous planning instances query execution times competitive with the native query that dramatically reduce search time for future planning. optimizer in each system, but can execute significantly faster Our key insight is that join ordering has a deep algorith- after learning (often by orders of magnitude). mic connection with Reinforcement Learning (RL) [47]. Join ACM Reference format: ordering’s sequential structure is the same problem structure Sanjay Krishnan1,2 , Zongheng Yang1 , Ken Goldberg1 , Joseph that underpins RL. We exploit this algorithmic connection M. Hellerstein1 , Ion Stoica1 1 RISELab, UC Berkeley 2 Computer to embed RL deeply into a traditional query optimizer; any- Science, University of Chicago skr@cs.uchicago.edu {zongheng, where an enumeration algorithm is used, a policy learned goldberg, hellerstein, istoica}@berkeley.edu . 2019. Learning from an RL algorithm can just as easily be applied. This in- to Optimize Join Queries With Deep Reinforcement Learn- sight enables us to achieve two key benefits. First, we can ing. In Proceedings of ACM Conference, Washington, DC, USA, seamlessly integrate our solution into many optimizers with July 2017 (Conference’17), 20 pages. the classical System R architecture. Second, we exploit the https://doi.org/10.1145/nnnnnnn.nnnnnnn nested structure of the problem to dramatically reduce the training cost, as compared to previous proposals for a “learn- Permission to make digital or hard copies of all or part of this work for ing optimizer”. personal or classroom use is granted without fee provided that copies are not To better understand the connection with RL, consider the made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components classical “bottom-up” dynamic programming solution to join of this work owned by others than ACM must be honored. Abstracting with ordering. The principle of optimality leads to an algorithm credit is permitted. To copy otherwise, or republish, to post on servers or to that incrementally builds a plan from optimal subplans of redistribute to lists, requires prior specific permission and/or a fee. Request size two, size three, and so on. Enumerated subplans are permissions from permissions@acm.org. memoized in a lookup table, which is consulted to construct Conference’17, July 2017, Washington, DC, USA a sequence of 1-step optimal decisions. Unfortunately, the © 2019 Association for Computing Machinery. ACM ISBN 978-x-xxxx-xxxx-x/YY/MM. . . $15.00 space and time complexities of exact memoization can be https://doi.org/10.1145/nnnnnnn.nnnnnnn prohibitive. Q-learning, an RL algorithm [47], relaxes the 

2 .requirement of exact memoization. Instead, it formulates optimal planning as a prediction problem: given the costs of previously enumerated subplans, which 1-step decision is most likely optimal? RL views the classic dynamic pro- gramming lookup table as a model—a data structure that summarizes enumerated subplans and predicts the value of the next decision. In concrete terms, Q-learning sets up a regression from the decision to join a particular pair of re- lations to the observed benefit of making that join on past data (i.e., impact on the final cost of the entire query plan). To validate this insight, we built an RL-based optimizer DQ that optimizes select-project-join blocks and performs join Figure 1: We consider 3 cost models for the Join Order ordering as well as physical operator selection. DQ observes Benchmark: (1) one with inexpensive index lookups, (2) one the planning results of previously executed queries and trains where the only physical operator is a hybrid hash join with an RL model to improve future search. We implement three limited memory, and (3) one that allows for the reuse of pre- versions of DQ to illustrate the ease of integration into exist- viously built hash tables. The figure plots the cost subopti- ing DBMSes: (1) A standalone version built on top of Apache mality w.r.t. optimal plans. The classical left-deep dynamic program fails on the latter two scenarios. We propose a re- Calcite [2], (2) a version integrated with PostgreSQL [3], and inforcement learning based optimizer, DQ, which can adapt (3) a version integrated with SparkSQL [7]. Deploying DQ to a specific cost model given appropriate training data. into existing production-grade systems (2) and (3) each re- quired changes of less than 300 lines of code and training data could be collected through the normal operation of the We are enthusiastic about the general trend of integrating DBMS with minimal overhead. learning techniques into database systems—not simply by One might imagine that training such a model is ex- black-box application of AI models to improve heuristics, tremely data-intensive. While RL algorithms are indeed noto- but by the deep integration of algorithmic principles that riously data-inefficient (typical RL settings, such as the Atari span the two fields. Such an integration can facilitate new games [38], require hundreds of thousands of training exam- DBMS architectures that take advantage of all of the benefits ples), we can exploit the optimal subplan structure specific of modern AI: learn from experience, adapt to new scenarios, to join optimization to collect an abundance of high-quality and hedge against uncertainty. Our empirical results with training data. From a single query that passes through a na- DQ span across multiple systems, multiple cost models, and tive optimizer, not only are the final plan and its total cost workloads. We show the benefits (and current limitations) collected as a training example, so are all of its subplans and, of an RL approach to join ordering and physical operator recursively, everything inside the exact memoization table. For selection. Understanding the relationships between RL and instance, planning an 18-relation join query in TPC-DS (Q64) classical methods allowed us to achieve these results in a data- through a bushy optimizer can yield up to 600,000 training efficient way. We hope that DQ represents a step towards a data points thanks to DQ’s Q-learning formulation. future learning query optimizer. We thoroughly study this approach on two workloads: Join Order Benchmark [29] and TPC-DS [5].DQ sees sig- 2 BACKGROUND nificant speedups in planning times (up to > 200×) rela- The classic join ordering problem is, of course, NP-hard, and tive to dynamic programming enumeration while essentially practical algorithms leverage heuristics to make the search matching the execution times of optimal plans computed by for a good plan efficient. The design and implementation of the native enumeration-based optimizers. These planning optimizer search heuristics are well-understood when the speedups allow for broadening the plan space to include cost model is roughly linear, i.e., the cost of a join is linear bushy plans and Cartesian products. In many cases, they in the size of its input relations. This assumption underpins lead to improved query execution times as well. DQ is partic- many classical techniques as well as recent work [27, 40, 44, ularly useful under non-linear cost models such as memory 49]. However, many practical systems have relevant non- limits or materialization. On two simulated cost models with linearities in join costs. For example, an intermediate result significant non-linearities, DQ improves on the plan quality exceeding the available memory may trigger partitioning, or of the next best heuristic over a set of 6 baselines by 1.7× and a relation may cross a size threshold that leads to a change 3×. Thus, we show DQ approaches the optimization time in physical join implementation. efficiency of programmed heuristics and the plan quality of It is not difficult to construct reasonable scenarios where optimal enumeration. classical heuristics dramatically fail (Figure 1). Consider 2 

3 .the query workload and dataset in the Join Order Bench- 2.2 Reinforcement Learning mark [29]. A popular heuristic from the original Selinger Bellman’s “Principle of Optimality” and the characterization optimizer is to prune the search space to only include left- of dynamic programming is one of the most important re- deep join orders. Prior work showed that left-deep plans are sults in computing [12]. In addition to forming the basis of extremely effective on this benchmark for cost models that relational query optimization, it has a deep connection to prefer index joins [29]. Experimentally, we found this to be a class of stochastic processes called Markov Decision Pro- true as well: the worst-case cost over the entire workload is cesses (MDPs), which formalize a wide range of problems only 2x higher than the true optimum (for an exponentially from path planning to scheduling. In an MDP model, an agent smaller search space). However, when we simply change the makes a sequence of decisions with the goal of optimizing a cost model to be more non-linear, consisting of (1) hybrid given objective (e.g., improve performance, accuracy). Each hash join operators that spill partitions to disk when data decision is dependent on the current state, and typically leads size exceeds available memory, or (2) hash join operators to a new state. The process is “Markovian” in the sense that that can re-use previously built hash tables, suddenly the the system’s current state completely determines its future left-deep heuristic is no longer a good idea—it is almost 50x progression. Formally, an MDP consists of a five-tuple: more costly than the true optimum. These results illustrate that in a practical sense, the search problem is unforgiving: various heuristics have different ⟨S, A, P(s, a), R(s, a), s 0 ⟩ weak spots where they fail by orders of magnitude relative to optimal. For example, success on such atypical or non- where S describes a set of states that the system can be in, A linear cost models may require searching over “bushy” plans, describes the set of actions the agent can take, s ′ ∼ P(s, a) not just left-deep ones. With new hardware innovations [8] describes a probability distribution over new states given and a move towards serverless RDBMS architectures [1], a current state and action, and s 0 defines a distribution of it is not unreasonable to expect a multitude of new query initial states. R(s, a) is the reward of taking action a in state cost models that significantly differ from existing literature, s. The reward measures the performance of the agent. The which might require a complete redesign of standard pruning objective of an MDP is to find a decision policy π : S → A, heuristics. Ideally, instead of a fixed heuristic, we would want a function that maps states to actions, with the maximum a strategy to guide the search space in a more data-driven expected reward: way—tailoring the search to a specific database instance, query workload, and observed join costs. This sets up the T −1 main premise of the paper: would it be possible to use data- arg max E R(st , at ) driven machine learning methods to identify such a heuristic π t =0 from data? subject to st +1 = P(st , at ), at = π (st ). 2.1 Example As with dynamic programming in combinatorial problems, We focus on the classical problem of searching for a query most MDPs are difficult to solve exactly. Note that the greedy plan made up of binary join operators and unary selections, solution, eagerly maximizing the reward at each step, might projections, and access methods. We will use the following be suboptimal in the long run. Generally, analytical solutions database of three relations denoting employee salaries as a to such problems scale poorly in the time horizon. running example throughout the paper: Reinforcement learning (RL) is a class of stochastic opti- mization techniques for MDPs [47]. An RL algorithm uses Emp(id, name, rank) Pos(rank, title, code) Sal(code, amount) sampling, taking randomized sequences of decisions, to build a model that correlates decisions with improvements in the Consider the following join query: optimization objective (cumulative reward). The extent to SELECT which the model is allowed to extrapolate depends on how * FROM Emp, Pos, Sal the model is parameterized. One can parameterize the model WHERE Emp.rank = Pos.rank with a table (i.e., exact parameterization) or one can use AND Pos.code = Sal.code any function approximator (e.g., linear functions, nearest neighbors, or neural networks). Using a neural network in There are many possible orderings to execute this query. For conjunction with RL, or Deep RL, is the key technique behind example, one could execute the example query as Emp ▷◁ recent results like learning how to autonomously play Atari (Sal ▷◁ Pos), or as Sal ▷◁ (Emp ▷◁ Pos). games [39] and the game of Go [45]. 3 

4 .2.3 Markov Model of Enumeration Symbol Definition Now, we will review standard “bottom-up” join enumeration, and then, we will make the connection to a Markov Deci- G A query graph. This is a state in the MDP. sion Process. Every join query can be described as a query c A join. This is an action. graph, where edges denote join conditions between tables G′ The resultant query graph after applying a join. and vertices denote tables. Any dynamic programming join J (c) A cost model that scores joins. optimizer implementation needs to keep track of its progress: Table 1: Notation used throughout the paper. what has already been done in a particular subplan (which relations were already joined up) and what options remain c 1 ◦ c 2 ... ◦ cT terminating in |V | = κG to minimize: (which relations–whether base or the result of joins–can still T be “joined in” with the subplan under consideration). The min J (c i ) c 1, ...,cT query graph formalism allows us to represent this state. i=1 subject to G i+1 = c(G i ). Definition 2.1 (Query Graph). A query graph G is an undi- Note how this problem statement exactly defines an MDP rected graph, where each relation R is a vertex and each join (albeit by convention a minimization problem rather than predicate ρ defines an edge between vertices. Let κG denote maximization). G is a representation of the state, c is a repre- the number of connected components of G. sentation of the action, the vertex merging process defines the state transition P(G, c), and the reward function is the negative cost −J . The output of an MDP is a function that Making a decision to join two subplans corresponds to maps a given query graph to the best next join. Before pro- picking two vertices that are connected by an edge and merg- ceeding, we summarize our notation in Table 1. ing them into a single vertex. Let G = (V , E) be a query graph. Applying a join c = (vi , v j ) to the graph G defines a new 2.4 Long Term Reward of a Join graph with the following properties: (1) vi and v j are re- To introduce how RL gives us a new perspective on this clas- moved from V , (2) a new vertex (vi + v j ) is added to V , and sical database optimization problem, let us first examine the (3) the edges of (vi + v j ) are the union of the edges incident greedy solution. A naive solution is to optimize each c i inde- to vi and v j . Each join reduces the number of vertices by pendently (also called Greedy Operator Optimization [40]). 1. Each plan can be described as a sequence of such joins The algorithm proceeds as follows: (1) start with the query c 1 ◦ c 2 ... ◦ cT until |V | = κG . The above description embraces graph, (2) find the lowest cost join, (3) update the query another System R heuristic: “avoiding Cartesian products”. graph and repeat until only one vertex is left. We can relax that heuristic by simply adding edges to G at The greedy algorithm, of course, does not consider how the start of the algorithm, to ensure it is fully connected. local decisions might affect future costs. For illustration, con- Going back to our running example, suppose we start with sider our running example query with the following simple a query graph consisting of the vertices (Emp, Pos, Sal). Let costs (assume a single join method with symmetric cost): the first join be c 1 = (Emp, Pos); this leads to a query graph where the new vertices are (Emp + Pos, Sal). Applying the J (EP) = 100, J (SP) = 90, J ((EP)S) = 10, J ((SP)E) = 50 only remaining possible join, we arrive at a single remaining The greedy solution would result in a cost of 140 (because it vertex Sal + (Emp + Pos) corresponding to the join plan neglects the future effects of a decision), while the optimal Sal ▷◁ (Emp ▷◁ Pos). solution has a cost of 110. However, there is an upside: this The join optimization problem is to find the best possi- greedy algorithm has a computational complexity of O(|V | 3 ), ble join sequence—i.e., the best query plan. Also note that despite the super-exponential search space. this model can be simply extended to capture physical op- The greedy solution is suboptimal because the decision erator selection as well. The set of allowed joins can be at each index fails to consider the long-term value of its typed with an eligible join type, e.g., c = (vi , v j , HashJoin) action. One might have to sacrifice a short term benefit for a or c = (vi , v j , IndexJoin). We assume access to a cost model long term payoff. Consider the optimization problem for a J (c) → R+ , i.e., a function that estimates the incremental particular query graph G: cost of a particular join. T V (G) = min J (c i ) (1) c 1, ...,cT i=1 Problem 1 (Join Optimization Problem). Let G define In classical treatments of dynamic programming, this func- a query graph and J define a cost model. Find a sequence tion is termed the value function. It is noted that optimal 4 

5 .behavior over an entire decision horizon implies optimal would hold: behavior from any starting index t > 1 as well, which is the Q(G, c) = J (c) + min ′ Q θ (G ′, c ′) basis for the idea of dynamic programming. Conditioned on c the current join, we can write in the following form: So, the learning process, or Q-learning, defines a loss at each V (G) = min Q(G, c) iteration: c L(Q) = ∥yi − Q θ (G, c)∥22 Q(G, c) = J (c) + V (G ′) i leading to the following recursive definition of the Q-function Then parameters of the Q-function can be optimized with (or cost-to-go function): gradient descent until convergence. RL yields two key benefits: (1) the search cost for a sin- Q(G, c) = J (c) + min ′ Q(G ′, c ′) (2) gle query relative to traditional query optimization is radi- c cally reduced, since the algorithm has the time-complexity Intuitively, the Q-function describes the long-term value of of greedy search, and (2) the parameterized model can po- each join: the cumulative cost if we act optimally for all tentially learn across queries that have “similar” but non- subsequent joins after the current join decision. Knowing Q identical subplans. This is because the similarity between is equivalent to solving the problem since local optimization subplans are determined by the query graph and join featur- minc ′ Q(G ′, c ′) is sufficient to derive an optimal sequence of izations, fG and fc ; thus if they are designed in a sufficiently join decisions. expressive way, then the neural network can be trained to If we revisit the greedy algorithm, and revise it hypotheti- extrapolate the Q-function estimates to an entire workload. cally as follows: (1) start with the query graph, (2) find the The specific choice of Q-learning is important here (com- lowest Q-value join, (3) update the query graph and repeat, pared to other RL algorithms). First, it allows us to take advan- then this algorithm has the same computational complexity tage of optimal substructures during training and greatly re- of O(|V | 3 ) but is provably optimal. To sketch out our solution, duce data needed. Second, compared to policy learning [33], we will use Deep RL to approximate a global Q-function (one Q-learning outputs a score for each join that appears in any that holds for all query graphs in a workload), which gives subplan rather than simply selecting the best join. This is us a polynomial-time algorithm for join optimization. more amenable to deep integration with existing query opti- mizers, which have additional state like interesting orders 2.5 Applying Reinforcement Learning and their own pruning of plans. Third, the scoring model al- An important class of reinforcement learning algorithms, lows for top-k planning rather than just getting the best plan. called Q-learning algorithms, allows us to approximate the Q- We note that the design of Q-learning variants is an active function from samples of data [47]. What if we could regress area of research in AI [21, 50], so we opted for the simplicity from features of (G, c) to the future cumulative cost based on of a Deep Q-learning approach and defer incorporation of a small number of observations? Practically, we can observe advanced variants to future work. samples of decision sequences containing (G, c, J (c), G ′) tu- ples, where G is the query graph, c is a particular join, J (c) 2.6 Reinforcement Learning vs. Supervised is the cost of the join, and G ′ is the resultant graph. Such a Learning sequence can be extracted from any final join plan and by evaluating the cost model on the subplans. Reinforcement Learning and Supervised Learning can seem Let’s further assume we have a parameterized model for very similar since the underlying inference methods in RL the Q-function, Q θ : algorithms are often similar to those used in supervised learning and statistical estimation. Here is how we justify our Q θ (fG , fc ) ≈ Q(G, c) terminology. In supervised learning, one has paired training where fG is a feature vector representing the query graph examples with ground-truth labels (e.g., an image with a and fc is a feature vector representing a particular join. θ labeled object). For join optimization, this would mean a is the model parameters that represent this function and dataset where the example is the current join graph and the is randomly initialized at the start. For each training tuple label is the next best join decision from an oracle. In the i, one can calculate the following label, or the “estimated” context of sequential planning, this problem setting is often Q-value: called Imitation Learning [42]; where one imitates an oracle yi = J (c) + min ′ Q θ (G ′, c ′) as best as possible. c As in [30], the term “Reinforcement Learning” refers to The {yi } can then be used as labels in a regression problem. a class of empirical solutions to Markov Decision Process If Q were the true Q-function, then the following recurrence problems where we do not have the ground-truth, optimal 5 

6 .next steps; instead, learning is guided by numeric “rewards” 3.1 Overview for next steps. In the context of join optimization, these Now, we describe what kind of training data is necessary rewards are subplan costs. RL rewards may be provided by a to learn a Q-function. In supervised regression, we collect real-world experiment, a simulation model, or some other data of the form (feature, values). The learned func- oracular process. In our work below, we explore different tion maps from feature to values. One can think of this reward functions including both real-world feedback (§5) as a stateless prediction, where the underlying prediction and simulation via traditional plan cost estimation (§3.3). problem does not depend on some underlying process state. RL purists may argue that access to any optimization or- On the other hand, in the Q-learning setting, there is state. acle moves our formulation closer to supervised learning So we have to collect training data of the form (state, than classical RL. We maintain this terminology because decision, new state, cost). Therefore, a training we see the pre-training procedure as a useful prior. Rather dataset has the following format (in Java notation): than expensive, ab initio learning from executions, we learn a useful (albeit imperfect) join optimization policy offline. List<Graph, Join, Graph', Cost> dataset This process bootstraps a more classical “learning-by-doing” RL process online that avoids executing grossly suboptimal In many cases like robotics or game-playing, RL is used in query plans. a live setting where the model is trained on-the-fly based on There is additionally subtlety in the choice of algorithm. concrete moves chosen by the policy and measured in prac- Most modern RL algorithms collect data episodically (execute tice. Q-learning is known as an “off-policy” RL method. This an entire query plan and observe the final result). This makes means that its training is independent of the data collection sense in fields like robotics or autonomous driving where process and can be suboptimal—as long as the training data actions may not be reversible or decomposable. In query sufficiently covers the decisions to be made. optimization, every query consists of subplans (each of which is its own “query”). Episodic data collection ignores this 3.2 Architecture and API compositional structure. DQ collects training data sampled from a cost model and a native optimizer. It builds a model which improves future planning instances. DQ makes relatively minimal assump- tions about the structure of the optimizer. Below are the API 3 OPTIMIZER ARCHITECTURE hooks that it requires implemented. Selinger’s optimizer design separated the problem of plan Workload Generation. A function that returns a list of training search from cost/selectivity estimation [44]. This insight queries of interest. DQ requires a relevant workload for allowed independent innovation on each topic over the years. training. In our experiments, we show that this workload In our initial work, we follow this lead, and intentionally can be taken from query templates or sampled from the focus on learning a search strategy only. Even within the database schema. search problem, we focus narrowly on the classical select- project-join kernel. This too is traditional in the literature, sample(): List<Queries> going back to Selinger [44] and continuing as recently as Neumann et al.’s very recent experimental work [40]. It is also Cost Sampling. A function that given a query returns a list of particularly natural for illustrating the connection between join actions and their resultant costs. DQ requires the sys- dynamic programming and Deep RL and implications for tem to have its own optimizer to generate training data. This query optimization. We intend for our approach to plug means generating feasible join plans and their associated directly into a Selinger-based optimizer architecture like costs. Our experiments evaluate integration with determin- that of PostgreSQL, DB2 and many other systems. istic enumeration, randomized, and heuristic algorithms. In terms of system architecture, DQ can be simply inte- grated as a learning-based replacement for prior algorithms train(query): List<Graph,Join,Graph',Cost> for searching a plan space. Like any non-exhaustive query optimization technique, our results are heuristic. The new Predicate Selectivity Estimation. A function that returns the concerns raised by our approach have to do with limitations selectivity of a particular single table predicate. DQ leverages of training, including overfitting and avoiding high-variance the optimizer’s own selectivity estimate for featurization plans. We use this section to describe the extensibility of (§4.1). our approach and what design choices the user has at her disposal. selectivity(predicate): Double 6 

7 . HashJoin HashJoin HashJoin Native HashJoin T4 HashJoin T4 IndexJoin T IndexJoin ({ , 3, }, {T 1, · · · ,T 4}; V ∗) Optimizer IndexJoin T3 IndexJoin T3 T T T1 T2 1 2 T1 T2 T1 T2 Plan from Relations Optimal Optimal Sub-plans Native Optimizer to Join Cost Figure 2: Training data collection is efficient (§3.3). Here, by leveraging the principle of optimality, three training examples are emitted from a single plan produced by a native optimizer. These examples share the same long-term cost and relations to join (i.e., making these local decisions eventually leads to joining {T 1, · · · ,T 4} with optimal cumulative cost V ∗ ). In our evaluation (§6), we will vary these exposed hooks of optimal sub-plans, then the learned Q-function may not to experiment with different implementations for each (e.g., accurately learn the downside of poor subplans. Likewise, comparing training on highly relevant data from a desired if purely random plans are sampled, the model might not workload vs. randomly sampling join queries directly from see very many instances of good plans. To encourage more the schema). “exploration”, during data collection noise can be injected into the optimizer to force it to enumerate more diverse subplans. 3.3 Efficient Training Data Generation We control this via a parameter ϵ, the probability of picking Training data generation may seem onerous, but in fact, a random join as opposed to a join with the lowest cost. As useful data is automatically generated as a consequence of the algorithm enumerates subplans, if rand() < ϵ then a running classical planning algorithms. For each join deci- random (valid) join is chosen on the current query graph; sion that the optimizer makes, we can get the incremental otherwise it proceeds with the lowest-cost join as usual. This cost of the join. Suppose, we run a classical bushy dynamic is an established technique to address such “covariate shift”, programming algorithm to optimize a k-way join, we not a phenomenon extensively studied in prior work [28]. only get a final plan but also an optimal plan for every single subplan enumerated along the way. Each query generates 4 REALIZING THE Q-LEARNING MODEL an optimal query plan for all of the subplans that compose Next, we present the mechanics of actually training and it, as well as observations of suboptimal plans that did not operating a Q-learning model. make the cut. This means that a single query generates a large amount of training examples. Figure 2 shows how the 4.1 Featurizing the Join Decision principle of optimality helps enhance a training dataset. Before we get into the details, we will give a brief motivation This data collection scheme differs from that of several of how we should think about featurization in a problem like popular RL algorithms such as PPO and Policy Gradients [43] this. The features should be sufficiently rich that they capture (and used in [33]). These algorithms train their models all relevant information to predict the future cumulative cost “episodically”, where they apply an entire sequence of deci- of a join decision. This requires knowing what the overall sions and observe the final cumulative reward. An analogy query is requesting, the tables on the left side of the proposed would be a graph search algorithm that does not backtrack join, and the tables on the right side of the proposed join. but resets to the starting node and tries the whole search It also requires knowing how single table predicates affect again. While general, this scheme not suited for the structure cardinalities on either side of the join. of join optimization, where an optimal plan is composed of optimal substructures. Q-learning, an algorithm that does Participating Relations: The overall intuition is to not rely on episodic data and can learn from offline data use each column name as a feature, because it identi- consisting of a hierarchy of optimal subplans, is a better fit fies the distribution of that column. The first step is to for join optimization. construct a set of features to represent which attributes In our experiments, we bootstrap planning with a bushy are participating in the query and in the particular join. dynamic program until the number of relations in the join Let A be the set of all attributes in the database (e.g., exceeds 10 relations. Then, the data generation algorithm {Emp.id, Pos.rank, ..., Sal .code, Sal .amount }). Each relation switches to a greedy scheme for efficiency for the last K − 10 rel (including intermediate join results) has a set of visible joins. Ironically, the data collected from such an optimizer attributes, Ar el ⊆ A, the attributes present in the output. might be “too good” (or too conservative) because it does Similarly, every query graph G can be represented by its not measure or learn from a diverse enough space of (costly, visible attributes AG ⊆ A. Each join is a tuple of two rela- hence risky) subplans. If the training data only consisted tions (L, R) and we can get their visible attributes AL and AR . 7 

8 .SELECT * AG = [E.id, E.name, E.rank, AL = [E.id, E.name, E.rank, FROM Emp, Pos, Sal P.rank, P.title, P.code, AL = [E.id, E.name, E.rank] P.rank, P.title, P.code] WHERE Emp.rank = [1 1 1 0 0 0 0 0] = [1 1 1 1 1 1 0 0] = Pos.rank S.code, S.amount] AND Pos.code = [1 1 1 1 1 1 1 1] AR = [P.rank, P.title, P.code] AR = [S.code, S.amount] = Sal.code = [0 0 0 1 1 1 0 0] = [0 0 0 0 0 0 1 1] (b) Query graph (a) Example query featurization (c) Features of E ▷◁ P (d) Features of (E ▷◁ P) ▷◁ S Figure 3: A query and its corresponding featurizations (§4.1). One-hot vectors encode the visible attributes in the query graph (AG ), the left side of a join (AL ), and the right side (AR ). Such encoding allows for featurizing both the query graph and a particular join. A partial join and a full join are shown. The example query covers all relations in the schema, so AG = A. Query: Query: relation and attribute σ corresponds to, by δr . For instance, <example query> <example query> if selection Emp.id > 200 is estimated to have a selectivity AND Emp.id > 200 feat_vec(IndexJoin(E ▷◁ P)) of 0.2, then the Emp.id slot in fG would be changed to 0.2. Selectivity(Emp.id>200) = 0.2 = AL ⊕ AR ⊕ [1 0] Figure 4a pictorially illustrates this scaling. fG = AG = [E.id, E.name, · · · ] Physical Operators: The next piece is to featurize the feat_vec(HashJoin(E ▷◁ P)) = [1 1 1 1 1 1 1 1] choice of physical operator. This is straightforward: we add = AL ⊕ AR ⊕ [0 1] another one-hot vector that indicates from a fixed set of → [.2 1 1 1 1 1 1 1] (b) Concatenation of implementations the type of join used (Figure 4b). (a) Selectivity scaling in physical operators in join Extensibility: In this paper, we focus only on the basic query graph features features form of featurization described above and study foreign key Figure 4: Accounting for selections and physical operators. equality joins.2 An ablation study as part of our evaluation Simple changes to the basic form of featurization are needed (Table 9) shows that the pieces we settled on all contribute to support selections (left) and physical operators (right). to good performance. That said, there is no architectural For example, assuming a system that chooses between only limitation in DQ that prevents it from utilizing other features. IndexJoin and HashJoin, a 2-dimensional one-hot vector is Any property believed to be relevant to join cost prediction concatenated to each join feature vector. Discussion in §4.1. can be added to our featurization scheme. For example, we Each of the attribute sets AG , AL , AR can then be represented can add an additional binary vector find to indicate which with a binary 1-hot encoding: a value 1 in a slot indicates attributes have indexes built. Likewise, physical properties that particular attribute is present, otherwise 0 represents like sort-orders can be handled by indicating which attributes its absence. Using ⊕ to denote concatenation, we obtain the are sorted in an operator’s output. Hardware environment query graph features, fG = AG , and the join decision fea- variables (e.g., available memory) can be added as scalars if tures, fc = AL ⊕ AR , and, finally, the overall featurization for deemed as important factors in determining the final best a particular (G, c) tuple is simply fG ⊕ fc . Figure 3 illustrates plan. Lastly, more complex join conditions such as inequality the featurization of our example query. conditions can also be handled (§8). Selections: Selections can change said distribution, i.e., (col, sel-pred) is different than (col, TRUE). To handle single table 4.2 Model Training predicates in the query, we have to tweak the feature repre- DQ uses a multi-layer perceptron (MLP) neural network to sentation. As with most classical optimizers, we assume that represent the Q-function. It takes as input the final featur- the optimizer eagerly applies selections and projections to ization for a (G, c) pair, fG ⊕ fc . Empirically, we found that a each relation. Next, we leverage the table statistics present two-layer MLP offered the best performance under a modest in most RDBMS. For each selection σ in a query we can ob- training time constraint (< 10 minutes). The model is trained tain the selectivity δ σ , which estimates the fraction of tuples with a standard stochastic gradient descent (SGD) algorithm. present after applying the selection.1 To account for selec- tions in featurization, we simply scale the slot in fG that the 1 We 2 Thisis due to our evaluation workloads containing only such joins. §8 consider selectivity estimation out of scope for this paper. See discus- sion in §3 and §7. discusses how DQ could be applied to more general join types. 8 

9 .4.3 Execution after Training inexpensive nature, partial re-training is a common strategy After training, we obtain a parameterized estimate of the applied in many machine learning applications. Q-function, Q θ (fG , fc ). For execution, we simply go back to the standard algorithm as in the greedy method but instead 5.2 Collecting Execution Data of using the local costs, we use the learned Q-function: (1) For fine-tuning, we collect a list of real-execution data, start with the query graph, (2) featurize each join, (3) find (Graph, Join, Graph’, OpTime), where instead the join with the lowest estimated Q-value (i.e., output from of the cost of the join, the real runtime attributed to the the neural net), (4) update the query graph and repeat. particular join operator is recorded. Per-operator runtimes This algorithm has the time-complexity of greedy enumer- can be collected by instrumenting the underlying system, ation except in greedy, the cost model is evaluated at each or using the system’s native analysis functionality (e.g., EX- iteration, and in our method, a neural network is evaluated. PLAIN ANALYZE in Postgres). One pleasant consequence is that DQ exploits the abundant vectorization opportunities in numerical computation. In each iteration, instead of invoking the neural net sequen- 6 EVALUATION tially on each join’s feature vector, DQ batches all candidate We extensively evaluate DQ to investigate the following joins (of this iteration) together, and invokes the neural net major questions: once on the batch. Modern CPUs, GPUs, and specialized ac- • How effective is DQ in producing plans, how good are celerators (e.g., TPUs [24]) all offer optimized instructions they, and under what conditions (§6.1.1, §6.1.2, §6.1.3)? for such single-instruction multiple-data (SIMD) workloads. • How efficient is DQ at producing plans, in terms of The batching optimization amortizes each invocation’s fixed runtimes and required data (§6.1.4, §6.1.5, §6.1.6)? overheads and has the most impact on large joins. • Do DQ’s techniques apply to real-world scenarios, systems, and workloads (§6.2, §6.3)? 5 FEEDBACK FROM EXECUTION We have described how DQ learns from sampling the cost To address the first two questions, we run experiments on model native to a query optimizer. However, it is well-known standalone DQ. The last question is evaluated with end-to- that a cost model (costs) may fail to correlate with reality end experiments on DQ-integrated Postgres and SparkSQL. (runtimes), due to poor cardinality estimates or unrealistic rules used in estimation. To correct these errors, the database 6.1 Standalone Optimization Experiments community has seen proposals of leveraging feedback from We implemented DQ and a wide variety of optimizer search execution [14, 35]. We can perform an analogous operation techniques previously benchmarked in Leis et al. [29] in a on learned Q-functions. Readers might be familiar with the standalone Java query optimizer harness. Apache Calcite concept of fine-tuning in the deep learning literature [54], is used for parsing SQL and representing the SQL AST. We where a network is trained on one dataset and “transferred” first evaluate standalone DQ and other optimizers for final to another with minimal re-training. DQ can optionally apply plan costs; unless otherwise noted, exploration (§3.3) and this technique to re-train itself on real execution runtimes real-execution feedback (§5) are turned off. We use the Join to correlate better with the operating environment. Order Benchmark (JOB) [29], which is derived from the real IMDB dataset (3.6GB in size; 21 tables). The largest table 5.1 Fine-tuning DQ has 36 million rows. The benchmark contains 33 templates Fine-tuning DQ consists of two steps: pre-training as usual and 113 queries in total. The joins have between 4 and 15 and re-training. First, DQ is pre-trained to convergence on relations, with an average of 8 relations per query. samples from the optimizer’s cost model; these are inexpen- We revisit a motivating claim from earlier: heuristics are sive to collect compared to real execution. Next, the weights well-understood when the cost model is linear but non- of the first two layers of the neural network are frozen, and linearities can lead to significant suboptimality. The experi- the output layer’s weights are re-initialized randomly. Re- ments intend to illustrate that DQ offers a form of robustness training is then started on samples of real execution runtimes, to cost model, meaning, that it prioritizes plans tailored to the which would only change the output layer’s weights. structure of the cost model, workload, and physical design— Intuitively, the process can be thought of as first using even when these plans are bushy. the cost model to learn relevant features about the general We consider 3 cost models: CM1 is a model for a main- structure of subplans (e.g., “which relations are generally memory database; CM2 additionally considers limited mem- beneficial to join?”). The re-trained output layer then projects ory hash joins where after a threshold the costs of spilling the effect of these features onto real runtimes. Due to its partitions to disk are considered; CM3 additionally considers 9 

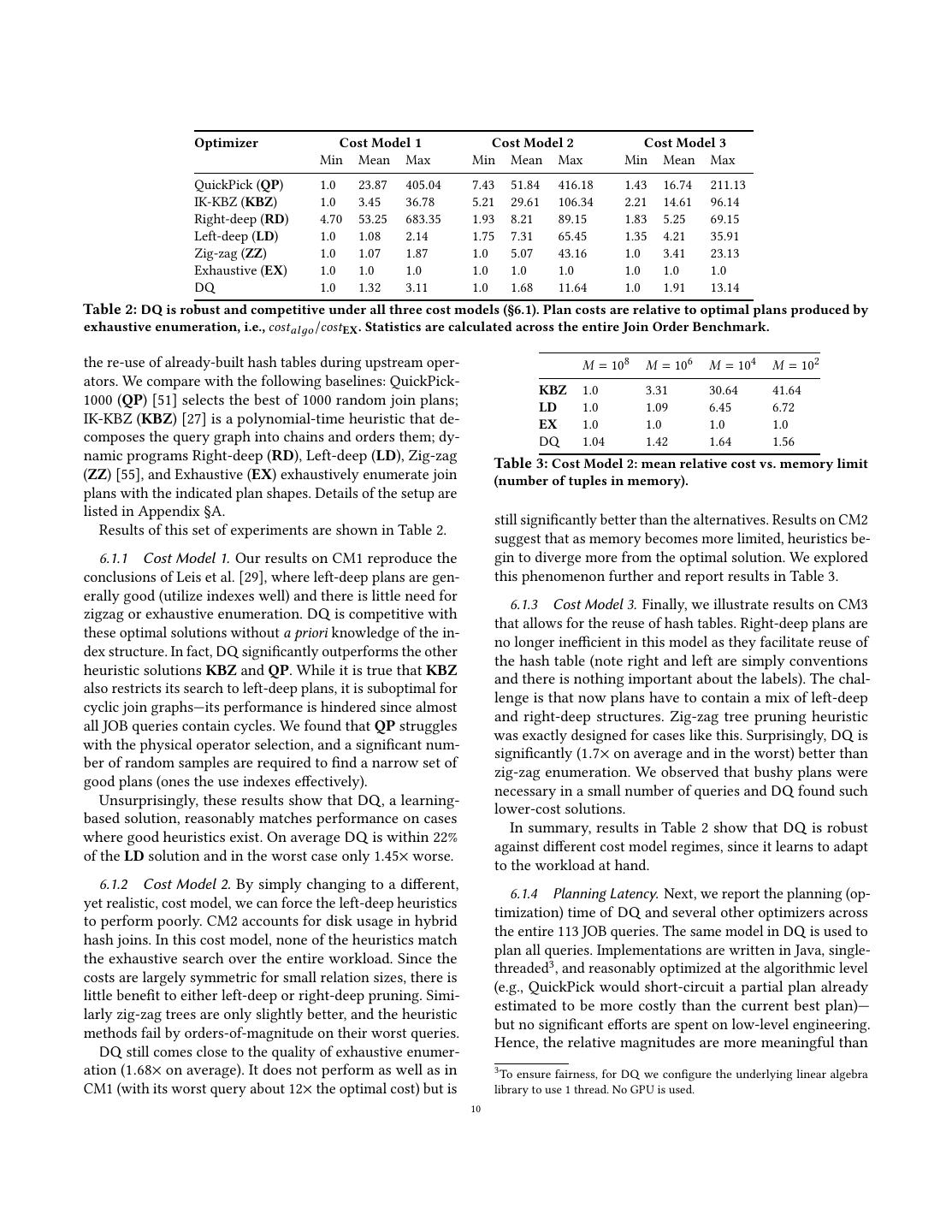
10 . Optimizer Cost Model 1 Cost Model 2 Cost Model 3 Min Mean Max Min Mean Max Min Mean Max QuickPick (QP) 1.0 23.87 405.04 7.43 51.84 416.18 1.43 16.74 211.13 IK-KBZ (KBZ) 1.0 3.45 36.78 5.21 29.61 106.34 2.21 14.61 96.14 Right-deep (RD) 4.70 53.25 683.35 1.93 8.21 89.15 1.83 5.25 69.15 Left-deep (LD) 1.0 1.08 2.14 1.75 7.31 65.45 1.35 4.21 35.91 Zig-zag (ZZ) 1.0 1.07 1.87 1.0 5.07 43.16 1.0 3.41 23.13 Exhaustive (EX) 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 DQ 1.0 1.32 3.11 1.0 1.68 11.64 1.0 1.91 13.14 Table 2: DQ is robust and competitive under all three cost models (§6.1). Plan costs are relative to optimal plans produced by exhaustive enumeration, i.e., costalдo /cost EX . Statistics are calculated across the entire Join Order Benchmark. the re-use of already-built hash tables during upstream oper- M = 108 M = 106 M = 104 M = 102 ators. We compare with the following baselines: QuickPick- KBZ 1.0 3.31 30.64 41.64 1000 (QP) [51] selects the best of 1000 random join plans; LD 1.0 1.09 6.45 6.72 IK-KBZ (KBZ) [27] is a polynomial-time heuristic that de- EX 1.0 1.0 1.0 1.0 composes the query graph into chains and orders them; dy- DQ 1.04 1.42 1.64 1.56 namic programs Right-deep (RD), Left-deep (LD), Zig-zag Table 3: Cost Model 2: mean relative cost vs. memory limit (ZZ) [55], and Exhaustive (EX) exhaustively enumerate join (number of tuples in memory). plans with the indicated plan shapes. Details of the setup are listed in Appendix §A. still significantly better than the alternatives. Results on CM2 Results of this set of experiments are shown in Table 2. suggest that as memory becomes more limited, heuristics be- 6.1.1 Cost Model 1. Our results on CM1 reproduce the gin to diverge more from the optimal solution. We explored conclusions of Leis et al. [29], where left-deep plans are gen- this phenomenon further and report results in Table 3. erally good (utilize indexes well) and there is little need for 6.1.3 Cost Model 3. Finally, we illustrate results on CM3 zigzag or exhaustive enumeration. DQ is competitive with that allows for the reuse of hash tables. Right-deep plans are these optimal solutions without a priori knowledge of the in- no longer inefficient in this model as they facilitate reuse of dex structure. In fact, DQ significantly outperforms the other the hash table (note right and left are simply conventions heuristic solutions KBZ and QP. While it is true that KBZ and there is nothing important about the labels). The chal- also restricts its search to left-deep plans, it is suboptimal for lenge is that now plans have to contain a mix of left-deep cyclic join graphs—its performance is hindered since almost and right-deep structures. Zig-zag tree pruning heuristic all JOB queries contain cycles. We found that QP struggles was exactly designed for cases like this. Surprisingly, DQ is with the physical operator selection, and a significant num- significantly (1.7× on average and in the worst) better than ber of random samples are required to find a narrow set of zig-zag enumeration. We observed that bushy plans were good plans (ones the use indexes effectively). necessary in a small number of queries and DQ found such Unsurprisingly, these results show that DQ, a learning- lower-cost solutions. based solution, reasonably matches performance on cases In summary, results in Table 2 show that DQ is robust where good heuristics exist. On average DQ is within 22% against different cost model regimes, since it learns to adapt of the LD solution and in the worst case only 1.45× worse. to the workload at hand. 6.1.2 Cost Model 2. By simply changing to a different, 6.1.4 Planning Latency. Next, we report the planning (op- yet realistic, cost model, we can force the left-deep heuristics timization) time of DQ and several other optimizers across to perform poorly. CM2 accounts for disk usage in hybrid the entire 113 JOB queries. The same model in DQ is used to hash joins. In this cost model, none of the heuristics match plan all queries. Implementations are written in Java, single- the exhaustive search over the entire workload. Since the threaded3 , and reasonably optimized at the algorithmic level costs are largely symmetric for small relation sizes, there is (e.g., QuickPick would short-circuit a partial plan already little benefit to either left-deep or right-deep pruning. Simi- estimated to be more costly than the current best plan)— larly zig-zag trees are only slightly better, and the heuristic but no significant efforts are spent on low-level engineering. methods fail by orders-of-magnitude on their worst queries. Hence, the relative magnitudes are more meaningful than DQ still comes close to the quality of exhaustive enumer- ation (1.68× on average). It does not perform as well as in 3 To ensure fairness, for DQ we configure the underlying linear algebra CM1 (with its worst query about 12× the optimal cost) but is library to use 1 thread. No GPU is used. 10 

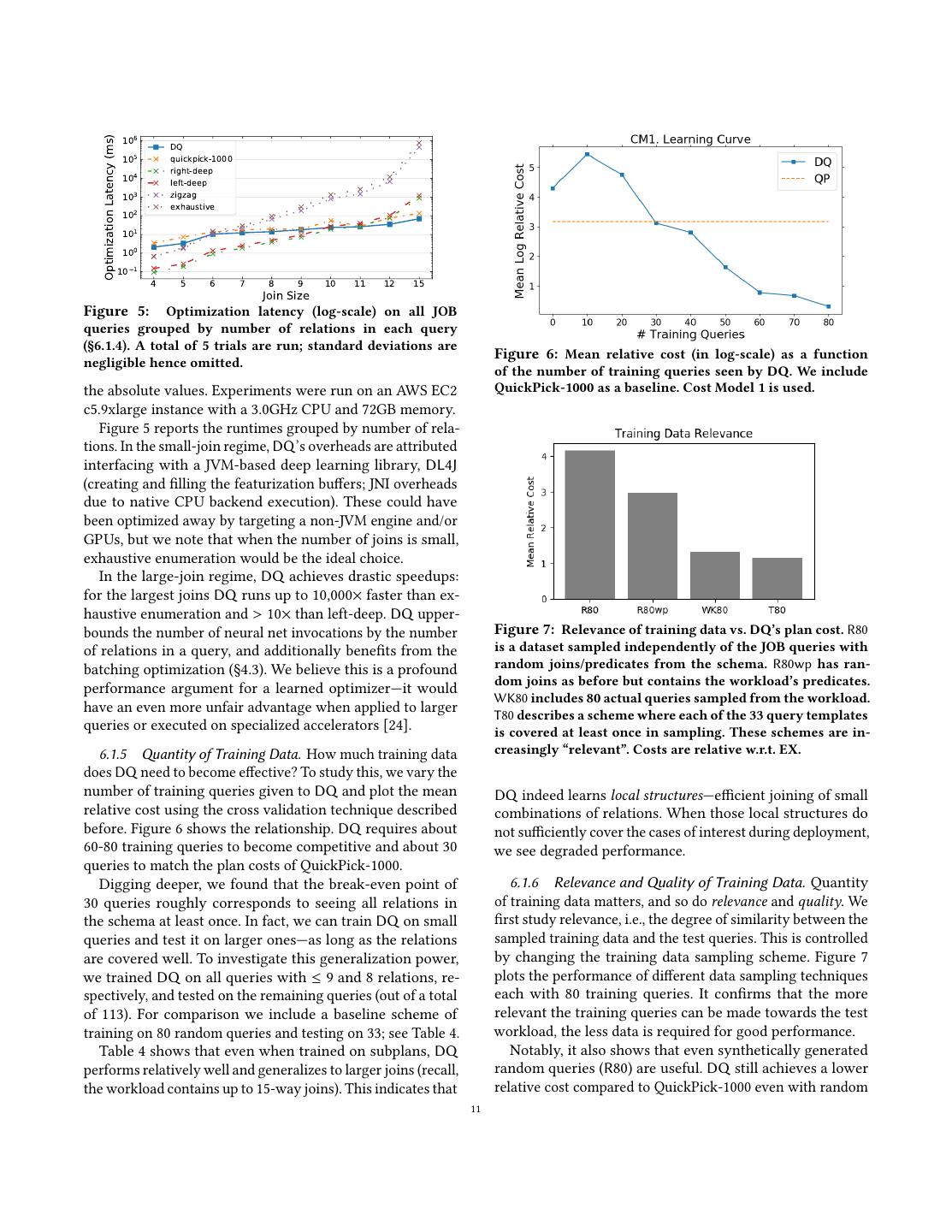
11 . 106 Optimization Latency (ms) DQ 105 quickpick-1000 right-deep 104 left-deep 103 zigzag exhaustive 102 101 100 10 1 4 5 6 7 8 9 10 11 12 15 Join Size Figure 5: Optimization latency (log-scale) on all JOB queries grouped by number of relations in each query (§6.1.4). A total of 5 trials are run; standard deviations are Figure 6: Mean relative cost (in log-scale) as a function negligible hence omitted. of the number of training queries seen by DQ. We include the absolute values. Experiments were run on an AWS EC2 QuickPick-1000 as a baseline. Cost Model 1 is used. c5.9xlarge instance with a 3.0GHz CPU and 72GB memory. Figure 5 reports the runtimes grouped by number of rela- tions. In the small-join regime, DQ’s overheads are attributed interfacing with a JVM-based deep learning library, DL4J (creating and filling the featurization buffers; JNI overheads due to native CPU backend execution). These could have been optimized away by targeting a non-JVM engine and/or GPUs, but we note that when the number of joins is small, exhaustive enumeration would be the ideal choice. In the large-join regime, DQ achieves drastic speedups: for the largest joins DQ runs up to 10,000× faster than ex- haustive enumeration and > 10× than left-deep. DQ upper- bounds the number of neural net invocations by the number Figure 7: Relevance of training data vs. DQ’s plan cost. R80 of relations in a query, and additionally benefits from the is a dataset sampled independently of the JOB queries with batching optimization (§4.3). We believe this is a profound random joins/predicates from the schema. R80wp has ran- dom joins as before but contains the workload’s predicates. performance argument for a learned optimizer—it would WK80 includes 80 actual queries sampled from the workload. have an even more unfair advantage when applied to larger T80 describes a scheme where each of the 33 query templates queries or executed on specialized accelerators [24]. is covered at least once in sampling. These schemes are in- 6.1.5 Quantity of Training Data. How much training data creasingly “relevant”. Costs are relative w.r.t. EX. does DQ need to become effective? To study this, we vary the number of training queries given to DQ and plot the mean DQ indeed learns local structures—efficient joining of small relative cost using the cross validation technique described combinations of relations. When those local structures do before. Figure 6 shows the relationship. DQ requires about not sufficiently cover the cases of interest during deployment, 60-80 training queries to become competitive and about 30 we see degraded performance. queries to match the plan costs of QuickPick-1000. Digging deeper, we found that the break-even point of 6.1.6 Relevance and Quality of Training Data. Quantity 30 queries roughly corresponds to seeing all relations in of training data matters, and so do relevance and quality. We the schema at least once. In fact, we can train DQ on small first study relevance, i.e., the degree of similarity between the queries and test it on larger ones—as long as the relations sampled training data and the test queries. This is controlled are covered well. To investigate this generalization power, by changing the training data sampling scheme. Figure 7 we trained DQ on all queries with ≤ 9 and 8 relations, re- plots the performance of different data sampling techniques spectively, and tested on the remaining queries (out of a total each with 80 training queries. It confirms that the more of 113). For comparison we include a baseline scheme of relevant the training queries can be made towards the test training on 80 random queries and testing on 33; see Table 4. workload, the less data is required for good performance. Table 4 shows that even when trained on subplans, DQ Notably, it also shows that even synthetically generated performs relatively well and generalizes to larger joins (recall, random queries (R80) are useful. DQ still achieves a lower the workload contains up to 15-way joins). This indicates that relative cost compared to QuickPick-1000 even with random 11 

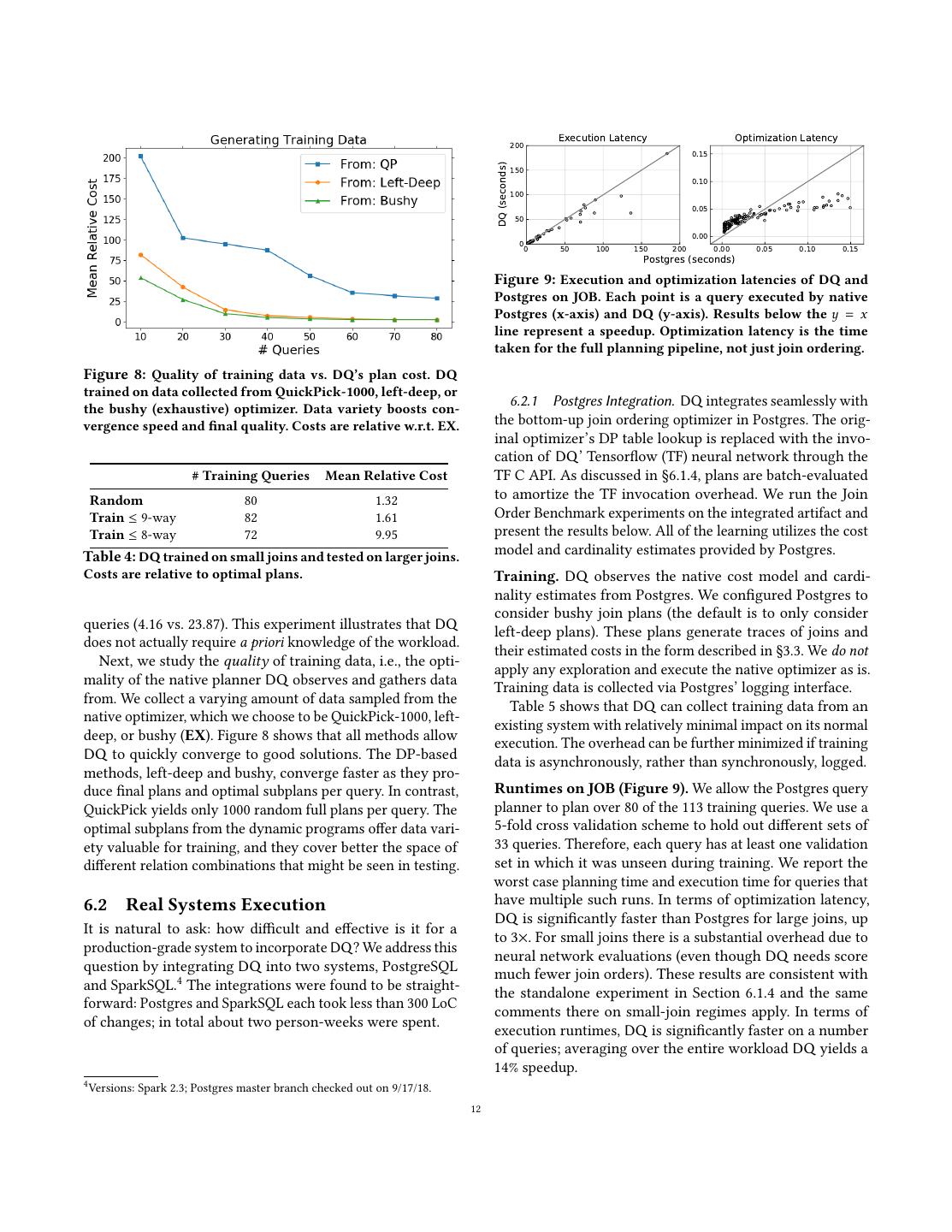
12 . 200 Execution Latency Optimization Latency 0.15 150 DQ (seconds) 0.10 100 0.05 50 0.00 00 50 100 150 200 0.00 0.05 0.10 0.15 Postgres (seconds) Figure 9: Execution and optimization latencies of DQ and Postgres on JOB. Each point is a query executed by native Postgres (x-axis) and DQ (y-axis). Results below the y = x line represent a speedup. Optimization latency is the time taken for the full planning pipeline, not just join ordering. Figure 8: Quality of training data vs. DQ’s plan cost. DQ trained on data collected from QuickPick-1000, left-deep, or the bushy (exhaustive) optimizer. Data variety boosts con- 6.2.1 Postgres Integration. DQ integrates seamlessly with vergence speed and final quality. Costs are relative w.r.t. EX. the bottom-up join ordering optimizer in Postgres. The orig- inal optimizer’s DP table lookup is replaced with the invo- cation of DQ’ Tensorflow (TF) neural network through the # Training Queries Mean Relative Cost TF C API. As discussed in §6.1.4, plans are batch-evaluated Random 80 1.32 to amortize the TF invocation overhead. We run the Join Train ≤ 9-way 82 1.61 Order Benchmark experiments on the integrated artifact and Train ≤ 8-way 72 9.95 present the results below. All of the learning utilizes the cost Table 4: DQ trained on small joins and tested on larger joins. model and cardinality estimates provided by Postgres. Costs are relative to optimal plans. Training. DQ observes the native cost model and cardi- nality estimates from Postgres. We configured Postgres to consider bushy join plans (the default is to only consider queries (4.16 vs. 23.87). This experiment illustrates that DQ left-deep plans). These plans generate traces of joins and does not actually require a priori knowledge of the workload. their estimated costs in the form described in §3.3. We do not Next, we study the quality of training data, i.e., the opti- apply any exploration and execute the native optimizer as is. mality of the native planner DQ observes and gathers data Training data is collected via Postgres’ logging interface. from. We collect a varying amount of data sampled from the Table 5 shows that DQ can collect training data from an native optimizer, which we choose to be QuickPick-1000, left- existing system with relatively minimal impact on its normal deep, or bushy (EX). Figure 8 shows that all methods allow execution. The overhead can be further minimized if training DQ to quickly converge to good solutions. The DP-based data is asynchronously, rather than synchronously, logged. methods, left-deep and bushy, converge faster as they pro- duce final plans and optimal subplans per query. In contrast, Runtimes on JOB (Figure 9). We allow the Postgres query QuickPick yields only 1000 random full plans per query. The planner to plan over 80 of the 113 training queries. We use a optimal subplans from the dynamic programs offer data vari- 5-fold cross validation scheme to hold out different sets of ety valuable for training, and they cover better the space of 33 queries. Therefore, each query has at least one validation different relation combinations that might be seen in testing. set in which it was unseen during training. We report the worst case planning time and execution time for queries that 6.2 Real Systems Execution have multiple such runs. In terms of optimization latency, DQ is significantly faster than Postgres for large joins, up It is natural to ask: how difficult and effective is it for a to 3×. For small joins there is a substantial overhead due to production-grade system to incorporate DQ? We address this neural network evaluations (even though DQ needs score question by integrating DQ into two systems, PostgreSQL much fewer join orders). These results are consistent with and SparkSQL.4 The integrations were found to be straight- the standalone experiment in Section 6.1.4 and the same forward: Postgres and SparkSQL each took less than 300 LoC comments there on small-join regimes apply. In terms of of changes; in total about two person-weeks were spent. execution runtimes, DQ is significantly faster on a number of queries; averaging over the entire workload DQ yields a 14% speedup. 4 Versions: Spark 2.3; Postgres master branch checked out on 9/17/18. 12 

13 . 25 Execution Latency Optimization Latency Median Max 1000 3 20 800 DQ (seconds) Postgres, no collection 19.17 ms 149.53 ms 2 Postgres, with collection 15 600 35.98 ms 184.22 ms 1 10 400 Table 5: Planning latency with collection turned off/on. 00 1 2 3 5 200 00 0 6.2.2 SparkSQL Integration. DQ is also integrated into 5 10 15 20 25 0 200 400 600 800 1000 SparkSQL, a distributed data analytics engine. To show that SparkSQL (seconds) DQ’s effectiveness applies to more than one workload, we Figure 10: Execution and optimization latencies of DQ evaluate the integrated result on TPC-DS. and SparkSQL on TPC-DS (SF1). We use an EC2 c5.9xlarge instance with 36 vCPUs. SparkSQL’s bushy dynamic pro- Training. SparkSQL 2.3 contains a cost-based optimizer gram takes 1000 seconds to plan the largest query (Q64, 18- which enumerates bushy plans for queries whose number of relation join); we include a zoomed-in view of the rest of the relations falls under a tunable threshold. We set this thresh- planning latencies. Results below the y = x line represent old high enough so that all queries are handled by this bushy a speedup. Across the workload, DQ’s mean speedup over dynamic program. To score plans, the optimizer invokes SparkSQL for execution is 1.0× and that for optimization is DQ’s trained neural net through TensorFlow Java. We use 3.6×. the native SparkSQL cost model and cardinality estimates. All algorithmic aspects of training data collection remain the same as the Postgres integration. Effectiveness on TPC-DS (Figure 10). We collect data from and evaluate on 97 out of all 104 queries in TPC-DS v2.4. The data files are generated with a scale factor of 1 and stored as columnar Parquet files. In terms of execution runtimes, DQ matches SparkSQL over the 97 queries (a mean speedup of 1.0×). In terms of optimization runtimes, DQ has a mean speedup of 3.6× but a max speedup of 250× on the query with largest number of joins (Q64). Note that the mean optimization speedup here is less drastic than JOB because Figure 11: Effects of fine-tuning DQ on JOB Q10c. A TPC-DS queries contain much less relations to join. modest amount of real execution using around 100 queries allows DQ to surpass both its original perfor- Discussion. In summary, results above show that DQ’s ef- mance (by 3×) as well as Postgres (by 3.5×). fective not only on the one workload designed to stress- test joins, but also on a well-established decision support Figure 11 shows the results as a function of the number workload. Further, we demonstrate the ease of integration of queries observed for real execution. Postgres emits a plan into production-grade systems including a RDBMS and a that executes in 70.0s, while baseline DQ emits a plan that distributed analytics engine. We hope these results provide executes in 60.1s. After fine-tuning, DQ emits a plan that motivation for developers of similar systems to incorporate executes in 20.3s, outperforming both Postgres and its orig- DQ’s learning-based join optimization technique. inal performance. This shows true runtimes are useful in correcting faulty cost model and/or cardinality estimates. 6.3 Fine-Tuning With Feedback Interestingly, training a version of DQ using only real run- Finally, we illustrate how DQ can overcome an inaccurate times failed to converge to a reasonable model—this suggests cost model by fine-tuning with feedback data (§5). We focus learning high-level features from inexpensive samples from on a specific JOB query, Q10c, where the cost model particu- the cost model is beneficial. larly deviates from the true runtime. Baseline DQ is trained on data collected over 112 queries, which is every query ex- 7 RELATED WORK cept for Q10c, as usual (i.e., values are costs from Postgres’ Application of machine learning in database internals is still native cost model). For fine-tuning we execute a varying the subject of significant debate this year and will continue amount of these queries and collect their actual runtimes. To to be a contentious question for years to come [11, 26, 32, 37]. encourage observing a variety of physical operators, we use An important question is what problems are amenable to ma- an exploration parameter of ϵ = 0.1 when observing run- chine learning solutions. We believe that query optimization times (recall from §3.3 exploration means with probability ϵ is one such sub-area. The problems considered are generally we form a random intermediate join). hard and orders-of-magnitude of performance are at stake. 13 

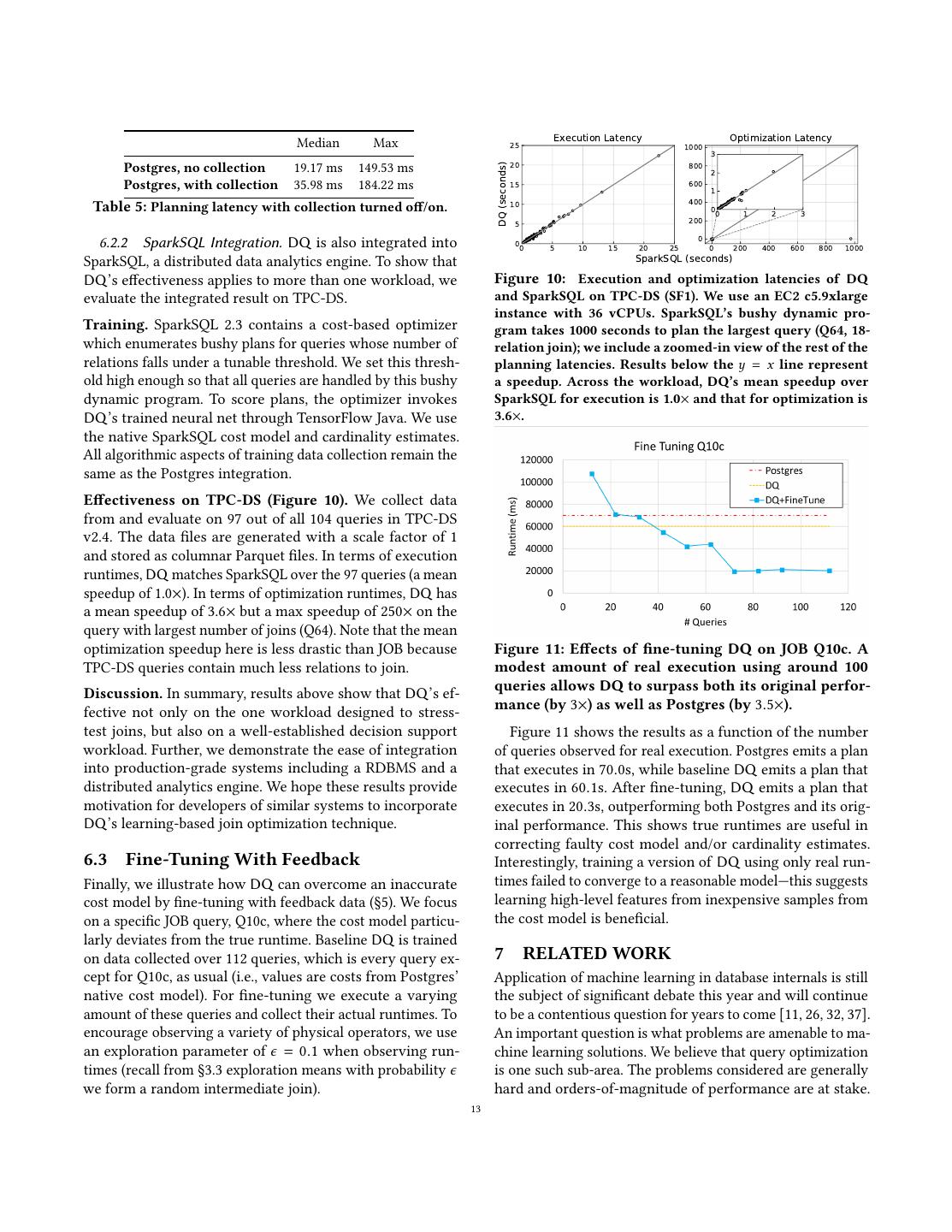
14 .In this setting, poor learning solutions will lead to slow but about 8,000 training queries to reach native PostgresâĂŹ cost not incorrect execution, so correctness is not a concern. on the 10 JOB queries. DQ exploits optimal substructures of Cost Function Learning We are certainly not the first to the problem and uses off-policy Q-learning to increase data- efficiency by two orders of magnitude: 80 training queries consider “learning” in the query optimizer and there are a number of alternative architectures that one may consider. to outperform PostgresâĂŹ real execution runtimes on the The precursors to this work are attempts to correct query entire JOB benchmark. optimizers through execution feedback. One of the seminal Adaptive Query Optimization Adaptive query process- works in this area is the LEO optimizer [35]. This optimizer ing [9, 16] as well as the related techniques to re-optimize uses feedback from the execution of queries to correct inac- queries during execution [10, 36] is another line of work curacies in its cost model. The underlying cost model is based that we think is relevant to the discussion. Reinforcement on histograms. The basic idea inspired several other impor- learning studies sequential problems and adaptive query op- tant works such as [14]. The sentiment in this research still timization is a sequential decision problem over tuples rather holds true today; when Leis et al. extensively evaluated the than subplans. We focus our study on optimization in fixed efficacy of different query optimization strategies they noted databases and the adaptivity that DQ offers is at a work- that feedback and cost estimation errors are still challenges load level. Continuously updating a neural network can be in query optimizers [29]. A natural first place to include challenging for very fine-grained adaptivity, e.g., processing machine learning would be what we call Cost Function Learn- different tuples in different ways. ing, where statistical learning techniques are used to correct Robustness There are a couple of branches of work that or replace existing cost models. This is very related to the study robustness to different parameters in query optimiza- problem of performance estimation of queries [6, 52, 53]. tion. In particular, the field of “parametric query optimiza- We actually investigated this by training a neural network tion” [22, 48], studies the optimization of piecewise linear to predict the selectivity of a single relation predicate. Results cost models. Interestingly, DQ is it is agnostic to this struc- were successful, albeit very expensive from a data perspec- ture. It learns a heuristic from data identifying different tive. To estimate selectivity on an attribute with 10k distinct regimes where different classes of plans work. We hope to values, the training set had to include 1000 queries. This ar- continue experiments and attempt to interpret how DQ is chitecture suffers from the problem of featurization of literals; partitioning the feature space into decisions. There is also a the results are heavily dependent on learning structure in deep link between this work and least expected cost (LEC) literal values from the database that are not always straight- query optimization [15]. Markov Decision Processes (the forward to featurize. This can be especially challenging for main abstraction in RL) are by definition stochastic and opti- strings or other non-numerical data types. A recent work- mize the LEC objective. shop paper does show some promising results in using Deep RL to construct a good feature representation of subqueries Join Optimization At Scale Scaling up join optimization but it still requires > 10k queries to train [41]. has been an important problem for several decades, most re- cently [40]. At scale, several randomized approaches can Learning in Query Optimization Recently, there has been be applied. There is a long history of randomized algo- several exciting proposals in putting learning inside a query rithms (e.g., the QuickPick algorithm [51]) and genetic al- optimizer. Ortiz et al. [41] applies deep RL to learn a repre- gorithms [13, 46]. These algorithms are pragmatic and it is sentation of queries, which can then be used in downstream often the case that commercial optimizers will leverage such query optimization tasks. Liu [31] and Kipf [25] use DNNs to a method after the number of tables grows beyond a certain learn cardinality estimates. Closer to our work is Marcus et point. The challenge with these methods is that their efficacy al.’s proposal of a deep RL-based join optimizer, ReJOIN [33], is hard to judge. We found that QuickPick often varied in which offered a preliminary view of the potential for deep performance on the same query quite dramatically. RL in this context. The early results reported in [33] top out Another heuristic approach is relaxation, or solving the at a 20% improvement in plan execution time of Postgres problem exactly under simplified assumptions. One straight- (compared to our 3x), and as of that paper they had only forward approach is to simply consider greedy search avoid- evaluated on 10 out of the 113 JOB queries that we study ing Cartesian products [17], which is also the premise of the here. DQ qualitatively goes beyond that work by offering IK-KBZ algorithms [23, 27]. Similar linearization arguments an extensible featurization scheme supporting physical join were also made in recent work [40, 49]. Existing heuristics selection. More fundamentally, DQ integrates the dynamic do not handle all types of non-linearities well, and this is programming of Q-learning into that of a standard query exactly the situation where learning can help. Interestingly optimizer, which allows us to use off-policy learning. Due enough, our proposed technique has a O(n 3 ) runtime, which to use of on-policy policy gradient methods, [33] requires 14 

15 .is similar to the linearizedDP algorithm described in [40]. of learning and query optimization in future work may shed We hope to explore the very large join regime in the future more insights. and an interesting direction is to compare DQ to recently proposed techniques like [40]. REFERENCES [1] Amazon Aurora Serverless. https://aws.amazon.com/rds/aurora/ serverless/. 8 DISCUSSION, LIMITATIONS, AND [2] Apache Calcite. https://calcite.apache.org/. CONCLUSION [3] PostgreSQL. https://www.postgresql.org/. [4] PostgreSQL: Genetic Query Optimizer. https://www.postgresql.org/ We presented our method with a featurization designed for docs/11/static/geqo.html. inner joins over foreign key relations as these were the ma- [5] TPC-DS. http://www.tpc.org/tpcds/. jor join queries in our benchmarks. This is not a fundamen- [6] M. Akdere, U. Çetintemel, M. Riondato, E. Upfal, and S. B. Zdonik. tal restriction and is designed to ease exposition. It is rela- Learning-based query performance modeling and prediction. In Data tively straightforward to extend this model to join conditions Engineering (ICDE), 2012 IEEE 28th International Conference on, pages 390–401. IEEE, 2012. composed of conjunctions of binary expressions. Assume [7] M. Armbrust, R. S. Xin, C. Lian, Y. Huai, D. Liu, J. K. Bradley, X. Meng, the maximum number of expressions in the conjunction is T. Kaftan, M. J. Franklin, A. Ghodsi, et al. Spark sql: Relational data capped at N . As before, let A be the set of all attributes in the processing in spark. In Proceedings of the 2015 ACM SIGMOD Inter- database. Each expression has two attributes and an opera- national Conference on Management of Data, pages 1383–1394. ACM, tor. As with featurizing the vertices we can 1-hot encode the 2015. [8] J. Arulraj and A. Pavlo. How to build a non-volatile memory database attributes present. We additionally have to 1-hot encode the management system. In Proceedings of the 2017 ACM International binary operators {=, , <, >}. For each of the expressions in Conference on Management of Data, pages 1753–1758. ACM, 2017. the conjunctive predicate, we concatenate the binary feature [9] R. Avnur and J. M. Hellerstein. Eddies: Continuously adaptive query vectors that have its operator and attributes. Since the maxi- processing. In ACM sigmod record, volume 29, pages 261–272. ACM, mum number of expressions in the conjunction capped at 2000. [10] S. Babu, P. Bizarro, and D. DeWitt. Proactive re-optimization. In N , we can get a fixed sized feature vector for all predicates. Proceedings of the 2005 ACM SIGMOD international conference on Man- More broadly, we believe DQ is a step towards a agement of data, pages 107–118. ACM, 2005. learning query optimizer. As illustrated by the Cascades [11] P. Bailis, K. S. Tai, P. Thaker, and M. Zaharia. Don’t throw out optimizer [19] and follow-on work, cost-based dynamic your algorithms book just yet: Classical data structures that can out- programming—whether bottom up or top-down with perform learned indexes. https://dawn.cs.stanford.edu/2018/01/11/ index-baselines/, 2017. memoization—needs not be restricted to select-project-join [12] R. Bellman. Dynamic programming. Princeton University Press, 1957. blocks. Most query optimizations can be recast into a space [13] K. Bennett, M. C. Ferris, and Y. E. Ioannidis. A genetic algorithm for of algebraic transformations amenable to dynamic program- database query optimization. Computer Sciences Department, Univer- ming, including asymmetric operators like outer joins, cross- sity of Wisconsin, Center for Parallel Optimization, 1991. block optimizations including order optimizations and “side- [14] S. Chaudhuri, V. Narasayya, and R. Ramamurthy. A pay-as-you-go framework for query execution feedback. Proceedings of the VLDB ways information passing”, and even non-relational opera- Endowment, 1(1):1141–1152, 2008. tors like PIVOT. The connection between RL and Dynamic [15] F. Chu, J. Halpern, and J. Gehrke. Least expected cost query opti- Programming presented in this paper can be easily leveraged mization: what can we expect? In Proceedings of the twenty-first ACM in those scenarios as well. Of course this blows up the search SIGMOD-SIGACT-SIGART symposium on Principles of database systems, space, and large spaces are ideal for solutions like the one pages 293–302. ACM, 2002. [16] A. Deshpande, Z. Ives, V. Raman, et al. Adaptive query processing. we proposed. Foundations and Trends® in Databases, 1(1):1–140, 2007. It is popular in recent AI research to try “end-to-end” learn- [17] L. Fegaras. A new heuristic for optimizing large queries. In Interna- ing, where problems that were traditionally factored into tional Conference on Database and Expert Systems Applications, pages subproblems (e.g., self-driving cars involve separate models 726–735. Springer, 1998. for localization, obstacle detection and lane-following) are [18] R. H. Gerber. Data-flow query processing using multiprocessor hash- partitioned algorithms. Technical report, Wisconsin Univ., Madison learned in a single unified model. One can imagine a simi- (USA), 1986. lar architectural ambition for an end-to-end learning query [19] G. Graefe. The cascades framework for query optimization. IEEE Data optimizer, which simply maps subplan features to measured Eng. Bull., 18(3):19–29, 1995. runtimes. This would require a significant corpus of run- [20] G. Graefe and W. McKenna. The volcano optimizer generator. Techni- time data to learn from, and changes to the featurization and cal report, COLORADO UNIV AT BOULDER DEPT OF COMPUTER SCIENCE, 1991. perhaps the deep network structure we used here. DQ is a [21] T. Hester, M. Vecerik, O. Pietquin, M. Lanctot, T. Schaul, B. Piot, D. Hor- pragmatic middle ground that exploits the structure of the gan, J. Quan, A. Sendonaris, G. Dulac-Arnold, et al. Deep q-learning join optimization problem. Further exploring the extremes from demonstrations. arXiv preprint arXiv:1704.03732, 2017. 15 

16 .[22] A. Hulgeri and S. Sudarshan. Parametric query optimization for linear [41] J. Ortiz, M. Balazinska, J. Gehrke, and S. S. Keerthi. Learning state and piecewise linear cost functions. In Proceedings of the 28th inter- representations for query optimization with deep reinforcement learn- national conference on Very Large Data Bases, pages 167–178. VLDB ing. In Proceedings of the Second Workshop on Data Management for Endowment, 2002. End-To-End Machine Learning, DEEM’18, pages 4:1–4:4, New York, NY, [23] T. Ibaraki and T. Kameda. On the optimal nesting order for computing USA, 2018. ACM. n-relational joins. ACM Transactions on Database Systems (TODS), [42] T. Osa, J. Pajarinen, G. Neumann, J. A. Bagnell, P. Abbeel, J. Peters, 9(3):482–502, 1984. et al. An algorithmic perspective on imitation learning. Foundations [24] N. P. Jouppi, C. Young, N. Patil, D. Patterson, G. Agrawal, R. Bajwa, and Trends® in Robotics, 7(1-2):1–179, 2018. S. Bates, S. Bhatia, N. Boden, A. Borchers, et al. In-datacenter perfor- [43] J. Schulman, F. Wolski, P. Dhariwal, A. Radford, and O. Klimov. Proxi- mance analysis of a tensor processing unit. In Computer Architecture mal policy optimization algorithms. arXiv preprint arXiv:1707.06347, (ISCA), 2017 ACM/IEEE 44th Annual International Symposium on, pages 2017. 1–12. IEEE, 2017. [44] P. G. Selinger, M. M. Astrahan, D. D. Chamberlin, R. A. Lorie, and T. G. [25] A. Kipf, T. Kipf, B. Radke, V. Leis, P. Boncz, and A. Kemper. Learned Price. Access path selection in a relational database management sys- cardinalities: Estimating correlated joins with deep learning. arXiv tem. In Proceedings of the 1979 ACM SIGMOD international conference preprint arXiv:1809.00677, 2018. on Management of data, pages 23–34. ACM, 1979. [26] T. Kraska, A. Beutel, E. H. Chi, J. Dean, and N. Polyzotis. The case [45] D. Silver, A. Huang, C. J. Maddison, A. Guez, L. Sifre, G. Van Den Driess- for learned index structures. In Proceedings of the 2018 International che, J. Schrittwieser, I. Antonoglou, V. Panneershelvam, M. Lanctot, Conference on Management of Data, pages 489–504. ACM, 2018. et al. Mastering the game of go with deep neural networks and tree [27] R. Krishnamurthy, H. Boral, and C. Zaniolo. Optimization of nonre- search. In Nature. Nature Research, 2016. cursive queries. In VLDB, volume 86, pages 128–137, 1986. [46] M. Steinbrunn, G. Moerkotte, and A. Kemper. Heuristic and ran- [28] M. Laskey, J. Lee, R. Fox, A. Dragan, and K. Goldberg. Dart: Noise domized optimization for the join ordering problem. The VLDB Jour- injection for robust imitation learning. Conference on Robot Learning nalâĂŤThe International Journal on Very Large Data Bases, 6(3):191–208, 2017, 2017. 1997. [29] V. Leis, A. Gubichev, A. Mirchev, P. Boncz, A. Kemper, and T. Neumann. [47] R. S. Sutton, A. G. Barto, et al. Reinforcement learning: An introduction. How good are query optimizers, really? Proceedings of the VLDB MIT press, 1998. Endowment, 9(3):204–215, 2015. [48] I. Trummer and C. Koch. Multi-objective parametric query optimiza- [30] S. Levine, P. Pastor, A. Krizhevsky, J. Ibarz, and D. Quillen. Learn- tion. Proceedings of the VLDB Endowment, 8(3):221–232, 2014. ing hand-eye coordination for robotic grasping with deep learning [49] I. Trummer and C. Koch. Solving the join ordering problem via mixed and large-scale data collection. The International Journal of Robotics integer linear programming. In Proceedings of the 2017 ACM Inter- Research, 37(4-5):421–436, 2018. national Conference on Management of Data, pages 1025–1040. ACM, [31] H. Liu, M. Xu, Z. Yu, V. Corvinelli, and C. Zuzarte. Cardinality es- 2017. timation using neural networks. In Proceedings of the 25th Annual [50] H. Van Hasselt, A. Guez, and D. Silver. Deep reinforcement learning International Conference on Computer Science and Software Engineering, with double q-learning. In AAAI, volume 2, page 5. Phoenix, AZ, 2016. pages 53–59. IBM Corp., 2015. [51] F. Waas and A. Pellenkoft. Join order selection (good enough is easy). [32] L. Ma, D. Van Aken, A. Hefny, G. Mezerhane, A. Pavlo, and G. J. Gordon. In British National Conference on Databases, pages 51–67. Springer, Query-based workload forecasting for self-driving database manage- 2000. ment systems. In Proceedings of the 2018 International Conference on [52] W. Wu, Y. Chi, H. Hacígümüş, and J. F. Naughton. Towards predicting Management of Data, pages 631–645. ACM, 2018. query execution time for concurrent and dynamic database workloads. [33] R. Marcus and O. Papaemmanouil. Deep reinforcement learning for Proceedings of the VLDB Endowment, 6(10):925–936, 2013. join order enumeration. arXiv preprint arXiv:1803.00055, 2018. [53] W. Wu, Y. Chi, S. Zhu, J. Tatemura, H. Hacigümüs, and J. F. Naughton. [34] R. Marcus and O. Papaemmanouil. Towards a hands-free query opti- Predicting query execution time: Are optimizer cost models really mizer through deep learning. arXiv preprint arXiv:1809.10212, 2018. unusable? In Data Engineering (ICDE), 2013 IEEE 29th International [35] V. Markl, G. M. Lohman, and V. Raman. LEO: An autonomic query Conference on, pages 1081–1092. IEEE, 2013. optimizer for DB2. IBM Systems Journal, 42(1):98–106, 2003. [54] J. Yosinski, J. Clune, Y. Bengio, and H. Lipson. How transferable are [36] V. Markl, V. Raman, D. Simmen, G. Lohman, H. Pirahesh, and M. Cil- features in deep neural networks? In Advances in neural information imdzic. Robust query processing through progressive optimization. processing systems, pages 3320–3328, 2014. In Proceedings of the 2004 ACM SIGMOD international conference on [55] M. Ziane, M. Zaït, and P. Borla-Salamet. Parallel query processing Management of data, pages 659–670. ACM, 2004. with zigzag trees. The VLDB JournalâĂŤThe International Journal on [37] M. Mitzenmacher. A model for learned bloom filters and related Very Large Data Bases, 2(3):277–302, 1993. structures. arXiv preprint arXiv:1802.00884, 2018. [38] V. Mnih, K. Kavukcuoglu, D. Silver, A. Graves, I. Antonoglou, D. Wier- stra, and M. Riedmiller. Playing atari with deep reinforcement learning. A STANDALONE OPTIMIZATION In arXiv, 2013. EXPERIMENT SETUP [39] V. Mnih, K. Kavukcuoglu, D. Silver, A. A. Rusu, J. Veness, M. G. Belle- mare, A. Graves, M. Riedmiller, A. K. Fidjeland, G. Ostrovski, et al. We consider three different cost models on the same work- Human-level control through deep reinforcement learning. In Nature. load: Nature Research, 2015. CM1: In the first cost model (inspired by [29]), we model [40] T. Neumann and B. Radke. Adaptive optimization of very large join queries. In Proceedings of the 2018 International Conference on Manage- a main-memory database that performs two types of joins: ment of Data, pages 677–692. ACM, 2018. index joins and in-memory hash joins. Let O describe the current operator, Ol be the left child operator, and O r be the right child operator. The costs are defined with the following 16 

17 .recursions: In our implementation of these cost models, we use true cardinalities on single-table predicates, and we leverage stan- ci j (O) = c(Ol ) + match(Ol , O r ) · |Ol | dard independence assumptions to construct more compli- cated cardinality estimates. (This is not a fundamental limi- chj (O) = c(Ol ) + c(O r ) + |O | tation of DQ. Results in §6.2 have shown that when Postgres and SparkSQL provide their native cost model and cardinality where c denotes the cost estimation function, | · | is the car- estimates, DQ is as effective.) The goal of this work is to eval- dinality function, and match denotes the expected cost of uate the join ordering process independent of the strength an index match, i.e., fraction of records that match the index or weakness of the underlying cardinality estimation. lookup (always greater than 1) multiplied by a constant fac- We consider the following baseline algorithms. These algo- tor λ (we chose 1.0). We assume indexes on the primary keys. rithms are not meant to be a comprehensive list of heuristics In this cost model, if an eligible index exists it is generally but rather representative of a class of solutions. desirable to use it, since match(Ol , O r ) · |Ol | rarely exceeds c(O r ) + |O | for foreign key joins. Even though the cost model (1) Exhaustive (EX): This is a dynamic program that ex- is nominally “non-linear”, primary tradeoff between the in- haustively enumerates all join plans avoiding Carte- dex join and hash join is due to index eligibility and not sian products. dependent on properties of the intermediate results. For the (2) left-deep (LD): This is a dynamic program that exhaus- JOB workload, unless λ is set to be very high, hash joins have tively enumerates all left-deep join plans. rare occurrences compared to index joins. (3) Right-Deep (RD): This is a dynamic program that ex- CM2: In the next cost model, we remove index eligibility haustively enumerates all right-deep join plans. from consideration and consider only hash joins and nested (4) Zig-Zag (ZZ): This is a dynamic program that exhaus- loop joins with a memory limit M. The model charges a cost tively enumerates all zig-zag trees (every join has when data requires additional partitioning, and further falls at least one base relation, either on the left or the back to a nested loop join when the smallest table exceeds right) [55]. the squared memory: (5) IK-KBZ (KBZ): This algorithm is a polynomial time algorithm that decomposes the query graph into chains   c(O l ) + c(O r ) + |O | if |O r | + |O l | ≤ M and orders the chains based on a linear approximation  = c(O l ) + c(O r ) + 2( |O r | + |O l |) + |O | if min( |O r |, |O l |) ≤ M   2 c join of the cost model [27]. |O r |  c(O l ) + c(O r ) + ( |O r | + M |O l |)    (6) QuickPick-1000 (QP): This algorithm randomly selects 1000 join plans and returns the best of them. 1000 The non-linearities in this model are size-dependent, so con- was selected to be roughly equivalent to the planning trolling the size of intermediate relations is important in the latency of DQ [51]. optimization problem. We set the memory limit M to 105 (7) Minimum Selectivity (MinSel): This algorithm selects tuples in our experiments. This limit is low in real-world the join ordering based on the minimum selectivity terms due to the small size of the benchmark data. However, heuristic [40]. While MinSel was fast, we found poor we intend for the results to be illustrative of what happens performance on the 3 cost models used in the paper. in the optimization problems. (8) Linearized Dynamic Program (LDP): This approach CM3: In the next cost model, we model a database that applies a dynamic program in the inner-loop of IK- accounts for the reuse of already-built hash tables. We use KBZ [40]. Not surprisingly, LDPâĂŹs results were the Gamma database convention where the left operator as highly correlated with those of IK-KBZ and Left-Deep the “build” operator and the right operator as the “probe” enumeration, so we chose to omit them from the main operator [18]. If the previous join has already built a hash body of the paper. table on an attribute of interest, then the hash join does not All of the algorithms consider join ordering without incur another cost. Cartesian products, so EX is an optimal baseline. We re- cnobuild = c(Ol ) + c(O r ) − |O r | + |O | port results in terms of the suboptimality w.r.t. EX, namely costalдo /cost EX . We present results on all 113 JOB queries. We also allow for index joins as in CM1. This model makes We train on 80 queries and test on 33 queries. We do 4-fold hash joins substantially cheaper in cases where re-use is cross validation to ensure that every test query is excluded possible. This model favors some subplans to be right-deep from the training set at least once. The performance of DQ is plans which maximize the reuse of the built hash tables. only evaluated on queries not seen in the training workload. Therefore, optimal solutions have both left-deep and right- Our standalone experiments are integrated with Apache deep segments. Calcite [2]. Apache Calcite provides libraries for parsing 17 

18 . Optimizer Cost Model 1 Cost Model 2 Cost Model 3 Min Mean Max Min Mean Max Min Mean Max QuickPick (QP) 1 23.87 405.04 7.43 51.84 416.18 1.43 16.74 211.13 IK-KBZ (KBZ) 1 3.45 36.78 5.21 29.61 106.34 2.21 14.61 96.14 Right-deep (RD) 4.7 53.25 683.35 1.93 8.21 89.15 1.83 5.25 69.15 Left-deep (LD) 1 1.08 2.14 1.75 7.31 65.45 1.35 4.21 35.91 Zig-zag (ZZ) 1 1.07 1.87 1 5.07 43.16 1 3.41 23.13 Exhaustive (EX) 1 1 1 1 1 1 1 1 1 DQ 1 1.32 3.11 1 1.68 11.64 1 1.91 13.14 Minimum Selectivity (MinSel) 2.43 59.86 1083.12 23.46 208.23 889.7 9.81 611.1 2049.13 IK-KBZ+DP (LDP) 1 1.09 2.72 2.1 10.03 105.32 2.01 3.99 32.19 Table 6: Extended results including omitted techniques for all three cost models. SQL, representing relational algebraic expressions, and a C ADDITIONAL STANDALONE Volcano-based query optimizer [19, 20]. Calcite does not han- EXPERIMENTS dle physical execution or storage and uses JDBC connectors In the subsequent experiments, we try to characterize when to a variety of database engines and file formats. We imple- DQ is expected to work and how efficiently. mented a package inside Calcite that allowed us to leverage its parsing and plan representation, but also augment it with C.1 Sensitivity to Training Data more sophisticated cost models and optimization algorithms. Standalone DQ is written in single-threaded Java. The ex- Classically, join optimization algorithms have been deter- tended results including omitted techniques are described in ministic. Except for QP, all of our baselines are deterministic Table 6. as well. Randomness in DQ (besides floating-point compu- tations) stems from what training data is seen. We run an experiment where we provide DQ with 5 different training B Cout COST MODEL datasets and evaluate on a set of 20 hold-out queries. We We additionally omitted experiments with a simplified cost report the max range (worst factor over optimal minus best model only searching for join orders and ignoring physical factor over optimal) in performance over all 20 queries in operator selection. We fed in true cardinalities to estimate Table 7. For comparison, we do the same with QP over 5 the selectivity of each of the joins, which is a perfect version trials (with a different random seed each time). of the “Cout ” model. We omitted these results as we did not see differences between the techniques and the goal of the CM1 CM2 CM3 study was to understand the performance of DQ over cost models that cause the heuristics to fail. In particular, we QP 2.11× 1.71× 3.44× found that threshold non-linearities as in CM3 cause the DQ 1.59× 1.13× 2.01× most problems. Table 7: Plan variance over trials. We found that while the performance of DQ does vary due to training data, the variance is relatively low. Even if Cout Mean we were to account for this worst case, DQ would still be QP 1.02 competitive in our macro-benchmarks. It is also substantially IK-KBZ 1.34 lower than that of QP, a true randomized algorithm. LD 1.02 ZZ 1.02 C.2 Sensitivity to Faulty Cardinalities Ex 1 In general, the cardinality/selectivity estimates computed DQ 1.03 by the underlying RDBMS do not have up-to-date accuracy. MinSel 1.11 All query optimizers, to varying degrees, are exposed to this issue since using faulty estimates during optimization may yield plans that are in fact suboptimal. It is therefore worthwhile to investigate this sensitivity and try to answer, 18 

19 .“is the neural network more or less sensitive than classical dynamic programs and heuristics?” In this microbenchmark, the optimizers are fed perturbed base relation cardinalities (explained below) during optimiza- tion; after the optimized plans are produced, they are scored by an oracle cost model. This means, in particular, DQ only sees noisy relation cardinalities during training and is tested on true cardinalities. The workload consists of 20 queries randomly chosen out of all JOB queries; the join sizes range from 6 to 11 relations. The final costs reported below are the average from 4-fold cross validation. The perturbation of base relation cardinalities works as follows. We pick N random relations, the true cardinality of each is multiplied by a factor drawn uniformly from {2, 4, 8, 16}. As N increases, the estimate noisiness increases (errors in the leaf operators get propagated upstream in a Figure 12: We plot the runtime in milliseconds of a single compounding fashion). Table 8 reports the final costs with query (q10c) with different variations of DQ (fully offline, fine tuning, and fully online). We found that the fine-tuned respect to estimate noisiness. approach was the most effective one. N =0 N =2 N =4 N =8 D DISCUSSION ABOUT POSTGRES KBZ 6.33 6.35 6.35 5.85 EXPERIMENT LD 5.51 5.53 5.53 5.60 EX 5.51 5.53 5.53 5.60 We also run a version of DQ where the model is only trained DQ 5.68 5.70 5.96 5.68 with online data (effectively the setting considered in Re- JOIN [33]). Even on an idealized workload of optimizing a Table 8: Costs (log10 ) when N relations have perturbed car- dinalities. single query (Query 10c), we could not get that approach to converge. We believe that the discrepancy from [33] is due to physical operator selection. In that work, the Postgres op- Observe that, despite a slight degradation in the N = 4 timizer selects the physical operators given the appropriate execution, DQ is not any more sensitive than the KBZ heuris- logical plans selected by the RL policy. With physical oper- tic. It closely imitates exhaustive enumeration—an expected ator selection, the learning problem becomes significantly behavior since its training data comes from EX’s plans com- harder (Figure 12). puted with the faulty estimates. We initially hypothesized the DQ outperforms the native Postgres optimizer in terms of execution times since it consid- C.3 Ablation Study ers bushy plans. This hypothesis only partially explains the Table 9 reports an ablation study of the featurization de- results. We run the same experiment where DQ is restricted scribed earlier (§4.1): to producing left-deep plans; in other words, DQ considers the same plan space as the native Postgres optimizer. We Graph Features Sel. Scaling Loss found that there was still a statistically significant speedup: No Predicates No No 0.087 Yes No 0.049 Mean Max Yes Yes 0.049 DQ:LD 1.09× 2.68× Predicates No No 0.071 DQ:EX 1.14× 2.72× Yes No 0.051 Yes Yes 0.020 Table 10: Execution time speedup over Postgres with dif- ferent plan spaces considered by DQ. Mean is the average Table 9: Feature ablation. speedup over the entire workload and max is the best case single-query speedup. Without features derived from the query graph (Figure 3b) and selectivity scaling (Figure 4a) the training loss is 3.5× We speculate that the speedup is caused by imprecision in more. These results suggest that all of the different features the Postgres cost model. As a learning technique, DQ may contribute positively for performance. smooth out inconsistencies in the cost model. 19 

20 . Finally, we compare with Postgres’ genetic optimizer (GEQ) on the 10 largest joins in JOB. DQ is about 7% slower in planning time, but nearly 10× faster in execution time. The difference in execution is mostly due to one outlier query on which GEQ is 37× slower. 20