- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
具有欧拉回路
展开查看详情
1 .欧拉图与哈密顿图 欧拉图 哈密顿图 最短路径问题 货郎担问题
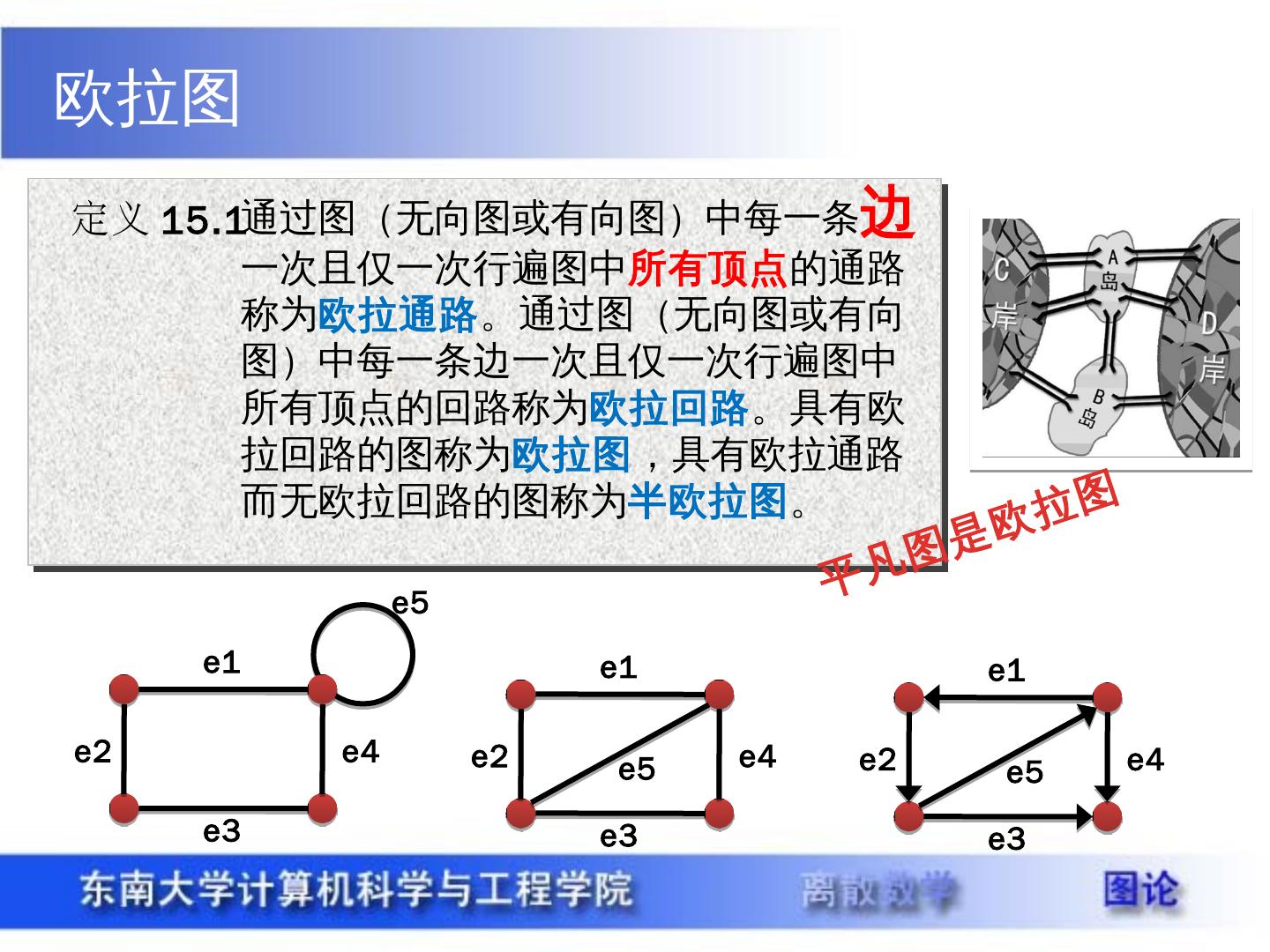
2 .欧拉图 定义 15.1 通过图(无向图或有向图)中每一条 边 一次且仅一次行遍图中 所有顶点 的通路称为 欧拉通路 。通过图(无向图或有向图)中每一条边一次且仅一次行遍图中所有顶点的回路称为 欧拉回路 。具有欧拉回路的图称为 欧拉图 ,具有欧拉通路而无欧拉回路的图称为 半欧拉图 。 平凡图是欧拉图 e1 e2 e3 e4 e5 e1 e2 e3 e4 e5 e1 e2 e3 e4 e5
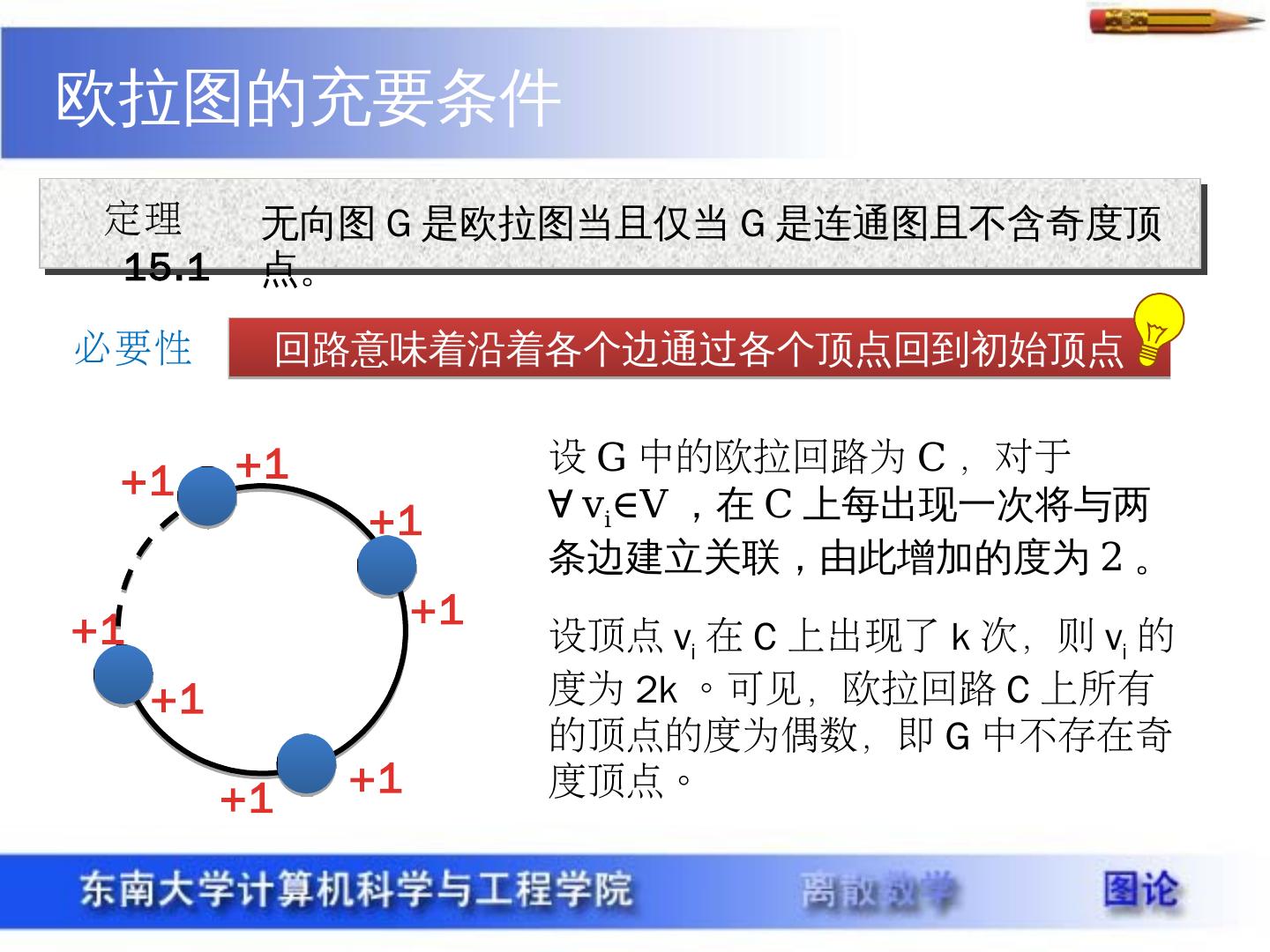
3 .欧拉图的充要条件 定理 15.1 无向图 G 是欧拉图当且仅当 G 是连通图且不含奇度顶点。 必要性 回路意味着沿着各个边通过各个顶点回到初始顶点 +1 +1 +1 +1 +1 +1 +1 +1 设 G 中的欧拉回路为 C ,对于 ∀ v i ∈V ,在 C 上每出现一次将与两条边建立关联,由此增加的度为 2 。 设顶点 v i 在 C 上出现了 k 次,则 v i 的度为 2k 。可见,欧拉回路 C 上所有的顶点的度为偶数,即 G 中不存在奇度顶点。
4 .欧拉图的充要条件 充分性 所有的顶点通过合理分配关联边(度)可以构造出一条欧拉回路 边的数量是无穷尽的,可以尝试用数学归纳法 边数 m 为 1 时,由于不存在奇度顶点, G 只能是包含唯一顶点的环。 设 m≤k ( k≥1 )时均可以构造出一条欧拉回路,需要证明 m=k+1 时结论也成立。由于 G 是连通图且不含奇度顶点,故 δ ( G ) ≥2 。 G 中必含有圈(定理 14.6 推论)。 设 C 为 G 中的一个圈,删除 C 中所有的边,则 C 上的所有顶点度数减少 2 ,且得到 G 的生成子图 G’ (定义 14.8 )。
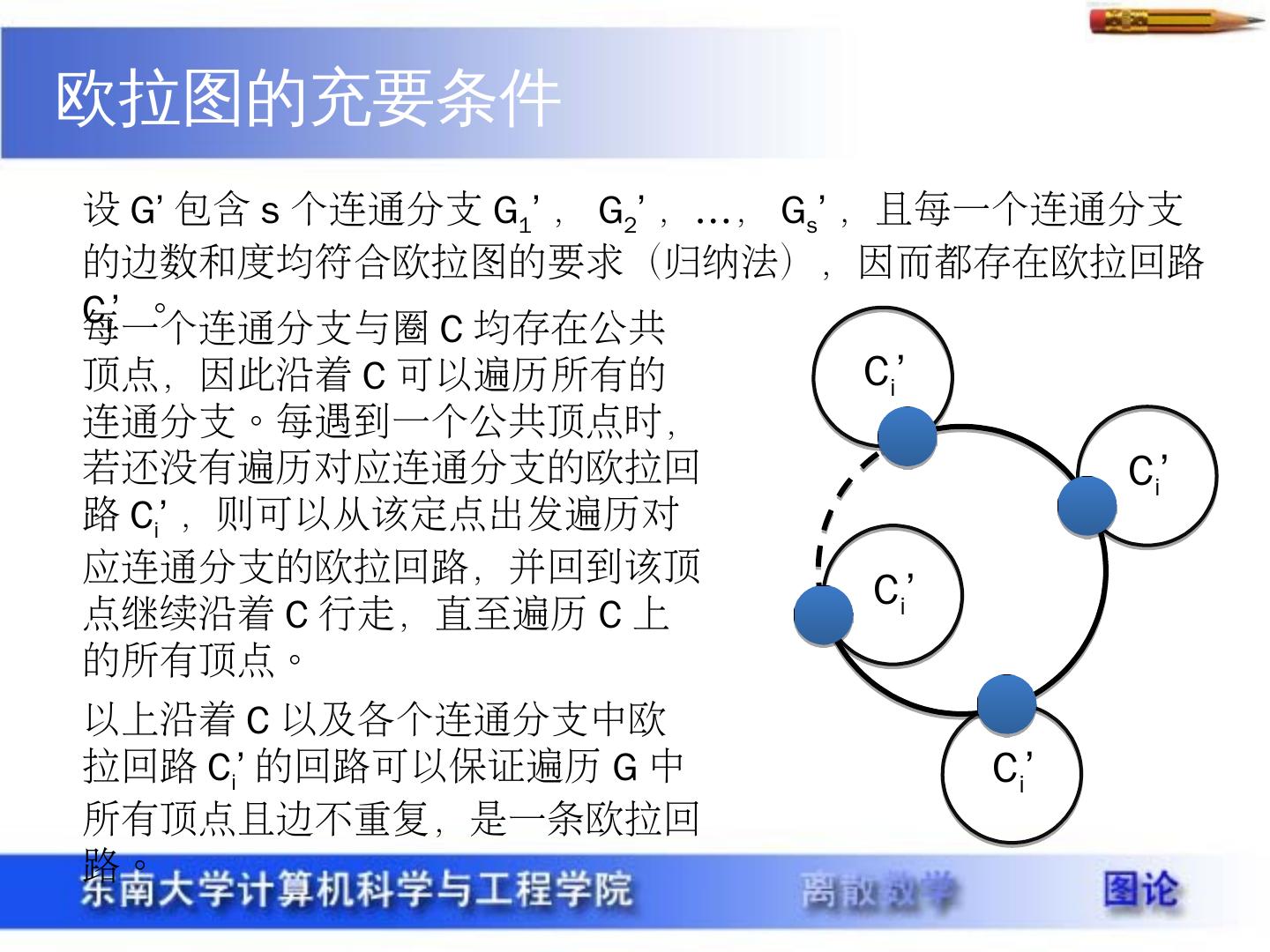
5 .欧拉图的充要条件 设 G’ 包含 s 个连通分支 G 1 ’ , G 2 ’ , … , G s ’ ,且每一个连通分支的边数和度均符合欧拉图的要求(归纳法),因而都存在欧拉回路 C i ’ 。 每一个连通分支与圈 C 均存在公共顶点,因此沿着 C 可以遍历所有的连通分支。每遇到一个公共顶点时,若还没有遍历对应连通分支的欧拉回路 C i ’ ,则可以从该定点出发遍历对应连通分支的欧拉回路,并回到该顶点继续沿着 C 行走,直至遍历 C 上的所有顶点。 C i ’ C i ’ C i ’ C i ’ 以上沿着 C 以及各个连通分支中欧拉回路 C i ’ 的回路可以保证遍历 G 中所有顶点且边不重复,是一条欧拉回路。
6 .PLAY 从以上证明不难看出:欧拉图是若干个边不重的圈之并,见示意图 .
7 .半欧拉图的充要条件 无向 G 是半欧拉图当且仅当 G 是连通图且仅含两个奇度顶点。 定理 15.2 必要性 含有欧拉通路而非回路,通路与回路什么区别? +1 +1 +1 +1 设 G 中的欧拉通路为 Γ ,对于除 Γ 的始点和终点外 ∀ v i ∈V ,在 Γ 上每出现一次将与两条边建立关联,由此增加的度为 2 。 设顶点 v i 在 C 上出现了 k 次,则 v i 的度为 2k 。 若 v i 是 Γ 的端点,由于端点之间不相邻,因此增加的度为 1 。若 v i 在 Γ 中出现 k 次,则 v i 的度为 2k+1 ,否则为 1 ,皆为奇数。 设 G 的两个奇度顶点为 v i 和 v j , 对 G 加新边 < v i , v j >, 则 G’=GU< v i , v j > 具有 欧拉回路 C’ 。而 C=C’ - < v i , v j > 则为 G 的一条欧拉通路。 充分性
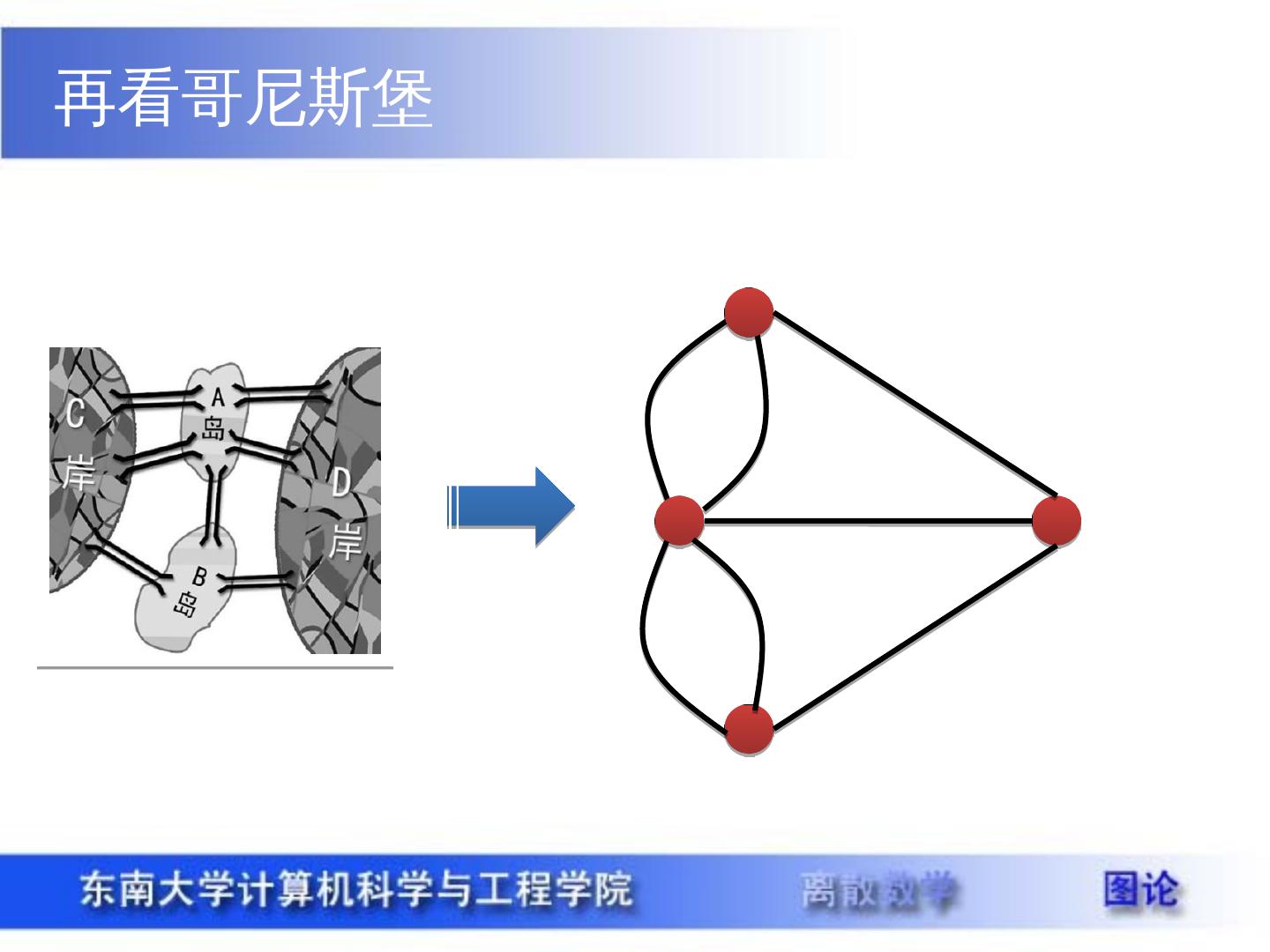
8 .再看哥尼斯堡
9 .跳马问题 2 3 4 4 4 4 3 2 3 4 6 6 6 6 4 3 4 6 8 8 8 8 6 4 4 6 8 8 8 8 6 4 4 6 8 8 8 8 6 4 4 6 8 8 8 8 6 4 3 4 6 6 6 6 4 3 2 3 4 4 4 4 3 2 度数为3的顶点8个, 其余均为偶数个顶点。 由欧拉定理可知: G 既不是欧拉图, 又不存在欧拉路径。 结论:在8 x 8的 棋盘上完成所有可能跳动仅一次是不可能的。
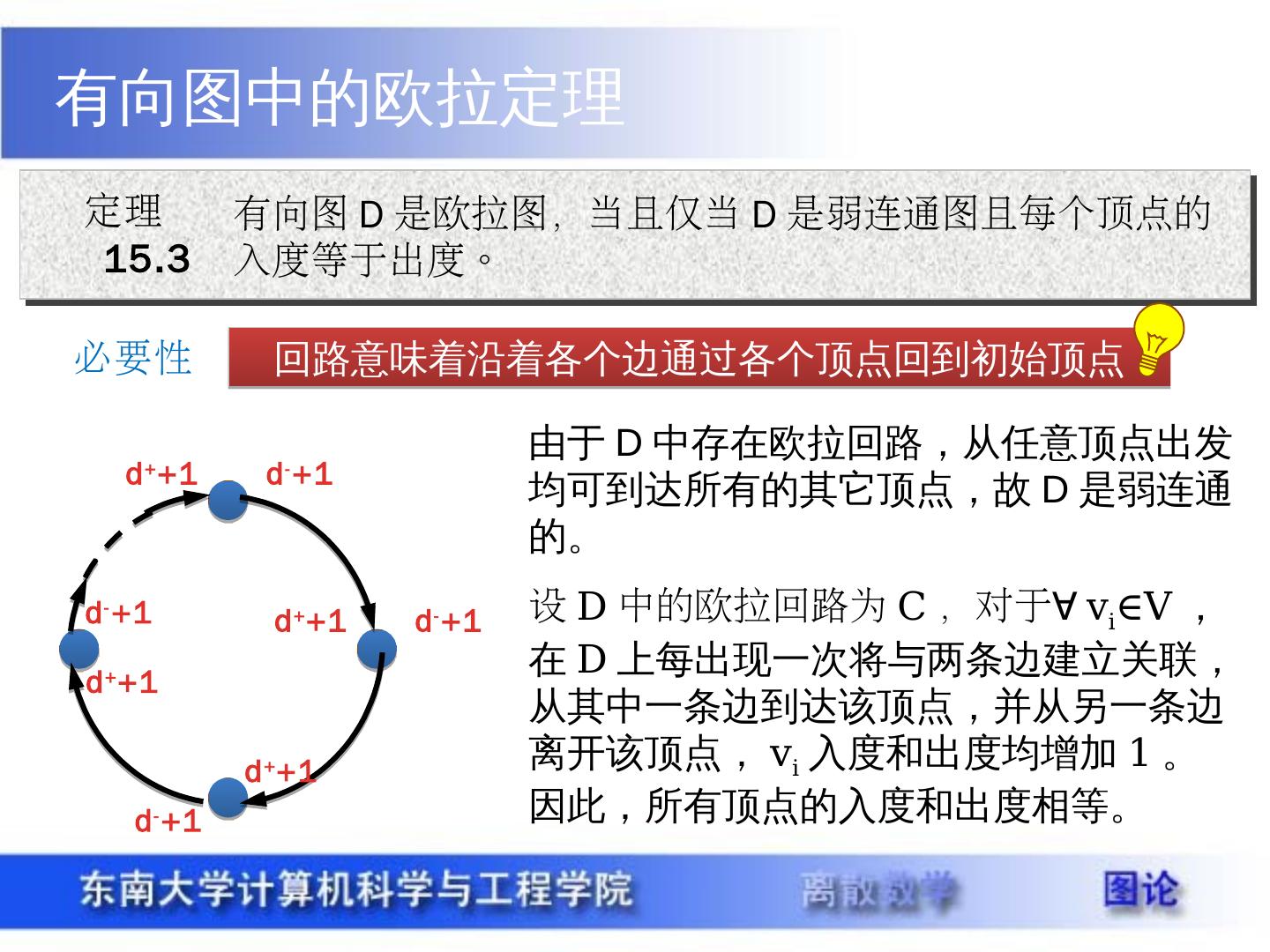
10 .有向图中的欧拉定理 定理 15.3 有向图 D 是欧拉图,当且仅当 D 是弱连通图且每个顶点的入度等于出度。 必要性 回路意味着沿着各个边通过各个顶点回到初始顶点 d + +1 d - +1 d + +1 d - +1 d + +1 d - +1 d + +1 d - +1 设 D 中的欧拉回路为 C ,对于 ∀ v i ∈V ,在 D 上每出现一次将与两条边建立关联,从其中一条边到达该顶点,并从另一条边离开该顶点, v i 入度和出度均增加 1 。因此,所有顶点的入度和出度相等。 由于 D 中存在欧拉回路,从任意顶点出发均可到达所有的其它顶点,故 D 是弱连通的。
11 .充分性 所有的顶点通过合理分配关联边(度)可以构造出一条欧拉回路 边的数量是无穷尽的,可以尝试用数学归纳法 有向图中的欧拉定理 边数 m 为 1 时, G 只能是包含唯一顶点的环。 设 m ≤k ( k≥1 )时均可以构造出一条欧拉回路,需要证明 m=k+1 时结论也成立。由于 G 是弱连通图且顶点的出度和入度相等,故 G 中必含有圈。 设 C 为 G 中的一个圈,删除 C 中所有的边,则 C 上的所有顶点入度和出度各减少 1 ,且得到 G 的生成子图 G’ (定义 14.8 )。
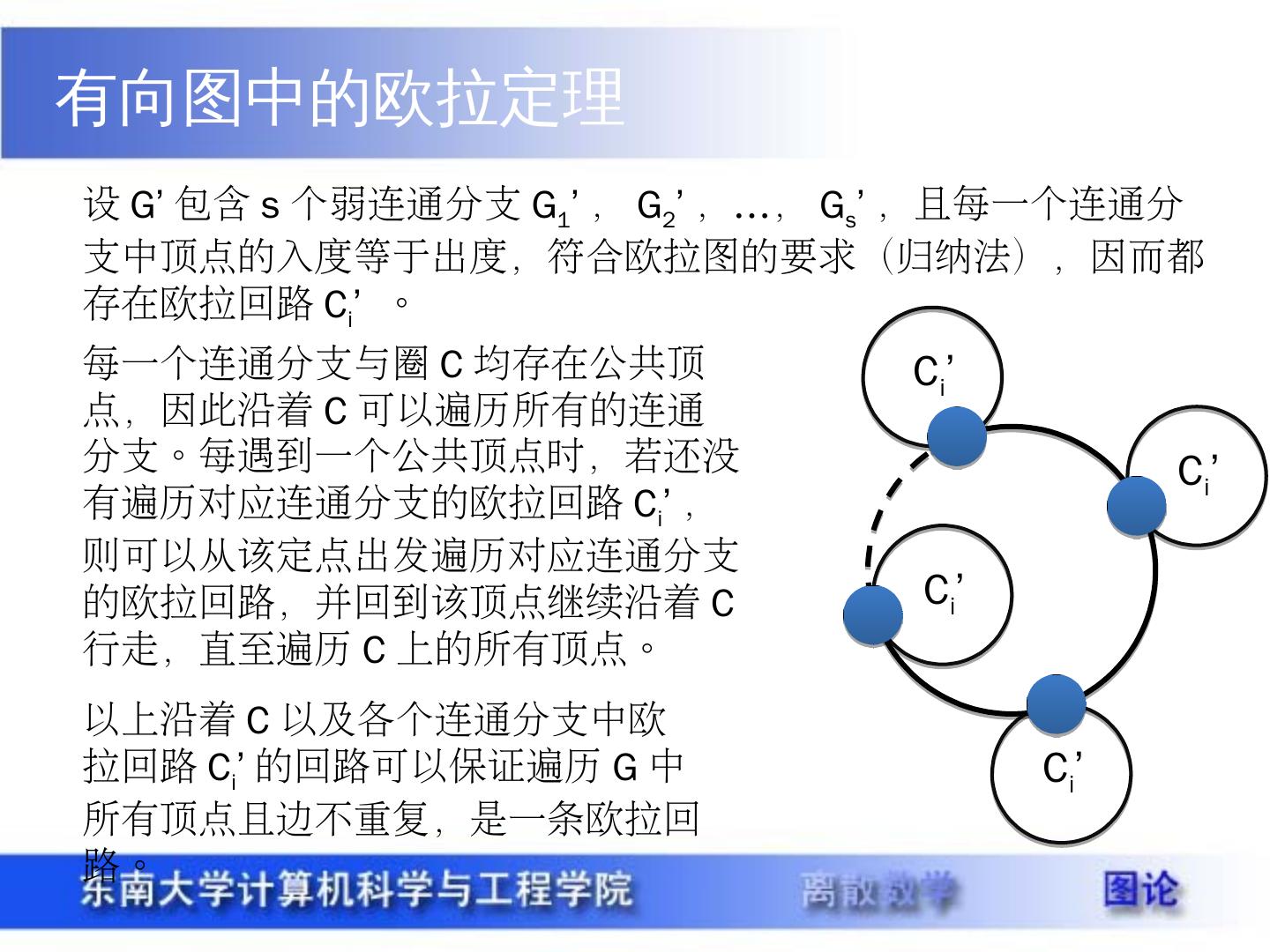
12 .有向图中的欧拉定理 设 G’ 包含 s 个弱连通分支 G 1 ’ , G 2 ’ , … , G s ’ ,且每一个连通分支中顶点的入度等于出度,符合欧拉图的要求(归纳法),因而都存在欧拉回路 C i ’ 。 每一个连通分支与圈 C 均存在公共顶点,因此沿着 C 可以遍历所有的连通分支。每遇到一个公共顶点时,若还没有遍历对应连通分支的欧拉回路 C i ’ ,则可以从该定点出发遍历对应连通分支的欧拉回路,并回到该顶点继续沿着 C 行走,直至遍历 C 上的所有顶点。 C i ’ C i ’ C i ’ C i ’ 以上沿着 C 以及各个连通分支中欧拉回路 C i ’ 的回路可以保证遍历 G 中所有顶点且边不重复,是一条欧拉回路。
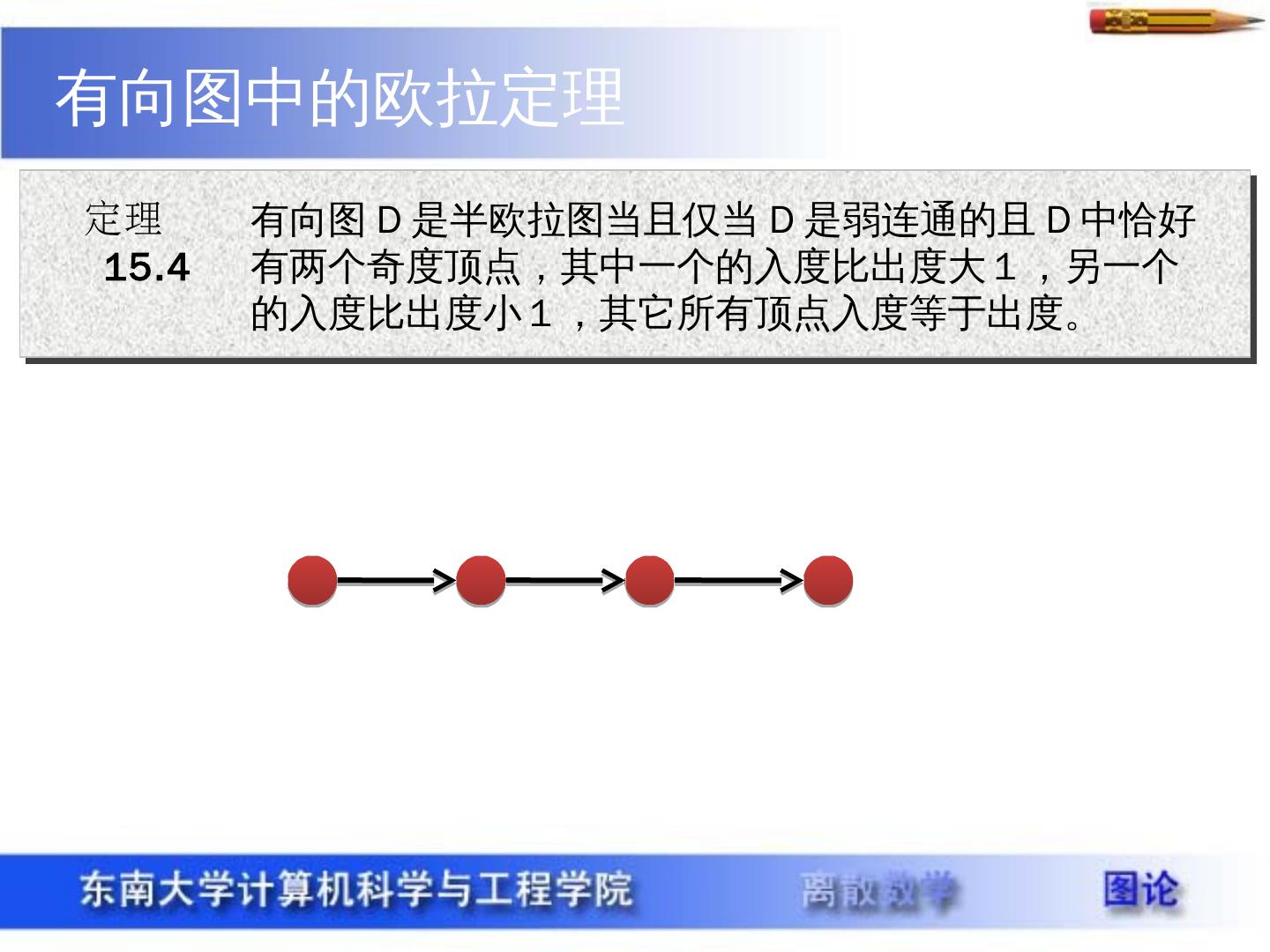
13 .定理 15.4 有向图中的欧拉定理 有向图 D 是半欧拉图当且仅当 D 是弱连通的且 D 中恰好有两个奇度顶点,其中一个的入度比出度大1,另一个的入度比出度小1,其它所有顶点入度等于出度。
14 .欧拉图的充要条件 定理 15.5 G 是非平凡的欧拉图当且仅当 G 是连通的且为若干个边不重的圈的并。 d+2
15 .关于欧拉图的等价命题 设 G 是非平凡连通图,以下三个命题等价: G 是欧拉图。 G 中每个顶点的度数均为偶数。 G 中所有的边包含在相互没有公共边的圈中。
16 .关于欧拉图的等价命题 设 G 是非平凡连通图,以下三个命题等价: G 是欧拉图。 G 中每个顶点的度数均为偶数。 G 中所有的边包含在相互没有公共边的圈中。
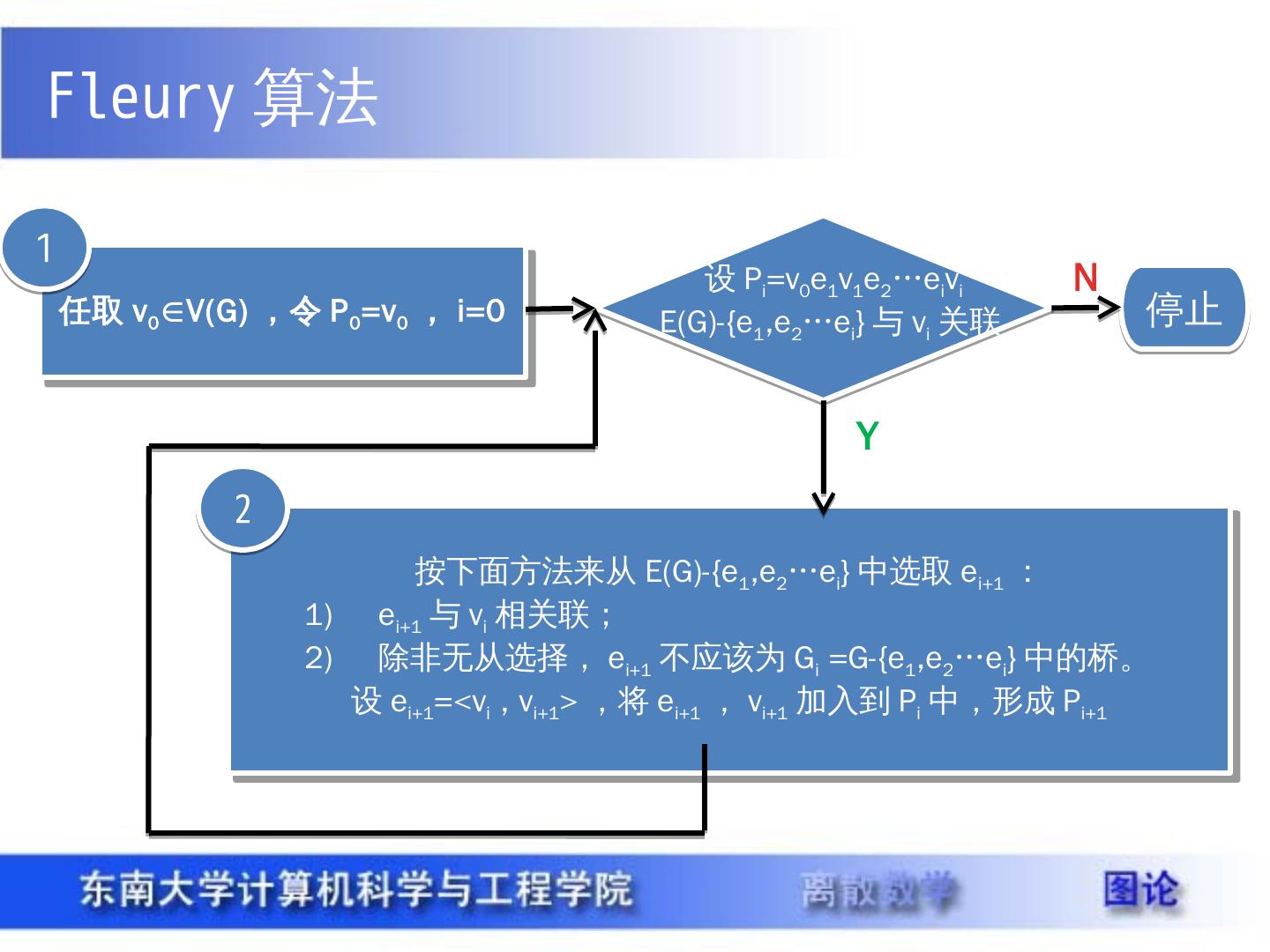
17 .Fleury 算法 任取 v 0 ∈V(G) ,令 P 0 =v 0 , i =0 1 设 P i =v 0 e 1 v 1 e 2 … e i v i E(G)-{e 1 ,e 2 … e i } 与 v i 关联 停止 N 按下面方法来从 E(G)-{e 1 ,e 2 … e i } 中选取 e i+1 : e i+1 与 v i 相关联; 除非无从选择, e i+1 不应该为 G i =G-{e 1 ,e 2 … e i } 中的桥。 设 e i+1 =<v i , v i+1 > ,将 e i+1 , v i+1 加入到 P i 中,形成 P i+1 2 Y
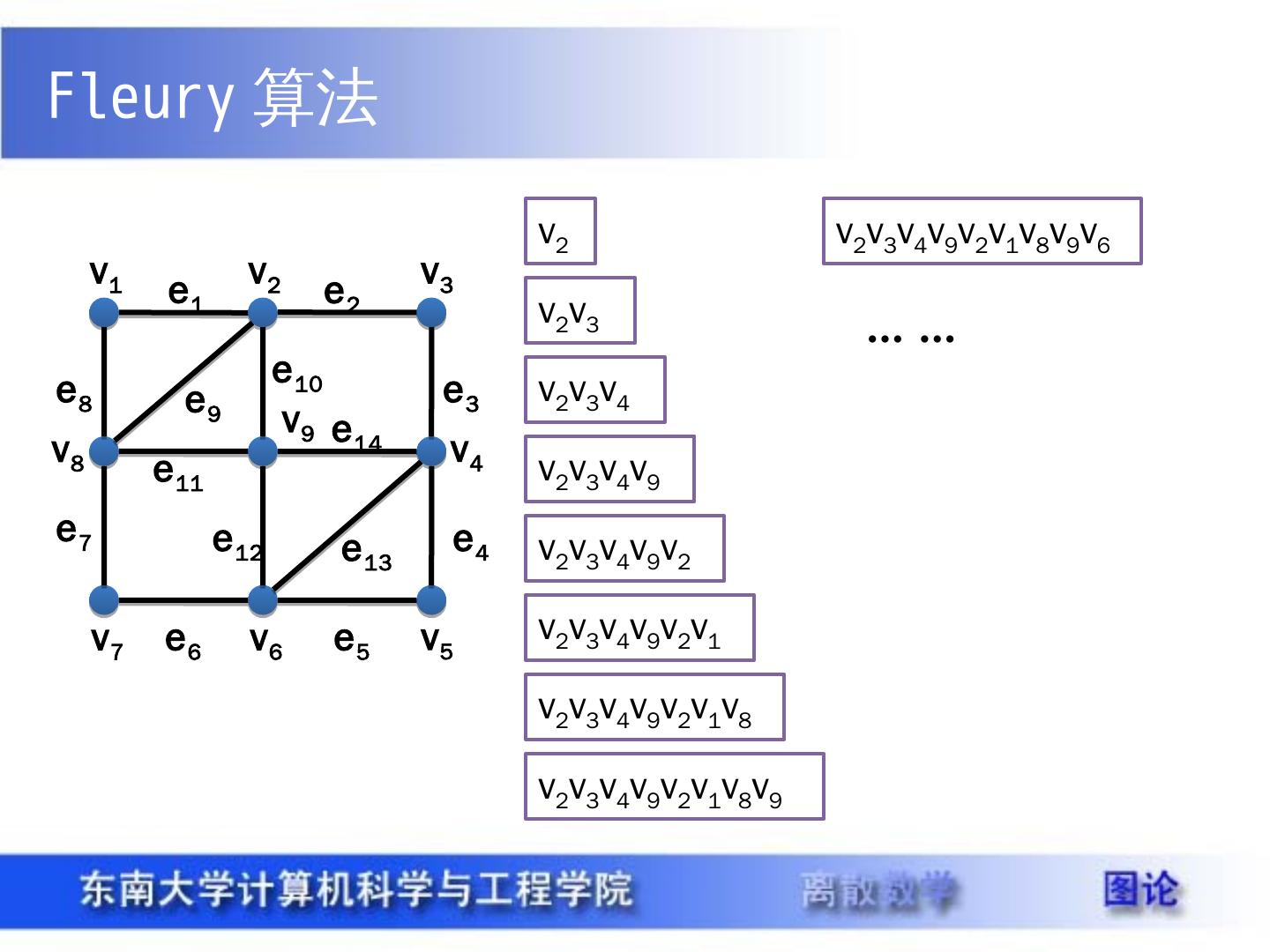
18 .Fleury 算法 v 1 v 2 v 3 v 4 v 5 v 6 v 7 v 8 v 9 e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 e 10 e 11 e 12 e 14 e 13 v 2 v 2 v 3 v 2 v 3 v 4 v 2 v 3 v 4 v 9 v 2 v 3 v 4 v 9 v 2 v 2 v 3 v 4 v 9 v 2 v 1 v 2 v 3 v 4 v 9 v 2 v 1 v 8 v 2 v 3 v 4 v 9 v 2 v 1 v 8 v 9 v 2 v 3 v 4 v 9 v 2 v 1 v 8 v 9 v 6 … …
19 .哈密顿图 定义 15.2 经过图(无向图或有向图)的 每一个顶点 一次且仅一次的通路称为哈密顿通路。经过图的每一个顶点一次且仅一次的回路称为哈密顿回路。具有哈密尔顿 回路 的图称为 哈密顿图 ,具有哈密顿 通路 但不具有哈密顿回路的图称为 半哈密顿图 。 平凡图是哈密顿图 欧拉图更加关注边,顶点在路径中可以重复; 问题来源于七桥遍历。 哈密顿图更加关注顶点,边在路径中可以缺失; 问题源自城市遍历。
20 .哈密顿图的必要条件 定理 15.6 设无向图 G=<V , E> 是哈密顿图,则对于任意 V 1 ⊂V 且 V 1 ≠Ø ,均有 p(G-V 1 )≤|V 1 | 从哈密顿图的定义出发:存在一条回路,遍历了所有顶点一次且仅一次。 …… …… 设 C 是 G 中的一条哈密顿回路,则 C 上遍历了 G 中的所有顶点,必同时包含 V 1 中所有顶点。 依次删除 V 1 中的顶点,若被删除顶点相邻,则 C 上的其它顶点仍然构成连通图, p(G-V 1 )=1 ;若被删除顶点不相邻, C 上处于被删除顶点之间的顶点若不存在与 C 上其它顶点的边则形成与 C 互不连通的子图。 当 V 1 中的顶点在 C 上互不相邻,且所有的间隔顶点均没有与 C 上其它顶点的边时形成的连通分支最多,即 p(G-V 1 )=|V 1 |
21 .半哈密顿图的必要条件 定理 15.6 推论 设无向图 G=<V , E> 是半哈密顿图,则对于任意 V 1 ⊂V 且 V 1 ≠Ø ,均有 p(G-V 1 )≤|V 1 |+1 通路与回路的区别表现在删除一个顶点的情况下 通路分割为两个连通分支,而回路则保持连通。
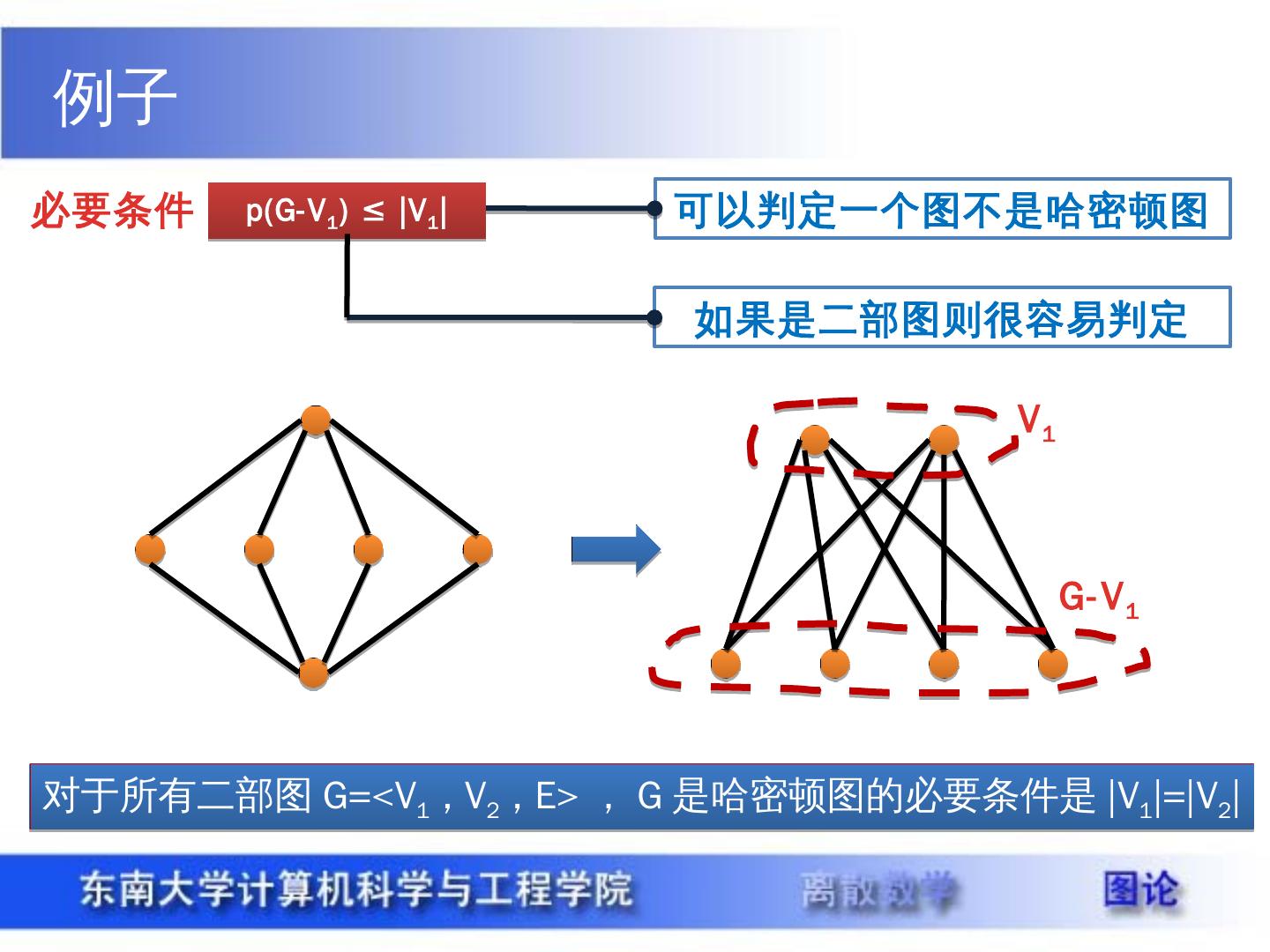
22 .例子 p(G-V 1 ) ≤ |V 1 | 必要条件 可以判定一个图不是哈密顿图 如果是二部图则很容易判定 G-V 1 V 1 对于所有二部图 G=<V 1 , V 2 , E> , G 是哈密顿图的必要条件是 |V 1 |=|V 2 |
23 .哈密顿通路存在的充分条件 定理 15.7 设无向图 G 是 n 阶无向简单图,若对于 G 中任意不相邻的顶点 u,v 均有 d(u)+d(v)≥n-1 ,则 G 中存在哈密顿通路。 d(u)+d(v)≥n-1 通路 无向简单图中顶点的最大度为 n-1 假设 G 不连通,则至少为两个连通分支 G 1 和 G 2 ,阶数分别为 n 1 和 n 2 。则 G 1 和 G 2 中顶点的最大度分别为 n 1 -1 和 n 2 -1 。若 u , v 分别在 G 1 和 G 2 中,则有: d(u)+d(v)≤n 1 +n 2 -2 = n-2 ,与 d(u)+d(v)≥n-1 矛盾。 哈密顿通路 所有顶点仅存在一次 1 、哈密顿通路是极大路径 2 、可以构造一条哈密顿通路 设 G 中的一条极大路径 Γ =v 1 v 2 …v l ,若 Γ 长度为 n-1 ,则其本身就是哈密顿通路; 若 l <n , 则 G 中存在 Γ 以外的顶点,那么是否可以将该顶点“链接”到 Γ 上,并形成一条更长的极大路径?如果可以,则通过不断“链接”其它顶点而构造出哈密顿通路。 证明线索: (1) 证 G 连通 (2) = v 1 v 2 … v l 为 G 中极大路径 . 若 l = n , 证毕 . (3) 否则,证 G 中存在过 上所有顶点的圈 C ,由 (1) 知 C 外顶点存在与 C 上某顶点相邻顶点,从而得比 更长的路径,重复 (2) –(3) ,最后得 G 中哈密顿通路 .
24 .哈密顿通路存在的充分条件 极大路径如何“链接”其它顶点? 重点是极大路径本身可构成一个圈 若 Γ 不是一个圈,即 v 1 与 v l 不相邻,设 v 1 和 v l 分别 与 v 2 到 v l-1 中的若干顶点相邻。由于 d(v 1 )+d(v l )≥n-1 ,因此与 v 1 和 v l 相邻的顶点数均不小于 2 ,且 v 1 和 v l 相邻的顶点中一定存在彼此相邻的情况。 因此可以构造一个圈 C 遍历 Γ 上所有顶点 由于 G 是连通图,设 Γ 外顶点 v l+1 与 C 上某一顶点 v t 相邻,则可以通过删除 v t 与 C 上两个相邻顶点之间任意一条边形成新的极大路径。 由于图 G 仍然满足连通且 d(v 1 )+d(v l )≥n-1 ,因此可通过不断构造圈将所有的其它顶点加入到极大路径中,最终构成哈密顿通路。 n-1
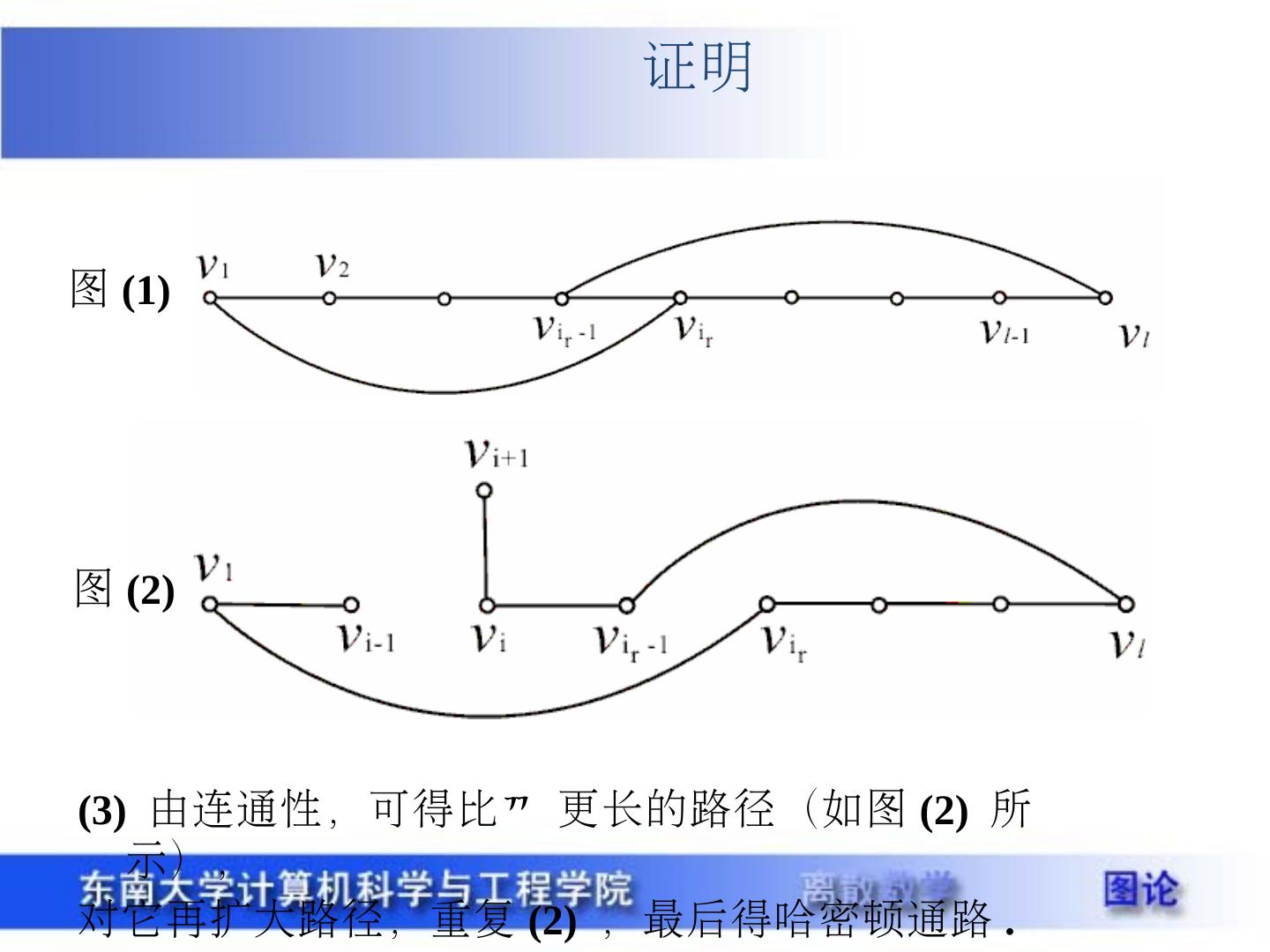
25 . 证明 图 (1) 图 (2) (3) 由连通性,可得比 更长的路径(如图 (2) 所示), 对它再扩大路径,重复 (2) ,最后得哈密顿通路 .
26 .哈密顿回路存在的充分条件 推论 设 G 为 n(n≥3) 阶无向简单图,若对于 G 中任意两个不相邻的顶点 u , v 均有 d(u)+d(v)≥n ,则 G 中存在哈密顿回路。 根据定理 15.7 可知, G 中存在哈密顿通路 Γ =v 1 v 2 … v n ,若 v 1 和 v n 不相邻,即不存在哈密顿回路。 v 1 与 Γ 上除 v n 以外的若干个顶点相邻, v n 与 Γ 上除 v 1 以外的若干个顶点相邻,两者的相邻顶点数至少为 2 且相邻顶点存在彼此相邻的情况。由此可以 构造一个包含 Γ 上所有顶点的圈 。 该圈即为哈密顿回路。 定理 15.8 设 u , v 为 n 阶无向简单图 G 中两个不相邻的顶点,且 d(u)+d(v)≥n ,则 G 为哈密顿图当且仅当 G∪ ( u,v ) 为哈密顿图( ( u,v ) 是加的新边) 不是任意
27 .例子 考虑在 7 天安排 7 门课程的考试,使得同一位老师所任的两门课程考试不排在接连的两天中,试证明如果没有老师担任多于 4 门课程,则符合上述要求的考试安排总是可能的。 某次国际会议中共有 8 人参加,他们来自不同的国家。他们中任何两个语言不通的人与其余的语言相通的人的人数之和大于等于 8 ,试证明可以将这 8 个人排在圆桌旁,使其中任何人都可以与左右的两人交谈。 哈密顿通路 哈密顿回路 设 G 是具有 7 个顶点的图,每个顶点对应于一门课程考试,如果这两个顶点对应的课程考试是由不同老师担任的,那么这两个顶点之间有一条边。 因为每个老师任课程数不超过 4 ,因此每个顶点的度数至少是 3 ,任意两个顶点的度数之和至少是 6 ,因此 G 总包含一条哈密尔顿通路,它对应于关于考试的一个合适的安排。
28 .竞赛图都有哈密顿通路 定理 15.9 n(n ≥2 ) 阶竞赛图中都有哈密顿通路。 设 D 为 n 阶竞赛图,对 n 作归纳证明。 n=2 时,仅有两个顶点,因此为哈密顿通路,结论成立。设 n=k 时结论亦成立,考察 n=k+1 的情况。 设 V(D)={v 1 , v 2 , … , v k , v k+1 } ,令 D 1 =D - v k+1 , D 1 中存在哈密顿通路 Γ 。若 Γ 上的任一顶点 v r 邻接到 v k+1 ,且 v r-1 邻接自 v k+1 ,则可以将 v k+1 由 v r-1 处接入 Γ 。否则,可以分别在 Γ 的始点或终点处连接 v k+1 。 1 、有向图 2 、完全图
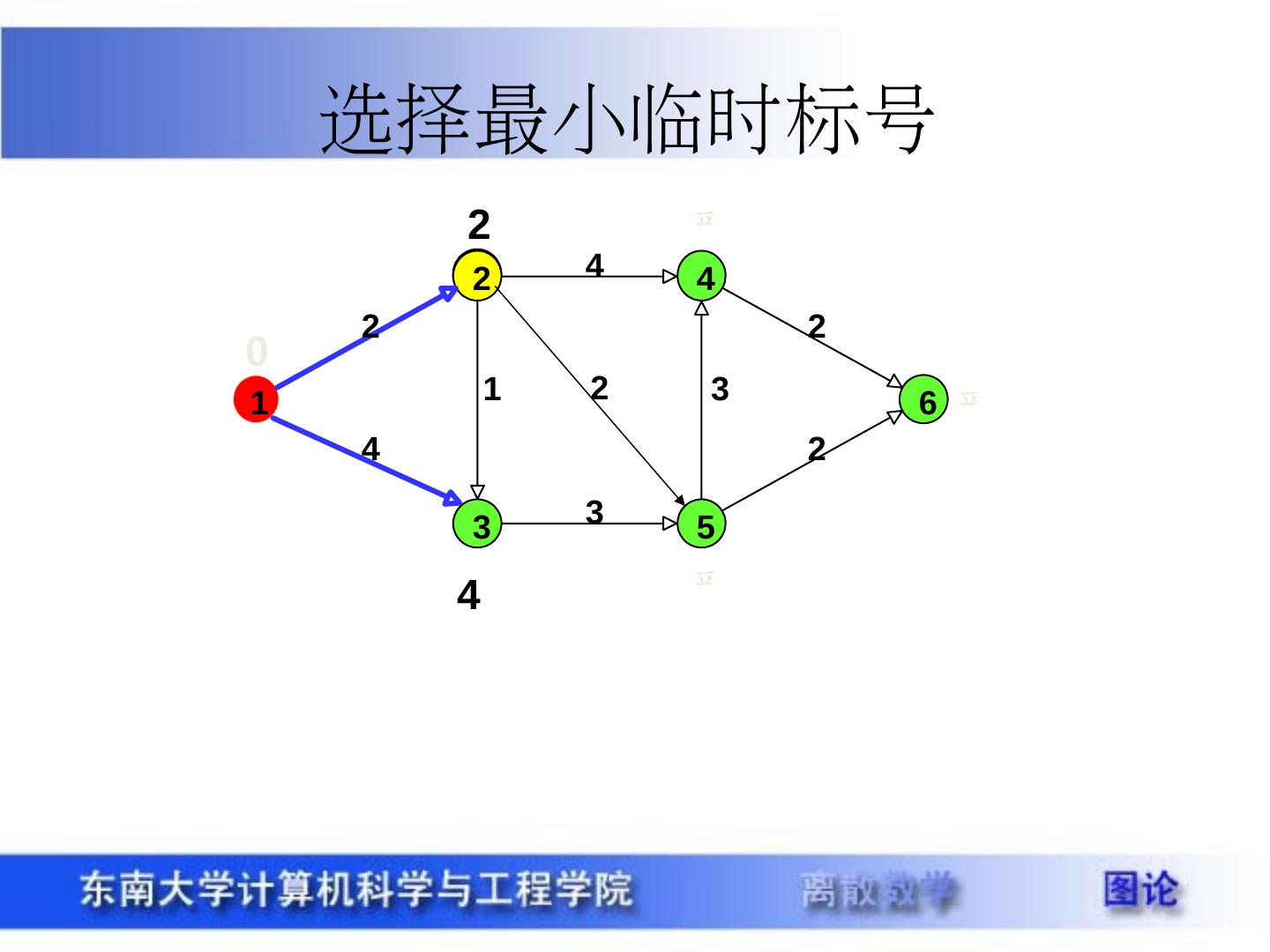
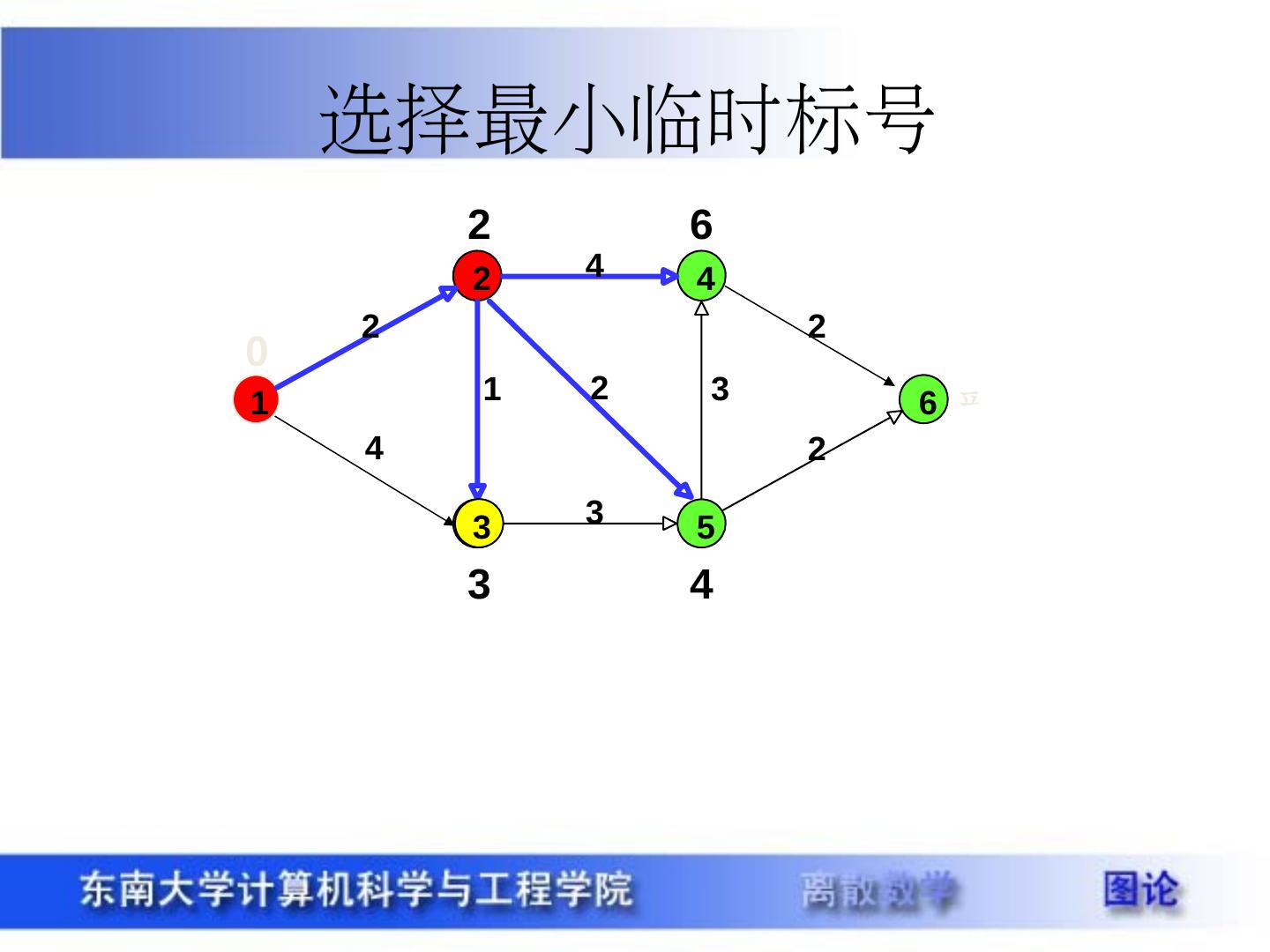
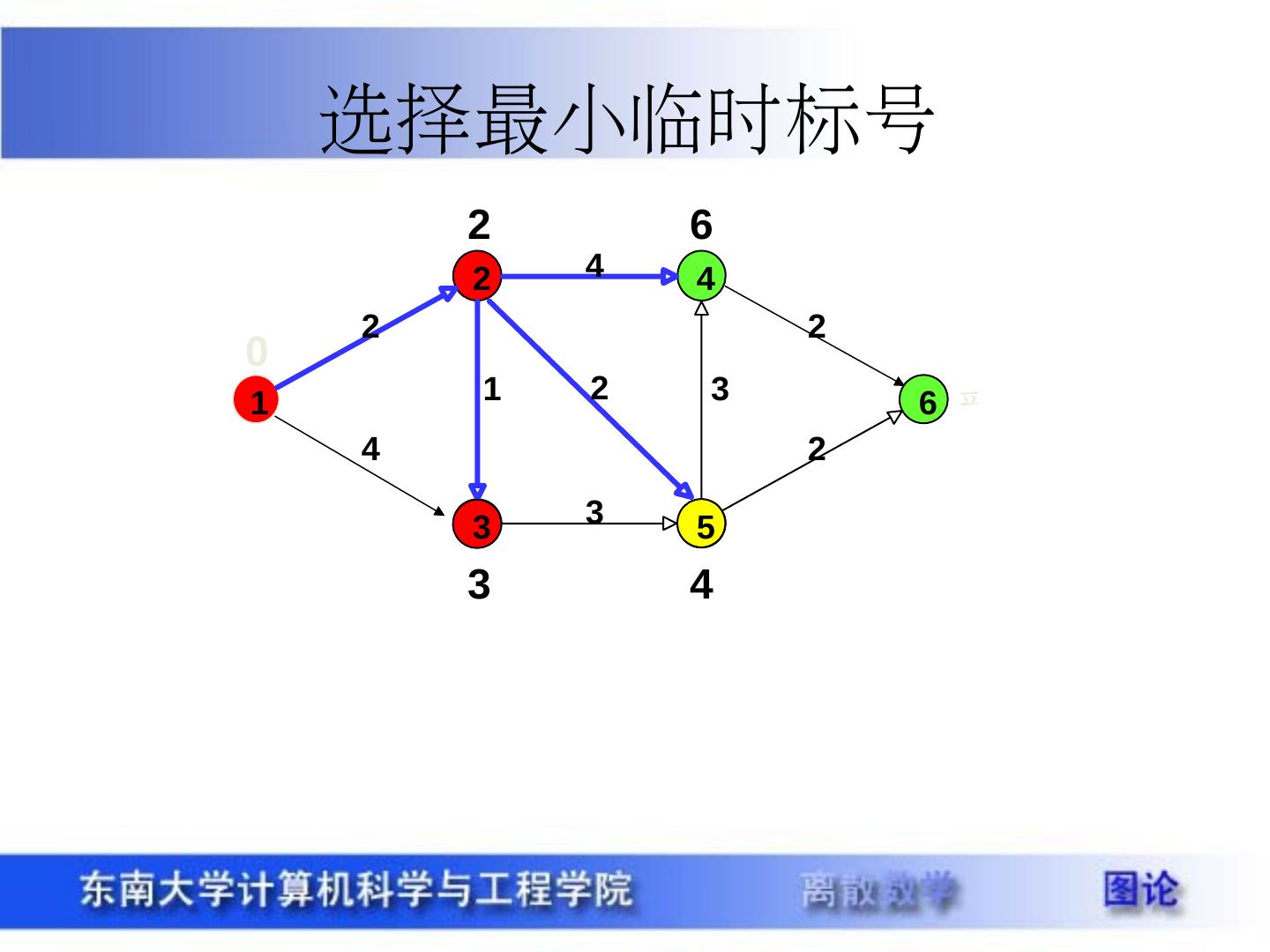
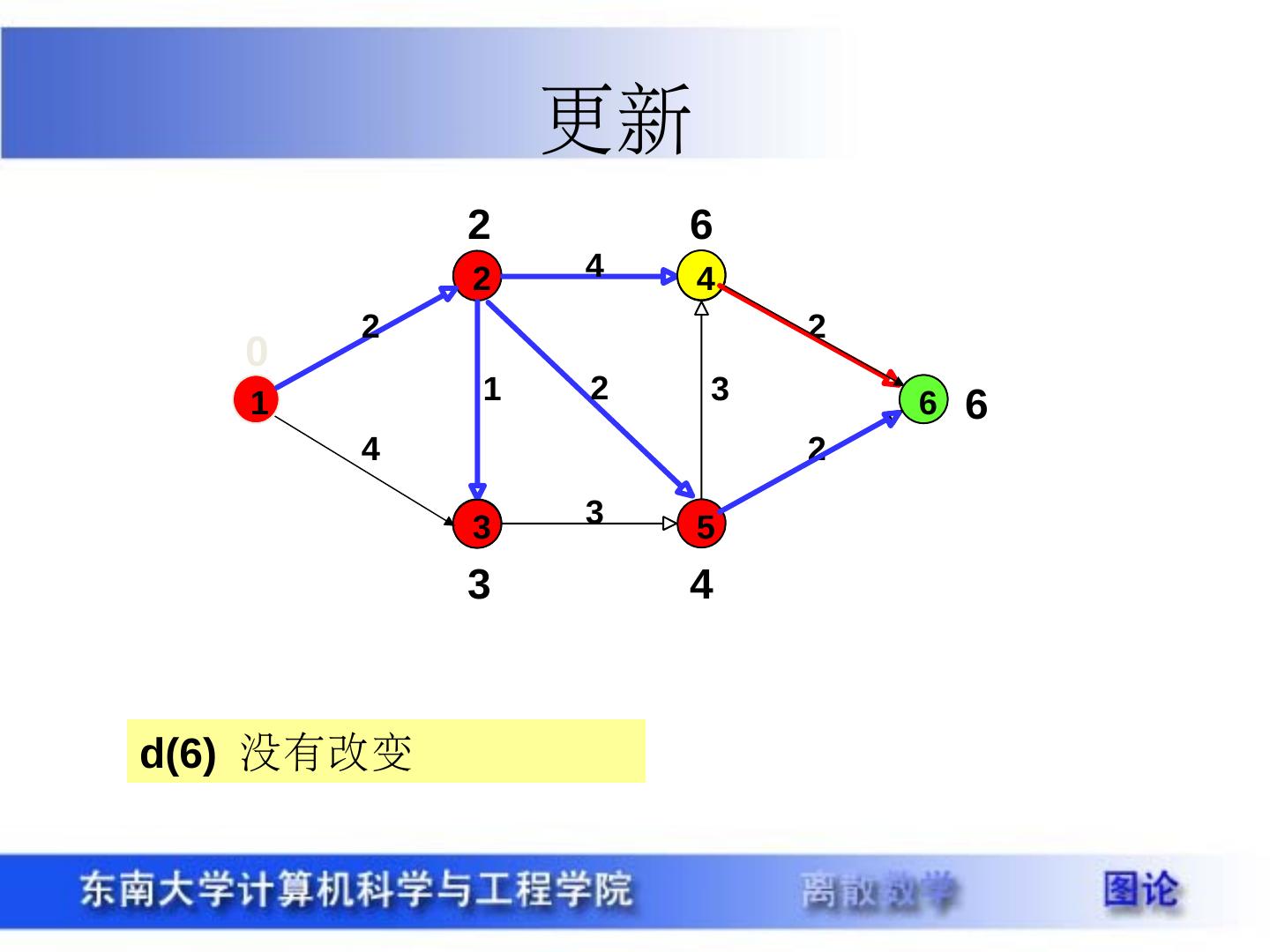
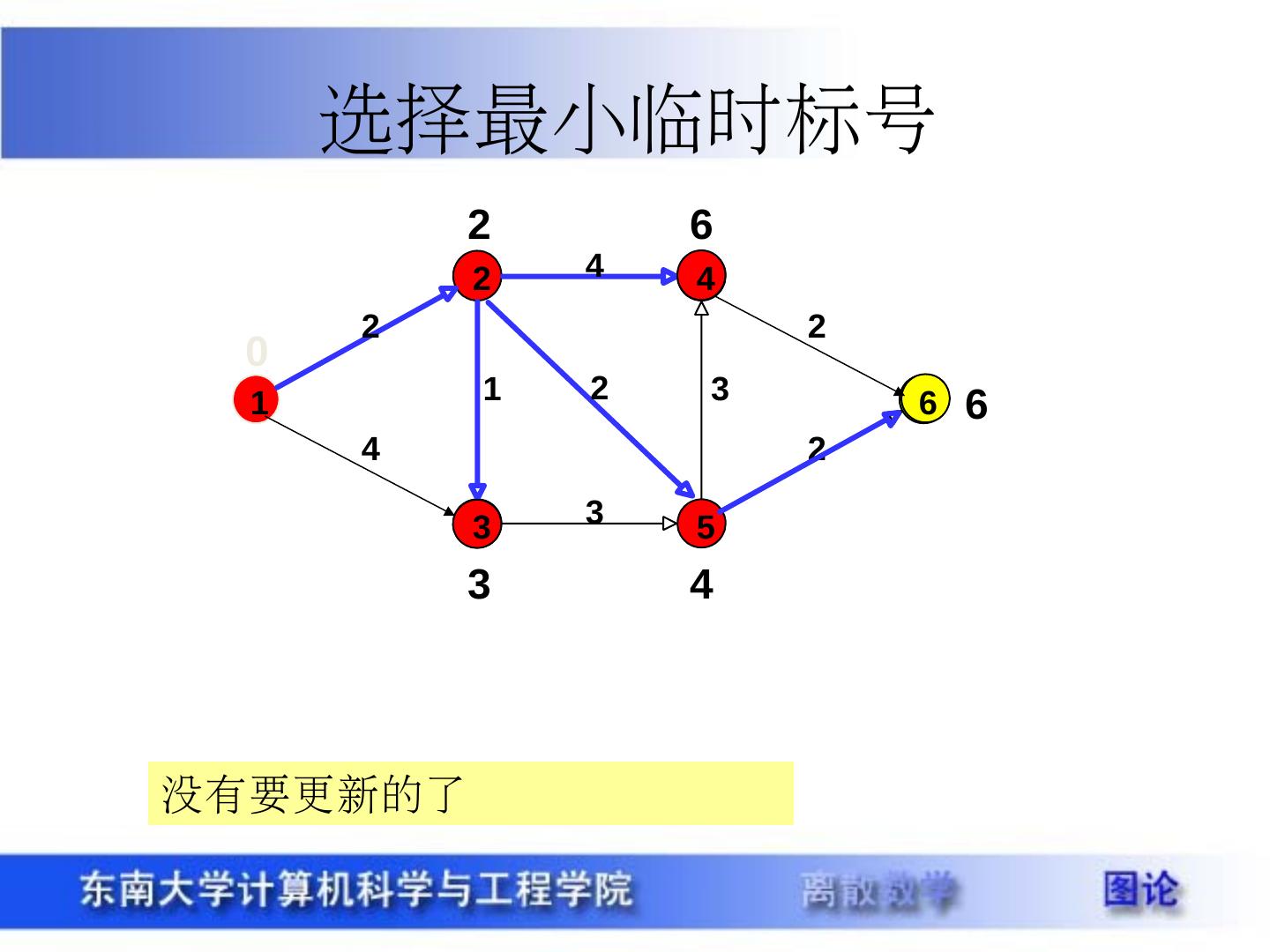
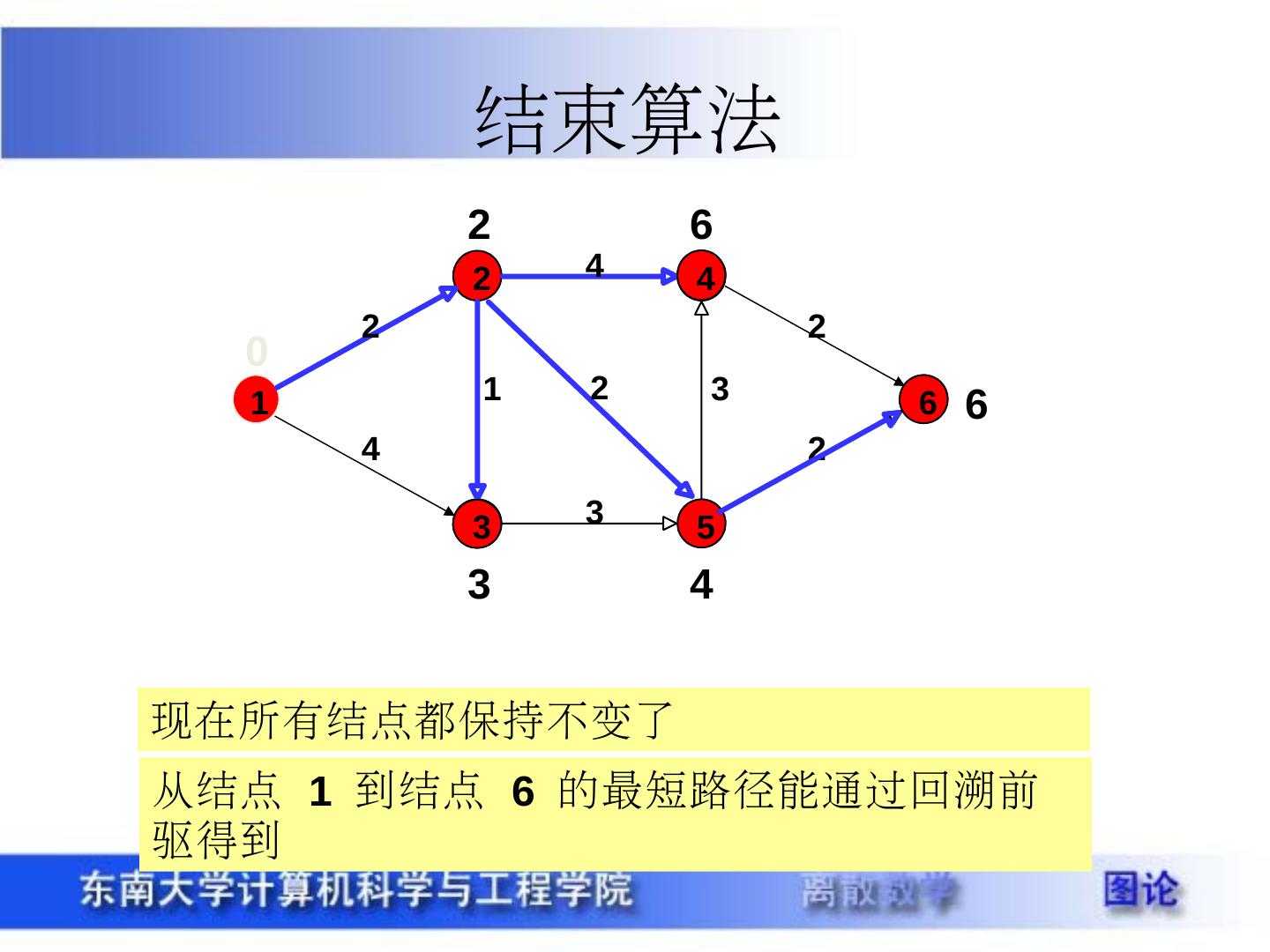
29 .带权图 定义 15.3 设图 G=<V , E> (无向图或有向图),给定 W:E->R ,对 G 的每一条边 e ,称 W(e) 为边 e 的权。把这样的图称为带权图,记作 G=<V , E , W> ,当 e=(u , v) ( <u , v> ),把 W(e) 记作 W(u , v) 。 设 P 是 G 中的一条通路, P 中所有边的权之和称为 P 的长度,记作 W(P) ,类似可定义回路 C 的长度。 Warcraft 最短路径 最经济路径 最可靠路径 最快路径