- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
了解图像的同态滤波。 - MING | JNU
展开查看详情
1 .多 媒 体 信 息 处 理 多 媒 体 信 息 处 理 基 础 图像增强 图像分割 形态学 图像处理 数字图像与视频压缩编码原理 数字音频编码技术及标准 数字图像与视频压缩编码标准 数字媒体文件格式 数字水印 基于内容的多媒体信息检索 理论基础 图像处理 多媒体数据压缩与文件格式 多媒体信息的内容保护与检索 结构框图 图 像 匹配
2 .2.1 引言 2.2 图像的灰度变换 2.3 图像平滑 2.4 图像锐化 2.5 图像的同态滤波 2.6 彩色增强 第 2 章 图像增强
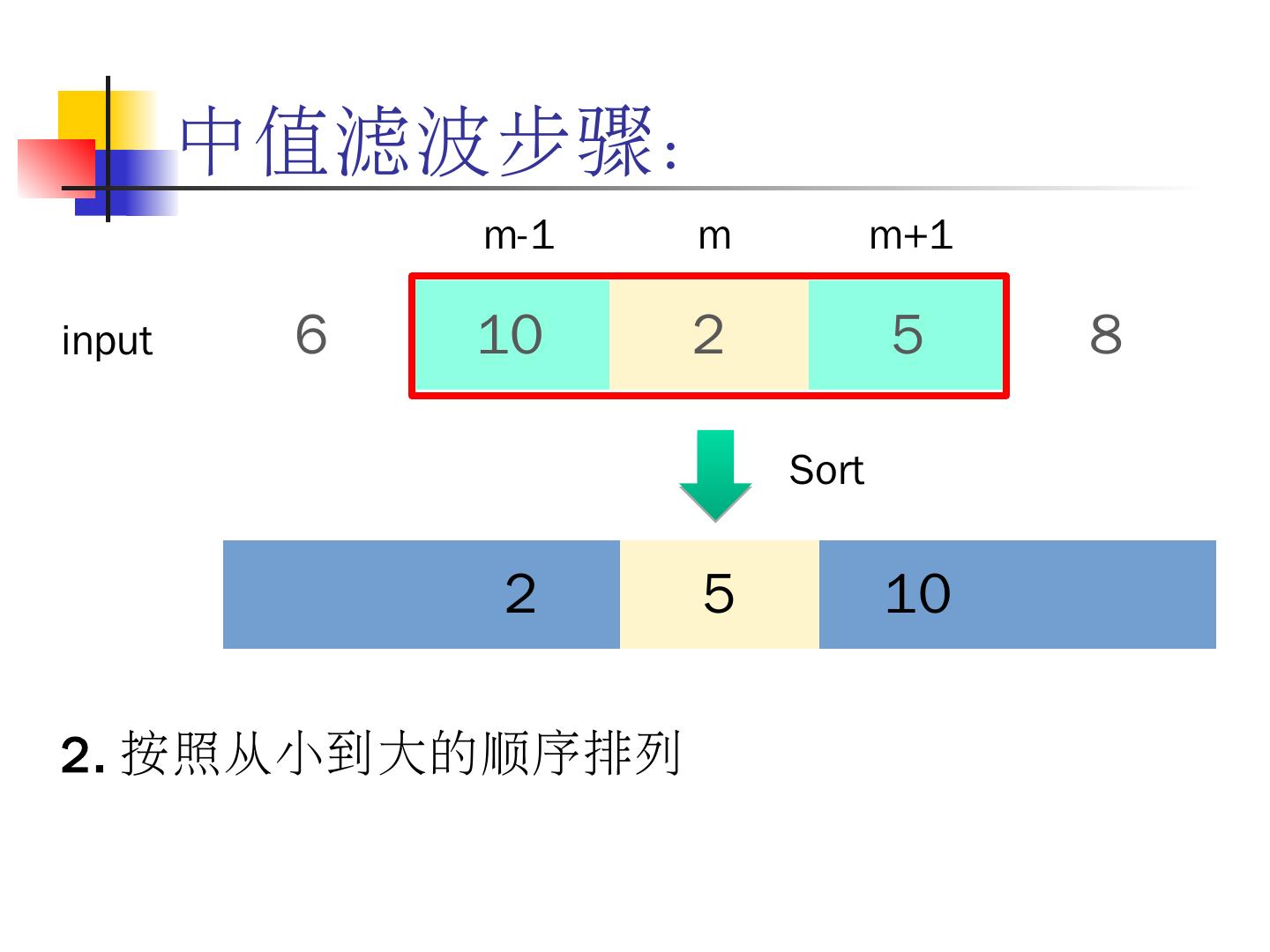
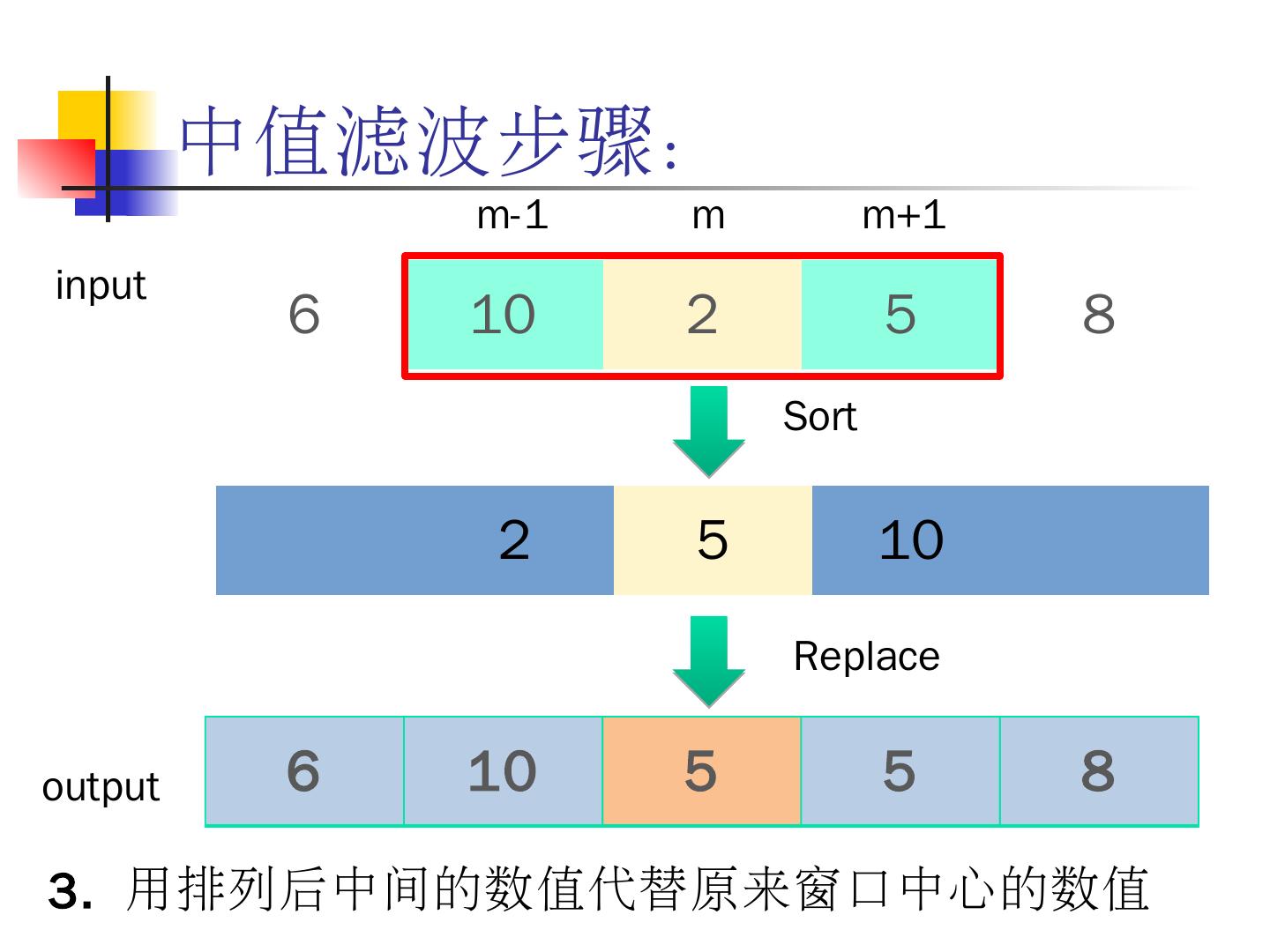
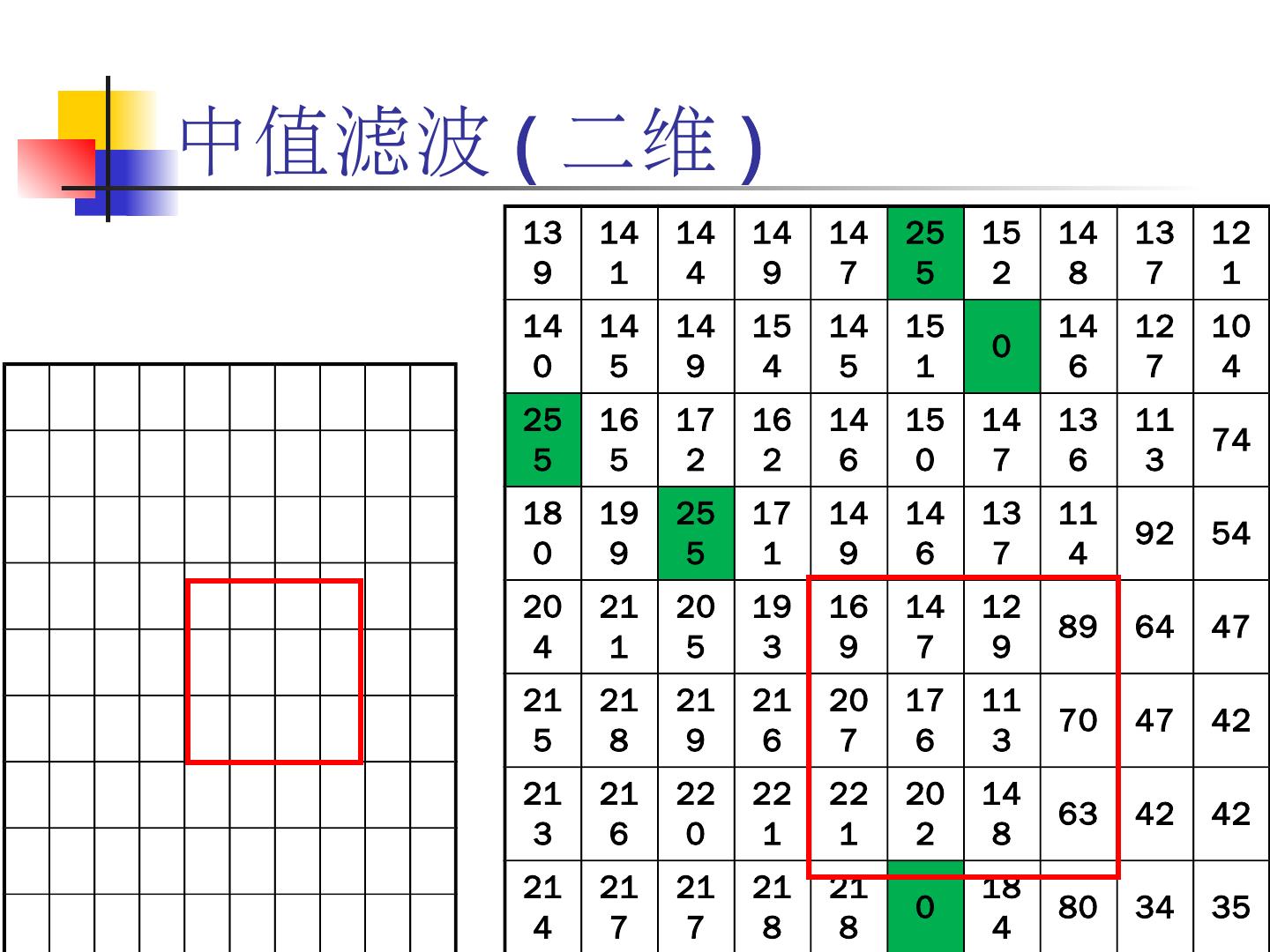
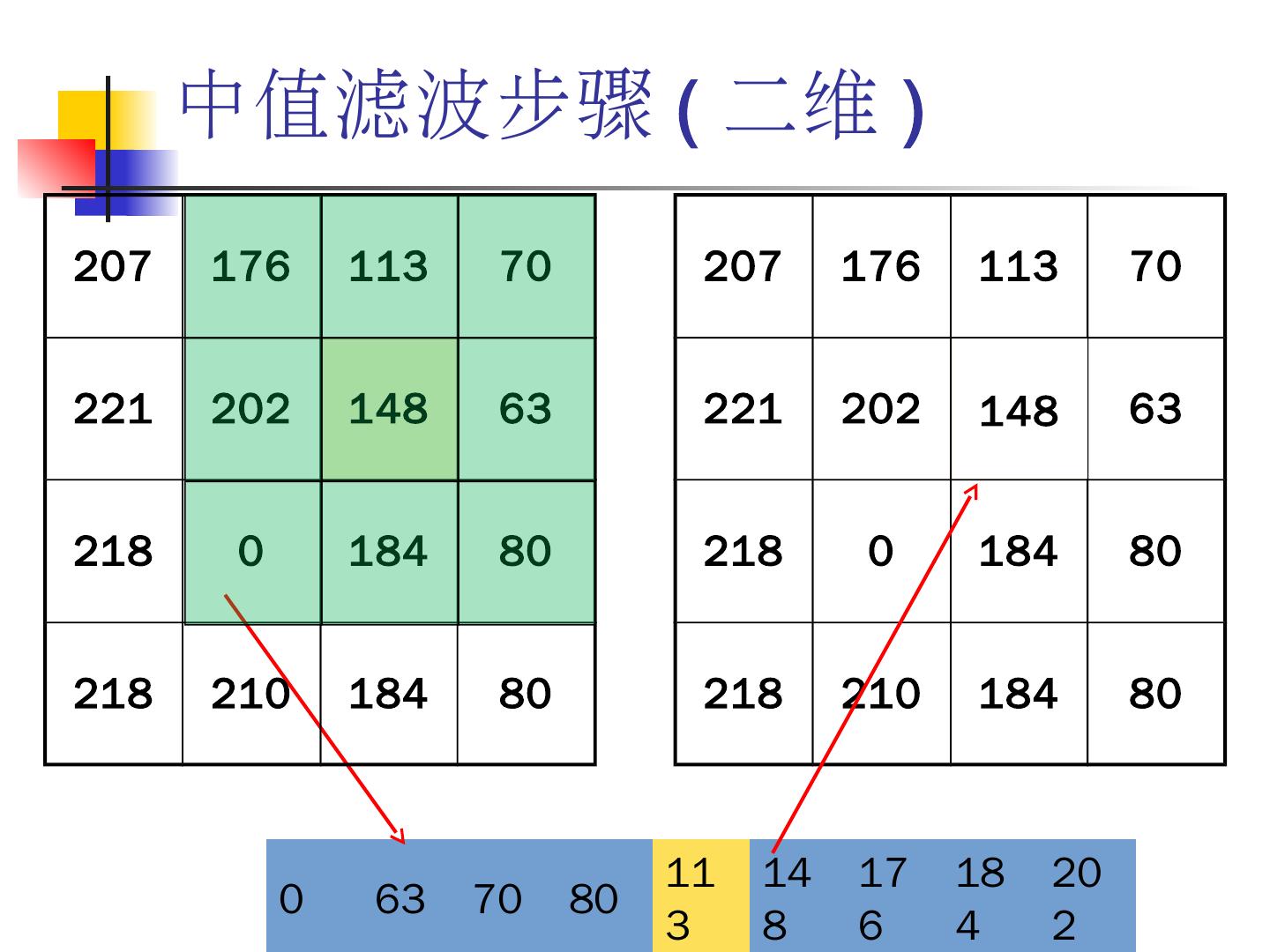
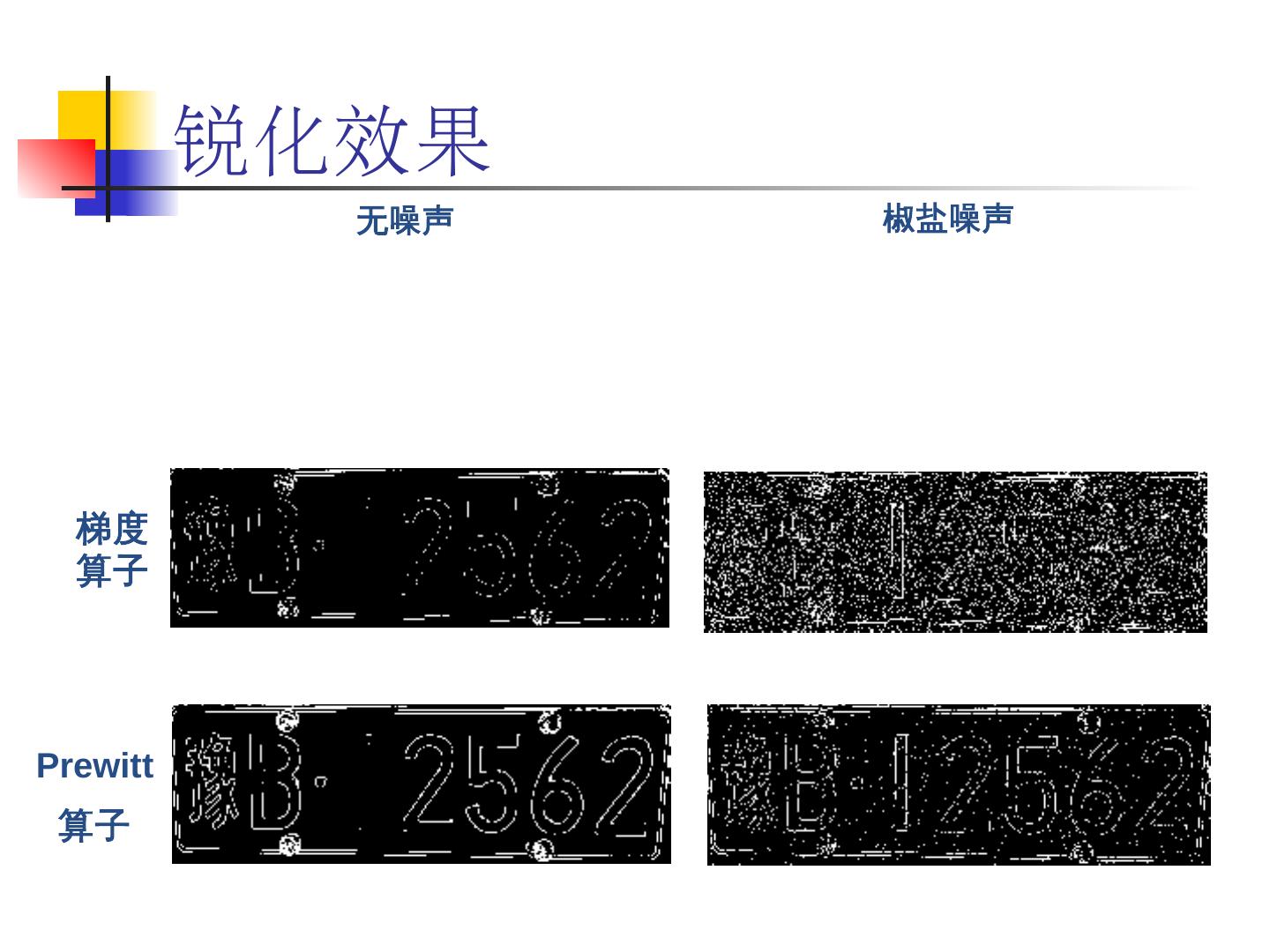
3 .掌握数字图像增强的基本方法和技术。 掌握数字图像灰度的线性与非线性变换的方法及应用。 熟悉直方图均衡化、直方图规定化的步骤。 掌握图像平滑的基本方法,如邻域平均法、中值滤波法、低通滤波。 掌握图像锐化的基本方法,如梯度运算、 Sobel 算子、拉普拉斯算子、高通滤波。 了解图像的同态滤波。 了解伪彩色增强、假彩色增强的基本方法。 本章学习目标
4 .图像增强 : 根据一定的要求将图像中感兴趣的部分加以 处理或突出 有用的图像特征(如边缘、轮廓、对比度等), 抑制 不需要的信息,以改善图像的主观视觉效果或便于后续的图像分析和识别。 图像复原 : 针对图像降质的具体原因,设法 补偿 降质因素,从而使改善后的图像尽可能地逼近原始图像。 改善降质图像(退化图像)的方法 : 2.1 引言
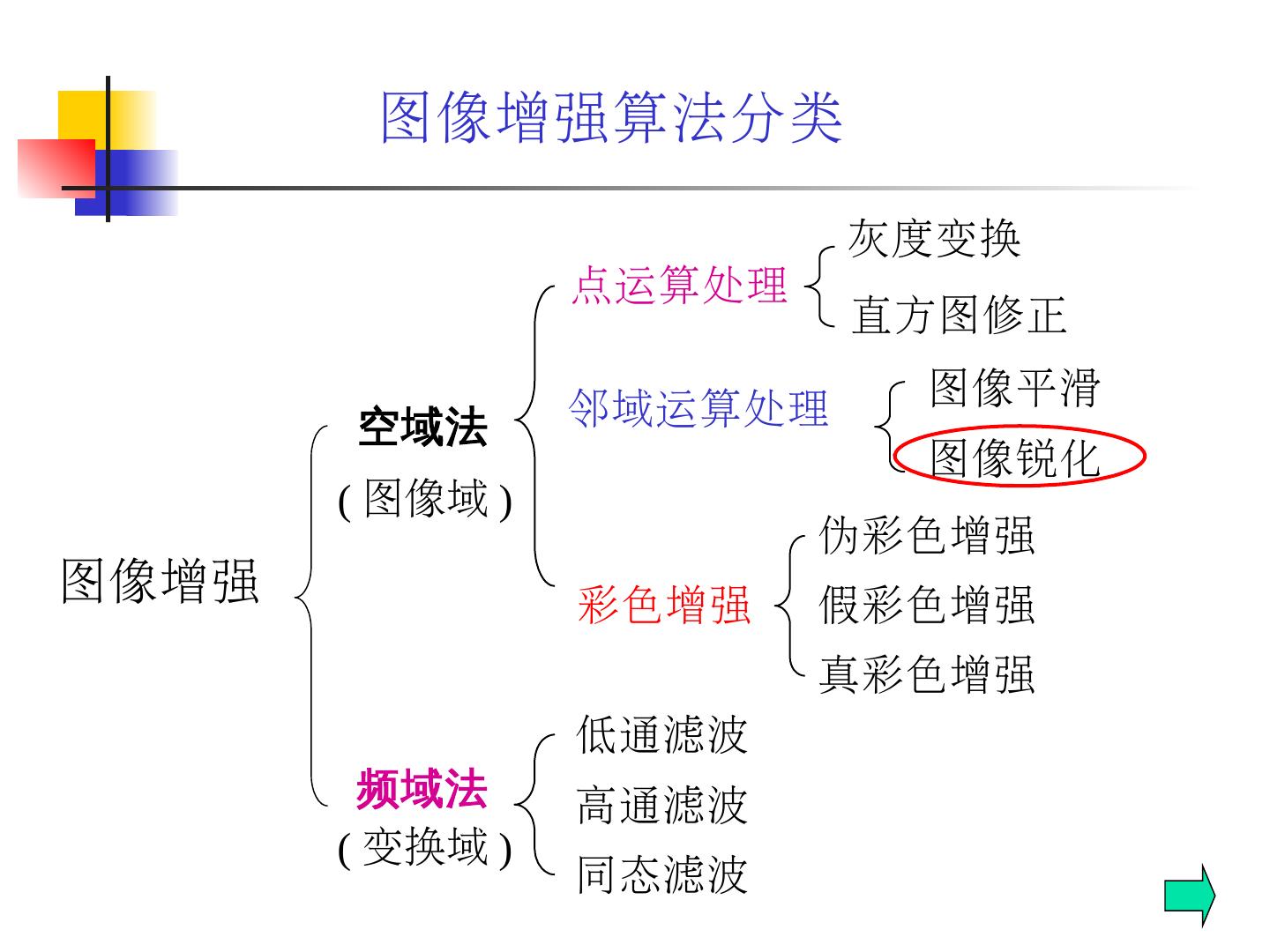
5 . ( 1 ) 空间域法 : 是在空间域内直接对图像的像素值进行运算操作。 点运算处理法: 是指直接对图像的各像素点逐一进行灰度变换的处理方法。例如,图像的 灰度变换 、 直方图修正 等都采用点运算处理法。 邻域运算处理法: 是对图像像素的某一邻域进行处理的方法。例如, 图像平滑 、 图像锐化 等都采用邻域运算处理法。 图像增强算法分类
6 .图像增强算法分类 ( 2 ) 频率域法 : 在 频率 域上对图像的变换系数进行处理,增强感兴趣的频率分量,然后再进行反变换到空间域,得到增强后的图像。 常用的方法包括 低通滤波 、 高通滤波 以及 同态滤波 等。
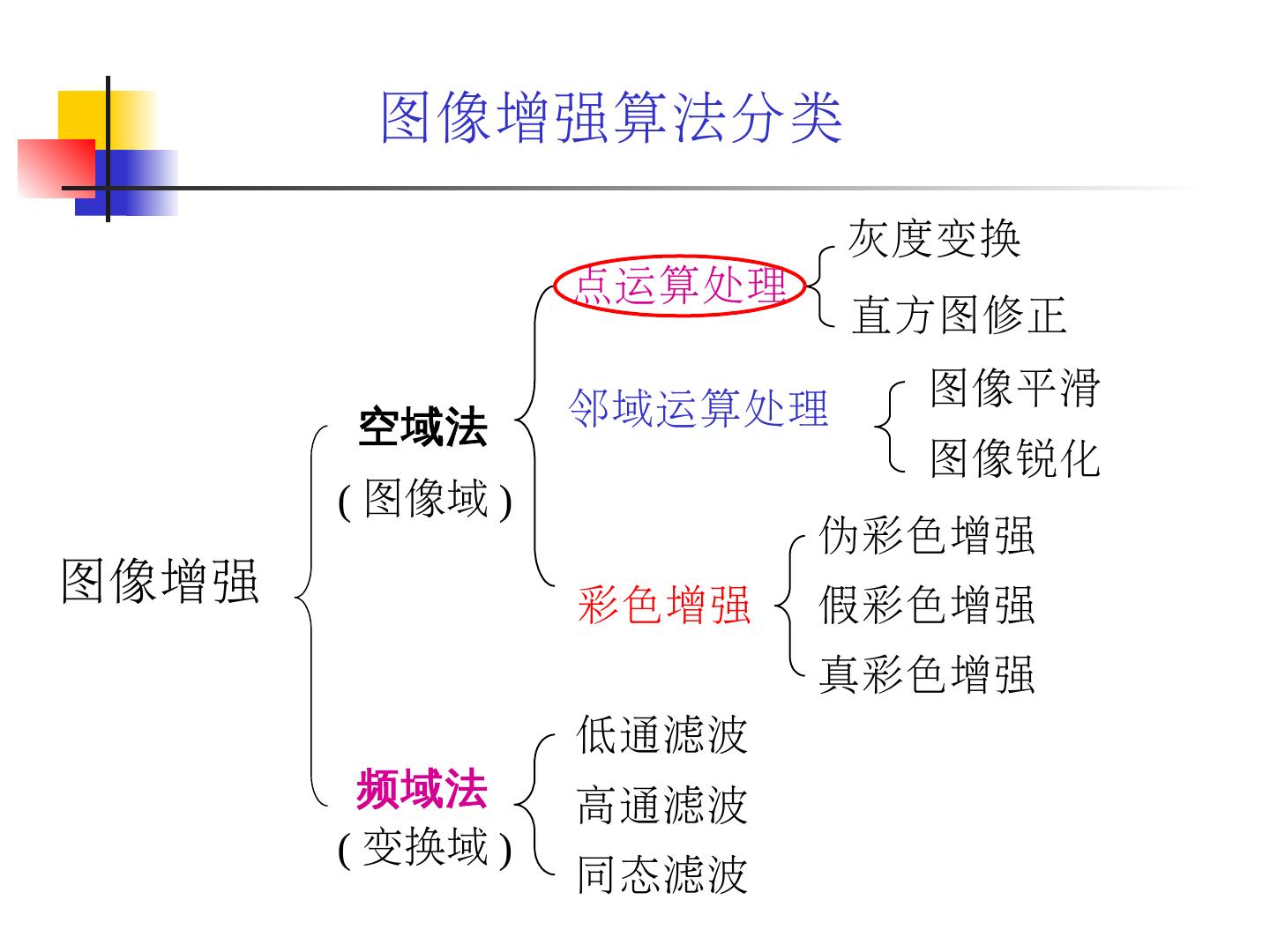
7 .图像增强算法分类 图像增强 点运算处理 灰度变换 直方图修正 邻域运算处理 图像平滑 图像锐化 彩色增强 假彩色增强 伪彩色增强 真彩色增强 空域法 ( 图像域 ) 频域法 低通滤波 高通滤波 同态滤波 ( 变换域 )
8 .
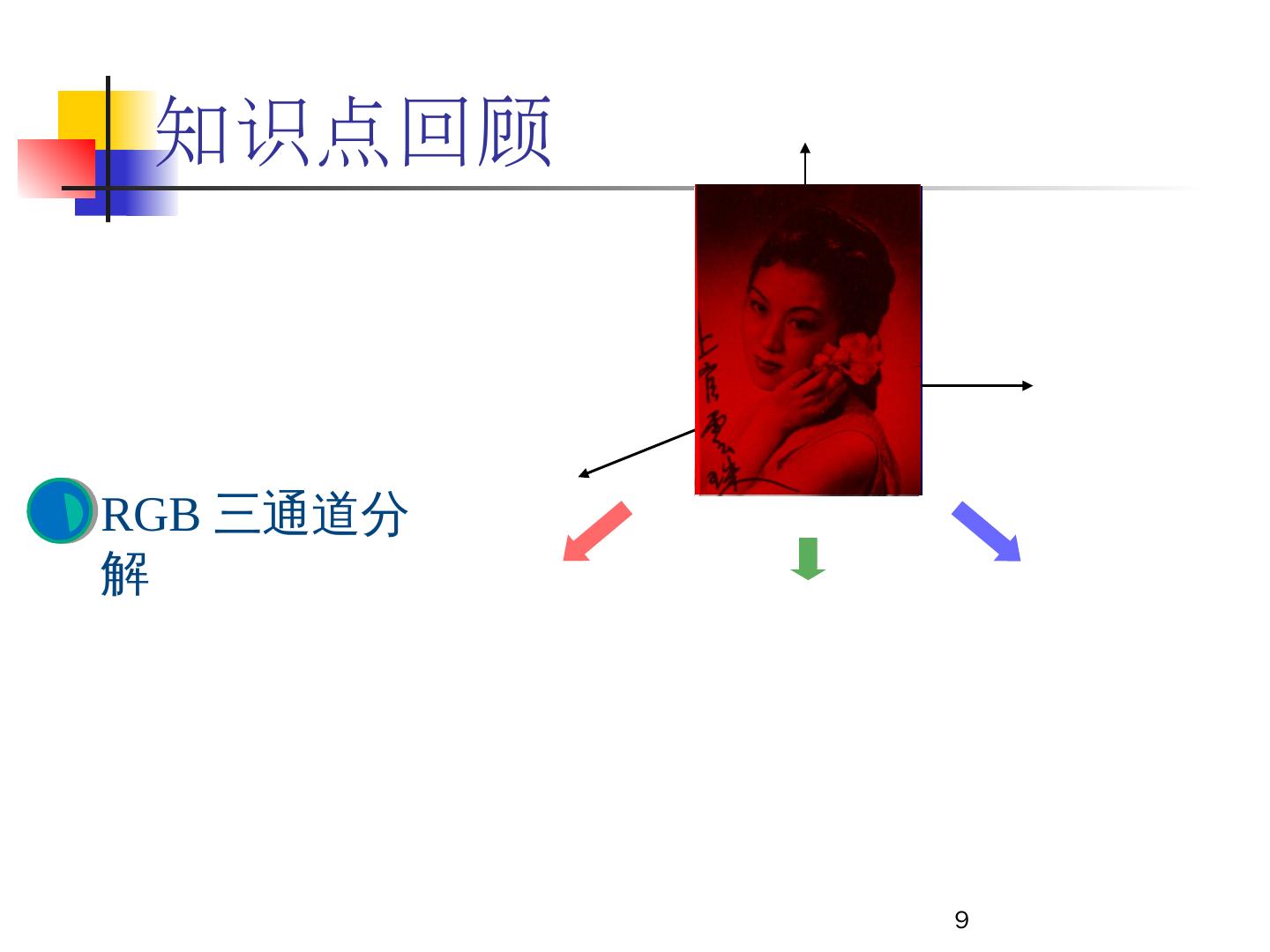
9 .9 知识点回顾 RGB 三通道分解
10 .10 知识点回顾 像素: 数字图像的最小元素
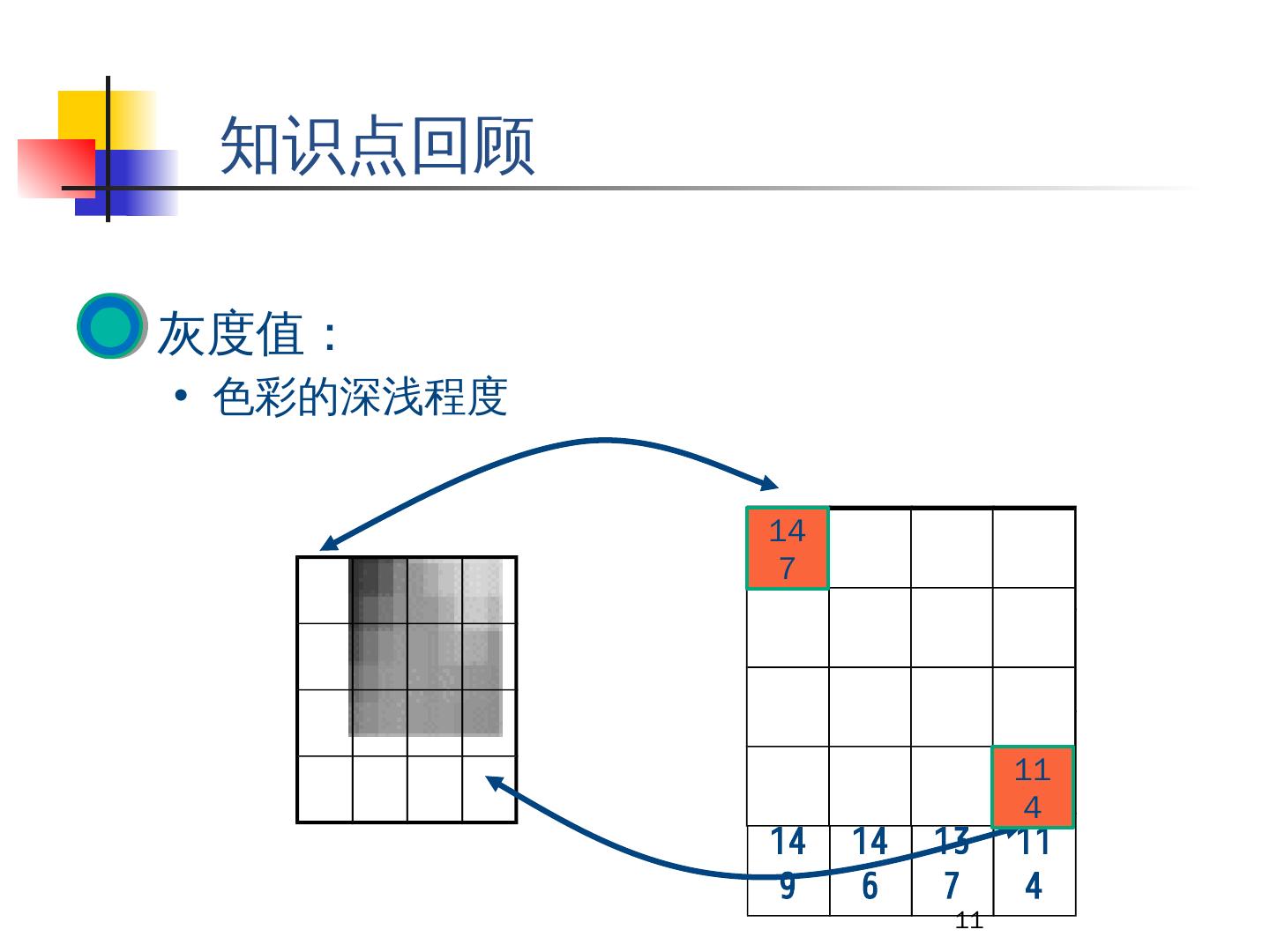
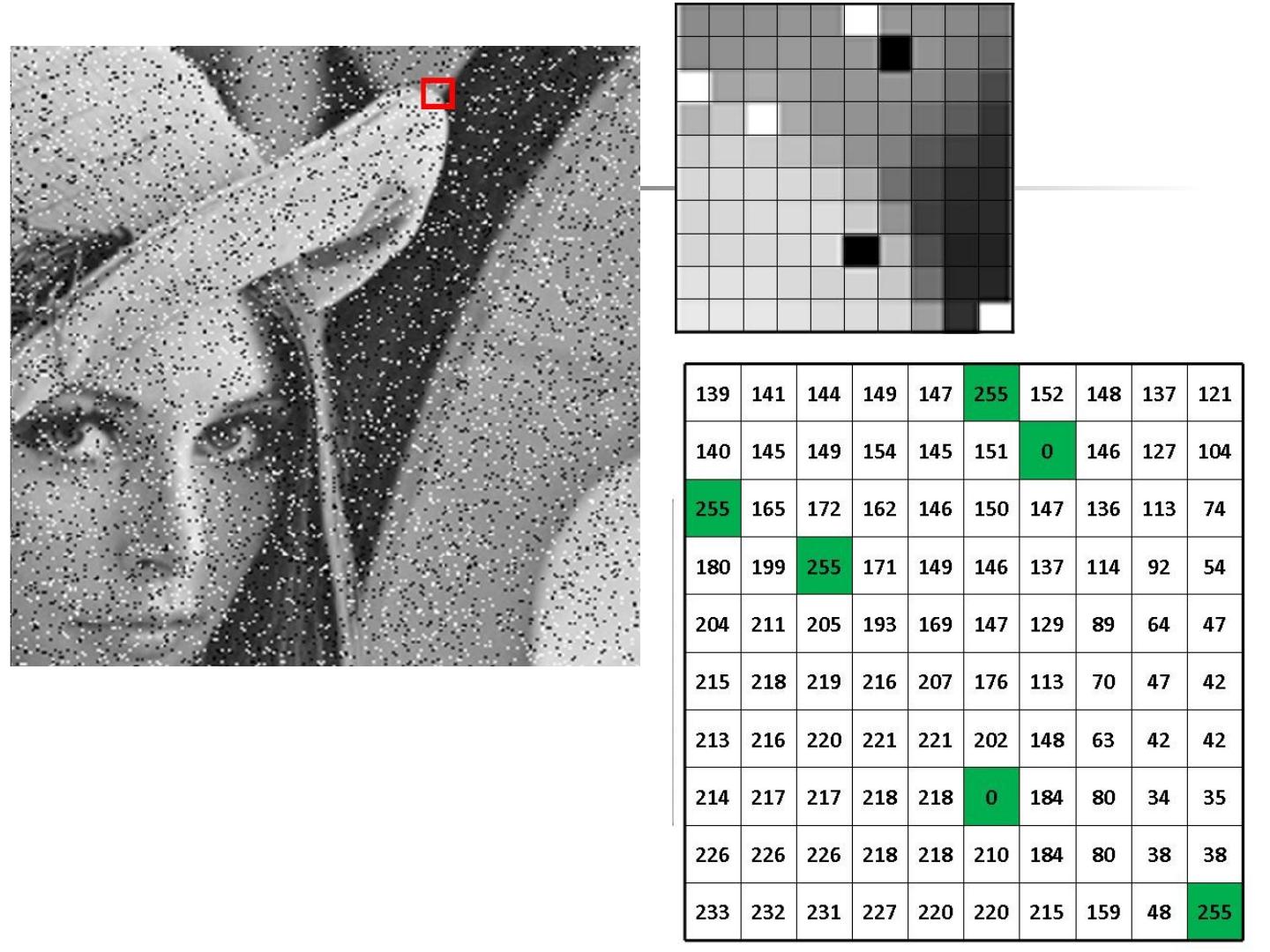
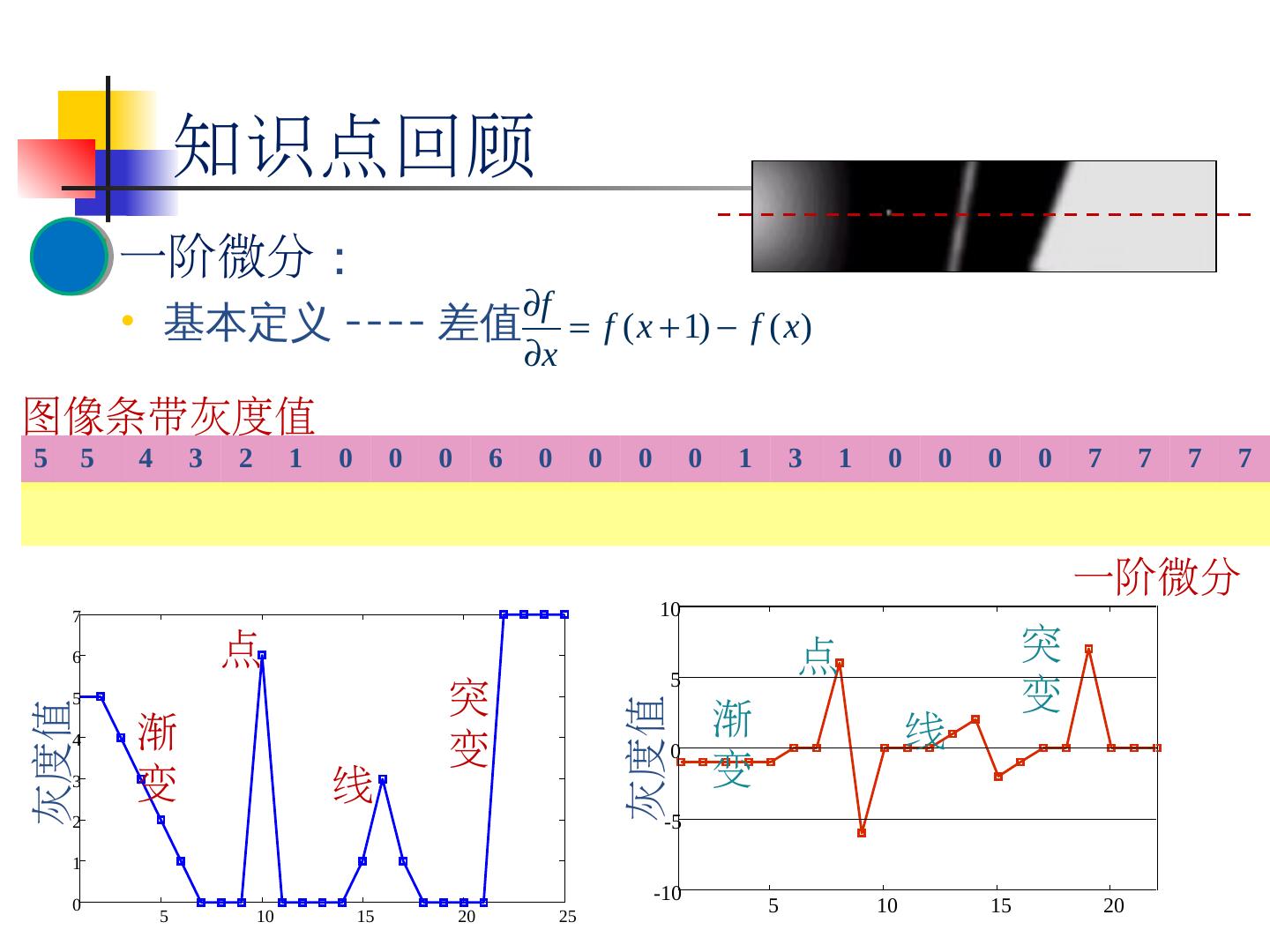
11 .11 147 149 152 148 145 151 150 146 146 150 147 136 149 146 137 114 灰度值: 色彩的深浅程度 知识点回顾 147 114
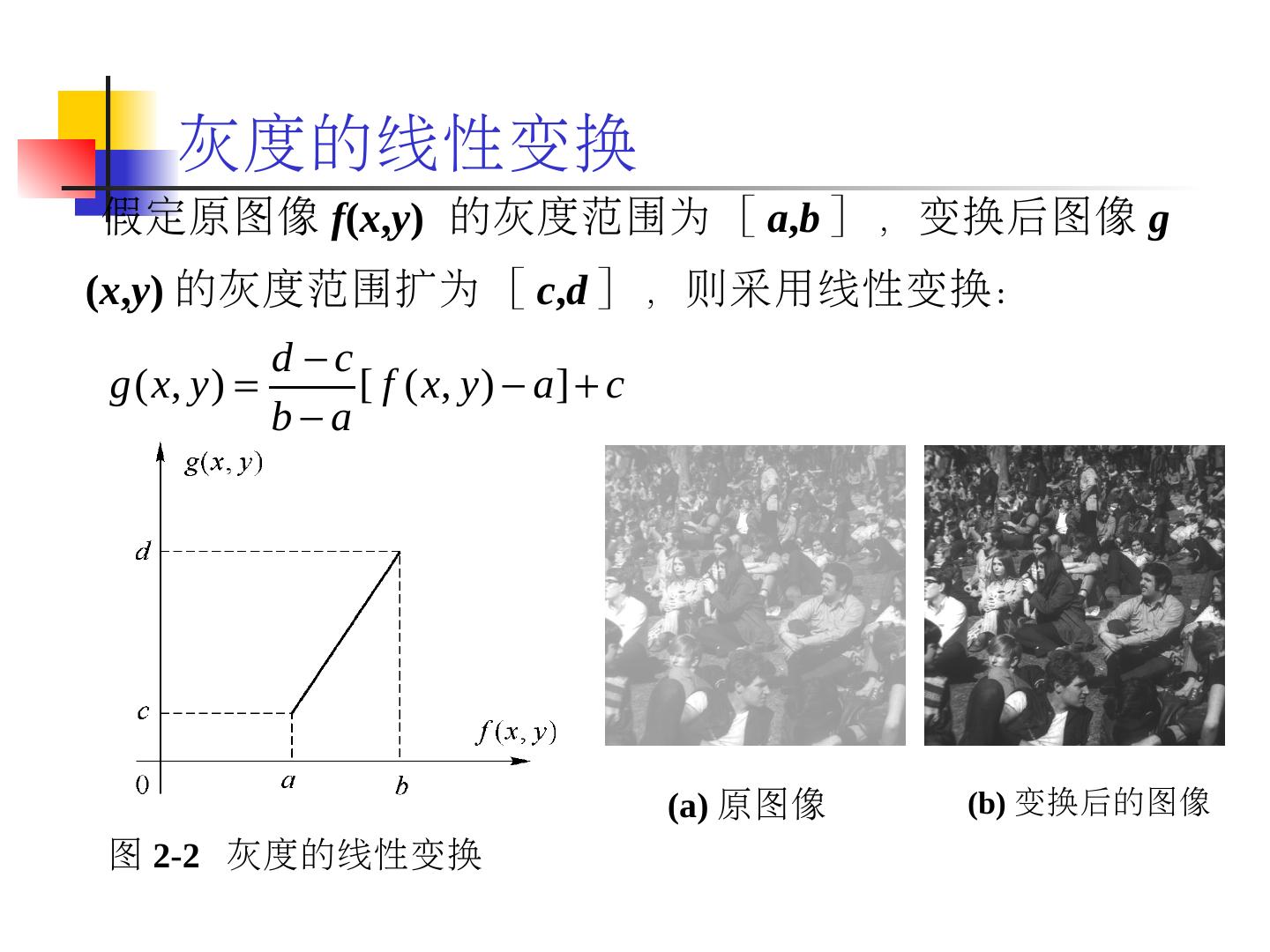
12 .灰度的线性变换 假定原图像 f ( x , y ) 的灰度范围为 [ a , b ] ,变换后图像 g ( x , y ) 的灰度范围扩为 [ c , d ] ,则采用线性变换: 图 2-2 灰度的线性变换 (a) 原图像 (b) 变换后的图像
13 . 若图像灰度在[ 0, M f ] 范围内,其中大部分像素的灰度级分布在区间[ a,b ],很小部分的灰度级超出了此区间,为改善增强的效果,可令 灰度的线性变换
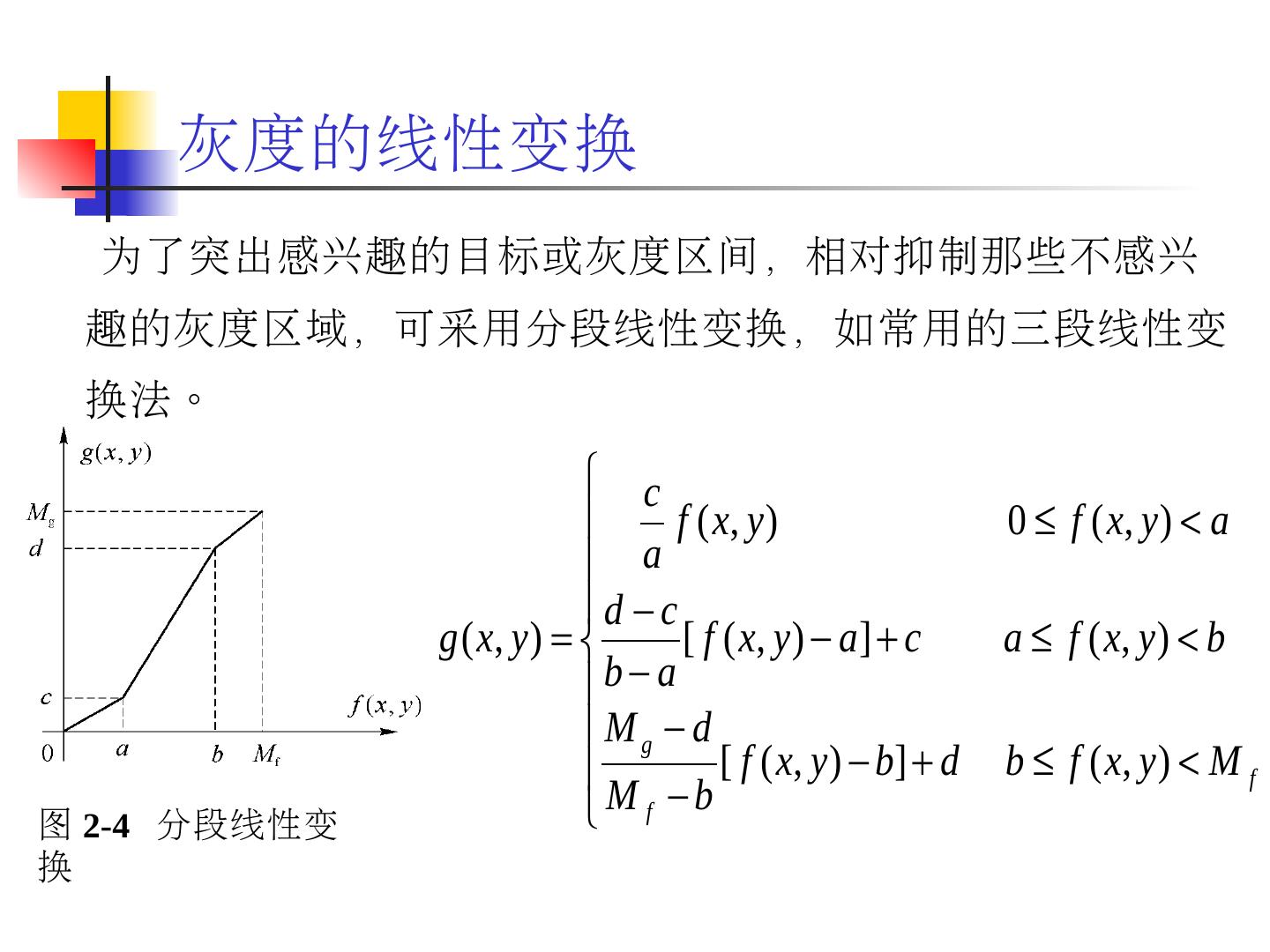
14 . 为了突出感兴趣的目标或灰度区间,相对抑制那些不感兴趣的灰度区域,可采用分段线性变换,如常用的三段线性变换法。 图 2-4 分段线性变换 灰度的线性变换
15 .采用非线性变换函数(例如对数函数、幂指数函数等) 对数变换式 a 、 b 、 c 是调整曲线的位置和形状的参数。 指数变换式 a 、 b 、 c 是调整曲线的位置和形状的参数。 灰度的非线性变换
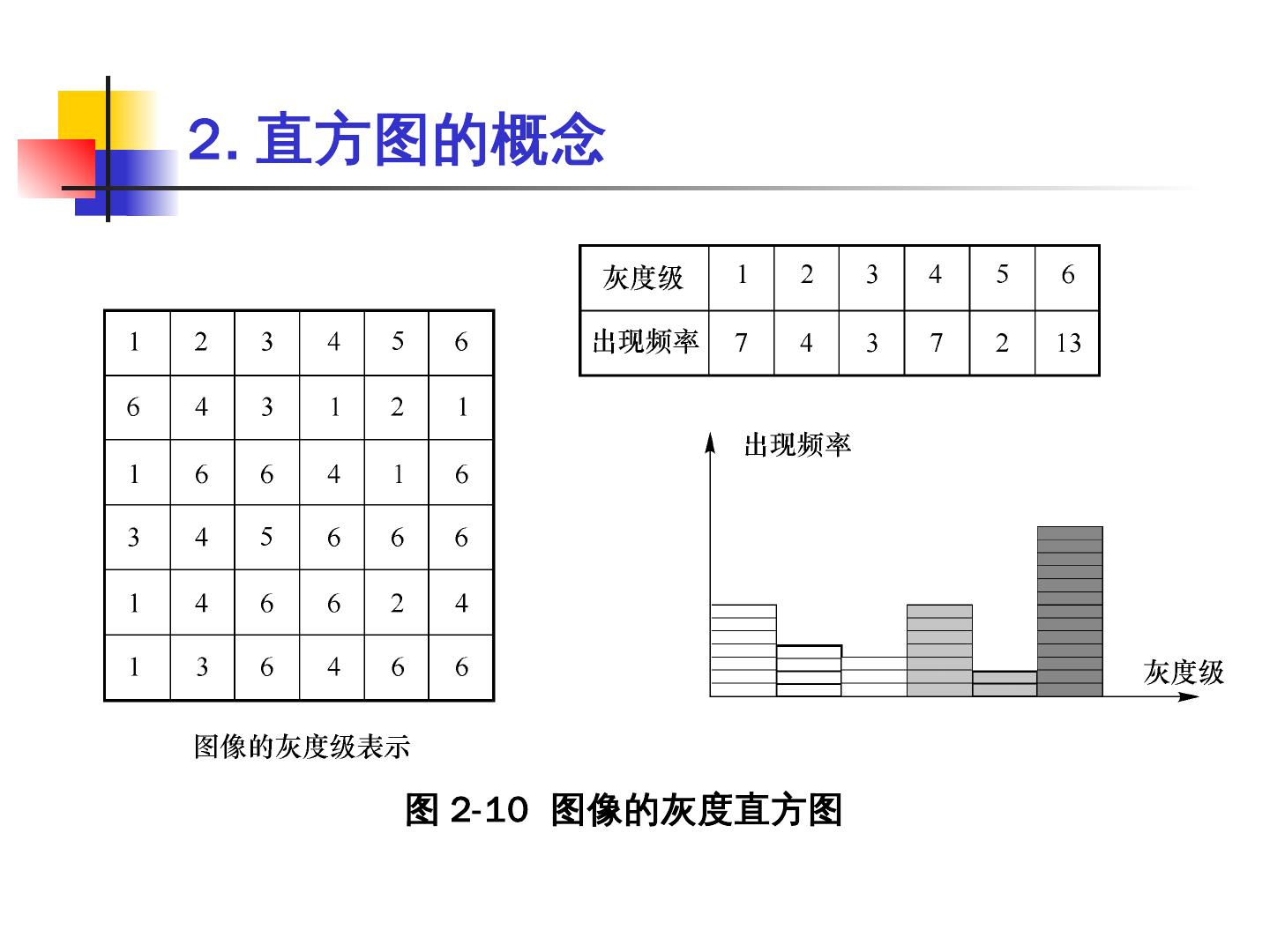
16 .直方图修正 1. 直方图的概念 如果将图像中像素亮度(灰度级)看成是一个随机变量,则其分布情况就反映了 图像的统计特性 。 灰度直方图是灰度级的函数,它表示图像中具有 某种灰度级的像素的个数 ,反映了图像中每种灰度级出现的 概率 。
17 .图 2-10 图像的灰度直方图 2. 直方图的概念
18 .设图像总像素个数为 n ,共有 L 级灰度, r k 为图像的第 k 级灰度值,并且具有灰度级 r k 的像素数为 n k ,则: 2. 灰度直方图的定义
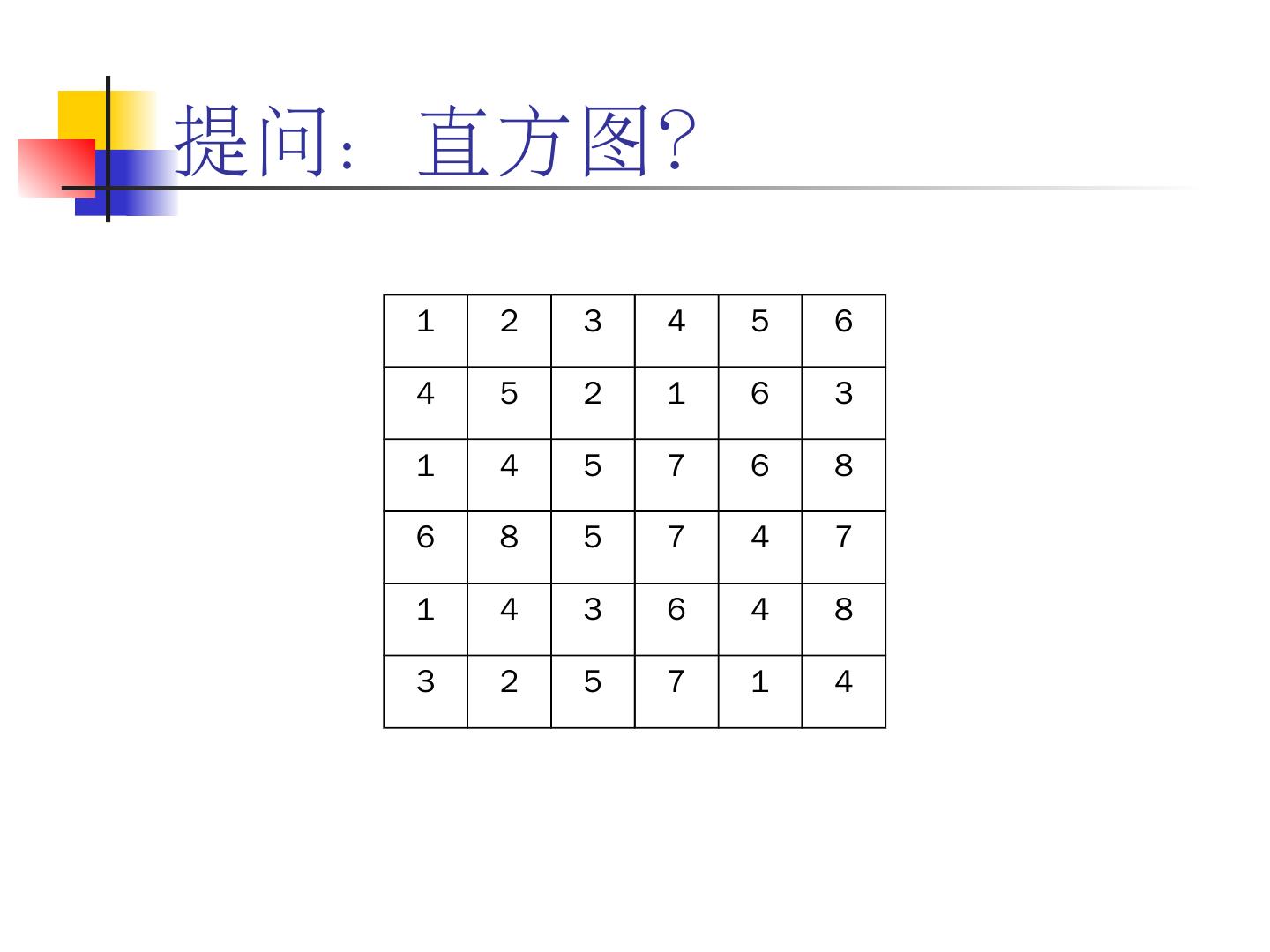
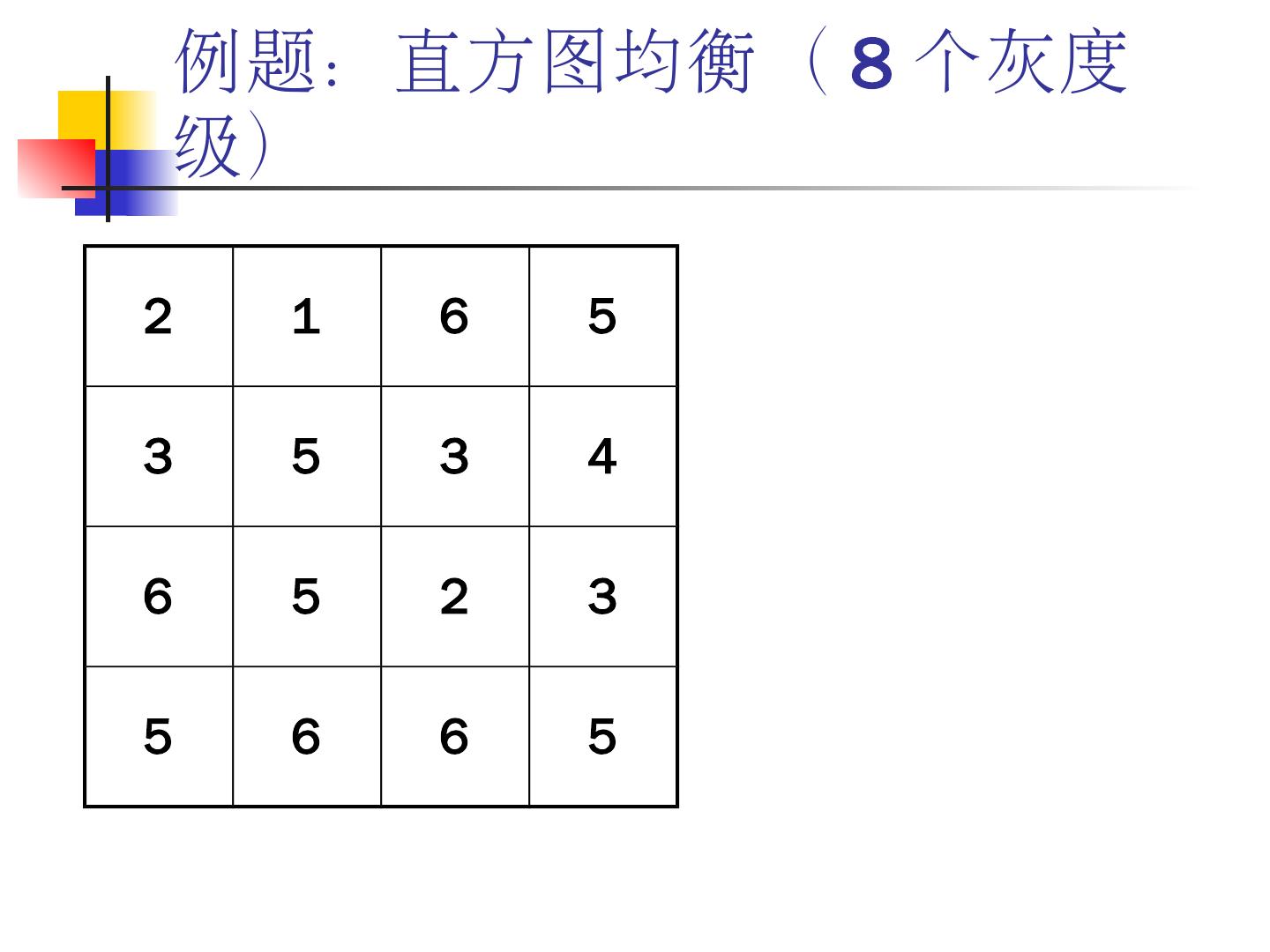
19 .提问:直方图? 1 2 3 4 5 6 4 5 2 1 6 3 1 4 5 7 6 8 6 8 5 7 4 7 1 4 3 6 4 8 3 2 5 7 1 4
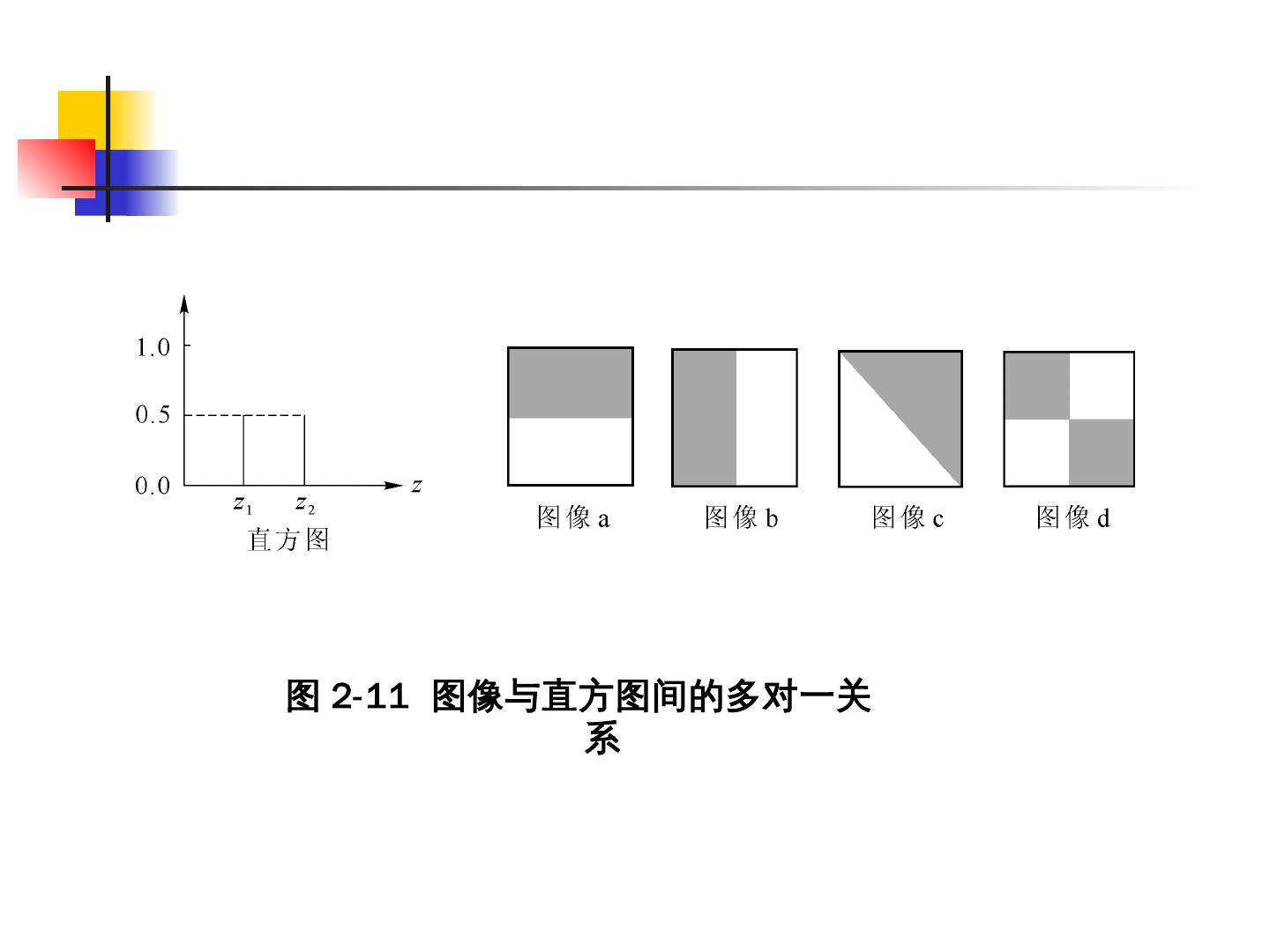
20 .( 1 )直方图是一幅图像中各像素灰度值出现的频数的 统计 结果,它只反映该图像中 不同灰度值出现的次数 ,而未反映某一灰度值像素所在的位置。 ( 2 )任一幅图像,都能唯一地确定出一幅与它对应的直方图,但不同的图像,可能有相同的直方图。 ( 3 )如果一幅图像由两个不连续的区域组成,并且每个区域的直方图已知,则整幅图像的直方图是这两个区域的直方图之和。 3. 直方图的性质
21 .图 2-11 图像与直方图间的多对一关系
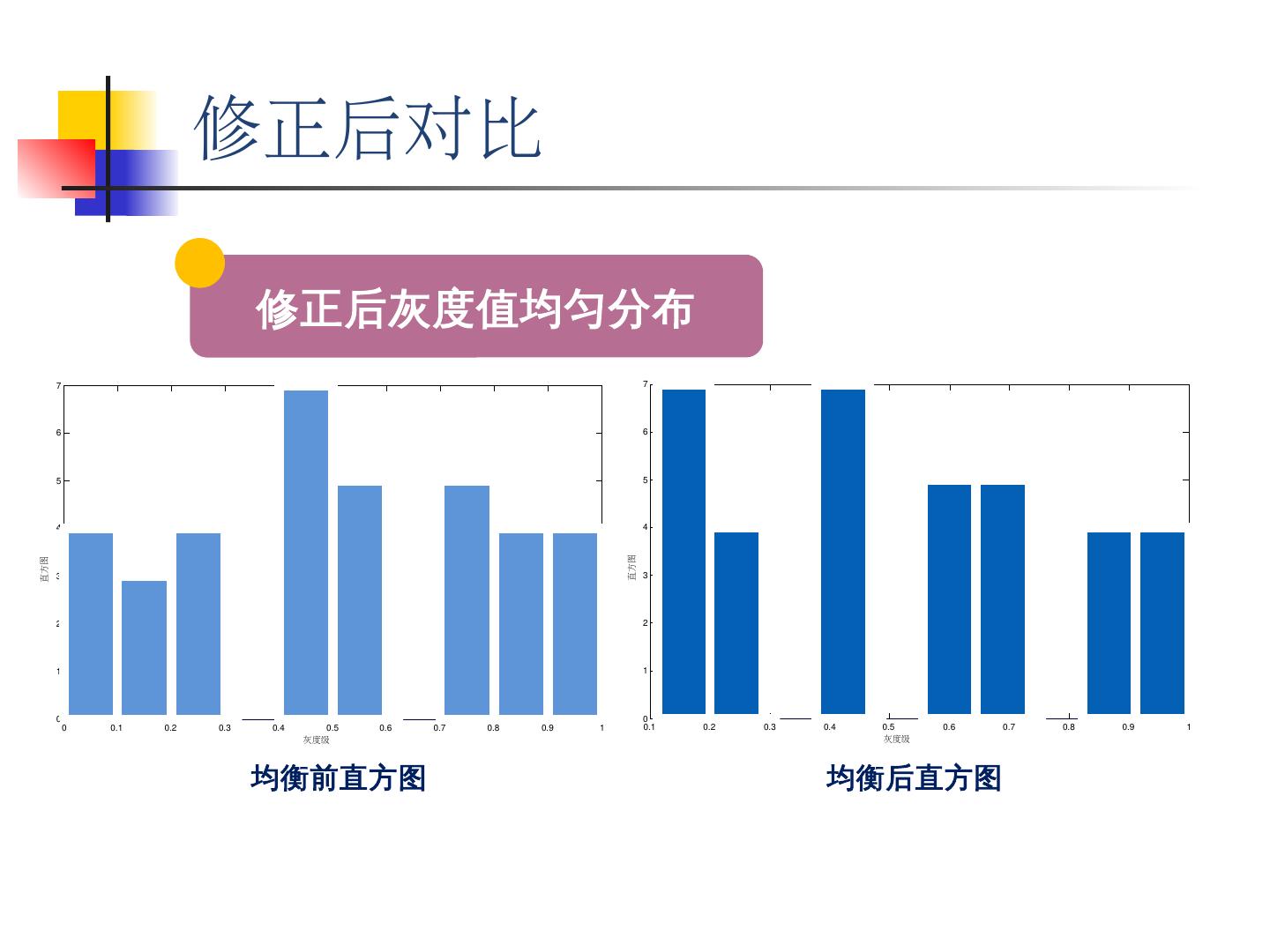
22 .直方图均衡化 : 将原图像的直方图通过变换函数修正为均匀的直方图, 从而增加像素灰度值的动态范围 , 达到增强图像整体对比度的效果 。 直方图均衡化 后,图像的直方图是平直的,即各灰度级具有相同的出现频数,那么由于灰度级具有均匀的概率分布,图像看起来就更清晰了。 4. 直方图均衡化
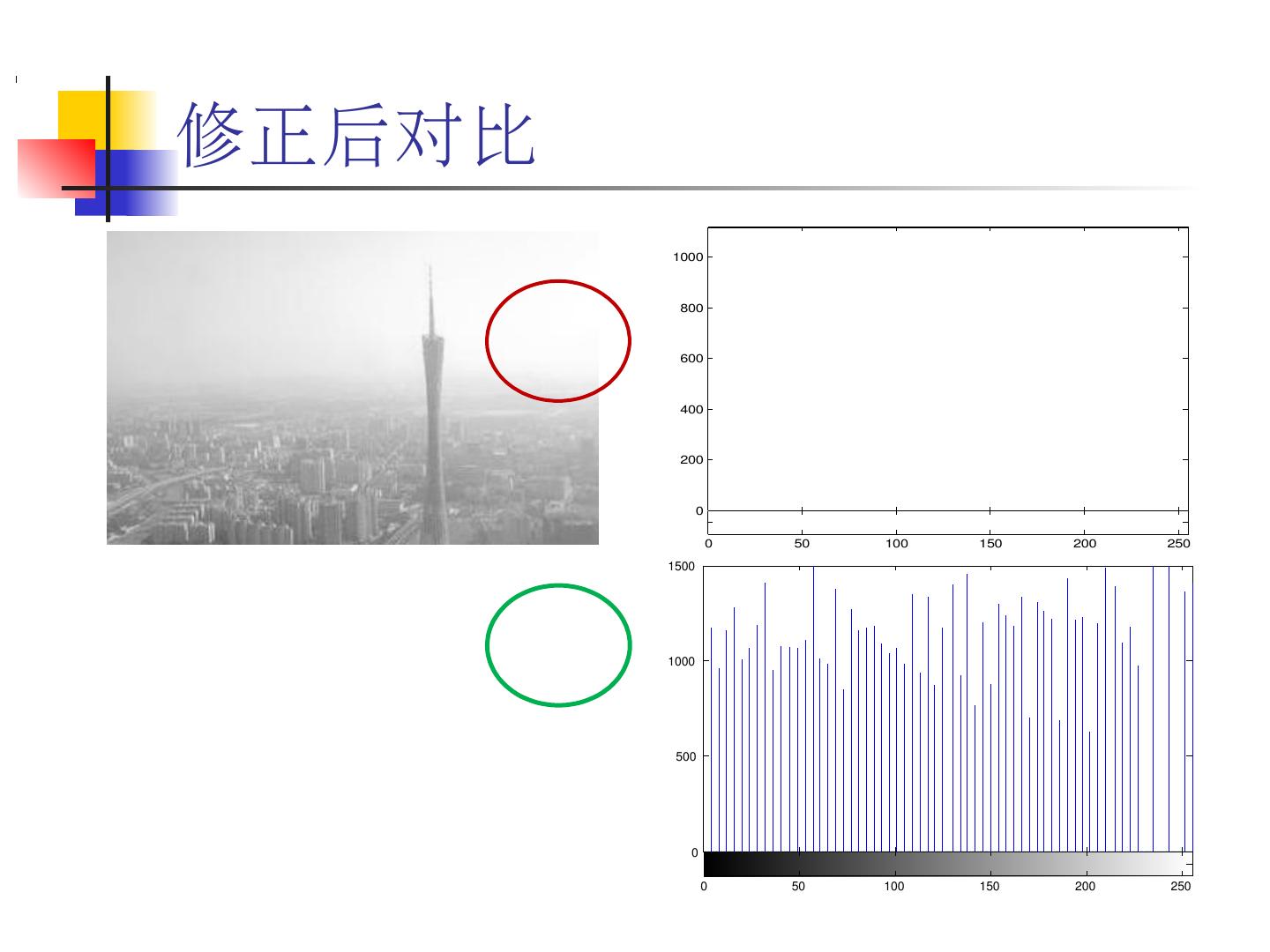
23 .2.1 引言 雾、霾等恶劣天气 对比度下降 清晰度下降 颜色改变 图片质量下降 是否有消除轻度雾霾的方法
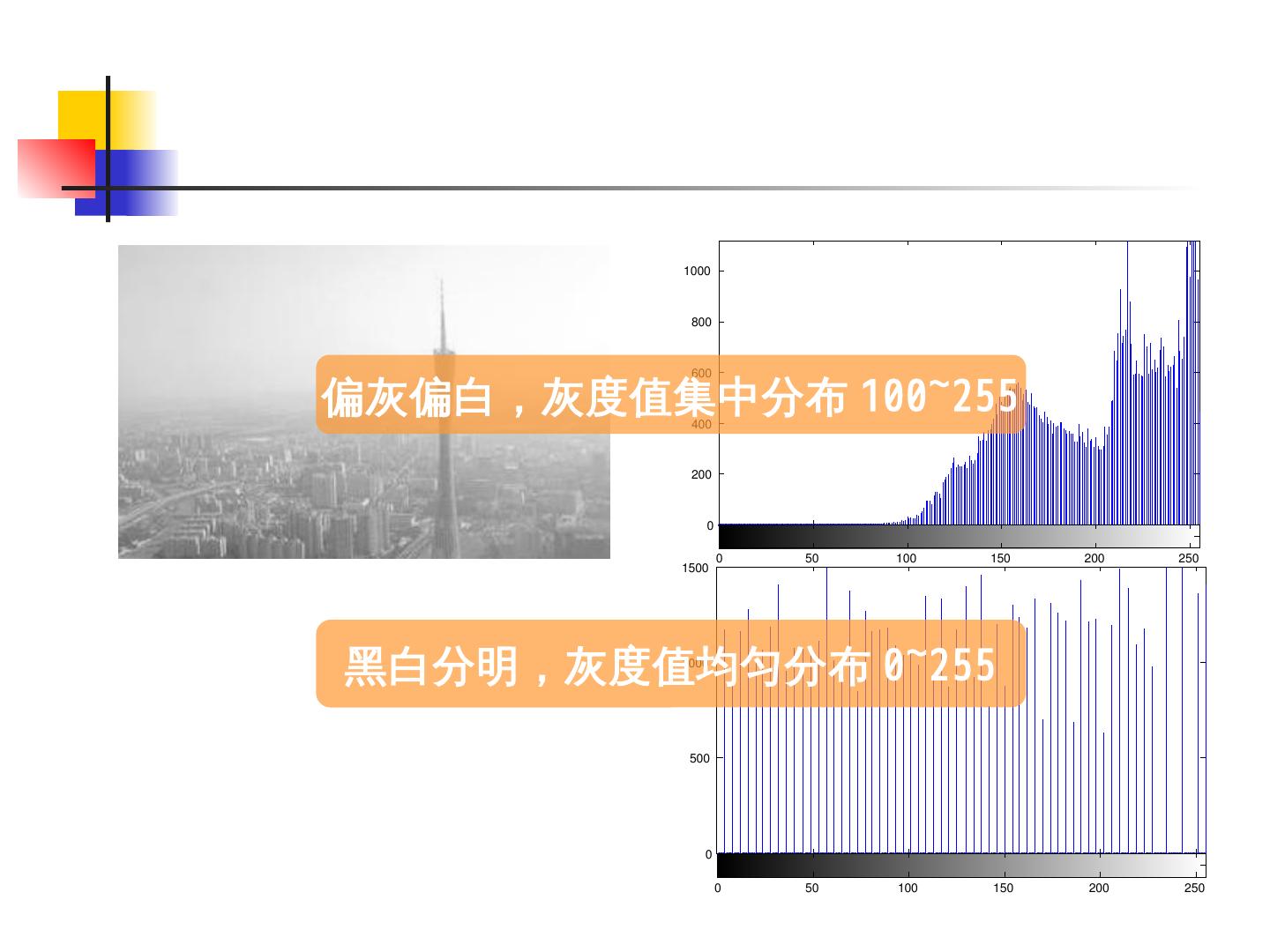
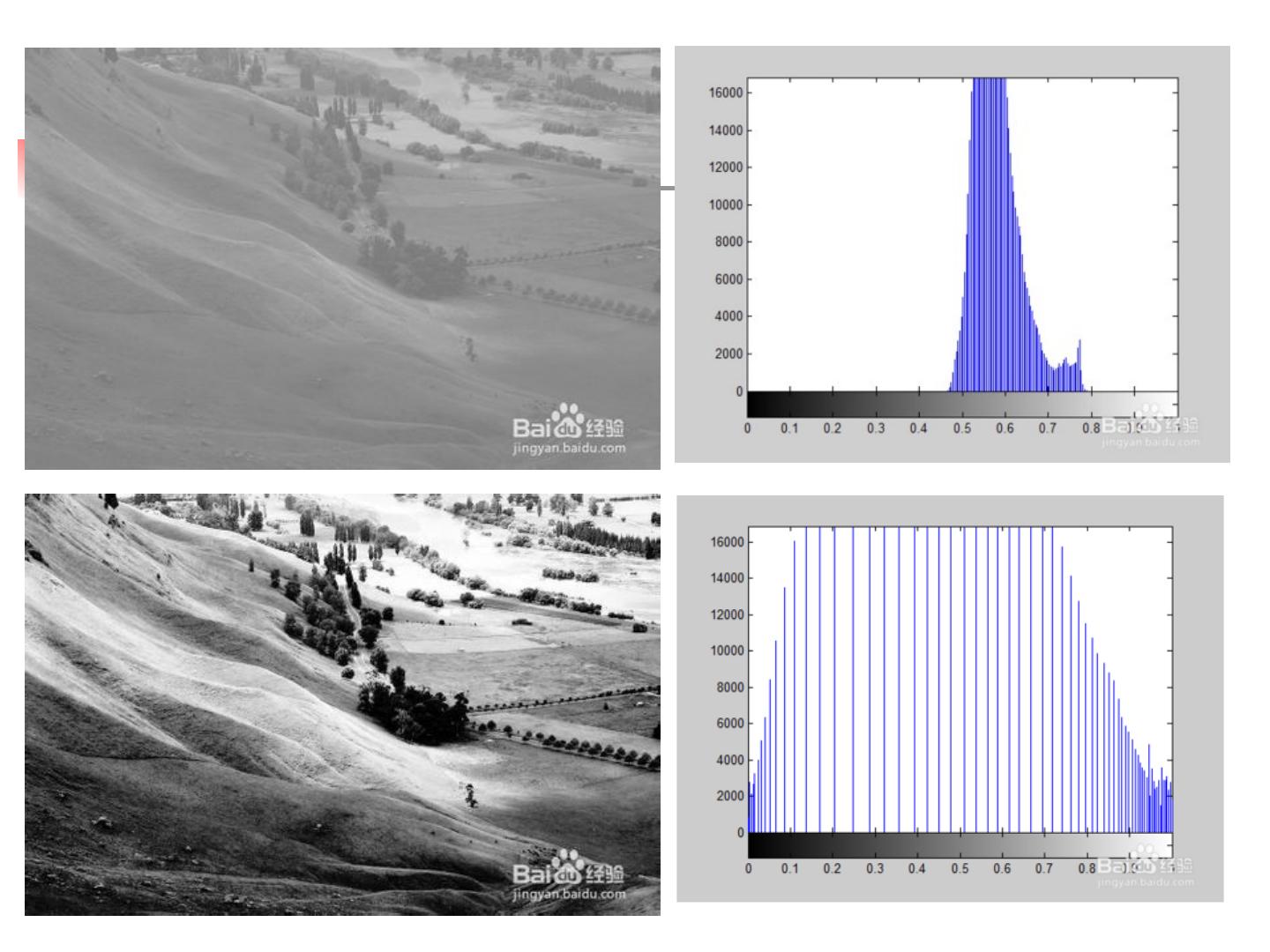
24 .0 500 1000 1500 0 50 100 150 200 250 0 200 400 600 800 1000 0 50 100 150 200 250 偏灰偏白,灰度值集中分布 100~255 黑白分明,灰度值均匀分布 0~255
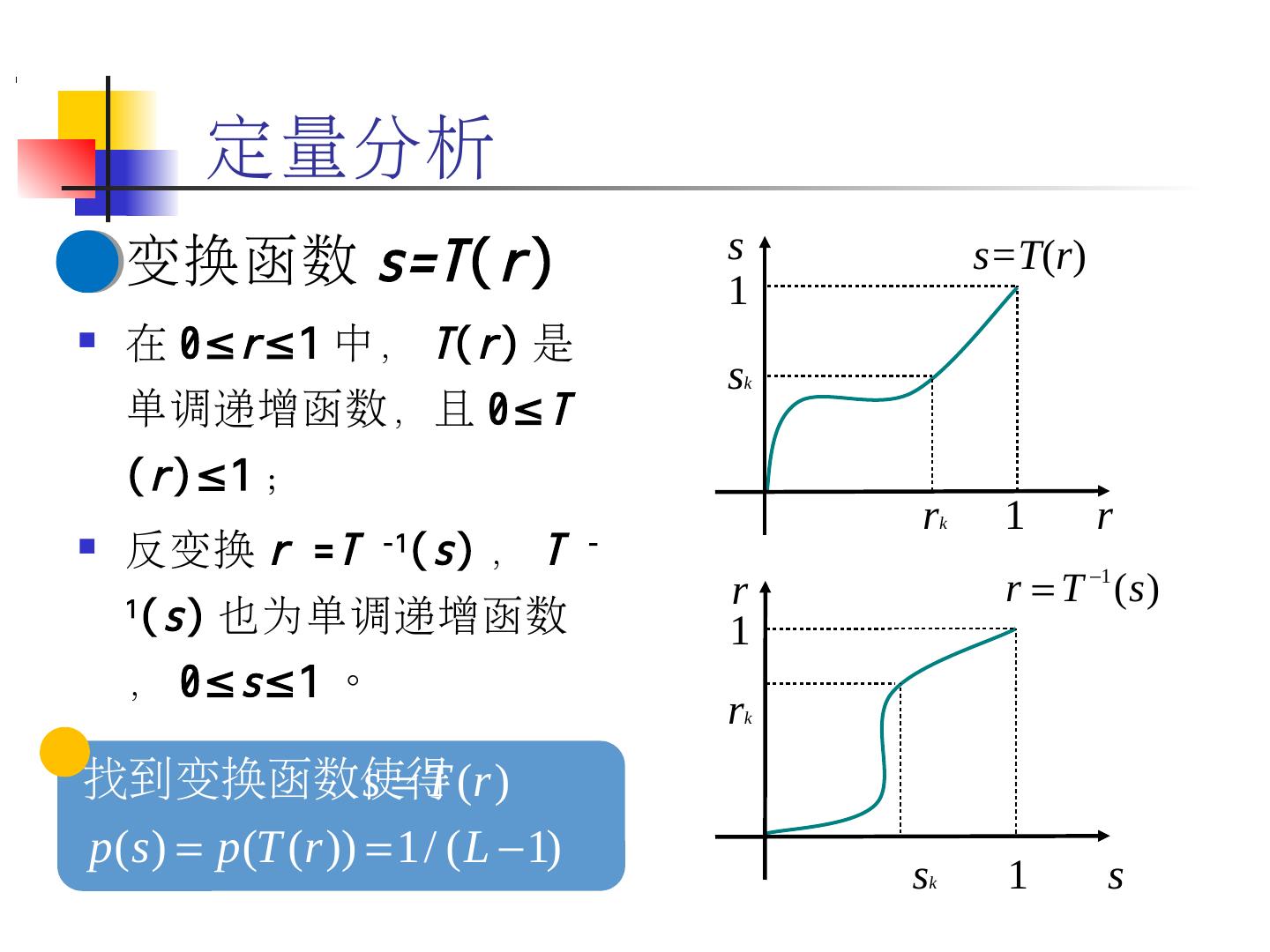
25 .25 定量分析 变换函数 s=T ( r ) 在 0≤ r ≤1 中, T ( r ) 是单调递增函数,且 0≤ T ( r )≤1 ; 反变换 r = T -1 ( s ) , T -1 ( s ) 也为单调递增函数, 0≤ s ≤1 。 r 1 r k s s k 1 s=T ( r ) r 1 r k s s k 1
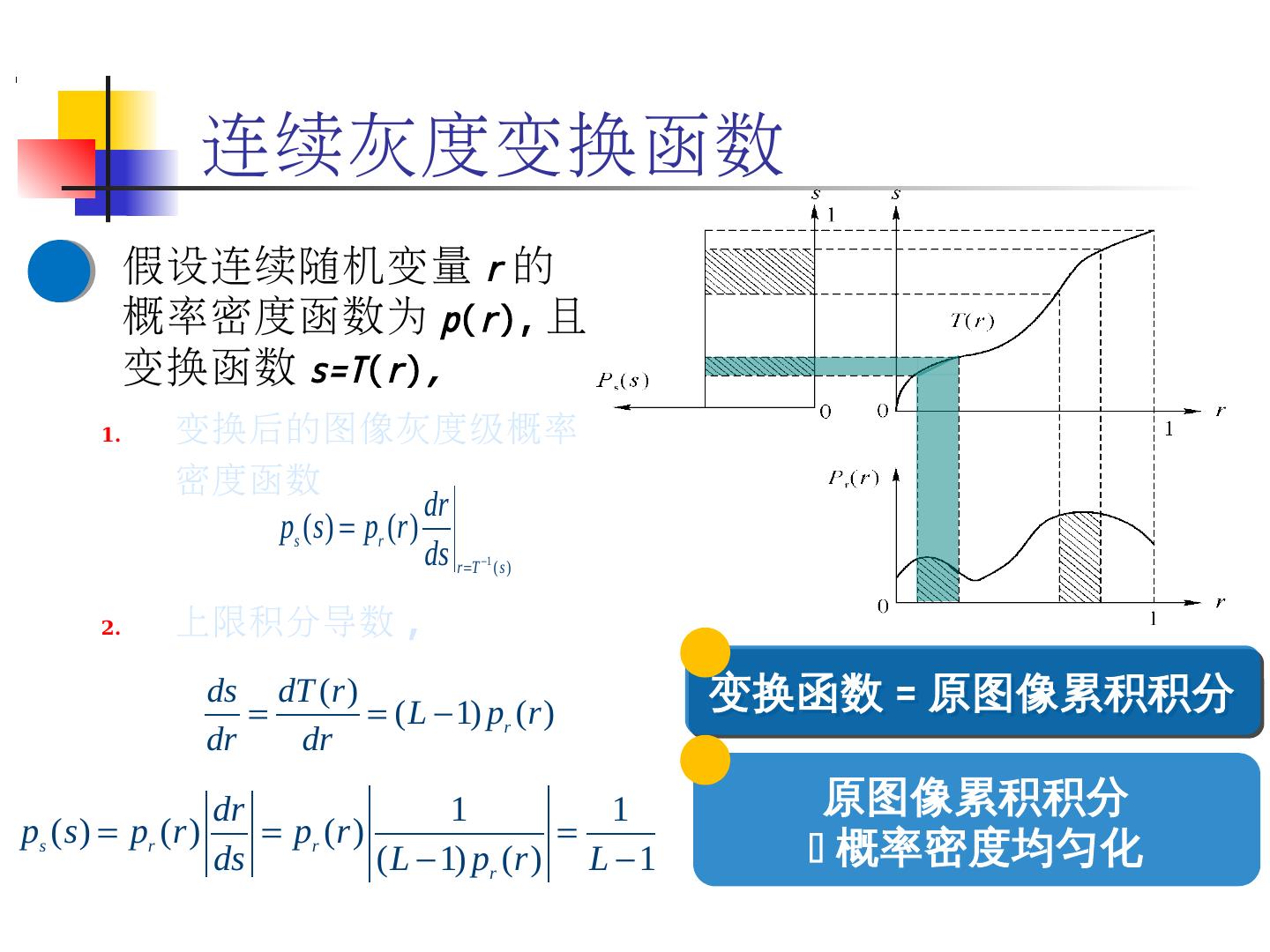
26 .26 连续灰度变换函数 假设连续随机变量 r 的概率密度函数为 p ( r ), 且变换函数 s=T ( r ) , 变换后的图像灰度级概率密度函数 上限积分导数 , 变换函数 = 原图像累积积分 原图像累积积分 概率密度均匀化
27 .为使变换后的灰度仍保持从黑到白的单一变化顺序,且变换范围与原先一致,以避免整体变亮或变暗。必须规定: ( 1 )在 0≤ r ≤1 中, T ( r ) 是单调递增函数,且 0≤ T ( r )≤1 ; ( 2 )反变换 r = T -1 ( s ) , T -1 ( s ) 也为单调递增函数, 0≤ s ≤1 。 用累计分布函数 (Cumulative Distribution Function, CDF) 作为灰度变换函数 s=T ( r ), 从而将原始图像的关于 灰度 r 的分布直方图 ,转换为关于 灰度 s 的均匀分布 。 累计分布函数
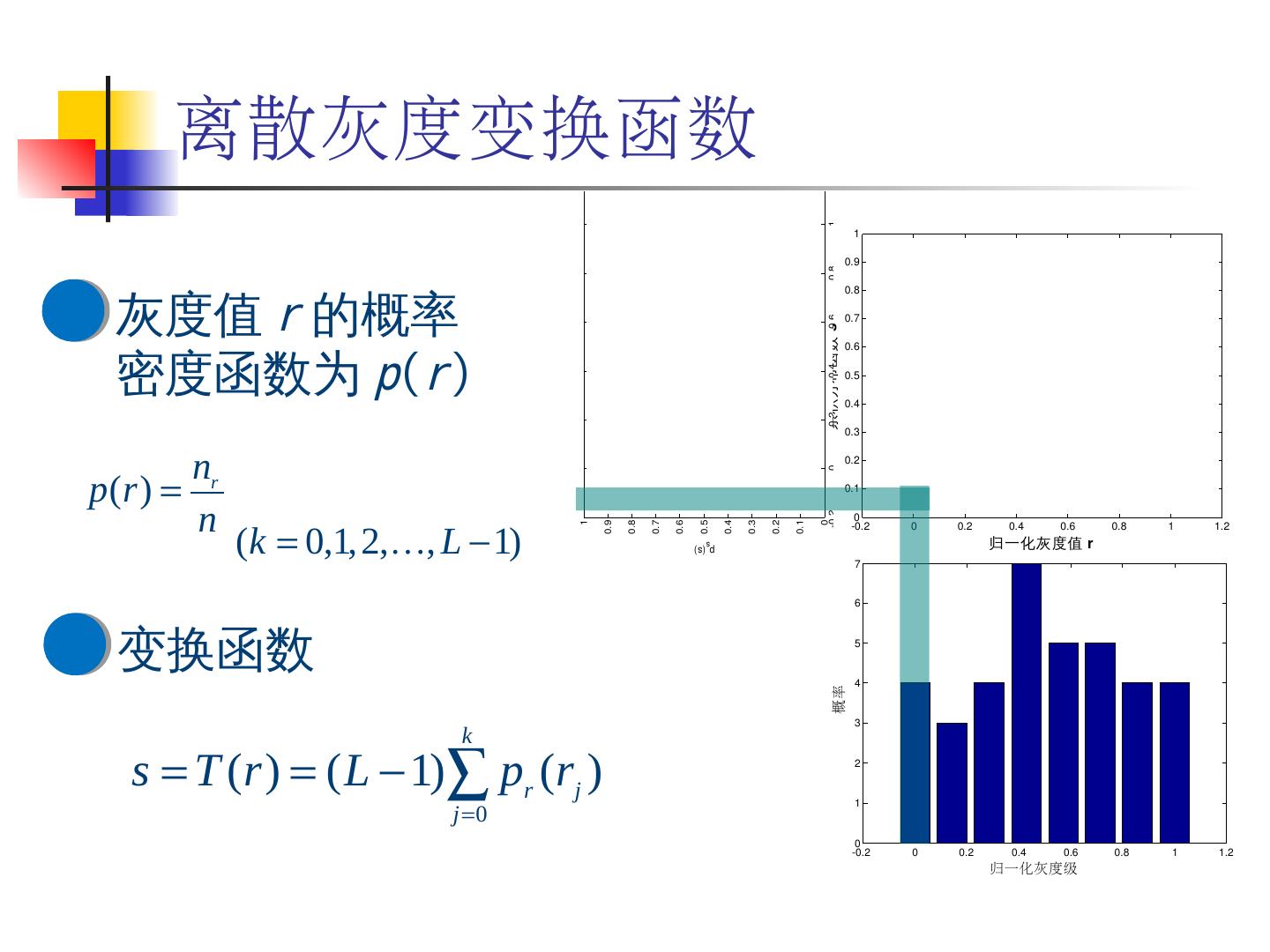
28 .28 -0.2 0 0.2 0.4 0.6 0.8 1 1.2 0 1 2 3 4 5 6 7 归一化灰度级 概率 离散灰度变换函数 灰度值 r 的概率密度函数为 p ( r ) 变换函数
29 .29 直方图修正步骤 -0.2 0 0.2 0.4 0.6 0.8 1 1.2 0 1 2 3 4 5 6 7 归一化灰度级 概率 归一化灰度级,并求灰度级 r k 的概率密度函数 , 累计积分 -0.2 0 0.2 0.4 0.6 0.8 1 1.2 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 归一化灰度级 累积积分