- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
LeetCode Solutions(Java)
展开查看详情
1 .LeetCode Solutions Program Creek Version 0.0
2 .Contents 1 Rotate Array in Java 7 2 Evaluate Reverse Polish Notation 9 3 Solution of Longest Palindromic Substring in Java 11 4 Solution Word Break 15 5 Word Break II 18 6 Word Ladder 20 7 Median of Two Sorted Arrays Java 23 8 Regular Expression Matching in Java 25 9 Merge Intervals 27 10 Insert Interval 29 11 Two Sum 31 12 Two Sum II Input array is sorted 32 13 Two Sum III Data structure design 33 14 3Sum 34 15 4Sum 36 16 3Sum Closest 38 17 String to Integer (atoi) 39 18 Merge Sorted Array 40 19 Valid Parentheses 42 20 Implement strStr() 43 2 | 181
3 . Contents 21 Set Matrix Zeroes 44 22 Search Insert Position 46 23 Longest Consecutive Sequence Java 47 24 Valid Palindrome 49 25 Spiral Matrix 52 26 Search a 2D Matrix 55 27 Rotate Image 56 28 Triangle 58 29 Distinct Subsequences Total 60 30 Maximum Subarray 62 31 Maximum Product Subarray 63 32 Remove Duplicates from Sorted Array 64 33 Remove Duplicates from Sorted Array II 67 34 Longest Substring Without Repeating Characters 69 35 Longest Substring Which Contains 2 Unique Characters 71 36 Palindrome Partitioning 73 37 Reverse Words in a String 75 38 Find Minimum in Rotated Sorted Array 76 39 Find Minimum in Rotated Sorted Array II 77 40 Find Peak Element 78 41 Min Stack 79 42 Majority Element 80 43 Combination Sum 82 44 Best Time to Buy and Sell Stock 83 45 Best Time to Buy and Sell Stock II 84 Program Creek 3 | 181
4 .Contents 46 Best Time to Buy and Sell Stock III 85 47 Best Time to Buy and Sell Stock IV 86 48 Longest Common Prefix 88 49 Largest Number 89 50 Combinations 90 51 Compare Version Numbers 92 52 Gas Station 93 53 Candy 95 54 Jump Game 96 55 Pascal’s Triangle 97 56 Container With Most Water 98 57 Count and Say 99 58 Repeated DNA Sequences 100 59 Add Two Numbers 101 60 Reorder List 105 61 Linked List Cycle 109 62 Copy List with Random Pointer 111 63 Merge Two Sorted Lists 114 64 Merge k Sorted Lists 116 65 Remove Duplicates from Sorted List 117 66 Partition List 119 67 LRU Cache 121 68 Intersection of Two Linked Lists 124 69 Java PriorityQueue Class Example 125 70 Solution for Binary Tree Preorder Traversal in Java 127 4 | 181 Program Creek
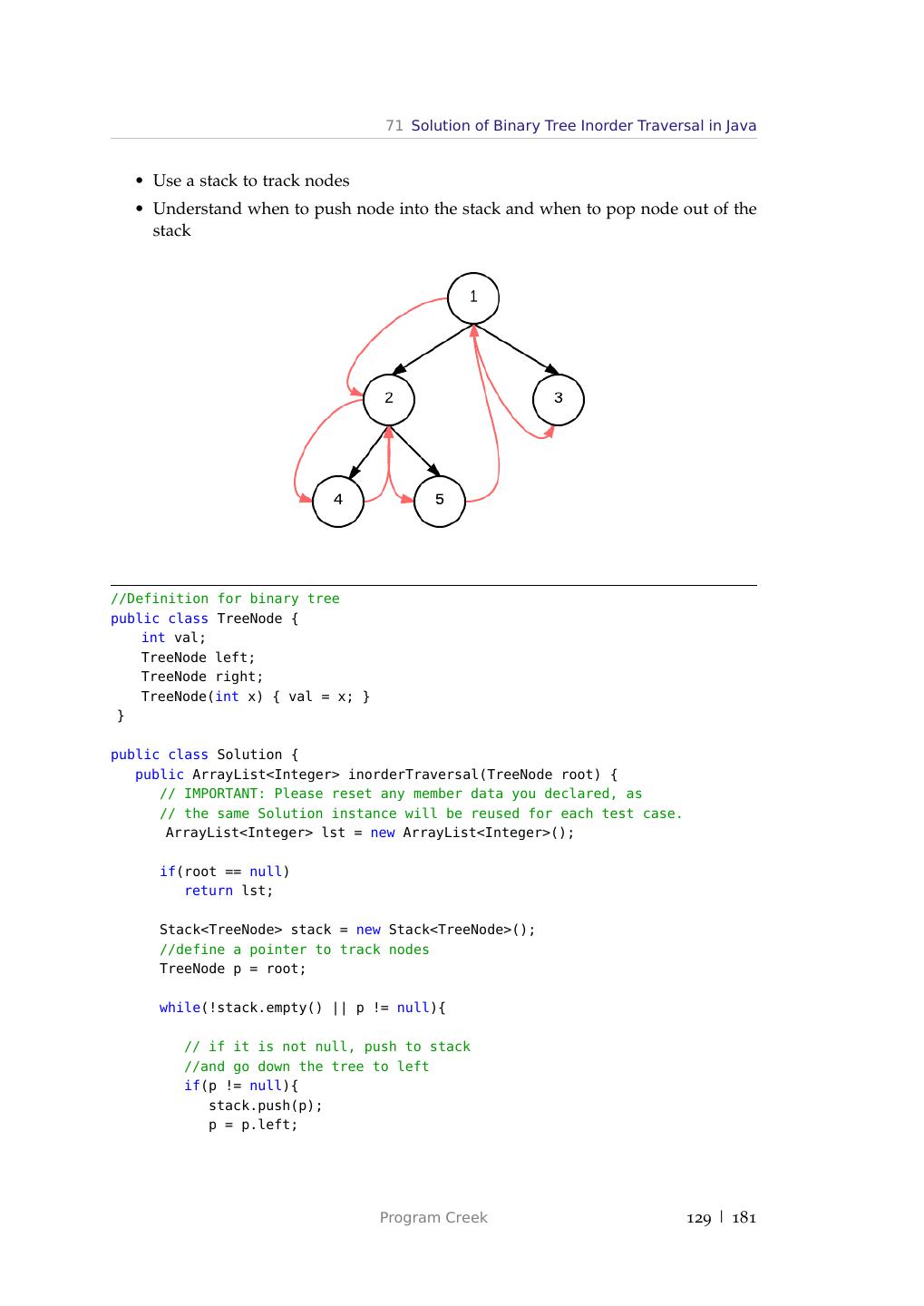
5 . Contents 71 Solution of Binary Tree Inorder Traversal in Java 128 72 Solution of Iterative Binary Tree Postorder Traversal in Java 130 73 Validate Binary Search Tree 131 74 Flatten Binary Tree to Linked List 133 75 Path Sum 134 76 Construct Binary Tree from Inorder and Postorder Traversal 136 77 Convert Sorted Array to Binary Search Tree 137 78 Convert Sorted List to Binary Search Tree 138 79 Minimum Depth of Binary Tree 140 80 Binary Tree Maximum Path Sum 142 81 Balanced Binary Tree 143 82 Symmetric Tree 145 83 Clone Graph Java 146 84 How Developers Sort in Java? 149 85 Solution Merge Sort LinkedList in Java 151 86 Quicksort Array in Java 154 87 Solution Sort a linked list using insertion sort in Java 156 88 Maximum Gap 158 89 Iteration vs. Recursion in Java 160 90 Edit Distance in Java 163 91 Single Number 165 92 Single Number II 166 93 Twitter Codility Problem Max Binary Gap 166 94 Number of 1 Bits 167 95 Reverse Bits 168 Program Creek 5 | 181
6 .Contents 96 Permutations 169 97 Permutations II 171 98 Permutation Sequence 173 99 Generate Parentheses 175 100 Reverse Integer 176 101 Palindrome Number 178 102 Pow(x, n) 179 6 | 181 Program Creek
7 .1 Rotate Array in Java You may have been using Java for a while. Do you think a simple Java array question can be a challenge? Let’s use the following problem to test. Problem: Rotate an array of n elements to the right by k steps. For example, with n = 7 and k = 3, the array [1,2,3,4,5,6,7] is rotated to [5,6,7,1,2,3,4]. How many different ways do you know to solve this problem? 1.1 Solution 1 - Intermediate Array In a straightforward way, we can create a new array and then copy elements to the new array. Then change the original array by using System.arraycopy(). public void rotate(int[] nums, int k) { if(k > nums.length) k=k%nums.length; int[] result = new int[nums.length]; for(int i=0; i < k; i++){ result[i] = nums[nums.length-k+i]; } int j=0; for(int i=k; i<nums.length; i++){ result[i] = nums[j]; j++; } System.arraycopy( result, 0, nums, 0, nums.length ); } Space is O(n) and time is O(n). 1.2 Solution 2 - Bubble Rotate Can we do this in O(1) space? This solution is like a bubble sort. public static void rotate(int[] arr, int order) { if (arr == null || order < 0) { throw new IllegalArgumentException("Illegal argument!"); 7 | 181
8 .1 Rotate Array in Java } for (int i = 0; i < order; i++) { for (int j = arr.length - 1; j > 0; j--) { int temp = arr[j]; arr[j] = arr[j - 1]; arr[j - 1] = temp; } } } However, the time is O(n*k). 1.3 Solution 3 - Reversal Can we do this in O(1) space and in O(n) time? The following solution does. Assuming we are given 1,2,3,4,5,6 and order 2. The basic idea is: 1. Divide the array two parts: 1,2,3,4 and 5, 6 2. Rotate first part: 4,3,2,1,5,6 3. Rotate second part: 4,3,2,1,6,5 4. Rotate the whole array: 5,6,1,2,3,4 public static void rotate(int[] arr, int order) { order = order % arr.length; if (arr == null || order < 0) { throw new IllegalArgumentException("Illegal argument!"); } //length of first part int a = arr.length - order; reverse(arr, 0, a-1); reverse(arr, a, arr.length-1); reverse(arr, 0, arr.length-1); } public static void reverse(int[] arr, int left, int right){ if(arr == null || arr.length == 1) return; while(left < right){ int temp = arr[left]; arr[left] = arr[right]; arr[right] = temp; left++; right--; 8 | 181 Program Creek
9 . } } 2 Evaluate Reverse Polish Notation The problem: Evaluate the value of an arithmetic expression in Reverse Polish Notation. Valid operators are +, -, *, /. Each operand may be an integer or another expression. Some examples: ["2", "1", "+", "3", "*"] -> ((2 + 1) * 3) -> 9 ["4", "13", "5", "/", "+"] -> (4 + (13 / 5)) -> 6 2.1 Naive Approach This problem is simple. After understanding the problem, we should quickly realize that this problem can be solved by using a stack. We can loop through each element in the given array. When it is a number, push it to the stack. When it is an operator, pop two numbers from the stack, do the calculation, and push back the result. The following is the code. It runs great by feeding a small test. However, this code 9 | 181
10 .2 Evaluate Reverse Polish Notation contains compilation errors in leetcode. Why? public class Test { public static void main(String[] args) throws IOException { String[] tokens = new String[] { "2", "1", "+", "3", "*" }; System.out.println(evalRPN(tokens)); } public static int evalRPN(String[] tokens) { int returnValue = 0; String operators = "+-*/"; Stack<String> stack = new Stack<String>(); for (String t : tokens) { if (!operators.contains(t)) { stack.push(t); } else { int a = Integer.valueOf(stack.pop()); int b = Integer.valueOf(stack.pop()); switch (t) { case "+": stack.push(String.valueOf(a + b)); break; case "-": stack.push(String.valueOf(b - a)); break; case "*": stack.push(String.valueOf(a * b)); break; case "/": stack.push(String.valueOf(b / a)); break; } } } returnValue = Integer.valueOf(stack.pop()); return returnValue; } } The problem is that switch string statement is only available from JDK 1.7. Leetcode apparently use versions below that. 10 | 181 Program Creek
11 .2.2 Accepted Solution If you want to use switch statement, you can convert the above by using the following code which use the index of a string "+-*/". public class Solution { public int evalRPN(String[] tokens) { int returnValue = 0; String operators = "+-*/"; Stack<String> stack = new Stack<String>(); for(String t : tokens){ if(!operators.contains(t)){ stack.push(t); }else{ int a = Integer.valueOf(stack.pop()); int b = Integer.valueOf(stack.pop()); int index = operators.indexOf(t); switch(index){ case 0: stack.push(String.valueOf(a+b)); break; case 1: stack.push(String.valueOf(b-a)); break; case 2: stack.push(String.valueOf(a*b)); break; case 3: stack.push(String.valueOf(b/a)); break; } } } returnValue = Integer.valueOf(stack.pop()); return returnValue; } } 11 | 181
12 .3 Solution of Longest Palindromic Substring in Java 3 Solution of Longest Palindromic Substring in Java Finding the longest palindromic substring is a classic problem of coding interview. In this post, I will summarize 3 different solutions for this problem. 3.1 Naive Approach Naively, we can simply examine every substring and check if it is palindromic. The time complexity is O(nˆ3). If this is submitted to LeetCode onlinejudge, an error mes- sage will be returned - "Time Limit Exceeded". Therefore, this approach is just a start, we need a better algorithm. public static String longestPalindrome1(String s) { int maxPalinLength = 0; String longestPalindrome = null; int length = s.length(); // check all possible sub strings for (int i = 0; i < length; i++) { for (int j = i + 1; j < length; j++) { int len = j - i; String curr = s.substring(i, j + 1); if (isPalindrome(curr)) { if (len > maxPalinLength) { longestPalindrome = curr; maxPalinLength = len; } } } } return longestPalindrome; } public static boolean isPalindrome(String s) { for (int i = 0; i < s.length() - 1; i++) { if (s.charAt(i) != s.charAt(s.length() - 1 - i)) { return false; } } return true; } 12 | 181 Program Creek
13 . 3 Solution of Longest Palindromic Substring in Java 3.2 Dynamic Programming Let s be the input string, i and j are two indices of the string. Define a 2-dimension array "table" and let table[i][j] denote whether substring from i to j is palindrome. Start condition: table[i][i] == 1; table[i][i+1] == 1 => s.charAt(i) == s.charAt(i+1) Changing condition: table[i+1][j-1] == 1 && s.charAt(i) == s.charAt(j) => table[i][j] == 1 Time O(nˆ2) Space O(nˆ2) public static String longestPalindrome2(String s) { if (s == null) return null; if(s.length() <=1) return s; int maxLen = 0; String longestStr = null; int length = s.length(); int[][] table = new int[length][length]; //every single letter is palindrome for (int i = 0; i < length; i++) { table[i][i] = 1; } printTable(table); //e.g. bcba //two consecutive same letters are palindrome for (int i = 0; i <= length - 2; i++) { if (s.charAt(i) == s.charAt(i + 1)){ table[i][i + 1] = 1; longestStr = s.substring(i, i + 2); } } printTable(table); //condition for calculate whole table for (int l = 3; l <= length; l++) { for (int i = 0; i <= length-l; i++) { Program Creek 13 | 181
14 .3 Solution of Longest Palindromic Substring in Java int j = i + l - 1; if (s.charAt(i) == s.charAt(j)) { table[i][j] = table[i + 1][j - 1]; if (table[i][j] == 1 && l > maxLen) longestStr = s.substring(i, j + 1); } else { table[i][j] = 0; } printTable(table); } } return longestStr; } public static void printTable(int[][] x){ for(int [] y : x){ for(int z: y){ System.out.print(z + " "); } System.out.println(); } System.out.println("------"); } Given an input, we can use printTable method to examine the table after each itera- tion. For example, if input string is "dabcba", the final matrix would be the following: 1 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 From the table, we can clear see that the longest string is in cell table[1][5]. 3.3 Simple Algorithm From Yifan’s comment below. Time O(nˆ2), Space O(1) public String longestPalindrome(String s) { if (s.isEmpty()) { return null; } if (s.length() == 1) { return s; } 14 | 181 Program Creek
15 . String longest = s.substring(0, 1); for (int i = 0; i < s.length(); i++) { // get longest palindrome with center of i String tmp = helper(s, i, i); if (tmp.length() > longest.length()) { longest = tmp; } // get longest palindrome with center of i, i+1 tmp = helper(s, i, i + 1); if (tmp.length() > longest.length()) { longest = tmp; } } return longest; } // Given a center, either one letter or two letter, // Find longest palindrome public String helper(String s, int begin, int end) { while (begin >= 0 && end <= s.length() - 1 && s.charAt(begin) == s.charAt(end)) { begin--; end++; } return s.substring(begin + 1, end); } 3.4 Manacher’s Algorithm Manacher’s algorithm is much more complicated to figure out, even though it will bring benefit of time complexity of O(n). Since it is not typical, there is no need to waste time on that. 4 Solution Word Break Given a string s and a dictionary of words dict, determine if s can be segmented into a space-separated sequence of one or more dictionary words. For example, given s = "leetcode", dict = ["leet", "code"]. Return true because "leetcode" can be segmented as "leet code". 15 | 181
16 .4 Solution Word Break 4.1 Naive Approach This problem can be solve by using a naive approach, which is trivial. A discussion can always start from that though. public class Solution { public boolean wordBreak(String s, Set<String> dict) { return wordBreakHelper(s, dict, 0); } public boolean wordBreakHelper(String s, Set<String> dict, int start){ if(start == s.length()) return true; for(String a: dict){ int len = a.length(); int end = start+len; //end index should be <= string length if(end > s.length()) continue; if(s.substring(start, start+len).equals(a)) if(wordBreakHelper(s, dict, start+len)) return true; } return false; } } Time: O(nˆ2) This solution exceeds the time limit. 4.2 Dynamic Programming The key to solve this problem by using dynamic programming approach: • Define an array t[] such that t[i]==true =>0-(i-1) can be segmented using dictio- nary • Initial state t[0] == true public class Solution { public boolean wordBreak(String s, Set<String> dict) { boolean[] t = new boolean[s.length()+1]; t[0] = true; //set first to be true, why? //Because we need initial state for(int i=0; i<s.length(); i++){ 16 | 181 Program Creek
17 . 4 Solution Word Break //should continue from match position if(!t[i]) continue; for(String a: dict){ int len = a.length(); int end = i + len; if(end > s.length()) continue; if(t[end]) continue; if(s.substring(i, end).equals(a)){ t[end] = true; } } } return t[s.length()]; } } Time: O(string length * dict size) One tricky part of this solution is the case: INPUT: "programcreek", ["programcree","program","creek"]. We should get all possible matches, not stop at "programcree". 4.3 Regular Expression The problem is supposed to be equivalent to matching the regexp (leet|code)*, which means that it can be solved by building a DFA in O(2m) ˆ and executing it in O(n). (Thanks to hdante.) Leetcode online judge does not allow using Pattern class though. public static void main(String[] args) { HashSet<String> dict = new HashSet<String>(); dict.add("go"); dict.add("goal"); dict.add("goals"); dict.add("special"); StringBuilder sb = new StringBuilder(); for(String s: dict){ sb.append(s + "|"); } String pattern = sb.toString().substring(0, sb.length()-1); Program Creek 17 | 181
18 . pattern = "("+pattern+")*"; Pattern p = Pattern.compile(pattern); Matcher m = p.matcher("goalspecial"); if(m.matches()){ System.out.println("match"); } } 4.4 The More Interesting Problem The dynamic solution can tell us whether the string can be broken to words, but can not tell us what words the string is broken to. So how to get those words? Check out Word Break II. 5 Word Break II Given a string s and a dictionary of words dict, add spaces in s to construct a sentence where each word is a valid dictionary word. Return all such possible sentences. For example, given s = "catsanddog", dict = ["cat", "cats", "and", "sand", "dog"], the solution is ["cats and dog", "cat sand dog"]. 5.1 Java Solution - Dynamic Programming This problem is very similar to Word Break. Instead of using a boolean array to track the match positions, we need to track the actual words. Then we can use depth first search to get all the possible paths, i.e., the list of strings. The following diagram shows the structure of the tracking array. 18 | 181
19 . 5 Word Break II public static List<String> wordBreak(String s, Set<String> dict) { //create an array of ArrayList<String> List<String> dp[] = new ArrayList[s.length()+1]; dp[0] = new ArrayList<String>(); for(int i=0; i<s.length(); i++){ if( dp[i] == null ) continue; for(String word:dict){ int len = word.length(); int end = i+len; if(end > s.length()) continue; if(s.substring(i,end).equals(word)){ if(dp[end] == null){ dp[end] = new ArrayList<String>(); } dp[end].add(word); } } } List<String> result = new LinkedList<String>(); if(dp[s.length()] == null) return result; Program Creek 19 | 181
20 . ArrayList<String> temp = new ArrayList<String>(); dfs(dp, s.length(), result, temp); return result; } public static void dfs(List<String> dp[],int end,List<String> result, ArrayList<String> tmp){ if(end <= 0){ String path = tmp.get(tmp.size()-1); for(int i=tmp.size()-2; i>=0; i--){ path += " " + tmp.get(i) ; } result.add(path); return; } for(String str : dp[end]){ tmp.add(str); dfs(dp, end-str.length(), result, tmp); tmp.remove(tmp.size()-1); } } 6 Word Ladder The problem: Given two words (start and end), and a dictionary, find the length of shortest trans- formation sequence from start to end, such that: Only one letter can be changed at a time Each intermediate word must exist in the dictionary For example, Given: start = "hit" end = "cog" dict = ["hot","dot","dog","lot","log"] As one shortest transformation is "hit" ->"hot" ->"dot" ->"dog" ->"cog", the program should return its length 5. Note: Return 0 if there is no such transformation sequence. All words have the same length. All words contain only lowercase alphabetic characters. This problem is a classic problem that has been asked frequently during interviews. 20 | 181
21 . 6 Word Ladder The following are two Java solutions. 6.1 Naive Approach In a simplest way, we can start from start word, change one character each time, if it is in the dictionary, we continue with the replaced word, until start == end. public class Solution { public int ladderLength(String start, String end, HashSet<String> dict) { int len=0; HashSet<String> visited = new HashSet<String>(); for(int i=0; i<start.length(); i++){ char[] startArr = start.toCharArray(); for(char c=’a’; c<=’z’; c++){ if(c==start.toCharArray()[i]){ continue; } startArr[i] = c; String temp = new String(startArr); if(dict.contains(temp)){ len++; start = temp; if(temp.equals(end)){ return len; } } } } return len; } } Apparently, this is not good enough. The following example exactly shows the problem. It can not find optimal path. The output is 3, but it actually only takes 2. Input: "a", "c", ["a","b","c"] Output: 3 Expected: 2 6.2 Breath First Search So we quickly realize that this looks like a tree searching problem for which breath first guarantees the optimal solution. Program Creek 21 | 181
22 .6 Word Ladder Assuming we have some words in the dictionary, and the start is "hit" as shown in the diagram below. We can use two queues to traverse the tree, one stores the nodes, the other stores the step numbers. Updated on 2/27/2015. public int ladderLength(String start, String end, HashSet<String> dict) { if (dict.size() == 0) return 0; dict.add(end); LinkedList<String> wordQueue = new LinkedList<String>(); LinkedList<Integer> distanceQueue = new LinkedList<Integer>(); wordQueue.add(start); distanceQueue.add(1); //track the shortest path int result = Integer.MAX_VALUE; while (!wordQueue.isEmpty()) { String currWord = wordQueue.pop(); Integer currDistance = distanceQueue.pop(); if (currWord.equals(end)) { result = Math.min(result, currDistance); } for (int i = 0; i < currWord.length(); i++) { char[] currCharArr = currWord.toCharArray(); for (char c = ’a’; c <= ’z’; c++) { 22 | 181 Program Creek
23 . currCharArr[i] = c; String newWord = new String(currCharArr); if (dict.contains(newWord)) { wordQueue.add(newWord); distanceQueue.add(currDistance + 1); dict.remove(newWord); } } } } if (result < Integer.MAX_VALUE) return result; else return 0; } 6.3 What learned from this problem? • Use breath-first or depth-first search to solve problems • Use two queues, one for words and another for counting 7 Median of Two Sorted Arrays Java LeetCode Problem: There are two sorted arrays A and B of size m and n respectively. Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)). 7.1 Java Solution This problem can be converted to the problem of finding kth element, k is (A’s length + B’ Length)/2. If any of the two arrays is empty, then the kth element is the non-empty array’s kth element. If k == 0, the kth element is the first element of A or B. For normal cases(all other cases), we need to move the pointer at the pace of half of an array length. public static double findMedianSortedArrays(int A[], int B[]) { int m = A.length; int n = B.length; 23 | 181
24 . if ((m + n) % 2 != 0) // odd return (double) findKth(A, B, (m + n) / 2, 0, m - 1, 0, n - 1); else { // even return (findKth(A, B, (m + n) / 2, 0, m - 1, 0, n - 1) + findKth(A, B, (m + n) / 2 - 1, 0, m - 1, 0, n - 1)) * 0.5; } } public static int findKth(int A[], int B[], int k, int aStart, int aEnd, int bStart, int bEnd) { int aLen = aEnd - aStart + 1; int bLen = bEnd - bStart + 1; // Handle special cases if (aLen == 0) return B[bStart + k]; if (bLen == 0) return A[aStart + k]; if (k == 0) return A[aStart] < B[bStart] ? A[aStart] : B[bStart]; int aMid = aLen * k / (aLen + bLen); // a’s middle count int bMid = k - aMid - 1; // b’s middle count // make aMid and bMid to be array index aMid = aMid + aStart; bMid = bMid + bStart; if (A[aMid] > B[bMid]) { k = k - (bMid - bStart + 1); aEnd = aMid; bStart = bMid + 1; } else { k = k - (aMid - aStart + 1); bEnd = bMid; aStart = aMid + 1; } return findKth(A, B, k, aStart, aEnd, bStart, bEnd); } 7.2 The Steps of the Algorithm Thanks to Gunner86. The description of the algorithm is awesome! 1) Calculate the medians m1 and m2 of the input arrays ar1[] and ar2[] respectively. 2) If m1 and m2 both are equal then we are done, and return m1 (or m2) 3) If m1 24 | 181
25 . 8 Regular Expression Matching in Java is greater than m2, then median is present in one of the below two subarrays. a) From first element of ar1 to m1 (ar1[0...|_n/2_|]) b) From m2 to last element of ar2 (ar2[|_n/2_|...n-1]) 4) If m2 is greater than m1, then median is present in one of the below two subarrays. a) From m1 to last element of ar1 (ar1[|_n/2_|...n-1]) b) From first element of ar2 to m2 (ar2[0...|_n/2_|]) 5) Repeat the above process until size of both the subarrays becomes 2. 6) If size of the two arrays is 2 then use below formula to get the median. Median = (max(ar1[0], ar2[0]) + min(ar1[1], ar2[1]))/2 8 Regular Expression Matching in Java Problem: Implement regular expression matching with support for ’.’ and ’*’. ’.’ Matches any single character. ’*’ Matches zero or more of the preceding element. The matching should cover the entire input string (not partial). The function prototype should be: bool isMatch(const char *s, const char *p) Some examples: isMatch("aa","a") return false isMatch("aa","aa") return true isMatch("aaa","aa") return false isMatch("aa", "a*") return true isMatch("aa", ".*") return true isMatch("ab", ".*") return true isMatch("aab", "c*a*b") return true 8.1 Analysis First of all, this is one of the most difficulty problems. It is hard to handle many cases. The problem should be simplified to handle 2 basic cases: • the second char of pattern is "*" • the second char of pattern is not "*" For the 1st case, if the first char of pattern is not ".", the first char of pattern and string should be the same. Then continue to match the left part. For the 2nd case, if the first char of pattern is "." or first char of pattern == the first i char of string, continue to match the left. Be careful about the offset. Program Creek 25 | 181
26 .8 Regular Expression Matching in Java 8.2 Java Solution 1 (Short) The following Java solution is accepted. public class Solution { public boolean isMatch(String s, String p) { if(p.length() == 0) return s.length() == 0; //p’s length 1 is special case if(p.length() == 1 || p.charAt(1) != ’*’){ if(s.length() < 1 || (p.charAt(0) != ’.’ && s.charAt(0) != p.charAt(0))) return false; return isMatch(s.substring(1), p.substring(1)); }else{ int len = s.length(); int i = -1; while(i<len && (i < 0 || p.charAt(0) == ’.’ || p.charAt(0) == s.charAt(i))){ if(isMatch(s.substring(i+1), p.substring(2))) return true; i++; } return false; } } } 8.3 Java Solution 2 (More Readable) public boolean isMatch(String s, String p) { // base case if (p.length() == 0) { return s.length() == 0; } // special case if (p.length() == 1) { // if the length of s is 0, return false if (s.length() < 1) { return false; } 26 | 181 Program Creek
27 . //if the first does not match, return false else if ((p.charAt(0) != s.charAt(0)) && (p.charAt(0) != ’.’)) { return false; } // otherwise, compare the rest of the string of s and p. else { return isMatch(s.substring(1), p.substring(1)); } } // case 1: when the second char of p is not ’*’ if (p.charAt(1) != ’*’) { if (s.length() < 1) { return false; } if ((p.charAt(0) != s.charAt(0)) && (p.charAt(0) != ’.’)) { return false; } else { return isMatch(s.substring(1), p.substring(1)); } } // case 2: when the second char of p is ’*’, complex case. else { //case 2.1: a char & ’*’ can stand for 0 element if (isMatch(s, p.substring(2))) { return true; } //case 2.2: a char & ’*’ can stand for 1 or more preceding element, //so try every sub string int i = 0; while (i<s.length() && (s.charAt(i)==p.charAt(0) || p.charAt(0)==’.’)){ if (isMatch(s.substring(i + 1), p.substring(2))) { return true; } i++; } return false; } } 27 | 181
28 .9 Merge Intervals 9 Merge Intervals Problem: Given a collection of intervals, merge all overlapping intervals. For example, Given [1,3],[2,6],[8,10],[15,18], return [1,6],[8,10],[15,18]. 9.1 Thoughts of This Problem The key to solve this problem is defining a Comparator first to sort the arraylist of Intevals. And then merge some intervals. The take-away message from this problem is utilizing the advantage of sorted list/ar- ray. 9.2 Java Solution class Interval { int start; int end; Interval() { start = 0; end = 0; } Interval(int s, int e) { start = s; end = e; } } public class Solution { public ArrayList<Interval> merge(ArrayList<Interval> intervals) { if (intervals == null || intervals.size() <= 1) return intervals; // sort intervals by using self-defined Comparator Collections.sort(intervals, new IntervalComparator()); ArrayList<Interval> result = new ArrayList<Interval>(); Interval prev = intervals.get(0); 28 | 181 Program Creek
29 . for (int i = 1; i < intervals.size(); i++) { Interval curr = intervals.get(i); if (prev.end >= curr.start) { // merged case Interval merged = new Interval(prev.start, Math.max(prev.end, curr.end)); prev = merged; } else { result.add(prev); prev = curr; } } result.add(prev); return result; } } class IntervalComparator implements Comparator<Interval> { public int compare(Interval i1, Interval i2) { return i1.start - i2.start; } } 10 Insert Interval Problem: Given a set of non-overlapping & sorted intervals, insert a new interval into the intervals (merge if necessary). Example 1: Given intervals [1,3],[6,9], insert and merge [2,5] in as [1,5],[6,9]. Example 2: Given [1,2],[3,5],[6,7],[8,10],[12,16], insert and merge [4,9] in as [1,2],[3,10],[12,16]. This is because the new interval [4,9] overlaps with [3,5],[6,7],[8,10]. 29 | 181