- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
cncc2018-AP-LLE
展开查看详情
1 . 无监督学习中的 选代表和被代表问题 - AP & LLE 张响亮 Xiangliang Zhang King Abdullah University of Science and Technology CNCC, Oct 25, 2018 Hangzhou, China
2 . Outline • Affinity Propagation (AP) [Frey and Dueck, Science, 2007] • Locally Linear Embedding (LLE) [Roweis and Saul, Science, 2000] 2
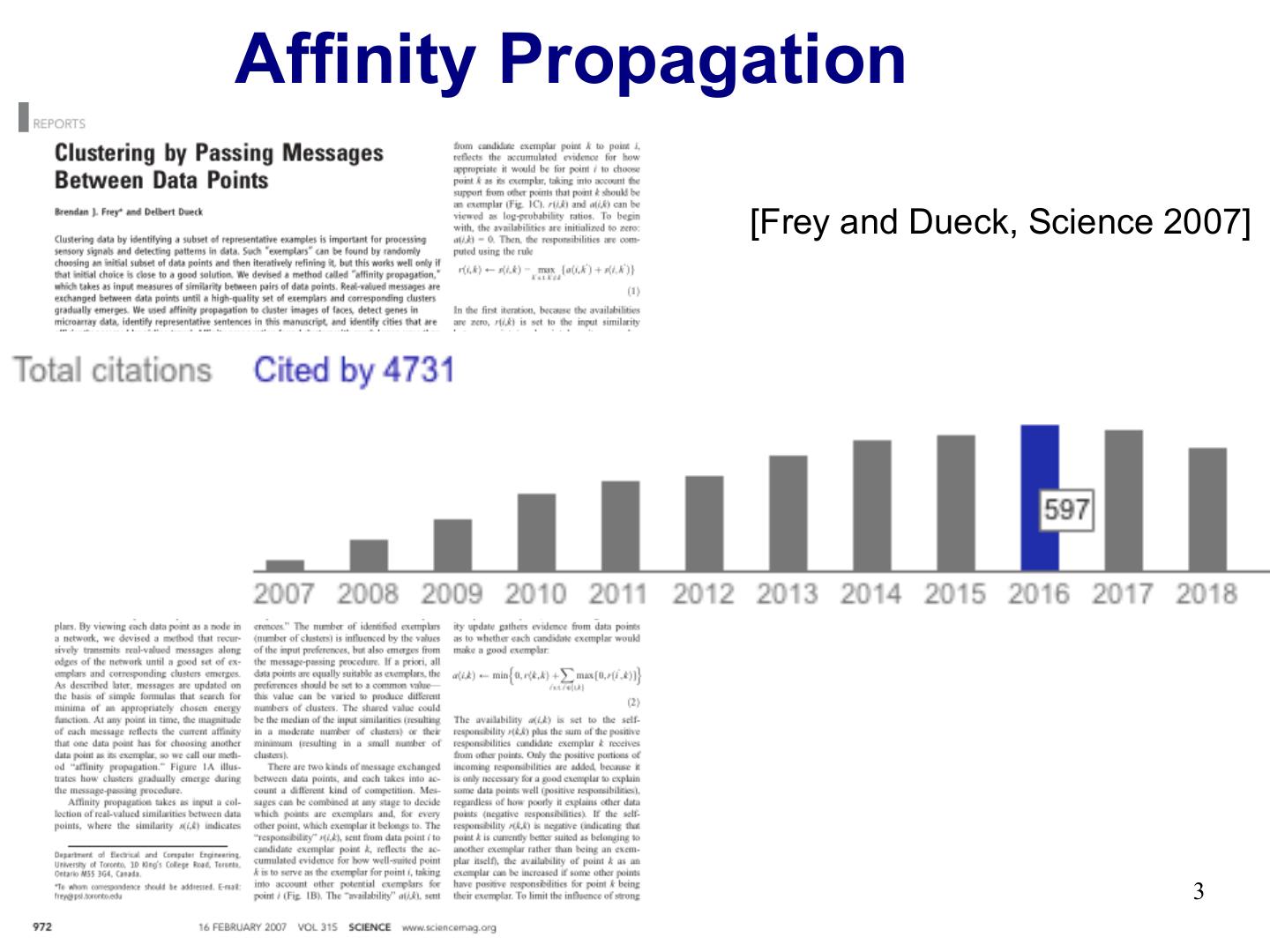
3 .Affinity Propagation [Frey and Dueck, Science 2007] 3
4 . Affinity Propagation [Frey and Dueck, NIPS 2005] We describe a new method that, for the first time to our knowledge, combines the advantages of model-based clustering and affinity-based clustering. Component Mixing coefficient 4
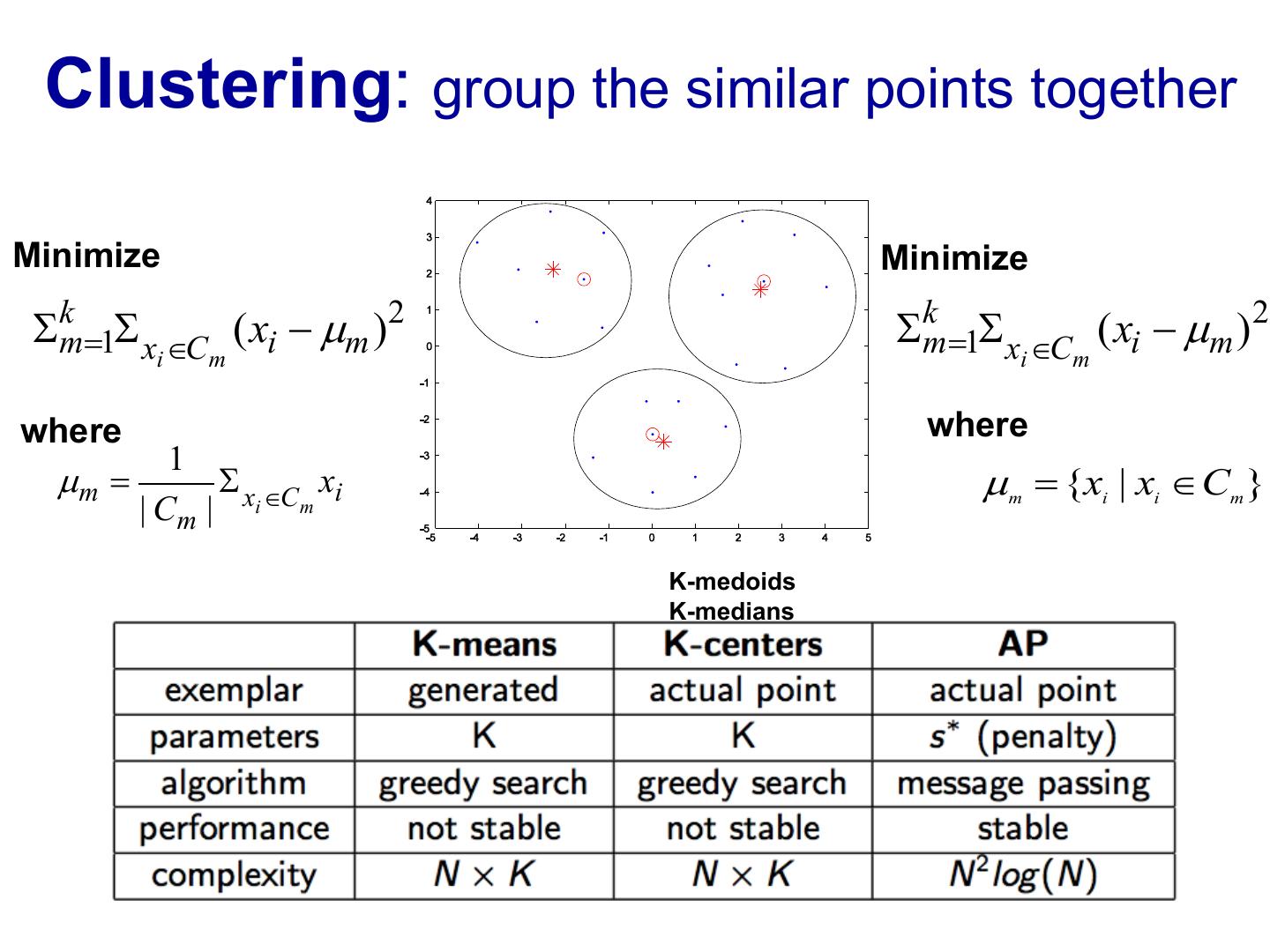
5 . Clustering: group the similar points together Minimize Minimize Skm=1S x ÎC ( xi - µm )2 Skm=1S x ÎC ( xi - µm )2 i m i m where where 1 µm = S x ÎC xi µm = {xi | xi Î Cm } | Cm | i m K-medoids K-medians
6 . Inspired by greedy k-medoids Data to cluster: The likelihood of belong to the cluster with center is the Bayesian prior probability that is a cluster center The responsibility of k-th component generating xi Assign xi with center si Choose a new center
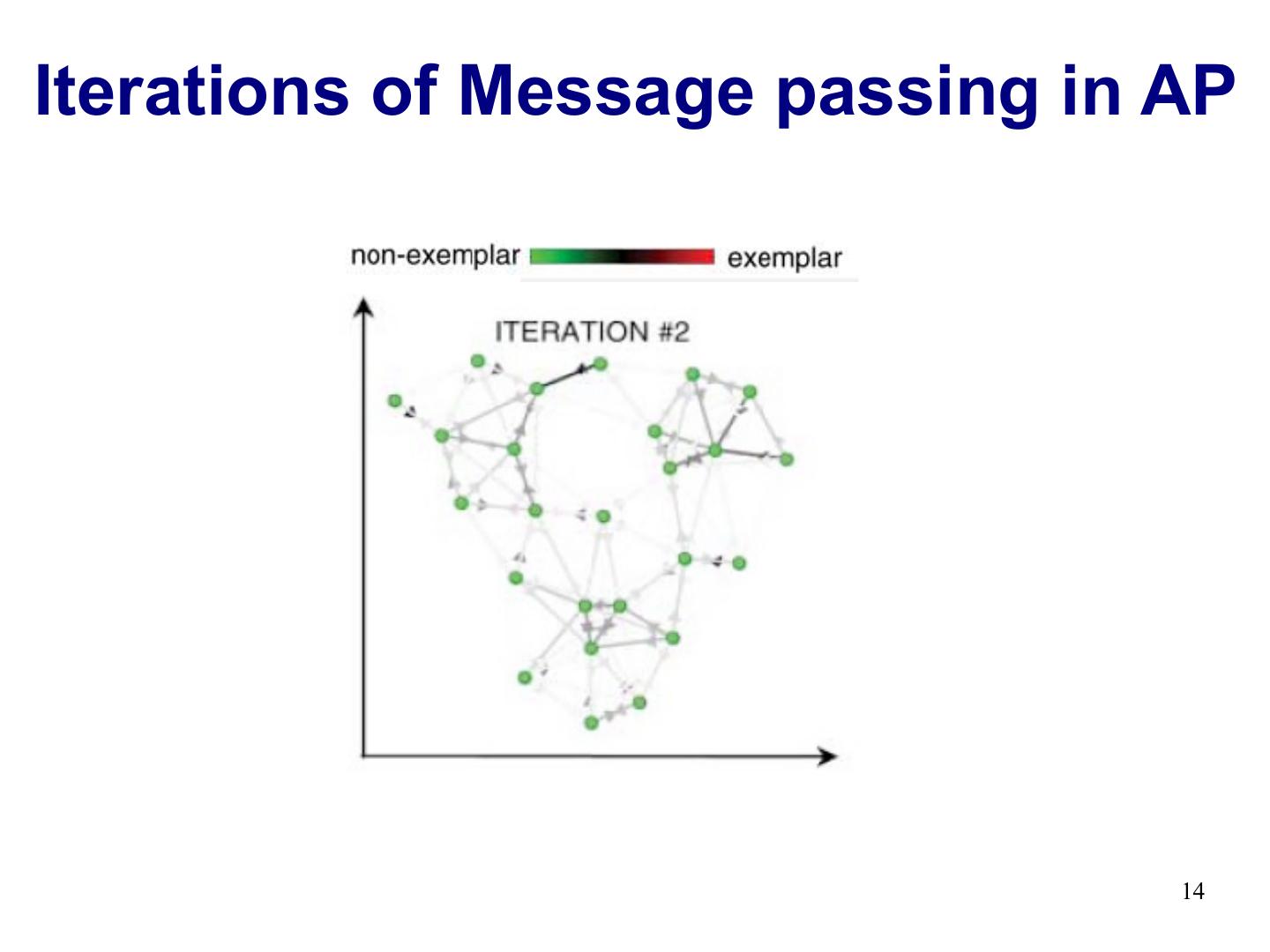
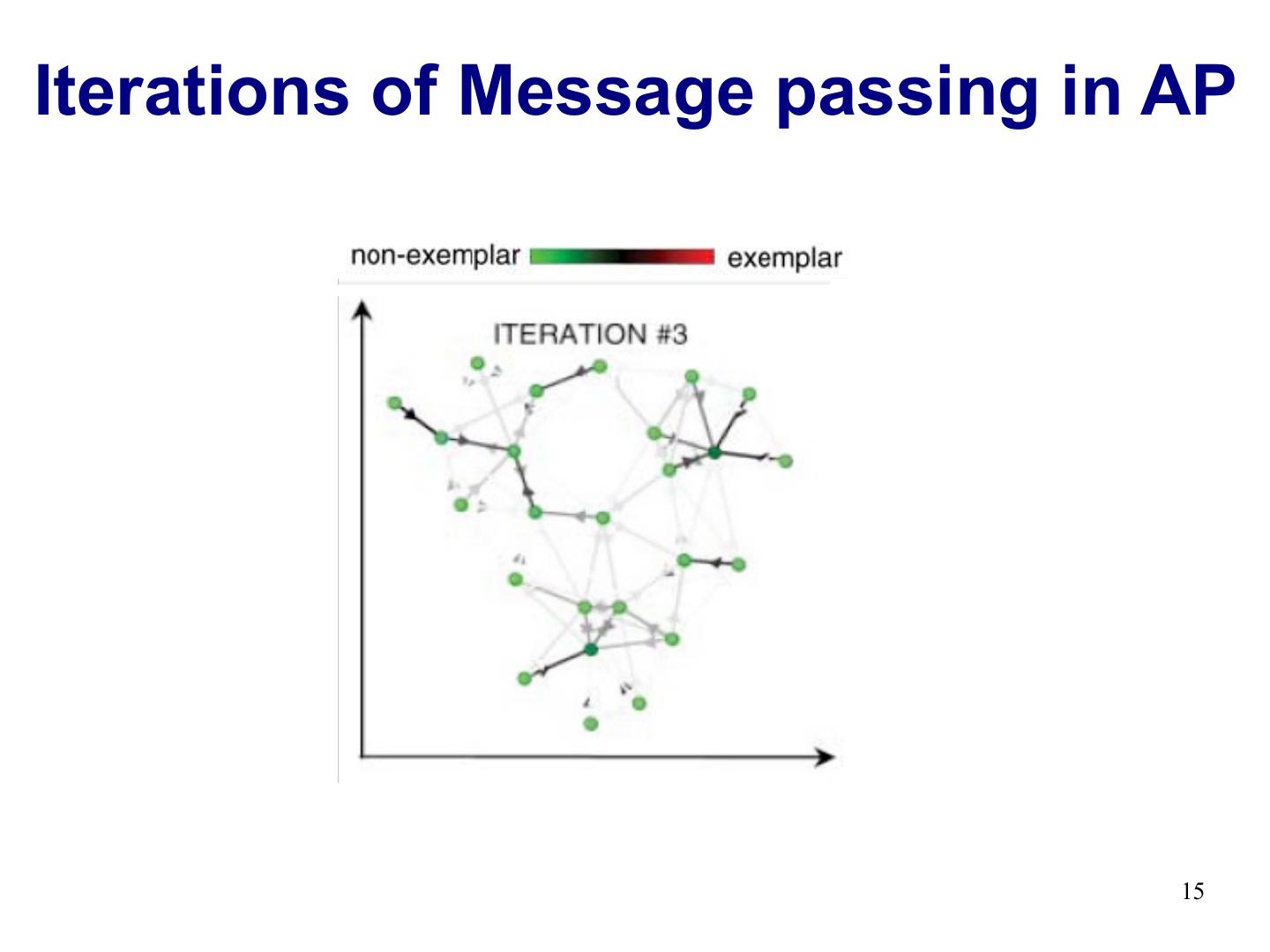
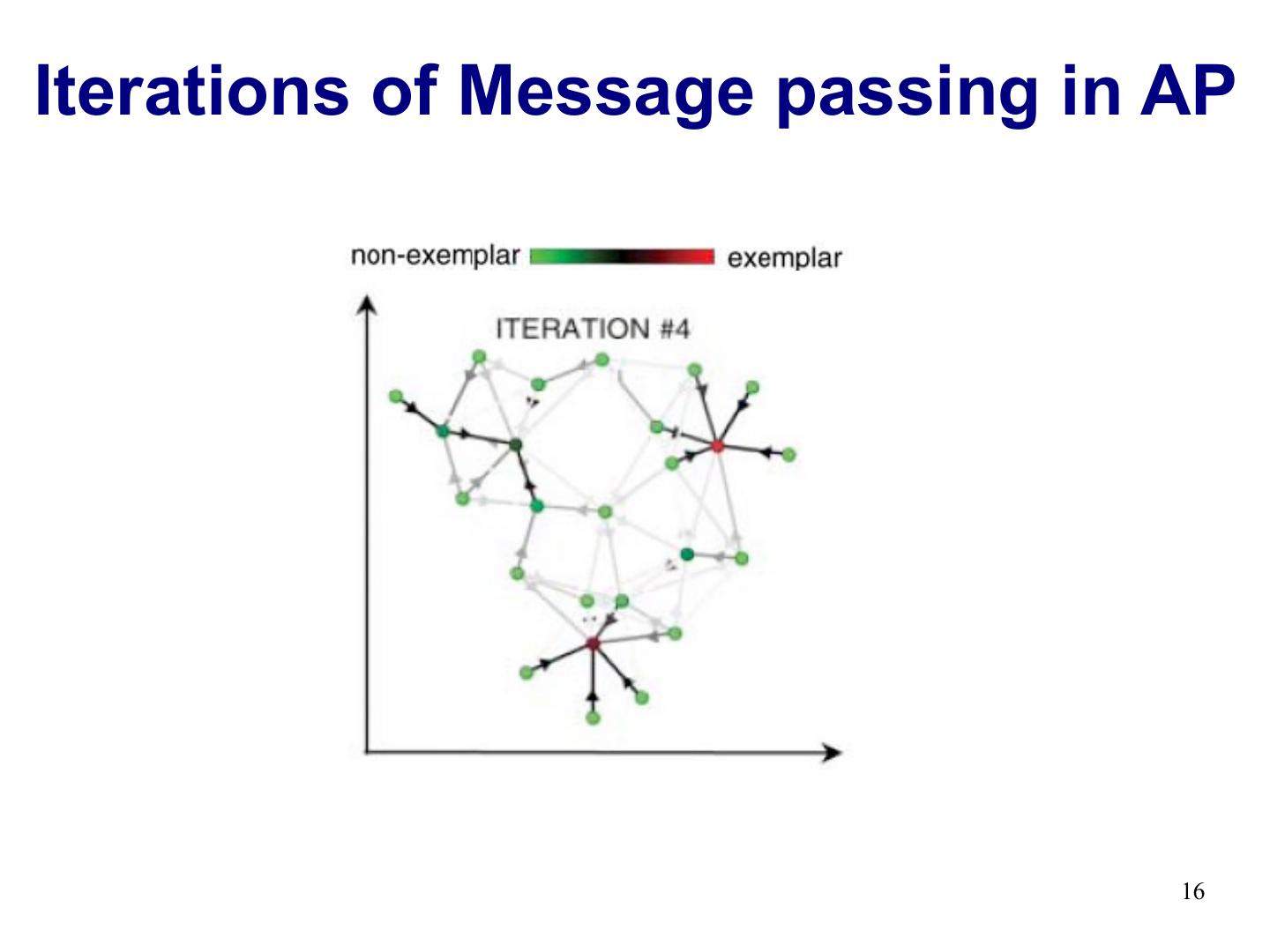
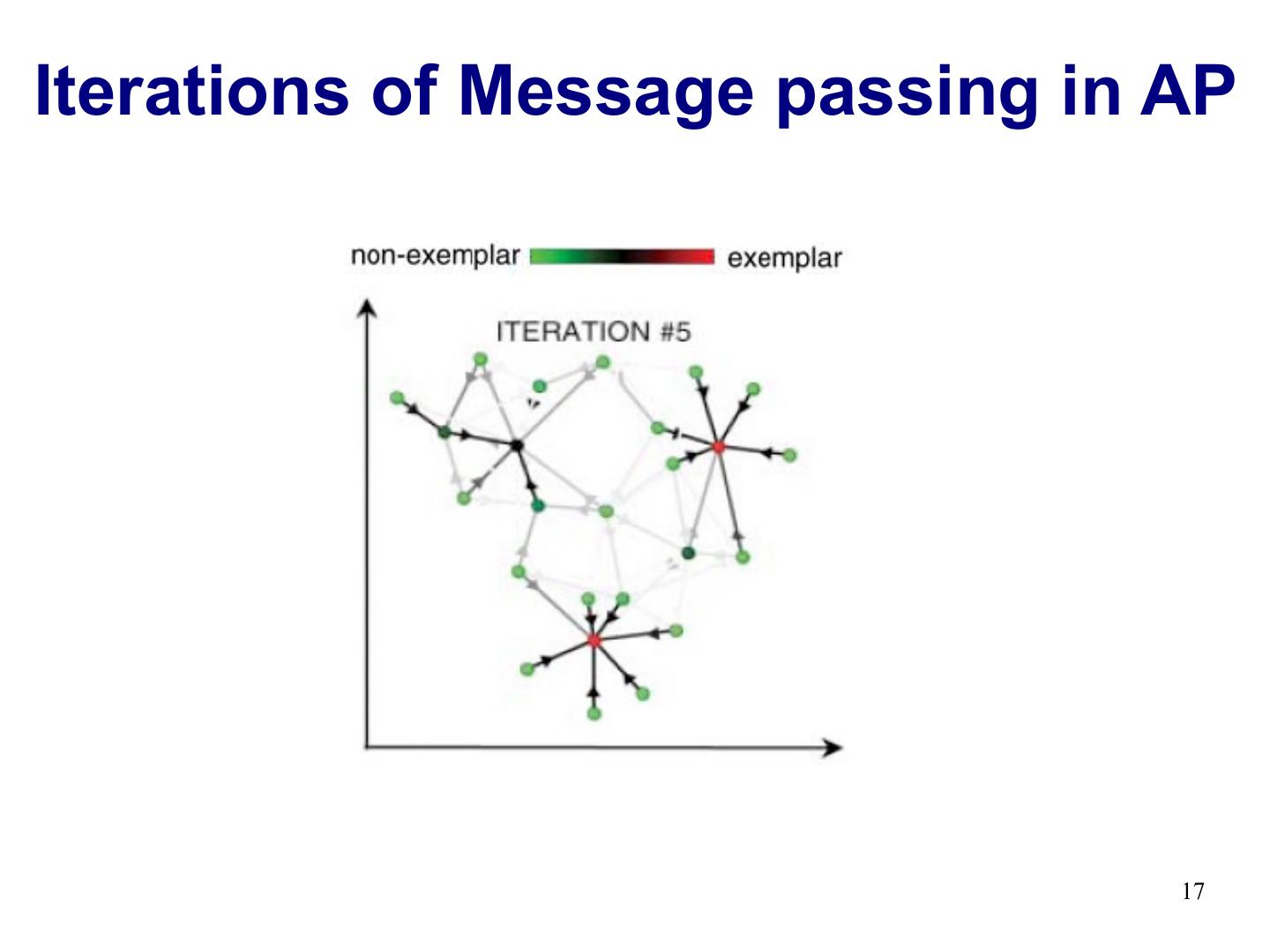
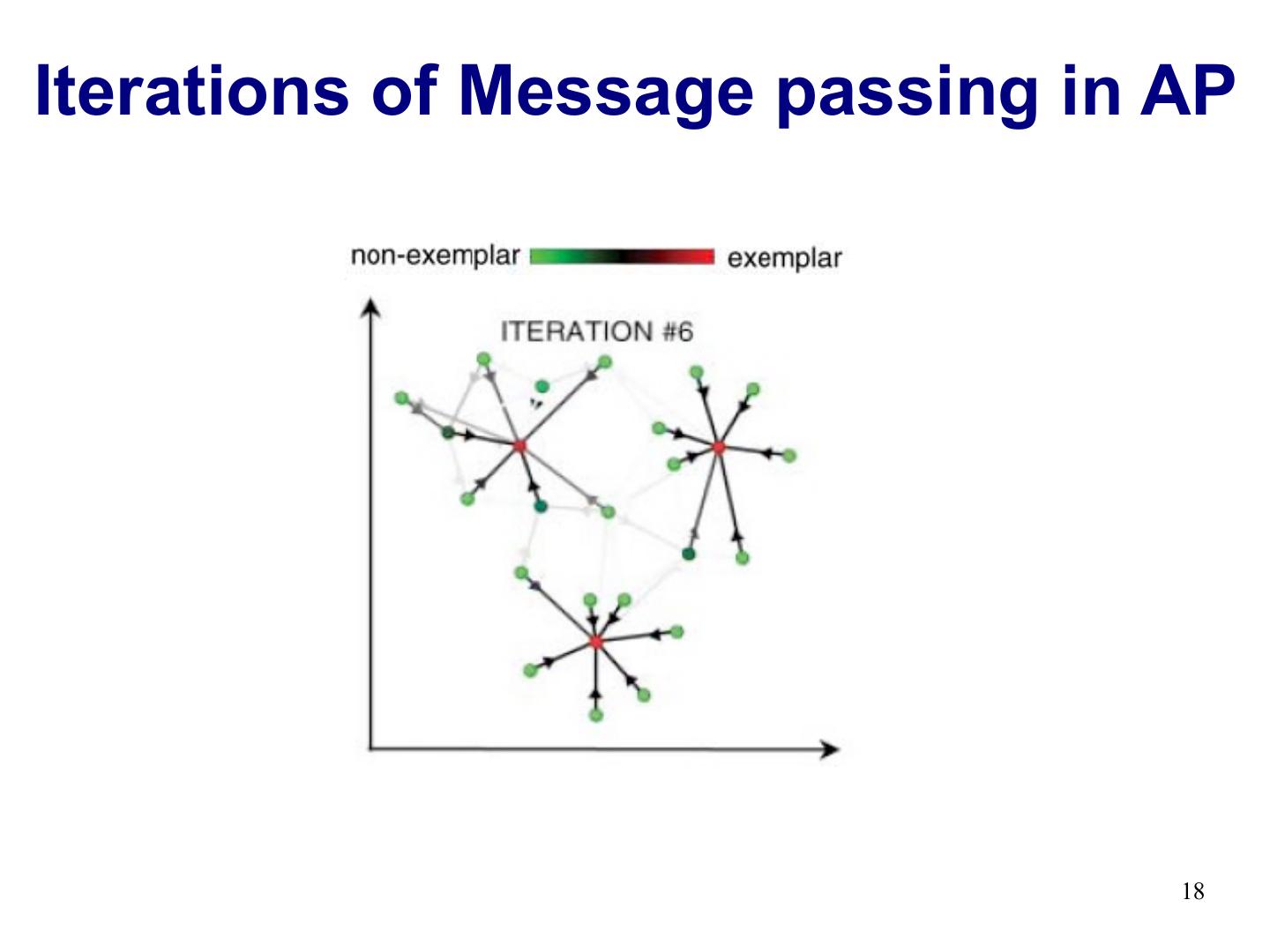
7 .Understanding the process Message sent from xi to each center/exemplar: preference to be with each exemplar Hard decision for cluster centers/exemplars Introduce: “availabilities”, which is sent from exemplars to other points, and provides soft evidence of the preference for each exemplar to be available as a center for each point
8 .The method presented in NIPS‘05 • Responsibilities are computed using likelihoods and availabilities • Availabilities are computed using responsibilities, recursively Affinities 8
9 .Interpretation by Factor Graph is the index of the exemplar for Should not be empty with a single exemplar Constraints: An exemplar must select itself as exemplar Objective function is 9
10 .Input and Output of AP in Science07 Preference (prior) 10
11 .AP: a message passing algorithm 11
12 .Iterations of Message passing in AP 12
13 .Iterations of Message passing in AP 13
14 .Iterations of Message passing in AP 14
15 .Iterations of Message passing in AP 15
16 .Iterations of Message passing in AP 16
17 .Iterations of Message passing in AP 17
18 .Iterations of Message passing in AP 18
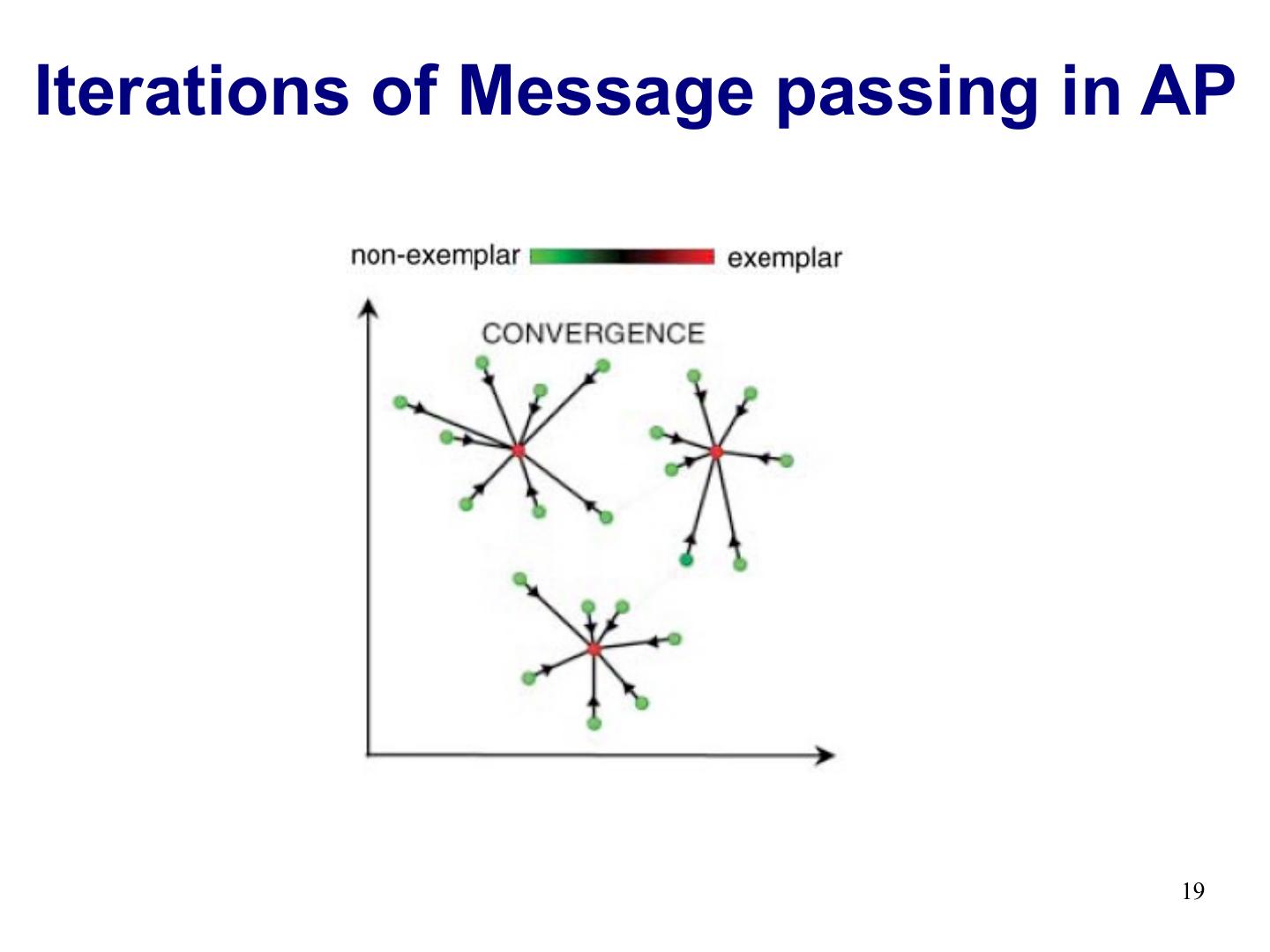
19 .Iterations of Message passing in AP 19
20 .Summary AP Xiangliang Zhang, KAUST CS340: Data Mining 20
21 .Extensive study of AP 21
22 . Outline • Affinity Propagation (AP) [Frey and Dueck, Science, 2007] • Locally Linear Embedding (LLE) [Roweis and Saul, Science, 2000] 22
23 .Locally Linear Embedding (LLE) [Roweis and Saul, Science, 2000] Saul and Roweis. Think globally, fit locally: unsupervised learning of low dimensional manifolds. JMLR 2003 23
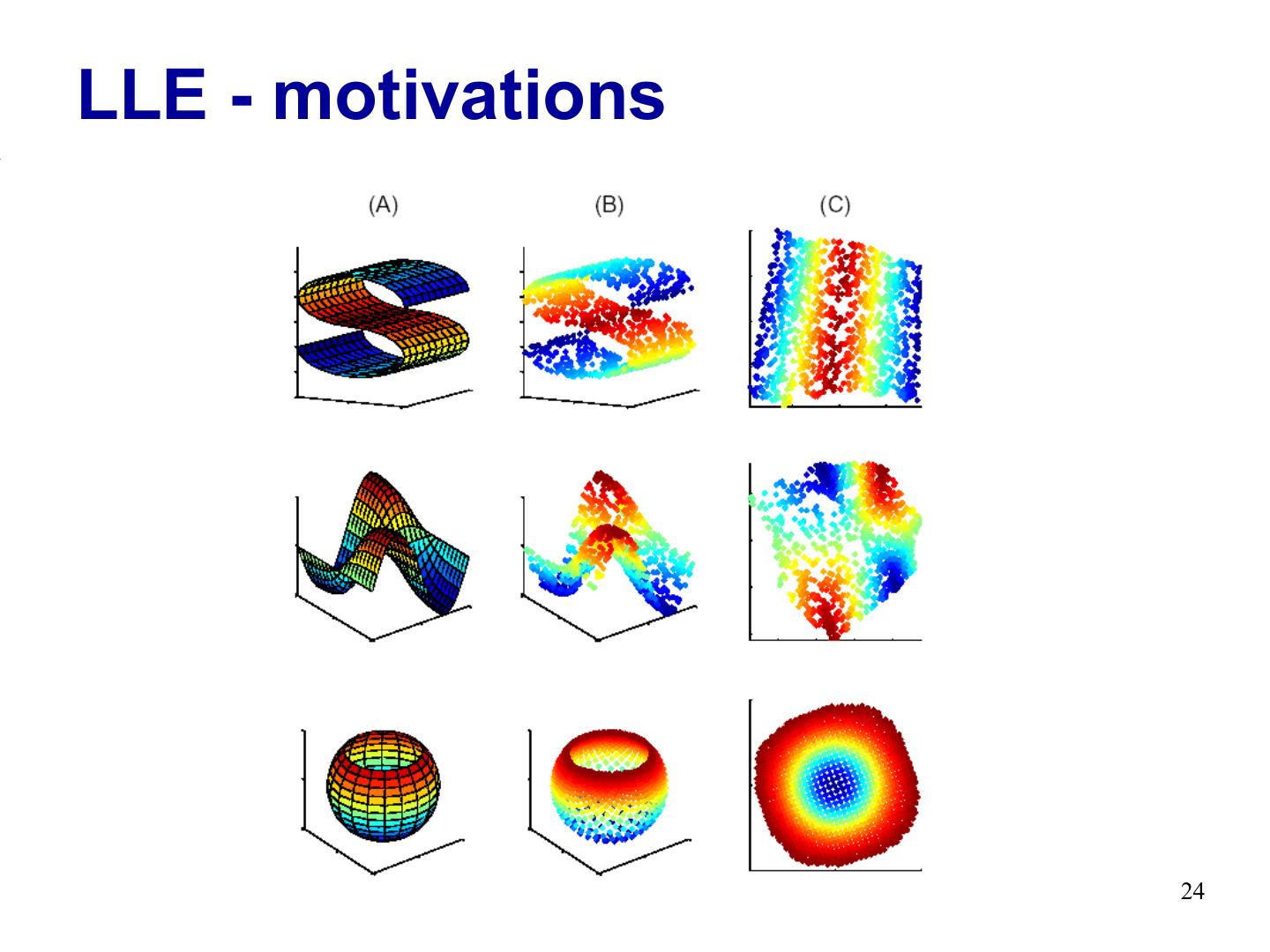
24 .LLE - motivations 24
25 . Inspired by MDS Multidimensional Scaling (MDS), find embedding of objects in low-dim space, preserving pairwise distance Given pairwise similarity Embedding to find Eliminate the need to estimate pairwise distances between widely separated data points? 25
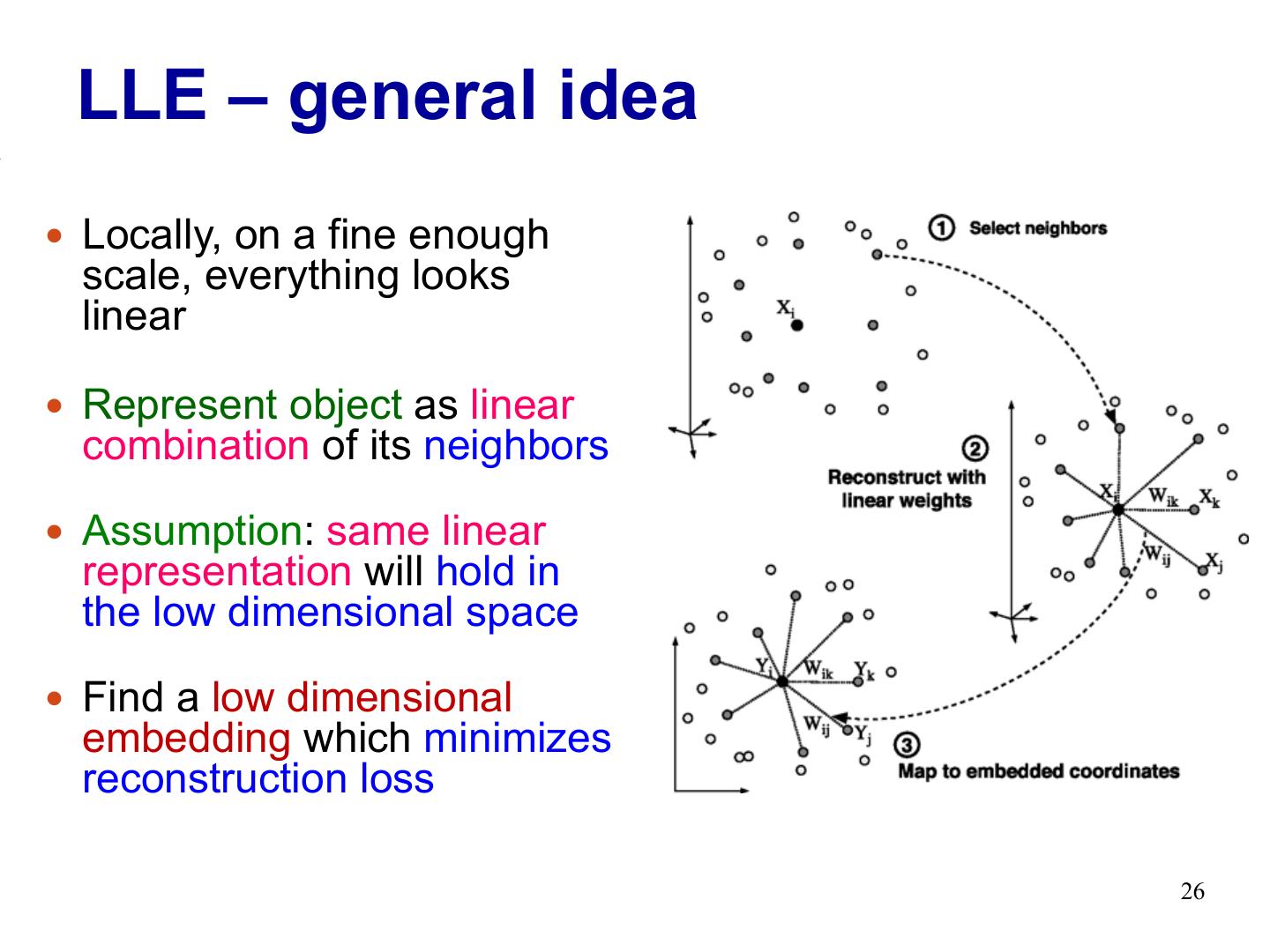
26 . LLE – general idea Locally, on a fine enough scale, everything looks linear Represent object as linear combination of its neighbors Assumption: same linear representation will hold in the low dimensional space Find a low dimensional embedding which minimizes reconstruction loss 26
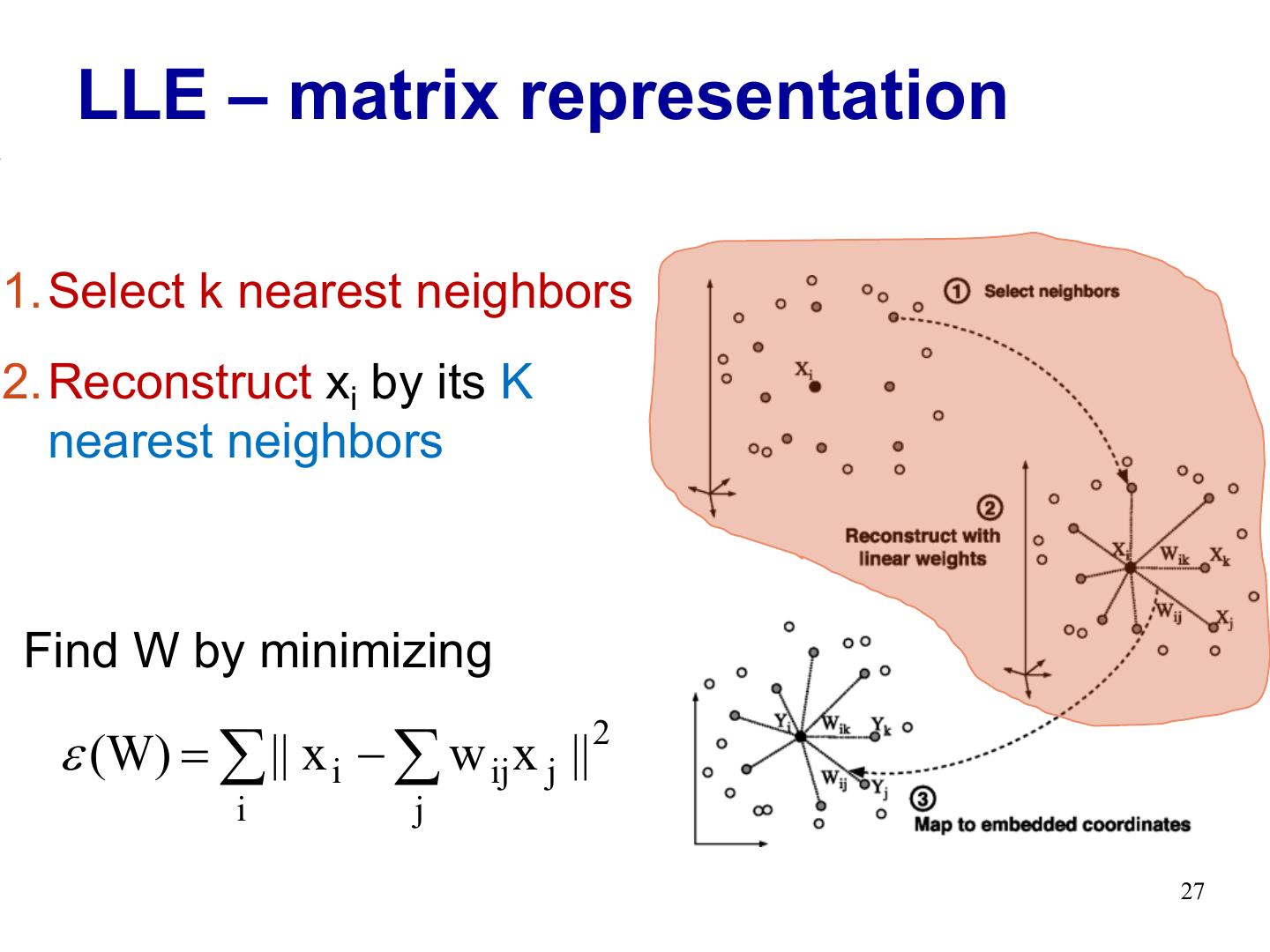
27 . LLE – matrix representation 1.Select k nearest neighbors 2.Reconstruct xi by its K nearest neighbors Find W by minimizing e (W) = å || x i - å w ij x j || 2 i j 27
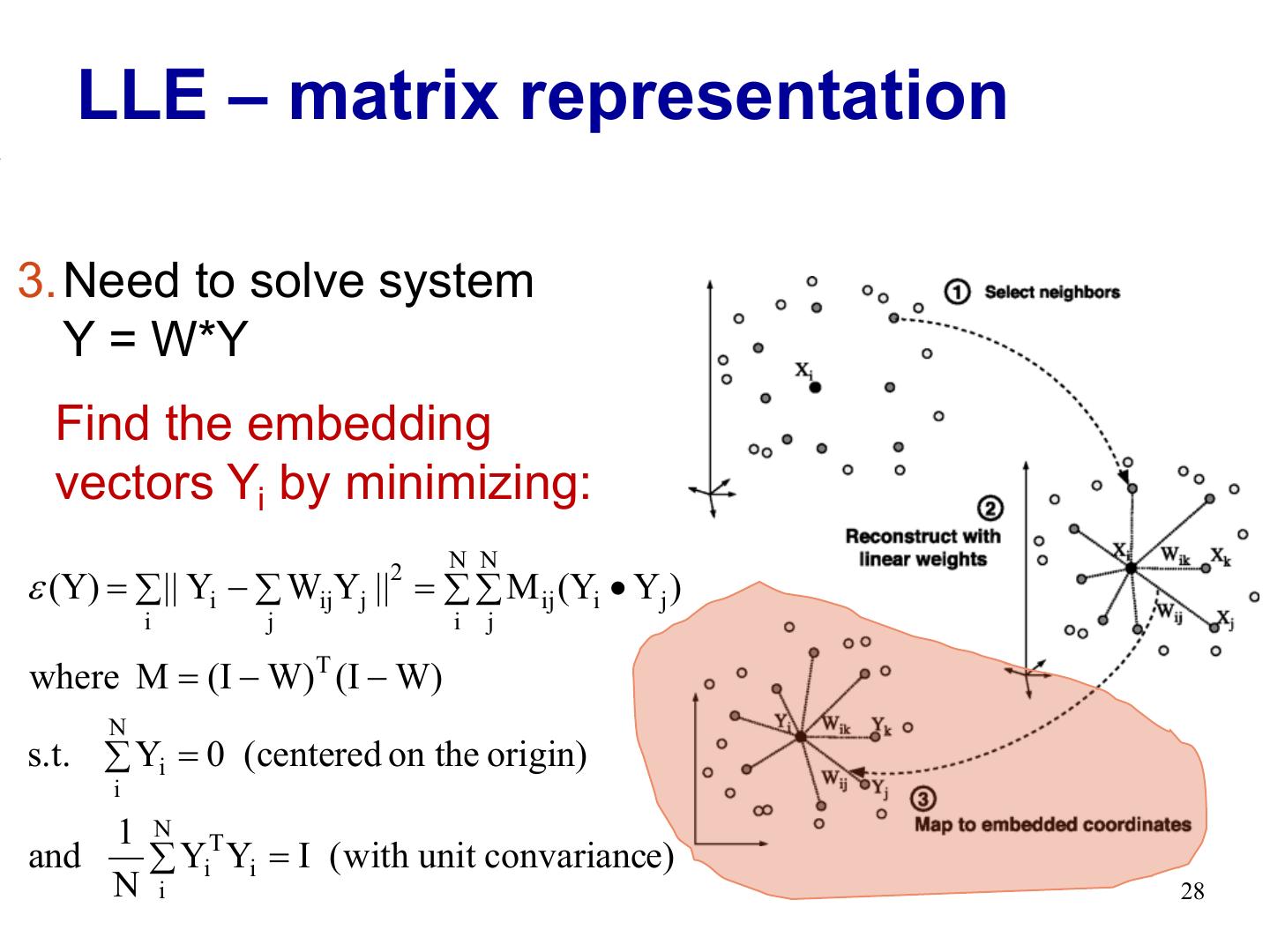
28 . LLE – matrix representation 3.Need to solve system Y = W*Y Find the embedding vectors Yi by minimizing: 2 N N e (Y) = å || Yi - å WijYj || = å å M ij (Yi • Yj ) i j i j where M = (I - W)T (I - W) N s.t. å Yi = 0 (centered on the origin) i 1 N T and å Yi Yi = I ( with unit convariance) N i 28
29 . LLE – algorithm summary 1. Find k nearest neighbors in X space 2. Solve for reconstruction weights W C-11 w= where C jk = ( x - h j )T ( x - h k ), and h j is one of x' s K nearest neighbors 1T C-11 3. Compute embedding coordinates Y using weights W: Create a sparse matrix M = (I-W)T(I-W) Set Y to be the eigenvectors corresponding to the bottom d non-zero eigenvectors of M 29