- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
计算机视觉:机器学习速成班
展开查看详情
1 .Machine Learning Crash Course Computer Vision Jia-Bin Huang, Virginia Tech Many slides from D. Hoiem, J. Hays
2 .Administrative stuffs HW 4 Due 11:59pm on Wed, November 2 nd
3 .What is a category? Why would we want to put an image in one? Many different ways to categorize To predict, describe, interact. To organize.
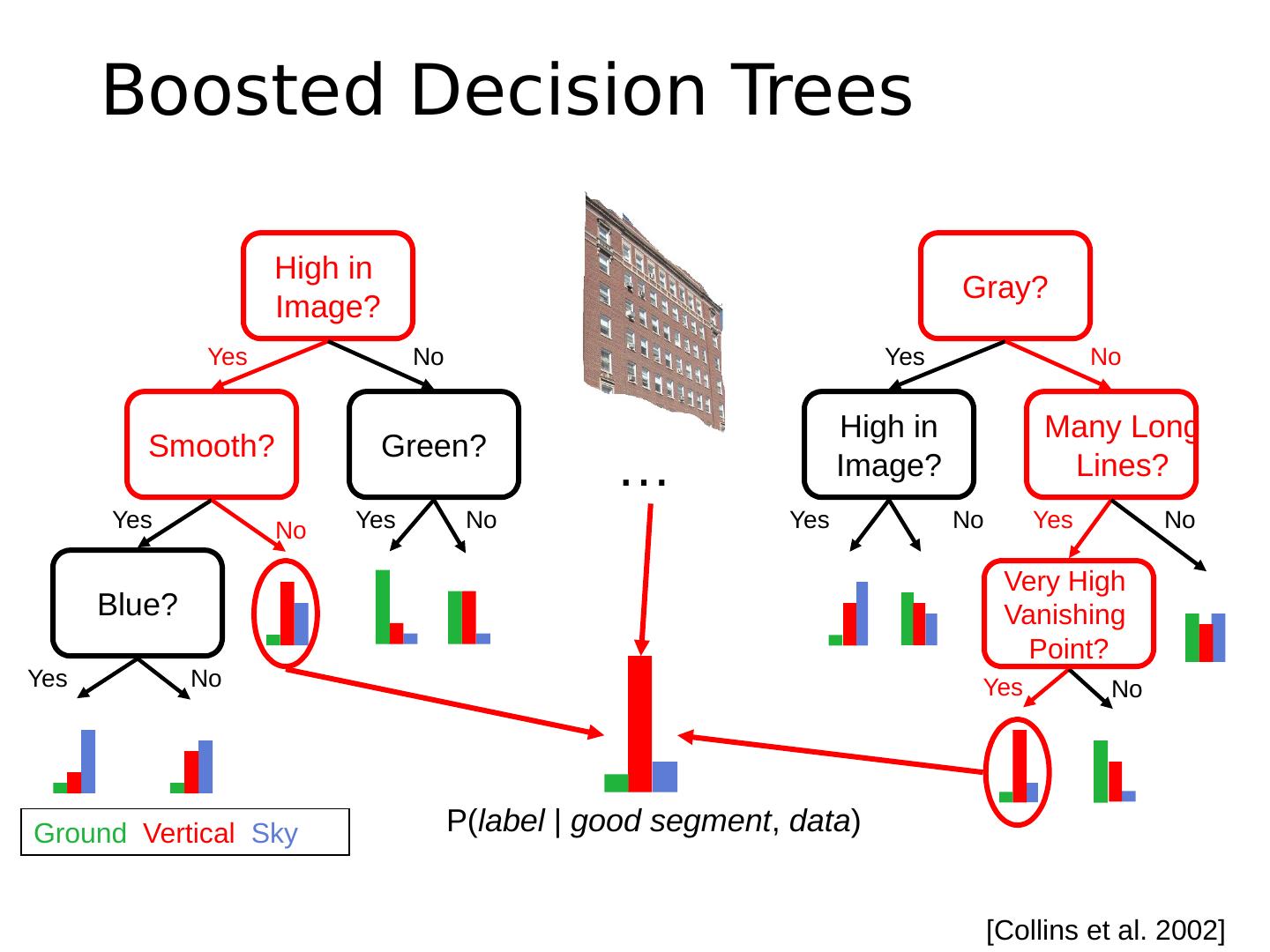
4 .Examples of Categorization in Vision Part or object detection E.g., for each window: face or non-face? Scene categorization Indoor vs. outdoor, urban, forest, kitchen, etc. Action recognition Picking up vs. sitting down vs. standing … Emotion recognition Region classification Label pixels into different object/surface categories Boundary classification Boundary vs. non-boundary Etc , etc.
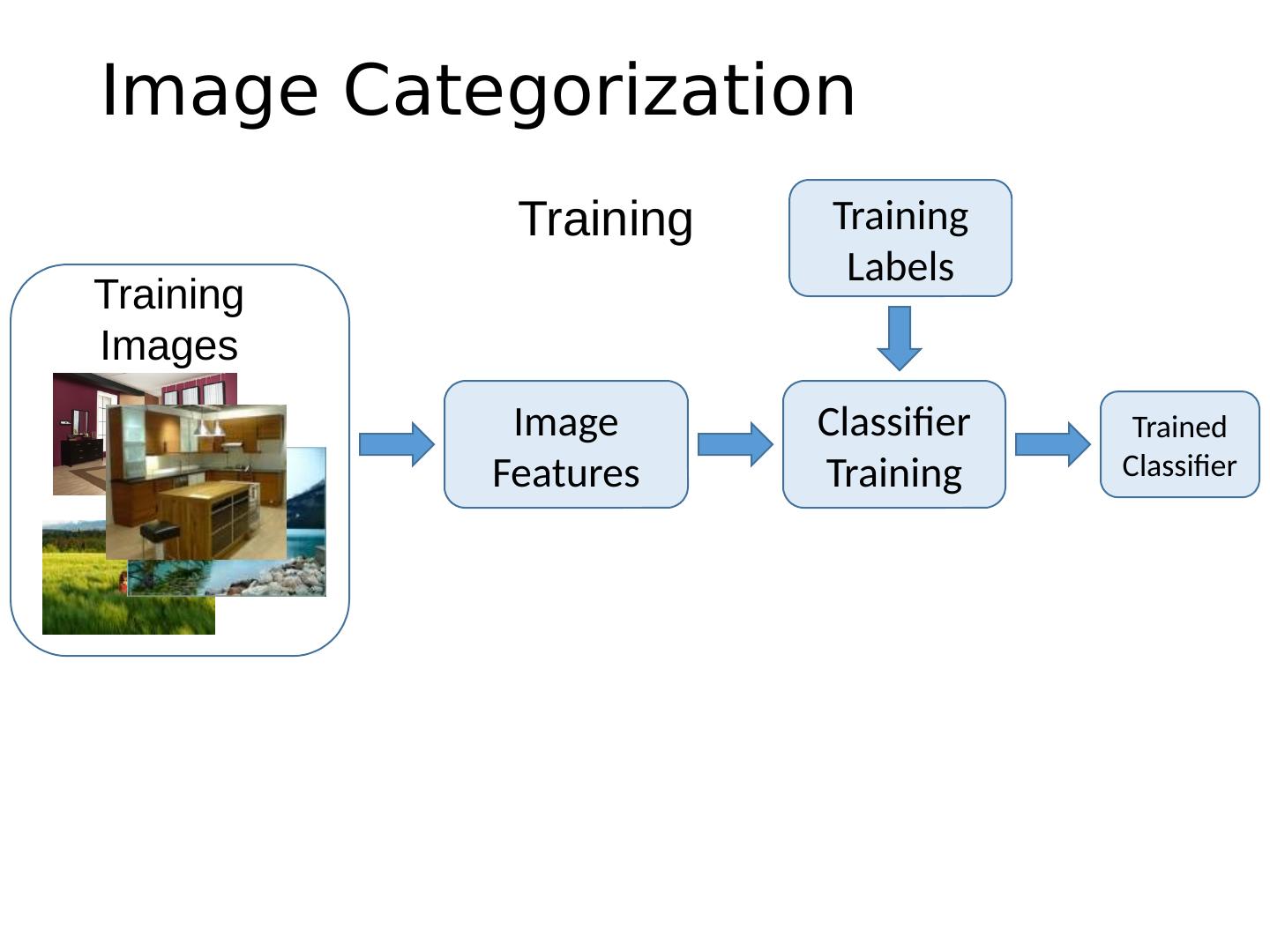
5 .Image Categorization Training Labels Training Images Classifier Training Training Image Features Trained Classifier
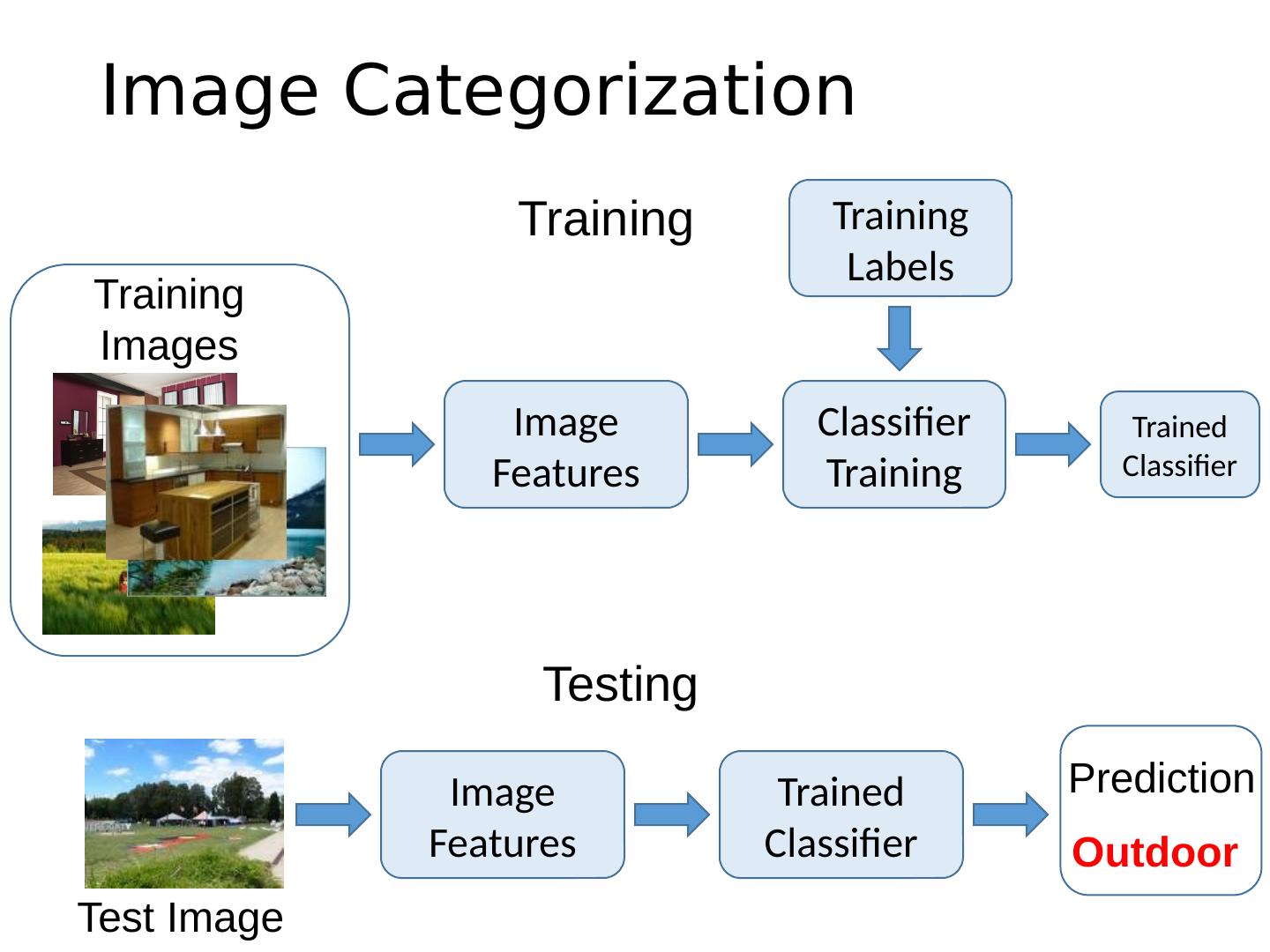
6 .Image Categorization Training Labels Training Images Classifier Training Training Image Features Image Features Testing Test Image Trained Classifier Trained Classifier Outdoor Prediction
7 .Feature design is paramount Most features can be thought of as templates, histograms (counts), or combinations Think about the right features for the problem Coverage Concision Directness
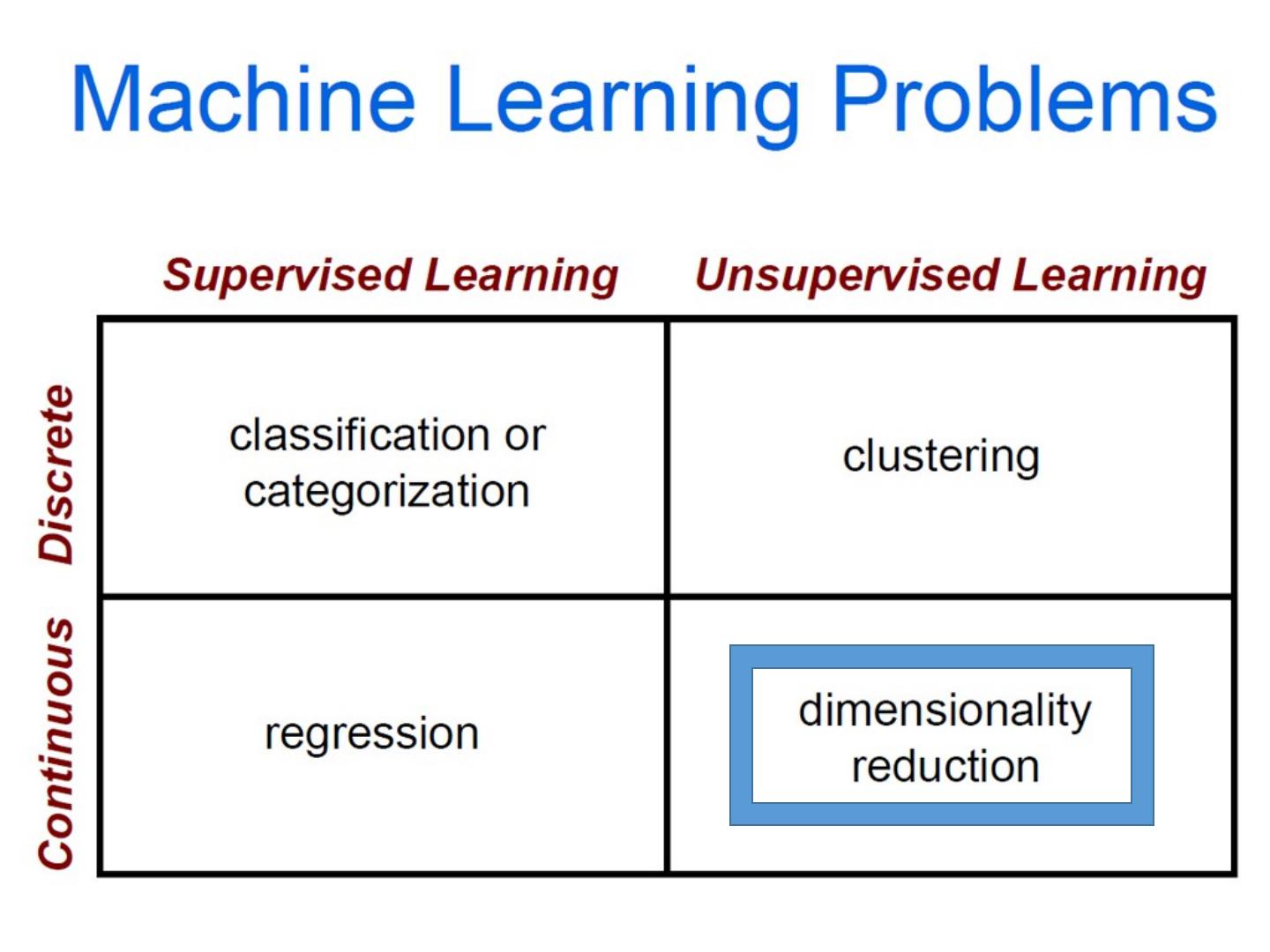
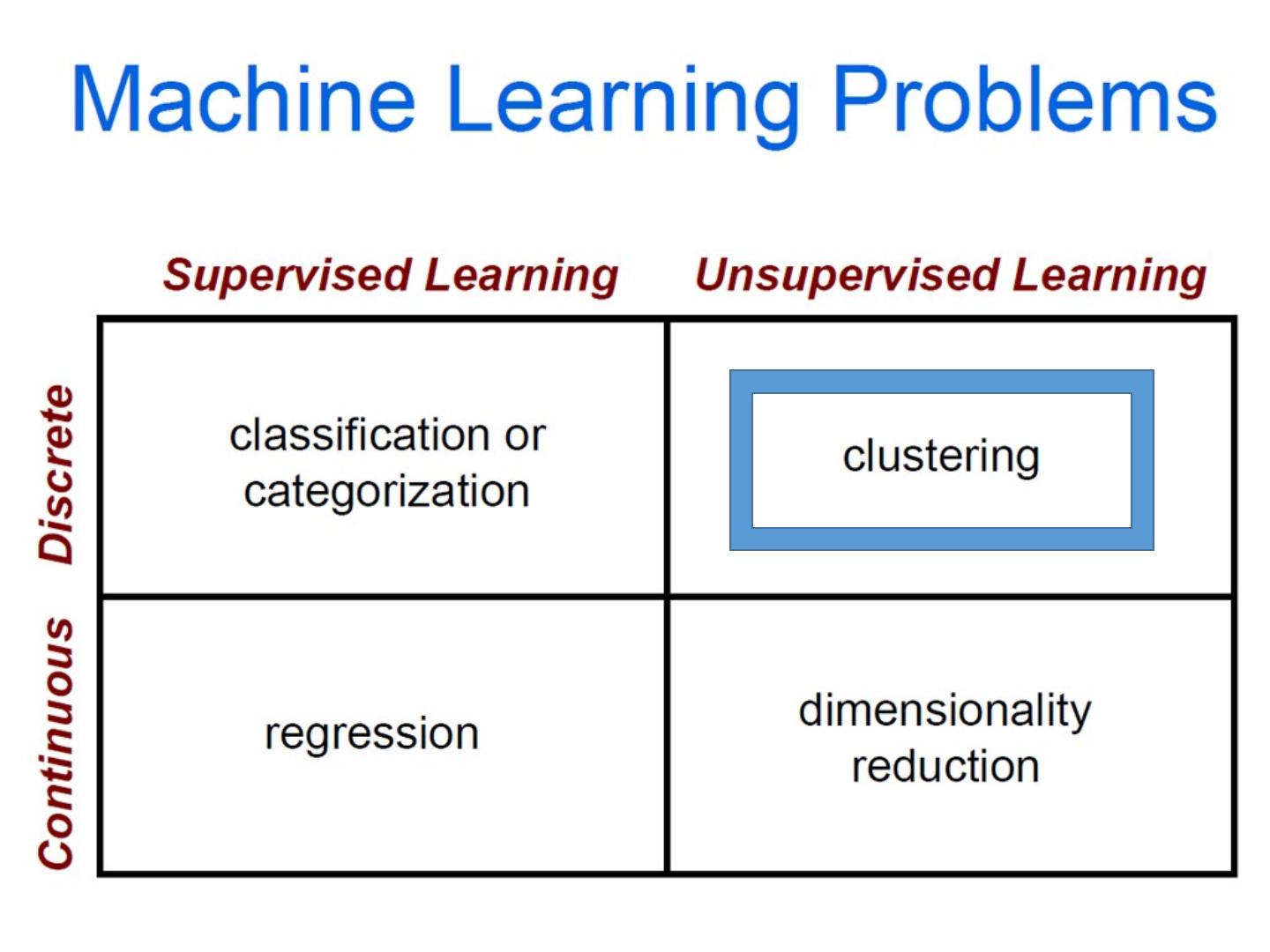
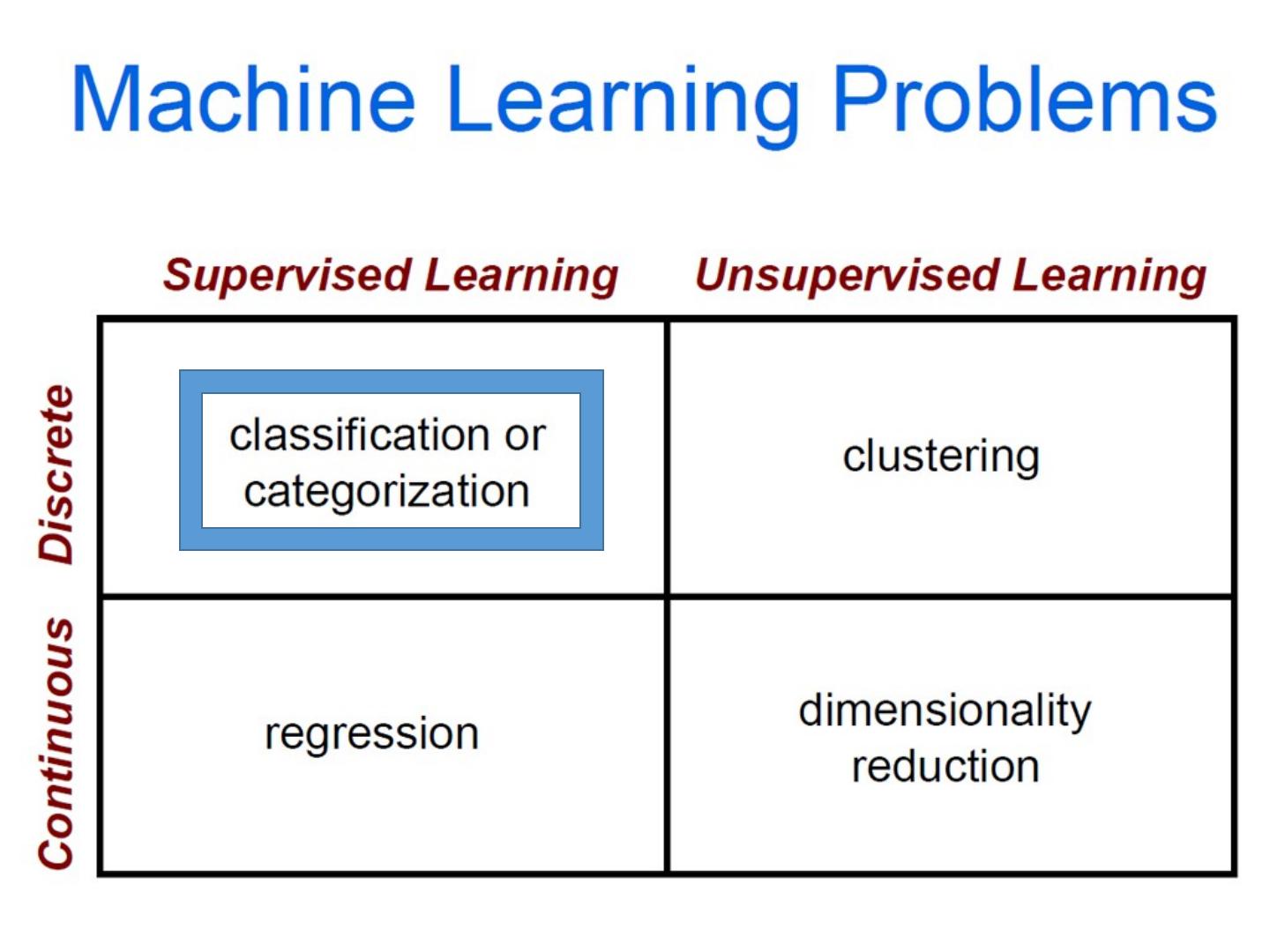
8 .Today’s class: Machine Learning Machine learning overview U nsupervised Learning Dimensionality reduction Clustering Supervised Learning Classification Regression
9 .
10 .“ If you were a current computer science student what area would you start studying heavily ?” Answer: Machine Learning. “ The ultimate is computers that learn” Bill Gates, Reddit AMA “Machine learning is the next Internet” Tony Tether, Director, DARPA “Machine learning is today’s discontinuity” Jerry Yang, CEO, Yahoo (C) Dhruv Batra 10 Slide Credit: Pedro Domingos , Tom Mitchel, Tom Dietterich
11 .(C) Dhruv Batra 11
12 .Machine Learning: Making predictions or decisions from Data
13 .Resources Disclaimer: This overview will not cover statistical underpinnings of learning methods. We’ve looking at ML as a tool. ML related courses at Virginia Tech ECE 5424 / 4424 - CS 5824 / 4824 Introduction to Machine Learning CS 4804 Introduction to Artificial Intelligence ECE 6504 Neural Networks and Deep Learning External courses Machine Learning by Andrew Ng https:// www.coursera.org/learn/machine-learning Learning from Data by Yaser S. Abu-Mostafa https:// www.edx.org/course/learning-data-introductory-machine-caltechx-cs1156x
14 .Impact of Machine Learning Machine Learning is arguably the greatest export from computing to other scientific fields.
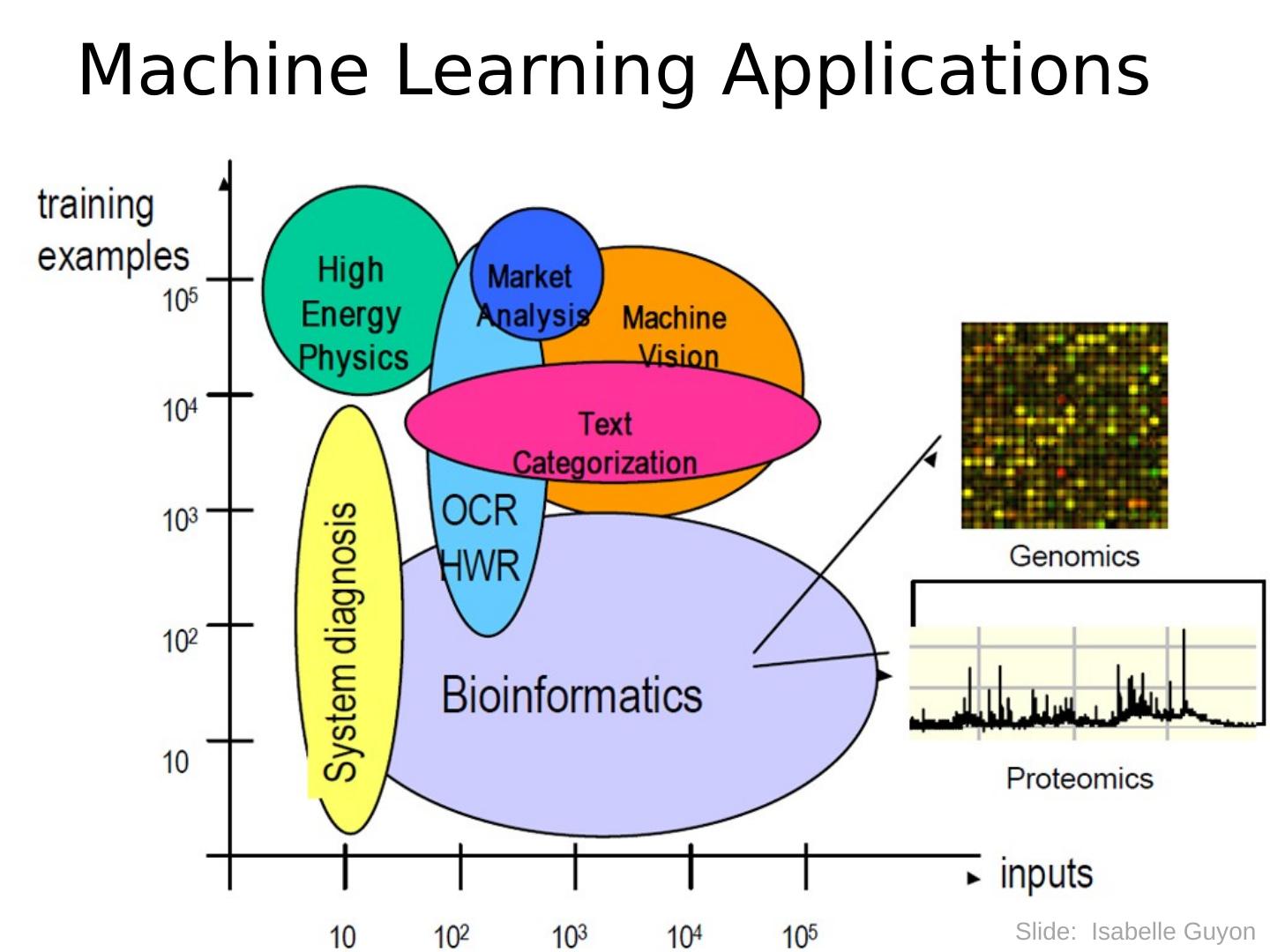
15 .Machine Learning Applications Slide: Isabelle Guyon
16 .Machine Learning Applications Slide: Isabelle Guyon
17 .Machine Learning Applications Slide: Isabelle Guyon
18 .Eigenfaces example Top eigenvectors: u 1 ,…u k Mean: μ
19 .Eigenfaces example Top eigenvectors: u 1 ,…u k Mean: μ
20 .Clustering Clustering: group together similar points and represent them with a single token Key Challenges: What makes two points/images/patches similar? How do we compute an overall grouping from pairwise similarities? Slide: Derek Hoiem
21 .Why do we cluster? Summarizing data Look at large amounts of data Patch-based compression or denoising Represent a large continuous vector with the cluster number Counting Histograms of texture, color, SIFT vectors Segmentation Separate the image into different regions Prediction Images in the same cluster may have the same labels Slide: Derek Hoiem
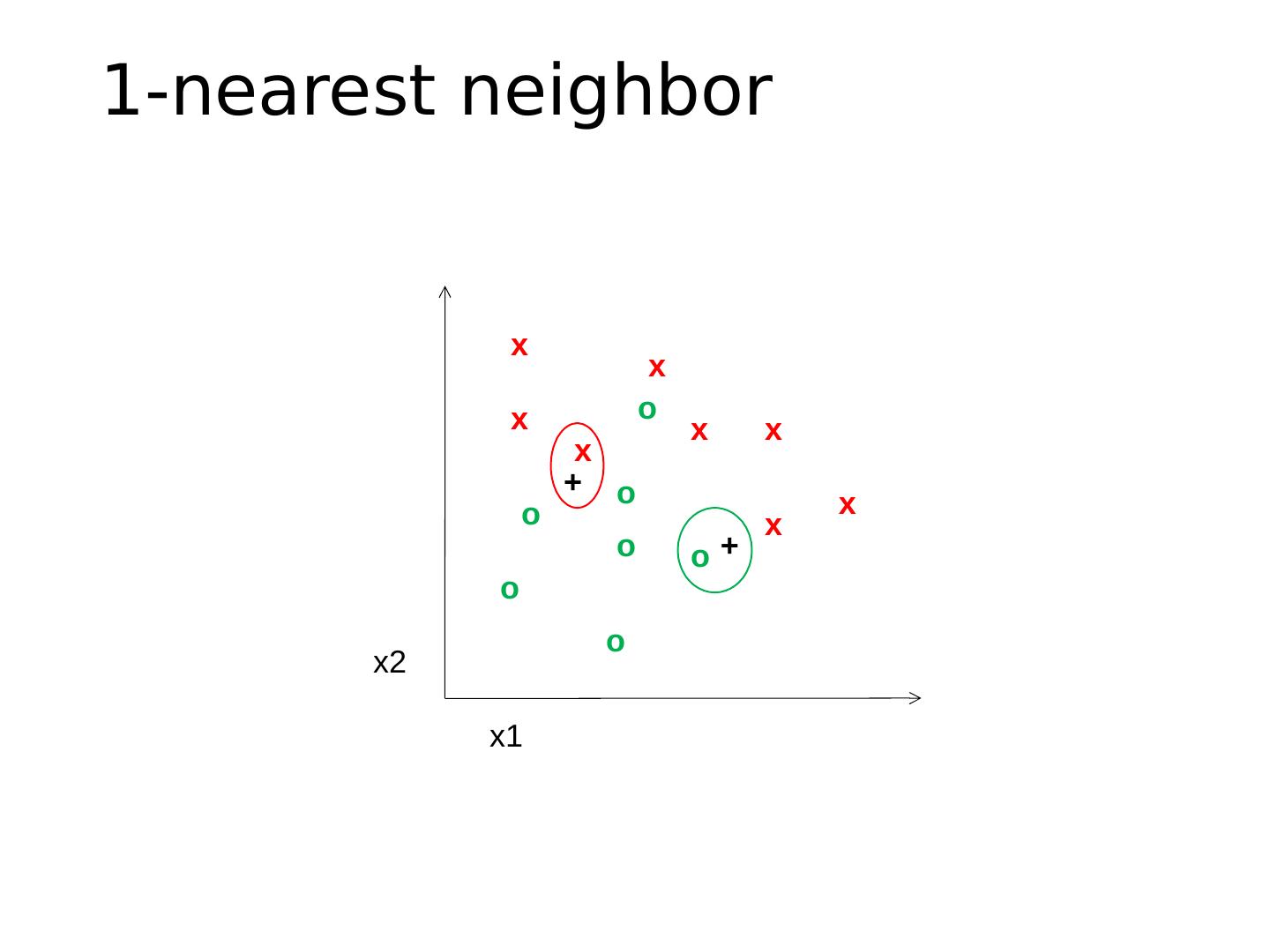
22 .How do we cluster? K-means Iteratively re-assign points to the nearest cluster center Agglomerative clustering Start with each point as its own cluster and iteratively merge the closest clusters Mean-shift clustering Estimate modes of pdf Spectral clustering Split the nodes in a graph based on assigned links with similarity weights Slide: Derek Hoiem
23 .How do we cluster? K-means Iteratively re-assign points to the nearest cluster center Agglomerative clustering Start with each point as its own cluster and iteratively merge the closest clusters Mean-shift clustering Estimate modes of pdf Spectral clustering Split the nodes in a graph based on assigned links with similarity weights Slide: Derek Hoiem
24 .The machine learning framework Apply a prediction function to a feature representation of the image to get the desired output: f( ) = “apple” f( ) = “tomato” f( ) = “cow” Slide credit: L. Lazebnik
25 .The machine learning framework y = f( x ) Training: given a training set of labeled examples {( x 1 ,y 1 ), …, ( x N ,y N )} , estimate the prediction function f by minimizing the prediction error on the training set Testing: apply f to a never before seen test example x and output the predicted value y = f( x ) output prediction function Image feature Slide credit: L. Lazebnik
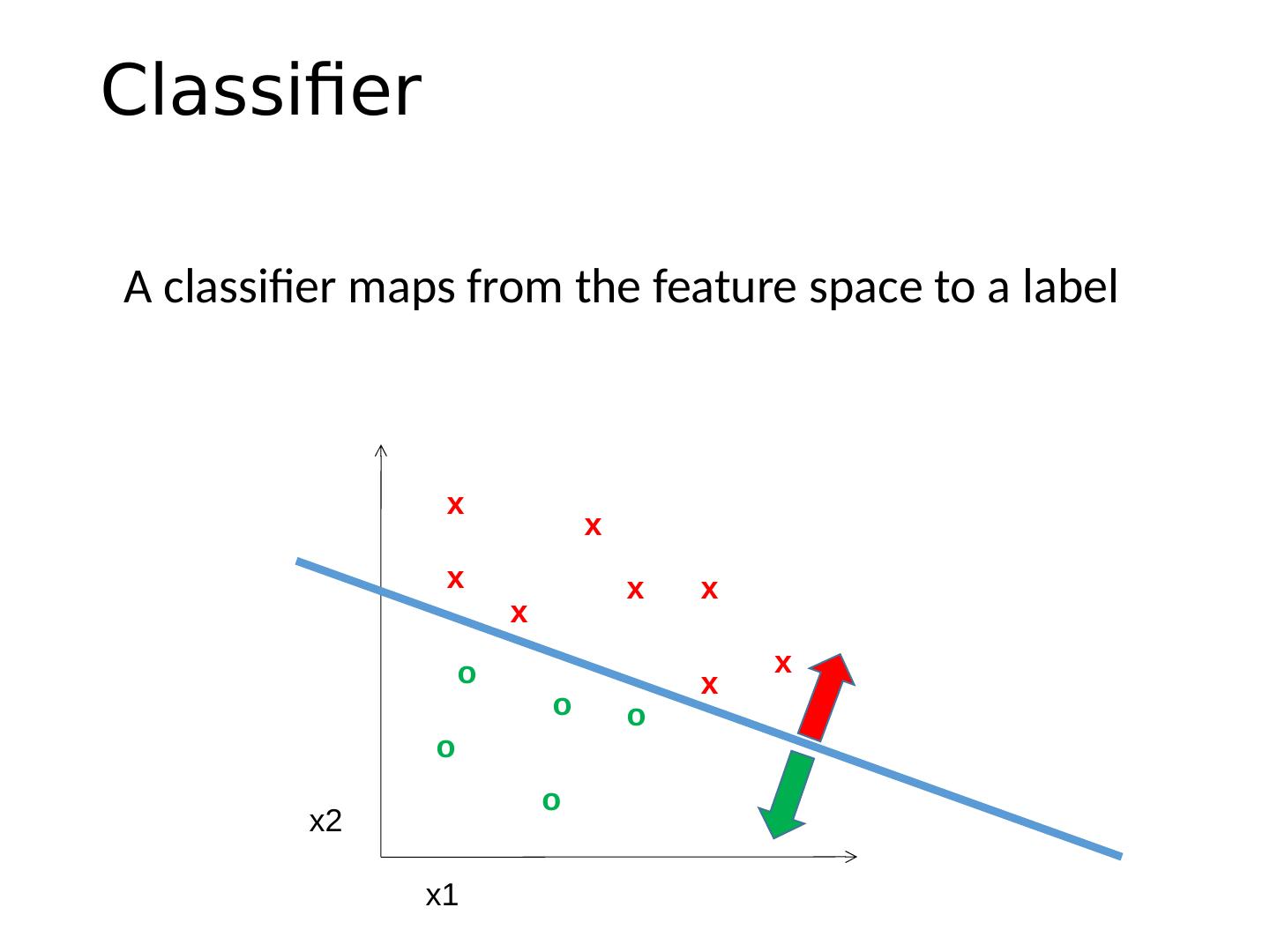
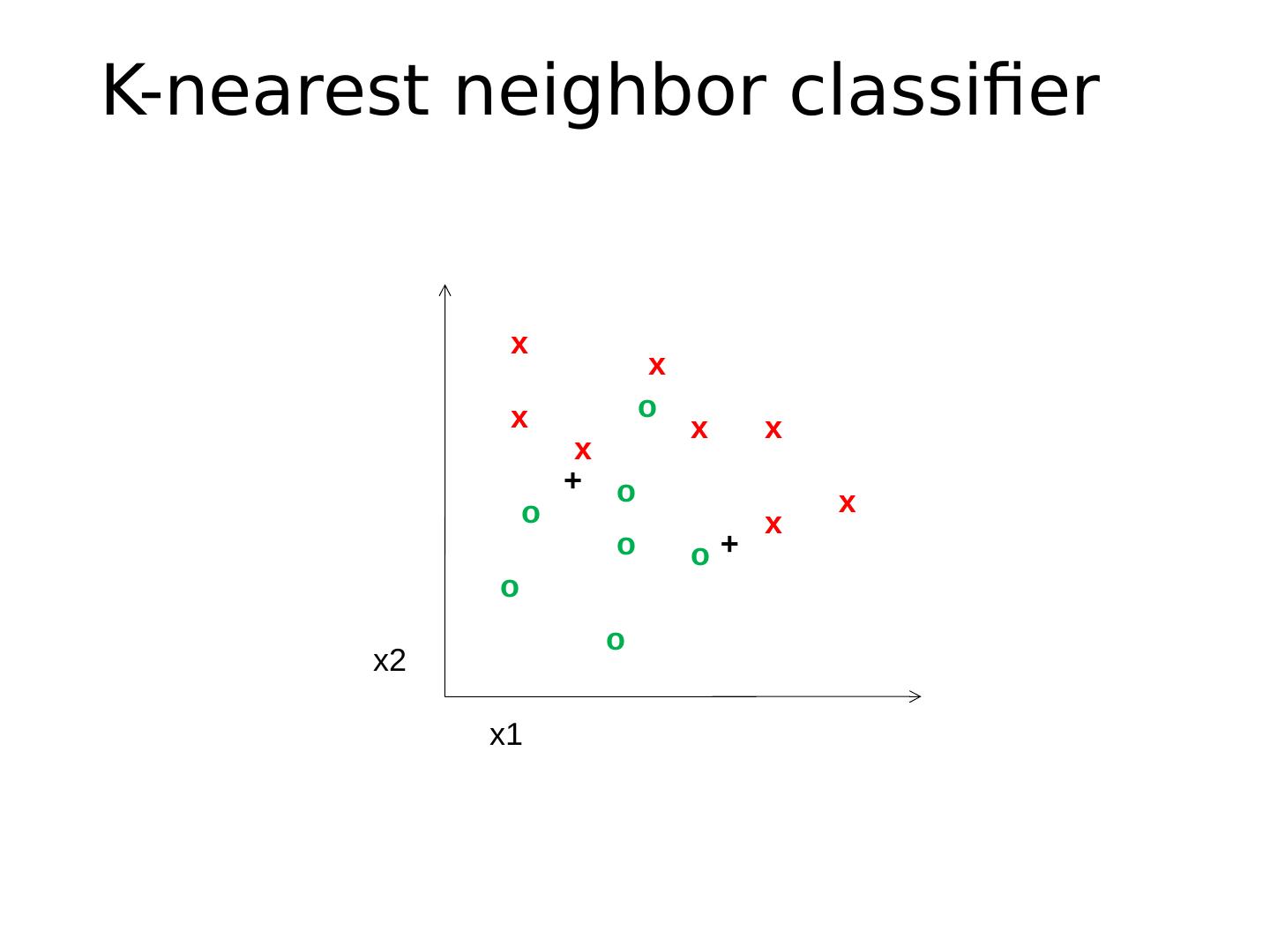
26 .Classifier A classifier maps from the feature space to a label x x x x x x x x o o o o o x2 x1
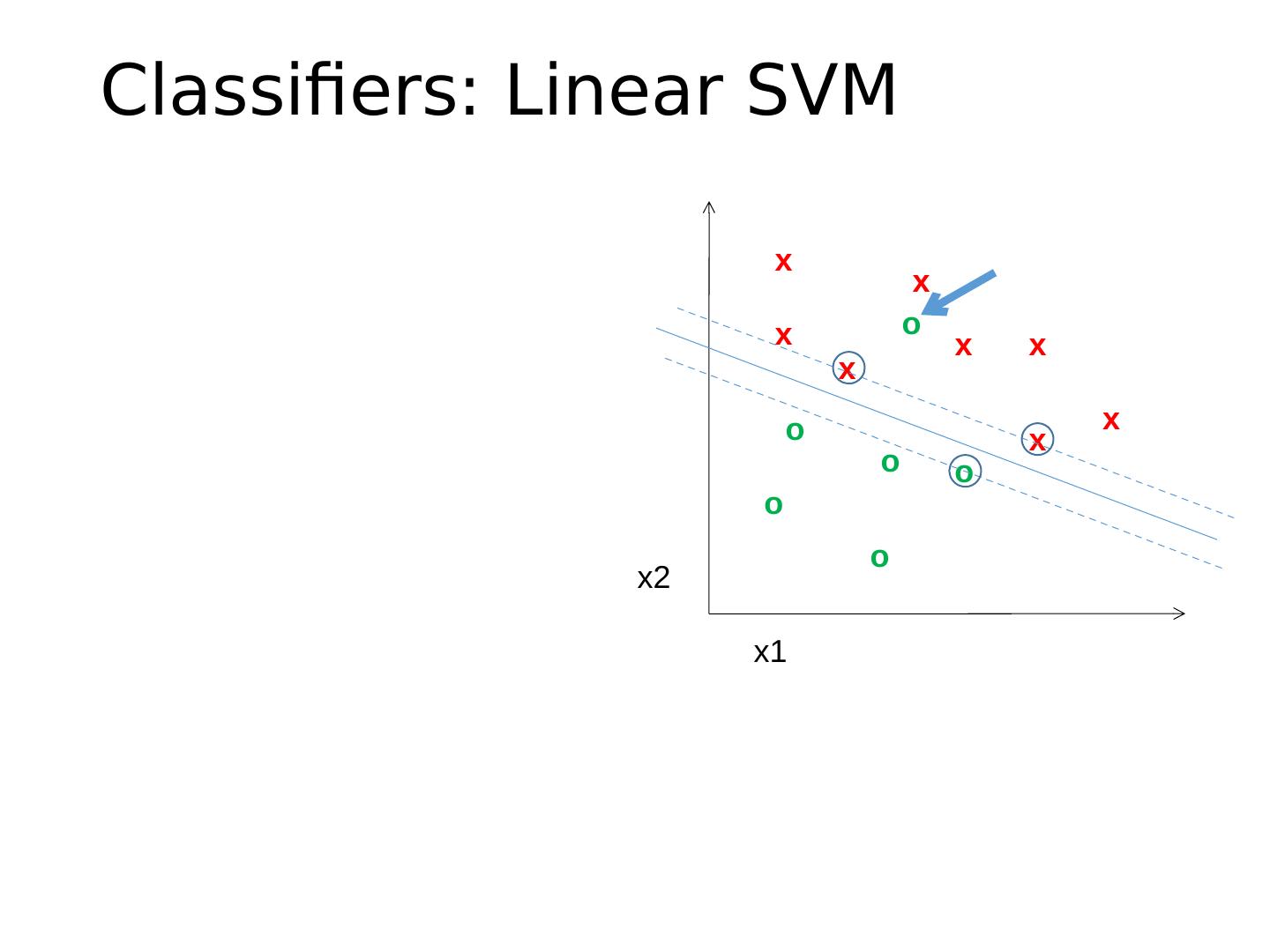
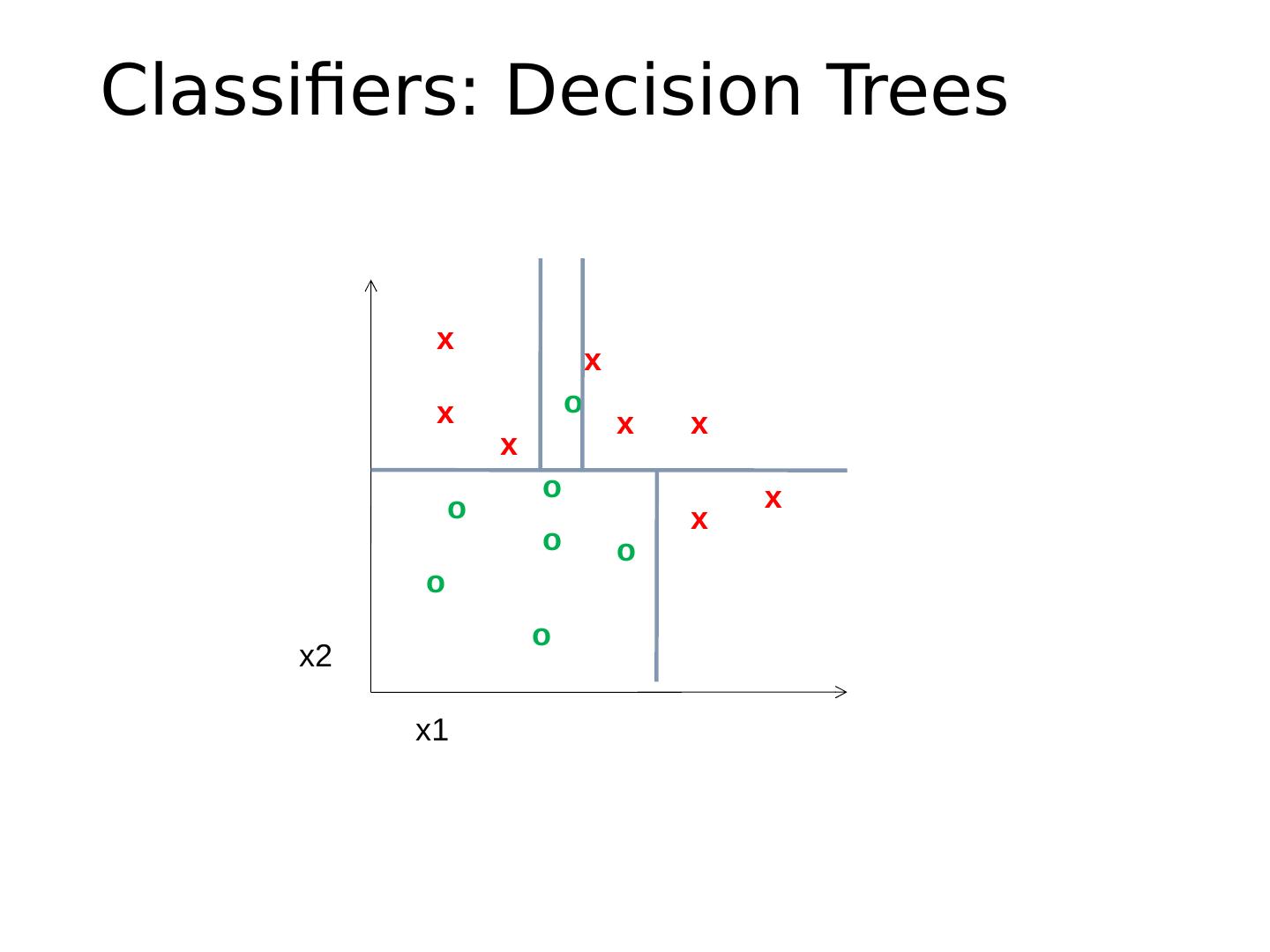
27 .Different types of classification Exemplar-based : transfer category labels from examples with most similar features What similarity function? What parameters? Linear classifier : confidence in positive label is a weighted sum of features What are the weights? Non-linear classifier : predictions based on more complex function of features What form does the classifier take? Parameters? Generative classifier : assign to the label that best explains the features (makes features most likely) What is the probability function and its parameters? Note: You can always fully design the classifier by hand, but usually this is too difficult. Typical solution: learn from training examples.
28 .One way to think about it… Training labels dictate that two examples are the same or different, in some sense Features and distance measures define visual similarity Goal of training is to learn feature weights or distance measures so that visual similarity predicts label similarity We want the simplest function that is confidently correct
29 .Exemplar-based Models Transfer the label(s) of the most similar training examples