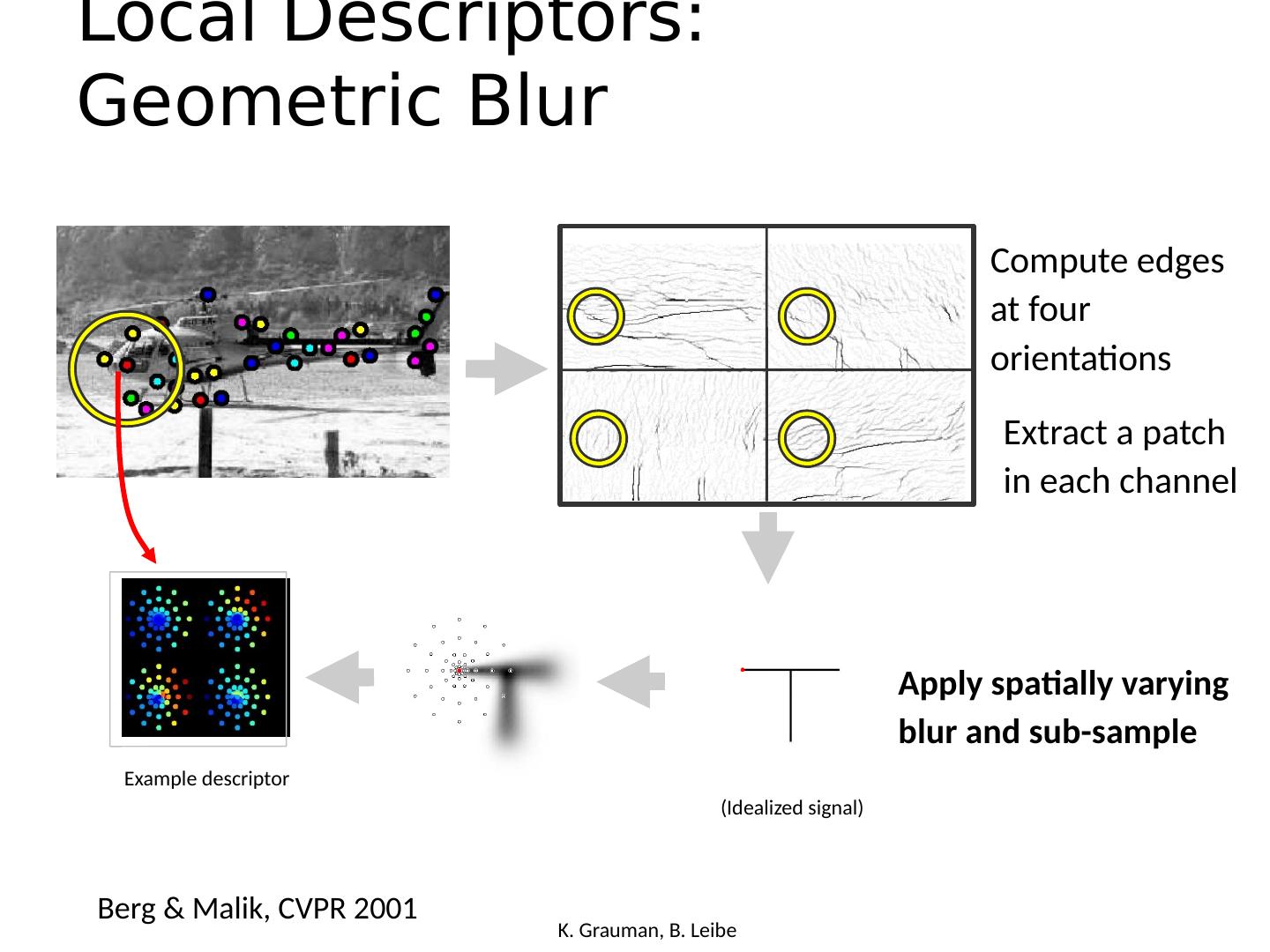
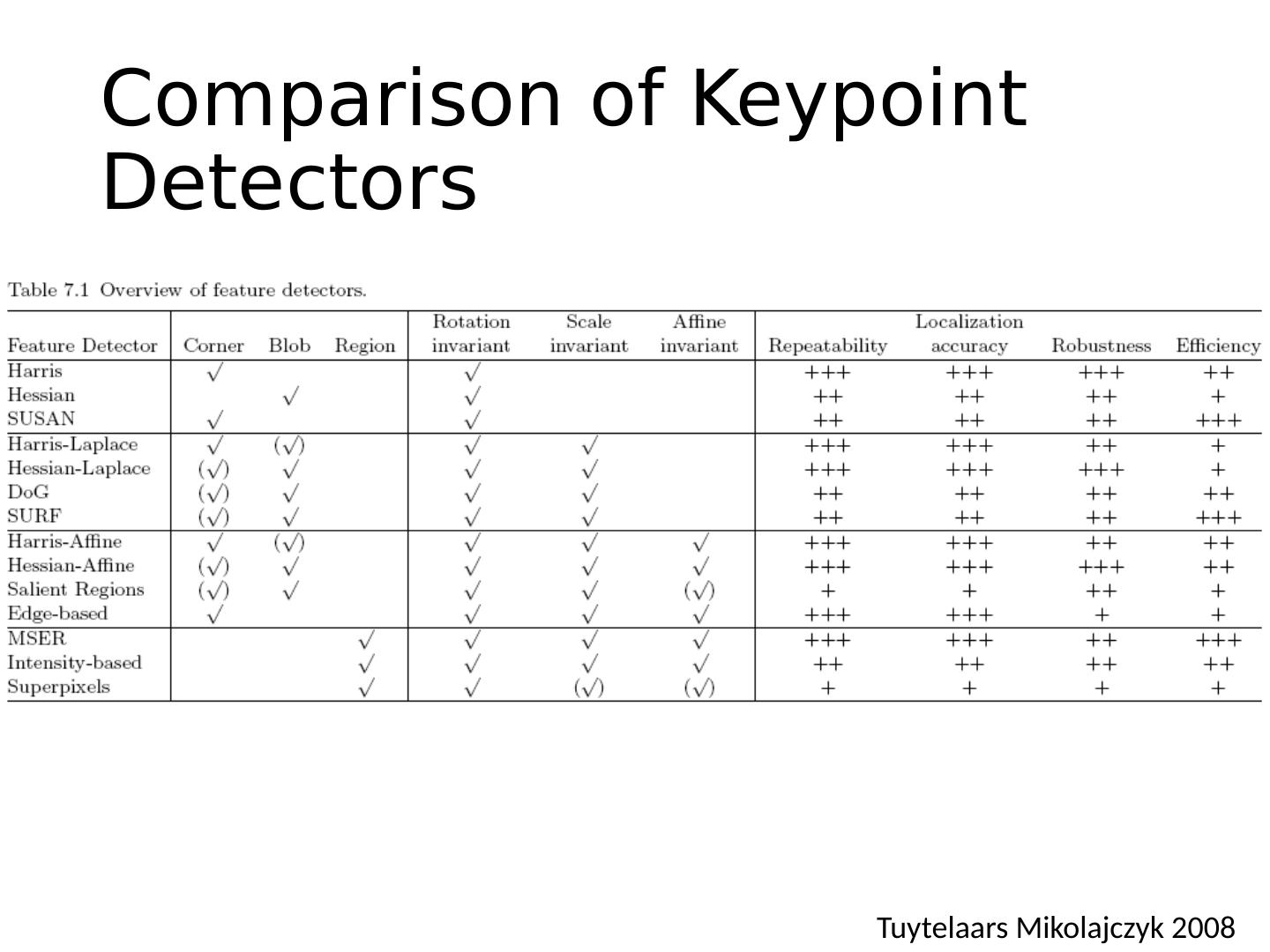
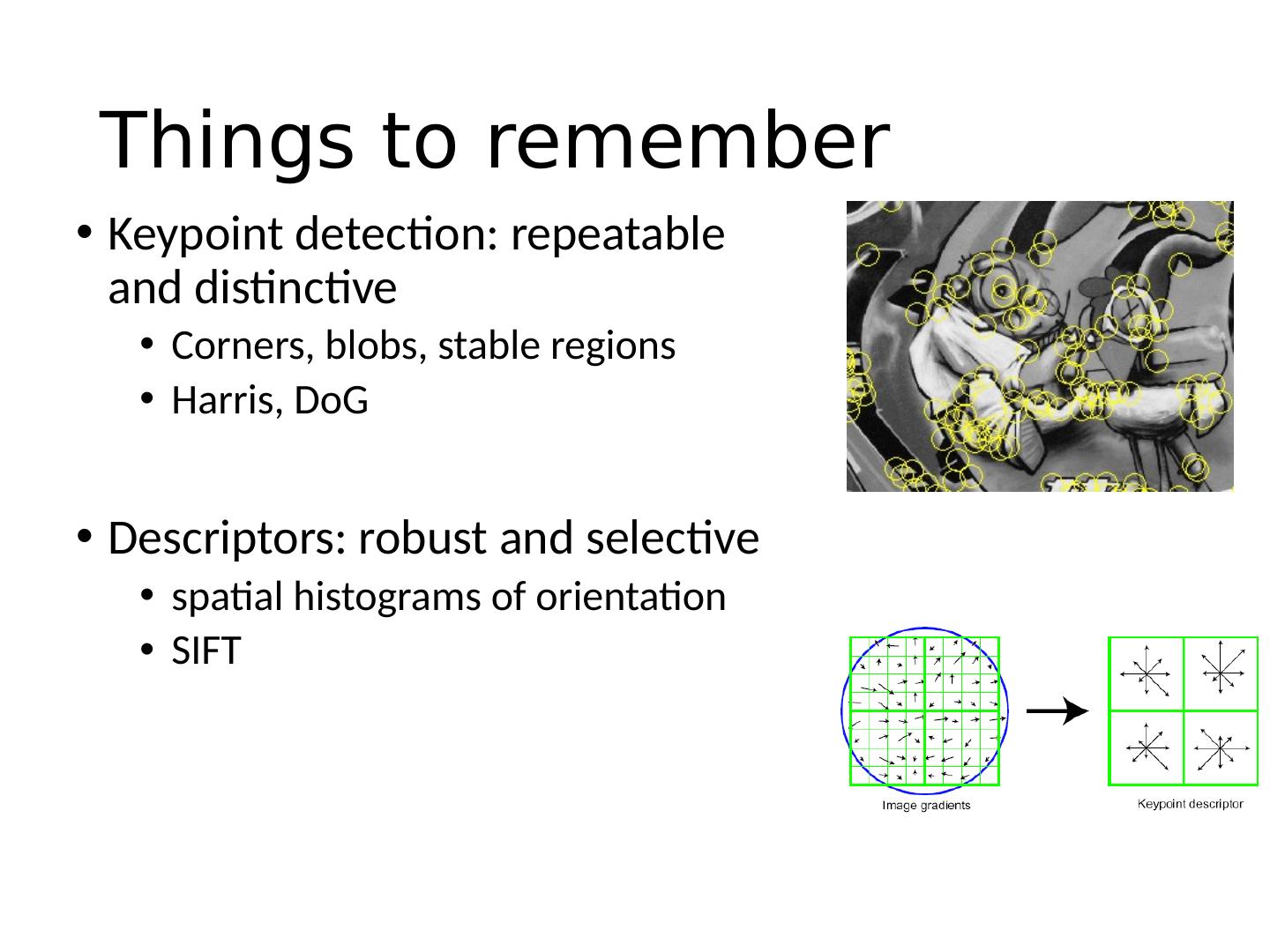
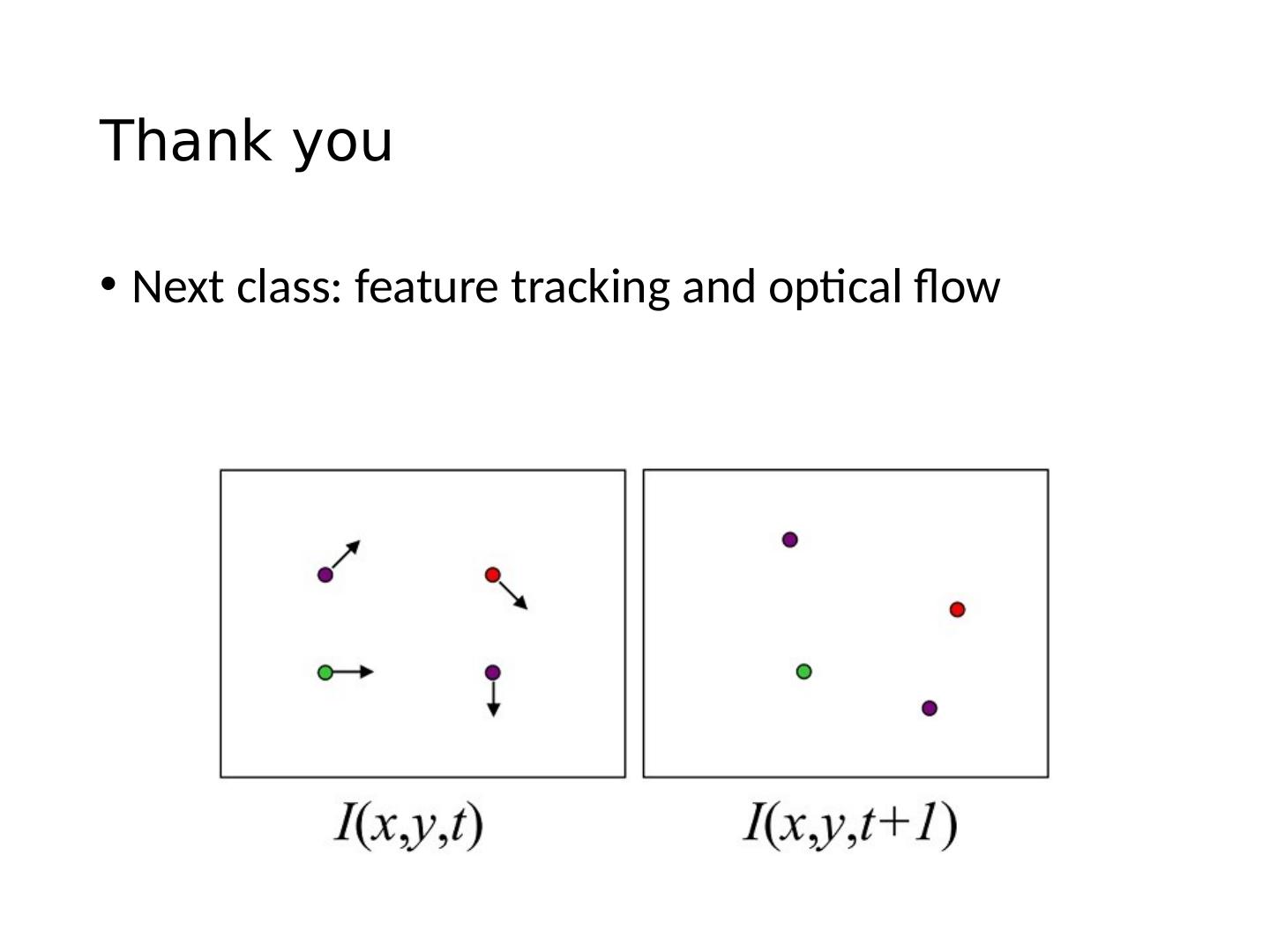
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
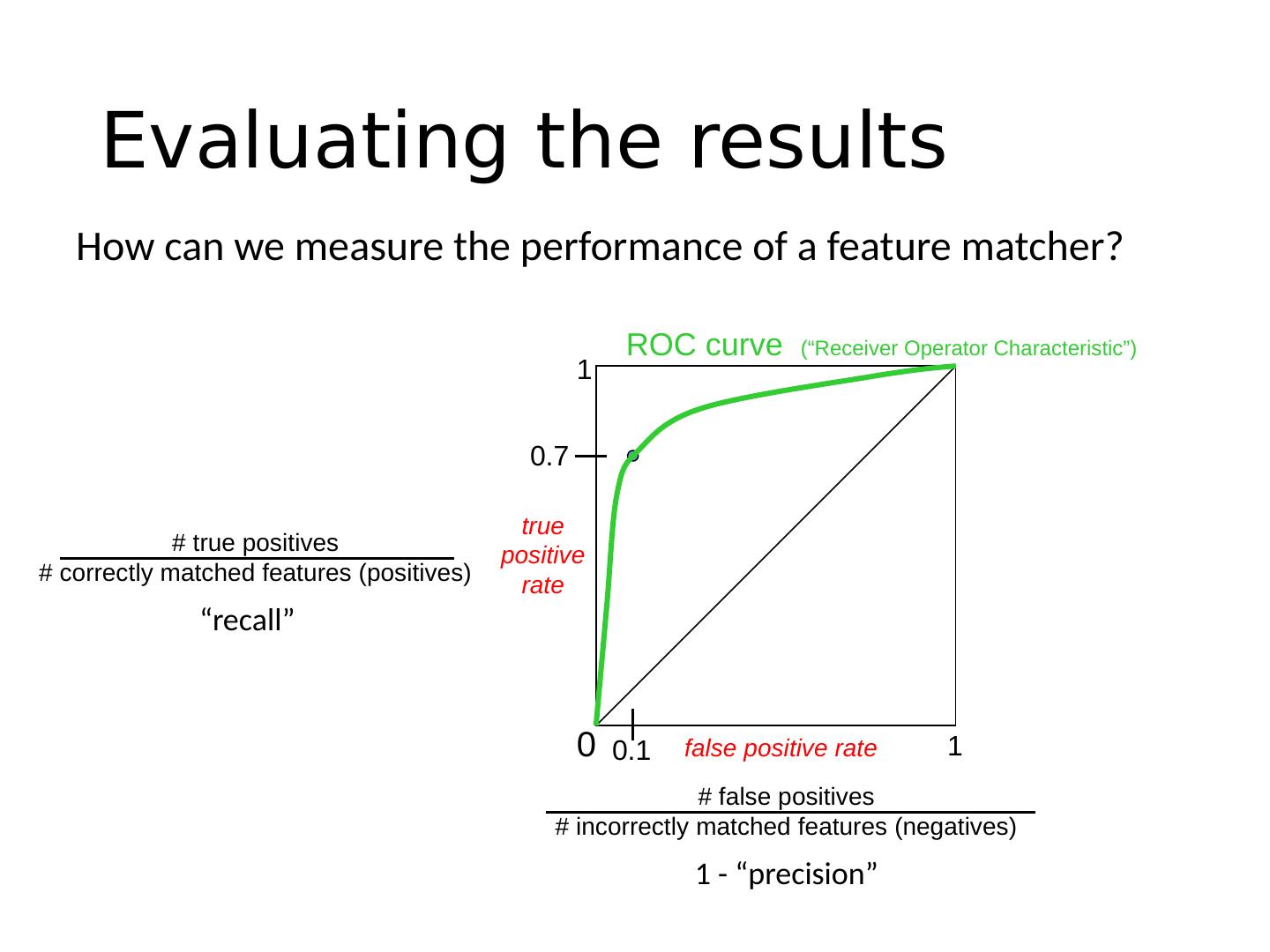
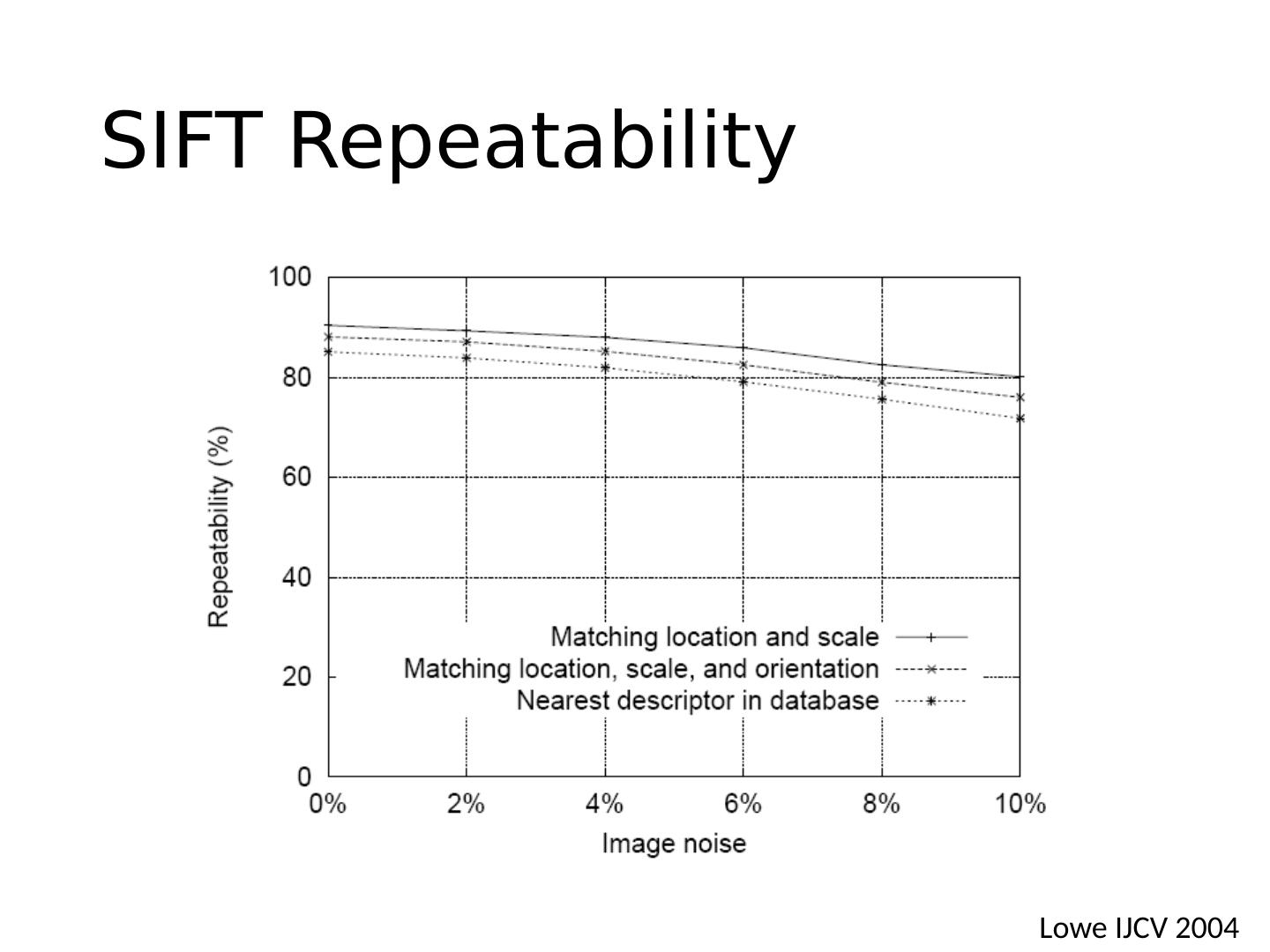
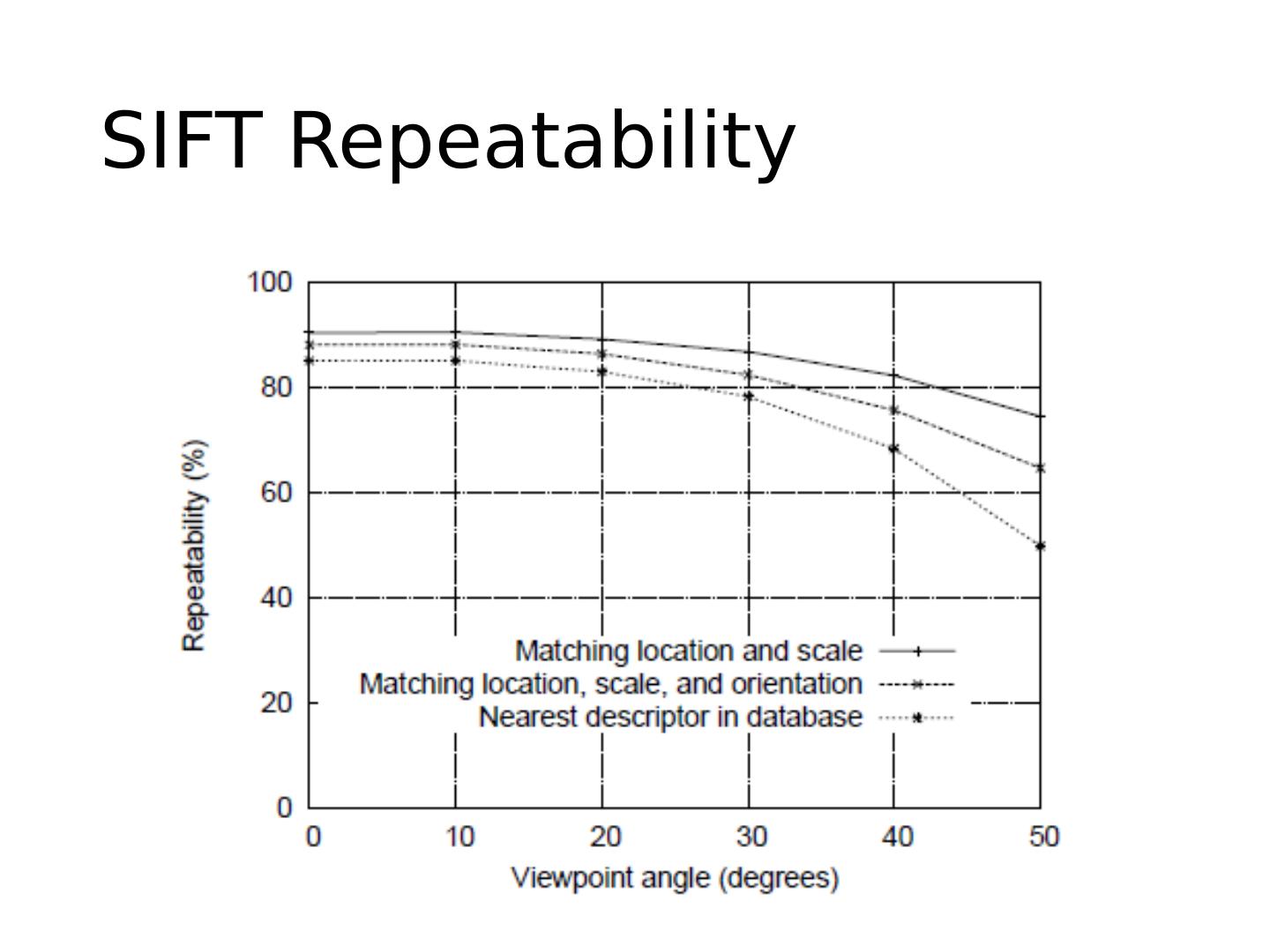
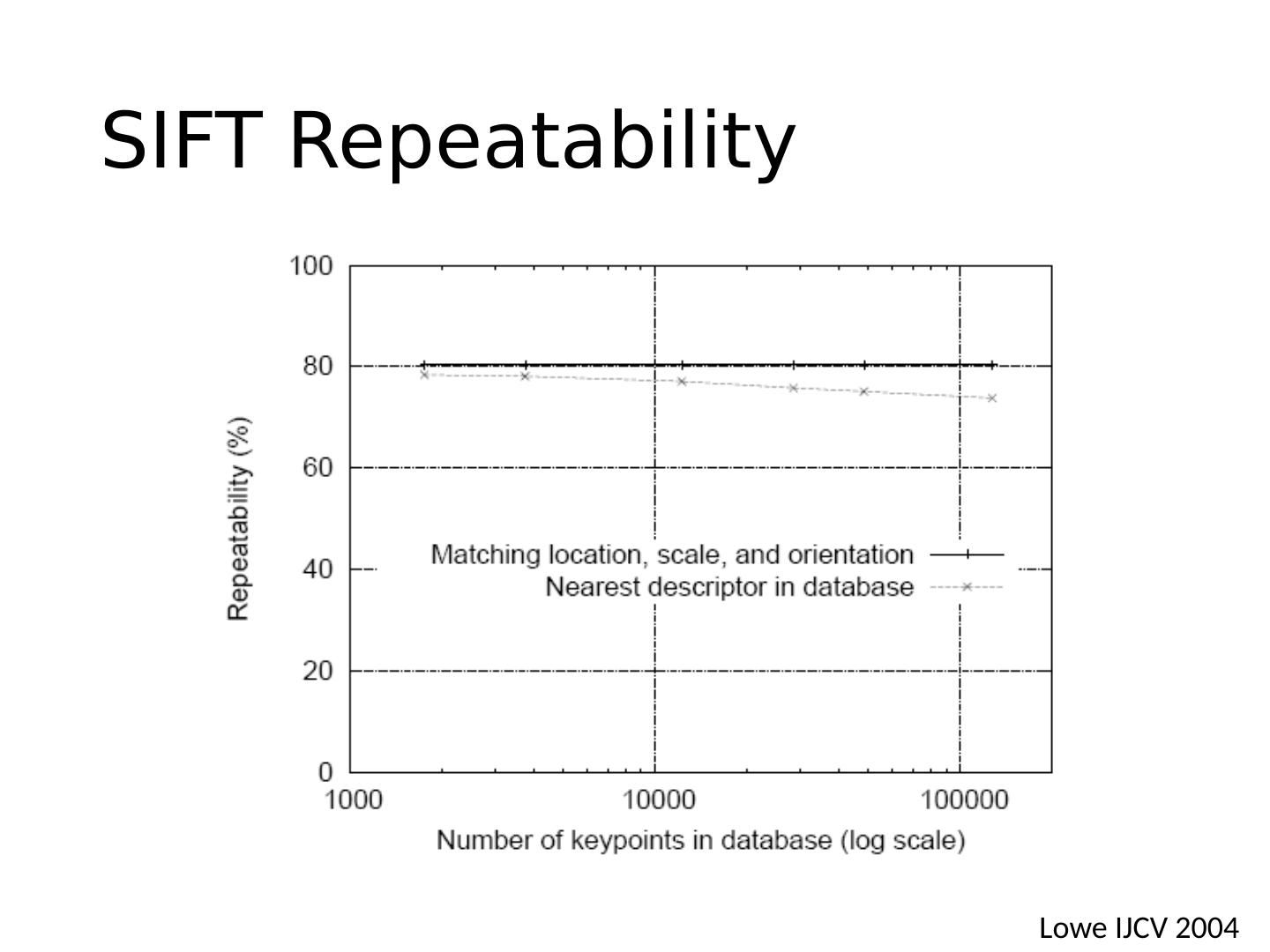
Interest Points
展开查看详情
1 .Interest Points Computer Vision Jia-Bin Huang, Virginia Tech Many slides from N Snavely, K. Grauman & Leibe , and D. Hoiem
2 .Administrative Stuffs HW 1 posted, due 11:59 PM Sept 19 Submission through Canvas Frequently Asked Questions for HW 1 posted on piazza Reading - Szeliski : 4.1
3 .What have we learned so far? Light and color What an image records Filtering in spatial domain Filtering = weighted sum of neighboring pixels Smoothing, sharpening, measuring texture Filtering in frequency domain Filtering = change frequency of the input image Denoising , sampling, image compression Image pyramid and template matching Filtering = a way to find a template Image pyramids for coarse-to-fine search and multi-scale detection Edge detection Canny edge = smooth -> derivative -> thin -> threshold -> link Finding straight lines, binary image analysis
4 .This module: Correspondence and Alignment Correspondence : matching points, patches, edges, or regions across images ≈ Slide credit: Derek Hoiem
5 .This module: Correspondence and Alignment Alignment/registration : solving the transformation that makes two things match better T Slide credit: Derek Hoiem
6 .The three biggest problems in computer vision? Registration Registration Registration Takeo Kanade (CMU)
7 .Example: automatic panoramas Credit: Matt Brown
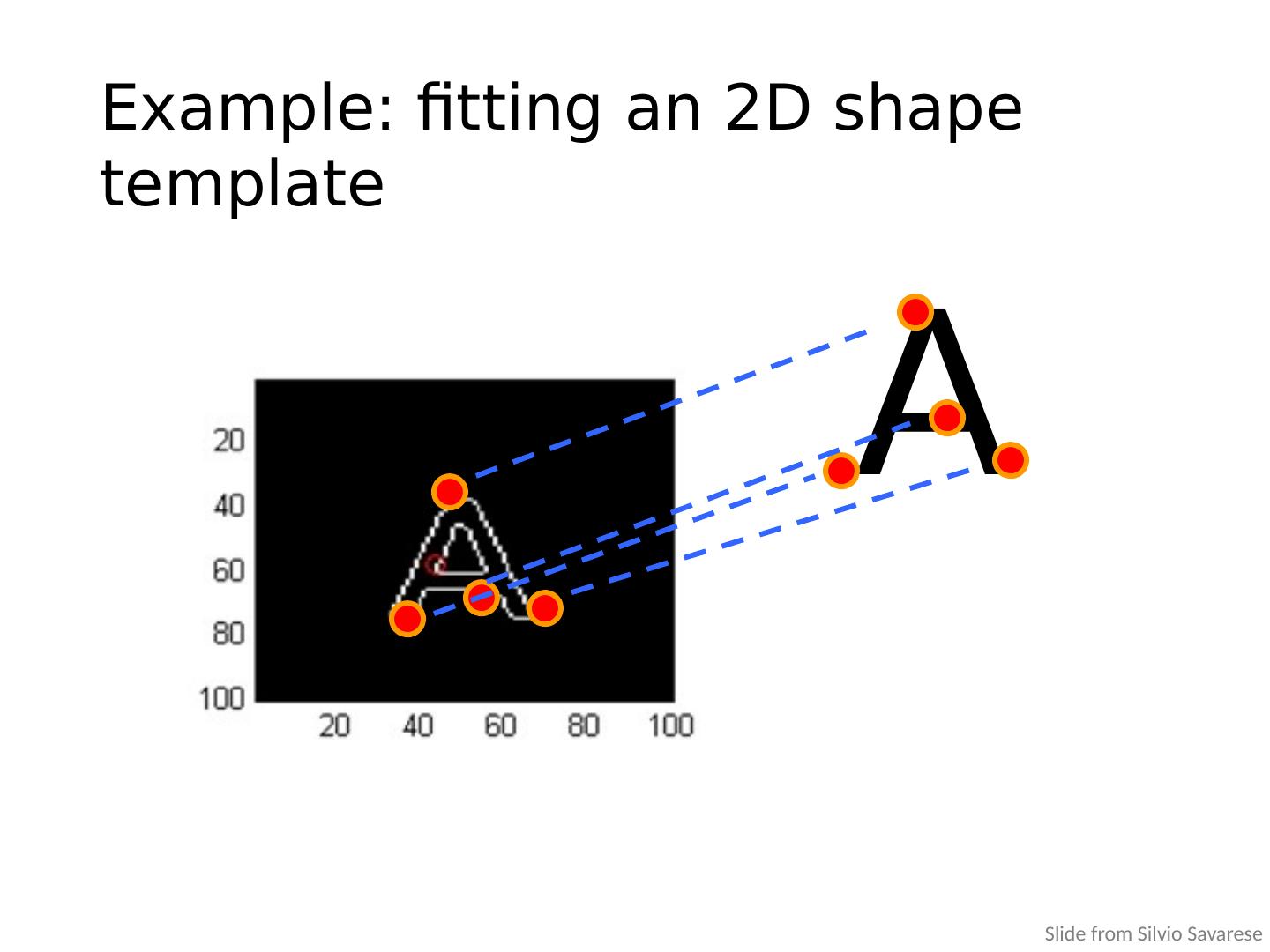
8 .A Example: fitting an 2D shape template Slide from Silvio Savarese
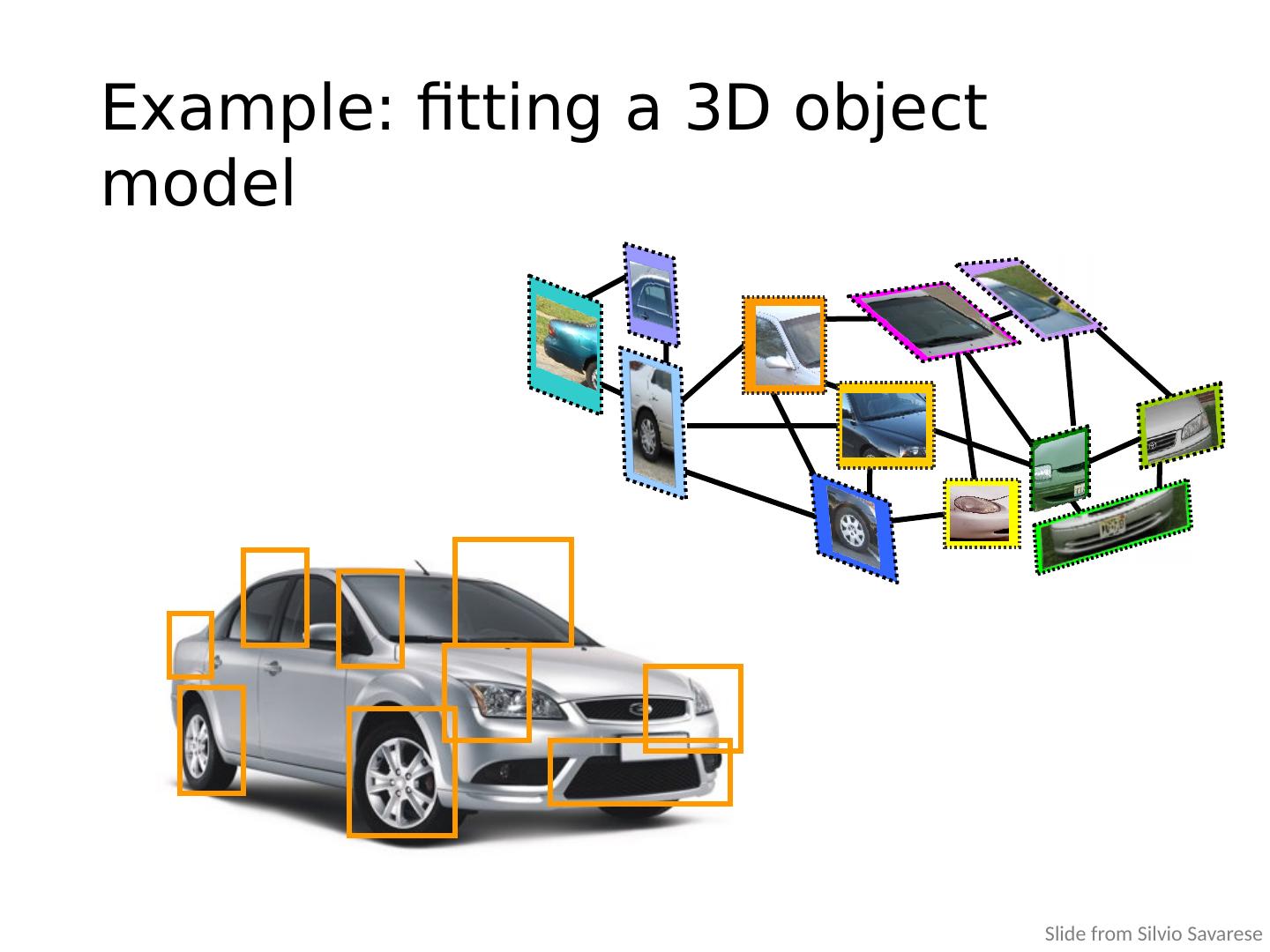
9 .Example: fitting a 3D object model Slide from Silvio Savarese
10 .Example: estimating “fundamental matrix” that corresponds two views Slide from Silvio Savarese
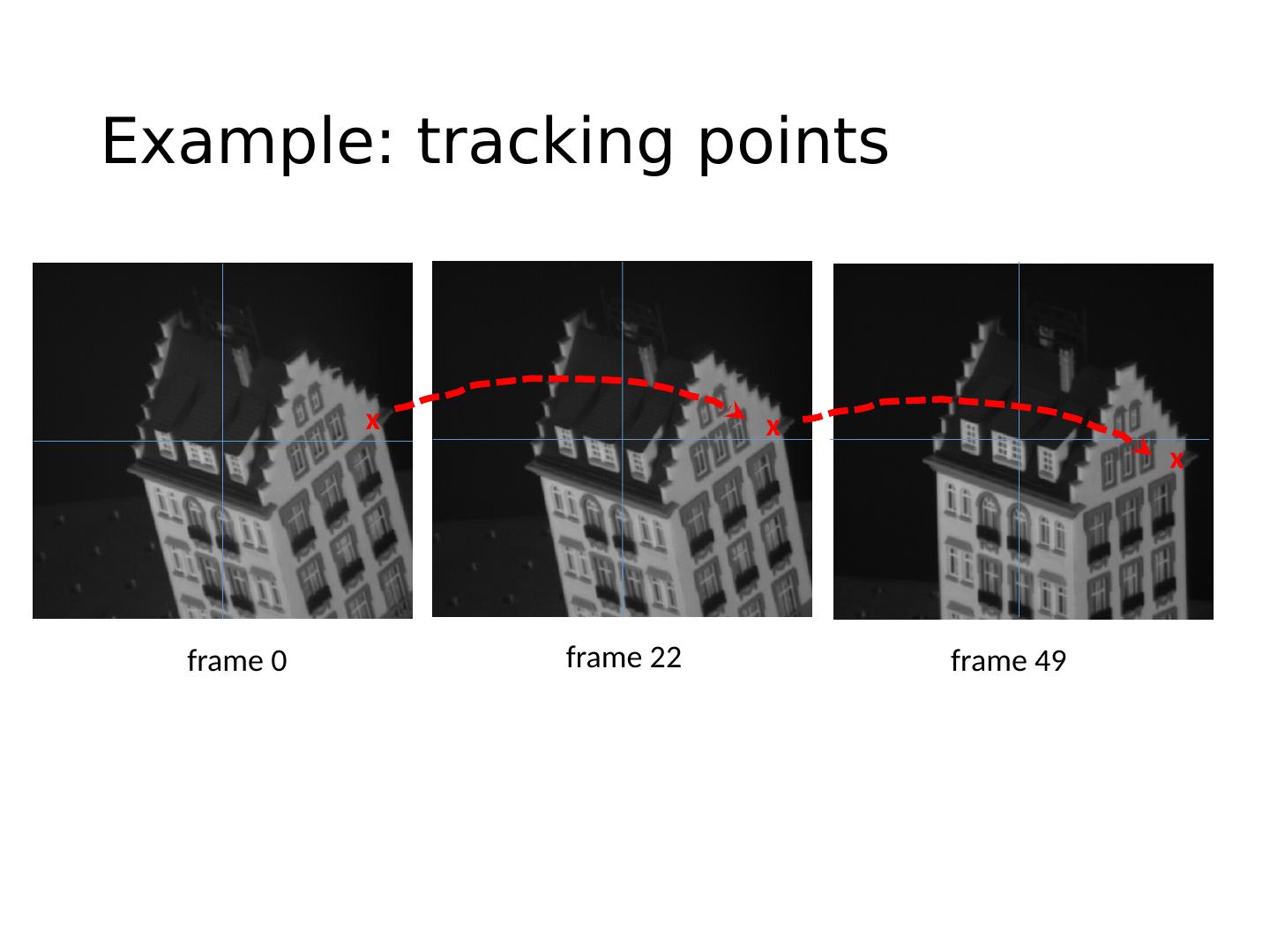
11 .Example: tracking points frame 0 frame 22 frame 49 x x x
12 .Today’s class What is interest point? Corner detection Handling scale and orientation Feature matching
13 .Why extract features? Motivation: panorama stitching We have two images – how do we combine them?
14 .Why extract features? Motivation: panorama stitching We have two images – how do we combine them? Step 1: extract features Step 2: match features
15 .Why extract features? Motivation: panorama stitching We have two images – how do we combine them? Step 1: extract features Step 2: match features Step 3: align images
16 .Image matching by Diva Sian by swashford TexPoint fonts used in EMF. Read the TexPoint manual before you delete this box.: A A A A A A
17 .Harder case by Diva Sian by scgbt
18 .Harder still?
19 .NASA Mars Rover images with SIFT feature matches Answer below (look for tiny colored squares…)
20 .Applications Keypoints are used for: Image alignment 3D reconstruction Motion tracking Robot navigation Indexing and database retrieval Object recognition
21 .Advantages of local features Locality features are local, so robust to occlusion and clutter Quantity hundreds or thousands in a single image Distinctiveness: can differentiate a large database of objects Efficiency real-time performance achievable
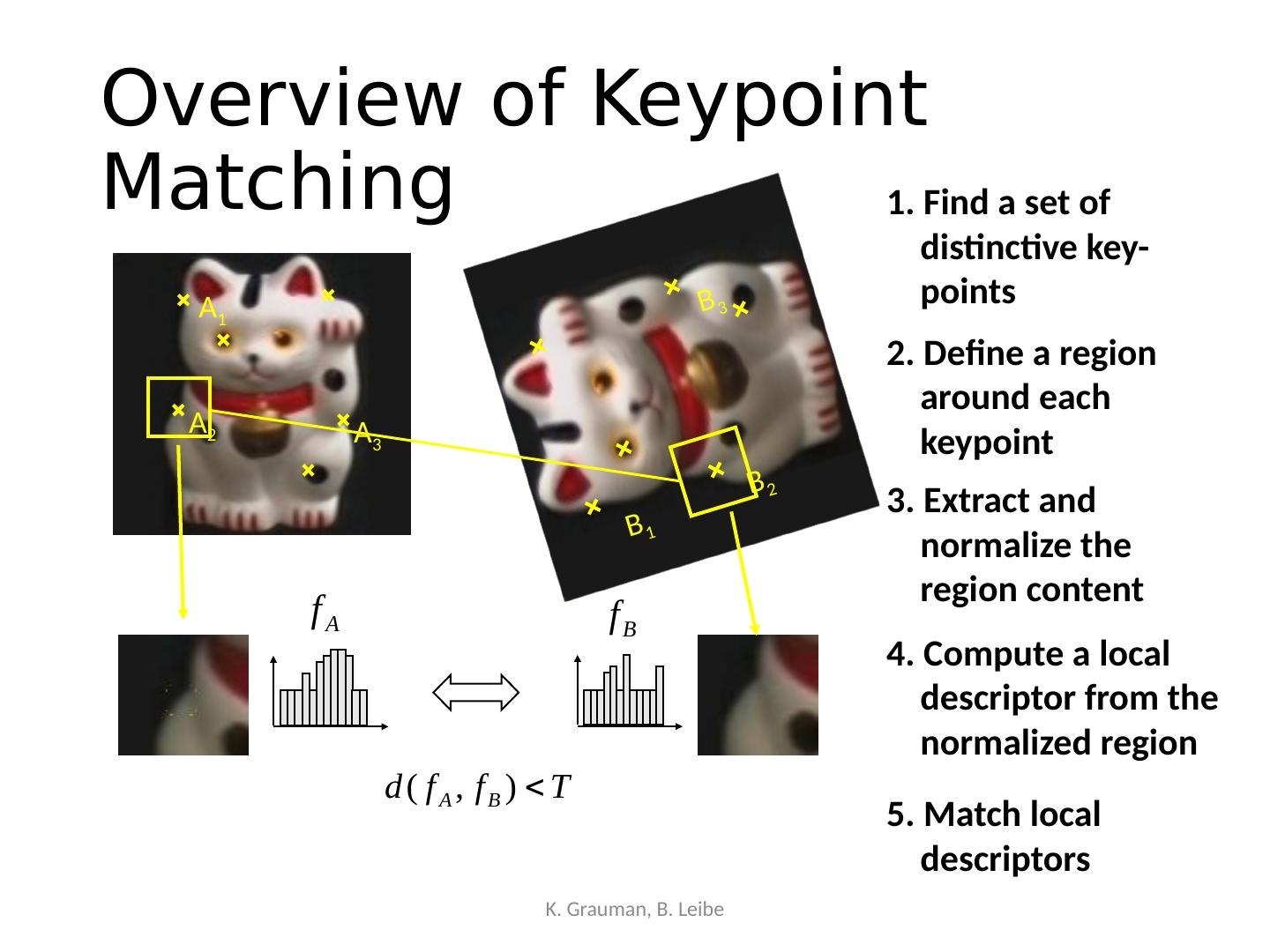
22 .Overview of Keypoint Matching K. Grauman, B. Leibe B 1 B 2 B 3 A 1 A 2 A 3 1. Find a set of distinctive key- points 3. Extract and normalize the region content 2. Define a region around each keypoint 4. Compute a local descriptor from the normalized region 5. Match local descriptors
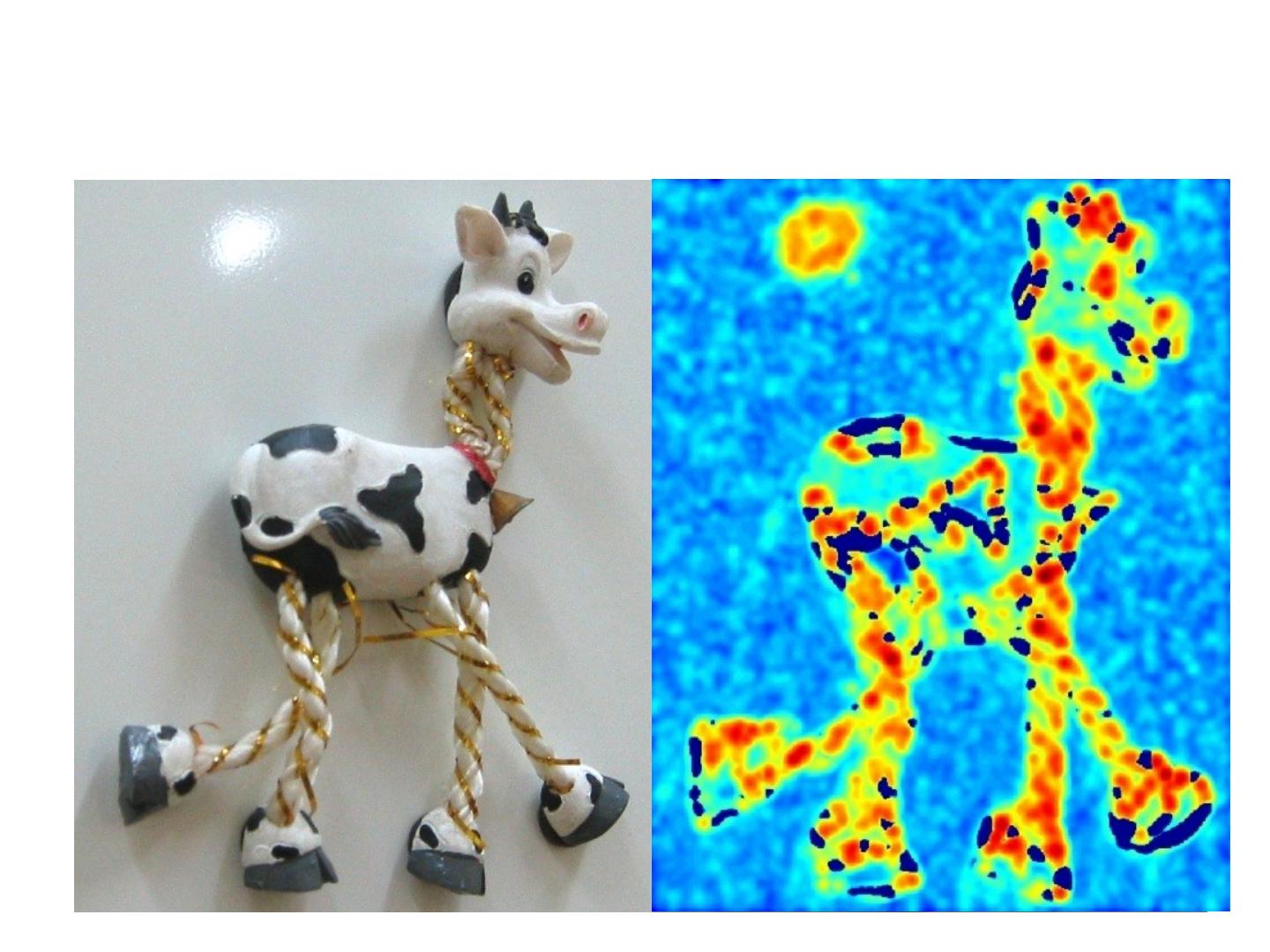
23 .Goals for Keypoints Detect points that are repeatable and distinctive
24 .Key trade-offs More Repeatable More Points B 1 B 2 B 3 A 1 A 2 A 3 Detection More Distinctive More Flexible Description Robust to occlusion Works with less texture Minimize wrong matches Robust to expected variations Maximize correct matches Robust detection Precise localization
25 .Choosing interest points Where would you tell your friend to meet you?
26 .Choosing interest points Where would you tell your friend to meet you?
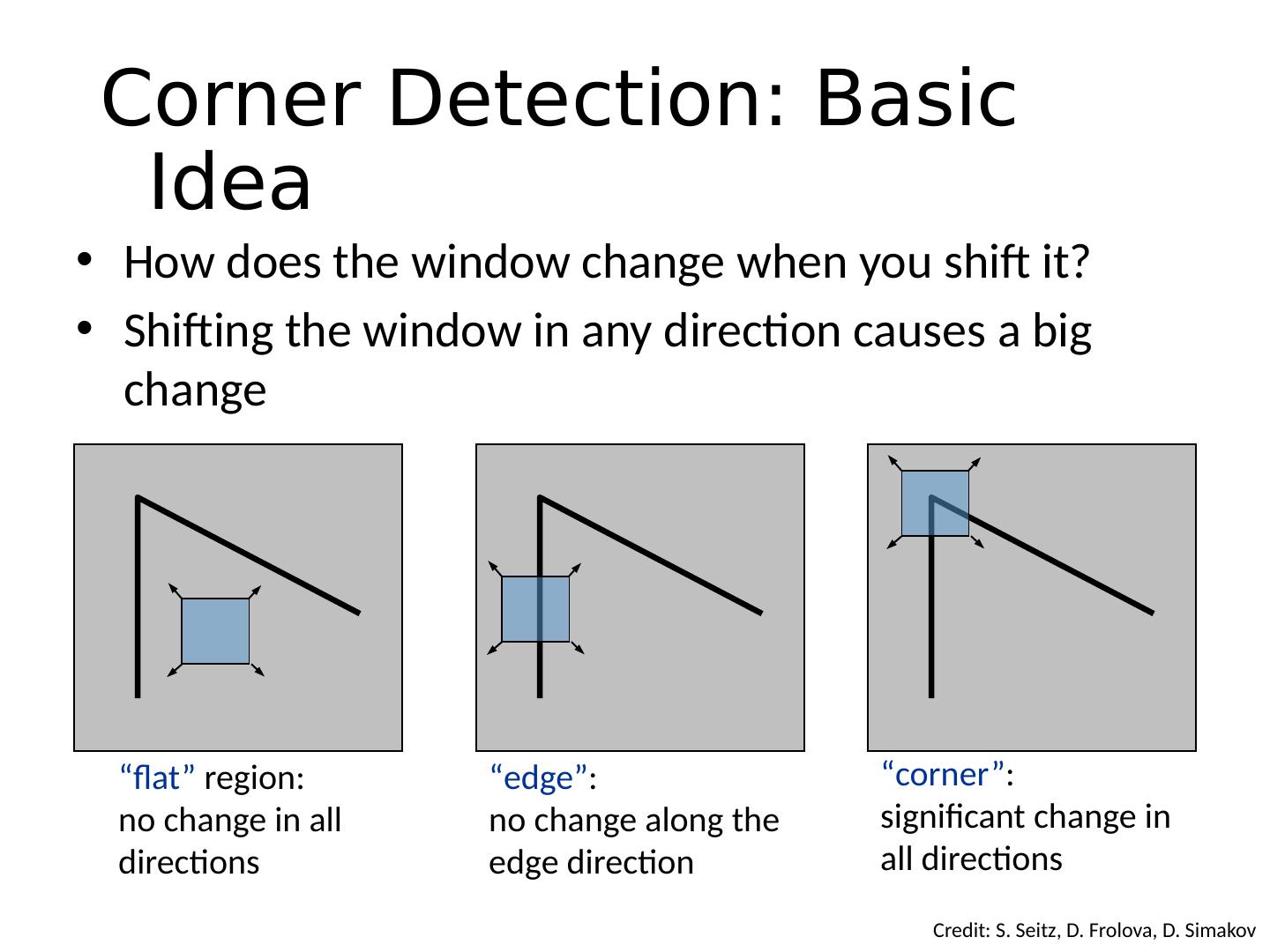
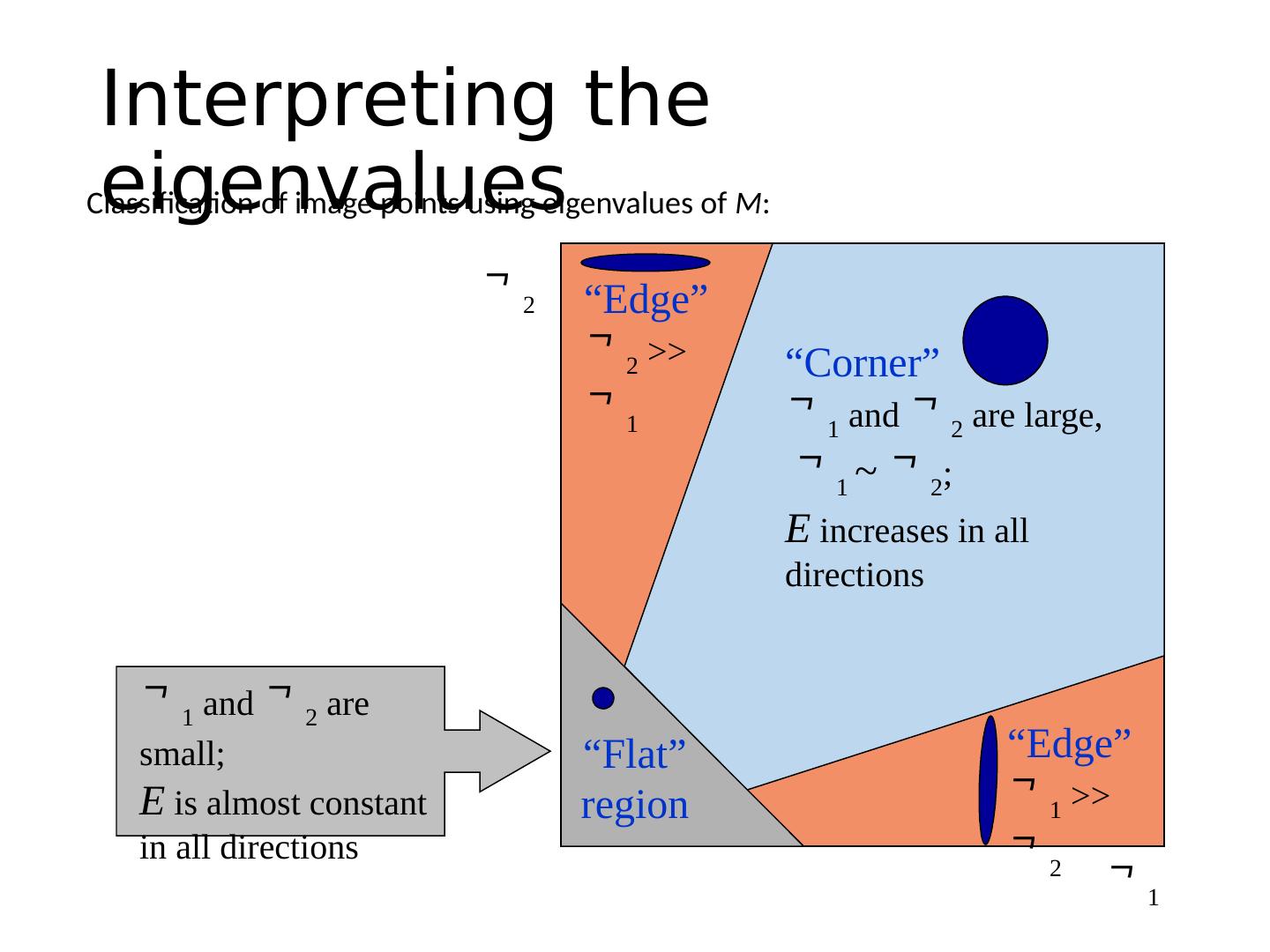
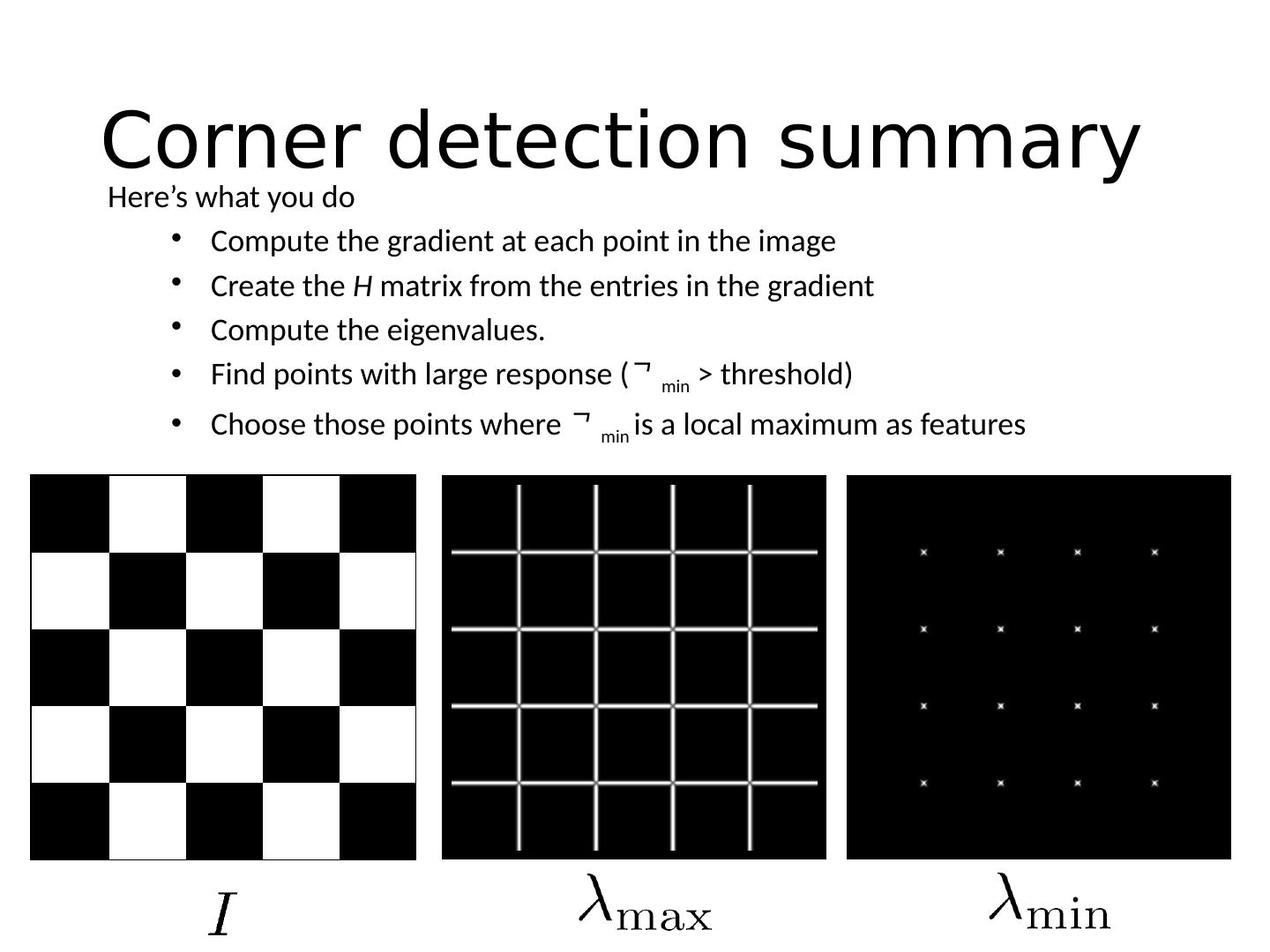
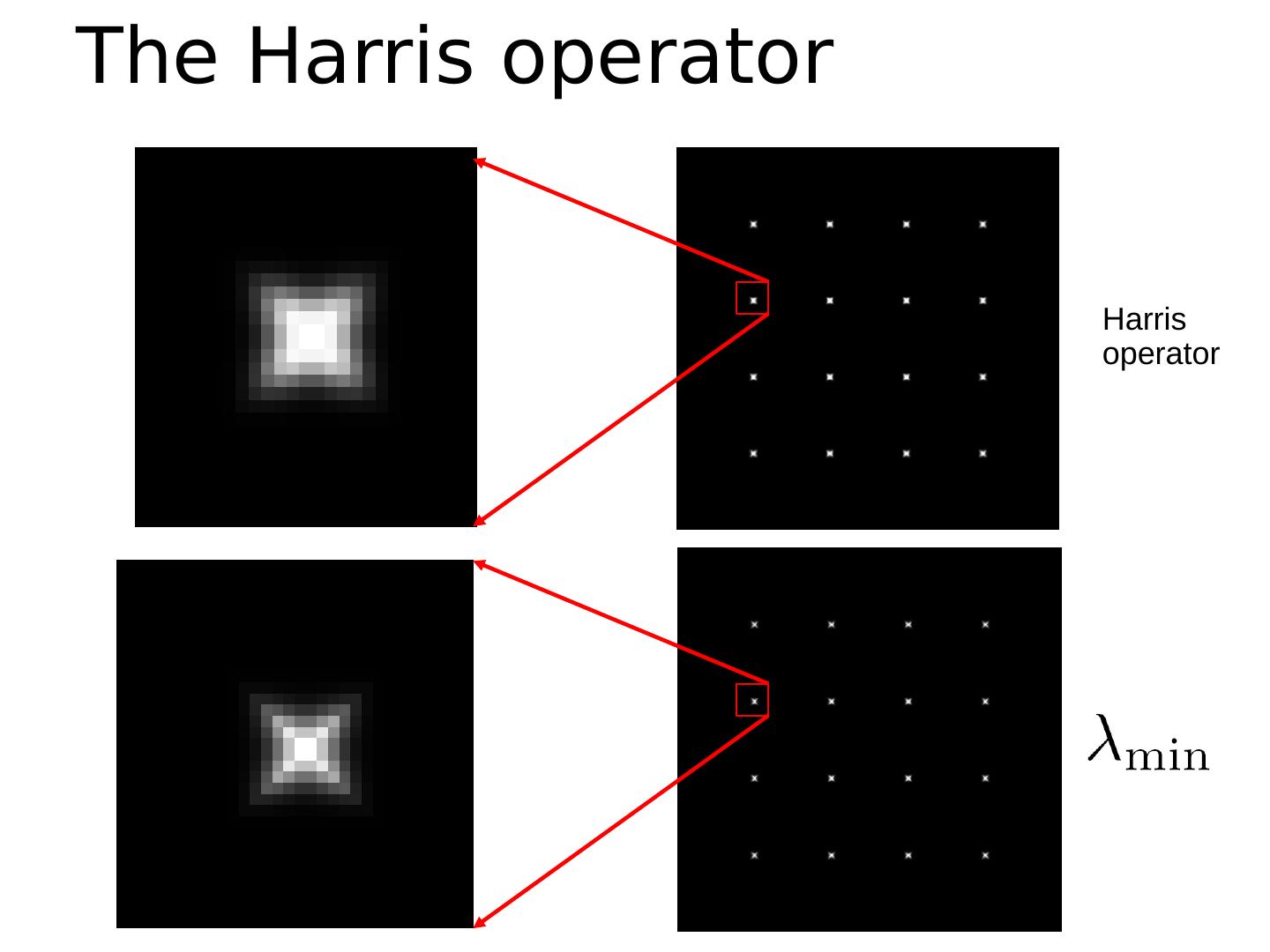
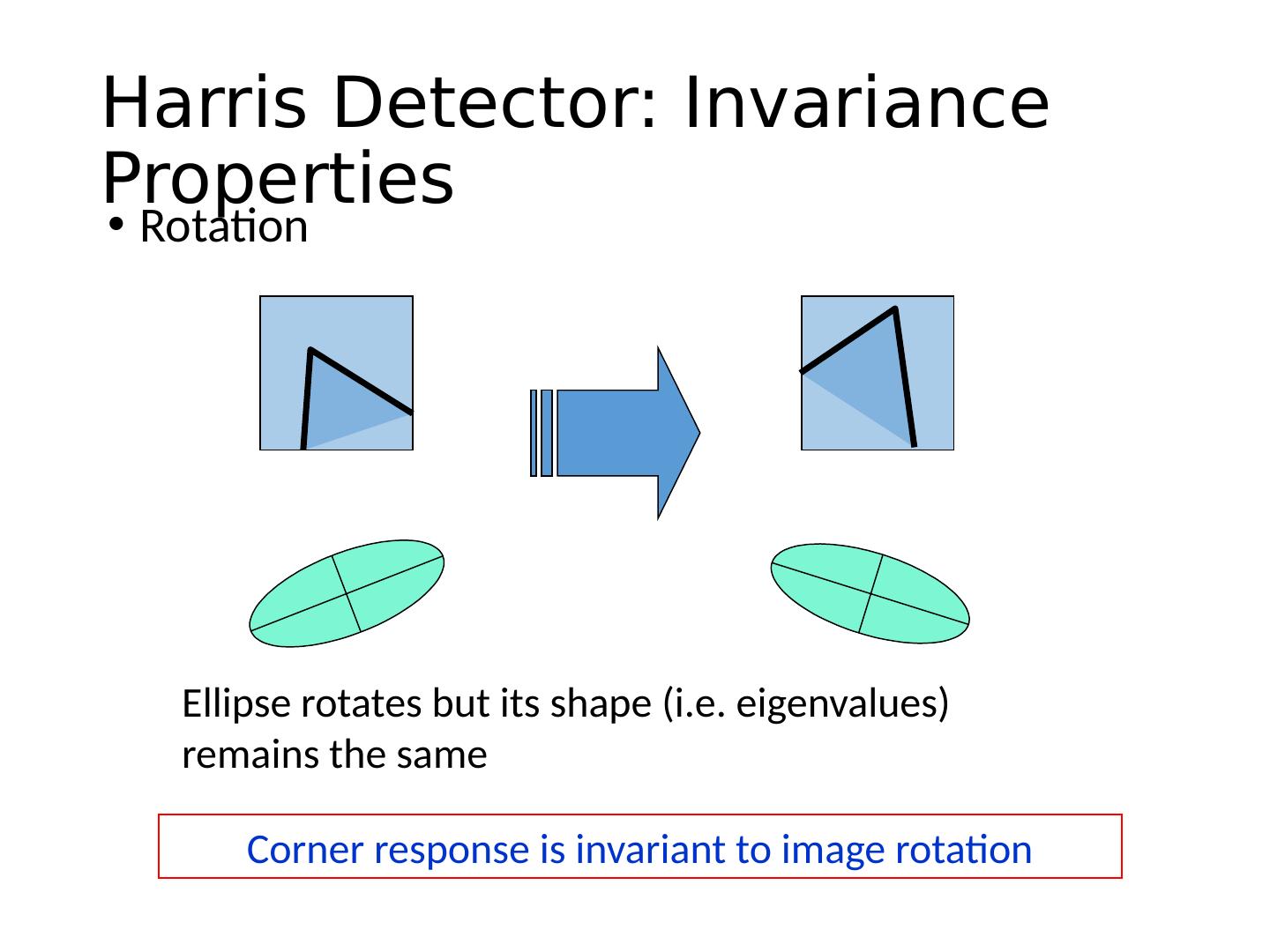
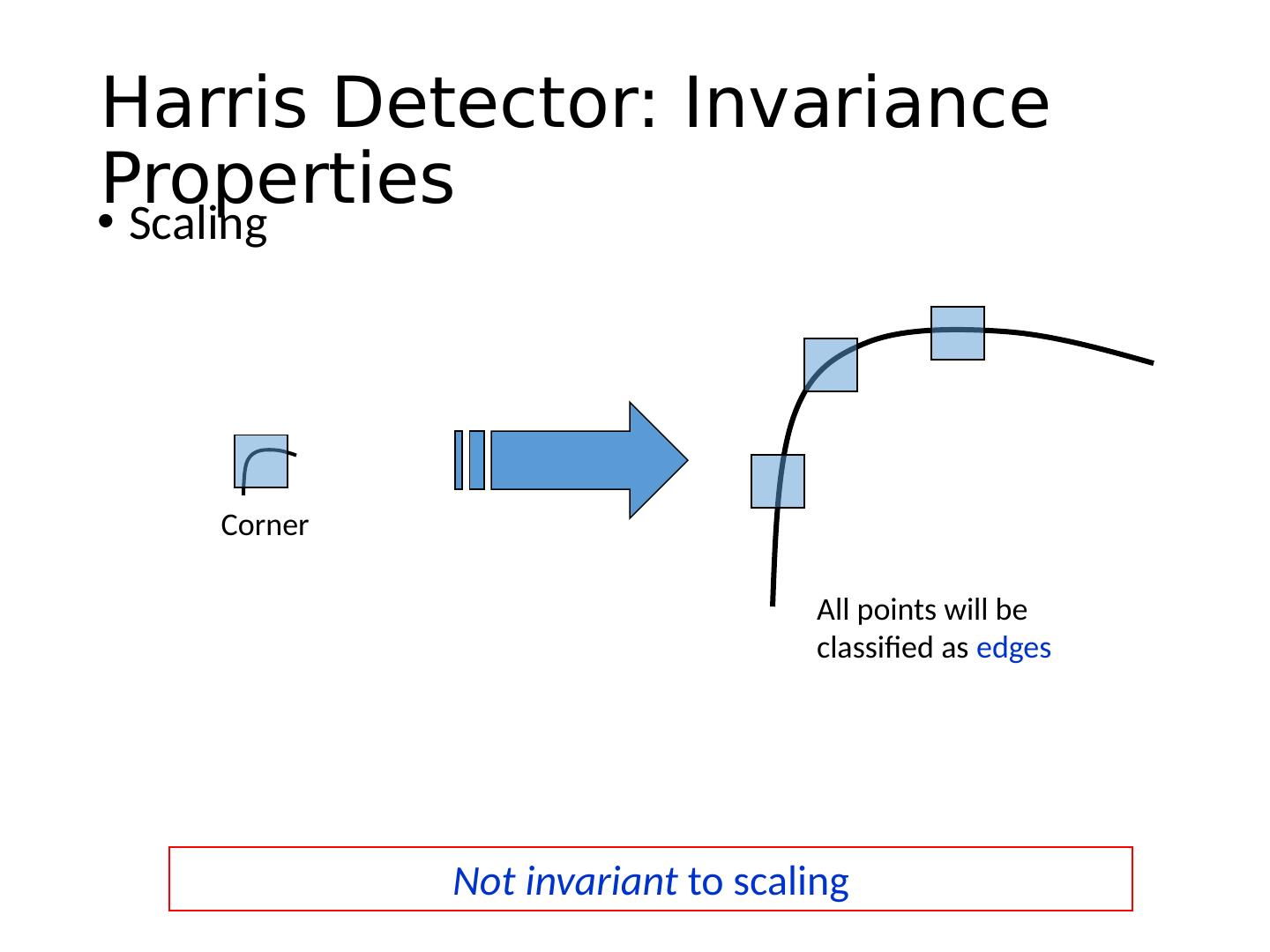
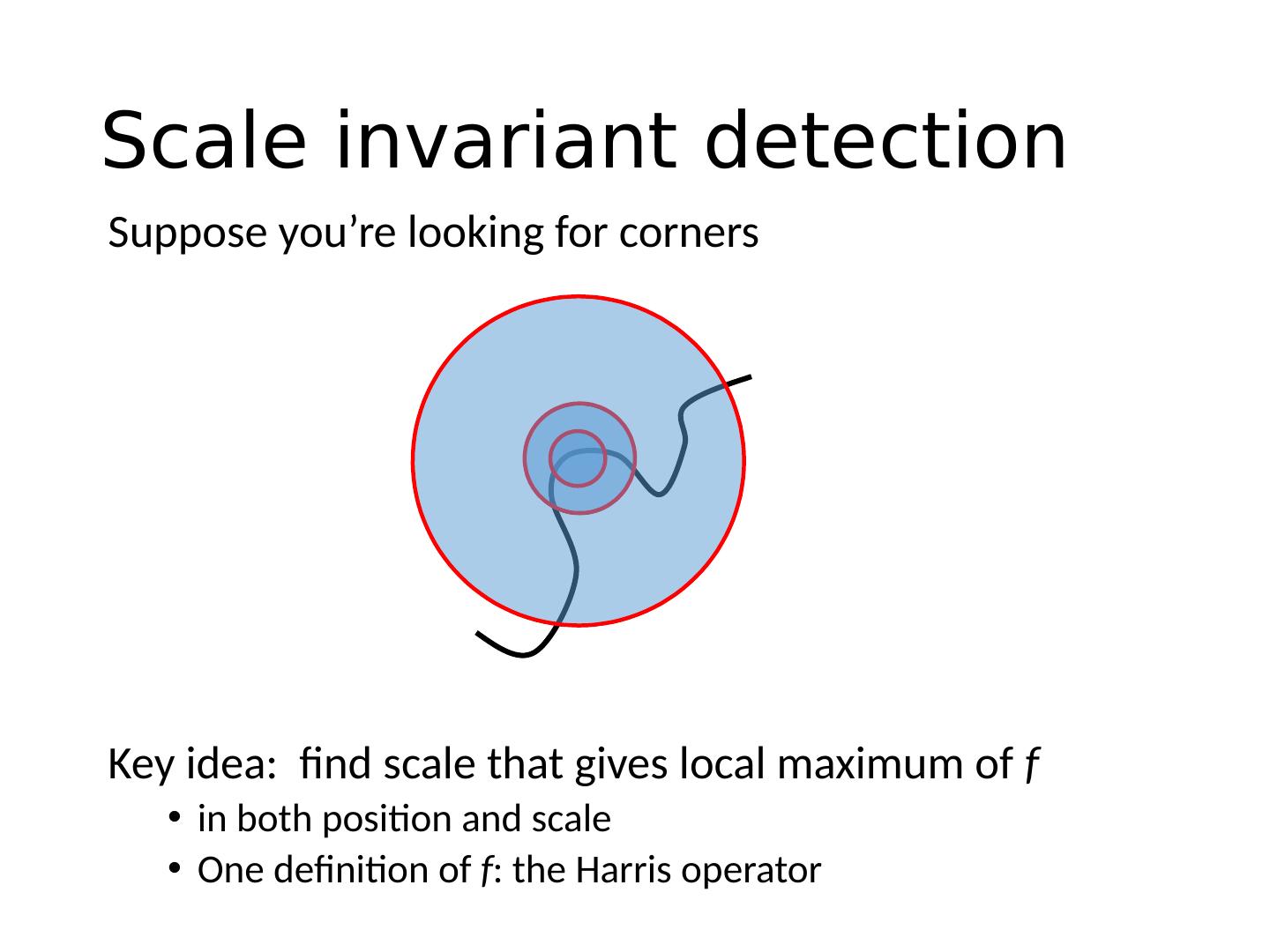
27 .Corner Detection: Basic Idea “flat” region: no change in all directions “edge” : no change along the edge direction “corner” : significant change in all directions How does the window change when you shift it? Shifting the window in any direction causes a big change Credit: S. Seitz, D. Frolova, D. Simakov
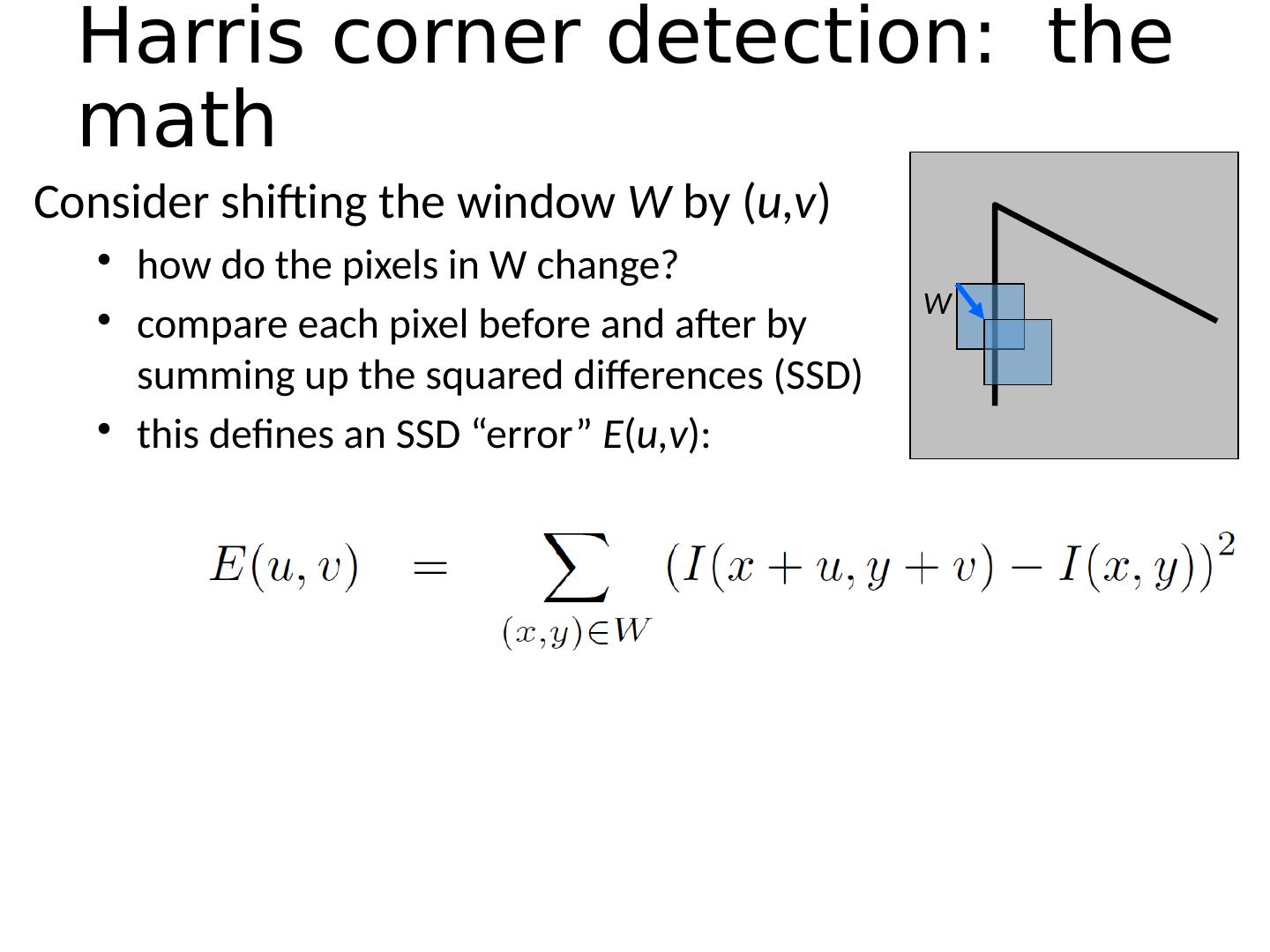
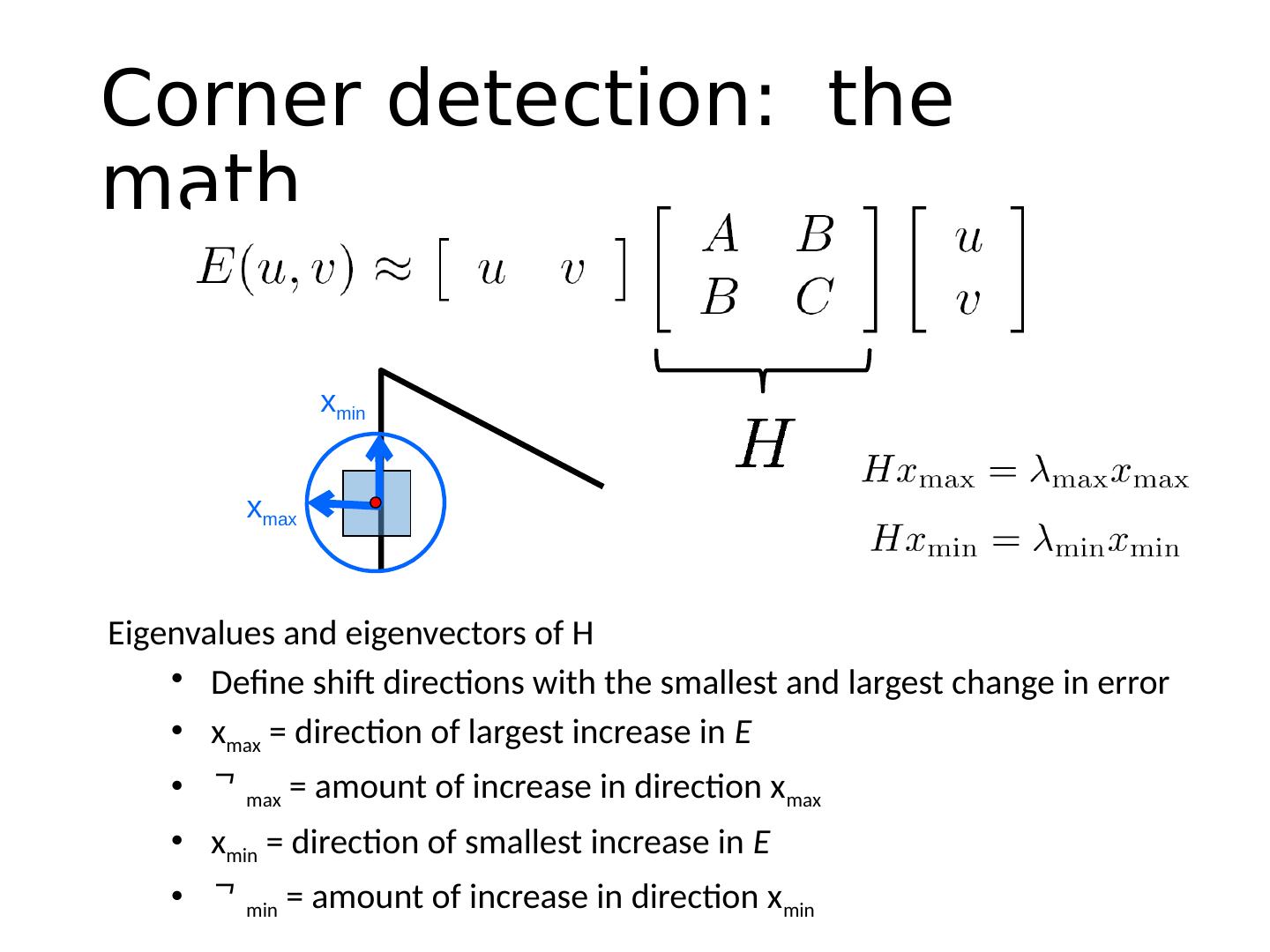
28 .Consider shifting the window W by ( u,v ) how do the pixels in W change? compare each pixel before and after by summing up the squared differences (SSD) this defines an SSD “error” E ( u,v ): Harris corner detection: the math W
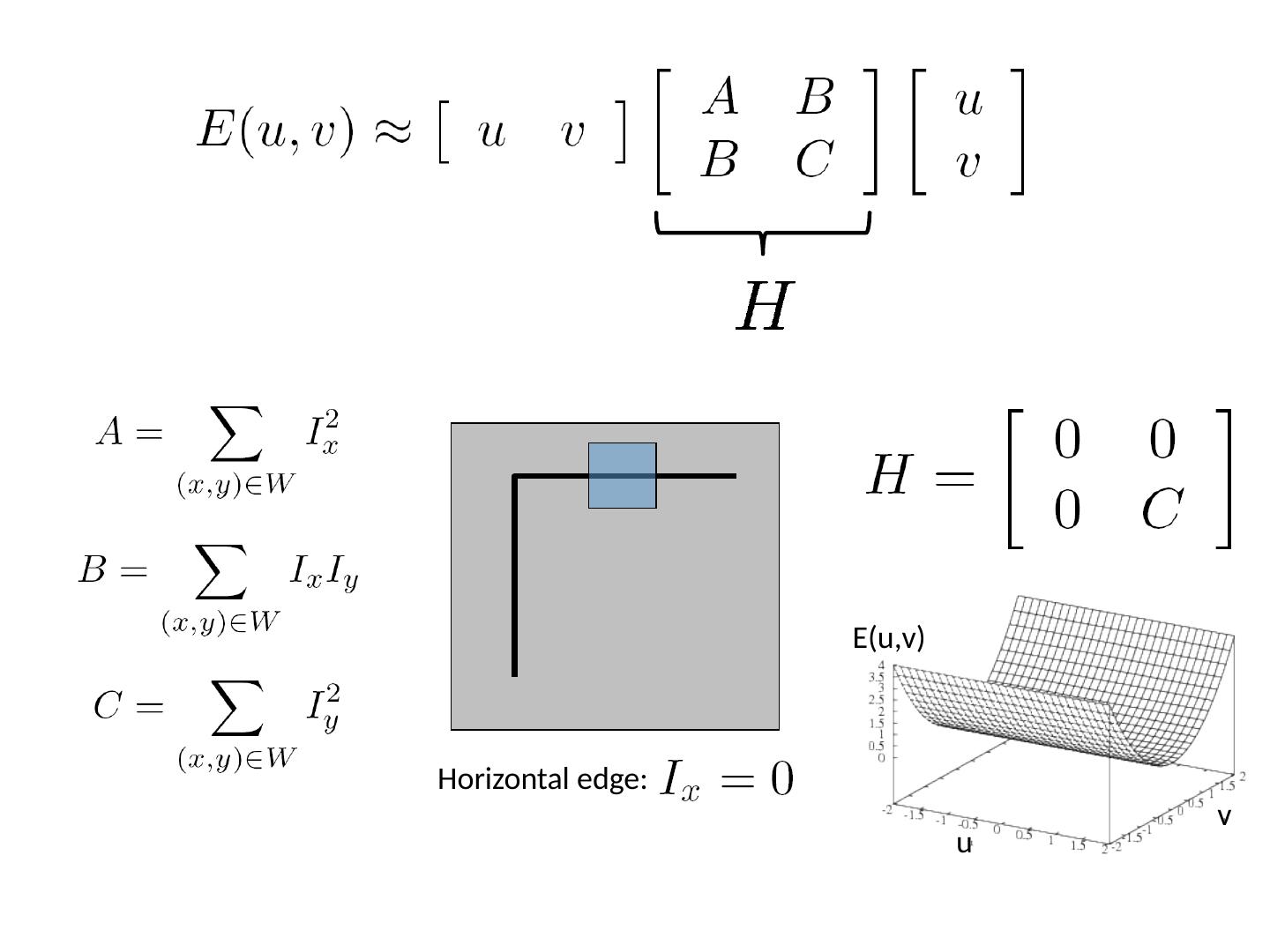
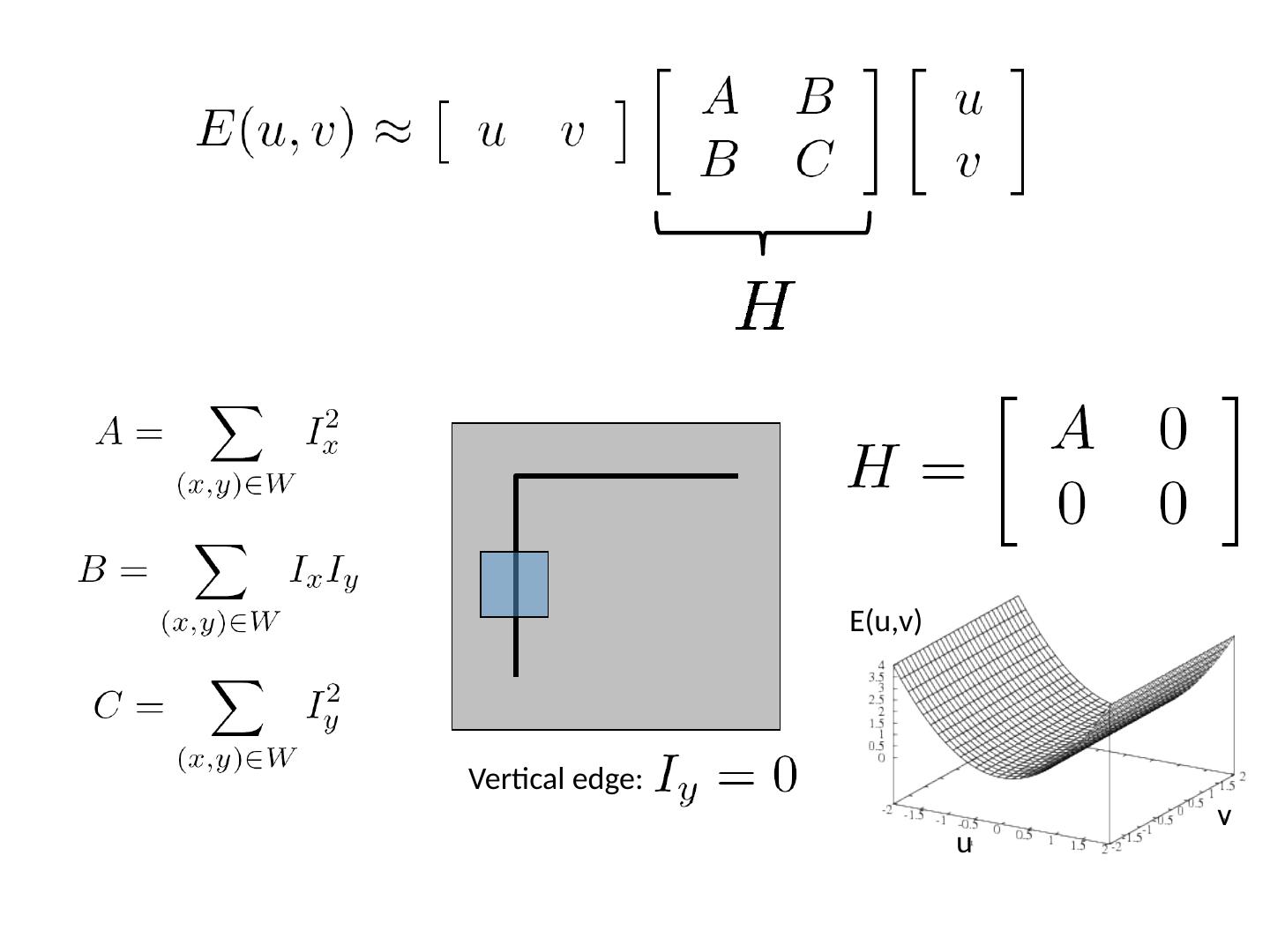
29 .Taylor Series expansion of I : If the motion (u,v) is small, then first order approximation is good Plugging this into the formula on the previous slide… Small motion assumption