- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Spectral Clustering
展开查看详情
1 .Spectral Clustering Shannon Quinn (with thanks to William Cohen of Carnegie Mellon University, and J . Leskovec , A. Rajaraman , and J . Ullman of Stanford University)
2 .Graph Partitioning Undirected graph Bi-partitioning task: Divide vertices into two disjoint groups Questions: How can we define a “good” partition of ? How can we efficiently identify such a partition? J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 2 1 3 2 5 4 6 A B 1 3 2 5 4 6
3 .Graph Partitioning What makes a good partition? Maximize the number of within-group connections Minimize the number of between-group connections J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 3 1 3 2 5 4 6 A B
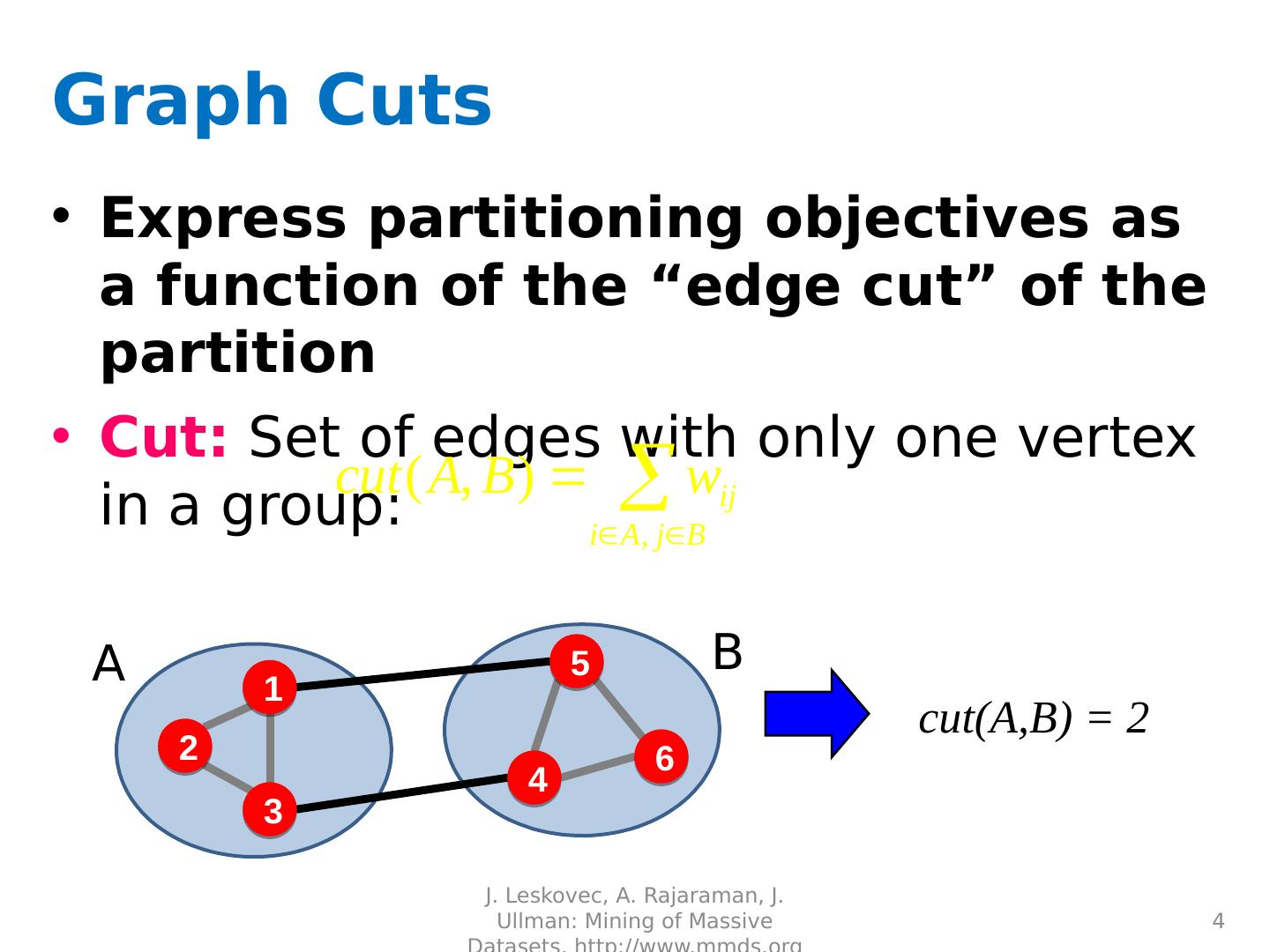
4 .A B Graph Cuts Express partitioning objectives as a function of the “edge cut” of the partition Cut: Set of edges with only one vertex in a group: J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 4 cut(A,B) = 2 1 3 2 5 4 6
5 .Graph Cut Criterion Criterion: Minimum-cut Minimize weight of connections between groups Degenerate case: Problem: Only considers external cluster connections Does not consider internal cluster connectivity J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 5 a rg min A,B cut(A,B) “Optimal cut” Minimum cut
6 .Graph Cut Criteria Criterion: Normalized-cut [Shi-Malik, ’97] Connectivity between groups relative to the density of each group : total weight of the edges with at least one endpoint in : Why use this criterion? Produces more balanced partitions How do we efficiently find a good partition? Problem: Computing optimal cut is NP-hard J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 6 [Shi- Malik ]
7 .Spectral Graph Partitioning A : adjacency matrix of undirected G A ij =1 if is an edge, else 0 x is a vector in n with components Think of it as a label/value of each node of What is the meaning of A x ? Entry y i is a sum of labels x j of neighbors of i J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 7
8 .What is the meaning of Ax ? j th coordinate of A x : Sum of the x -values of neighbors of j Make this a new value at node j Spectral Graph Theory: Analyze the “spectrum” of matrix representing Spectrum: Eigenvectors of a graph, ordered by the magnitude (strength) of their corresponding eigenvalues : J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 8
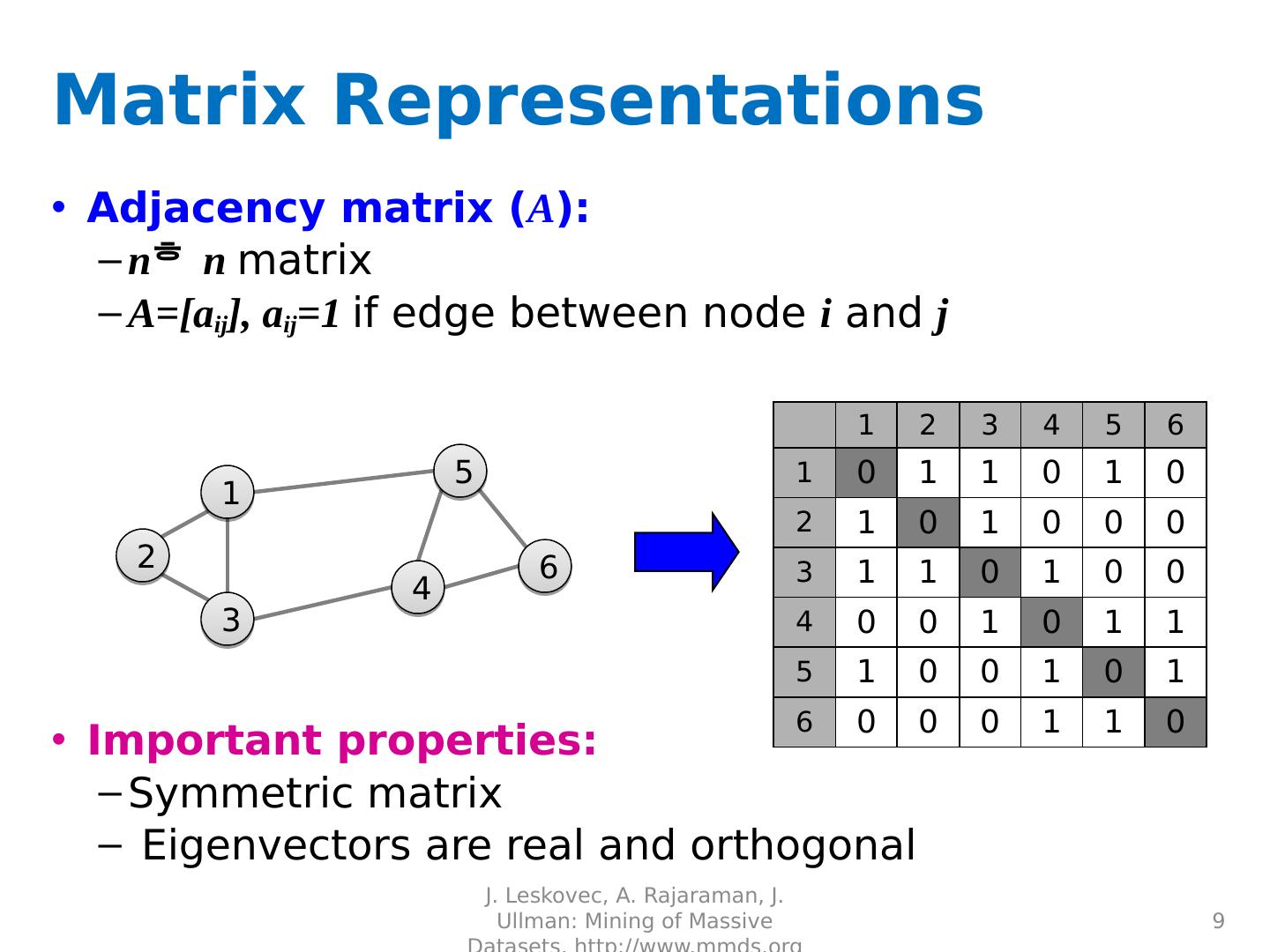
9 .Matrix Representations Adjacency matrix ( A ): n n matrix A=[ a ij ], a ij =1 if edge between node i and j Important properties: Symmetric matrix Eigenvectors are real and orthogonal J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 9 1 3 2 5 4 6 1 2 3 4 5 6 1 0 1 1 0 1 0 2 1 0 1 0 0 0 3 1 1 0 1 0 0 4 0 0 1 0 1 1 5 1 0 0 1 0 1 6 0 0 0 1 1 0
10 .Matrix Representations Degree matrix (D): n n diagonal matrix D=[ d ii ], d ii = degree of node i J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 10 1 3 2 5 4 6 1 2 3 4 5 6 1 3 0 0 0 0 0 2 0 2 0 0 0 0 3 0 0 3 0 0 0 4 0 0 0 3 0 0 5 0 0 0 0 3 0 6 0 0 0 0 0 2
11 .Matrix Representations Laplacian matrix (L): n n symmetric matrix What is trivial eigenpair ? Important properties: Eigenvalues are non-negative real numbers Eigenvectors are real and orthogonal J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 11 1 3 2 5 4 6 1 2 3 4 5 6 1 3 -1 -1 0 -1 0 2 -1 2 -1 0 0 0 3 -1 -1 3 -1 0 0 4 0 0 -1 3 -1 -1 5 -1 0 0 -1 3 -1 6 0 0 0 -1 -1 2
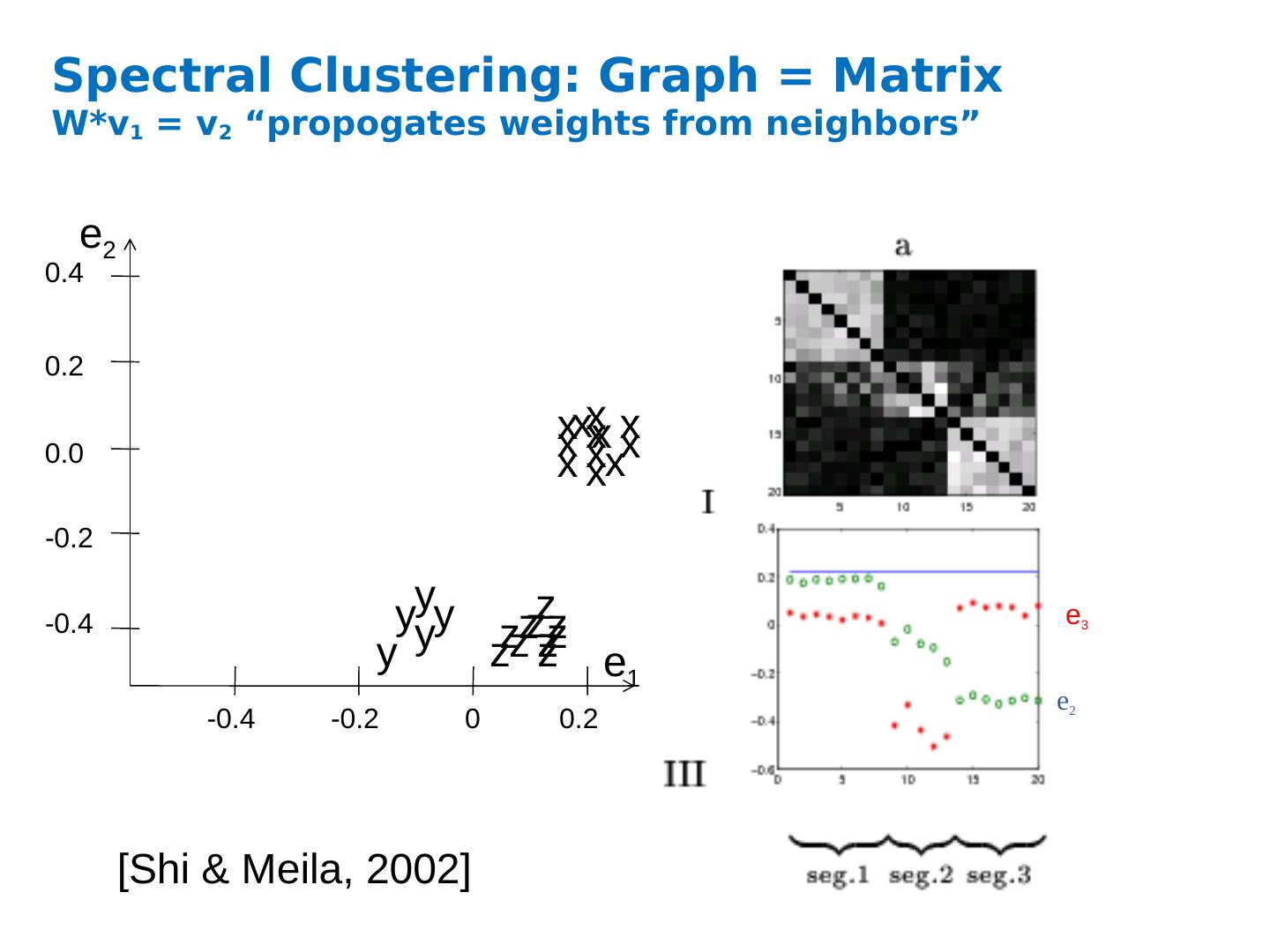
12 .Spectral Clustering: Graph = Matrix W*v 1 = v 2 “ propogates weights from neighbors” [Shi & Meila, 2002 ] e 2 e 3 -0.4 -0.2 0 0.2 -0.4 -0.2 0.0 0.2 0.4 x x x x x x y y y y y x x x x x x z z z z z z z z z z z e 1 e 2
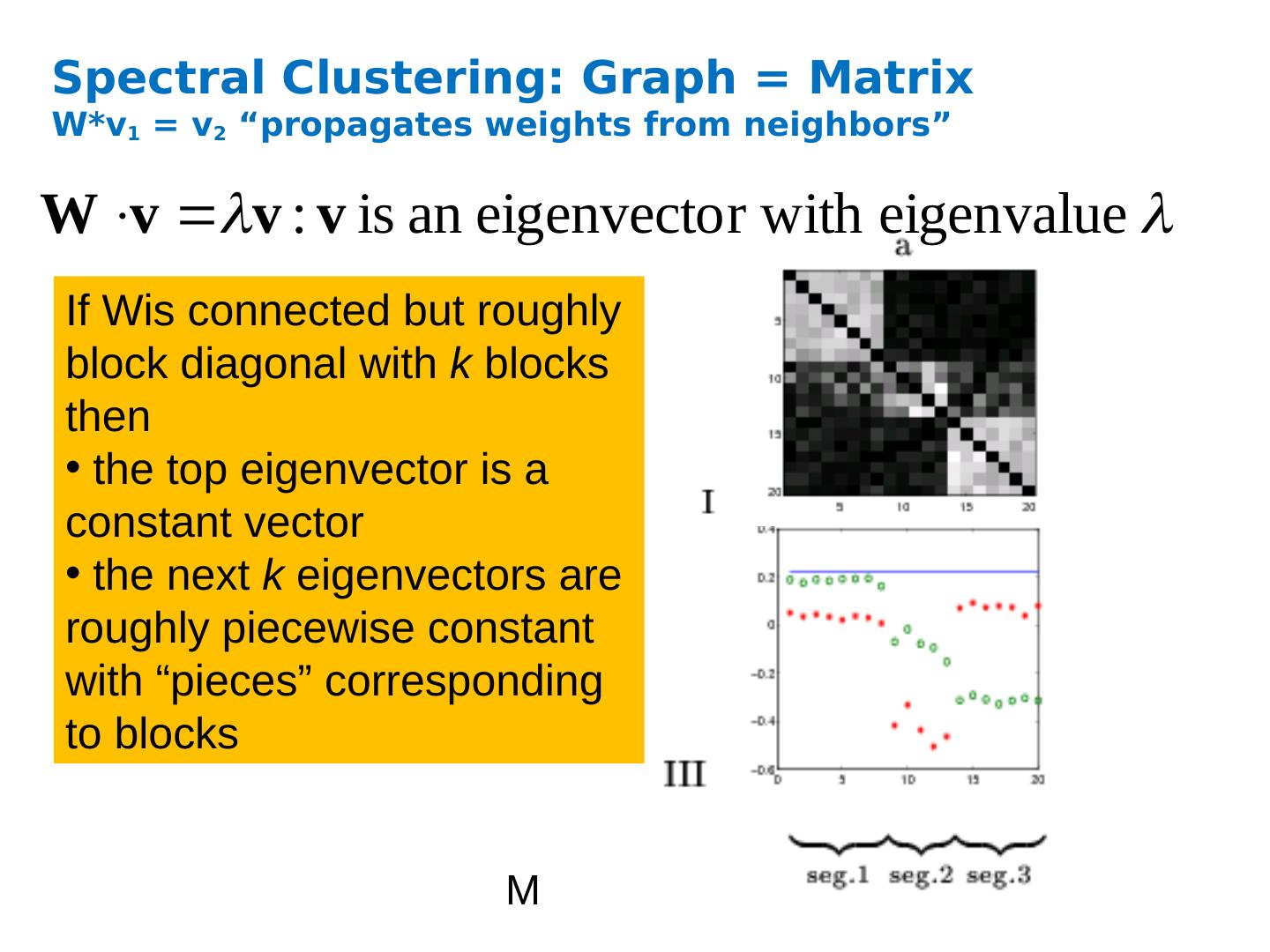
13 .Spectral Clustering: Graph = Matrix W*v 1 = v 2 “propagates weights from neighbors” M If Wis connected but roughly block diagonal with k blocks then the top eigenvector is a constant vector the next k eigenvectors are roughly piecewise constant with “pieces” corresponding to blocks
14 .Spectral Clustering: Graph = Matrix W*v 1 = v 2 “propagates weights from neighbors” M If W is connected but roughly block diagonal with k blocks then the “top” eigenvector is a constant vector the next k eigenvectors are roughly piecewise constant with “pieces” corresponding to blocks Spectral clustering: Find the top k+1 eigenvectors v 1 ,…, v k+1 Discard the “top” one Replace every node a with k -dimensional vector x a = < v 2 ( a ) ,…, v k+1 ( a ) > Cluster with k -means
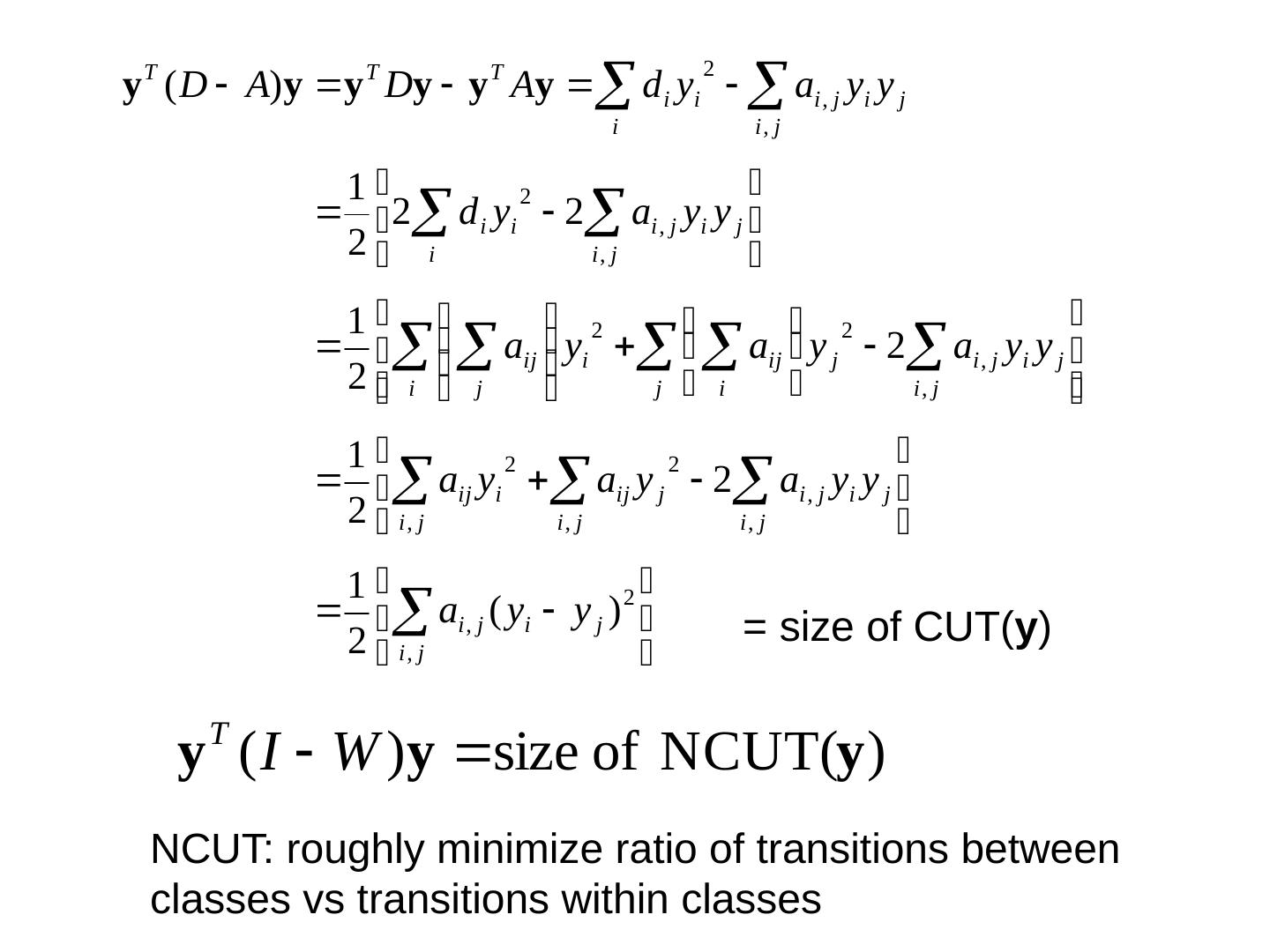
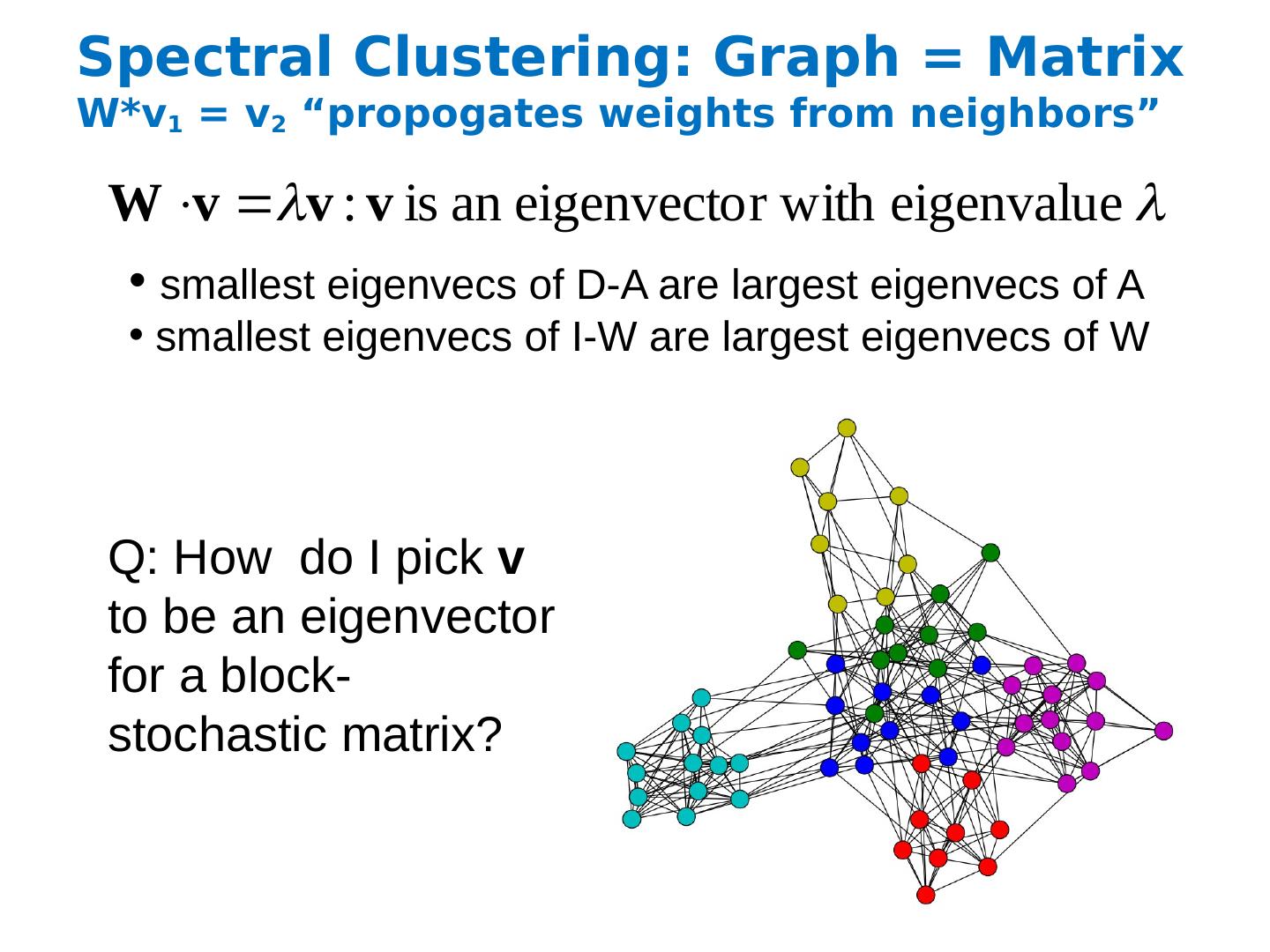
15 .Spectral Clustering: Graph = Matrix W*v 1 = v 2 “ propogates weights from neighbors” smallest eigenvecs of D-A are largest eigenvecs of A smallest eigenvecs of I-W are largest eigenvecs of W Suppose each y(i)=+1 or -1 : Then y is a cluster indicator that splits the nodes into two what is y T (D-A) y ?
16 .= size of CUT( y ) NCUT: roughly minimize ratio of transitions between classes vs transitions within classes
17 .So far… How to define a “good” partition of a graph? Minimize a given graph cut criterion How to efficiently identify such a partition? Approximate using information provided by the eigenvalues and eigenvectors of a graph Spectral Clustering 17 J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org
18 .Spectral Clustering Algorithms Three basic stages: 1) Pre-processing Construct a matrix representation of the graph 2) Decomposition Compute eigenvalues and eigenvectors of the matrix Map each point to a lower-dimensional representation based on one or more eigenvectors 3) Grouping Assign points to two or more clusters, based on the new representation J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 18
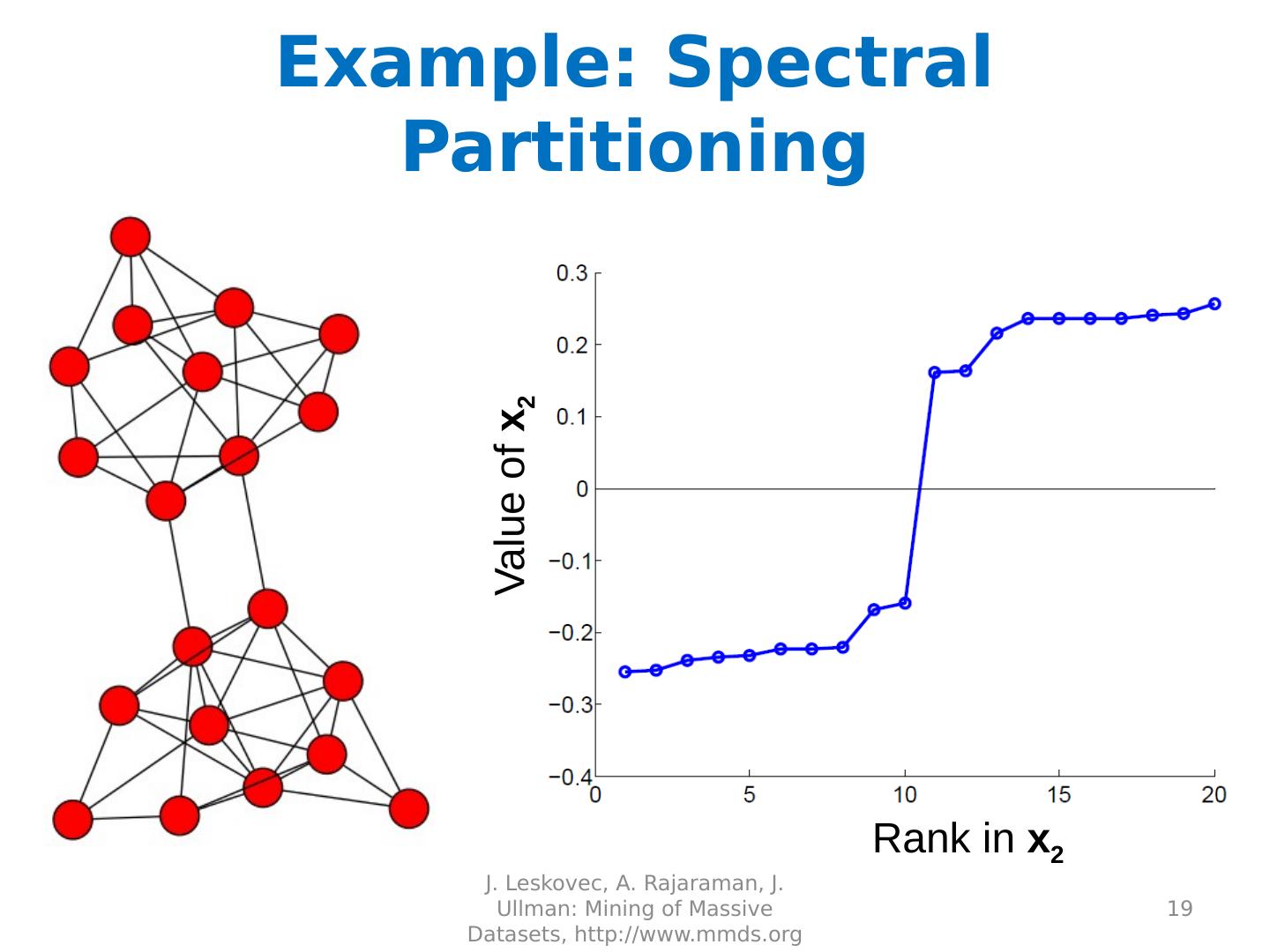
19 .Example: Spectral Partitioning J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 19 Rank in x 2 Value of x 2
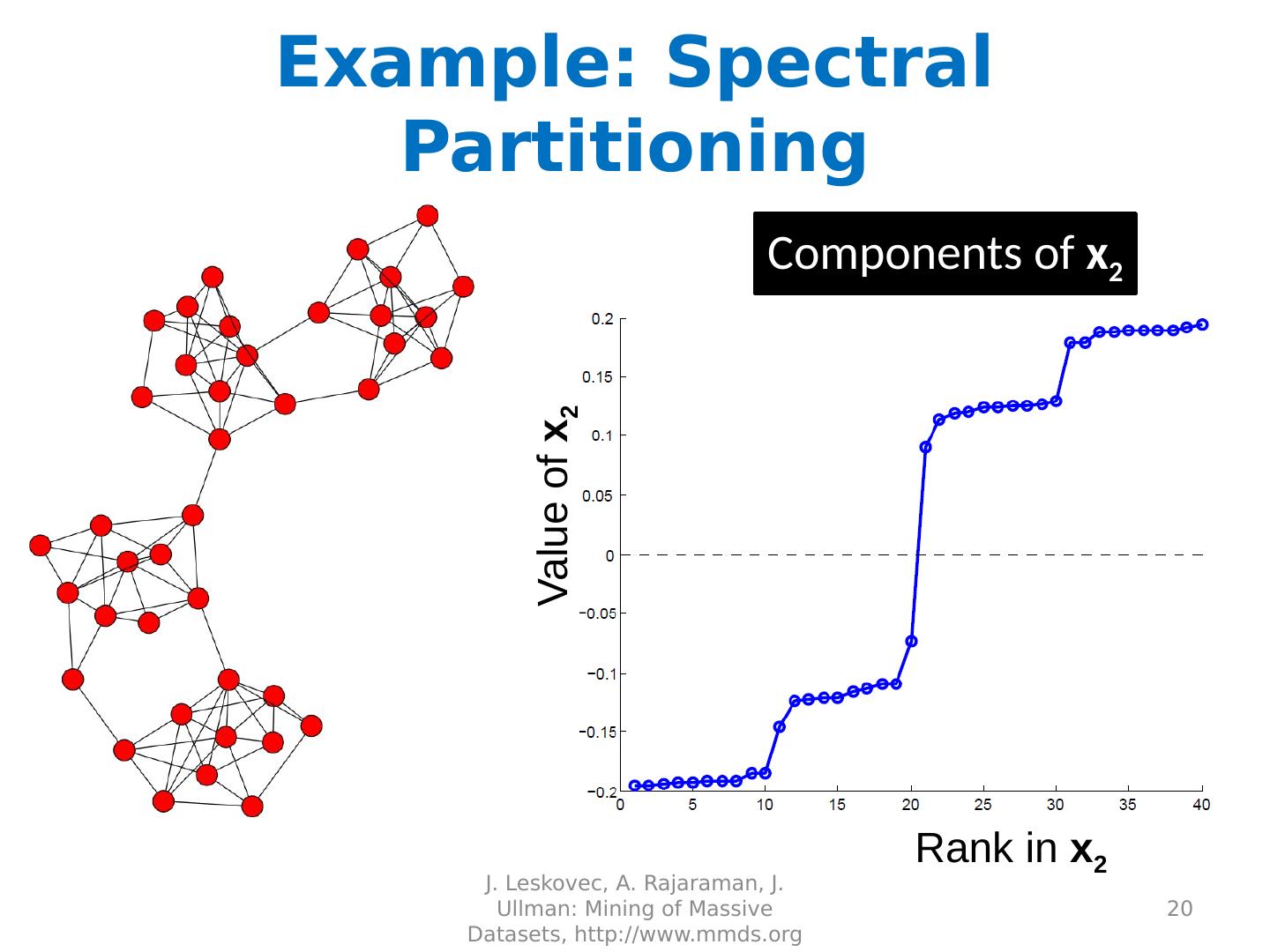
20 .Example: Spectral Partitioning J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 20 Rank in x 2 Value of x 2 Components of x 2
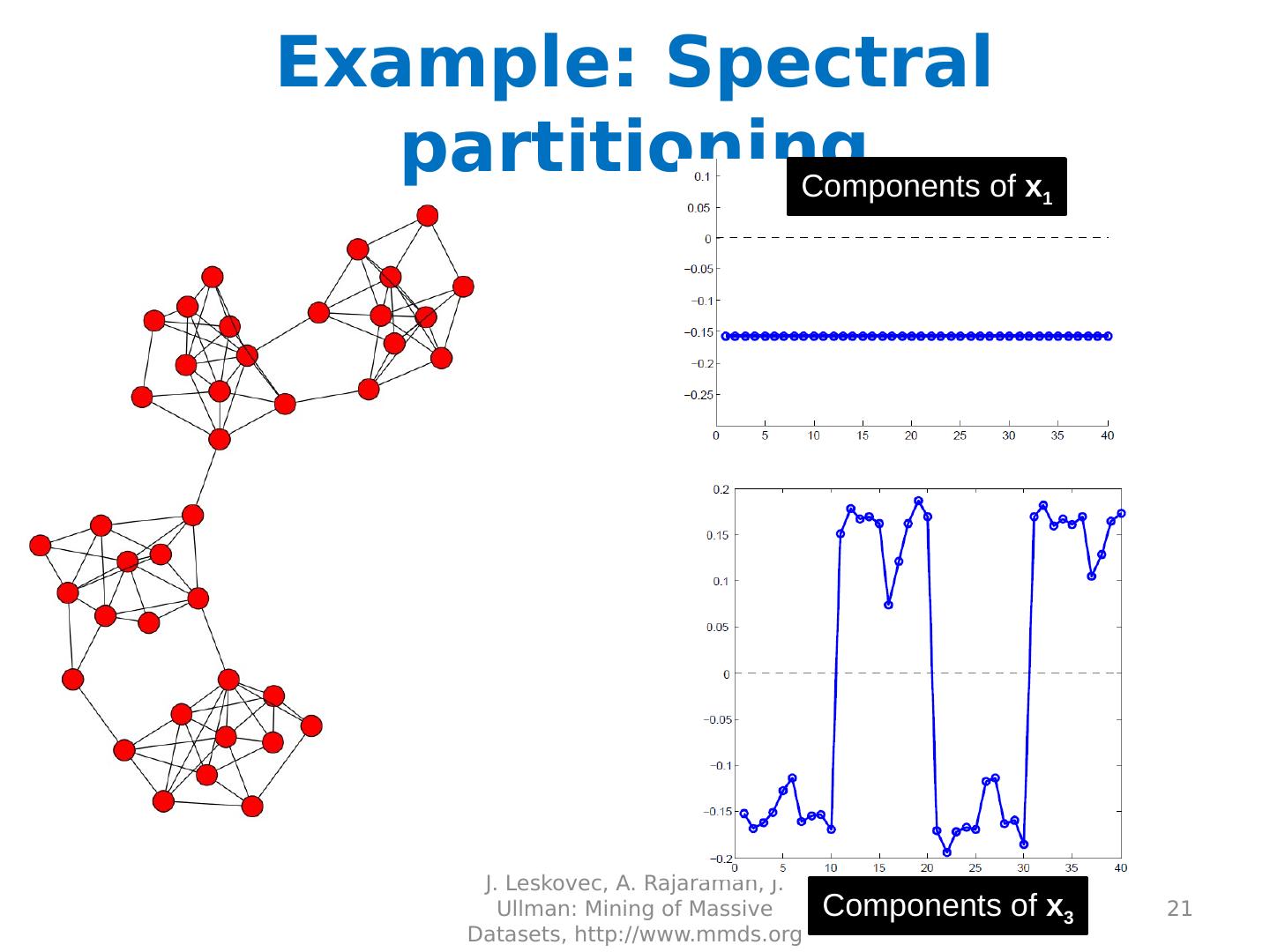
21 .Example: Spectral partitioning J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 21 Components of x 1 Components of x 3
22 .k-Way Spectral Clustering How do we partition a graph into k clusters? Two basic approaches: Recursive bi-partitioning [Hagen et al., ’92] Recursively apply bi-partitioning algorithm in a hierarchical divisive manner Disadvantages: Inefficient, unstable Cluster multiple eigenvectors [Shi- Malik , ’00] Build a reduced space from multiple eigenvectors Commonly used in recent papers A preferable approach… J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 22
23 .Why use multiple eigenvectors? Approximates the optimal cut [Shi- Malik , ’00] Can be used to approximate optimal k -way normalized cut Emphasizes cohesive clusters Increases the unevenness in the distribution of the data Associations between similar points are amplified, associations between dissimilar points are attenuated The data begins to “approximate a clustering” Well-separated space Transforms data to a new “embedded space”, consisting of k orthogonal basis vectors Multiple eigenvectors prevent instability due to information loss J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 23
24 .Spectral Clustering: Graph = Matrix W*v 1 = v 2 “ propogates weights from neighbors” Q: How do I pick v to be an eigenvector for a block-stochastic matrix? smallest eigenvecs of D-A are largest eigenvecs of A smallest eigenvecs of I-W are largest eigenvecs of W
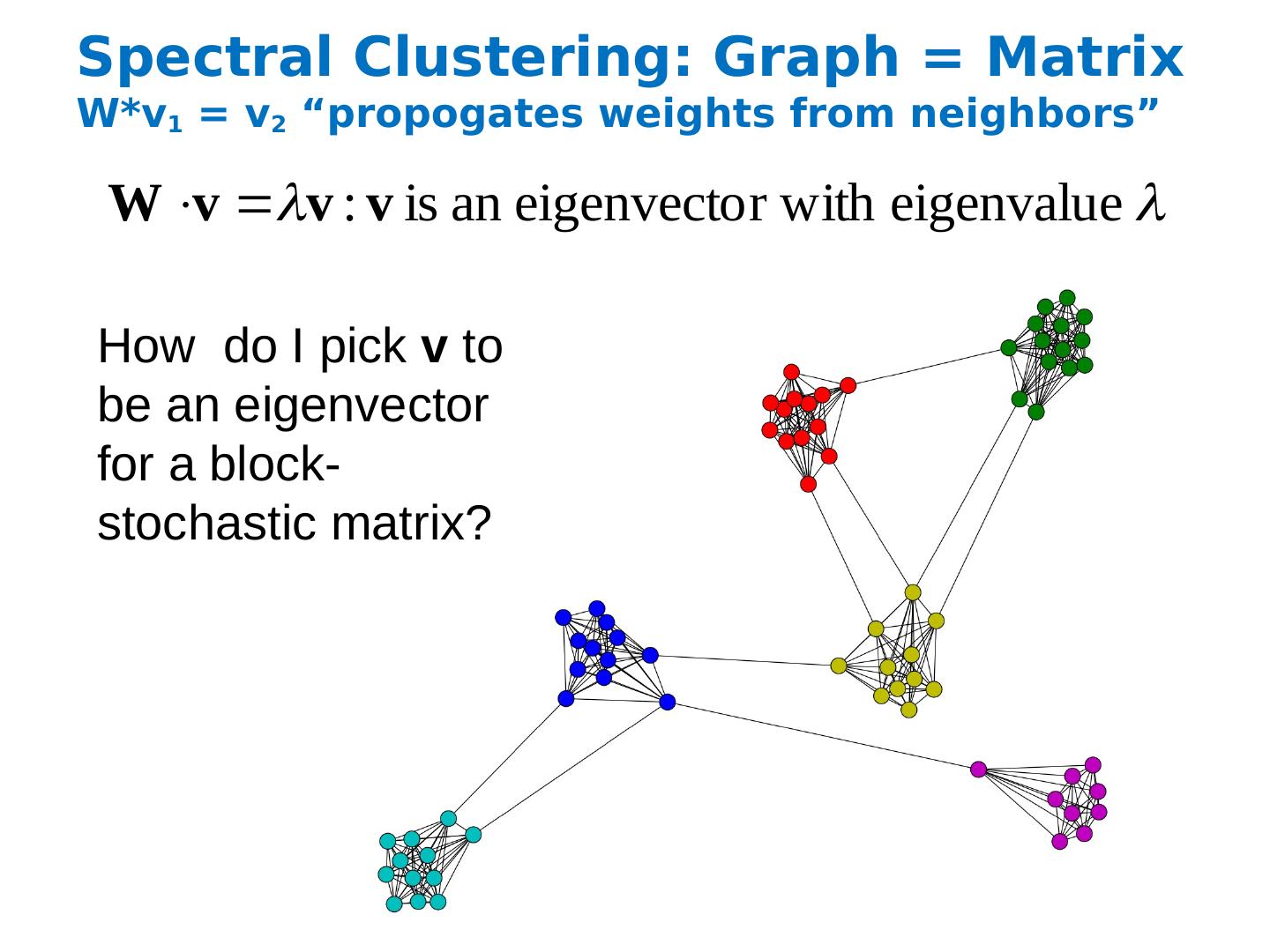
25 .Spectral Clustering: Graph = Matrix W*v 1 = v 2 “ propogates weights from neighbors” How do I pick v to be an eigenvector for a block-stochastic matrix?
26 .Spectral Clustering: Graph = Matrix W*v 1 = v 2 “ propogates weights from neighbors” smallest eigenvecs of D-A are largest eigenvecs of A smallest eigenvecs of I-W are largest eigenvecs of W Suppose each y(i)=+1 or -1 : Then y is a cluster indicator that cuts the nodes into two what is y T (D-A) y ? The cost of the graph cut defined by y what is y T (I-W) y ? Also a cost of a graph cut defined by y How to minimize it? Turns out: to minimize y T X y / ( y T y ) find smallest eigenvector of X But: this will not be +1/-1, so it’s a “relaxed” solution
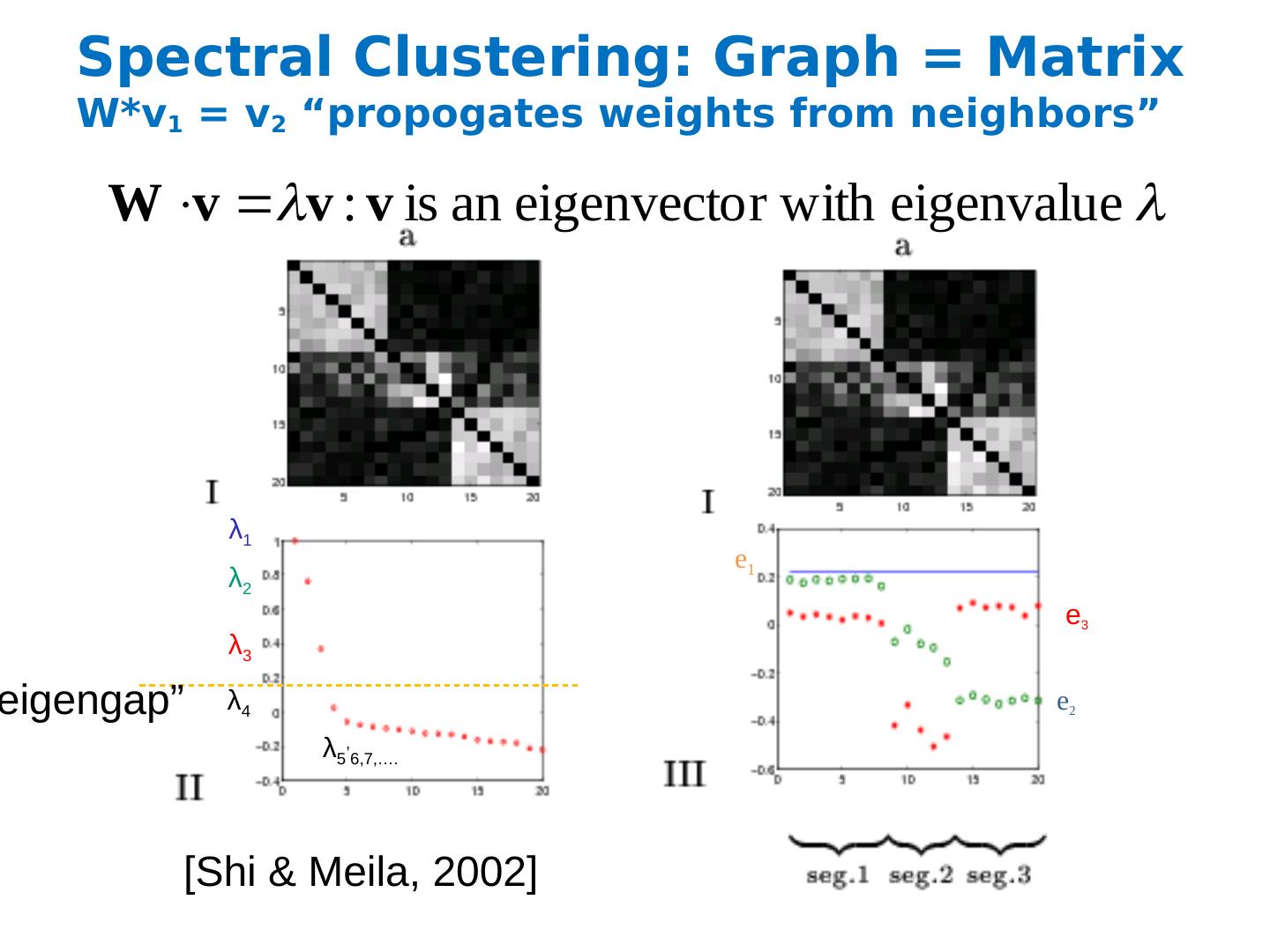
27 .Spectral Clustering: Graph = Matrix W*v 1 = v 2 “ propogates weights from neighbors” [Shi & Meila, 2002 ] λ 2 λ 3 λ 4 λ 5 , 6 ,7,…. λ 1 e 1 e 2 e 3 “ eigengap ”
28 .Some more terms If A is an adjacency matrix (maybe weighted) and D is a (diagonal) matrix giving the degree of each node Then D-A is the ( unnormalized ) Laplacian W=AD -1 is a probabilistic adjacency matrix I-W is the (normalized or random-walk) Laplacian etc…. The largest eigenvectors of W correspond to the smallest eigenvectors of I-W So sometimes people talk about “ bottom eigenvectors of the Laplacian ”
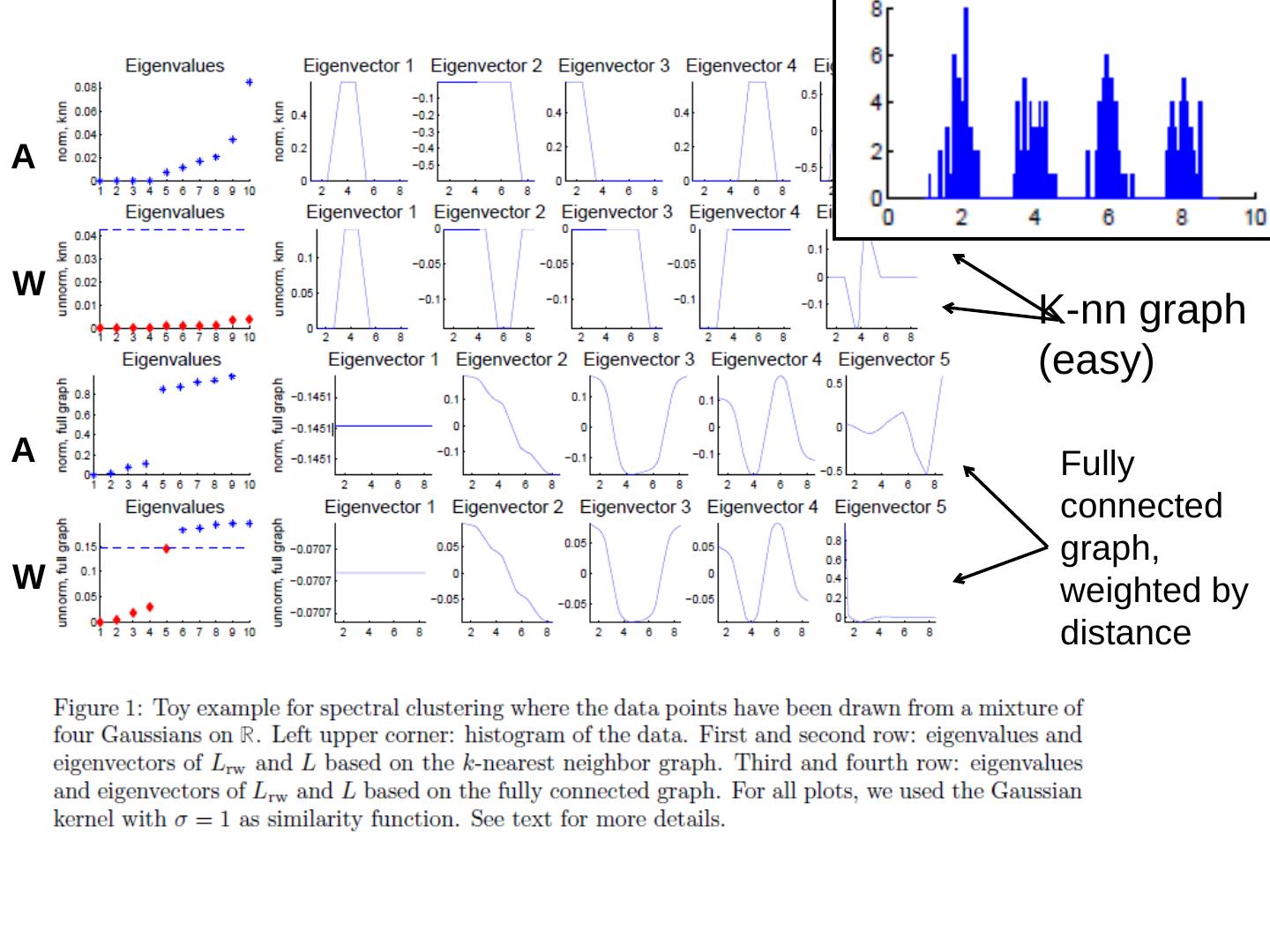
29 .A W A W K-nn graph (easy) Fully connected graph, weighted by distance