- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Semi-Supervised Learning With Graphs
展开查看详情
1 .Semi-Supervised Learning With Graphs Shannon Quinn (with thanks to William Cohen at CMU)
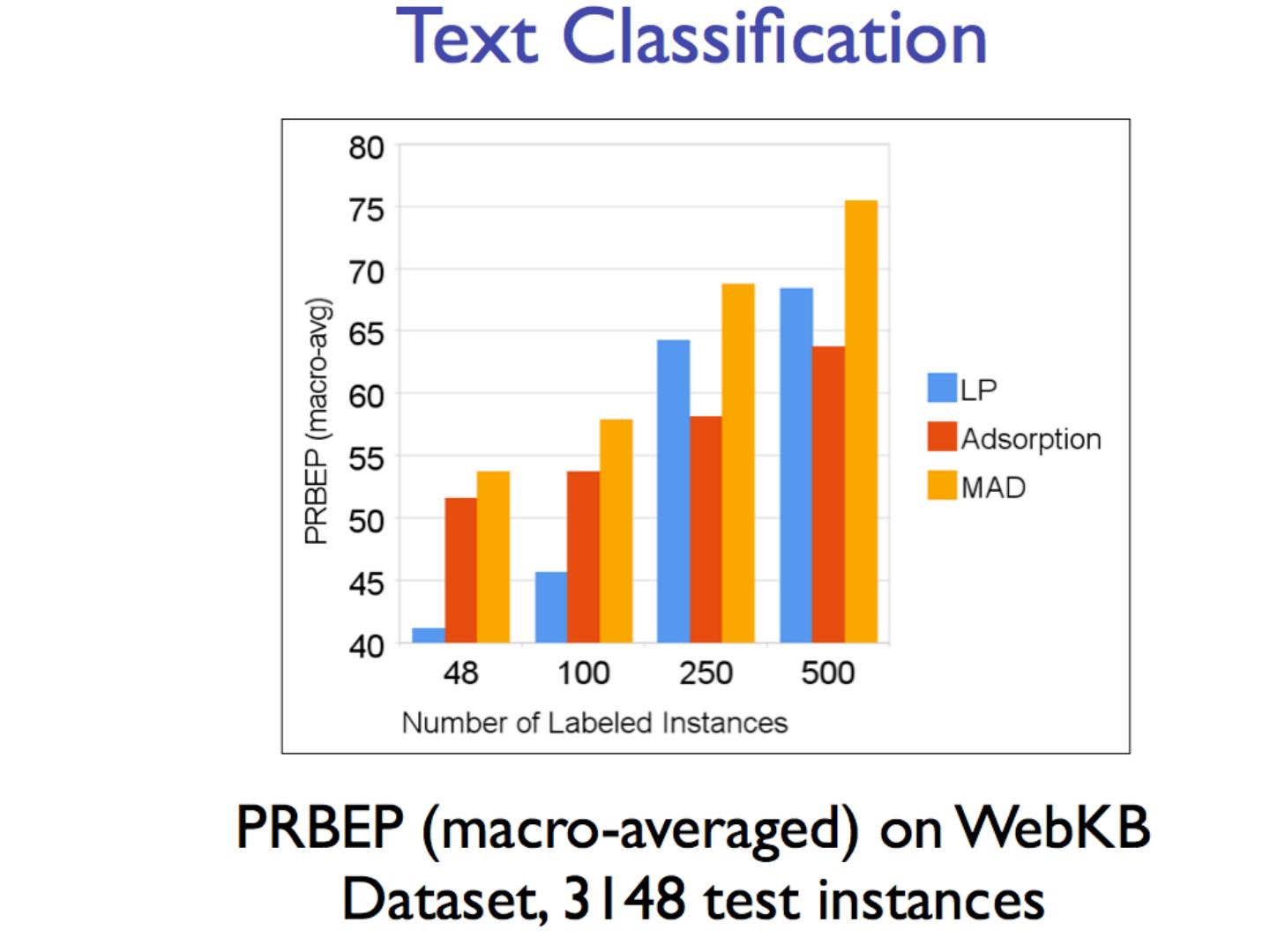
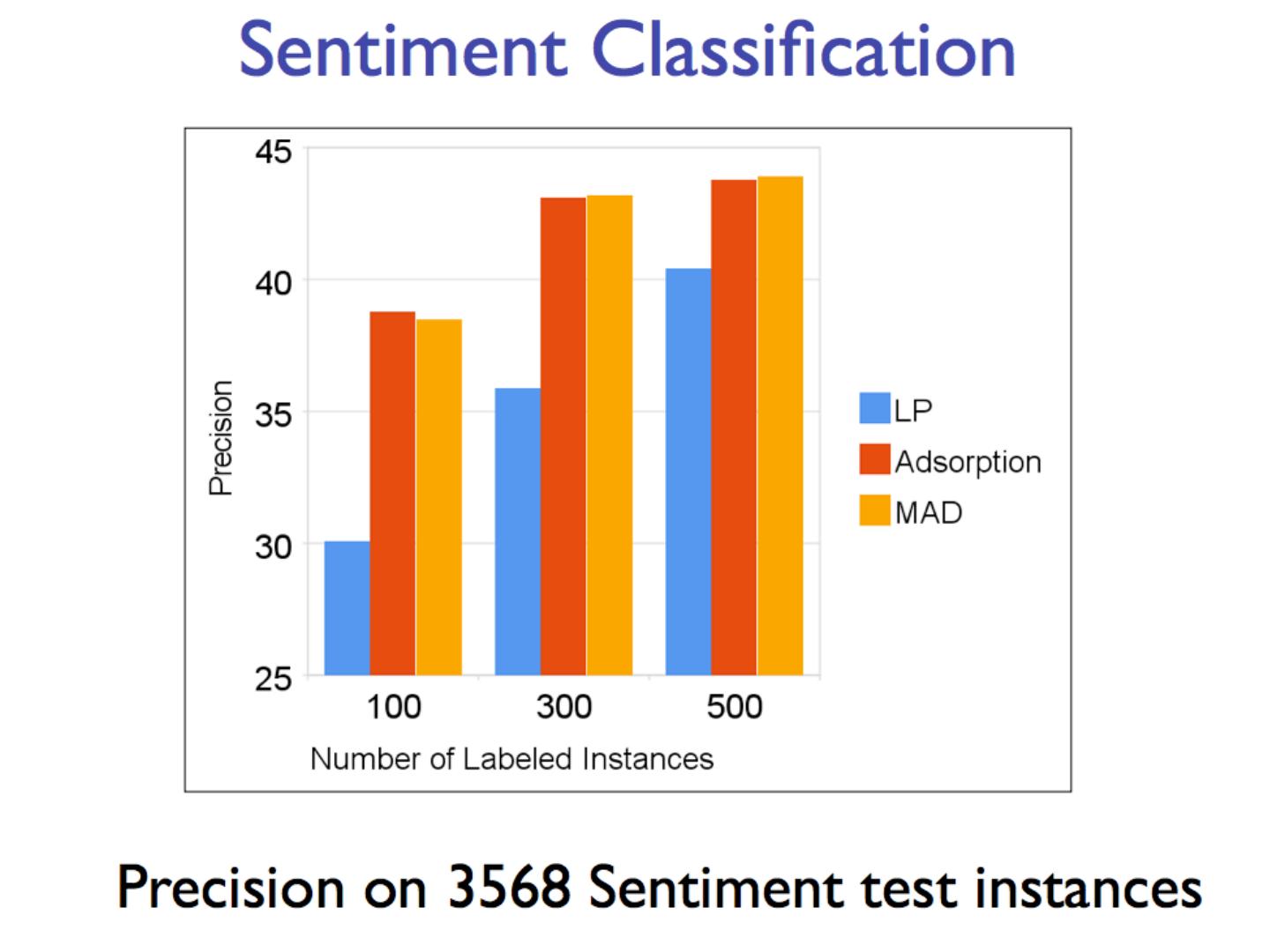
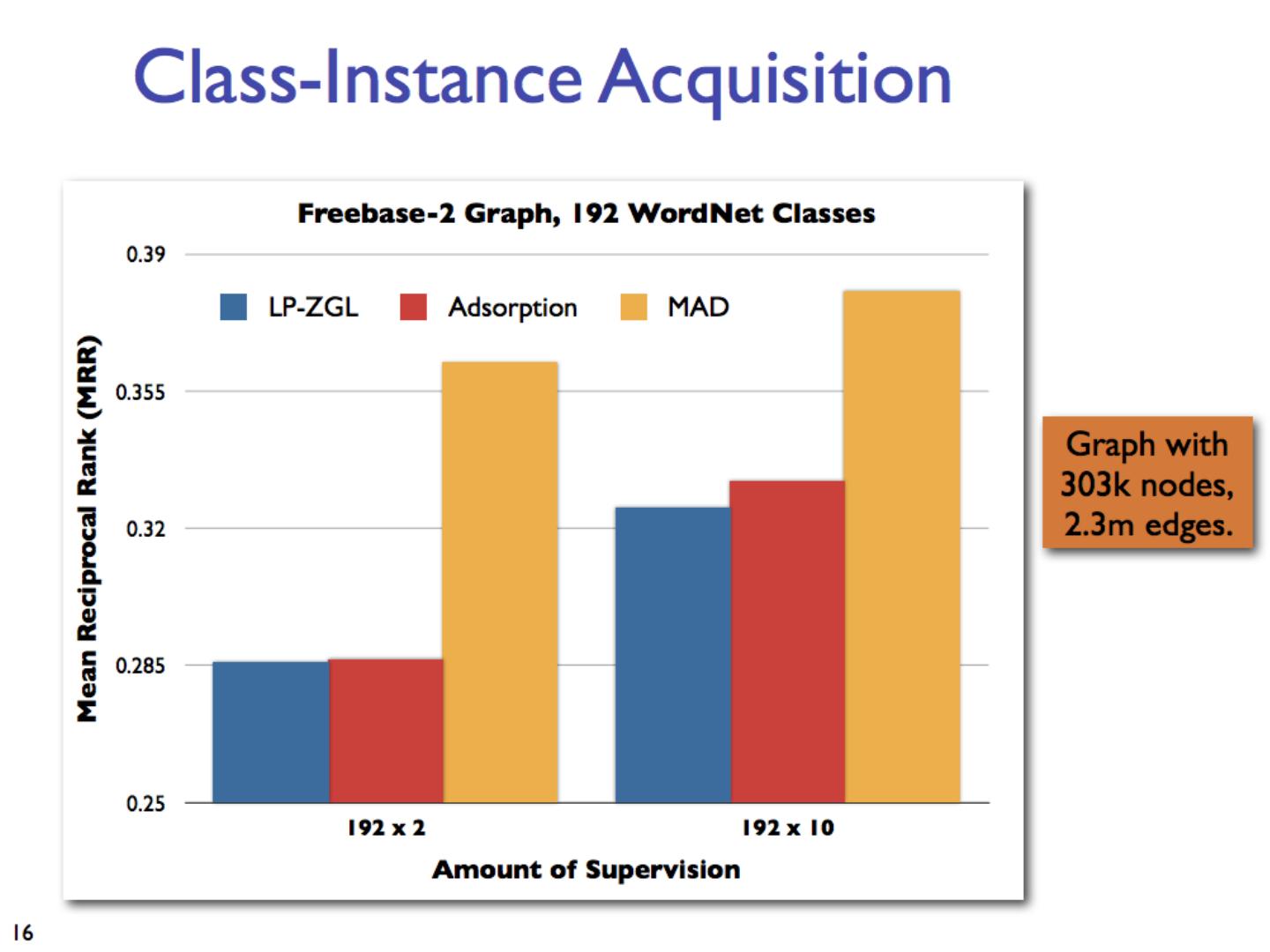
2 .Semi-supervised learning A pool of labeled examples L A (usually larger) pool of unlabeled examples U Can you improve accuracy somehow using U?
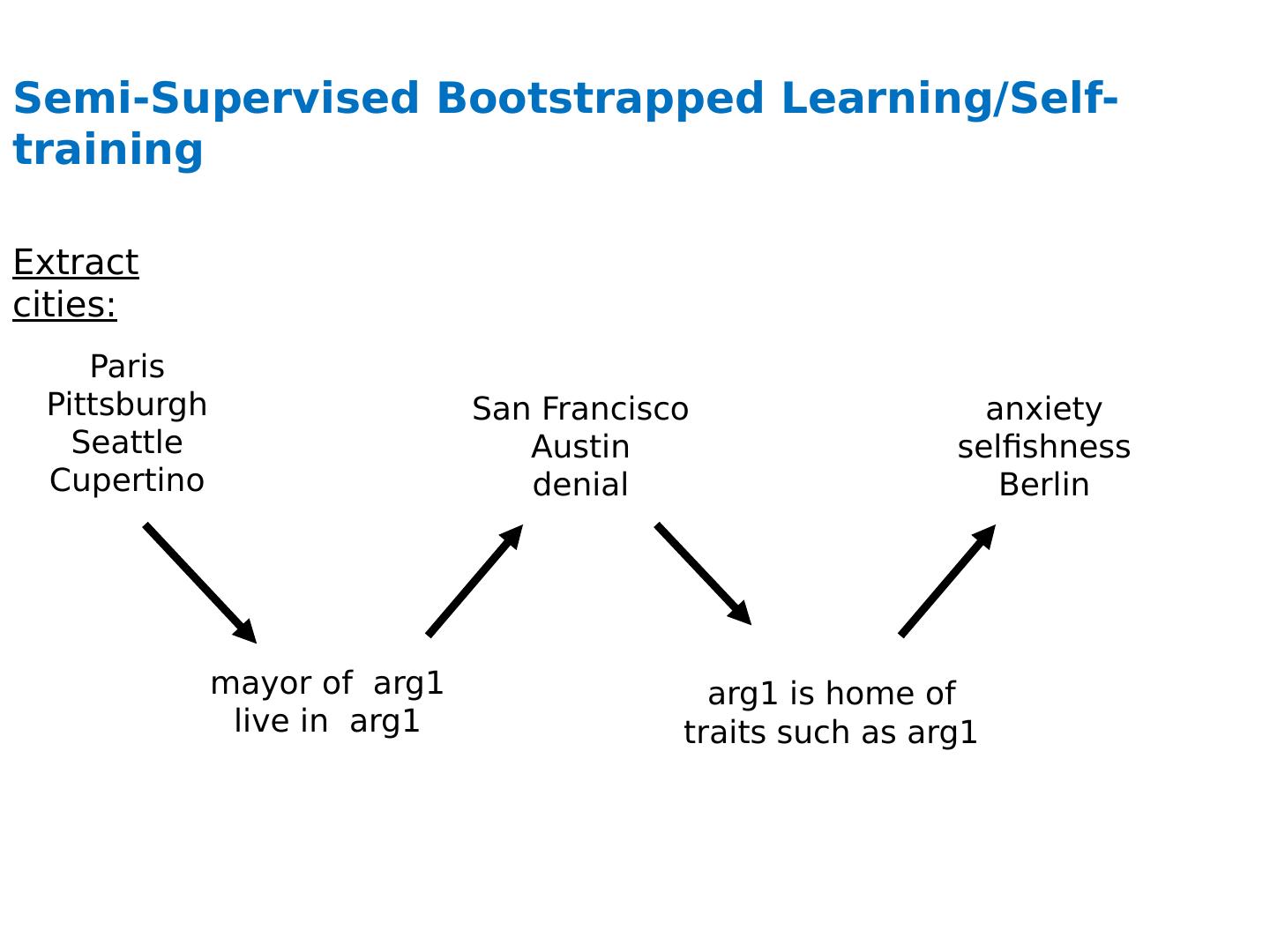
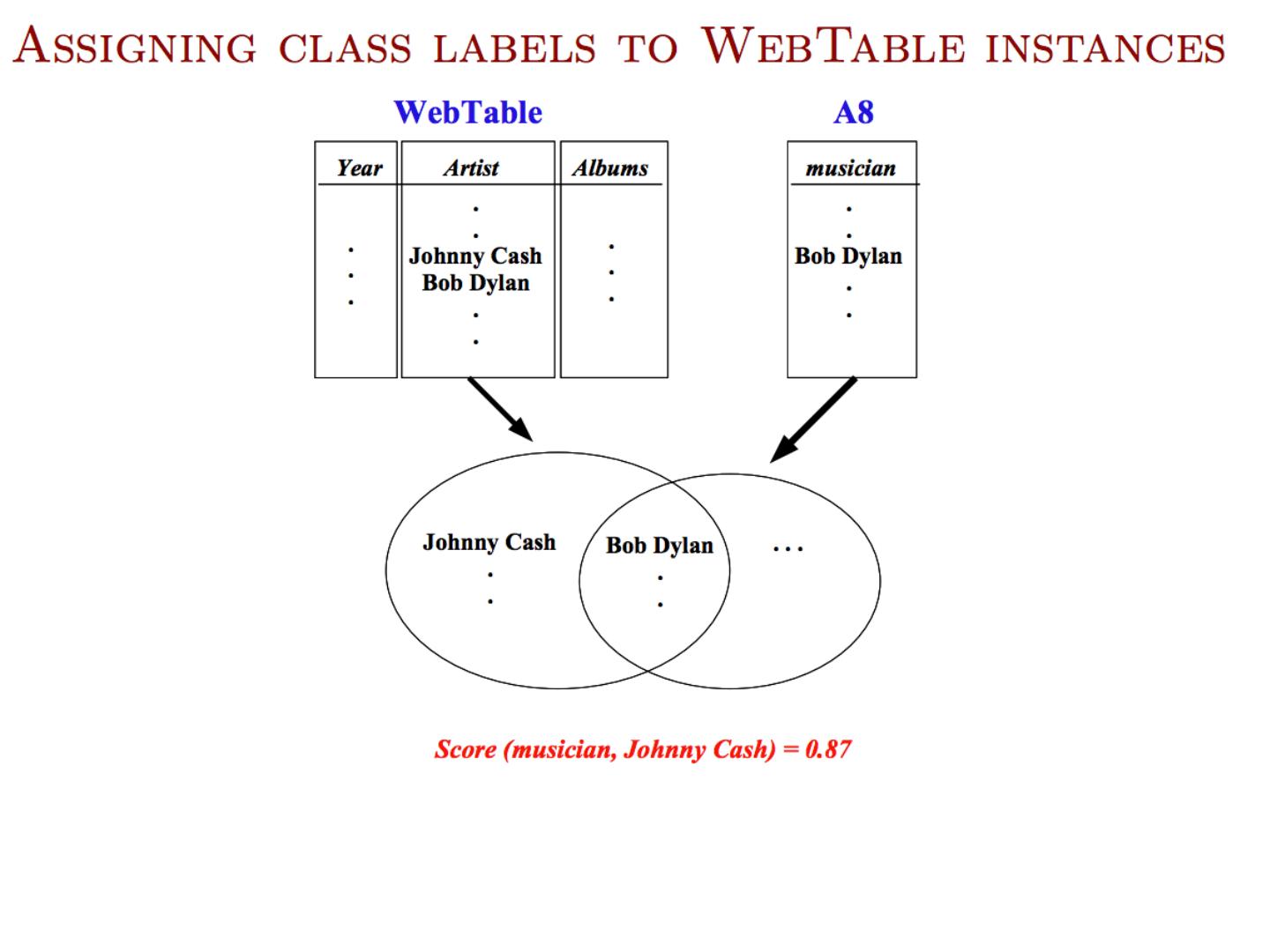
3 .Semi-Supervised Bootstrapped Learning/Self-training Paris Pittsburgh Seattle Cupertino mayor of arg1 live in arg1 San Francisco Austin denial arg1 is home of traits such as arg1 anxiety selfishness Berlin Extract cities:
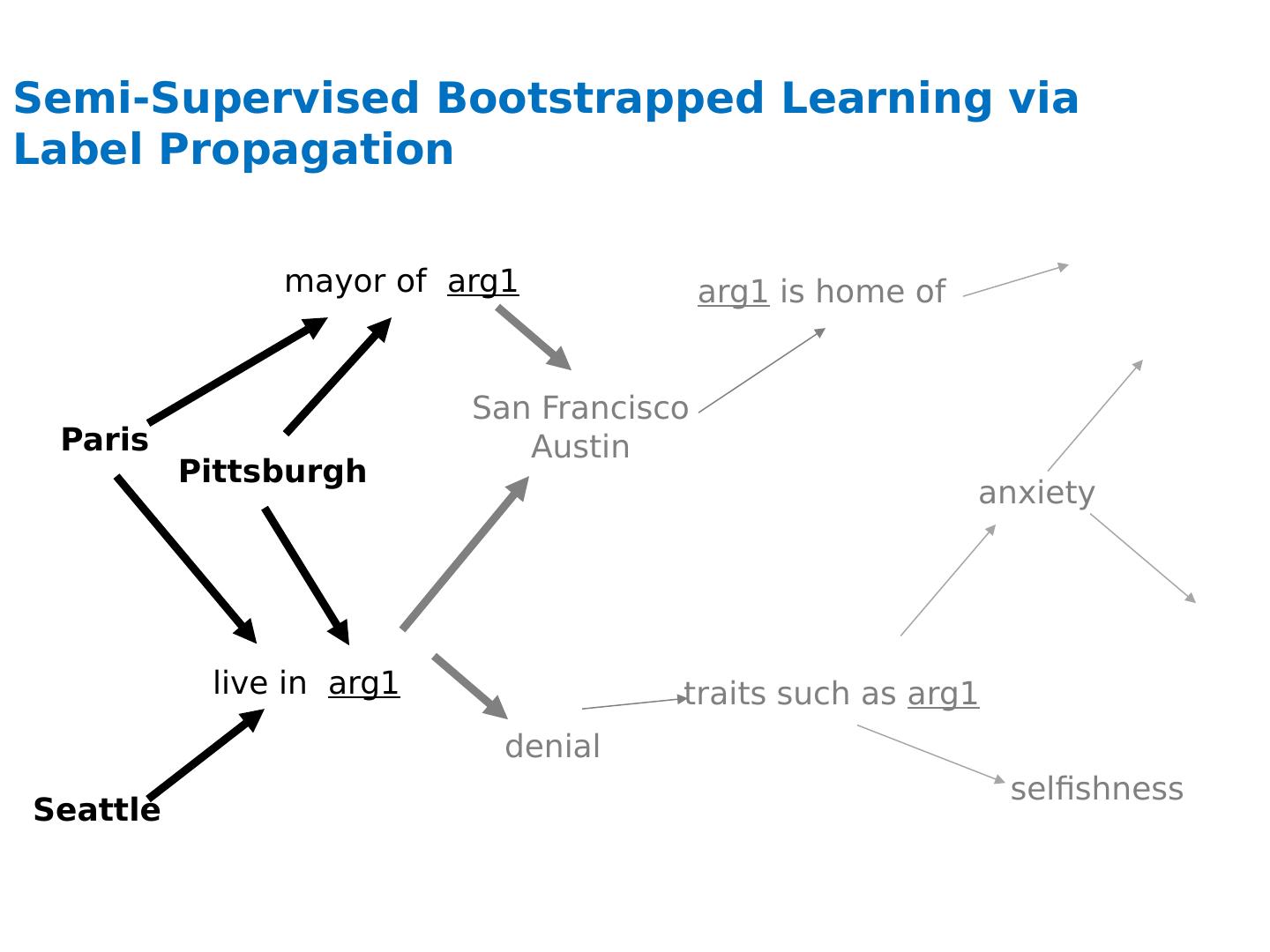
4 .Semi-Supervised Bootstrapped Learning via Label Propagation Paris live in arg1 San Francisco Austin traits such as arg1 anxiety mayor of arg1 Pittsburgh Seattle denial arg1 is home of selfishness
5 .Semi-Supervised Bootstrapped Learning via Label Propagation Paris live in arg1 San Francisco Austin traits such as arg1 anxiety mayor of arg1 Pittsburgh Seattle denial arg1 is home of selfishness Nodes “ near ” seeds Nodes “ far from ” seeds Information from other categories tells you “ how far ” (when to stop propagating) arrogance traits such as arg1 denial selfishness
6 .Semi-Supervised Learning as Label Propagation on a (Bipartite) Graph Paris live in arg1 San Francisco Austin traits such as arg1 anxiety mayor of arg1 Pittsburgh Seattle denial arg1 is home of selfishness Propagate labels to nearby nodes X is “ near ” Y if there is a high probability of reaching X from Y with a random walk where each step is either (a) move to a random neighbor or (b) jump back to start node Y, if you ’ re at an NP node rewards multiple paths penalizes long paths penalizes high-fanout paths I like arg1 beer Propagation methods: “ personalized PageRank ” (aka damped PageRank, random-walk-with-reset)
7 .ASONAM-2010 (Advances in Social Networks Analysis and Mining)
8 .Network Datasets with Known Classes UBMCBlog AGBlog MSPBlog Cora Citeseer
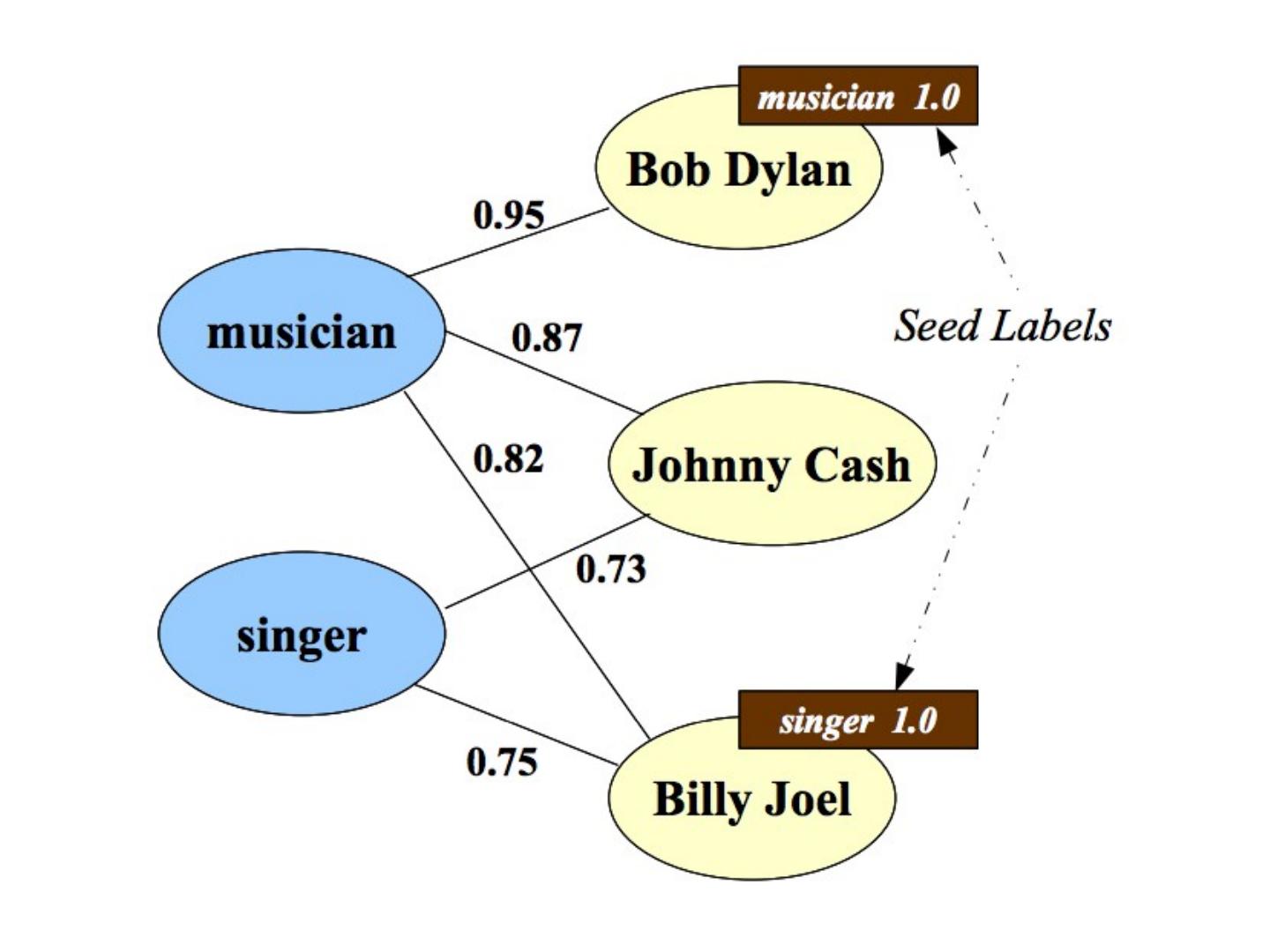
9 .RWR - fixpoint of: Seed selection order by PageRank, degree, or randomly go down list until you have at least k examples/class
10 .CoEM /HF/ wvRN One definition [ MacSkassy & Provost, JMLR 2007] :…
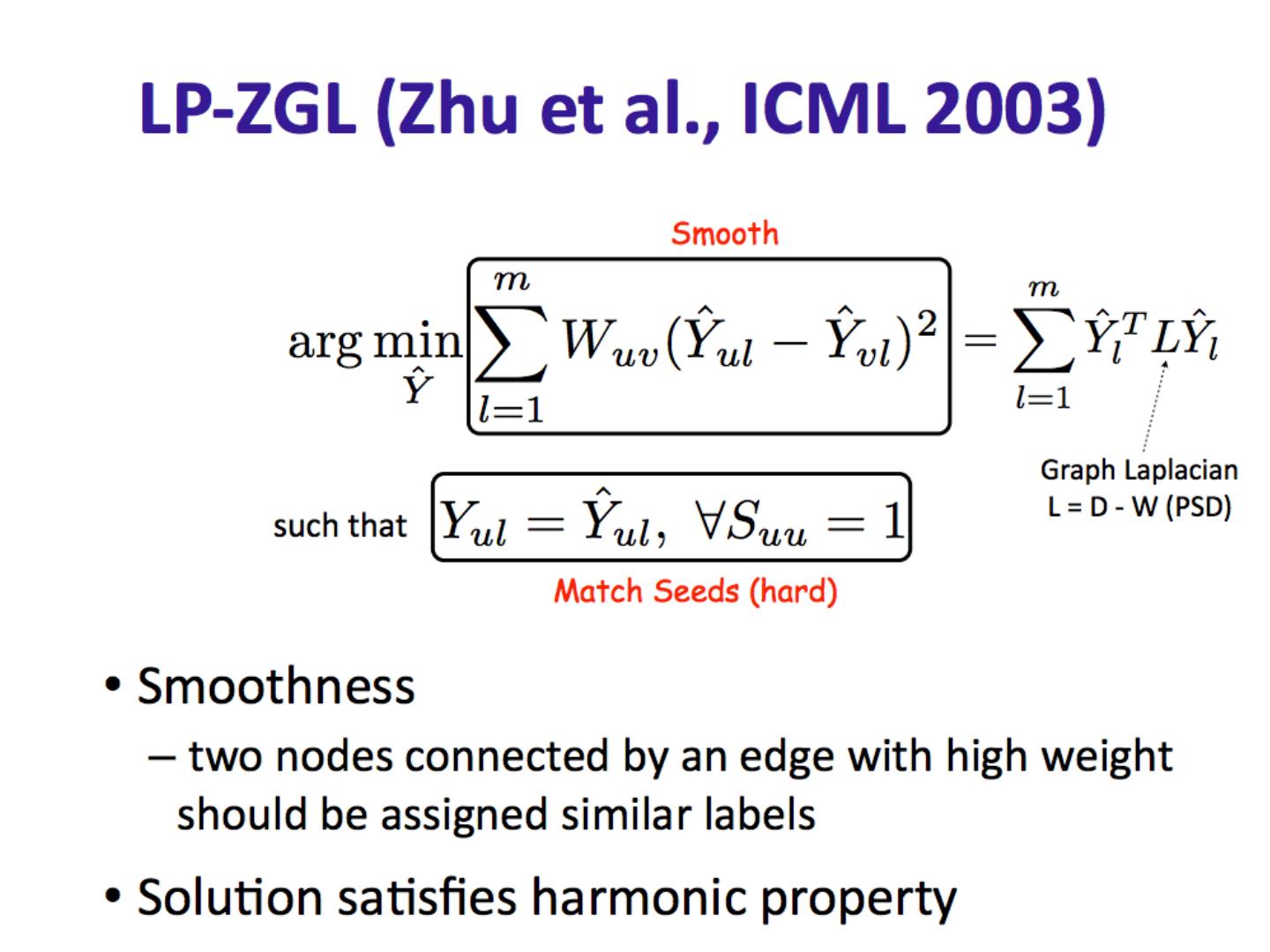
11 .CoEM /HF/ wvRN Another definition in [X. Zhu, Z. Ghahramani , and J. Lafferty, ICML 2003] A harmonic field – the score of each node in the graph is the harmonic, or linearly weighted, average of its neighbors’ scores (harmonic field, HF)
12 .CoEM /HF/ wvRN Another justification of the same algorithm…. … start with co-training with a naïve Bayes learner
13 .
14 .
15 .
16 .How to do this minimization? First, differentiate to find min is at Jacobi method : To solve Ax=b for x Iterate: … or:
17 .How to do this minimization? First, differentiate to find min is at Jacobi method : To solve Ax=b for x Iterate: … or:
18 .How to do this minimization? First, differentiate to find min is at Jacobi method : To solve Ax=b for x Iterate: … or:
19 .How to do this minimization? First, differentiate to find min is at Jacobi method : To solve Ax=b for x Iterate: … or:
20 .How to do this minimization? First, differentiate to find min is at Jacobi method : To solve Ax=b for x Iterate: … or:
21 .How to do this minimization? First, differentiate to find min is at Jacobi method : To solve Ax=b for x Iterate: … or:
22 .How to do this minimization? First, differentiate to find min is at Jacobi method : To solve Ax=b for x Iterate: … or:
23 .How to do this minimization? First, differentiate to find min is at Jacobi method : To solve Ax=b for x Iterate: … or:
24 .How to do this minimization? First, differentiate to find min is at Jacobi method : To solve Ax=b for x Iterate: … or:
25 .From SemiSupervised to Unsupervised Learning
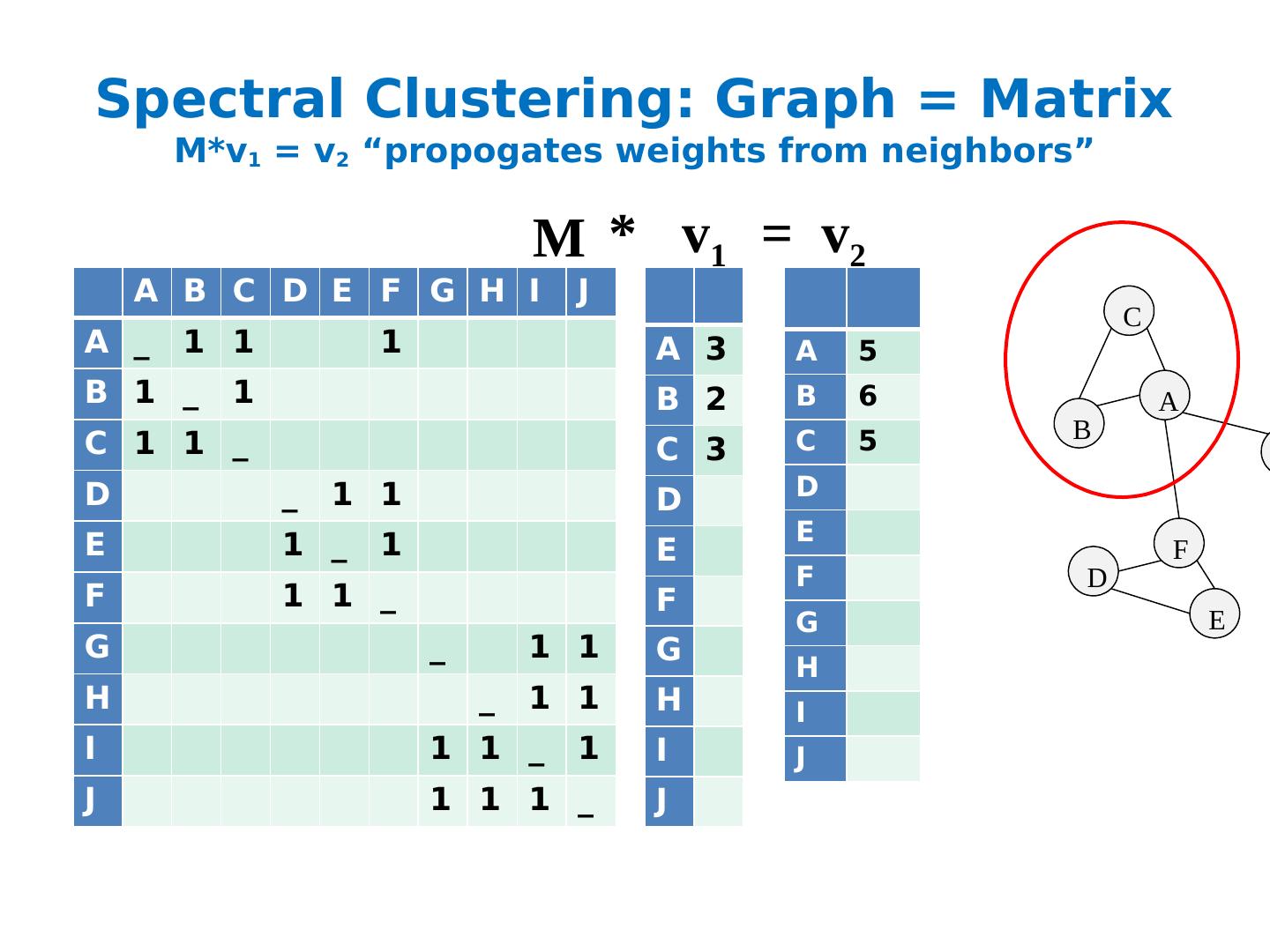
26 .Spectral Clustering: Graph = Matrix M*v 1 = v 2 “ propogates weights from neighbors ” H A B C D E F G H I J A _ 1 1 1 B 1 _ 1 C 1 1 _ D _ 1 1 E 1 _ 1 F 1 1 _ G _ 1 1 H _ 1 1 I 1 1 _ 1 J 1 1 1 _ A B C F D E G I J A 3 B 2 C 3 D E F G H I J M M v 1 A 5 B 6 C 5 D E F G H I J v 2 * =
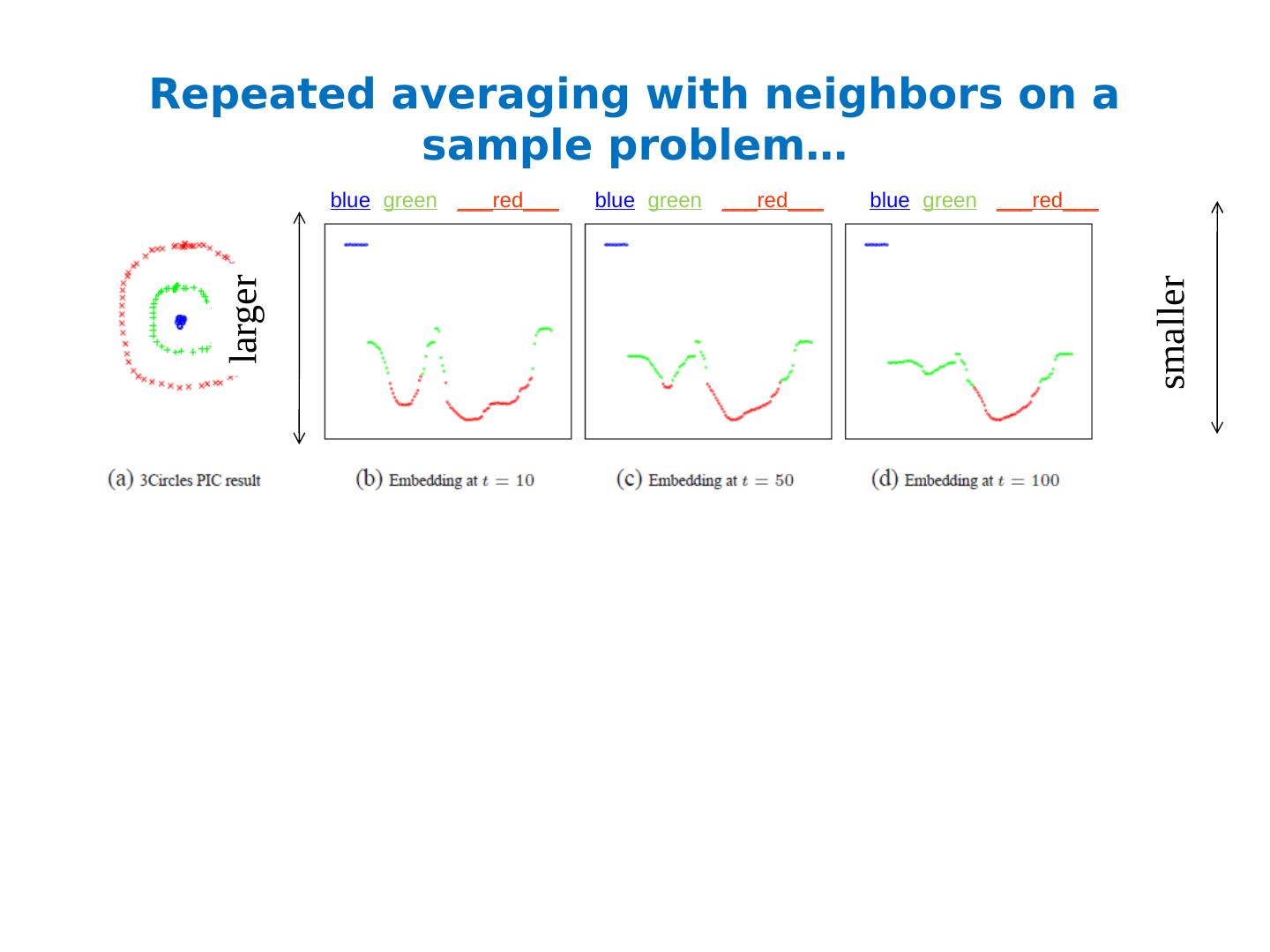
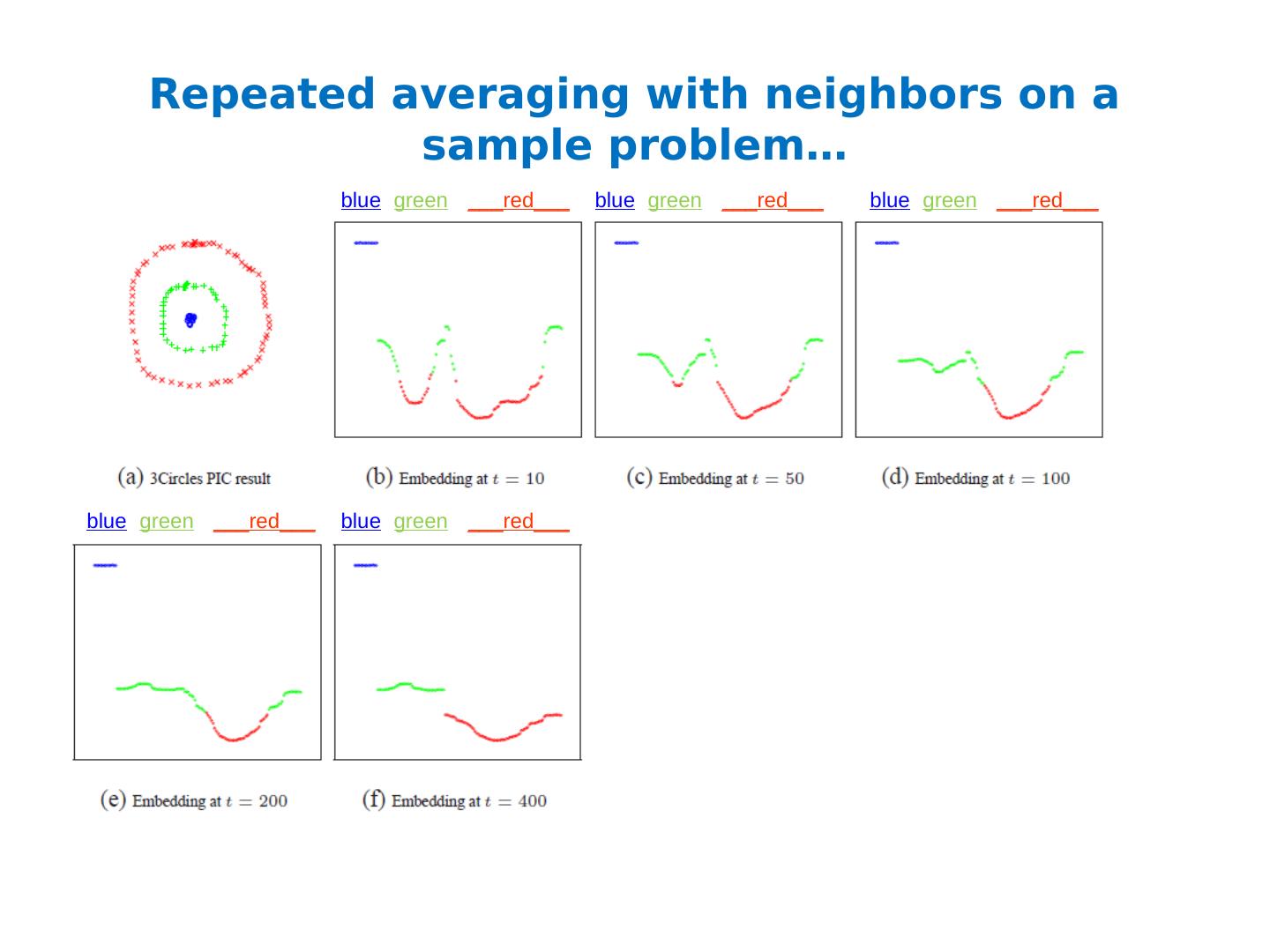
27 .Repeated averaging with neighbors as a clustering method Pick a vector v 0 (maybe at random) Compute v 1 = Wv 0 i.e., replace v 0 [x] with weighted average of v 0 [y] for the neighbors y of x Plot v 1 [x] for each x Repeat for v 2 , v 3 , … Variants widely used for semi-supervised learning clamping of labels for nodes with known labels Without clamping, will converge to constant v t What are the dynamics of this process?
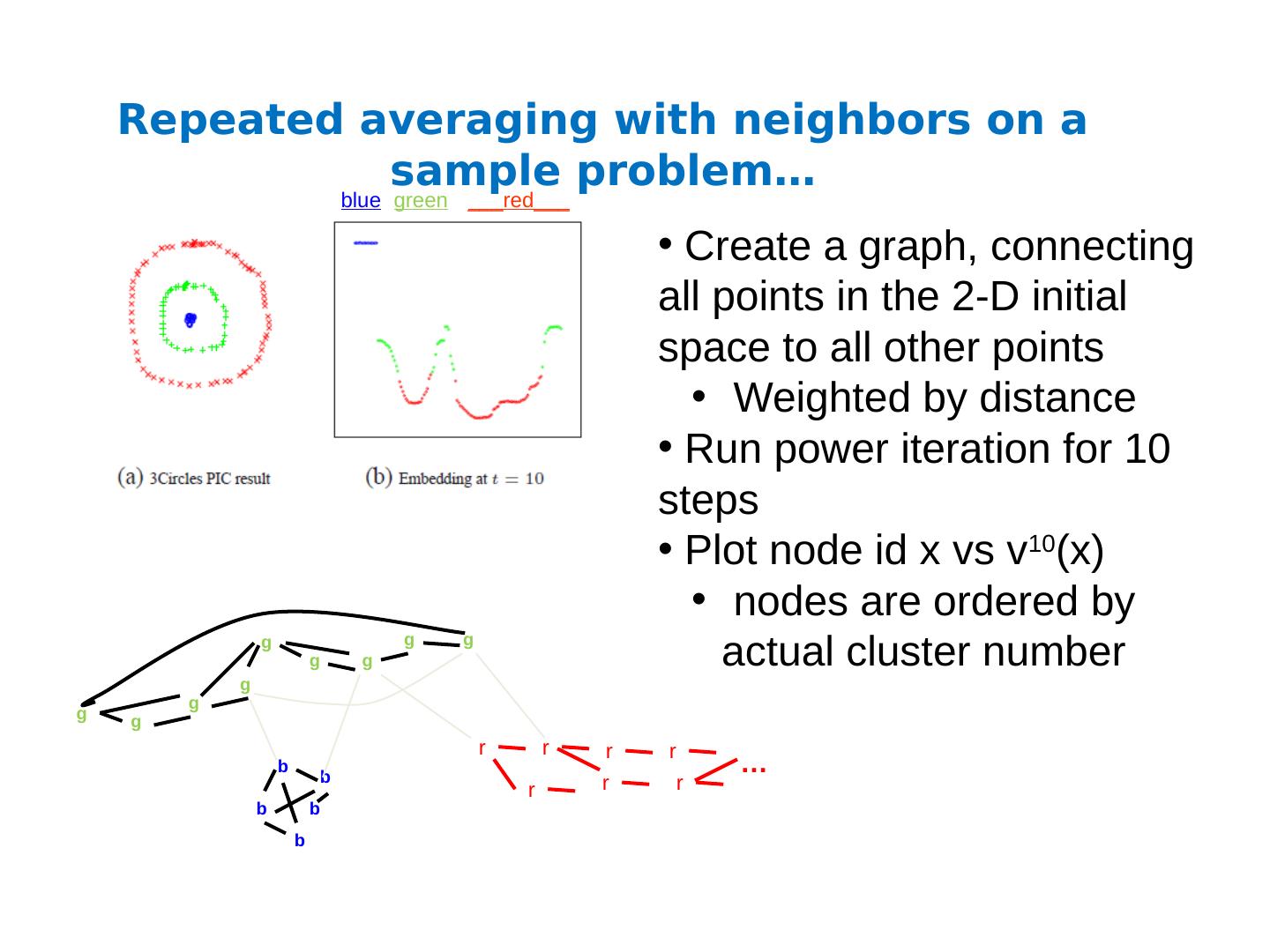
28 .Repeated averaging with neighbors on a sample problem… Create a graph, connecting all points in the 2-D initial space to all other points Weighted by distance Run power iteration for 10 steps Plot node id x vs v 10 (x) nodes are ordered by actual cluster number b b b b b g g g g g g g g g r r r r r r r … blue green ___red___
29 .Repeated averaging with neighbors on a sample problem… blue green ___red___ blue green ___red___ blue green ___red___ smaller larger