- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Naïve Bayes and Hadoop
展开查看详情
1 .Naïve Bayes and Hadoop Shannon Quinn
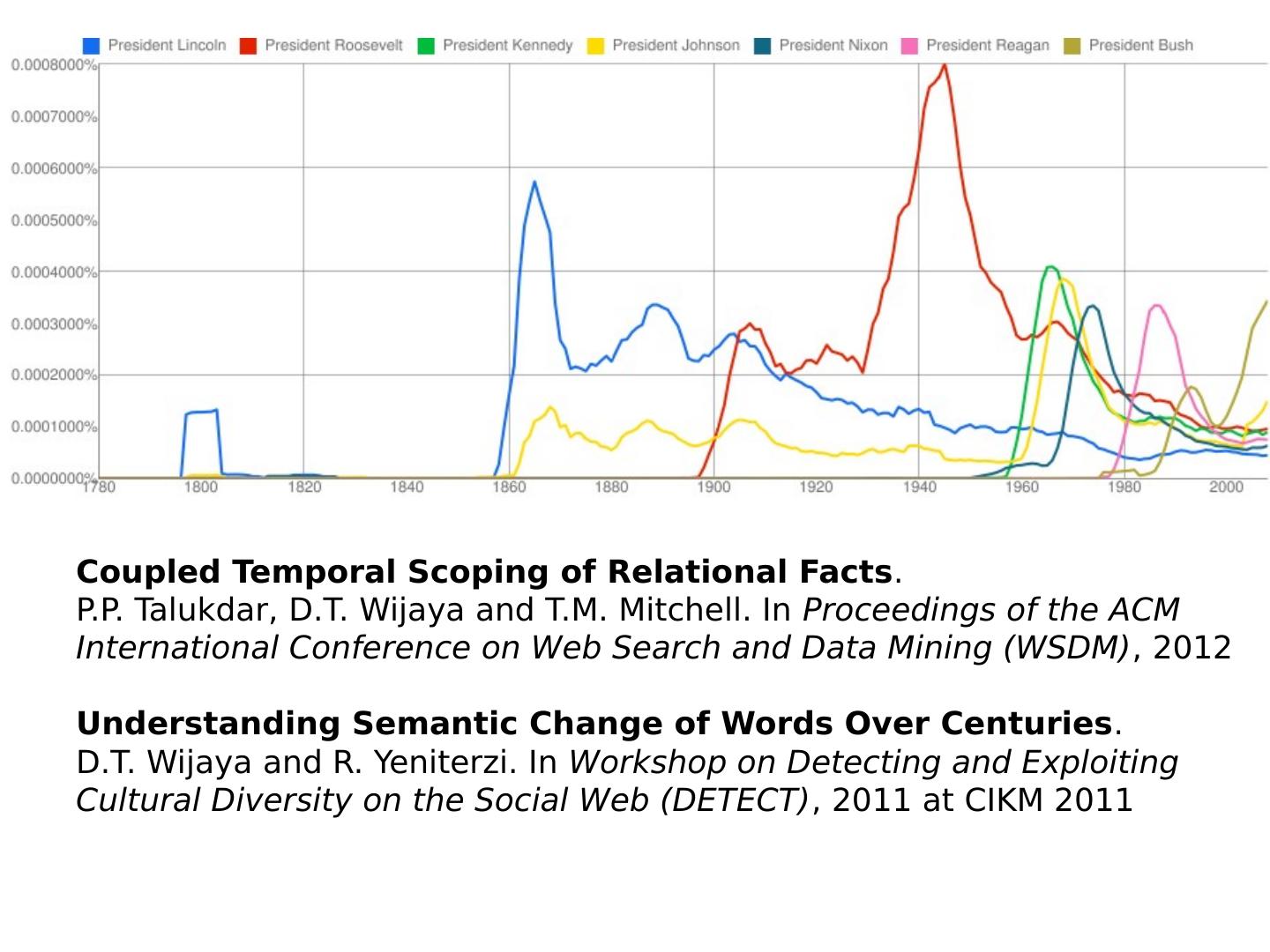
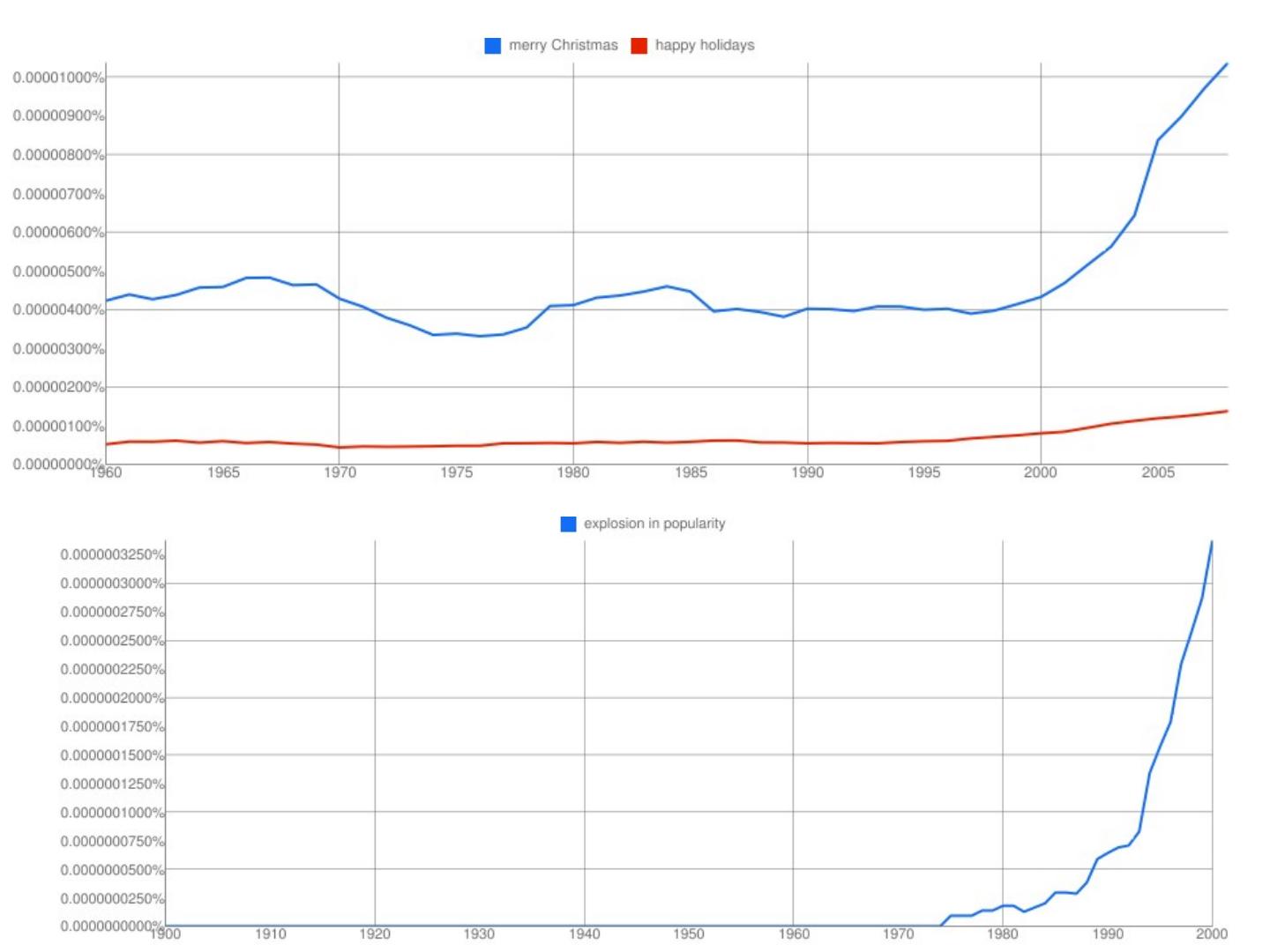
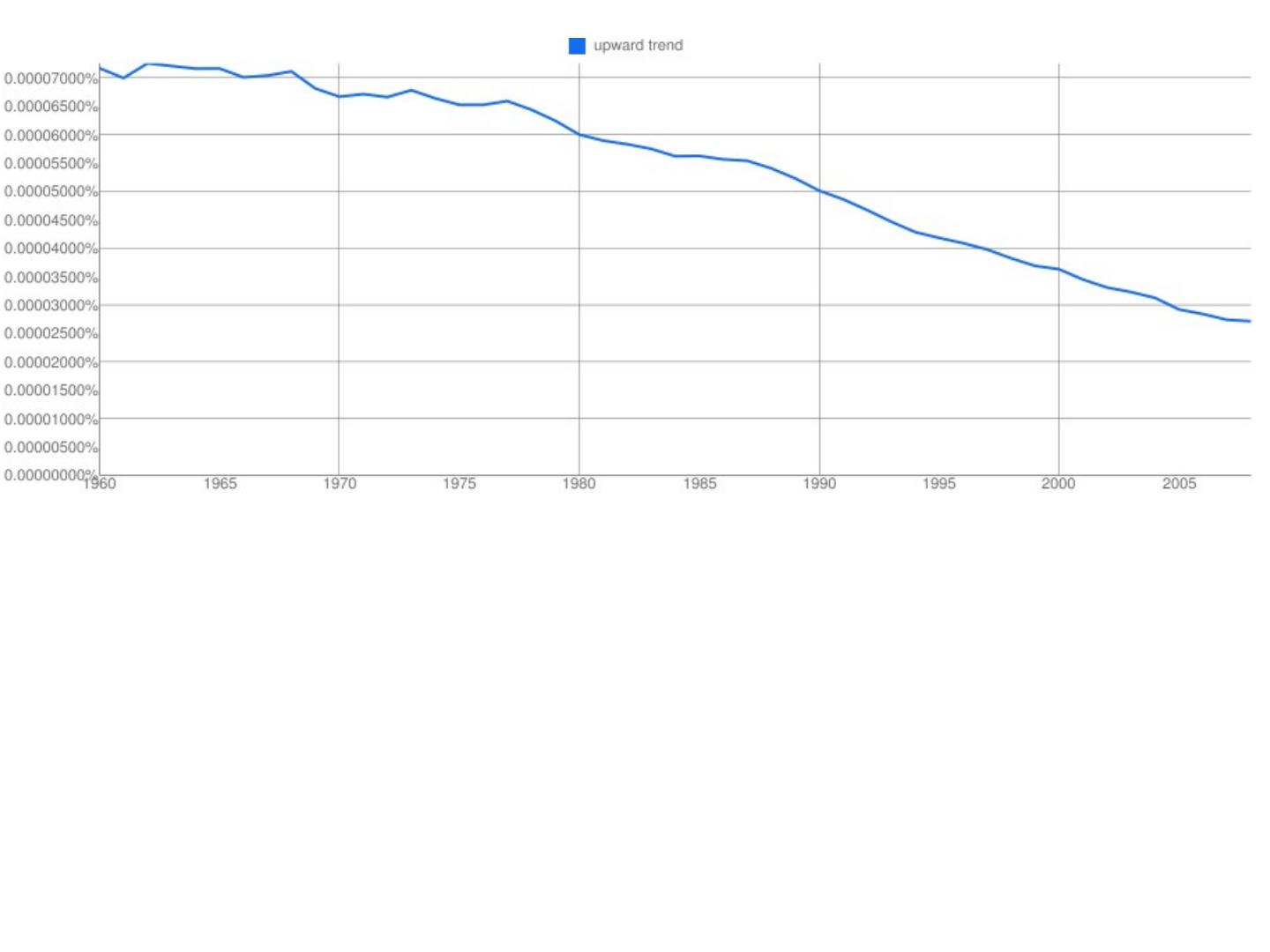
2 .http://xkcd.com/ngram-charts/
3 .Coupled Temporal Scoping of Relational Facts . P.P. Talukdar , D.T. Wijaya and T.M. Mitchell. In Proceedings of the ACM International Conference on Web Search and Data Mining (WSDM) , 2012 Understanding Semantic Change of Words Over Centuries . D.T. Wijaya and R. Yeniterzi . In Workshop on Detecting and Exploiting Cultural Diversity on the Social Web (DETECT) , 2011 at CIKM 2011
4 .
5 .
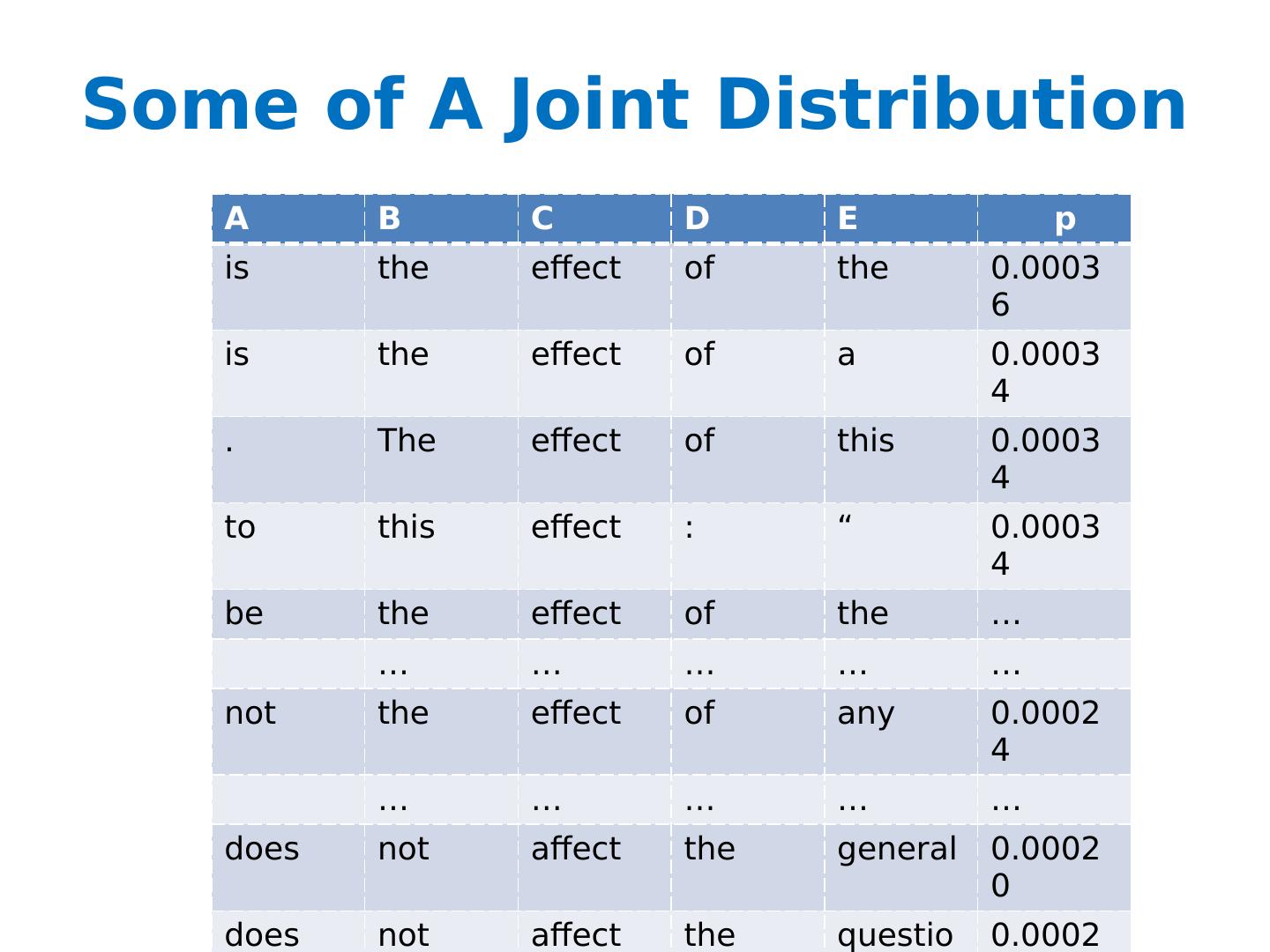
6 .Some of A Joint Distribution A B C D E p is the effect of the 0.00036 is the effect of a 0.00034 . The effect of this 0.00034 to this effect : “ 0.00034 be the effect of the … … … … … … not the effect of any 0.00024 … … … … … does not affect the general 0.00020 does not affect the question 0.00020 any manner affect the principle 0.00018
7 .Flashback Abstract : Predict whether income exceeds $50K/yr based on census data. Also known as "Census Income" dataset. [ Kohavi , 1996] Number of Instances: 48,842 Number of Attributes: 14 (in UCI’s copy of dataset) + 1; 3 (here) Size of table: 2 15 =32768 (if all binary) avg of 1.5 examples per row Actual m = 1,974,927, 360 (if continuous attributes binarized )
8 .Copyright © Andrew W. Moore Naïve Density Estimation The problem with the Joint Estimator is that it just mirrors the training data (and is *hard* to compute). We need something which generalizes more usefully. The naïve model generalizes strongly: Assume that each attribute is distributed independently of any of the other attributes.
9 .Copyright © Andrew W. Moore Using the Naïve Distribution Once you have a Naïve Distribution you can easily compute any row of the joint distribution. Suppose A, B, C and D are independently distributed. What is P(A ^ ~B ^ C ^ ~D) ?
10 .Copyright © Andrew W. Moore Using the Naïve Distribution Once you have a Naïve Distribution you can easily compute any row of the joint distribution. Suppose A, B, C and D are independently distributed. What is P(A ^ ~B ^ C ^ ~D) ? P(A) P(~B) P(C) P(~D)
11 .Copyright © Andrew W. Moore Naïve Distribution General Case Suppose X 1 ,X 2 ,…, X d are independently distributed. So if we have a Naïve Distribution we can construct any row of the implied Joint Distribution on demand . How do we learn this?
12 .Copyright © Andrew W. Moore Learning a Naïve Density Estimator Another trivial learning algorithm! MLE Dirichlet (MAP)
13 .Copyright © Andrew W. Moore Independently Distributed Data Review: A and B are independent if Pr(A,B )= Pr(A)Pr(B ) Sometimes written: A and B are conditionally independent given C if Pr(A,B|C )= Pr(A|C )* Pr(B|C ) Written
14 .Bayes Classifiers If we can do inference over Pr(X,Y )… … in particular compute Pr(X|Y ) and Pr(Y ). We can compute
15 .Can we make this interesting? Yes! Key ideas: Pick the class variable Y Instead of estimating P(X 1 ,…, X n ,Y ) = P(X 1 )*…* P(X n )*Y, estimate P(X 1 ,…, X n |Y ) = P(X 1 |Y)*…* P(X n |Y ) Or, assume P(X i |Y )=Pr(X i |X 1 ,…,X i-1 ,X i+1 ,… X n ,Y ) Or, that X i is conditionally independent of every X j , j!= i , given Y. How to estimate? MLE
16 .The Naïve Bayes classifier – v1 Dataset: each example has A unique id id Why? For debugging the feature extractor d attributes X 1 ,…, X d Each X i takes a discrete value in dom (X i ) One class label Y in dom (Y) You have a train dataset and a test dataset
17 .The Naïve Bayes classifier – v1 You have a train dataset and a test dataset Initialize an “event counter” ( hashtable ) C For each example id, y, x 1 ,…., x d in train: C(“ Y =ANY”) ++; C(“ Y=y”) ++ For j in 1..d : C(“ Y=y ^ X j = x j ”) ++ For each example id, y, x 1 ,…., x d in test: For each y’ in dom (Y): Compute Pr (y’,x 1 ,…., x d ) = Return the best y’
18 .The Naïve Bayes classifier – v1 You have a train dataset and a test dataset Initialize an “event counter” ( hashtable ) C For each example id, y, x 1 ,…., x d in train: C(“ Y =ANY”) ++; C(“ Y=y”) ++ For j in 1..d : C(“ Y=y ^ X j = x j ”) ++ For each example id, y, x 1 ,…., x d in test: For each y’ in dom (Y): Compute Pr (y’,x 1 ,…., x d ) = Return the best y’ This will overfit , so …
19 .The Naïve Bayes classifier – v1 You have a train dataset and a test dataset Initialize an “event counter” ( hashtable ) C For each example id, y, x 1 ,…., x d in train: C(“ Y =ANY”) ++; C(“ Y=y”) ++ For j in 1..d : C(“ Y=y ^ X j = x j ”) ++ For each example id, y, x 1 ,…., x d in test: For each y’ in dom (Y): Compute Pr (y’,x 1 ,…., x d ) = Return the best y’ where: q j = 1/| dom ( X j )| q y = 1/| dom (Y)| m=1 This will underflow, so …
20 .The Naïve Bayes classifier – v1 You have a train dataset and a test dataset Initialize an “event counter” ( hashtable ) C For each example id, y, x 1 ,…., x d in train: C(“ Y =ANY”) ++; C(“ Y=y”) ++ For j in 1..d : C(“ Y=y ^ X j = x j ”) ++ For each example id, y, x 1 ,…., x d in test: For each y’ in dom (Y): Compute log Pr (y’,x 1 ,…., x d ) = Return the best y’ where: q j = 1/| dom ( X j )| q y = 1/| dom (Y)| m=1
21 .The Naïve Bayes classifier – v2 For text documents, what features do you use? One common choice: X 1 = first word in the document X 2 = second word in the document X 3 = third … X 4 = … … But: Pr( X 13 = hockey|Y =sports ) is probably not that different from Pr( X 11 = hockey|Y =sports )…so instead of treating them as different variables, treat them as different copies of the same variable
22 .The Naïve Bayes classifier – v2 For text documents, what features do you use? One common choice: X 1 = first word in the document X 2 = second word in the document X 3 = third … X 4 = … … But: Pr( X 13 = hockey|Y =sports ) is probably not that different from Pr( X 11 = hockey|Y =sports )…so instead of treating them as different variables, treat them as different copies of the same variable
23 .The Naïve Bayes classifier – v2 You have a train dataset and a test dataset Initialize an “event counter” ( hashtable ) C For each example id, y, x 1 ,…., x d in train: C(“ Y =ANY”) ++; C(“ Y=y”) ++ For j in 1..d : C(“ Y=y ^ X j = x j ”) ++ For each example id, y, x 1 ,…., x d in test: For each y’ in dom (Y): Compute Pr (y’,x 1 ,…., x d ) = Return the best y’
24 .The Naïve Bayes classifier – v2 You have a train dataset and a test dataset Initialize an “event counter” ( hashtable ) C For each example id, y, x 1 ,…., x d in train: C(“ Y =ANY”) ++; C(“ Y=y”) ++ For j in 1..d : C(“ Y=y ^ X= x j ”) ++ For each example id, y, x 1 ,…., x d in test: For each y’ in dom (Y): Compute Pr (y’,x 1 ,…., x d ) = Return the best y’
25 .The Naïve Bayes classifier – v2 You have a train dataset and a test dataset Initialize an “event counter” ( hashtable ) C For each example id, y, x 1 ,…., x d in train: C(“ Y =ANY”) ++; C(“ Y=y”) ++ For j in 1..d : C(“ Y=y ^ X= x j ”) ++ For each example id, y, x 1 ,…., x d in test: For each y’ in dom (Y): Compute log Pr (y’,x 1 ,…., x d ) = Return the best y’ where: q j = 1/|V| q y = 1/| dom (Y)| m=1
26 .Complexity of Naïve Bayes You have a train dataset and a test dataset Initialize an “event counter” ( hashtable ) C For each example id, y, x 1 ,…., x d in train: C(“ Y =ANY”) ++; C(“ Y=y”) ++ For j in 1..d : C(“ Y=y ^ X= x j ”) ++ For each example id, y, x 1 ,…., x d in test: For each y’ in dom (Y): Compute log Pr (y’,x 1 ,…., x d ) = Return the best y’ where: q j = 1/|V| q y = 1/| dom (Y)| m=1 Complexity: O( n), n= size of train Complexity: O(| dom (Y)|*n’), n’= size of test Sequential reads Sequential reads
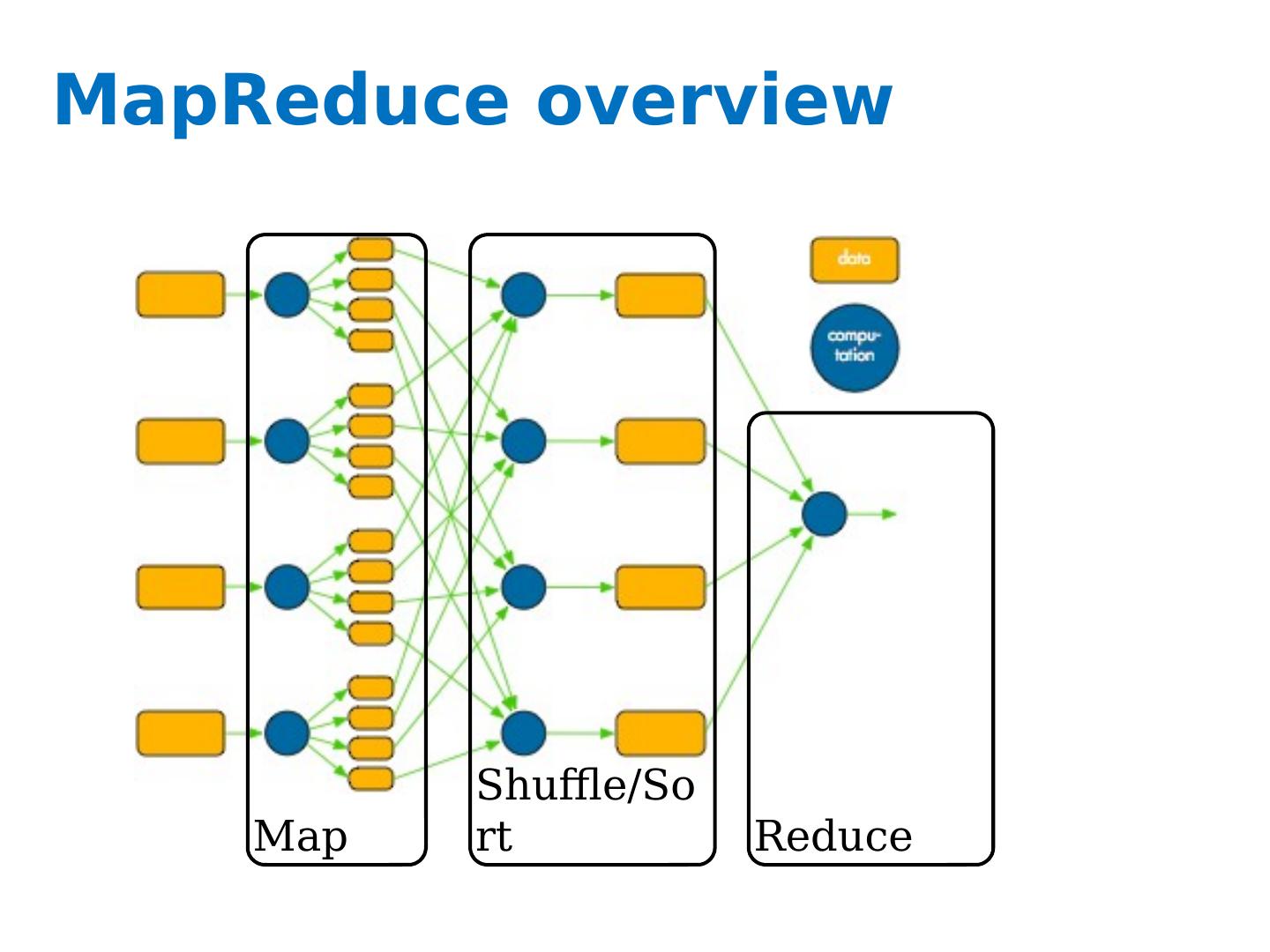
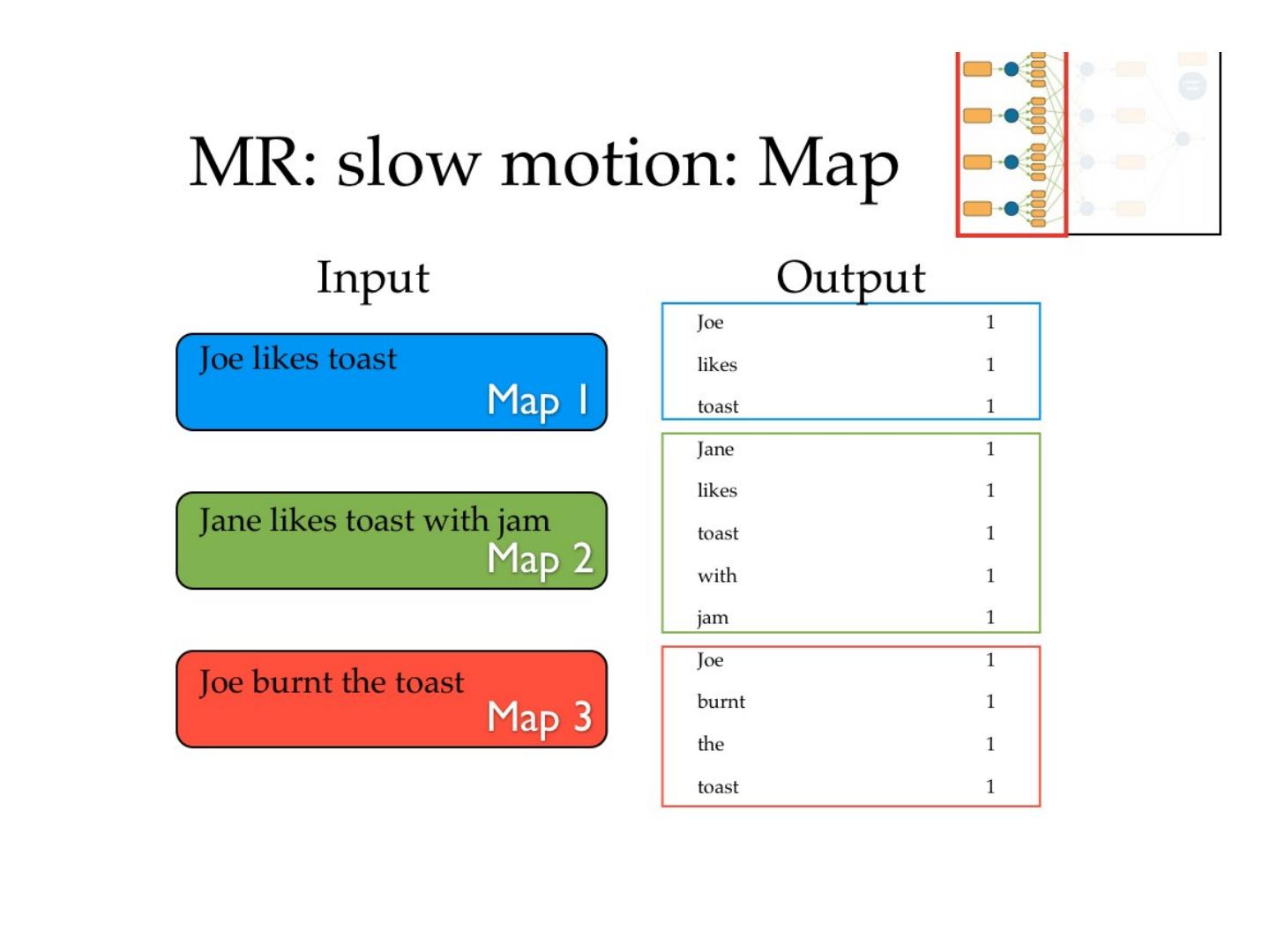
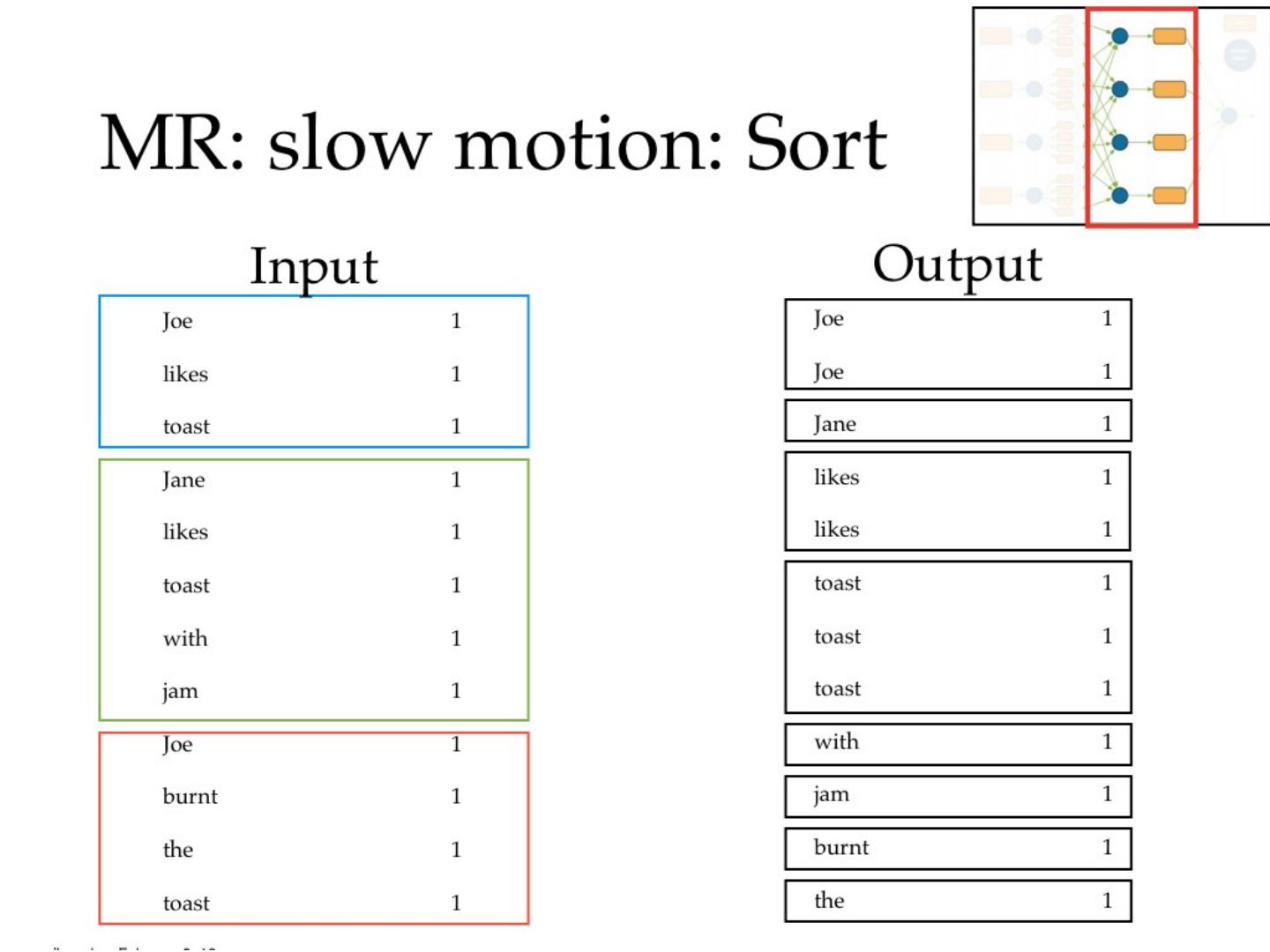
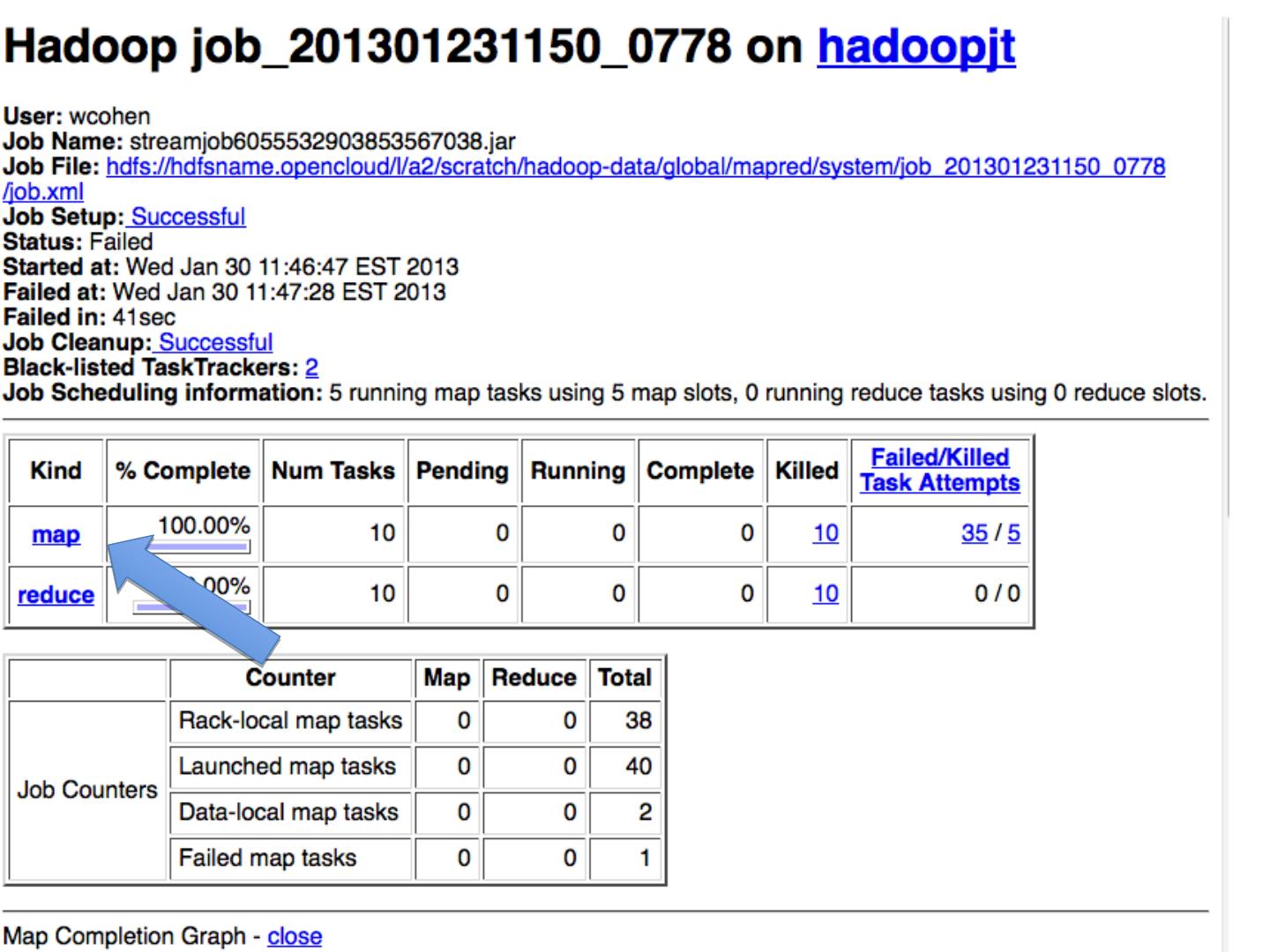
27 .MapReduce !
28 .Inspiration not Plagiarism This is not the first lecture ever on Mapreduce I borrowed from William Cohen, who borrowed from Alona Fyshe , and she borrowed from: Jimmy Lin http://www.umiacs.umd.edu/~jimmylin/cloud-computing/SIGIR-2009/Lin-MapReduce-SIGIR2009.pdf Google http://code.google.com/edu/submissions/mapreduce-minilecture/listing.html http://code.google.com/edu/submissions/mapreduce/listing.html Cloudera http://vimeo.com/3584536
29 .Inspiration not Plagiarism This is not the first lecture ever on Mapreduce I borrowed from William Cohen, who borrowed from Alona Fyshe , and she borrowed from: Jimmy Lin http://www.umiacs.umd.edu/~jimmylin/cloud-computing/SIGIR-2009/Lin-MapReduce-SIGIR2009.pdf Google http://code.google.com/edu/submissions/mapreduce-minilecture/listing.html http://code.google.com/edu/submissions/mapreduce/listing.html Cloudera http://vimeo.com/3584536