More on Data Streams

1 .More on Data Streams Shannon Quinn (with thanks to J. Leskovec , A. Rajaraman , J. Ullman: Mining of Massive Datasets, http:// www.mmds.org )

2 .Data Streams In many data mining situations, we do not know the entire data set in advance Stream Management is important when the input rate is controlled externally: Google queries Twitter or Facebook status updates We can think of the data as infinite and non-stationary (the distribution changes over time) J. Leskovec , A. Rajaraman , J. Ullman: Mining of Massive Datasets, http:// www.mmds.org 2

3 .3 The Stream Model Input elements enter at a rapid rate, at one or more input ports (i.e., streams ) We call elements of the stream tuples The system cannot store the entire stream accessibly Q: How do you make critical calculations about the stream using a limited amount of (secondary) memory? J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org

4 .Side note: NB is a Streaming Alg. Naïve Bayes (NB) is an example of a stream algorithm In Machine Learning we call this: Online Learning Allows for modeling problems where we have a continuous stream of data We want an algorithm to learn from it and slowly adapt to the changes in data Idea: Do slow updates to the model (NB, SVM, Perceptron) makes small updates So: First train the classifier on training data. Then: For every example from the stream, we slightly update the model (using small learning rate) J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 4

5 .General Stream Processing Model J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 5 Processor Limited Working Storage . . . 1, 5, 2, 7, 0, 9, 3 . . . a, r, v, t, y, h, b . . . 0, 0, 1, 0, 1, 1, 0 time Streams Entering. Each is stream is composed of elements / tuples Ad-Hoc Queries Output Archival Storage Standing Queries

6 .Problems on Data Streams Types of queries one wants on answer on a data stream: (we’ll do these today) Sampling data from a stream Construct a random sample Queries over sliding windows Number of items of type x in the last k elements of the stream J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 6

7 .Problems on Data Streams Other types of queries one wants on answer on a data stream: Filtering a data stream Select elements with property x from the stream Counting distinct elements Number of distinct elements in the last k elements of the stream Estimating moments Estimate avg./std. dev. of last k elements Finding frequent elements J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 7

8 .Applications (1) Mining query streams Google wants to know what queries are more frequent today than yesterday Mining click streams Yahoo wants to know which of its pages are getting an unusual number of hits in the past hour Mining social network news feeds E.g., look for trending topics on Twitter, Facebook J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 8

9 .Applications ( 2) Sensor Networks Many sensors feeding into a central controller Telephone call records Data feeds into customer bills as well as settlements between telephone companies IP packets monitored at a switch Gather information for optimal routing Detect denial-of-service attacks J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 9

10 .Sampling from a Data Stream Since we can not store the entire stream , one obvious approach is to store a sample Two different problems: (1) Sample a fixed proportion of elements in the stream (say 1 in 10) (2) Maintain a random sample of fixed size over a potentially infinite stream At any “time” k we would like a random sample of s elements What is the property of the sample we want to maintain? For all time steps k , each of k elements seen so far has equal prob. of being sampled J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 10

11 .Sampling a Fixed Proportion Problem 1: Sampling fixed proportion Scenario: Search engine query stream Stream of tuples : (user, query, time) Answer questions such as: How often did a user run the same query in a single days Have space to store 1/10 th of query stream Naïve solution: Generate a random integer in [0..9] for each query Store the query if the integer is 0 , otherwise discard J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 11

12 .Problem with Naïve A pproach Simple question: What fraction of queries by an average search engine user are duplicates? Suppose each user issues x queries once and d queries twice (total of x +2 d queries) Correct answer: d /( x + d ) Proposed solution: We keep 10% of the queries Sample will contain x /10 of the singleton queries and 2 d /10 of the duplicate queries at least once But only d /100 pairs of duplicates d/100 = 1/10 ∙ 1/10 ∙ d Of d “duplicates” 18d/100 appear exactly once 18d/100 = (( 1/10 ∙ 9/10 )+( 9/10 ∙ 1/10)) ∙ d So the sample-based answer is   12

13 .Solution: Sample Users Solution: Pick 1/10 th of users and take all their searches in the sample Use a hash function that hashes the user name or user id uniformly into 10 buckets J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 13

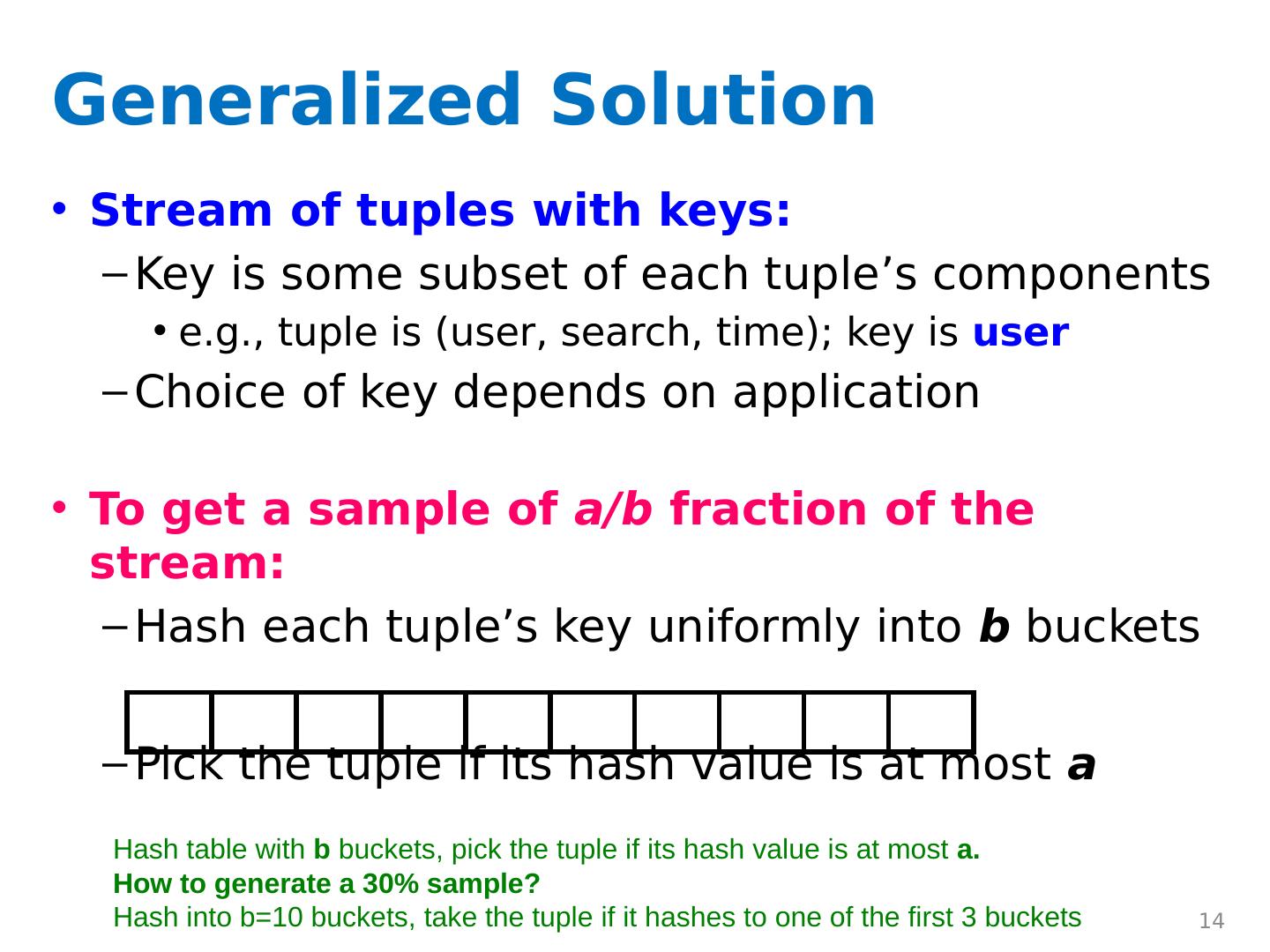
14 .Generalized Solution Stream of tuples with keys: Key is some subset of each tuple’s components e.g., tuple is (user, search, time); key is user Choice of key depends on application To get a sample of a/b fraction of the stream: Hash each tuple’s key uniformly into b buckets Pick the tuple if its hash value is at most a 14 Hash table with b buckets, pick the tuple if its hash value is at most a. How to generate a 30% sample? Hash into b=10 buckets, take the tuple if it hashes to one of the first 3 buckets

15 .Maintaining a fixed-size sample Problem 2: Fixed-size sample Suppose we need to maintain a random sample S of size exactly s tuples E.g., main memory size constraint Why? Don’t know length of stream in advance Suppose at time n we have seen n items Each item is in the sample S with equal prob. s/n 15 How to think about the problem: say s = 2 Stream: a x c y z k c d e g… At n= 5, each of the first 5 tuples is included in the sample S with equal prob. At n= 7, each of the first 7 tuples is included in the sample S with equal prob . Impractical solution would be to store all the n tuples seen so far and out of them pick s at random

16 .Solution: Fixed Size Sample Algorithm (a.k.a. Reservoir Sampling) Store all the first s elements of the stream to S Suppose we have seen n-1 elements, and now the n th element arrives ( n > s ) With probability s/n , keep the n th element, else discard it If we picked the n th element, then it replaces one of the s elements in the sample S , picked uniformly at random Claim: This algorithm maintains a sample S with the desired property: After n elements, the sample contains each element seen so far with probability s/n 16

17 .Proof: By Induction We prove this by induction: Assume that after n elements, the sample contains each element seen so far with probability s/n We need to show that after seeing element n+1 the sample maintains the property Sample contains each element seen so far with probability s /(n+1) Base case: After we see n=s elements the sample S has the desired property Each out of n=s elements is in the sample with probability s/s = 1 J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 17

18 .Proof: By Induction Inductive hypothesis: After n elements, the sample S contains each element seen so far with prob. s/n Now element n+1 arrives Inductive step: For elements already in S , probability that the algorithm keeps it in S is: So, at time n , tuples in S were there with prob. s/n Time n  n+1 , tuple stayed in S with prob. n/(n+1) So prob. tuple is in S at time n+1 =   J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 18 Element n+1 discarded Element n+1 not discarded Element in the sample not picked

19 .Sliding Windows A useful model of stream processing is that queries are about a window of length N – the N most recent elements received Interesting case: N is so large that the data cannot be stored in memory, or even on disk Or, there are so many streams that windows for all cannot be stored Amazon example: For every product X we keep 0/1 stream of whether that product was sold in the n - th transaction We want answer queries, how many times have we sold X in the last k sales J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 19

20 .Sliding Window: 1 Stream Sliding window on a single stream: J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 20 q w e r t y u i o p a s d f g h j k l z x c v b n m q w e r t y u i o p a s d f g h j k l z x c v b n m q w e r t y u i o p a s d f g h j k l z x c v b n m q w e r t y u i o p a s d f g h j k l z x c v b n m Past Future N = 6

21 .21 Counting Bits ( 1) Problem: Given a stream of 0 s and 1 s Be prepared to answer queries of the form How many 1s are in the last k bits? where k ≤ N Obvious solution: Store the most recent N bits When new bit comes in, discard the N +1 st bit 0 1 0 0 1 1 0 1 1 1 0 1 0 1 0 1 1 0 1 1 0 1 1 0 Past Future J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org Suppose N=6

22 .Counting Bits ( 2) You can not get an exact answer without storing the entire window Real Problem: What if we cannot afford to store N bits? E.g. , we’re processing 1 billion streams and N = 1 billion But we are happy with an approximate answer 22 J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 0 1 0 0 1 1 0 1 1 1 0 1 0 1 0 1 1 0 1 1 0 1 1 0 Past Future

23 .An attempt: Simple solution Q: How many 1s are in the last N bits? A simple solution that does not really solve our problem: Uniformity assumption Maintain 2 counters: S : number of 1s from the beginning of the stream Z : number of 0s from the beginning of the stream How many 1s are in the last N bits? But, what if stream is non-uniform? What if distribution changes over time?   J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 23 0 1 0 0 1 1 1 0 0 0 1 0 1 0 0 1 0 0 0 1 0 1 1 0 1 1 0 1 1 1 0 0 1 0 1 0 1 1 0 0 1 1 0 1 0 N Past Future

24 .DGIM Method DGIM solution that does not assume uniformity We store bits per stream Solution gives approximate answer, never off by more than 50% Error factor can be reduced to any fraction > 0, with more complicated algorithm and proportionally more stored bits   J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 24 [ Datar , Gionis , Indyk , Motwani ]

25 .Summary Sampling a fixed proportion of a stream Sample size grows as the stream grows Sampling a fixed-size sample Reservoir sampling Counting the number of 1s in the last N elements Exponentially increasing windows Extensions: Number of 1s in any last k (k < N) elements Sums of integers in the last N elements J. Leskovec, A. Rajaraman, J. Ullman: Mining of Massive Datasets, http://www.mmds.org 25

26 .Beyond Naïve Bayes: Some Other Efficient [Streaming] Learning Methods Shannon Quinn (with thanks to William Cohen)

27 .Rocchio’s algorithm Relevance Feedback in Information Retrieval , SMART Retrieval System Experiments in Automatic Document Processing, 1971, Prentice Hall Inc .

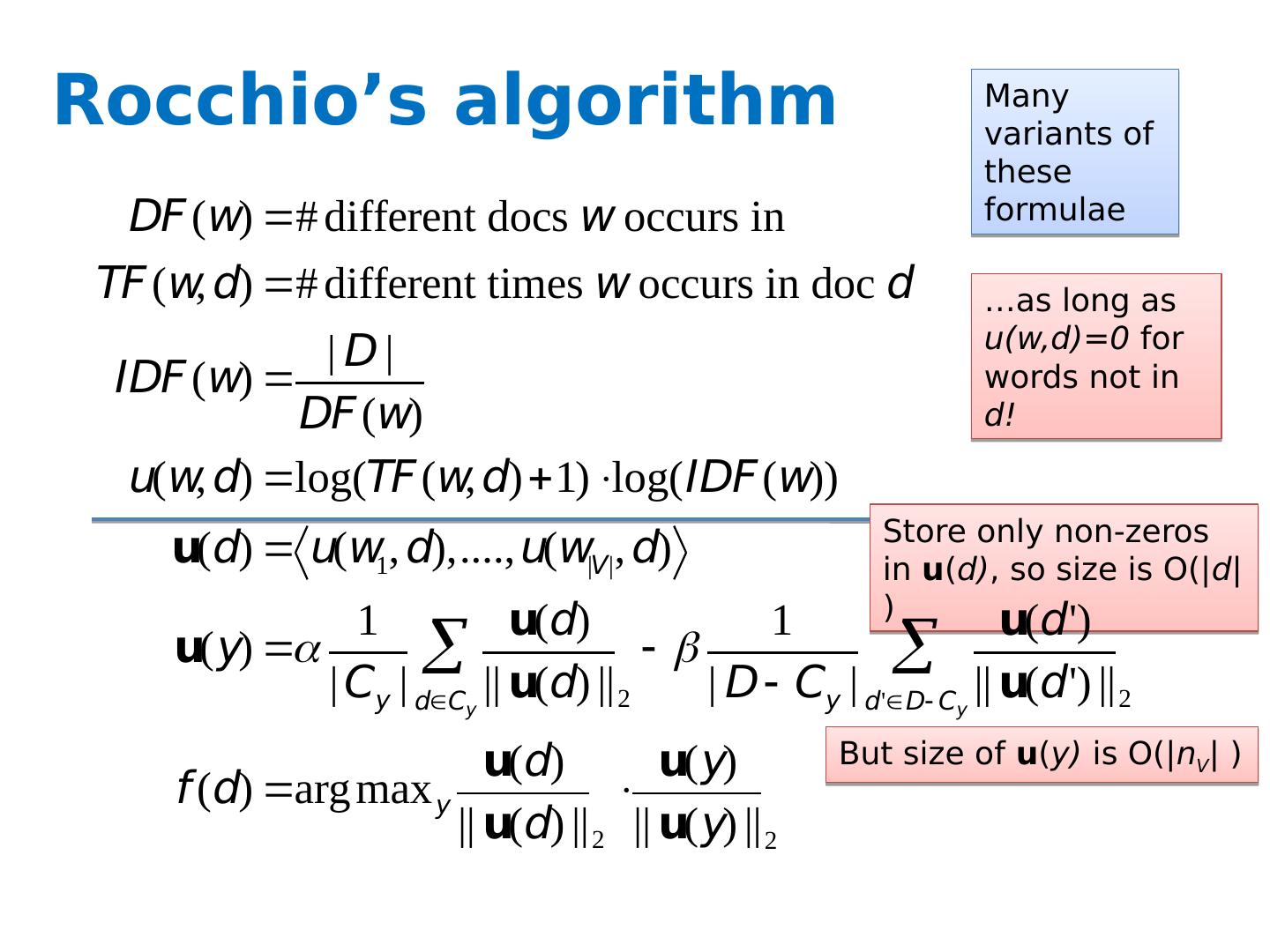
28 .Rocchio’s algorithm Many variants of these formulae …as long as u( w,d )=0 for words not in d! Store only non-zeros in u ( d) , so size is O(| d | ) But size of u ( y ) is O(| n V | )

29 .Rocchio’s algorithm Given a table mapping w to DF(w) , we can compute v ( d ) from the words in d… and the rest of the learning algorithm is just adding…