- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
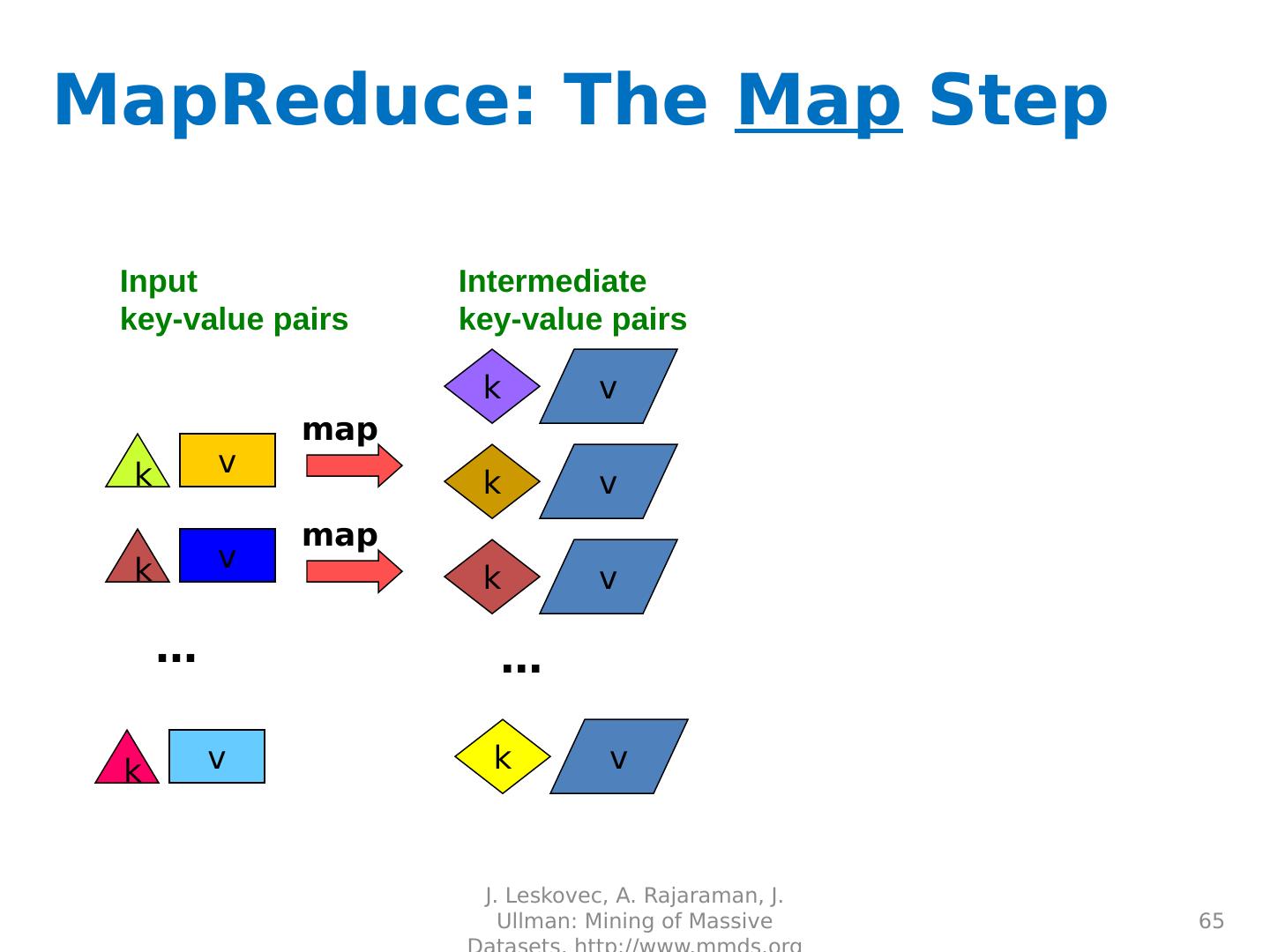
Basics of MapReduce
展开查看详情
1 .Basics of MapReduce Shannon Quinn
2 .Today Naïve Bayes with huge feature sets i.e. ones that don’t fit in memory Pros and cons of possible approaches Traditional “DB” (actually, key-value store) Memory-based distributed DB Stream-and-sort counting Other tasks for stream-and-sort … MapReduce ?
3 .Complexity of Naïve Bayes You have a train dataset and a test dataset Initialize an “event counter” ( hashtable ) C For each example id, y, x 1 ,…., x d in train: C(“ Y =ANY”) ++; C(“ Y=y”) ++ For j in 1..d : C(“ Y=y ^ X= x j ”) ++ For each example id, y, x 1 ,…., x d in test: For each y’ in dom (Y): Compute log Pr (y’,x 1 ,…., x d ) = Return the best y’ where: q j = 1/|V| q y = 1/| dom (Y)| m=1 Complexity: O( n), n= size of train Complexity: O(| dom (Y)|*n’), n’= size of test Assume hashtable holding all counts fits in memory Sequential reads Sequential reads
4 .What’s next How to implement Naïve Bayes Assuming the event counters do not fit in memory Why? Micro: 0.6G memory Standard : S: 1.7Gb L: 7.5Gb XL: 15Mb Hi Memory : XXL: 34.2 XXXXL: 68.4
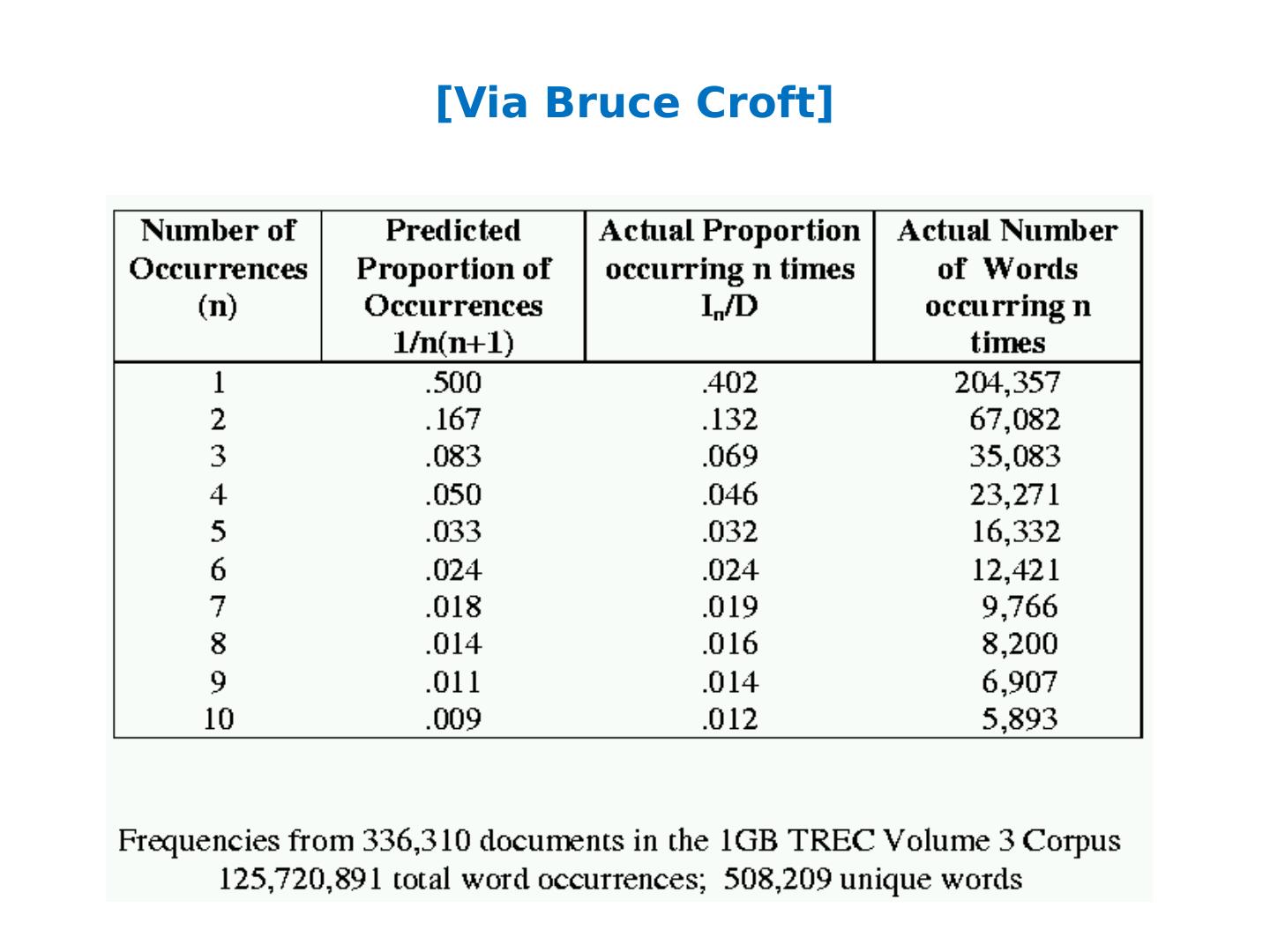
5 .What’s next How to implement Naïve Bayes Assuming the event counters do not fit in memory Why? Zipf’s law: many words that you see, you don’t see often.
6 .[Via Bruce Croft]
7 .What’s next How to implement Naïve Bayes Assuming the event counters do not fit in memory Why? Heaps’ Law: If V is the size of the vocabulary and the n is the length of the corpus in words: Typical constants: K 1/10 1/ 100 0.4 0.6 (approx. square-root) Why? Proper names, missspellings , neologisms, … Summary: For text classification for a corpus with O(n) words, expect to use O( sqrt (n)) storage for vocabulary. Scaling might be worse for other cases (e.g., hypertext, phrases, …)
8 .What’s next How to implement Naïve Bayes Assuming the event counters do not fit in memory Possible approaches: Use a database? (or at least a key-value store)
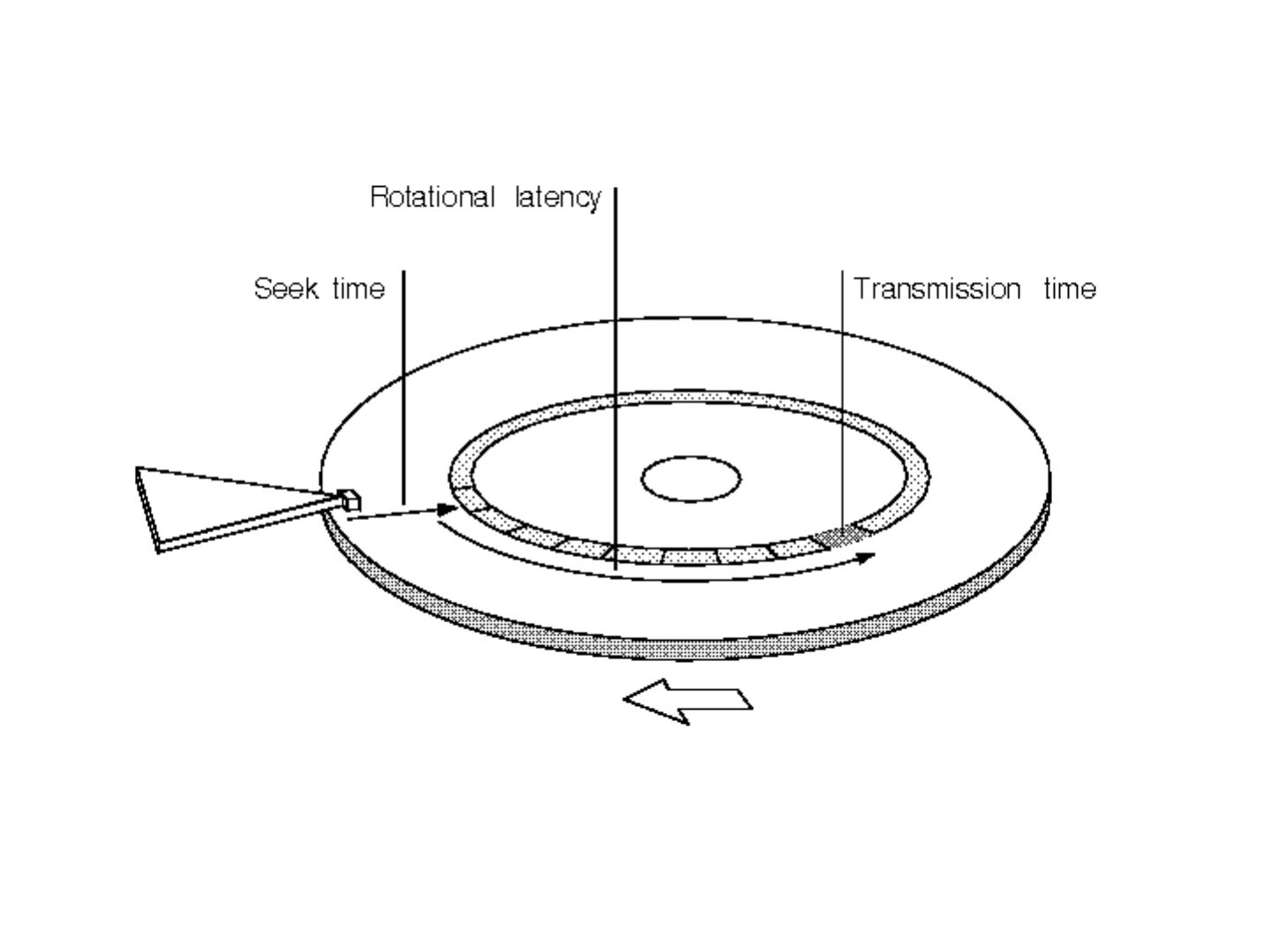
9 .Numbers (Jeff Dean says) Everyone Should Know ~= 10x ~= 15x ~= 100,000x 40x
10 .Using a database for Big ML We often want to do random access on big data E.g., different versions of examples for q/a E.g., spot-checking parameter weights to see if they are sensible Simplest approach: Sort the data and use binary search O(log 2 n) seeks to find query row
11 .Using a database for Big ML We often want to do random access on big data E.g., different versions of examples for q/a E.g., spot-checking parameter weights to see if they are sensible Almost-as-simple idea based on fact that disk seek time ~= reading 1Mb Let K=rows/Mb (e.g., K=1000) Scan through data once and record the seek position of every K- th row in an index file (or memory) To find row r: Find the r’, last item in the index smaller than r Seek to r’ and read the next megabyte Cheap since index is size n/1000 Cost is ~= 2 seeks
12 .Using a database for Big ML Summary: we’ve gone from ~= 1 seek (best possible) to ~= 2 seeks---plus finding r’ in the index. If index is O(1Mb) then finding r’ is also like 1 seek So we’re paying about 3 seeks per random access in a Gb What if the index is still large? Build (the same sort of index) for the index! Now we’re paying 4 seeks for each random access into a Tb ….and repeat recursively if you need This is called a B-tree It only gets complicated when we want to delete and insert.
13 .
14 .
15 .Numbers (Jeff Dean says) Everyone Should Know ~= 10x ~= 15x ~= 100,000x 40x Best case (data is in same sector/block)
16 .A single large file can be spread out among many non-adjacent blocks/sectors… and then you need to seek around to scan the contents of the file… Question: What could you do to reduce this cost?
17 .What’s next How to implement Naïve Bayes Assuming the event counters do not fit in memory Possible approaches: Use a database? Counts are stored on disk, not in memory …So, accessing a count might involve some seeks Caveat: many DBs are good at caching frequently-used values, so seeks might be infrequent ….. O(n*scan) O(n*scan*4*seek)
18 .What’s next How to implement Naïve Bayes Assuming the event counters do not fit in memory Possible approaches: Use a memory-based distributed database? Counts are stored on disk, not in memory …So, accessing a count might involve some seeks Caveat: many DBs are good at caching frequently-used values, so seeks might be infrequent ….. O(n*scan) O(n*scan*???)
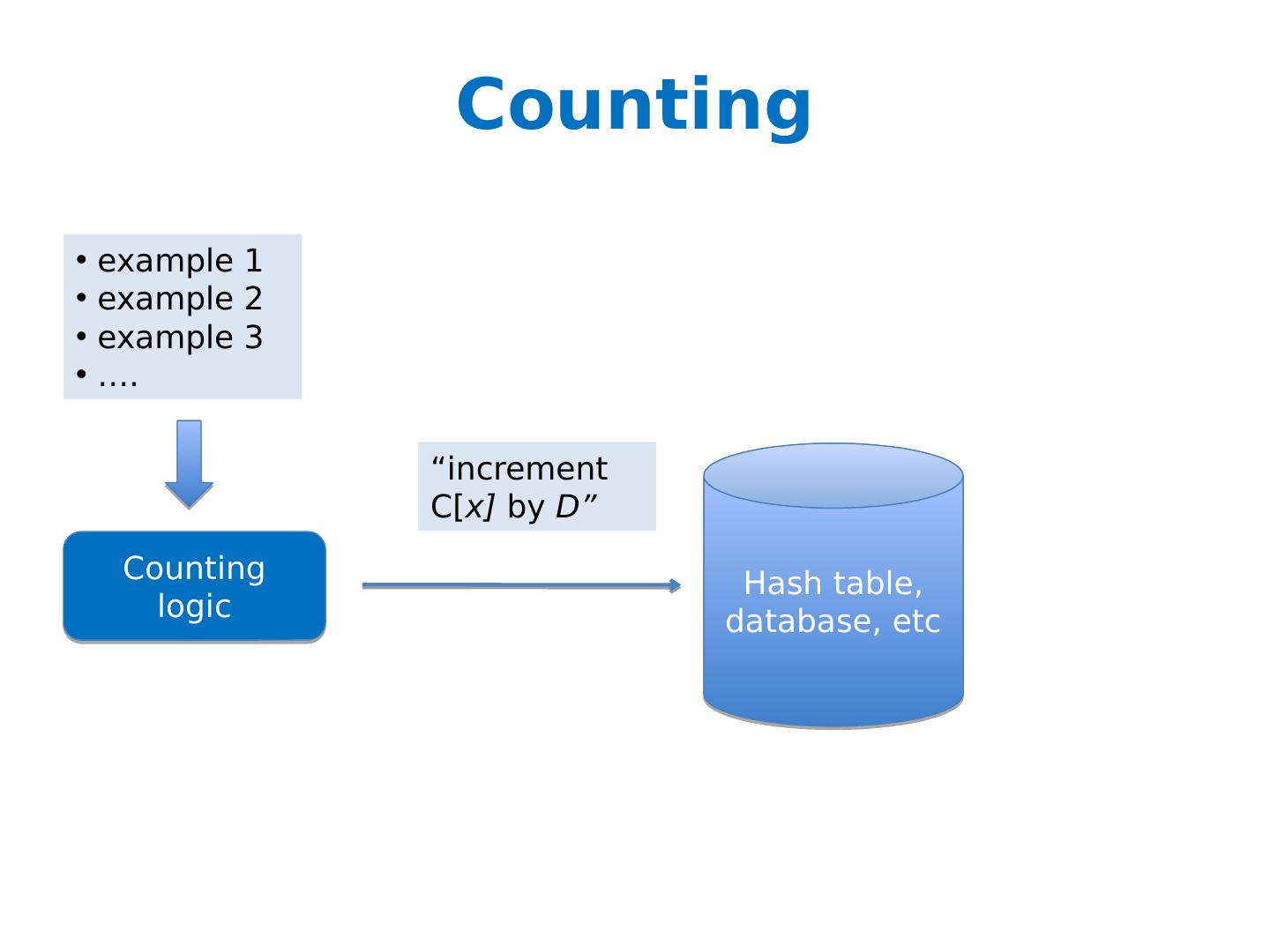
19 .Counting example 1 example 2 example 3 …. Counting logic Hash table, database, etc “increment C[ x] by D”
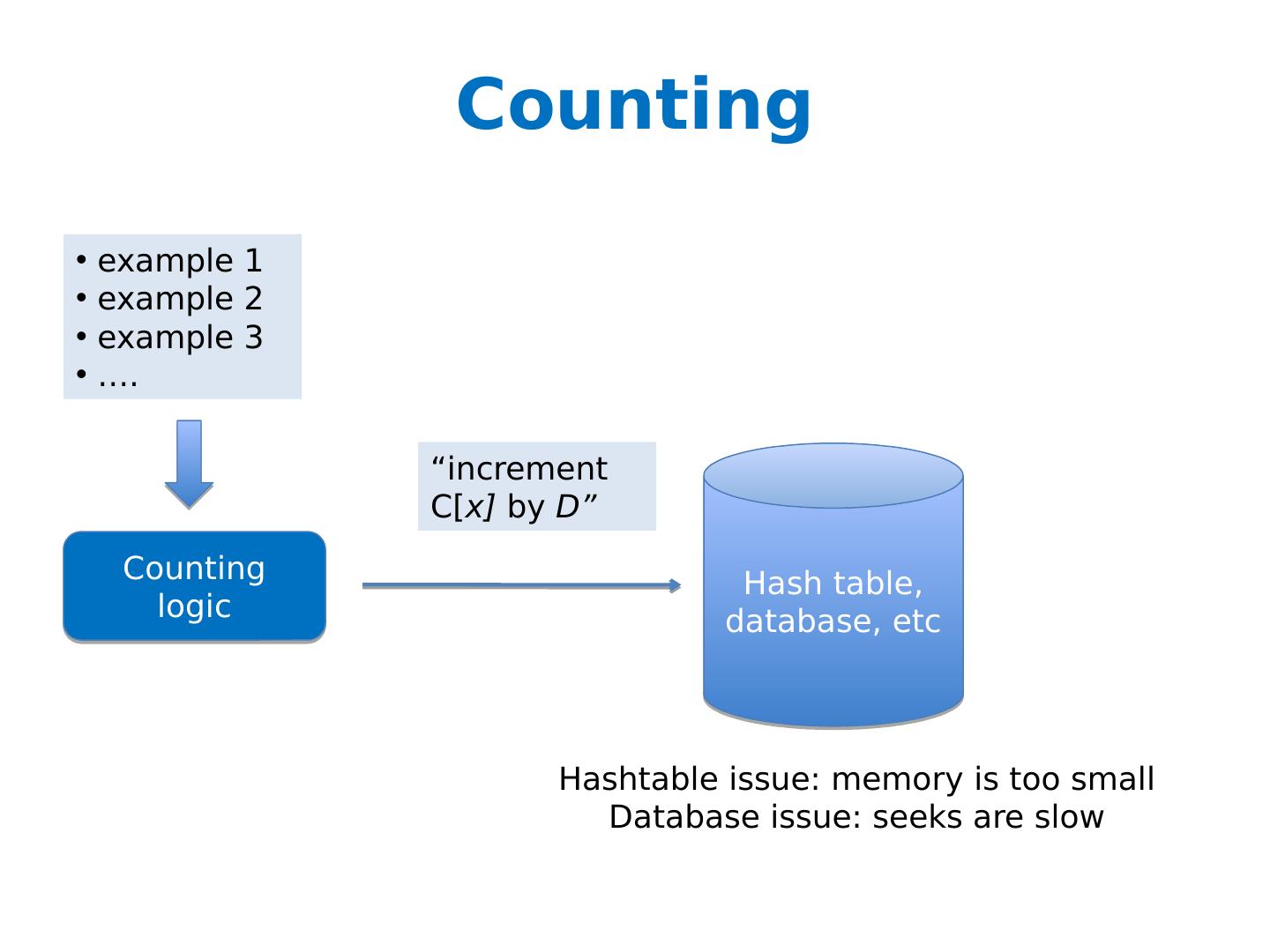
20 .Counting example 1 example 2 example 3 …. Counting logic Hash table, database, etc “increment C[ x] by D” Hashtable issue: memory is too small Database issue: seeks are slow
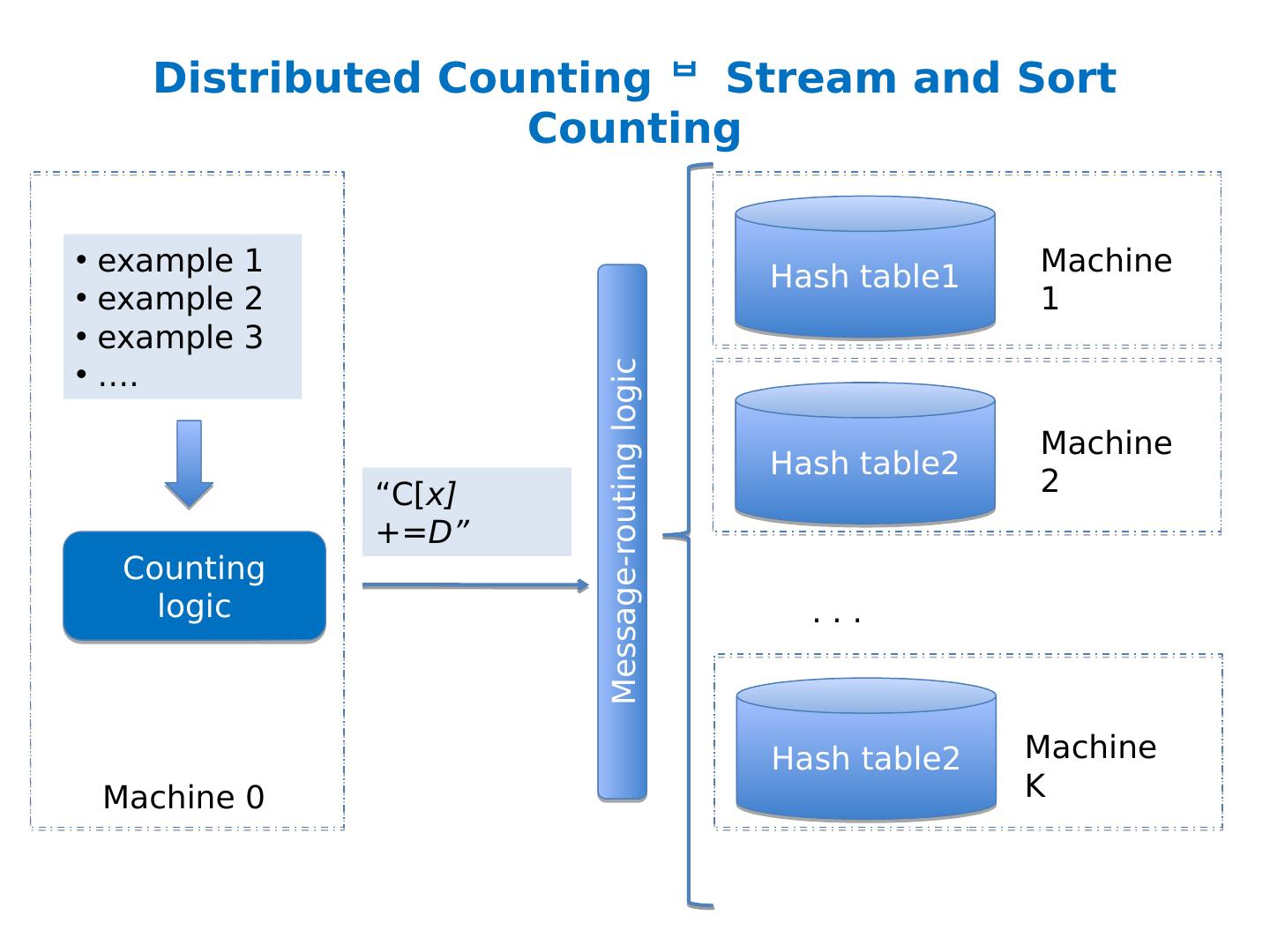
21 .Distributed Counting example 1 example 2 example 3 …. Counting logic Hash table1 “increment C[ x] by D” Hash table2 Hash table2 Machine 1 Machine 2 Machine K . . . Machine 0 Now we have enough memory….
22 .Distributed Counting example 1 example 2 example 3 …. Counting logic Hash table1 “increment C[ x] by D” Hash table2 Hash table2 Machine 1 Machine 2 Machine K . . . Machine 0 New issues: Machines and memory cost $$! Routing increment requests to right machine Sending increment requests across the network Communication complexity
23 .Distributed Counting example 1 example 2 example 3 …. Counting logic Hash table1 “increment C[ x] by D” Hash table2 Hash table2 Machine 1 Machine 2 Machine K . . . Machine 0 New issues: Machines and memory cost $$! Routing increment requests to right machine Sending increment requests across the network Communication complexity
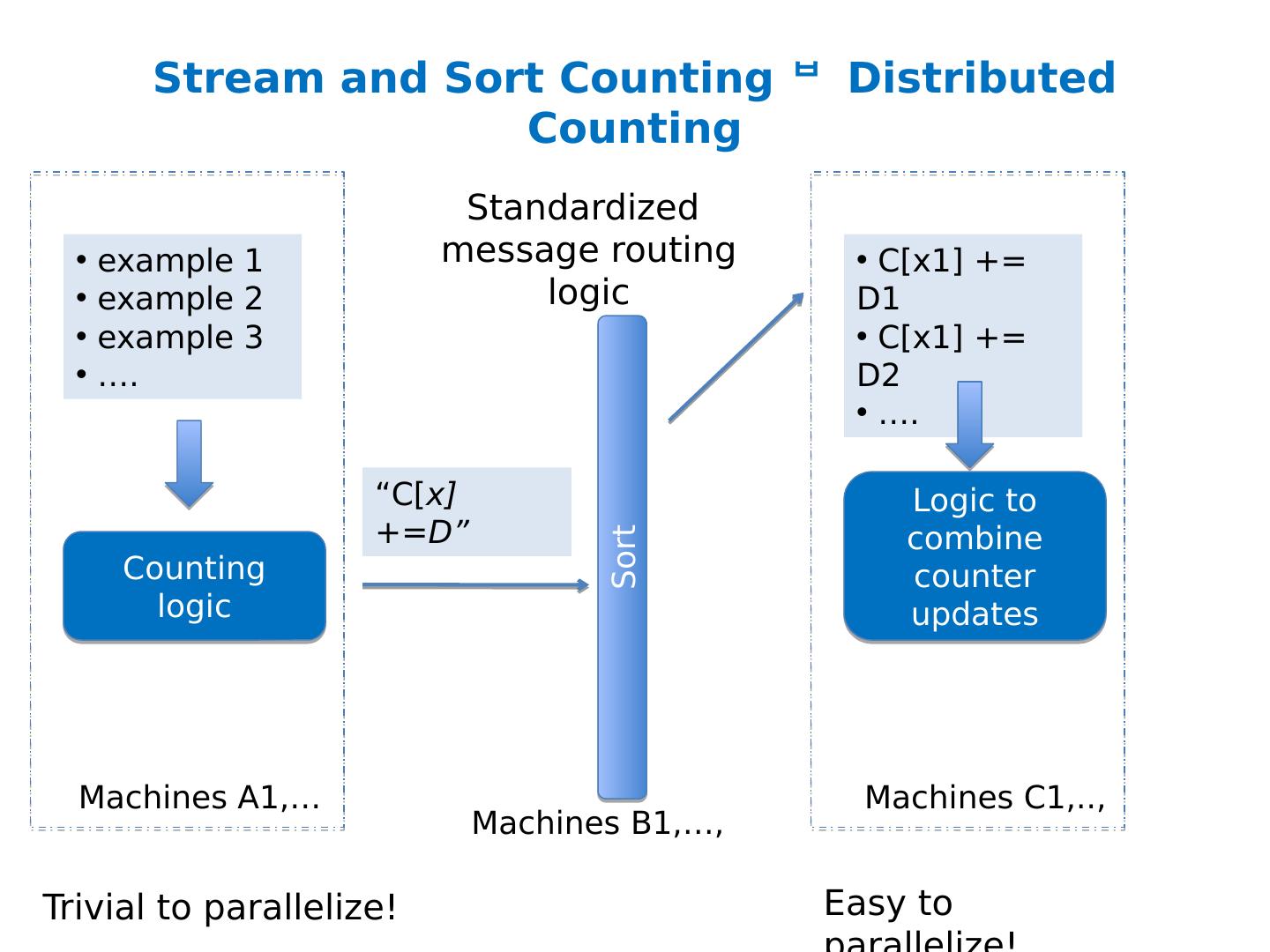
24 .What’s next How to implement Naïve Bayes Assuming the event counters do not fit in memory Possible approaches: Use a memory-based distributed database? Extra cost: Communication costs: O(n) … but that’s “ok” Extra complexity: routing requests correctly Note: If the increment requests were ordered seeks would not be needed! O(n*scan) O(n* scan+n *send) 1) Distributing data in memory across machines is not as cheap as accessing memory locally because of communication costs. 2) The problem we’re dealing with is not size. It’s the interaction between size and locality: we have a large structure that’s being accessed in a non-local way.
25 .What’s next How to implement Naïve Bayes Assuming the event counters do not fit in memory Possible approaches: Use a memory-based distributed database? Extra cost: Communication costs: O(n) … but that’s “ok” Extra complexity: routing requests correctly Compress the counter hash table? Use integers as keys instead of strings? Use approximate counts? Discard infrequent/unhelpful words? Trade off time for space somehow? Observation: if the counter updates were better-ordered we could avoid using disk Great ideas which we’ll discuss more later O(n*scan) O(n* scan+n *send)
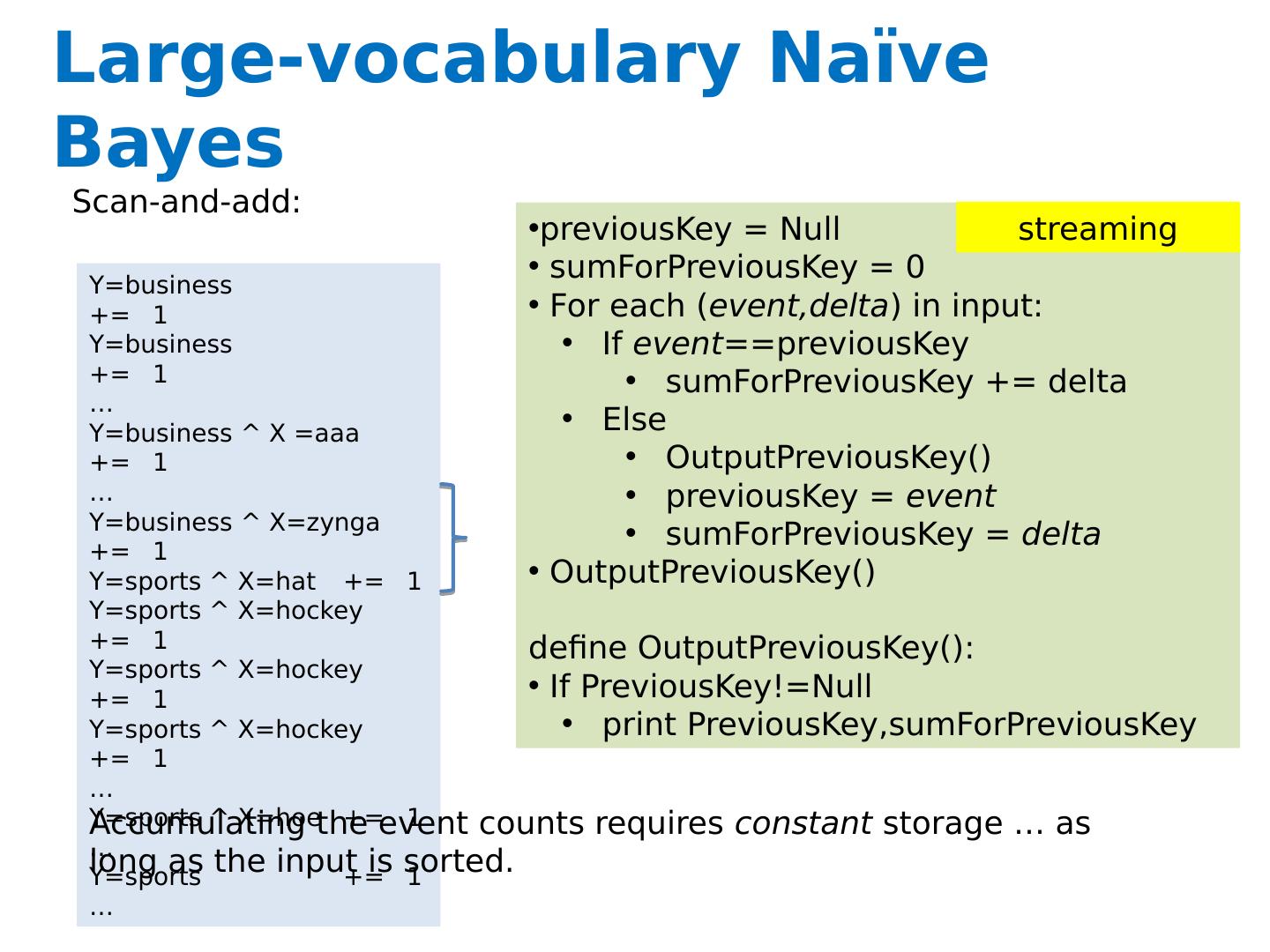
26 .Large-vocabulary Naïve Bayes One way trade off time for space: Assume you need K times as much memory as you actually have Method: Construct a hash function h(event) For i =0,…,K-1 : Scan thru the train dataset Increment counters for event only if h(event) mod K == i Save this counter set to disk at the end of the scan After K scans you have a complete counter set Comment: this works for any counting task, not just naïve Bayes What we’re really doing here is organizing our “messages” to get more locality…. Counting
27 .Large-vocabulary Naïve Bayes One way trade off time for space: Assume you need K times as much memory as you actually have Method: Construct a hash function h(event) For i =0,…,K-1 : Scan thru the train dataset Increment counters for event only if h(event) mod K == i Save this counter set to disk at the end of the scan After K scans you have a complete counter set Comment: this works for any counting task, not just naïve Bayes What we’re really doing here is organizing our “messages” to get more locality…. Counting
28 .Large vocabulary counting Another approach: Start with Q: “what can we do for large sets quickly”? A: sorting It’s O(n log n), not much worse than linear You can do it for very large datasets using a merge sort sort k subsets that fit in memory, merge results, which can be done in linear time
29 .Large-vocabulary Naïve Bayes Create a hashtable C For each example id, y, x 1 ,…., x d in train: C(“ Y =ANY”) ++; C(“ Y=y”) ++ For j in 1..d : C(“ Y=y ^ X= x j ”) ++